1 Introduction

The understanding of magnetism at nanoscale is scientifically attractive not only because the quantum mechanical properties of the individual spins become significant, but also for the emergence of new phenomena from confinement and proximity, such as giant magnetoresistance (GMR), spintronics, and superparamagnetism [1,2,3,4]. The significant advances in the availability of strategies for the synthesis and characterization of materials have led to the massive interest in magnetic nanoparticles. Currently, magnetic nanostructures such as nanodisc, nanotubes, nanorods, nanowires, and nanocomposites are widely used as active components in magnetic refrigeration, magnetic diagnosis, drug delivery, catalysis, ferrofluids, sensors, energy storage, logic circuits, etc. [5,6,7,8]. Apart from the above, manipulating the size and shape of the nanostructures place them close to the biological entity such as gene, protein, and cell. This offers an upper hand for magnetic nanoparticles in biomedical applications such as magnetic hyperthermia, magnetic resonance imaging, tissue engineering, cell tracking, and bioseparation [9, 10]. Additionally, the large surface of the magnetic nanostructures finds potential application in wastewater treatment as nanoabsorbent, energy harvesting, heat transfer, ferrofluids, photocatalysis, pigmentation, etc. [11,12,13,14,15,16].

The two key factors which dominate the magnetic properties of nanoparticles are the finite-size effects and the surface effects [5, 7]. Finite-size effects result from the quantum confinement of electrons such as single-domain limit and superparamagnetic limit, while the surface effects are related to symmetry breaking of the crystal structure at the boundary. The large fraction of atoms residing at the surface of the nanoparticle control the surface interface effects [4, 5, 7].

In perovskite rare earth manganites, nanoparticles display exotic features such as superparamagnetism, spin glass behaviour, low-field saturation magnetization, low-field magnetoresistance, and large coercivity which are different from their bulk counterparts [17, 18]. These striking characteristics make them suitable for application in magnetic hyperthermia, solid oxide fuel cells, magnetic memory devices, spintronic devices, and magnetic sensors [18]. The feasibility to tune the magnetic transition spread over a broad temperature range and the melting of the robust charge ordering (CO) state in the nanoparticles enable their potential for magnetic refrigeration application [18,19,20]. Recently tailoring the ferroelectricity in hexagonal manganite thin films has been realized to be suitable for photovoltaic application [21].

Among rare earth manganites, Pr1-xSrxMnO3 has attracted extra attention owing to its resemblance to the prototype La1-xSrxMnO3 (LSMO). The parent compound PrMnO3 is an antiferromagnetic (AFM) insulator with TN ≈ 100 K. Systematic replacement of Pr3+ by Sr2+ (i.e. Pr1-xSrxMnO3) changes the magnetic ground state and the system exhibits a second order paramagnetic (PM) to ferromagnetic (FM) transition for Sr2+ content 0.20 ≤ x ≤ 0.45 [22,23,24]. In the present study, we focus our attention on Pr0.6Sr0.4MnO3 (PSMO)-derived composition. PSMO is a room temperature metallic FM with TC = 310 K, TMI = 260 K and exhibits moderate magnetoresistance (MR) of 40% for H = 80 kOe [25, 26]. It is reported to undergo a structural transition from orthorhombic structure (space group Pnma) to monoclinic (space group I2/a) structure at (TS) = 88 K [27]. It shows both normal and inverse magnetocaloric effect (MCE) in the same sample which is interesting from a practical application point of view as magnetic cooling can be achieved from both adiabatic magnetization and demagnetization in different temperature ranges [26, 28].

Contrary to PrMnO3, BiMnO3 is an FM insulator with TC = 100 K and crystallizes in a monoclinic structure [29, 30]. Sr2+ substitution for Bi3+ (i.e. Bi1-xSrxMnO3) reduces FM and induces charge ordered (CO) AFM for wide concentration of Sr2+ (i.e. 0.25 ≤ x ≤ 0.80) [31, 32]. Bi0.75Sr0.25MnO3 is a well-known CO-AFM showing the highest CO temperature, TCO = 625 K among manganites which is robust and stable in an external field as high as 30 T [31, 33]. For x = 0.40, i.e. Bi0.6Sr0.4MnO3 (BSMO), the compound shows a PM-to-AFM transition at TN = 150 K and CO transition at TCO ≈ 600 K [31, 33]. Previous reports on Bi3+-doped LaSrMnO3 [34, 35], LaCaMnO3 [36, 37], PrSrMnO3 [38, 39] demonstrate a transition in the magnetic ground state from FM metallic to AFM insulating with competitive coexistence of FM and AFM clusters for intermediate concentration of Bi3+ [34,35,36,37,38,39]. Across the phase coexistence, the material exhibits a large MR (≈100%) and MCE probably due to the melting of the CO state. In the partial doping concentration of Bi3+, the system shows predominantly FM features with a systematic drop in TC and net magnetization [34,35,36,37,38,39]. However, in the case of NdSrMnO3 [40], NdCaMnO3 [41], Bi3+ doping drives the system to be robust CO. The observed unusual behaviour of bismuth manganites is attributed to the presence of 6 s lone pair electrons in the outermost orbital of Bi3+ [42].

In view of the contrasting properties of PSMO and BSMO, in the present work, the effect of particle size reduction on the magnetic properties of 20% Bi3+-doped Pr0.6Sr0.4MnO3 (PSMO) is investigated in detail. 20% Bi3+ when substituted in the case of FM La0.7Sr0.3MnO3, retains dominant FM state both in the bulk form and in the nanoparticles [43]. However, in the case of FM LaCaMnO3 [37, 44] and PrSrMnO3 [39], AFM and FM phase separation has been noticed. Previous reports on Bi-substituted PSMO [38, 39, 45] reveal that for partial Bi3+ substitution TC reduces and MR improves. For a higher concentration of Bi3+, multiple magnetic interactions are observed [39]. In our previous studies on magnetic phase coexistence, the Bi3+-substituted LSMO nanoparticles reveal an overall drop in net magnetization with size reduction while the metamagnetic M–H behaviour of the system remains significantly unaltered [46,47,48]. Contrary to that, we find in the present study the suppression in the metamagnetic M–H response with the decrease in particle size. Therefore, a detailed study of the present system was warranted, and we here present our analysis of X-ray diffraction studies and magnetization data discuss the results to reveal the role of particle size reduction on the structure, magnetization, magnetic correlations, and magnetocaloric effect (MCE) of Pr0.4Bi0.2Sr0.4MnO3 nanoparticles.

2 Experimental details

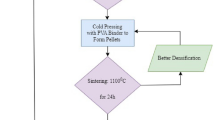
Pr0.4Bi0.2Sr0.4MnO3 (PB20SMO) nanoparticles have been prepared using a top-down approach in a two-step process. Initially, polycrystalline bulk samples were prepared by the solid-state reaction of Pr6O11, Bi2O3, SrCO3, and MnO2 (all 99.9% purity) weighed stoichiometrically according to the following equation.

(0.067 Pr6O11) + (0.1 Bi2O3) + (0.4 SrCO3) + MnO2 → Pr0.4Bi0.2Sr0.4MnO3 + xCO2 (↑).

These oxides were mixed thoroughly using agate mortar pestle with the help of isopropyl alcohol, to get a homogeneous mixture. The obtained mixture was calcined at 800 °C, 900 °C, and 1000 °C, respectively, for 24 h each with intermediate grinding. The powders were then pressed into rectangular pellets and were sintered at 1100 °C for 24 h.

In the second step, the pellets were then crushed into a fine powder and were subjected to high-energy planetary ball milling to prepare nanoparticles. The powders were taken in tungsten carbide jars of 50 ml volume along with 10 mm tungsten carbide balls such that the ball mass-to-sample mass ratio was maintained as 20:1. The ball milling was performed at the main disc speed of 300 rpm. The milling time was varied from 0 to 240 min, and a small quantity of sample was taken out a certain interval of time up to 240 min.

The obtained nanoparticles are characterized for their crystal structure and phase purity using room temperature X-ray diffraction (XRD) measurements taken on a M/s. Bruker D2 Phaser powder X-ray diffractometer with Cu-Kα radiation in the 2θ range of 20 °–80 ° with a step size of 0.02°. Magnetic measurements were taken on a M/s quantum design, superconducting quantum interference device (SQUID)-based vibrating sample magnetometer (VSM) in magnetic fields up to ± 70 kOe and in the temperature range 2–380 K.

3 Results and discussions

3.1 Room temperature X-ray diffraction

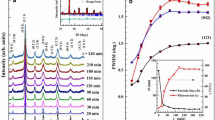
Figure 1a shows the room temperature XRD patterns of bulk and ball-milled PB20SMO samples. The XRD peaks display a systematic broadening with increase in milling time (tm), suggesting reduction in particle size (D) and concomitant inducement of microstrain (ε) in the lattice. The full width at half maximum (FWHM) of the selected reflections, i.e. (1 2 1), (2 0 2), and (0 4 2), plotted as a function of tm (Fig. 1b) shows a sudden rise in the value during the beginning of ball milling compared to higher tm. This indicates a substantial drop in D occurs during the initial phase of ball milling compared to higher tm.

Fig. 1
figure 1

a Room temperature XRD patterns of bulk and ball-milled PB20SMO. b A plot showing the variation in FWHM of (1 2 1), (0 4 2), and (2 0 2) diffraction peaks for bulk and ball-milled PB20SMO. c Rietveld refined XRD patterns of PB20SMO-t (t = 0, 20, 120, and 240 min)

Full size image

To derive the structural parameters, the obtained XRD patterns have been subjected to Rietveld refinement method using the FullProf program [49]. Figure 1c shows the XRD profiles for selected PB20SMO-t (t = 0, 20, 120, and 240 min) along with the pattern calculated through Rietveld refinement method. The XRD patterns have been indexed considering the orthorhombic structure in Pnma space group. As all the Bragg peaks could be indexed using this structure, contamination in the sample during ball milling can be ruled out. This indicates that all the samples studied here are of single phase. The unit cell parameters and reliability values of Rietveld refinement are summarized in Table 1.

Table 1 Rietveld refined unit cell parameters and reliability values of Rietveld refinement of X-ray diffraction patterns for PB20SMO-t refined using orthorhombic structure, space group Pnma
Full size table

For better estimation of D and ε using XRD, the instrumental resolution file (IRF) was obtained by measuring a NIST standard sample (corundum), before starting the Rietveld refinement of PB20SMO. For subsequent PB20SMO samples, only the quantities influenced by the sample properties were refined. The TCH pseudo-Voigt peak shape function [50] was considered for both standard and our samples. On supplying the IRF file during Rietveld refinement, Fullprof generates a volume average of particle size (D) and microstrain (ε) through the integral breadth method in a microstructure file (*.mic file) [50]. Figure 2 shows the variation in D and ε as a function of tm. A sudden drop in the D has been noticed as the tm changes from 0 to 60 min while the ε exhibits monotonous increment up to 150 min of ball milling and then tends to saturate. The substantial drop in D could be attributed to the enhanced rate of dislocation densities (δ) and defects induced due to the constant collision between the sample mass and balls with the walls of the jar [51, 52]. From D, an estimation of δ can be obtained from the relation \(\delta = \frac{1}{{D}^{2}}\) [53]. Inset in Fig. 2 shows the variation in \(\delta\) with tm. As tm increases from 0 to 240 min, \(\delta\) shows substantial increase from 1013 to 1015 lines/m2. Also, since the dimension of the feed size before ball milling is larger compared to after each milling time, a huge drop in D and a rise in ε is witnessed during the initial phase of ball milling. Further, the degree of crystallinity (DC) has been estimated using the relation \(\left(DC\right)=\frac{Area of crystalline peaks}{Area of all peaks (crystalline+amorphous)}\). DC decreases from 92 to 66% as tm increases (Table 1). Thus, based on the estimated D from XRD, four samples obtained after t = 0, 20, 120, and 240 min of ball milling having particle size D = 160, 36, 17, and 12 nm, respectively, were chosen to study, in detail, the influence of particle size reduction on the magnetic properties.

Fig. 2
figure 2

The variation of particle size and microstrain is shown as a function of milling time for PB20SMO. Inset shows the variation in dislocation density with milling time

Full size image

3.2 Magnetization studies

Figure 3 shows the dc magnetization plots for PB20SMO-D samples (D = 160, 36, 17, 12 nm) in the temperature range of 3–380 K in an applied field of 100 Oe. The magnetization has been recorded under zero field-cooled (ZFC) and field-cooled (FC) state of the samples. All samples show a well-defined PM-to-FM transition (TC) which drops from 264 K for D = 160 nm to 210 K for D = 12 nm (inset (ii) in Fig. 3a). Compared to PSMO which has TC = 308 K [28, 54], 20% Bi3+ substitution reduces the TC to 264 K. Also, the low-temperature structural transition which was seen as a drop in ZFC and FC curve for PSMO [26, 28] is suppressed with Bi3+ substitution. However, the bulk PB20SMO-160 (D = 160 nm) sample shows a hump in FC at T ˂ 200 K which could be attributed to the disordered antiferromagnetic (AFM) interactions in the system. Similar low-temperature hump in FC curve has been noticed in case of La0.7-xBixSr0.3MnO3 (x = 0.30 and 0.35) [46, 48, 55]. The decrease in TC with Bi3+ substitution can be explained considering the increase in unit cell volume. As seen from the XRD analysis, the unit cell volume increases from 229.214 to 231.011 Å3 as x changes from 0 to 0.20 [54]. This elongates the Mn–O–Mn chains, thus reducing the hopping of eg electrons. The double exchange coupling weakens, thereby resulting in the decrease of TC. Also, the highly covalent 6s lone pair character of Bi3+ is expected to create localization of electrons around the Bi3+-rich region which leads to AFM coupling, thereby decreasing the FM character of PSMO.

Fig. 3
figure 3

A plot of temperature-dependent dc magnetization for a bulk and b ball-milled PB20SMO in an applied field of 100 Oe. Inset (i) in 3 a shows the enlarged view of low-temperature hump. Inset (ii) in 3(a) shows variation in TC and width of dM/dT as a function of D−1. The line connecting the points is a guide to eyes. Inset in 3 b shows temperature variation of MFC−MZFC

Full size image

Further, the sharp magnetic transition recorded for the bulk sample broadens with the decrease in D which can be seen as the increase in the FWHM of dM/dT curve (inset (ii) in Fig. 3a). This may be due to the weak magnetic interaction among the spins on the surface of the nanoparticles. Also, a large bifurcation between ZFC and FC curves noticed in all samples specifies the presence of inhomogeneity in the system. The strength of the inhomogeneity can be quantified as MFC – MZFC (inset in Fig. 3b) which is higher for PB20SMO-36 and PB20SMO-17 samples.

The high-temperature inverse magnetic susceptibility ( \({\chi }^{-1}\)) has been analysed using the Curie–Weiss (CW) law [56], \(\chi =\frac{C}{T-{\theta }_{p}}\), C is Curie’s constant, and θp is Curie–Weiss temperature. Figure 4 shows the \({\chi }^{-1}\) vs T plots for PB20SMO-D. From the slope of the linear fit in the temperature range 310 ˂ T ˂ 380 K, the values of θp have been determined. Inset in Fig. 4 shows the θp vs D−1 plot. The positive values of θp demonstrate the dominant FM interactions in the system. With a decrease in D, the θp value decreases suggest a weakening of FM interaction with size reduction. Additionally, it is interesting to note that all samples show a deviation from the CW behaviour exhibiting a downturn, below a certain temperature (TG) in each sample’s case. This may be accounted as the presence of short-range FM correlations above TC. Most reports assign this anomaly to the Griffith’s like singularity in the system [57,58,59,60] while some literature suggests the presence of FM polarons above TC could result in \(\chi\)−1(T) downturn [61,62,63]. In general, the existence of GP like behaviour is characterized by a downturn in \({\chi }^{-1}\)(T), which is sharp for lower applied fields and subdue with an increase in the magnitude of applied magnetic field. Also, the low field \({\chi }^{-1}\) shows a temperature dependence given by the power law [57],

$$\begin{array}{*{20}c} {\chi^{ - 1} \propto \left( {T - T_{C}^{R} } \right)^{{\left( {1 - \lambda } \right)}} } & { 0 \le \lambda \le 1} \\ \end{array}$$
(1)

where \({T}_{C}^{R}\) is the critical temperature of a random ferromagnet and the exponent \(\lambda\) determines the deviation from CW law. The temperature at which \({\chi }^{-1}\)(T) deviates from linearity is known as Griffith’s temperature, TG. The TG in the present case decreases with a decrease in particle size. Figure 5 shows the \(\chi\)−1 vs T plots in different applied magnetic fields for PB20SMO-D. A systematic softening of the downturn has been noticed with an increase in the magnitude of applied magnetic field. This may be understood as in higher applied fields the magnetic contribution from PM matrix enhances and dominates the embedded FM clusters, hence driving towards linear variation in \(\chi\)−1 vs T. Using the procedure described in Ref [57], the value of \(\lambda\) has been estimated from the plot of \(\chi\)−1 vs [(T/ \({T}_{C}^{R}\))–1] in double logarithmic scale (inset in each panel of Fig. 5). The slope of the linear fit gives the value of \(\lambda\) tabulated in Table 2. The estimated value of \(\lambda\) is in good agreement with the reported literature [57,58,59,60], thereby suggesting the applicability of GP model to explain the deviation in \(\chi\)−1(T). Also, the magnitude of \(\lambda\) is found to increase with particle size reduction implying the enhancement in the strength of GP like singularity. On the contrary, Souza et al. [61] suggested that GP like treatment for accounting the \({\chi }^{-1}\)(T) downturn is inappropriate and proposed the presence of FM polarons, intrinsic to manganites due to structural and chemical disorder to be responsible to \(\chi\)−1(T) deviation from CW behaviour. Later, Rozenberg et. al. [64, 65] and Aga Shahee et al. [66] supported the above hypothesis. Since conductivity in manganites above TMI is accounted by the hopping of small polarons, it appears as if both the proposed models hold. However, the magnitude of resistivity and polaron activation energy Ea of a ferromagnetic manganite is found to increase with a decrease in D [67,68,69], thus suspecting the applicability of the FM polarons hypothesis.

Fig. 4
figure 4

Temperature evolution of inverse magnetic susceptibility for PB20SMO-D; the solid line indicates the linear fit to the CW law. Inset b shows the variation in θp as a function of D−1

Full size image
Fig. 5
figure 5

A plot of temperature evolution of inverse magnetic susceptibility in different magnetic fields for PB20SMO. Inset in each panel shows inverse susceptibility versus [(T/ \({T}_{C}^{R}\))–1] in double logarithmic scale and solid line represent the linear fit

Full size image
Table 2 Values of TC, θp, TG, λ, MS, and other calculated microstructural parameters for bulk and ball-milled PB20SMO samples
Full size table

To gain deeper insights into the magnetic interactions, field-dependent isothermal magnetization loops were recorded for PB20SMO-D at different temperatures (Fig. 6a–d). For PB20SMO-160, the M–H behaviour at 300 K is nonlinear and unsaturated suggesting the presence of weak magnetic interactions in the system. On lowering the temperature to T ˂ TC, i.e. 200 K, the M–H response shows a significant spontaneous moment (M0) with unsaturated magnetization suggesting the coexistence of FM and AFM interactions in the system. At T = 100 K and 50 K, the M–H loops represent distinct behaviour with open loops along the positive and negative field sweep. The magnetization in the virgin loop remains unsaturated even in the field as high at 70 kOe with notable spontaneous moment signifying the alignment of residual FM domains parallel to the applied magnetic field. In the reverse field sweep (demagnetization curve), the sample remains in a high state down to 10 kOe and then rapidly drops to zero at H = 0 kOe. In the negative field sweep, a response similar to the positive field sweep has been noticed; however, the area under the loop along with the forward and reverse field sweep is less compared to the positive field sweep. The observed M–H response implies the presence of metamagnetic magnetization with the ramping field. This suggests field-induced AFM-to-FM transition in the system. At T = 3 K, a clear step like feature has been observed in the virgin curve at critical field HCR = 50 kOe. Along the demagnetization path, the system remains in a high magnetic state down to 9 kOe field and then drops to zero at zero field. When the field is increased in the negative direction, the magnetization curve is similar to the demagnetization curve of the positive field and follows a similar pathway with further field sweep. This indicates that the field-induced transition from the AFM to FM state is irreversible and the induced FM phase is stable at this temperature. The net magnetization at 3 K is less compared to that at 50 K and 100 K and indicates an increase in the volume fraction of AFM interactions at 3 K.

Fig. 6
figure 6

Field-dependent magnetization plots for PB20SMO-D, a D = 160 nm, b D = 36 nm, c D = 17 nm, and d D = 12 nm at different temperatures

Full size image

For PB20SMO-36, the recorded magnetization with the ramping field is similar to that of PB20SMO-160 but a small drop in the open-loop area has been noticed. In the case of PB20SMO-17 and PB20SMO-12, the M–H is highly unsaturated signifying the increased surface disorder that leads to the reduced magnetic interaction. Also, it is interesting to note that the difference between the virgin curve and loop which was clearly identified in the bulk sample tend to merge in ball-milled sample implying the increase in the strength of AFM interaction or surge in the surface disorder due to ball milling that brings down the strength of FM interaction in the nanoparticles. Further, the net magnetization has been found to systematically increase with a decrease in temperature contrary to PB20SMO-160 and PB20SMO-36.

Figure 7 shows the temperature evolution of (a) saturation magnetization (MS) and (b) coercivity (HC). On lowering the temperature from 300 K, an overall increase in the value of MS and HC is noticed. The elevation in MS with a decrease in T corroborates the PM-to-FM transition in all the samples while a small drop in MS at a lower temperature for D = 160 and 36 nm ratifies the hump recorded in the FC curve below T = 200 K for PB20SMO-160 (inset (ii) in Fig. 3a). The HC values plotted as a function D (inset in Fig. 7b) display a rise with a drop in D due to the increased surface anisotropy because of the lattice strain and broken bonds as the D comes down [70]. In general, with a decrease in D, HC increases and attains a maximum value for a critical particle size DC where nanoparticles show a transition from multidomain to single-domain state. For further decrease in D, HC drops. Inset in Fig. 7b shows the variation in HC vs D−1 fitted to HC = m + n/D, where m and n are constants. Linear variation in HC vs D−1 (inset in Fig. 7b) suggests the multidomain nature of the nanoparticles [43, 71].

Fig. 7
figure 7

Temperature evolution a MS and b HC for bulk and ball-milled PB20SMO. Inset in b shows the variation in HC as a function of particle size (D) and D−1. Solid line represents the linear fit

Full size image

The law of approach to saturation (LAS) fit [72],

$$M = M_{S} \left( { 1 - \frac{a}{H} - \frac{b}{{H^{2} }} } \right) + \chi_{p} H$$
(2)

given to the demagnetization curves in the first quadrant provide more insights into the magnetic behaviour. The term \({M}_{S}\) in the above relation refers to the saturation magnetization, a/H corresponds to the structural defects while b/H2 is related to the uniaxial magneto-crystalline anisotropy given as [73] \(K=\sqrt{\frac{15}{4}b{M}_{s}^{2}}\) (erg/cm) and \({\chi }_{p}H\) is the high field susceptibility. Figure 8 shows the LAS fit given to the M–H curves at 3 K and the fitting parameters are summarized in Table 2. A rise in the a/H values specifies an increase in the structural defects due to ball milling. The estimated K values are of the order 105 erg/cm3 and decrease with particle size reduction due to disorder in the core of the nanoparticles. Further a substantial drop in MS from 2.1 μB/f.u. to 0.2 μB/f.u. has been noticed with a drop in D (Fig. 9). MS plotted as a function of D−1 (inset in Fig. 9) shows a linear variation specifying a strong impact of particle size on the MS of the sample.

Fig. 8
figure 8

M–H loops for bulk and ball-milled PB20SMO at 3 K. Solid line represents the fit given to the law of approach to saturation. Inset shows the variation in K as a function of D−1

Full size image
Fig. 9
figure 9

A plot showing variation of MS as a function particle size (D). Inset shows the linear fit (solid line) given to MS vs D−1

Full size image

The range of magnetic interaction with particle size reduction can be interpreted from the M2 vs H/M (i.e. Arrott’s plots) [57, 66]. If the linear interpolation of the high-field-magnetization region of M2 vs H/M yields a positive slope, it represents the presence of spontaneous moment with long-range FM order while the negative slope represents short-range FM correlations in the system. As shown in Fig. 10, the intercept value for PB20SMO-160 and PB20SMO-36 is negative at T = 300 K ˃ TC and positive for T ≤ 200 K ˂ TC, demonstrating that the magnetic interactions above TC are short-ranged while those below TC the system exhibit long-range FM order. Similarly, for PB20SMO-17, the intercept has negative value at T ˃ 200 K and transforms to be positive T ˂ 100 K signifying a crossover in the range of FM interactions across magnetic ordering. However, for PB20SMO-12, the intercept is negative at all temperatures demonstrate the FM interactions to be short-ranged due to increased surface disorder because to ball milling.

Fig. 10
figure 10

A plot of M2 vs. H/M (Arrott’s plot) for PB20SMO-D

Full size image

The magnetic entropy change \(\Delta S\) has been determined from iso-field magnetization using Maxwell’s thermodynamic relation [74],

$$\Delta S \left( {T, H} \right) = S_{M} \left( {T,H} \right) - S_{M} \left( {T,0} \right) = \mathop \smallint \limits_{0}^{H} \left( {\frac{\partial M}{{\partial T}}} \right)_{H} dH$$
(3)

where M is the magnetization, H is the applied magnetic field, and T is the temperature. According to Maxwell relation, the change in magnetic entropy upon application of magnetic field is related to magnetization with respect to the temperature through

$$\left( {\frac{\partial S}{{\partial H}}} \right)_{T} = - \left( {\frac{\partial M}{{\partial T}}} \right)_{H}$$

Most frequently magnetization isotherms recorded across the TC/TN and specific heat measurements are used to estimate the \(\Delta S\) values [74]. However, some recent reports suggest the estimation of \(\Delta S\) from iso-field magnetization [75, 76]. A close overlap in the estimation of \(\Delta S\) from isothermal and iso-field magnetization validates the application of the latter approach to estimate the MCE. Figure 11 a-d shows the variation of \(\Delta S\) as a function of temperature in different applied fields (i.e. H = 10 kOe and 50 kOe). As expected, a large change in \(\Delta S\) has been observed in the vicinity of TC. The bulk PB20SMO shows a maximum entropy change \({\Delta S}_{M}\) of 2.43 J/kg-K for H = 50 kOe which drops to 0.24 J/kg-K as particle size reduces (table. 3) along with broadening of \(\Delta S\) curve. The relative cooling power (RCP) defined as RCP = \(\Delta {\mathrm{S}}_{\mathrm{M}} \times {\delta \mathrm{T}}_{\mathrm{FWHM}}\), where \({\delta \mathrm{T}}_{\mathrm{FWHM}}\) is the full width half maximum of \(\Delta S\) curve, also drops with a decrease in the particle size (table 3).

Fig. 11
figure 11

Variation in magnetic entropy change (ΔS) plotted as a function of temperature for bulk and ball-milled P20SMO at different applied magnetic field (H = 10, 50 kOe)

Full size image
Table 3 Values of \(\Delta {S}_{M}, {\delta T}_{FWHM}, \mathrm{and} RCP\) for different applied magnetic fields for bulk and ball-milled PB20SMO
Full size table

A sudden variation in \(\Delta S\) across TC could be accounted for by considering the change in magnetization and the spin–lattice coupling across the magnetic ordering temperature [74]. The variation in the Mn–O–Mn bond angle and Mn–O bond length with temperature results in the volume change, thereby influencing the \(\Delta S\) values. A comparison of the obtained \(\Delta {S}_{M}\) with few reported studies is summarized in table 4 [77,78,79,80,81,82,83,84]. The \(\Delta {S}_{M}\) value in the present study is less compared to PSMO which indicates that Bi3+ addition suppresses the net magnetization of the system.

Table 4 A comparison of \(\Delta {S}_{M} \mathrm{and} RCP\) values for different samples
Full size table

From the above results, it can be noticed that with an increase in tm, the dislocation density and microstrain increase while the degree of crystallinity drops. Correspondingly a decrease in TC, MS, K, and \(\Delta S\) has been observed while HC values display a monotonous increase. Also, a transition in the range of magnetic interactions from long range to short range has been noticed. A similar variation in the magnetic properties with a decrease in particle size has been previously reported in the case of manganites [28, 71, 73, 85,86,87,88] and other oxides [89,90,91,92]. The observed characteristic could be accounted for by considering the core–shell structure of the nanoparticles [93], according to which each nanoparticle has a FM/AFM grain surrounded by a non-magnetic shell comprised of broken bonds and randomly oriented magnetic spins.

Assuming the net magnetization of the shell to be zero, an estimate of shell thickness (t) can be attained from the relation [94],

$$t = \frac{D}{2 } \left( {1 - \left( {\frac{{M_{{S \left( {Nano} \right)}} }}{{M_{{S \left( {Bulk} \right)}} }}} \right)^{1/3} } \right)$$
(4)

where D is the particle size, MS (Bulk) and MS (Nano) corresponds to the saturation magnetization of bulk and nanoparticles, respectively. The MS (Bulk) value is obtained from the intercept of MS vs D−1 plot (inset in Fig. 10). The estimated obtained values of t are tabulated in Table 2. Figure 12 shows the variation of t/D (i.e. shell thickness/particle size) as a function of D. The t/D ratio increases monotonously with a drop in D. A linear dependence of t/D with D−1 suggests a direct impact of size reduction on the thickness of the non-magnetic shell that strongly controls the magnetic properties of the nanoparticles.

Fig. 12
figure 12

Variation in t/D as a function of particle size (D). Inset shows the linear fit given to t vs D−1

Full size image

Since it has been well understood that with a decrease in D, the surface effects dominate compared to the core. The growth in dislocation density, vacancies, lattice defects, and low crystallinity adds to the surface defects which increases the separation between the FM core. This, in turn, reduces the magnetic interaction among them resulting in the drop of net magnetization, TC and \(\Delta {S}_{M}\) with broad magnetic transitions. However, the metamagnetic magnetization loops noticed for bulk and ball-milled PB20SMO demonstrate the observed behaviour to be a characteristic of magnetic interaction among the cores. Since it has been well established that PSMO is a metallic FM [12] and BSMO is a CO-AFM [16], PB20SMO represents a solid solution in both parent phases, thus showing the magnetic state of both phases. Similar coexistence of FM and AFM phases has been reported in case of Bi-substituted LaCaMnO3 [22, 34], LaSrMnO3 [20, 41], NdSr/CaMnO3 [25, 26] for a particular concentration of Bi3+. Even though Bi3+ is diamagnetic and the Mn3+/Mn4+ concentration is unaltered with Bi3+ substitution, the presence of 6s lone pair electrons of Bi3+ leads to the localization of charges across the Bi–O bonds. The antiparallel spin orientation between localized electrons and Mn3+/Mn4+ results in AFM superexchange coupling between Mn–O–Mn chains around Bi3+-rich regions, thereby driving the system towards AFM.

Further, the scientific conflict in assigning the sharp downturn observed in χ−1 (T) to either GP like singularity or the presence of FM polarons demands the presence of quenched disorder in the system [43,44,45,46,47,48,49,50,51,52,53]. Generally, in most of the manganites, A-site substitution that leads to the structural distortion due to the tilting of MnO6 octahedra is expected to be the cause of quenched disorder while some reports suggest the competitive coexistence of the FM and AFM phases [44] and the magnetic interactions among the different magnetic ions due to B-site substitution [43] also results in quenched disorder. In the present case, the tilting of MnO6 octahedra along with FM and AFM phase coexistence due to Bi3+ ions could be considered as the source of quenched disorder in bulk PB20SMO. Additionally, the broken Mn–O–Mn network due to ball milling also adds to the quenched disorder in PB20SMO nanoparticles. The local FM fluctuations resulted from the random spatial variation in the magnetic exchange interactions due to particle size reduction result in the formation of short-range FM domains embedded in the PM matrix.

4 Conclusions

Systematic analysis of the magnetization data has been carried out to understand the role of particle size reduction on the magnetic correlations and magnetocaloric properties of Pr0.4Bi0.2Sr0.4MnO3. As the particle size decreases from 160 to 12 nm, TC drops from 264 to 213 K along with a drastic reduction in the net magnetization from 2.12 to 0.41 μB/f.u. and \(\Delta {S}_{M}\) from 2.43 to 0.24 J/kg-K. Correspondingly a suppression in the metamagnetic M–H loops has been observed which suggests a reduced magnetic interaction among the nanoparticles. The observed properties can be explained due to the formation of a non-magnetic shell around the FM/AFM core. Additionally, a sharp downturn noticed in the inverse susceptibility suggests the presence of short-range FM correlations above TC.