Skip to main content

Advertisement

SpringerLink
Log in

Steady-State Bifurcation of a Non-parallel Flow Involving Energy Dissipation over a Hartmann Boundary Layer

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

Abstract

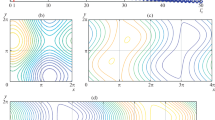
A plane non-parallel vortex flow in a square fluid domain is examined. The energy dissipation of the flow is dominated by viscosity and linear friction effect of a Hartmann layer. This is a traditional Navier–Stokes flow when the linear friction effect is not involved, whereas it is a magnetohydrodynamic flow when the energy dissipation is fundamentally dominated by the friction. It is proved that linear critical values of a spectral problem are nonlinear thresholds leading to the onset of secondary steady-state flows, the nonlinear phenomenon observed in laboratory experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Bondarenko, N.F., Gak, M.Z., Dolzhanskii, F.V.: Laboratory and theoretical models of a plane periodic flow. Izv. Akad. Nauk SSSR Fiz. Atmos. Okeana 15, 1017–1026 (1979)

  • Cerretelli, C., Williamson, C.H.K.: The physical mechanism for vortex merging. J. Fluid Mech. 475, 41–77 (2003)

    Article  MathSciNet  Google Scholar 

  • Chen, Z.M.: Bifurcating steady-state solutions of the dissipative quasi-geostrophic equation in Lagrangian formulation. Nonlinearity 29, 3132–3147 (2016)

    Article  MathSciNet  Google Scholar 

  • Chen, Z.M.: Instability of two-dimensional square eddy flows. Phys. Fluids 31, 044107 (2019)

    Article  Google Scholar 

  • Chen, Z.M., Price, W.G.: Supercritical regimes of liquid-metal fluid motions in electromagnetic fields: wall-bounded flows. Proc. R. Soc. Lond. A 458, 2735–2757 (2002)

    Article  MathSciNet  Google Scholar 

  • Chen, Z.M., Price, W.G.: Secondary fluid flows driven electromagnetically in a two-dimensional extended duct. Proc. R. Soc. Lond. A 461, 1659–1683 (2005)

    MathSciNet  MATH  Google Scholar 

  • Crandall, M.G., Rabinowitz, P.H.: Bifurcation from simple eigenvalues. J. Funct. Anal. 8, 321–340 (1971)

    Article  MathSciNet  Google Scholar 

  • Iudovich, V.I.: Example of the generation of a secondary stationary or periodic flow when there is loss of stability of the laminar flow of a viscous incompressible fluid. J. Appl. Math. Mech. 29, 527–544 (1965)

    Article  Google Scholar 

  • Kraichnan, R.H.: Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417 (1967)

    Article  Google Scholar 

  • Meunier, P., Le Dizès, S., Leweke, T.: Physics of vortex merging. Comptes Rendus Physique 6, 431–450 (2005)

    Article  Google Scholar 

  • Orszag, S.A., Patera, A.T.: Secondary instability of wall bounded shear flows. J. Fluid Mech. 128, 347–385 (1983)

    Article  Google Scholar 

  • Rabinowitz, P.H.: Existence and nonuniqueness of rectangular solutions of the Bénard problem. Arch. Rational Mech. Anal. 29, 32–57 (1968)

    Article  MathSciNet  Google Scholar 

  • Sommeria, J.: Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139–168 (1986)

    Article  Google Scholar 

  • Sommeria, J., Verron, J.: An investigation of nonlinear interactions in a two-dimensional recirculating flow. Phys. Fluids 27, 1918 (1984)

    Article  Google Scholar 

  • Thess, A.: Instabilities in two-dimensional spatially periodic flows. Part II: Square eddy lattice. Phys. Fluids A 4, 1396 (1992)

    Article  MathSciNet  Google Scholar 

  • Verron, J., Sommeria, J.: Numerical simulation of a two-dimensional turbulence experiment in magnetohydrodynamics. Phys. Fluids 30, 732 (1987)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Shenzhen University, Shenzhen, 518060, China

    Zhi-Min Chen

Authors
  1. Zhi-Min Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhi-Min Chen.

Additional information

Communicated by Tim Healey.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, ZM. Steady-State Bifurcation of a Non-parallel Flow Involving Energy Dissipation over a Hartmann Boundary Layer. J Nonlinear Sci 31, 91 (2021). https://doi.org/10.1007/s00332-021-09752-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00332-021-09752-y

Keywords

Mathematics Subject Classification

Search

Navigation