A hierarchical intervention scheme based on epidemic severity in a community network

Abstract

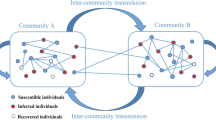
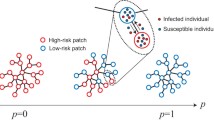
As there are no targeted medicines or vaccines for newly emerging infectious diseases, isolation among communities (villages, cities, or countries) is one of the most effective intervention measures. As such, the number of intercommunity edges (${\textit{NIE}}$) becomes one of the most important factor in isolating a place since it is closely related to normal life. Unfortunately, how ${\textit{NIE}}$ affects epidemic spread is still poorly understood. In this paper, we quantitatively analyzed the impact of ${\textit{NIE}}$ on infectious disease transmission by establishing a four-dimensional ${\textit{SIR}}$ edge-based compartmental model with two communities. The basic reproduction number $R_{0}(\langle l\rangle )$ is explicitly obtained subject to ${\textit{NIE}}$ $\langle l\rangle$. Furthermore, according to $R_{0}(0)$ with zero ${\textit{NIE}}$, epidemics spread could be classified into two cases. When $R_{0}(0)>1$ for the case 2, epidemics occur with at least one of the reproduction numbers within communities greater than one, and otherwise when $R_0(0)<1$ for case 1, both reproduction numbers within communities are less than one. Remarkably, in case 1, whether epidemics break out strongly depends on intercommunity edges. Then, the outbreak threshold in regard to ${\textit{NIE}}$ is also explicitly obtained, below which epidemics vanish, and otherwise break out. The above two cases form a severity-based hierarchical intervention scheme for epidemics. It is then applied to the SARS outbreak in Singapore, verifying the validity of our scheme. In addition, the final size of the system is gained by demonstrating the existence of positive equilibrium in a four-dimensional coupled system. Theoretical results are also validated through numerical simulation in networks with the Poisson and Power law distributions, respectively. Our results provide a new insight into controlling epidemics.

Appendix

1.1 Appendix A

In this subsection, we apply the linear system at disease-free equilibrium of Eq. (19) to verify the basic reproduction number in (25). The Jacobian matrix at disease-free equilibrium $E_{0}=(1, 1, 1, 1)$ of model Eq. (19) is

$$\begin{aligned} \textrm{J}= \begin{pmatrix} J_{11}&{}\beta _{11}{\tilde{G}_{12}^{'}(1)}&{}0&{}0\\ 0&{}-(\beta _{12}+\gamma _{2})&{}\beta _{12}G_{21}^{'}(1)&{}\beta _{12}{\tilde{G}_{22}^{'}(1)}\\ \beta _{21}{\tilde{G}_{11}^{'}(1)}&{}\beta _{21}G_{12}^{'}(1)&{}-(\beta _{21}+\gamma _{1})&{}0\\ 0&{}0&{}\beta _{22}{\tilde{G}_{21}^{'}(1)}&{}J_{44} \end{pmatrix}, \end{aligned}$$

where $J_{11} = -(\beta _{11}+\gamma _{1})+\beta _{11}G_{11}^{'}(1)$, $J_{44} = -(\beta _{22}+\gamma _{2})+\beta _{22}G_{22}^{'}(1)$.

Its characteristic equation is

$$\begin{aligned} \lambda ^{4}+a_{1}\lambda ^{3}+a_{2}\lambda ^{2}+a_{3}\lambda +a_{4}=0, \end{aligned}$$

(30)

where

$$\begin{aligned} a_{1}&=(\beta _{11}+\gamma _{1})+(\beta _{12}+\gamma _{2})+(\beta _{21}+\gamma _{1})+(\beta _{22}+\gamma _{2})-\beta {11}G_{11}^{'}(1)\\&\quad -\beta _{22}G_{22}^{'}(1),\\ a_{2}&=(\beta _{11}+\gamma _{1})(\beta _{12}+\gamma _{2})+(\beta _{11}+\gamma _{1})(\beta _{21}+\gamma _{1})+(\beta _{11}+\gamma _{1})(\beta _{22}+\gamma _{2})\\&\quad +(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1}) +(\beta _{12}+\gamma _{2})(\beta _{22}+\gamma _{2})+(\beta _{21}+\gamma _{1})(\beta _{22}+\gamma _{2})\\&\quad -(\beta _{12}+\gamma _{2})\beta _{11}G_{11}^{'}(1)-(\beta _{21}+\gamma _{1})\beta _{11}G_{11}^{'}(1-(\beta _{22}+\gamma _{2})\beta _{11}G_{11}^{'}(1)\\&\quad -(\beta _{11}+\gamma _{1})\beta _{22}G_{22}^{'}(1)-(\beta _{12}+\gamma _{2})\beta _{22}G_{22}^{'}(1)-(\beta _{21}+\gamma _{1})\beta _{22}G_{22}^{'}(1)\\&\quad +\beta _{11}G_{11}^{'}(1)\beta _{22}G_{22}^{'}(1)-\beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1),\\ a_{3}&=(\beta _{11}+\gamma _{1})(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1}) +(\beta _{11}+\gamma _{1})(\beta _{12}+\gamma _{2})(\beta _{22}+\gamma _{2})\\&\quad +(\beta _{11}+\gamma _{1})(\beta _{21}+\gamma _{1})(\beta _{22}+\gamma _{2})+(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1})(\beta _{22}+\gamma _{2})\\&\quad -(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1})\beta _{11}G_{11}^{'}(1)-(\beta _{21}+\gamma _{1})(\beta _{22}+\gamma _{2})\beta _{11}G_{11}^{'}(1)\\&\quad -(\beta _{12}+\gamma _{2})G_{22}^{'}(1)\beta _{11}G_{11}^{'}(1)-(\beta _{11}+\gamma _{1})(\beta _{21}+\gamma _{1})\beta _{22}G_{22}^{'}(1)\\&\quad -(\beta _{11}+\gamma _{1})(\beta _{12}+\gamma _{2})\beta _{22}G_{22}^{'}(1)-(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1})\beta _{22}G_{22}^{'}(1)\\&\quad -(\beta _{11}+\gamma _{1})\beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1)-(\beta _{22}+\gamma _{2})\beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1)\\&\quad +(\beta _{12}+\gamma _{2})\beta _{11}G_{11}^{'}(1)\beta _{22}G_{22}^{'}(1)+(\beta _{21}+\gamma _{1})\beta _{11}G_{11}^{'}(1)\beta _{22}G_{22}^{'}(1)\\&\quad +\beta _{11}G_{11}^{'}(1)\beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1)+\beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1)\beta _{22}G_{22}^{'}(1)\\&\quad -\beta _{11}{\tilde{G}_{11}^{'}(1)}\beta _{21}{\tilde{G}_{12}^{'}(1)} \beta _{12}G_{21}^{'}(1)-\beta _{12}{\tilde{G}_{21}^{'}(1)}\beta _{22}{\tilde{G}_{22}^{'}(1)}\beta _{21}G_{12}^{'}(1),\\ \end{aligned}$$

$$\begin{aligned} a_{4}&=(\beta _{11}+\gamma _{1})(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1})(\beta _{22}+\gamma _{2})-(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1}) \\ {}&\quad \times (\beta _{22}+\gamma _{2})\beta _{11}G_{11}^{'}(1)-(\beta _{11}+\gamma _{1})(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1})\beta _{22}G_{22}^{'}(1) \\ {}&\quad +(\beta _{22}+\gamma _{2})\beta _{11}G_{11}^{'}(1)\beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1)+(\beta _{11}+\gamma _{1})\beta _{22}G_{22}^{'}(1) \\ {}&\quad \times \beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1)-(\beta _{11}+\gamma _{1}) (\beta _{22}+\gamma _{2})\beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1) \\ {}&\quad +(\beta _{12}+\gamma _{2})(\beta _{21}+\gamma _{1})\beta _{11}G_{11}^{'}(1)\beta _{22}G_{22}^{'}(1)- (\beta _{22}+\gamma _{2})\beta _{11}{\tilde{G}_{11}^{'}(1)}\\&\quad \times \beta _{21}{\tilde{G}_{12}^{'}(1)}\beta _{12} G_{21}^{'}(1)-(\beta _{11}+\gamma _{1})\beta _{12}{\tilde{G}_{21}^{'}(1)}\beta _{22}{\tilde{G}_{22}^{'}(1)} \beta _{21}G_{12}^{'}(1) \\ {}&\quad +\beta _{11}{\tilde{G}_{11}^{'}(1)} \beta _{21}{\tilde{G}_{12}^{'}(1)}\beta _{12}G_{21}^{'}(1)\beta _{22}G_{22}^{'}(1) +\beta _{12}{\tilde{G}_{21}^{'}(1)}\beta _{22} {\tilde{G}_{22}^{'}(1)}\\&\quad \times \beta _{11}G_{11}^{'}(1)\beta _{21}G_{12}^{'}(1)-\beta _{11}G_{11}^{'}(1) \beta _{12}G_{21}^{'}(1)\beta _{21}G_{12}^{'}(1)\beta _{22}G_{22}^{'}(1) \\ {}&\quad -\beta _{11}G_{11}^{*'}(1)\beta _{12}{\tilde{G}_{21}^{'}(1)}\beta _{21}{\tilde{G}_{12}^{'}(1)}\beta _{22}{\tilde{G}_{22}^{'}(1)}. \end{aligned}$$

As the complexity of the fourth order Eq. (30), the stability of disease-free equilibrium is hard to verify by Routh–Hurwitz criterion. However, for the type of edge-based equations, reference Rattana et al. (2014) has indicated that the case of $a_{4}=0$ in fourth order equation (30) is equivalent to $R_{0}=1$. Therefore, when $a_{4}=0$ in (30), we obtain

$$\begin{aligned} R_{0}&=\frac{\beta _{11}}{\beta _{11}+\gamma _{1}}\frac{\beta _{12}}{\beta _{12}+\gamma _{2}}\frac{\beta _{21}}{\beta _{21}+\gamma _{1}}\frac{\beta _{22}}{\beta _{22}+\gamma _{2}}\left( \tilde{G}_{11}^{ '}(1)+\tilde{G}_{12}^{'}(1)-1\right) \nonumber \\&\quad \times \left( \tilde{G}_{21}^{ '}(1)+\tilde{G}_{22}^{ '}(1)-1\right) +\frac{\beta _{11}}{\beta _{11}+\gamma _{1}}\frac{\beta _{12}}{\beta _{12}+\gamma _{2}}\frac{\beta _{21}}{\beta _{21}+\gamma _{1}}G_{21}^{'}(1)\nonumber \\&\quad \times \left( \tilde{G}_{11}^{ '}(1)+\tilde{G}_{12}^{ '}(1)-1\right) +\frac{\beta _{12}}{\beta _{12}+\gamma _{2}}\frac{\beta _{21}}{\beta _{21}+\gamma _{1}}\frac{\beta _{22}}{\beta _{22}+\gamma _{2}}G_{12}^{'}(1)\nonumber \\&\quad \times \left( \tilde{G}_{21}^{ '}(1)+\tilde{G}_{22}^{ '}(1)-1\right) +\frac{\beta _{12}}{\beta _{12}+\gamma _{2}}G_{21}^{'}(1)\frac{\beta _{21}}{\beta _{21}+\gamma _{1}}G_{12}^{'}(1) \nonumber \\&\quad +\frac{\beta _{11}}{\beta _{11}+\gamma _{1}}G_{11}^{'}(1)+\frac{\beta _{22}}{\beta _{22}+\gamma _{2}}G_{22}^{'}(1)-\frac{\beta _{11}}{\beta _{11}+\gamma _{1}}G_{11}^{'}(1)\frac{\beta _{22}}{\beta _{22}+\gamma _{2}}G_{22}^{'}(1). \end{aligned}$$

It indirectly verifies the validity of $R_{0}$ in (25), although the analysis lacks strict proof.