SIR dynamics in random networks with communities

Abstract

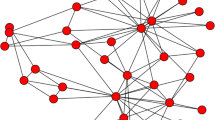
This paper investigates the effects of the community structure of a network on the spread of an epidemic. To this end, we first establish a susceptible–infected–recovered (SIR) model in a two-community network with an arbitrary joint degree distribution. The network is formulated as a probability generating function. We also obtain the sufficient conditions for disease outbreak and extinction, which involve the first-order and second-order moments of the degree distribution. As an example, we then study the effect of community structure on epidemic spread in a complex network with a Poisson joint degree distribution. The numerical solutions of the SIR model well agree with stochastic simulations based on the Monte Carlo method, confirming that the model is reliable and accurate. Finally, by strengthening the community structure in the simulation, i.e. fixing the total degree distribution and reducing the number ratio of the external edges, we can increase or decrease the final cumulative epidemic incidence depending on the transmissibility of the virus between humans and the community structure at that point. Why community structure can affect disease dynamics in a complicated way is also discussed. In any case, for large-scale epidemics, strengthening the community structure to reduce the size of disease is undoubtedly an effective way.

Appendices

Appendix A: the dynamics of SIR epidemic model in a network with two communities

In this section, we develop an SIR-epidemic model involving the variables $\theta _{mn}$, $p^{I_m}_{S_n}$ and $p^{S_m}_{S_n}$, $m,n=1,2$. The method used is similar to that (Volz 2008).

Firstly, we introduce the dynamics of $\theta _{mn}$, $m,n=1,2.$ Consider a susceptible node ego in community l at time t with a joint degree (k, j), there are a set of k internal arcs $(\text{ ego }^l,\text{ alter }^{in}_{1})$, $(\text{ ego }^l,\text{ alter }^{in}_{2})$, $\cdots$, $(\text{ ego }^l, \text{ alter }^{in}_{k})$ and a set of j external arcs $(\text{ ego }^l,\text{ alter }^{out}_{1})$, $(\text{ ego }^l,\text{ alter }^{out}_{2})$, $\cdots$, $(\text{ ego }^l,\text{ alter }^{out}_{j})$ corresponding to the ego. We assume that for each arc $(\text{ ego }^l,\text{ alter }^{in}_{m})$ for $m=1,2,\cdots , k$ and $(\text{ ego }^l,\text{ alter }^{out}_{n})$ for $n=1,2,\cdots , j$, there will be uniform probabilities $p^{I_l}_{S_l}=M^{I_l}_{S_l}/M^{in}_{S_l}$ and $p^{I_n}_{S_l}=M^{I_n}_{S_l}/M^{out}_{S_l}$ for $n\ne l$ that $alter^{in}_{m}$ and $alter^{out}_{n}$ are infectious, respectively. In a time dt, an expected number $\gamma (k p^{I_l}_{S_l}+j p^{I_n}_{S_l})dt$ for $n\ne l$ of these will be such that the infectious alter transmits to ego. Consequently, the hazard for ego becoming infected at time t is

$$\begin{aligned} \lambda ^l_{(k,j)}(t)=\gamma (k p^{I_l}_{S_l}+j p^{I_n}_{S_l}), \ \ \ \ \ l,n=1,2,\ \ \ n\ne l \end{aligned}$$

(42)

Now let $u^l_{(k,j)}(t)$ represent the fraction of nodes with joint degree (k, j) in community l which remain susceptible at time t. Using Eq. (42), we have

$$\begin{aligned} u^l_{(k,j)}(t)= & {} \exp \left( {-\int _0^t\lambda _{(k,j)}(\tau )d\tau }\right) =\exp (-\int _0^t\gamma \left( k p^{I_l}_{S_l}+j p^{I_n}_{S_l}\right) d\tau )\nonumber \\= & {} \exp \left( -\int _0^t\gamma p^{I_l}_{S_l}d\tau \right) ^k \cdot \exp \left( -\int _0^t\gamma p^{I_n}_{S_l}d\tau \right) ^j,\ \ \ \ \ l,n=1,2,\ n\ne l\nonumber \\ \end{aligned}$$

(43)

Subsequently, let

$$\begin{aligned} \theta _{ln}=\exp \left( {-\int _0^t\gamma p^{I_n}_{S_l}d\tau }\right) , l,n=1,2. \end{aligned}$$

(44)

Then

$$\begin{aligned} u^l_{(k,j)}(t)=(\theta _{ll})^k\cdot (\theta _{ln})^j,\ \ \ \ n\ne l \end{aligned}$$

Thus, the fraction of nodes which remain susceptible at time t in community l for $l=1, 2$ are

$$\begin{aligned} \left\{ \begin{array}{ll} s_1=\sum \limits _{k,j}P_1(k,j)\theta _{11}^k\theta _{12}^j=\frac{N}{N_1}G(\theta _{11}, \theta _{12}, 0, 0), \ \ \ \ \, \ &{}\ \ \\ s_2=\sum \limits _{k,j}P_2(k,j)\theta _{22}^k\theta _{21}^j=\frac{N}{N_2}G(0, 0, \theta _{22}, \theta _{21}), \ \ \ \ \, \ &{} \ \ \end{array}\right. \end{aligned}$$

(45)

respectively and the fraction of nodes which remain susceptible in the whole network at time t is

$$\begin{aligned} s=\sum \limits _{l,n=1}^2\sum \limits _{n\ne l}\sum \limits _{k,j}\frac{N_l}{N}P_l(k,j)\theta _{ll}^k\theta _{ln}^j=G(\theta _{11},\theta _{12},\theta _{22},\theta _{21}). \end{aligned}$$

Similarly, for $l,n=1,2$ and $n\ne l$, we have

$$\begin{aligned} A^{in}_{S_l}= & {} N_l\sum \limits _{k,j}kP_l{(k,j)\theta _{ll}^k\theta _{ln}^j}=NG_l{(\theta _{ll},\theta _{ln})}\theta _{ll},\nonumber \\ A^{out}_{S_l}= & {} N_l\sum \limits _{k,j}jP_l{(k,j)\theta _{ll}^k\theta _{ln}^j}=NG^l{(\theta _{ll},\theta _{ln})}\theta _{ln}. \end{aligned}$$

(46)

In terms of $A^{in}_l=NG_l{(1,1)}$ and Eq. (46), we have

$$\begin{aligned} M^{in}_{S_l}=\frac{G_l{(\theta _{ll},\theta _{ln})}\theta _{ll}}{G_l{(1,1)}},\ \ \ M^{out}_{S_l}=\frac{G^l{(\theta _{ll},\theta _{ln})}\theta _{ln}}{G^l{(1,1)}} \end{aligned}$$

(47)

According to Eq. (44), the dynamics of $\theta _{ln}$, $l, n=1, 2$ is

$$\begin{aligned} \dot{\theta }_{ln}=-\gamma \theta _{ln}p^{I_n}_{S_l}, \ \ \ \ \ l,n=1,2, \end{aligned}$$

(48)

which depends on the variable $p^{I_n}_{S_l}$. To close the above system, we have to calculate the dynamics of $p^{I_n}_{S_l}$.

Second, we introduce the dynamics of $p^{I_n}_{S_l}$ for $l,n=1,2$. The definition of $p^{I_n}_{S_l}$ is

$$\begin{aligned} p^{I_n}_{S_l}=\left\{ \begin{array}{ll} \frac{M^{I_l}_{S_l}}{M^{in}_{S_l}},&{}\ \ n=l\\ \frac{M^{I_n}_{S_l}}{M^{out}_{S_l}},&{} \ \ n\ne l\end{array}\right. . \end{aligned}$$

(49)

Hence,

(50)

From Eq. (47), we easily get

$$\begin{aligned} \dot{ M^{in}_{S_l}}=\frac{G_{ll}{(\theta _{ll},\theta _{ln})}\dot{\theta }_{ll}\theta _{ll}+G_l^l{(\theta _{ll},\theta _{ln})} \dot{\theta }_{ln}\theta _{ll}+G_l(\theta _{ll},\theta _{ln})\dot{\theta }_{ll}}{G_l{(1,1)}} \end{aligned}$$

(51)

and

$$\begin{aligned} \dot{ M^{out}_{S_l}}=\frac{G_l^l{(\theta _{ll},\theta _{ln})}\dot{\theta }_{ll}\theta _{ln}+G^{ll}{(\theta _{ll},\theta _{ln})} \dot{\theta }_{ln}\theta _{ln}+G^l(\theta _{ll},\theta _{ln})\dot{\theta }_{ln}}{G^l{(1,1)}} \end{aligned}$$

(52)

where $l,n=1,2$ and $n\ne l$.

The dynamics of $M^{I_n}_{S_l}$ for l, $n=1,2$ depends on the state of excessive neighbors (not counting the alter $I_n$ in the chosen arc $(S_l, I_n)$) of the ego node $S_l$ for an random chosen arc $(S_l, I_n)$ in $A^{I_n}_{S_l}$ for l, $n=1,2$. The following notations in Table 2 are needed to clarify subsequent calculations.

Table 2 Symbols

The PGF for the excessive degree distribution of the ego node $S_l$ in the selected arc $(S_l, I_n)$ are

$$\begin{aligned}&g_{S_1I_1}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}\nonumber \\&\quad =\frac{G_1{((p^{S_1}_{S_1}X_{S_1}+p^{I_1}_{S_1}X_{I_1}+p^{R_1}_{S_1}X_{R_1})\theta _{11},(p^{S_2}_{S_1}X_{S_2}+p^{I_2}_{S_1}X_{I_2}+p^{R_2}_{S_1}X_{R_2})\theta _{12})}}{G_1{(\theta _{11},\theta _{12})}},\nonumber \\ \end{aligned}$$

(53)

$$\begin{aligned}&g_{S_1I_2}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}\nonumber \\&\quad =\frac{G^1{((p^{S_1}_{S_1}X_{S_1}+p^{I_1}_{S_1}X_{I_1}+p^{R_1}_{S_1}X_{R_1})\theta _{11},(p^{S_2}_{S_1}X_{S_2}+p^{I_2}_{S_1}X_{I_2}+p^{R_2}_{S_1}X_{R_2})\theta _{12})}}{G^1{(\theta _{11},\theta _{12})}},\nonumber \\ \end{aligned}$$

(54)

$$\begin{aligned}&g_{S_2I_1}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}\nonumber \\&\quad =\frac{G^2{((p^{S_2}_{S_2}X_{S_2}+p^{I_2}_{S_2}X_{I_2}+p^{R_2}_{S_2}X_{R_2})\theta _{22},(p^{S_1}_{S_2}X_{S_1}+p^{I_1}_{S_2}X_{I_1}+p^{R_1}_{S_2}X_{R_1})\theta _{21})}}{G^2{(\theta _{22},\theta _{21})}},\nonumber \\ \end{aligned}$$

(55)

$$\begin{aligned}&g_{S_2I_2}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}\nonumber \\&\quad =\frac{G_2{((p^{S_2}_{S_2}X_{S_2}+p^{I_2}_{S_2}X_{I_2}+p^{R_2}_{S_2}X_{R_2})\theta _{22},(p^{S_1}_{S_2}X_{S_1}+p^{I_1}_{S_2}X_{I_1}+p^{R_1}_{S_2}X_{R_1})\theta _{21})}}{G_2{(\theta _{22},\theta _{21})}}.\nonumber \\ \end{aligned}$$

(56)

The derivation of the Eq. (53) is presented in the “Appendix B” as an example.

Because arcs are distributed polynomially to nodes in sets S, I, R, we have $g_{S_1I_1}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}=g_{S_1S_1}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}$, which is easy to verify by repeating the calculation in Eq. (53).

By Eqs. (53) and (54), we have

$$\begin{aligned} \delta _{S_lI_l}(S_l)= & {} \frac{\partial g_{S_lI_l}(X_{S_l},X_{I_l},X_{R_l},X_{S_n},X_{I_n},X_{R_n})}{\partial X_{S_l}}|_{X_{S_l}=X_{I_l}=X_{R_l}=X_{S_n}=X_{I_n}=X_{R_n}=1} \nonumber \\= & {} \frac{G_{ll}(\theta _{ll},\theta _{ln})p^{S_l}_{S_l}\theta _{ll}}{G_l(\theta _{ll},\theta _{ln})},\nonumber \\ \delta _{S_lI_l}(I_l)= & {} \frac{\partial g_{S_lI_l}(X_{S_l},X_{I_l},X_{R_l},X_{S_n},X_{I_n},X_{R_n})}{\partial X_{I_l}}|_{X_{S_l}=X_{I_l}=X_{R_l}=X_{S_n}=X_{I_n}=X_{R_n}=1} \nonumber \\= & {} \frac{G_{ll}(\theta _{ll},\theta _{ln})p^{I_l}_{S_l}\theta _{ll}}{G_l(\theta _{ll},\theta _{ln})},\nonumber \\ \delta _{S_lI_n}(I_l)= & {} \frac{\partial g_{S_lI_n}(X_{S_l},X_{I_l},X_{R_l},X_{S_n},X_{I_n},X_{R_n})}{\partial X_{I_l}} |_{X_{S_l}=X_{I_l}=X_{R_l}=X_{S_n}=X_{I_n}=X_{R_n}=1} \nonumber \\= & {} \frac{G_l^l(\theta _{ll},\theta _{ln})p^{I_l}_{S_l}\theta _{ll}}{G^l(\theta _{ll},\theta _{ln})},\nonumber \\ \delta _{S_lI_n}(S_l)= & {} \frac{ \partial g_{S_lI_n}(X_{S_l},X_{I_l},X_{R_l},X_{S_n},X_{I_n},X_{R_n})}{\partial X_{S_l}}|_{X_{S_l}=X_{I_l}=X_{R_l}=X_{S_n}=X_{I_n}=X_{R_n}=1} \nonumber \\= & {} \frac{G_l^l(\theta _{ll},\theta _{ln})p^{S_l}_{S_l}\theta _{ll}}{G^l(\theta _{ll},\theta _{ln})}. \end{aligned}$$

(57)

We next obtain the dynamics of $M_{S_l}^{I_l}$. Volz (2008) introduces the approach to model SIR dynamics on networks. Here, we briefly present this approach.

There are three reasons for the reduction of the fraction of arcs between $S_l$ and $I_l$. One reason is the newly infectious nodes in community l. In a time infinitesimal dt, the fraction of newly infectious nodes is $-\dot{s}_l$. According to Eq. (45), we can obtain

$$\begin{aligned} \dot{s}_l=\frac{N}{N_l}G_l(\theta _{ll},\theta _{ln})\dot{\theta }_{ll}+\frac{N}{N_l}G^l(\theta _{ll},\theta _{ln})\dot{\theta }_{ln}, \end{aligned}$$

(58)

in which $-\frac{N}{N_l}G_l(\theta _{ll},\theta _{ln})\dot{\theta }_{ll}$ describes a fraction nodes infected by infectious alters in community l and $-\frac{N}{N_l}G^l(\theta _{ll},\theta _{ln})\dot{\theta }_{ln}$ describes a fraction nodes infected by infectious alters in community n for $l\ne n$. Therefore, $M^{I_l}_{S_l}$ decreases at rate

$$\begin{aligned}&-\frac{N}{N_l}G_l(\theta _{ll},\theta _{ln})\dot{\theta }_{ll}\frac{\delta _{S_lI_l}(I_l)}{\frac{N}{N_l}G_l{(1,1)}} -\frac{N}{N_l}G^l(\theta _{ll},\theta _{ln})\dot{\theta }_{ln}\frac{\delta _{S_lI_n}(I_l)}{\frac{N}{N_l}G_l{(1,1)}}\nonumber \\&\quad =-\frac{G_l(\theta _{ll},\theta _{ln})}{G_l{(1,1)}}\delta _{S_lI_l}(I_l)\dot{\theta }_{ll} -\frac{G^l(\theta _{ll},\theta _{ln})}{G_l{(1,1)}}\delta _{S_lI_n}(I_l)\dot{\theta }_{ln}. \end{aligned}$$

(59)

Because $\delta _{S_lI_l}(I_l)$ does not count the arc along which a node was infected, another reason is the transmission from the infectious alter to the susceptible ego in this arc, which results in a reduction at a rate

$$\begin{aligned} \gamma {M^{I_l}_{S_l}}. \end{aligned}$$

The third reason is the recovery of the infectious alter in the arcs, which brings about a reduction at a rate

$$\begin{aligned} \mu I_l\frac{M^{I_l}_{S_l}}{I_l}=\mu M^{I_l}_{S_l}. \end{aligned}$$

On the other hand, the increase of $M^{I_l}_{S_l}$ is only due to the infection of the fraction of the susceptible egos which have excessive susceptible neighbors. So ${M^{I_l}_{S_l}}$ increases at the rate

$$\begin{aligned}&-\frac{N}{N_l}G_l(\theta _{ll},\theta _{ln})\dot{\theta }_{ll}\frac{\delta _{S_lI_l}(S_l)}{\frac{N}{N_l}G_l{(1,1)}} -\frac{N}{N_l}G^l(\theta _{ll},\theta _{ln})\dot{\theta }_{ln}\frac{\delta _{S_lI_n}(S_l)}{\frac{N}{N_l}G_l{(1,1)}}\nonumber \\&\quad =-\frac{G_l(\theta _{ll},\theta _{ln})}{G_l{(1,1)}}\delta _{S_lI_l}(S_l)\dot{\theta }_{ll} -\frac{G^l(\theta _{ll},\theta _{ln})}{G_l{(1,1)}}\delta _{S_lI_n}(S_l)\dot{\theta }_{ln}. \end{aligned}$$

(60)

From Eqs. (48), (59)–(60), we have

$$\begin{aligned} \dot{M}^{I_l}_{S_l}= & {} -(\gamma +\mu ) M^{I_l}_{S_l}-\frac{G_l(\theta _{ll},\theta _{ln})}{G_l{(1,1)}}(\delta _{S_lI_l}(S_l)-\delta _{S_lI_l}(I_l))\dot{\theta }_{ll}\nonumber \\&-\frac{G^l(\theta _{ll},\theta _{ln})}{G_l{(1,1)}}(\delta _{S_lI_n}(S_l)-\delta _{S_lI_n}(I_l))\dot{\theta }_{ln}\nonumber \\= & {} \gamma \frac{(p^{S_l}_{S_l}-p^{I_l}_{S_l})\theta _{ll}}{G_l{(1,1)}} (G_{ll}(\theta _{ll},\theta _{ln}) \theta _{ll}p^{I_l}_{S_l}\nonumber \\&+G_l^l(\theta _{ll},\theta _{ln})\theta _{ln}p^{I_n}_{S_l})-(\gamma +\mu ) M^{I_l}_{S_l}. \end{aligned}$$

(61)

Now applying Eqs. (47), (48), (51) and (61) to Eq. (50), we obtain the dynamics of $p^{I_l}_{S_l}$, i.e.

$$\begin{aligned} \frac{dp^{I_l}_{S_l}}{dt}= & {} \frac{\gamma \theta _{ll}p^{I_l}_{S_l}p^{S_l}_{S_l}G_{ll}{(\theta _{ll},\theta _{ln})}}{G_l{(\theta _{ll},\theta _{ln})}} +\frac{\gamma \theta _{ln}p^{I_n}_{S_l}p^{S_l}_{S_l}G_l^l{(\theta _{ll},\theta _{ln})}}{G_l{(\theta _{ll},\theta _{ln})}} -(\gamma +\mu )p^{I_l}_{S_l}+\gamma ({p}^{I_l}_{S_l})^2\nonumber \\= & {} \frac{\gamma \theta _{ll}p^{I_l}_{S_l}p^{S_l}_{S_l}G_{ll}{(\theta _{ll},\theta _{ln})}}{G_l{(\theta _{ll},\theta _{ln})}} +\frac{\gamma \theta _{ln}p^{I_n}_{S_l}p^{S_l}_{S_l}G_l^l{(\theta _{ll},\theta _{ln})}}{G_l{(\theta _{ll},\theta _{ln})}}-\gamma p^{I_l}_{S_l}(1-p^{I_l}_{S_l})-\mu p^{I_l}_{S_l}.\nonumber \\ \end{aligned}$$

(62)

Similarly, we can obtain the dynamics of $p^{I_n}_{S_l}$, $p^{S_l}_{S_l}$ and $p^{S_n}_{S_l}$ for $l\ne n$ and $l, n=1, 2$.

Appendix B: the PGF for the excessive degree distribution of the ego node in an arc

We give PGF for the excessive degree distribution of the ego node $S_l$ in an arc $(S_l, I_n)$, which is a conditional PGF involving the state of the ego node.

Table 3 Random variables

For an arbitrary chosen arc $\xi$, define some random variables. Easy to find, we list them in Table 3. Let A, B and C represent the state of a node and they may be S, I or R. Let $P(i_1, j_1, l_1, i_2, j_2, l_2\mid \xi )$ be the conditional probability that $\xi _{S_1}=i_1$, $\xi _{I_1}=j_1$, $\xi _{R_1}=l_1$, $\xi _{S_2}=i_2$, $\xi _{I_2}=j_2$ and $\xi _{R_2}=l_2$ for an arbitrary chosen arc $\xi$. The amount of excessive neighbors in state S, I and R and in community l, $l=1,2$, of ego node in state A and in the chosen arc are distributed polynomially with probability $p^{I_l}_{A}$, $p^{S_l}_{A}$ and $p^{R_l}_{A}=1-p^{I_l}_{A}-p^{S_l}_{A}$, $l=1,2$, respectively.

The PGF for the excessive degree distribution of the ego node $S_1$ in the chosen arc $(S_1, I_1)$, is

$$\begin{aligned}&g_{S_1I_1}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}\nonumber \\&\quad =\sum \limits _{i_1+m_1\le {k}}\sum \limits _{i_2+m_2\le {j}}P(i_1,m_1-1,l_1,i_2,m_2,l_2|S_1I_1)\nonumber \\&\qquad X_{S_1}^{i_1}X_{I_1}^{m_1-1}X_{R_1}^{l_1}X_{S_2}^{i_2}X_{I_2}^{m_2}X_{R_2}^{l_2}. \end{aligned}$$

(63)

From the definition of the conditional probability, we have

$$\begin{aligned} P(i_1,m_1-1,l_1,i_2,m_2,l_2|S_1I_1)= & {} \frac{P(i_1, m_1-1, l_1, i_2, m_2, l_2,S_1I_1)}{P(S_1I_1)}. \end{aligned}$$

(64)

Grounded on total probability formula, we have

$$\begin{aligned} P(i_1, m_1-1, l_1, i_2, m_2, l_2,S_1I_1)=\sum \limits _{k,j}P_1\cdot P_2\cdot P_3\cdot P_4\cdot P_5 \end{aligned}$$

(65)

and

$$\begin{aligned} P(S_1I_1)=\sum \limits _{k,j} P_2\cdot P_3\cdot P_4\cdot P_5, \end{aligned}$$

(66)

where

$$\begin{aligned} P_1= & {} P(i_1, m_1-1, l_1, i_2, m_2, l_2|\vartheta _2=I_1,\vartheta _1=S,d=(k,j),\eta =1)\nonumber \\ P_2= & {} P(\vartheta _2=I_1|\vartheta _1=S,d=(k,j),\eta =1)=p_{S_1}^{I_1},\nonumber \\ P_3= & {} P(\vartheta _1=S|d=(k,j),\eta =1)=\theta ^k_{11}\theta ^j_{12},\nonumber \\ P_4= & {} P(d=(k,j)|\eta =1)=\frac{N_1kP_1(k,j)}{N_1\frac{N}{N_1}(G_1+G^1)}, \nonumber \\ P_5= & {} P(\eta =1)=\frac{G_1+G^1}{\sum \nolimits ^2_{l=1}{(G_l+G^l)}}. \end{aligned}$$

(67)

Since the amount of excessive neighbors of ego node in state S and in the chosen arc $(S_1,I_1)$ are distributed polynomially with probability $p_{S_1}^{S_l}$, $p_{S_1}^{I_l}$, $p^{R_l}_{S_1}=1-p^{S_l}_{S_1}-p_{S_1}^{I_l}$, $l=1,2$, respectively, we have

$$\begin{aligned} P_1= & {} P(i_1, m_1-1, l_1, i_2, m_2, l_2|\vartheta _2=I_1,\vartheta _1=S,d=(k,j),\eta =1)\nonumber \\= & {} \frac{(k-1)!j!{(p_{S_1}^{S_1})}^{i_1}{(p_{S_1}^{I_1})}^{m_1-1}{(p_{S_1}^{R_1})}^{k-i_1-m_1}{(p_{S_1}^{S_2})}^{i_2}{(p_{S_1}^{I_2})}^{m_2} {(p_{S_1}^{R_2})}^{j-i_2-m_2}}{i_1!(m_1-1)!(k-i_1-m_1)!i_2!m_2!(j-i_2-m_2)!}.\nonumber \\ \end{aligned}$$

(68)

From Eqs. (63), (64), (65), (66) and (67), we have

$$\begin{aligned}&g_{S_1I_1}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}\nonumber \\&\quad =\sum \limits _{i_1+m_1\le {k}}\sum \limits _{i_2+m_2\le {j}}\frac{\sum \nolimits _{k,j}P_1\cdot P_2\cdot P_3\cdot P_4\cdot P_5}{\sum \nolimits _{k,j} P_2\cdot P_3\cdot P_4\cdot P_5}X_{S_1}^{i_1}X_{I_1}^{m_1-1}X_{R_1}^{l_1}X_{S_2}^{i_2}X_{I_2}^{m_2}X_{R_2}^{l_2} \nonumber \\&\quad =\frac{\sum \nolimits _{k,j}\sum \nolimits _{i_1+m_1\le {k}}\sum \nolimits _{i_2+m_2\le {j}}P_1\cdot \theta ^k_{11}\theta ^j_{12}{kP_1(k,j)} p_{S_1}^{I_1}X_{S_1}^{i_1}X_{I_1}^{m_1-1}X_{R_1}^{l_1}X_{S_2}^{i_2}X_{I_2}^{m_2}X_{R_2}^{l_2}}{\sum \nolimits _{k,j} \theta ^k_{11}\theta ^j_{12} p_{S_1}^{I_1}\cdot {kP_1(k,j)}} \nonumber \\&\quad =\frac{\sum \nolimits _{k,j}\theta ^k_{11}\theta ^j_{12}{P_1(k,j)}\sum \nolimits _{i_1+m_1\le {k}}\sum \nolimits _{i_2+m_2\le {j}}kp_{S_1}^{I_1}P_1\cdot X_{S_1}^{i_1}X_{I_1}^{m_1-1}X_{R_1}^{l_1}X_{S_2}^{i_2}X_{I_2}^{m_2}X_{R_2}^{l_2} }{\sum \nolimits _{k,j} \theta ^k_{11}\theta ^j_{12}\cdot {kp_{S_1}^{I_1}P_1(k,j)}}.\nonumber \\ \end{aligned}$$

(69)

Furthermore, Eq. (68) leads to

$$\begin{aligned} \sum \limits _{i_1+m_1\le {k}}\sum \limits _{i_2+m_2\le {j}}kp_{S_1}^{I_1}P_1\cdot X_{S_1}^{i_1}X_{I_1}^{m_1-1}X_{R_1}^{l_1}X_{S_2}^{i_2}X_{I_2}^{m_2}X_{R_2}^{l_2}=\varDelta _1\cdot \varDelta _2,\end{aligned}$$

(70)

where

$$\begin{aligned} \varDelta _1= & {} \sum \limits _{i_1+m_1\le k}\frac{k!p_{S_1}^{I_1}{(p_{S_1}^{S_1}X_{S_1})}^{i_1}{(p_{S_1}^{I_1}X_{I_1})}^{m_1-1}{(p_{S_1}^{R_1}X_{R_1})}^{k-i_1-m_1} }{i_1!(m_1-1)!(k-i_1-m_1)!}\nonumber \\= & {} \frac{d{(p^{S_1}_{S_1}X_{S_1}+p^{I_1}_{S_1}X_{I_1}+p^{R_1}_{S_1}X_{R_1})^k}}{dX_{I_1}} \end{aligned}$$

(71)

and

$$\begin{aligned} \varDelta _2= & {} \sum \limits _{i_2+m_2\le j}\frac{j!{(p_{S_1}^{S_2}X_{S_2})}^{i_2}{(p_{S_1}^{I_2}X_{I_2})}^{m_2} {(p_{S_1}^{R_2}X_{R_2})}^{j-i_2-m_2}}{i_2!m_2!(j-i_2-m_2)!}\nonumber \\= & {} (p^{S_2}_{S_1}X_{S_2}+p^{I_2}_{S_1}X_{I_2}+p^{R_2}_{S_1}X_{R_2})^j \end{aligned}$$

(72)

Thus, from Eqs. (70), (71) and (72), we have

$$\begin{aligned}&\sum \limits _{k,j}\theta ^k_{11}\theta ^j_{12}{P_1(k,j)}\varDelta _1\varDelta _2 \nonumber \\&\quad =\sum \limits _{k,j}\theta ^k_{11}\theta ^j_{12}{P_1(k,j)}\frac{d{(p^{S_1}_{S_1}X_{S_1}+p^{I_1}_{S_1}X_{I_1}+p^{R_1}_{S_1}X_{R_1})^k}}{dX_{I_1}} \nonumber \\&\qquad (p^{S_2}_{S_1}X_{S_2}+p^{I_2}_{S_1}X_{I_2}+p^{R_2}_{S_1}X_{R_2})^j\nonumber \\&\quad =\frac{N}{N_1}G_1{(\alpha \theta _{11},\beta \theta _{12})}p^{I_1}_{S_1}\theta _{11}, \end{aligned}$$

(73)

where $\alpha =p^{S_1}_{S_1}X_{S_1}+p^{I_1}_{S_1}X_{I_1}+p^{R_1}_{S_1}X_{R_1}$ and $\beta =p^{S_2}_{S_1}X_{S_2}+p^{I_2}_{S_1}X_{I_2}+p^{R_2}_{S_1}X_{R_2}$. As in the above analysis, we have

$$\begin{aligned} \sum \limits _{k,j} \theta ^k_{11}\theta ^j_{12}p_{S_1}^{I_1}\cdot {kP_1(k,j)} =\frac{N}{N_1}{G_1{(\theta _{11},\theta _{12})p_{S_1}^{I_1}\theta _{11}}}. \end{aligned}$$

(74)

From Eqs. (69), (73) and (74), we have

$$\begin{aligned}&g_{S_1I_1}{(X_{S_1},X_{I_1},X_{R_1},X_{S_2},X_{I_2},X_{R_2})}=\frac{\sum \nolimits _{k,j}\theta ^k_{11}\theta ^j_{12}{P_1(k,j)}\varDelta _1\varDelta _2 }{\sum \nolimits _{k,j} \theta ^k_{11}\theta ^j_{12}p_{S_1}^{I_1}\cdot {kP_1(k,j)}}\nonumber \\&\quad =\frac{G_1{((p^{S_1}_{S_1}X_{S_1}+p^{I_1}_{S_1}X_{I_1}+p^{R_1}_{S_1}X_{R_1})\theta _{11},(p^{S_2}_{S_1}X_{S_2}+p^{I_2}_{S_1}X_{I_2}+p^{R_2}_{S_1}X_{R_2})\theta _{12})}}{G_1{(\theta _{11},\theta _{12})}}.\nonumber \\ \end{aligned}$$

(75)