Sensitivity of the dynamics of the general Rosenzweig–MacArthur model to the mathematical form of the functional response: a bifurcation theory approach

Abstract

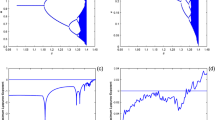
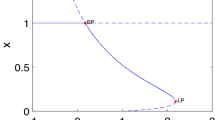
The equations in the Rosenzweig–MacArthur predator–prey model have been shown to be sensitive to the mathematical form used to model the predator response function even if the forms used have the same basic shape: zero at zero, monotone increasing, concave down, and saturating. Here, we revisit this model to help explain this sensitivity in the case of three response functions of Holling type II form: Monod, Ivlev, and Hyperbolic tangent. We consider both the local and global dynamics and determine the possible bifurcations with respect to variation of the carrying capacity of the prey, a measure of the enrichment of the environment. We give an analytic expression that determines the criticality of the Hopf bifurcation, and prove that although all three forms can give rise to supercritical Hopf bifurcations, only the Trigonometric form can also give rise to subcritical Hopf bifurcation and has a saddle node bifurcation of periodic orbits giving rise to two coexisting limit cycles, providing a counterexample to a conjecture of Kooji and Zegeling. We also revisit the ranking of the functional responses, according to their potential to destabilize the dynamics of the model and show that given data, not only the choice of the functional form, but the choice of the number and/or position of the data points can influence the dynamics predicted.