Abstract
In this paper, we study a discrete predator–prey system with modified Holling–Tanner functional response. We derive conditions of existence for flip bifurcations and Hopf bifurcations by using the center manifold theorem and bifurcation theory. Numerical simulations including bifurcation diagrams, maximum Lyapunov exponents, and phase portraits not only illustrate the correctness of theoretical analysis, but also exhibit complex dynamical behaviors and biological phenomena. This suggests that the small integral step size can stabilize the system into the locally stable coexistence. However, the large integral step size may destabilize the system producing far richer dynamics. This also implies that when the intrinsic growth rate of prey is high, the model has bifurcation structures somewhat similar to the classic logistic one.
Similar content being viewed by others
1 Introduction
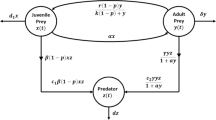
Predator–prey interactions have long been studied and continue to be one of the dominant themes in both biology and mathematical biology due to their universal existence and importance [1]. Recently, a predator–prey system with modified Holling–Tanner functional response was given in [2, 3] as follows:
where r, K, k, a, b, c, s, h are positive constants, and u and v represent the population densities of prey and predator, respectively. The prey grows logistically with carrying capacity K and intrinsic growth rate r in the absence of predator. The predator consumes the prey according to the functional response of Beddington–DeAngelis type \(kuv / (a + bu + cv)\) and grows logistically with intrinsic growth rate s, and cv measures the mutual interference between predators. The parameters k, a, b, and c are the consumption rate, the saturation constant, the saturation constant for an alternative prey, and the predator interference, respectively. The carrying capacity \(u / h\) of predator is proportional to the population size of the prey. The parameter h is the number of preys required to support one predator at equilibrium when v equals \(u / h\). The term \(v / u\) measures the loss in the predator population due to rarity of its favorite food.
Applying the following scaling to (1),
it becomes of the following form:
However, for a mathematical biology model, if the size of population is rarely small, or the population has no overlapping generation, or people study population changes within certain intervals of time, the discrete-time model would indeed be more suitable and realistic than the continuous-time model [4–12]. On the other hand, numerical solutions or approximate solutions of discrete-time models can be obtained more easily, and much work has shown that discrete-time prey–predator models can produce a much richer set of patterns than those observed in continuous-time models [13–18]. Thus, it is necessary to consider the corresponding discrete model of system (2). Using the forward Euler scheme to system (2), we therefore obtain the following discrete-time model:
where δ is the integral step size. In this paper, we mainly focus on the dynamical behavior of system (3) in the interior of the first quadrant of R2. More precisely, we discuss the stability of fixed points of system (3) and rigorously prove that the map (3) undergoes the flip bifurcation and Hopf bifurcation by using the center manifold theorem and bifurcation theory. Meanwhile, resent numerical simulations not only to illustrate our results of theoretical analysis, but also to explore complex dynamical behaviors.
The outline of this paper is as follows. In Sect. 2, we investigate in detail the existence and local stability of fixed points of model (3). In Sect. 3, we derive sufficient conditions for the existence of flip bifurcation and Hopf bifurcation. In Sect. 4, we present numerical simulations to check our results of theoretical analysis and exhibit some complex and new dynamical behaviors. In the end, we give a brief conclusion in Sect. 5.
2 Existence and stability of fixed points
From a biological point of view, system (3) must have positive values of u and v. We have the following result.
Theorem 2.1
Assume that \(\Omega = \{ (u,v)|u > 0,v > 0,r \delta u + \beta \delta v - (1 + r\delta) < 0\}\). Then Ω is an invariant set for system (3) if δ and s are enough small.
Proof
Suppose that \((u_{0},v_{0}) \in \Omega \). Then \((u_{1},v_{1}) > 0\) if δ is small enough, where
Let \(L = r\delta u_{1} + \beta \delta v_{1} - (1 + r\delta)\). Then
If δ is small enough, then it follows that
Since \(v_{0} < \frac{1 + r\delta }{\beta \delta } \), we have
If s is small enough, then we have
Thus \(H = ( s - \frac{hv_{0}}{u_{0}} ) - \frac{ru_{0}}{a + u_{0} + mv_{0}} < 0\).
Let \(L(u_{0}) = - r^{2}\delta^{2}u_{0}^{2} + r\delta (1 + r\delta)u _{0} + \delta (1 + r\delta)H\). Then \(L(u_{0}) = \delta (1 + r\delta)H < 0\).
Therefore, \(L < 0\) if δ is small enough. Then \((u_{1},v_{1}) \in \Omega \) if δ and s are small enough, that is, Ω is an invariant set for system (3).
It is clear that the fixed points of model (3) satisfy the following equations:
□
Lemma 2.1
For all parameter values, system (3) has two fixed points, the boundary fixed point \(A(1,0)\) and the unique positive fixed point \(B(u_{*},v_{*})\) defined by
Now, we perform the linear stability analysis of system (3) at each fixed point. The Jacobian matrix J of (3) evaluated at any point \((u,v)\) is given by
where
Moreover, the characteristic equation of \(J(u, v)\) can be written as
where \(p(u,v) = - ( a_{11} + a_{22} ) \), \(q(u,v) = a_{11}a _{22} - a_{12}a_{21}\).
Lemma 2.2
([11])
Let \(F(\lambda) = \lambda^{2} + P\lambda + Q\), where P and Q are constants. Suppose that \(F(1) > 0\) and \(\lambda_{1}\) and \(\lambda_{2}\) are two roots of \(F(\lambda) = 0\). Then
-
(i)
\(\vert \lambda_{1} \vert < 1\) and \(\vert \lambda_{2} \vert < 1\) if and only if \(F( - 1) > 0\) and \(Q < 1\);
-
(ii)
\(\vert \lambda_{1} \vert < 1\) and \(\vert \lambda_{2} \vert > 1\) (or \(\vert \lambda_{1} \vert > 1\) and \(\vert \lambda_{2} \vert < 1\)) if and only if \(F( - 1) < 0\);
-
(iii)
\(\vert \lambda_{1} \vert > 1\) and \(\vert \lambda_{2} \vert > 1\) if and only if \(F( - 1) > 0\) and \(Q > 1\);
-
(iv)
\(\lambda_{1} = - 1\) and \(\vert \lambda_{2} \vert \ne 1\) if and only if \(F( - 1) = 0\) and \(P \ne 0\), 2;
-
(v)
\(\lambda_{1}\) and \(\lambda_{2}\) are the conjugate complex roots and \(\vert \lambda_{1} \vert = \vert \lambda_{2} \vert = 1\) if and only if \(P^{2} - 4Q < 0\) and \(Q = 1\).
Suppose that \(\lambda_{1}\) and \(\lambda_{2}\) are two roots of (5), which are called eigenvalues of the fixed point \((u,v)\). The point \((u,v)\) is a sink if \(\vert \lambda_{1} \vert < 1\) and \(\vert \lambda_{2} \vert < 1\). A sink is locally asymptotic stable. The point \((u,v)\) is a source if \(\vert \lambda_{1} \vert > 1\) and \(\vert \lambda_{2} \vert > 1\). A source is locally unstable. The point \((u,v)\) is a saddle if \(\vert \lambda_{1} \vert > 1\) and \(\vert \lambda_{2} \vert < 1\) (or \(\vert \lambda_{1} \vert < 1\) and \(\vert \lambda _{2} \vert > 1\)), and \((u,v)\) is nonhyperbolic if either \(\vert \lambda_{1} \vert = 1\) or \(\vert \lambda_{2} \vert = 1\).
Theorem 2.2
The eigenvalues of the fixed point \(A(1,0)\) are \(\lambda_{1} = 1 - \delta r\) and \(\lambda_{2} = 1 + \delta s\).
-
(i)
\(A(1,0)\) is a saddle if \(0 < \delta < \frac{2}{r}\);
-
(ii)
\(A(1,0)\) is a source if \(\delta > \frac{2}{r}\);
-
(iii)
\(A(1,0)\) is nonhyperbolic if \(\delta = \frac{2}{r}\).
Let
It can be easily seen that one of the eigenvalues of \(A(1,0)\) is −1 and the other is neither 1 nor −1 when all parameters of system (3) locate in \(F_{A}\). Then the center manifold of system (3) at \(A(1,0)\) is \(v = 0\) when parameters are in \(F_{A}\). The map (3) restricted to this center manifold is the classic logistic model \(u \to ru(1 - u)\). It is well known that the predator population becomes extinct and the prey undergoes the period-doubling bifurcation to chaos by choosing the bifurcation parameter r. Therefore, the fixed point \(A(1,0)\) can undergo flip bifurcation when parameters vary in a small neighborhood of \(F_{A}\).
The characteristic equation of the Jacobian matrix \(J(u,v)\) evaluated at the unique positive fixed point \(B(u_{*},v_{*})\) can be written as
where
Let
Then
Theorem 2.3
-
(i)
\(B(u_{*},v_{*})\) is a sink if one of the following conditions holds:
-
(i.1)
\(- 2\sqrt{Hs} < G < 0\) and \(0 < \delta < - \frac{G}{Hs}\);
-
(i.2)
\(G < - 2\sqrt{Hs}\) and \(0 < \delta < \frac{ - G - \sqrt{G^{2} - 4Hs}}{Hs}\);
-
(i.1)
-
(ii)
\(B(u_{*},v_{*})\) is a source if one of the following conditions holds:
-
(ii.1)
\(- 2\sqrt{Hs} < G < 0\) and \(\delta > - \frac{G}{Hs}\);
-
(ii.2)
\(G < - 2\sqrt{Hs}\) and \(\delta > \frac{ - G + \sqrt{G^{2} - 4Hs}}{Hs}\);
-
(ii.3)
\(G \ge 0\);
-
(ii.1)
-
(iii)
\(B(u_{*},v_{*})\) is a saddle if the following conditions hold:
$$ G < - 2\sqrt{Hs} \quad \textit{and}\quad \frac{ - G - \sqrt{G^{2} - 4Hs}}{Hs} < \delta < \frac{ - G + \sqrt{G ^{2} - 4Hs}}{Hs}; $$ -
(iv)
\(B(u_{*},v_{*})\) is nonhyperbolic if one of the following conditions holds:
-
(iv.1)
\(G < - 2\sqrt{Hs}\) and \(\delta = \frac{ - G \pm \sqrt{G^{2} - 4Hs}}{Hs}\) and \(\delta \ne - \frac{2}{G}, - \frac{4}{G}\);
-
(iv.2)
\(- 2\sqrt{Hs} < G < 0\) and \(\delta = - \frac{G}{Hs}\).
-
(iv.1)
From the Jury criterion and the preceding analysis it can be easily seen that one of the eigenvalues of the unique positive fixed point \(B(u_{*},v_{*})\) is −1 and the other is neither 1 nor −1 if (iv.1) of Theorem 2.3 holds. When (iv.2) of Theorem 2.3 is true, the eigenvalues of the unique positive fixed point \(B(u_{*},v_{*})\) are a pair of conjugate complex numbers with modulus one.
Let
and
Then the unique positive fixed point \(B(u_{*},v_{*})\) may undergo the flip bifurcation when parameters vary in a small neighborhood of \(F_{B1}\) or \(F_{B2}\).
Let
Then the unique positive fixed point \(B(u_{*},v_{*})\) may undergo the Hopf bifurcation when the parameters vary in a small neighborhood of \(H_{B}\).
3 Flip bifurcation and Hopf bifurcation
Based on the previous analysis, in this section, we mainly focus on the flip bifurcation and Hopf bifurcation of the unique positive fixed point \(B(u_{*},v_{*})\). Then, we choose the integral step size δ as a bifurcation parameter for investigating the Flip bifurcation and Hopf bifurcation of \(B(u_{*},v_{*})\) by using the center manifold theorem and bifurcation theory.
We first discuss the flip bifurcation of system (3) at \(B(u_{*},v_{*})\) when the parameters vary in a small neighborhood of \(F_{B1}\). Similar arguments can be applied to the other case of \(F_{B2}\).
Taking the parameters \((\delta ,\beta ,a,h,m,r,s)\) arbitrarily from \(F_{B1}\), we consider system (3) with \(( \delta, \beta, a, h, m, r, s) \in F_{B1}\) described by
Then the map (7) has a unique positive fixed point \(B(u_{*},v_{*})\) with eigenvalues \(\lambda_{1} = - 1\) and \(\lambda_{2} = 3 + G\delta_{1}\) with \(\vert \lambda_{2} \vert \ne 1\) by Theorem 2.3.
Choosing \(\delta_{*}\) as a bifurcation parameter, we consider a perturbation of (7) as follows:
where \(\vert \delta_{*} \vert \ll 1\) is a small perturbation parameter.
Assume that \(U = u - u_{*}\),\(V = v - v_{*}\). Then we transform the fixed point \(B(u_{*},v_{*})\) of the map (8) into the origin. For convenience, we rewrite U and V as u and v, respectively. Then we have
where
and \(\delta = \delta_{1}\).
We construct the invertible matrix
and apply the translation \((u, v)^{T} = T(\tilde{u}, \tilde{v})^{T}\). Then the map (9) can be changed into
where
and \(u = a_{12}\tilde{u} + a_{12}\tilde{v}\), \(v = - (1 + a_{11}) \tilde{u} + (\lambda_{2} - a_{11})\tilde{v}\).
Next, we apply the center manifold theorem [19] to determine the dynamics of the fixed point \((\tilde{u},\tilde{v}) = (0,0)\) at \(\delta_{*} = 0\). Then there exists a center manifold of the map (11), which can be represented as follows:
Assume that
where \(O(( \vert \tilde{u} \vert + \vert \delta_{*} \vert )^{3})\) is a function of order at least three in their variables \((\tilde{u}, \delta_{*})\).
Then, the center manifold must satisfy
Substituting (11) and (12) into (13) and comparing the coefficients of (12), we obtain
Therefore, the map (10) restricted to the center manifold \(W^{c}(0,0)\) is given by
where
Let \(\alpha_{1} = ( \frac{\partial^{2}F}{\partial \tilde{u}\partial \delta_{*}} + \frac{1}{2}\frac{\partial F}{\partial \delta_{*}}\frac{\partial^{2}F}{\partial \tilde{u}^{2}} ) \vert _{(0,0)} = h_{2}\) and \(\alpha_{2} = ( \frac{1}{6}\frac{ \partial^{3}F}{\partial \tilde{u}^{3}} + ( \frac{1}{2}\frac{ \partial^{2}F}{\partial \tilde{u}^{2}} ) ^{2} ) \vert _{(0,0)} = h_{5} + h_{1}^{2}\).
Then we have the following results.
Theorem 3.1
If \(\alpha_{1} \ne 0\) and \(\alpha_{2} \ne 0\), then the map (3) undergoes a flip bifurcation at the unique positive fixed point \(B(u_{*},v_{*})\) when the parameter δ varies in a small neighborhood of \(F_{B1}\). Moreover, if \(\alpha_{2} > 0\) (resp., \(\alpha_{2} < 0\)), then the period-2 orbits that bifurcate from \(B(u_{*},v_{*})\) are stable (resp., unstable).
Next, we discuss the Hopf bifurcation of \(B(u_{*},v_{*})\) when the parameters \((\delta ,\beta ,a,h,m,r,s)\) vary in a small neighborhood of \(H_{B}\). Taking the parameters \((\delta ,\beta ,a,h,m,r,s)\) arbitrary from \(H_{B}\), we consider system (3) with \(( \delta, \beta, a, h, m, r, s) \in H_{B}\) represented by
Then the map (15) has a unique positive fixed point \(B(u_{*},v_{*})\).
Then we choose \(\bar{\delta }_{*}\) as a bifurcation parameter and consider a perturbation of (15) as follows:
where \(\vert \bar{\delta }_{*} \vert \ll 1\) is a small perturbation parameter.
Assume that \(U = u - u_{*}\) and \(V = v - v_{*}\). Then we transform the fixed point \(B(u_{*},v_{*})\) of the map (16) into the origin. For convenience, we rewrite U and V as u and v, respectively. Then we have
where \(a_{11}\), \(a_{12}\), \(a_{13}\), \(a_{14}\), \(a_{15}\), \(a_{16}\), \(a_{17}\), \(a_{18}\), \(a_{19}\), \(a_{21}\), \(a_{22}\), \(a_{23}\), \(a_{24}\), \(a_{25}\), \(a_{26}\), \(a_{27}\), \(a_{28}\), \(a_{29}\) are given in (10) by substituting δ for \(\delta_{2} + \bar{\delta }_{*}\).
Then the characteristic equation associated with the linearization of model (17) at \((u,v) = (0,0)\) is given by
where
Since \(( \delta, \beta, a, h, m, r, s) \in H_{B}\), there exists a pair of complex conjugate eigenvalues λ, λ̄ with modulus 1 at \((u,v) = (0,0)\) by Theorem 2.3, where
Then we have \(\vert \lambda \vert = \sqrt{q(\bar{\delta }_{*})}\), \(l = \frac{\mathrm{d} \vert \lambda \vert }{\mathrm{d}\bar{ \delta }_{*}} \vert _{\bar{\delta }_{*} = 0} = - \frac{G}{2} > 0\).
In addition, we require that when \(\bar{\delta }_{*} = 0\), \(\lambda ^{n}\), \(\bar{\lambda }^{n} \ne 1\), \(n = 1,2,3,4\), which is equivalent to \(p(0) \ne - 2,0,1,2\). Note that \(( \delta, \beta, a, h, m, r, s) \in H_{B}\), so \(p(0) \ne - 2,2\). Thus we only need to satisfy \(p(0) \ne 0,1\), which leads to
In the following, we investigate the normal form of the map (17) at \(\bar{\delta }_{*} = 0\). Put \(\mu = 1 + \frac{G\delta_{2}}{2}\) and \(\omega = \frac{\delta_{2}}{2}\sqrt{4Hs - G^{2}}\). Using the translation
the model (17) becomes
where
and \(u = a_{12}\tilde{u}\), \(v = (\mu - a_{11})\tilde{u} - \omega \tilde{v}\).
Let
Then the map (20) can undergo the Hopf bifurcation when the following discriminatory quantity is not zero:
where
From the preceding analysis and theorem in [20] we have the following result.
Theorem 3.2
If condition (19) holds and \(\gamma \ne 0\), then the map (3) undergoes a Hopf bifurcation at the unique positive fixed point \(B(u_{*},v_{*})\) when the parameter δ varies in a small neighborhood of \(H_{B}\). Moreover, if \(\gamma < 0\) (resp., \(\gamma > 0\)), then an attracting (resp., repelling) invariant closed curve bifurcates from the fixed point for \(\delta > \delta_{2}\) (resp., \(\delta > \delta_{2}\)).
4 Numerical simulations
In this section, we present the bifurcation diagrams, phase portraits, and maximum Lyapunov exponents for system (3) to illustrate our theoretical analysis and show the complex dynamical behaviors by using numerical simulations. The bifurcation parameters are considered for the following three cases:
-
(i)
Varying δ in the range \(1 \le \delta \le 1.4\) and fixing \(r = 2\), \(\beta = 0.5\), \(a = 0.2\), \(m = 0.2\), \(s = 0.6\), \(h = 2\).
-
(ii)
Varying δ in the range \(2 \le \delta \le 3\) and fixing \(r = 1\), \(\beta = 0.5\), \(a = 0.2\), \(m = 0.2\), \(s = 0.6\), \(h = 2\).
-
(iii)
Varying r in the range \(2 \le r \le 2.99\) and fixing \(\delta = 1\), \(\beta = 0.5\), \(a = 0.2\), \(m = 0.2\), \(s = 0.6\), \(h = 2\).
Case (i). On the basis of Lemma 2.1, we know that the map (3) has one unique positive fixed point. By calculation the flip bifurcation of system (3) emerges from the fixed point \((u_{*},v_{*}) = (0.9410621, 0.28231863)\) at \(\delta = 1.156171665\) with \(\alpha_{1} = - 1.729846926\), \(\alpha_{2} = 0.7258371266\), and \(( \delta, \beta, a, h, m, r, s) \in F_{B_{1}}\), which illustrates Theorem 3.1. From Figs. 1(a), (b) we observe that the fixed point \(B(u_{*},v_{*})\) is stable for \(0 < \delta < 1.156171665\) and loses its stability at the flip bifurcation parameter value \(\delta = 1.156171665\). Also, there is a cascade of period −2, 4, 6, 8, 16 orbits emerging. The maximum Lyapunov exponents corresponding to Figs. 1(a), (b) are shown in Fig. 1(c). The phase portraits associated with Figs. 1(a), (b) are displayed in Fig. 2. It can be seen from Fig. 2 that there are chaotic sets when \(\delta = [1.399, 1.4]\). Further, Fig. 1(d) shows that if \(\delta = [1.399, 1.4]\), then the maximum Lyapunov exponents are larger than 0, which confirms the existence of chaotic sets.
(a) Flip bifurcation diagram of map (3) in the \((\delta,u)\) plane with initial value \((0.9510621, 0.29231863)\). (b) Flip bifurcation diagram of map (3) in the \((\delta,v)\) plane. (c) Maximum Lyapunov exponents corresponding to (a) and (b). (d) Local amplification of (c) for \(\delta \in [1.39,1.4]\)
Phase portraits for various values of δ corresponding to Figs. 1(a), (b)
Case (ii). According to Lemma 2.1, we know that the map (3) has one unique positive fixed point. After calculation, the Hopf bifurcation emerges from the fixed point \((u_{*},v_{*}) = (0.8833954475, 0.2650186342)\) at \(\delta = 2.560064295\) with \(\gamma = - 0.503038999\) and \(( \delta, \beta, a, h, m, r, s) \in H_{B}\). This shows the correctness of Theorem 3.2. From Figs. 3(a), (b) we observe that the fixed point \(B(u_{*},v_{*})\) is stable for \(0 < \delta < 2.560064295\) and loses its stability at the Hopf bifurcation parameter value \(\delta = 2.560064295\). Then an attracting invariant cycle bifurcates from the fixed point since \(\gamma = - 0.503038999 < 0\) by Theorem 3.2. The maximum Lyapunov exponents corresponding to Figs. 3(a), (b) are calculated and shown in Fig. 3(c). Figure 3(d) is a local amplifications for \(\delta \in [2.75,2.9]\). It can be easily seen from Figs. 3(c), (d) that the maximum Lyapunov exponents are nonnegative for the parameter \(\delta \in [2.87,2.98]\), which implies the existence of chaos. Also, we observe from Fig. 4 that there are period-10, period-20, period-30, and period-73 orbits and attracting chaotic sets.
(a) Hopf bifurcation diagram of map (3) in the \((\delta,u)\) plane with initial value \((0.8933954475, 0.2750186342)\). (b) Hopf bifurcation diagram of map (3) in the \((\delta,v)\) plane. (c) Maximum Lyapunov exponents corresponding to Figs. 3(a), (b). (d) Local amplification diagram of (a) for \(\delta \in [2.75,2.9]\)
Phase portraits for various values of δ corresponding to Figs. 3(a), (c)
Case (iii). The bifurcation diagrams of system (3) in the \((r,u)\) and \((r,v)\) planes for \(2 \le r \le 2.86\) are disposed in Figs. 5(a), (b). The maximum Lyapunov exponent corresponding to Fig. 5(a) is computed and plotted in Fig. 5(c), and the local amplification diagram corresponding to (c) for \(\delta \in [2.8,2.6]\) is shown in Fig. 5(d). From Figs. 5(a), (b) we can see that there is a cascade of period-doubling emerging. From Fig. 5(d) we see that the maximum Lyapunov exponents corresponding to \(r = 2.85\) are greater than 0, which implies the existence of chaotic sets.
5 Conclusion
In this paper, we have mainly considered the complex behaviors of a predator–prey system with modified Holling–Tanner functional response in R2. By using the center manifold theorem and bifurcation theory we prove that the unique positive fixed point of system (3) can undergo flip bifurcation and Hopf bifurcation. Most importantly, when the integral step size δ is chosen as a bifurcation parameter, numerical simulations show that system (3) shows very rich nonlinear dynamical behaviors including stable coexistence, period-doubling bifurcation leading to chaos, attracting invariant circles, and even stranger chaotic attractors. According to Figs. 1 and 2, we can observe that the small integral step size δ can stabilize the dynamical system (3), but the large integral step size may destabilize the system producing more complex dynamical behaviors. Then it reminds of us that the integral step size may play a key role in exploring the dynamical behaviors. In addition, from Fig. 5 we can see that the appropriately intrinsic growth rate r of prey can stabilize the dynamical system (3). However, the high intrinsic growth rate may destabilize system (3). From a biological point of view, when the prey population is submitted to the high intrinsic growth rate, the number of preys are abundant, and the prey consumption by predator may have a marginal effect on the dynamics of prey. Hence, the dynamical behavior of prey mainly depends on the population itself. Then, system (3) becomes the classic logistic model and exhibits the period-doubling leading to chaos.
References
Berryman, A.A.: The origins and evolution of predator–prey theory. Ecology 73, 1530–1535 (1992)
Shi, H., Li, W., Lin, G.: Positive steady states of a diffusive predator–prey system with modified Holling–Tanner functional response. Nonlinear Anal., Real World Appl. 11, 3711–3721 (2010)
Yang, W.: Global asymptotical stability and persistent property for a diffusive predator–prey system with modified Leslie–Gower functional response. Nonlinear Anal., Real World Appl. 14, 1323–1330 (2013)
Zhang, L., Zhang, C., Zhao, M.: Dynamic complexities in a discrete predator–prey system with lower critical point for the prey. Math. Comput. Simul. 105, 119–131 (2014)
Choo, S.: Global stability in n-dimensional discrete Lotka–Volterra predator–prey models. Adv. Differ. Equ. 2014, 11 (2014)
Cao, H., Zhou, Y., Ma, Z.: Bifurcation analysis of a discrete SIS model with bilinear incidence depending on new infection. Math. Biosci. Eng. 10, 1399–1417 (2013)
Ren, J., Yu, L., Siegmund, S.: Bifurcations and chaos in a discrete predator–prey model with Crowley–Martin functional response. Nonlinear Dyn. 90, 19–41 (2017)
Huang, T., Zhang, H., Yang, H., Wang, N., Zhang, F.: Complex patterns in a space- and time-discrete predator-prey model with Beddington-DeAngelis functional response. Commun. Nonlinear Sci. 43, 182–199 (2017)
Huang, J., Liu, S., Ruan, S., Xiao, D.: Bifurcations in a discrete predator–prey model with nonmonotonic functional response. J. Math. Anal. Appl. 464, 201–230 (2018)
Din, Q.: Complexity and chaos control in a discrete-time prey–predator model. Commun. Nonlinear Sci. 49, 113–134 (2017)
Cheng, L., Cao, H.: Bifurcation analysis of a discrete-time ratio-dependent predator–prey model with Allee effect. Commun. Nonlinear Sci. Numer. Simul. 38, 288–302 (2016)
Liu, X., Xiao, D.: Complex dynamic behaviors of a discrete-time predator–prey system. Chaos Solitons Fractals 32, 80–94 (2007)
Cui, Q., Zhang, Q., Qiu, Z., Hu, Z.: Complex dynamics of a discrete-time predator-prey system with Holling IV functional response. Chaos Solitons Fractals 87, 158–171 (2016)
Jana, D.: Chaotic dynamics of a discrete predator–prey system with prey refuge. Appl. Math. Comput. 224, 848–865 (2013)
Asheghi, R.: Bifurcations and dynamics of a discrete predator–prey system. J. Biol. Dyn. 8, 161–186 (2014)
He, Z., Lai, X.: Bifurcation and chaotic behavior of a discrete-time predator–prey system. Nonlinear Anal., Real World Appl. 12, 403–417 (2011)
Liu, X., Liu, Y., Li, Q.: Multiple bifurcations and chaos in a discrete prey–predator system with generalized Holling III functional response. Discrete Dyn. Nat. Soc. 2015, 1–10 (2015)
Zhuo, X., Zhang, F.: Stability for a new discrete ratio-dependent predator–prey system. Qual. Theory Dyn. Syst. 17, 189–202 (2018)
Carr, J.: Application of Center Manifold Theorem. Springer, New York (1981)
Robinson, C.: Dynamical Systems, Stability, Symbolic Dynamics and Chaos, 2nd edn. CRC Press, Boca Raton (1999)
Funding
This work was supported by the National Natural Science Foundation of China (no. 11461058) and by Sichuan Minzu College (nos. XYZB17001 and sfkc201701).
Author information
Authors and Affiliations
Contributions
JZ is responsible for the model formulation and study planning. JZ and YY have done the calculation, the proof, and the simulation. Both authors have read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
Both authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, J., Yan, Y. Stability and bifurcation analysis of a discrete predator–prey system with modified Holling–Tanner functional response. Adv Differ Equ 2018, 402 (2018). https://doi.org/10.1186/s13662-018-1819-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1819-0