On the use of a spacetime modeling for heat equation applied to self-heating computation with comparison to experimental results

Abstract

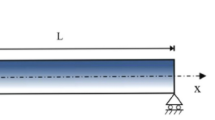
Self-heating phenomenonrepresents thermal evolution in materials resulting from mechanical loading. It is presentlyinvestigated during fatigue tests at 20 kHz. The aim of this article is to compare the variation of temperature, in the range 20 to 80 ^∘C, of a material body due to self-heating computed from an innovative point of view: requiring a covariant formulation of the thermomechanical behavior, we propose a spacetime approach for heat conduction and heat equation based on spacetime thermodynamics. In this article, we prove the feasibility to use such a spacetime framework to solve thermal problems. Thus computational methods performed with FEniCS platform, using finite element method, lead to a numerical approach for investigating self-heating. The integral form of the spacetime problem with the adapted boundary conditions directly usable are provided for heat conduction problem. The identification process of the parameters obtained from the experimental data of fatigue tests is also particularly studied to obtain the best accuracy and reliability of the numerical simulations, presently applied to metallic material (C65 steel) and 1D beam (60 mm length). Moreover, by use of optimization techniques, some numerical values for these input parameters are obtained, especially the characteristic time (in the range 40 to 130 s) and the heat source related to thermomechanical phenomena (intrinsic dissipation in the range 0.3 to 12 ^∘C ⋅ s^− 1). They have been successfully used to obtain spacetime temperature distributions in comparison to experimental measurements.

Appendix: Covariant derivative and rate of deformation

The covariant derivative of respectively, a scalar density $\mathcal {S}$ denoted $\nabla _{\lambda } \mathcal {S}$, and a second-rank tensor density $\boldsymbol {\mathcal {T}}$ denoted $\nabla _{\lambda } \mathcal {T}^{\mu \nu }$ is given by:

$$ \begin{array}{@{}rcl@{}} \nabla_{\lambda} \mathcal{S}&=&\frac{\partial \mathcal{S}}{\partial x^{\lambda}} -W{\Gamma}^{\kappa}_{\kappa \lambda}\mathcal{S} \end{array} $$

(45a)

$$ \begin{array}{@{}rcl@{}} \nabla_{\lambda} \mathcal{T}^{\mu\nu} &=& \frac{\partial \mathcal{T}^{\mu\nu}}{\partial x^{\lambda}} + {\Gamma}^{\mu}_{\kappa \lambda}\mathcal{T}^{\kappa\nu} +{\Gamma}^{\nu}_{\kappa \lambda}\mathcal{T}^{\mu\kappa} -W{\Gamma}^{\kappa}_{\kappa \lambda}\mathcal{T}^{\mu\nu} \end{array} $$

(45b)

where W is the weight of the tensor density (W = 0 for temperature field) and ${\Gamma }^{\alpha }_{\beta \gamma }$ are the coefficients of the metric connection identified with Christoffel’s symbols given by:

$$ \begin{array}{@{}rcl@{}} {\Gamma}^{\mu}_{\kappa \lambda}=\frac{1}{2}g^{\mu \alpha} \left( \frac{\partial g_{\alpha \kappa}}{\partial x^{\lambda}} + \frac{\partial g_{\alpha \lambda}}{\partial x^{\kappa}} - \frac{\partial g_{\kappa \lambda}}{\partial x^{\alpha}} \right) ={\Gamma}^{\mu}_{\lambda \kappa} \end{array} $$

(46)

Note that in this case ∇_λg^μν = 0 and that for every point of the spacetime domain, for an inertial observer, all Christoffel’s symbols vanish.

It is important to stress out that, as a consequence of the absence of gravitation, the Riemann curvature tensor of this spacetime domain is equal to zero, although the Christoffel’s symbols may not. In other words, the considered spacetime is Euclidean, thus flat, whether the observer is inertial ($\Rightarrow {\Gamma }^{\mu }_{\kappa \lambda }=0$), or not ($\Rightarrow {\Gamma }^{\mu }_{\kappa \lambda }\neq 0$) [19].

A covariant transport corresponding to the projection of the covariant derivative on the proper time u^λ∇_λ(.) is also defined. In an inertial coordinate system z^μ, in which the Christoffel’s symbols vanish, the covariant transport may be rewritten as:

$$ \begin{array}{@{}rcl@{}} u^{\lambda } \nabla_{\lambda} (.)=\frac{d(.)}{ds}= u^{\lambda} \frac{\partial }{\partial z^{\lambda}}(.)=u^{4} \frac{\partial }{\partial z^{4}}(.)+u^{i} \frac{\partial }{\partial z^{i}}(.) \end{array} $$

(47)

We further introduce the four-tensor rate of deformation d, a generalization of the symmetric part of the velocity gradient:

$$ \begin{array}{@{}rcl@{}} d^{\mu}_{\phantom{a}\nu}&=&\frac{1}{2}(\nabla_{\nu} u^{\mu}+\nabla_{\mu} u^{\nu}) \end{array} $$

(48)