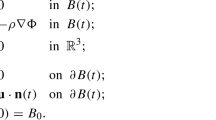Abstract
Without any symmetry assumptions on the initial data we construct global-in-time unique solutions to the vacuum free boundary three-dimensional isentropic compressible Euler equations when the adiabatic exponent \(\gamma \) lies in the interval \((1,\frac{5}{3}]\). Our initial data lie sufficiently close to the expanding compactly supported affine motions recently constructed by Sideris and they satisfy the physical vacuum boundary condition.
Similar content being viewed by others
Notes
Affine motions in the absence of free boundaries have been used before to understand qualitative behavior of solutions in fluid mechanics, for instance see Majda [32].
In the absence of free boundaries, gas expansion also plays an important role in the global results in [12, 39]. The full nonlinear analysis of stabilizing effects of the fluid expansion in the context of general relativistic cosmological models was initiated by Rodnianski and Speck [36] and extended further in [11, 14, 27, 35, 41].
One could introduce a more geometric language so that \(\text {curl}_{\Lambda }\) and \(\Lambda \nabla \) are “natural” operators with respect to a given metric structure, but for the sake of conciseness we choose not to.
References
Chen, G.-Q.: Remarks on R. J. DiPerna’s paper: convergence of the viscosity method for isentropic gas dynamics [Comm. Math. Phys. 91 (1983), no. 1, 1–30; MR0719807 (85i:35118)]. Proc. Am. Math. Soc. 125(10), 2981–2986 (1997)
Chiodaroli, E., De Lellis, C., Kreml, O.: Global ill-posedness of the isentropic system of gas dynamics. Commun. Pure Appl. Math. 68(7), 1157–1190 (2015)
Christodoulou, D.: The Formation of Shocks in 3-Dimensional Fluids. EMS Monographs in Mathematics. EMS Publishing House, Zürich (2007)
Christodoulou, D., Miao, S.: Compressible Flow and Euler’s Equations, Surveys in Modern Mathematics, vol. 9. International Press, Vienna (2014)
Coutand, D., Shkoller, S.: Well-posedness in smooth function spaces for the moving-boundary 1-D compressible Euler equations in physical vacuum. Commun. Pure Appl. Math. 64(3), 328–366 (2011)
Coutand, D., Shkoller, S.: Well-posedness in smooth function spaces for the moving boundary three-dimensional compressible Euler equations in physical vacuum. Arch. Ration. Mech. Anal. 206(2), 515–616 (2012)
Dacorogna, B., Moser, J.: On a partial differential equation involving the Jacobian determinant. Ann. Inst. H. Poincaré Anal. Non Linéaire 7(1), 1–26 (1990)
Dafermos, C.: Hyperbolic Conservation Laws in Continuum Physics. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 325, 2nd edn. Springer, Berlin (2005)
DiPerna, R.J.: Convergence of the viscosity method for isentropic gas dynamics. Commun. Math. Phys. 91, 1–30 (1983)
Eggers, J., Fontelos, A.M.: The role of self-similarity in singularities of partial differential equations. Nonlinearity 22, R1–R44 (2009)
Friedrich, H.: Sharp asymptotics for Einstein-\(\lambda \)-dust flows. Commun. Math. Phys. 350, 803–844 (2017)
Grassin, M.: Global smooth solutions to Euler equations for a perfect gas. Indiana Univ. Math. J. 47, 1397–1432 (1998)
Hadžić, M., Jang, J.: Nonlinear stability of expanding star solutions in the radially-symmetric mass-critical Euler-Poisson system. Commun. Pure Appl. Math. 71(5), 827–891 (2018)
Hadžić, M., Speck, J.: The global future stability of the FLRW solutions to the Dust-Einstein system with a positive cosmological constant. J. Hyp. Differ. Equ. 12(1), 87–188 (2015)
Huang, H., Marcati, P., Pan, R.: Convergence to the Barenblatt solution for the compressible Euler equations with damping and vacuum. Arch. Ration. Mech. Anal. 176, 1–24 (2005)
Jang, J., Masmoudi, N.: Well-posedness for compressible Euler equations with physical vacuum singularity. Commun. Pure Appl. Math. 62, 1327–1385 (2009)
Jang, J., Masmoudi, N.: Vacuum in gas and fluid dynamics. In: Proceedings of the IMA Summer School on Nonlinear Conservation Laws and Applications, pp. 315–329. Springer (2011)
Jang, J., Masmoudi, N.: Well and ill-posedness for compressible Euler equations with vacuum. J. Math. Phys. 53(11), 115625 (2012)
Jang, J., Masmoudi, N.: Well-posedness of compressible Euler equations in a physical vacuum. Commun. Pure Appl. Math. 68(1), 61–111 (2015)
Kufner, A., Malgranda, L., Persson, L.-E.: The Hardy Inequality. Vydavatelský Servis, Plzen (2007)
Lindblad, H.: Well posedness for the motion of a compressible liquid with free surface boundary. Commun. Math. Phys. 260, 319–392 (2005)
Lions, P.L., Perthame, B., Souganidis, P.E.: Existence and stability of entropy solutions for the hyperbolic systems of isentropic gas dynamics in Eulerian and Lagrangian coordinates. Commun. Pure Appl. Math. 49(6), 599–638 (1996)
Liu, T.-P.: Compressible flow with damping and vacuum. Jpn. J. Appl. Math. 13, 25–32 (1996)
Liu, T.-P., Smoller, J.: On the vacuum state for isentropic gas dynamics equations. Adv. Math. 1, 345–359 (1980)
Liu, T.-P., Yang, T.: Compressible Euler equations with vacuum. J. Differ. Equ. 140, 223–237 (1997)
Liu, T.-P., Yang, T.: Compressible flow with vacuum and physical singularity. Methods Appl. Anal. 7, 495–509 (2000)
Lübbe, C., Valiente-Kroon, J.A.: A conformal approach for the analysis of the nonlinear stability of pure radiation cosmologies. Ann. Phys. 328, 1–25 (2013)
Luk, J., Speck, J.: Shock formation in solutions to the \(2D\) compressible Euler equations in the presence of non-zero vorticity. Invent. Math. (to appear). arXiv:1610.00737
Luo, T., Xin, Z., Zeng, H.: Well-posedness for the motion of physical vacuum of the three-dimensional compressible Euler equations with or without self-gravitation. Arch. Ration. Mech. Anal. 213(3), 763–831 (2014)
Luo, T., Zeng, H.: Global existence of smooth solutions and convergence to barenblatt solutions for the physical vacuum free boundary problem of compressible euler equations with damping. Commun. Pure Appl. Math. 69(7), 1354–1396 (2016)
Majda, A.: Compressible Fluid Flow and Systems of Conservation Laws in Several Space Variables, Volume 53 of Applied Mathematical Sciences. Springer, New York (1984)
Majda, A.: Vorticity and the mathematical theory of incompressible fluid flow. Commun. Pure Appl. Math. 39(S, suppl.), S187–S220 (1986)
Makino, T., Ukai, S., Kawashima, S.: Sur la solution à support compact de l’équations d’Euler compressible. Jpn. J. Appl. Math. 3, 249–257 (1986)
Merle, F., Raphaël, P., Szeftel, J.: Stable self similar blow up dynamics for \(L^2\)-supercritical NLS equations. Geom. Funct. Anal. 20(4), 1028–1071 (2010)
Oliynyk, T.: Future stability of the FLRW fluid solutions in the presence of a positive cosmological constant. Commun. Math. Phys. 346, 293–312 (2016)
Rodnianski, I., Speck, J.: The nonlinear future stability of the FLRW family of solutions to the irrotational Euler–Einstein system with a positive cosmological constant. J. Eur. Math. Soc. 15(6), 2369–2462 (2013)
Rozanova, O.: Solutions with Linear Profile of Velocity to the Euler Equations in Several Dimensions. Hyperbolic Problems: Theory, Numerics, Applications, pp. 861–870. Springer, Berlin (2003)
Shkoller, S., Sideris, T.C.: Global existence of near-affine solutions to the compressible Euler equations. Preprint arXiv:1710.08368
Serre, D.: Solutions classiques globales des équations d’Euler pour un fluide parfait compressible. Ann. l’Inst. Fourier 47, 139–153 (1997)
Serre, D.: Expansion of a compressible gas in vacuum. Bull. Inst. Math. Acad. Sin. Taiwan 10, 695–716 (2015)
Speck, J.: The nonlinear future stability of the FLRW family of solutions to the Euler–Einstein system with a positive cosmological constant. Sel. Math. 18(3), 633–715 (2012)
Sideris, T.C.: Formation of singularities in three-dimensional compressible fluids. Commun. Math. Phys. 101(4), 475–485 (1985)
Sideris, T.C.: Spreading of the free boundary of an ideal fluid in a vacuum. J. Differ. Equ. 257(1), 1–14 (2014)
Sideris, T.C.: Global existence and asymptotic behavior of affine motion of 3D ideal fluids surrounded by vacuum. Arch. Ration. Mech. Anal. 225(1), 141–176 (2017)
Acknowledgements
The authors express their gratitude to P. Raphaël for fruitful discussions and for pointing out connections to the treatment of self-similar singular behavior for nonlinear Schrödinger equations. They also thank C. Dafermos for his feedback and pointing out important references. JJ is supported in part by NSF Grants DMS-1608492 and DMS-1608494 and a von Neumann fellowship of the Institute for Advanced Study through the NSF grant DMS-1128155. MH acknowledges the support of the EPSRC Grant EP/N016777/1.
Author information
Authors and Affiliations
Corresponding author
Appendices
A Asymptotic-in-\(\tau \) behavior of affine solutions
In this section we collect some of the basic properties of affine motions that are used at many places in our estimates. Their proofs are rather straightforward and follow directly from the description of the asymptotic behavior of the solutions of (2.18) from [44].
We remind the reader that for any \(M\in {\mathbb {M}}^{3\times 3}\) we denote by \(\Vert M\Vert \) the Hilbert–Schmidt norm of the matrix M.
Lemma A.1
(Asymptotic behavior of A, \(\Gamma ^*= O^{-1} O_\tau \), and \(\Lambda = O^{-1} O^{-\top }\)) For any \(\gamma \in (1,\frac{5}{3}]\) and any pair of initial conditions \((A(0),\dot{A}(0))\in {\mathrm{GL}}^+(3)\times {\mathbb {M}}^{3\times 3}\) there exist matrices \(A_0,A_1,M(t)\) such that the unique solution A(t) to the Cauchy problem
can be written in the form
where \(A_0,A_1\) are both time-independent and M(t) satisfies the bounds
Moreover
where
Furthermore there exists a constant \(C>0\) such that
where \(d_i\), \(i=1,2,3\), are the eigenvalues of the matrix \(\Lambda \) and \(P\in \text {SO}(3)\) satisfies \(\Lambda = P^\top Q P,\) \(Q = {\mathrm{diag}}(d_i)\).
Proof
Asymptotic behavior (A.3)–(A.4) and bound (A.5) are a consequence of Theorem 3 and Lemma 6 from [44].
Proof of (A.6) Since \( O = \frac{A}{\mu }\) we have
where we used the formula
Therefore, from (A.3) and (A.4) it is easy to obtain the following asymptotics:
This implies that
where we made use of (A.4) again. Recalling that \( \frac{d\tau }{dt} = \frac{1}{\mu } \) we obtain the following asymptotic behavior \( O_\tau \sim _{\tau \rightarrow \infty } \frac{A_0}{t(\tau )}. \) Using (A.3) again it follows that
Since
and \( O \sim \frac{A_0+tA_1}{\mu }\) we conclude that
where we used (A.13). Therefore
where \( \mu _1 = (\det A_1)^{\frac{1}{3}}, \) and this completes the proof of (A.6). Proof of (A.7) is similar.
Proof of (A.7)–(A.9) From the definition of \(\Lambda \) we have
where we used the symmetry of \(\Lambda \) in the last equality. Since \(\Vert \Lambda \Vert \lesssim 1\) it follows by part (i) that \(\Vert \Lambda _\tau \Vert \lesssim e^{-\mu _1\tau }\). To bound \(\Lambda _{\tau \tau }\) we note that by (A.14) \( \Lambda _{\tau \tau } = - 2 \Lambda _\tau (\Gamma ^*)^\top - 2\Lambda (\Gamma _\tau ^*)^\top . \) Since both \(\Vert \Lambda _\tau \Vert \) and \(\Vert \Gamma ^*\Vert \) decay exponentially, it remains to prove the decay of \(\Vert \Gamma _\tau ^*\Vert \). From \(\Gamma ^* = O^{-1}O_\tau \) it follows that \(\Gamma _\tau ^*=-(\Gamma ^*)^2 + O^{-1}O_{\tau \tau }\), and therefore it remains to prove the decay of \(\Vert O_{\tau \tau }\Vert \). A simple calculation shows that
Using the asymptotic behavior (A.12), (2.18), we can refine the asymptotics (A.12) to show that \(A_t \text {Tr}(A^{-1}A_t)+A \partial _t\text {Tr}(A^{-1}A_t) = O(t^{2-3\gamma })\) and therefore from the above equation it follows that
This yields the second bound in (A.7). Bounds (A.8) (A.9) follow by similar arguments using (A.3), while (A.10) is a direct consequence of (A.8). \(\square \)
B Commutators
In order to evaluate various commutator terms that arise from commuting differential operators  with the usual Cartesian derivatives or apply the Leibniz rule we shall rely on the fact that the high-order Sobolev norms expressed in polar coordinates are equivalent to the usual high-order Sobolev norms on the support of function \(\psi \).
with the usual Cartesian derivatives or apply the Leibniz rule we shall rely on the fact that the high-order Sobolev norms expressed in polar coordinates are equivalent to the usual high-order Sobolev norms on the support of function \(\psi \).
Lemma B.1
Let  be a collection of the standard Cartesian, normal, and tangential vector-fields. For any two vector fields \(X_k,X_\ell \in {\mathcal {X}}\), \(k,\ell = 1,\ldots ,7\) there commutator satisfies the following relationship
be a collection of the standard Cartesian, normal, and tangential vector-fields. For any two vector fields \(X_k,X_\ell \in {\mathcal {X}}\), \(k,\ell = 1,\ldots ,7\) there commutator satisfies the following relationship

where the functions \(c^m_{k\ell }\), \(c_{k\ell }\), are \(C^\infty \) on the exterior of any ball around the origin \(r=0\).
Proof
The proof is a simple consequence of the following direct calculations. For any \(i,j\in \{1,2,3\}\) we have

\(\square \)
Lemma B.1 is a technical tool allowing us to bound the lower order commutators in our energy estimates.
Using the product rule and the relationship \(\mathscr {A}=[D\eta ]^{-1}\) it is easy to see that the following formulas hold
Similarly, for any \(j=1,2,3\) we have

Therefore, if \(\beta =(0,0,0)\) we have the formula

If \(|\beta | > 0\), then with \(e_1=(1,0,0)\), \(e_2 = (0,1,0)\), and \(e_3=(0,0,1)\) we obtain

where \(c_{a'\beta '},c_{\beta '}\) are positive universal constants and the Einstein summation convention does not apply to the index j. Finally, the high-order commutators appearing on the right-hand side in the identities (B.4)–(B.5) can be expressed as a linear combination of the elements of \({\mathcal {X}}\) with smooth coefficients away from zero. In other words, for any \(j=1,2,3\) the following commutator identity holds:

for some universal coefficients \(C^j_{a',\beta ',\ell }\) which are smooth on the exterior of any ball around the origin \(r=0\). Formula (B.6) is a direct consequence of Lemma B.1.
C Weighted spaces, Hardy inequalities, and Sobolev embeddings
In this section, we recall Hardy inequalities and embedding results of weighted function spaces. First of all, we state the Hardy inequality near \(r=1\).
Lemma C.1
(Hardy inequality [20]) Let k be a real number and g a function satisfying \(\int _0^1 (1-r)^{k +2}(g^2 + g'^2) dr < \infty \).
If \(k > -1\), then we have \( \int _0^1 (1-r)^{k} g^2 dr \le C \int _0^1 (1-r)^{k+2} (g^2 + |g'|^2) dr \).
If \(k < -1\), then g has a trace at \(r=1\) and \( \int _0^1 (1-r)^{k} (g - g(1))^2 dr \le C \int _0^1 (1-r)^{k+2} |g'|^2 dr\).
Since w depends only on r and w behaves like a distance function \(1-r\), using Lemma C.1, we in particular get
for any nonnegative real number \(k> -1\) and for any \(u\in C^\infty (B_1(\mathbf{0}){\setminus } B_{\frac{1}{4}}(\mathbf{0}))\). We can apply (C.1) to  and thereafter apply (C.1) repeatedly to the right-hand side. As a consequence for any \(-1< k < \alpha +a\),
and thereafter apply (C.1) repeatedly to the right-hand side. As a consequence for any \(-1< k < \alpha +a\),

Upon choosing \(m = \lceil a+\alpha -k \rceil \) where \(\lceil \ \rceil \) is the ceiling function, we obtain

for any \(u\in C^\infty (B_1(\mathbf{0}){\setminus } B_{\frac{1}{4}}(\mathbf{0}))\).
As a consequence of (C.3), we obtain the weighted Sobolev–Hardy inequality:
Proposition C.2
For any \(u\in C^\infty (B_1(\mathbf{0}))\), we have


We omit the technical details of the proof, as it follows from standard estimates relying on the \(H^2(\Omega )\hookrightarrow L^\infty (\Omega )\) continuous embedding and the Hardy inequality (C.3).
D Starting from Lagrangian formulation
Consider the Lagrangian formulation of the E\(_\gamma \)-system [6, 19]:
where \(\mathscr {A}_\zeta \) and \({\mathscr {J}}_\zeta \) are induced by the flow map \(\partial _t\zeta (t,y)=\mathbf{{u}}(t,\zeta (t,y))\) (\(\mathbf{u}\) is the original fluid velocity appearing in (1.1)) and \(w=(\rho _0 {\mathscr {J}}_\zeta (0))^{\gamma -1}\ge 0\) is an enthalpy function that depends only on the initial data. To find affine motions (with center of mass at 0) one makes the ansatz \( \zeta (t,y)= A(t) y\) [44]. With \(\mathscr {A}_{\zeta }^\top =[D\zeta ]^{-\top }= A(t)^{-\top }\) and \({\mathscr {J}}_{\zeta }=\det A\), by plugging this ansatz into (D.1), we obtain
Since w is independent of t, (D.2) will be satisfied if we demand
which precisely yields the affine motions (1.5)–(1.6) (discovered by Sideris when \(\mathbf{a}\equiv 0\)) which form the set \({\mathscr {S}}\) with the center of mass fixed at the origin.
In order to study the stability of elements of \({\mathscr {S}}\) we want to realize them as time-independent background solutions. Given such an affine motion A we modify the flow map \(\zeta \) and define \(\eta := A^{-1} \zeta \). Since \(\mathscr {A}_\zeta ^\top = A^{-\top } \mathscr {A}_\eta ^\top \) and \({\mathscr {J}}_\zeta = (\det A) {\mathscr {J}}_\eta \), we obtain
By using (D.3) we can rewrite the previous equation in the form
where \(\Lambda =\det A^{\frac{2}{3}} A^{-1}A^{-T}\).
We rescale the time variable t so that \(1+t\sim e^{\mu _1\tau }\) by setting \(\frac{d\tau }{d t} = (\det A)^{-\frac{1}{3}}\). Then (D.4) can be written as
We now recall \(A^{-1} A_\tau = \mu ^{-1} \mu _\tau I + O^{-1}O_\tau \) where \( A= \mu O\) and \(\mu = (\det A)^{\frac{1}{3}}\) (see Sect. 2.1). The equation for \(\eta \) reads
where \(\Gamma ^*=O^{-1}O_\tau \). It is clear that \(\eta (y)\equiv y\) corresponds to Sideris’ affine motions, and equation (D.6) is nothing but (2.35). By considering \(\uptheta =\eta -y\), we obtain the \(\uptheta \)-Eq. (2.38).
Rights and permissions
About this article
Cite this article
Hadžić, M., Jang, J. Expanding large global solutions of the equations of compressible fluid mechanics. Invent. math. 214, 1205–1266 (2018). https://doi.org/10.1007/s00222-018-0821-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-018-0821-1