Measurements of Quantum Hamiltonians with Locally-Biased Classical Shadows

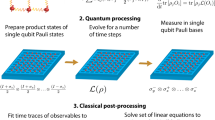
Abstract

Obtaining precise estimates of quantum observables is a crucial step of variational quantum algorithms. We consider the problem of estimating expectation values of quantum Hamiltonians, obtained on states prepared on a quantum computer. We propose a novel estimator for this task, which is locally optimised with knowledge of the Hamiltonian and a classical approximation to the underlying quantum state. Our estimator is based on the concept of classical shadows of a quantum state, and has the important property of not adding to the circuit depth for the state preparation. We test its performance numerically for molecular Hamiltonians of increasing size, finding a sizable reduction in variance with respect to current measurement protocols that do not increase circuit depths.

1 Introduction

Estimating observables of interest for quantum states prepared on a quantum processor is a central subroutine in a variety of quantum algorithms. Improving the precision of the measurement process is a pressing need, considering the fast-paced increase in size of current quantum devices. One key application is the energy estimation of complex molecular Hamiltonians, a staple of variational quantum eigensolvers (VQE) [1,2,3,4]. Readout of quantum information on quantum processors is available only through single-qubit projective measurements. The outcomes of these single-qubit measurements are combined to estimate quantum observables described by linear combinations of Pauli operators. Naively, each Pauli operator can be estimated independently by appending a quantum circuit composed of one layer of single-qubit gates at the end of state preparation, before readout.

A series of recent efforts [5,6,7,8,9,10,11,12] has shown that savings in the number of measurements can be obtained for the estimation of complex observables, at the expense of increasing circuit depths. This increase in circuit depth can defy the purpose of variational quantum algorithms, which aim to keep gate counts low [13].

Other strategies, more amenable to execution on near-term devices, have considered reducing the number of measurements while simultaneously not increasing circuit depth. These strategies are based on grouping together Pauli operators that can be measured in the same single-qubit basis. This Pauli grouping approach was introduced in [3] and explored thoroughly in [14] for chemistry systems. Machine learning techniques have also recently been used to tackle the measurement problem [15], with no increase in circuit depth. The machine learning approach is based upon the assumption that fermionic neural-network states can capture quantum correlations in ground states of molecular systems [16].

The measurement problem has been considered in the context of predicting collections of generic observables on reduced density matrices [17,18,19,20,21]. The best asymptotic scalings up to poly-logarithmic factors are obtained in [17], where it is proposed to characterise a quantum state through random measurements; the measurement outcomes are later used to evaluate expectation values of arbitrary observables.

In this article we introduce an estimator that recovers, in expectation, mean values of observables on quantum states prepared on quantum computers. The protocol is based on classical shadows using random Pauli measurements introduced in [17] and referred to as classical shadows in this present article. We show how sampling from random measurement bases in the original protocol can be locally biased towards certain bases on each individual qubit. We name this technique locally-biased classical shadows. We show how to optimise the estimator’s local bias on each qubit based on the knowledge of a target observable and a classical approximation of the quantum state, named reference state. We also prove that this optimisation has a convex cost function in certain regimes. We benchmark our optimisation procedure in the setting of quantum chemistry Hamiltonians, where reference states can be obtained from the Hartree–Fock solution, or multi-reference states, obtained with perturbation theory. We finally compare the variance of our estimator to previous methods for estimating average values that do not increase circuit depth, obtaining consistent improvements.

1.1 Outline of the paper

Section 2 reviews classical shadows using random Pauli measurements in a notation convenient to this current article. Section 3 provides the construction of the locally-biased classical shadows and calculates the expectation and variance associated with the estimator introduced. Section 4 shows how to optimise the estimator. Section 5 benchmarks our estimator for molecular energies on molecules of increasing sizes. Section 6 finishes with closing remarks. Appendix A reviews the methods for molecular energy estimation to which we compare our estimator.

2 Classical Shadows Using Random Pauli Measurements

Classical shadows using random Pauli measurements has been introduced in [17]. This section reproduces the procedure in a different style. Since we are only concerned with estimating one specific observable, we do not mention the aspect of a snapshot, nor the efficient description using the symplectic representation, nor the notion of median of means.

The problem that we want to address is the estimation of ${{\,\mathrm{tr}\,}}(\rho O)$ for a given n-qubit state $\rho$ and an observable O decomposed as a linear combination of Pauli terms:

$$\begin{aligned} O = \sum _{Q \in \{I,X,Y,Z\}^{\otimes n}} \alpha _Q Q \end{aligned}$$

(1)

where $\alpha _Q\in {\mathbb {R}}$. Notationally, for a Pauli operator Q as above and for a given qubit $i\in \{1,2,\dots ,n\}$ we shall write $Q_i$ for the i^th single-qubit Pauli operator so that $Q=\otimes _i Q_i$. We denote the support of such an operator ${{\,\mathrm{supp}\,}}(Q) = \{i | Q_i \ne I\}$ and its weight ${{\,\mathrm{wt}\,}}(Q)= |{{\,\mathrm{supp}\,}}(Q)|$. An n-qubit Pauli operator Q is said to be full-weight if ${{\,\mathrm{wt}\,}}(Q)=n$.

This task of estimating ${{\,\mathrm{tr}\,}}(\rho O)$ is accomplished with classical shadows of [17] as described in Algorithm 1. Briefly, one randomly selects a Pauli basis for each of the n-qubits in which to measure the quantum state; this is irrespective of the operator O. Then, after measurement, non-zero estimates can be provided for all Pauli operators which qubit-wise commute with the measurement bases. All other Pauli operators are implicitly provided with the zero estimator for their expectation values.

We introduce the function from [17, Eq. E28]. For two n-qubit Pauli operators P, Q define, for each qubit i,

$$\begin{aligned} f_i(P,Q) = {\left\{ \begin{array}{ll} 1 &{} \hbox { if } P_i=I \hbox { or } Q_i=I; \\ 3 &{} \hbox { if } P_i=Q_i \ne I; \\ 0 &{} \text {else}. \end{array}\right. } \end{aligned}$$

(2)

and extend this to the multi-qubit setting by declaring $f(P,Q) = \prod _{i=1}^n f_i(P,Q)$. Also, given a full-weight Pauli operator P, we let $\mu (P,i)\in \{\pm 1\}$ denote the eigenvalue measurement when qubit i is measured in the $P_i$ basis. For a subset $A\subseteq \{1,2,\dots , n\}$ declare

$$\begin{aligned} \mu (P,A) = \prod _{i\in A} \mu (P,i) \end{aligned}$$

(3)

with the convention that $\mu (P,\varnothing )=1$.

As shown in [17], the output of this algorithm is an unbiased estimator of the desired expectation value, that is, ${\mathbb {E}}(\nu )={{\,\mathrm{tr}\,}}{(\rho O)}$.

3 Locally-Biased Classical Shadows

In this section we generalise classical shadows by observing that the randomisation procedure of the Pauli measurements can be biased in the measurement basis for each qubit. We build an estimator based on biased measurements, which in expectation recovers ${{\,\mathrm{tr}\,}}(\rho O)$. We then proceed to calculate its variance.

As in Sect. 2, we wish to estimate ${{\,\mathrm{tr}\,}}(\rho O)$ for a given state $\rho$ and an observable $O=\sum _Q \alpha _Q Q$. For each qubit $i \in \{1,2,\dots ,n\}$, consider a probability distribution $\beta _i$ over $\{X,Y,Z\}$ and denote by $\beta _{i}(P_i)$ the probability associated with each Pauli $P_i\in \{X,Y,Z\}$. We write $\beta$ for the collection $\{ \beta _i \}_{i=1}^n$ and note that $\beta$ may be considered a probability distribution on full-weight Pauli operators by associating with $P\in \{X,Y,Z\}^{\otimes n}$ the probability $\beta (P) = \prod _i \beta _{i}(P_i)$.

We generalise the function introduced in Eq. (2). For two n-qubit Pauli operators P, Q and a product probability distribution $\beta$, define, for each qubit i,

$$\begin{aligned} f_i(P,Q,\beta ) = {\left\{ \begin{array}{ll} 1 &{} \hbox { if } P_i=I \hbox { or } Q_i=I; \\ (\beta _i(P_i))^{-1} &{} \hbox { if } P_i=Q_i \ne I; \\ 0 &{} \text {else}. \end{array}\right. } \end{aligned}$$

(4)

In this article, we will assume that $(\beta _i(P_i))^{-1}>0$ in order to avoid ay division-by-zero edge cases. (Note that such cases are irrelevant when we consider Sect. 4.) We extend this to the multi-qubit setting by declaring

$$\begin{aligned} f(P,Q, \beta ) = \prod _{i=1}^n f_i(P,Q,\beta ). \end{aligned}$$

(5)

Algorithm 2 describes an estimator via locally-biased classical shadows. Note that the (uniform) classical shadows case is retrieved when $\beta _i(P_i) = \frac{1}{3}$ for every qubit $i\in \{1,2,\dots , n\}$ and every Pauli term $P_i\in \{X,Y,Z\}$.

Algorithm 3 recovers the expectation ${{\,\mathrm{tr}\,}}(\rho O)$, as shown in the following lemma.

Lemma 1

The estimator $\nu$ from Algorithm 2 with a single sample $(S=1)$ satisfies

$$\begin{aligned} {\mathbb {E}}(\nu ) = \sum _Q \alpha _Q {{\,\mathrm{tr}\,}}(\rho Q) \qquad \text {and} \qquad {\mathbb {E}}(\nu ^2) = \sum _{Q,R} f(Q,R,\beta ) \alpha _Q\alpha _R {{\,\mathrm{tr}\,}}(\rho QR). \end{aligned}$$

(6)

Proof

Let ${\mathbb {E}}_P$ denote the expected value over the distribution $\beta (P)$. Let ${\mathbb {E}}_{\mu (P)}$ denote the expected value over the measurement outcomes for a fixed Pauli basis P. Using the fact that $\beta (P)$ is a product distribution one can easily check that

$$\begin{aligned} {\mathbb {E}}_P f(P,Q,\beta ) = 1, \end{aligned}$$

(7)

$$\begin{aligned} {\mathbb {E}}_P f(P,Q,\beta ) f(P,R,\beta ) = f(Q,R,\beta ) \end{aligned}$$

(8)

for any $Q,R\in \{I,X,Y,Z\}^{\otimes n}$.

Let us say that an n-qubit Pauli operator Q agrees with a basis $P\in \{X,Y,Z\}^{\otimes n}$ iff $Q_i\in \{I,P_i\}$ for any qubit i. Note that $f(P,Q,\beta )=0$ unless Q agrees with P. For any n-qubit Pauli operators Q, R that agree with a basis P one has

$$\begin{aligned} {\mathbb {E}}_{\mu (P)} \mu (P,\mathrm {supp}(Q)) ={{\,\mathrm{tr}\,}}{(\rho Q)} \end{aligned}$$

(9)

and

$$\begin{aligned} {\mathbb {E}}_{\mu (P)} \mu (P,\mathrm {supp}(Q)) \mu (P,\mathrm {supp}(R))={{\,\mathrm{tr}\,}}{(\rho QR)}. \end{aligned}$$

(10)

To get the last equality, observe that $\mu (P,A)\mu (P,A')=\mu (P,A\ominus A')$ for any subsets of qubits $A,A'$, where $A\ominus A'$ is the symmetric difference of A and $A'$. The assumption that both Q and R agree with the same basis P implies that $\mathrm {supp}(Q)\ominus \mathrm {supp}(R)=\mathrm {supp}(QR)$. Now Eq. (10) follows from Eq. (9).

By definition, the expected value in Eq. (6) is a composition of the expected values over a Pauli basis P and over the measurement outcomes $\mu (P)$, that is, ${\mathbb {E}}= {\mathbb {E}}_P {\mathbb {E}}_{\mu (P)}$. Using the above identities one gets

$$\begin{aligned} {\mathbb {E}}(\nu )= {\mathbb {E}}_P {\mathbb {E}}_{\mu (P)} \nu = \sum _Q \alpha _Q {{\,\mathrm{tr}\,}}{(\rho Q)} {\mathbb {E}}_P f(P,Q,\beta ) = \sum _Q \alpha _Q {{\,\mathrm{tr}\,}}{(\rho Q)} \end{aligned}$$

Here the second equality is obtained using Eq. (9) and the linearity of expected values. The third equality follows from Eq. (7). Likewise,

$$\begin{aligned} {\mathbb {E}}(\nu ^2)= & {} {\mathbb {E}}_P {\mathbb {E}}_{\mu (P)} \nu ^2 = \sum _{Q,R} \alpha _Q \alpha _R {{\,\mathrm{tr}\,}}{(\rho QR)} {\mathbb {E}}_P f(P,Q,\beta ) f(P,R,\beta ) \\= & {} \sum _{Q,R} \alpha _Q \alpha _R f(Q,R,\beta ) {{\,\mathrm{tr}\,}}{(\rho QR)}. \end{aligned}$$

Here the second equality is obtained using Eq. (10) and observing that that $f(P,Q,\beta )f(P,R,\beta )=0$ unless both Q and R agree with P. The third equality follows from Eq. (8). $\square$

Recall that in the context of using a quantum processor, we aim to use the random variable $\nu$ to estimate ${{\,\mathrm{tr}\,}}(\rho O)$ to some (additive) precision $\varepsilon$. This dictates the number of samples S required. Specifically, for fixed $\rho ,O$, we require $S=O(\varepsilon ^{-2} {{\,\mathrm{Var}\,}}(\nu ^{(s)}))$ where ${{\,\mathrm{Var}\,}}(\nu ^{(s)})$ is obviously independent of the specific sample s. For future reference, we record explicitly the variance of $\nu$ for a single sample $(S=1)$. Lemma 1 establishes

$$\begin{aligned} {{\,\mathrm{Var}\,}}(\nu ) = \left( \sum _{Q,R} f(Q,R,\beta ) \alpha _Q \alpha _R {{\,\mathrm{tr}\,}}(\rho Q R)\right) - \left( {{\,\mathrm{tr}\,}}(\rho O) \right) ^2. \end{aligned}$$

(11)

Remark 1

In [17, Proposition 3], the authors aim to upper-bound this variance independently of the state $\rho$. In the uniform setting, this is achieved with an application of Cauchy-Schwarz and it leads to a bound of $4^k \Vert O\Vert ^2_\infty$ where k is the weight of the operator.

4 Optimised Locally-Biased Classical Shadows

In this section we show how the locally-biased classical shadows introduced in Sect. 3 can be optimised when one has partial knowledge about the underlying quantum state. This partial information is obtained efficiently with a classical computation. This is the case of VQE for molecular Hamiltonians if one initialises the variational procedure from a reference state, which can be, for example, the Hartree–Fock solution, a generic fermionic Gaussian state [22], or perturbative Møller–Plesset solutions. Our method can be also extended to generic many-body Hamiltonians, considering for example the generation of reference states with semidefinite programming [23]. On a more general note, the existence of a good reference state is the assumption of all algorithms that target ground state properties of interacting many-body problems, including quantum phase estimation.

In this setting, we optimise the probability distributions $\beta = \{\beta _i\}_{i=1}^n$ to obtain the smallest variance on a given reference state. To do this, we consider the variance calculated in Eq. (11) and extract from it the component which, associated with the reference state, explicitly depends on the distributions $\beta$. We proceed to optimise this cost function, thereby minimising the variance, noting that a negligible restriction of the cost function that we use leads to a convex optimisation problem. Finally, we use the optimised distributions $\beta ^*$ to build molecular energy estimators as defined in Algorithm 3.

To set notation, we introduce a molecular Hamiltonian, H, acting on n qubits. We write

$$\begin{aligned} H = \sum _{P \in \{I,X,Y,Z\}^{\otimes n}} \alpha _P P \end{aligned}$$

(12)

and denote by $H_0$ the traceless part of H.

4.1 Single-reference optimisation

We first consider the case in which the reference state is a product state of the form $\frac{1}{2^n}\otimes _{i=1}^n(I + m_i P_i)$ where $m_i \in \{\pm 1\}$ and $P_i\in \{X,Y,Z\}$. This is the case if a VQE targeting a molecular Hamiltonian in the molecular basis is initialised with the Hartree–Fock state. In this case $P_i=Z$. Motivated by this, we use the label “HF” and, for ease of reading, we assume that $P_i=Z$. However we remark that the results here can be generalised out of the quantum chemistry domain.

We are given a reference product state $\rho _{\mathrm {HF}} = \frac{1}{2^n}\otimes _{i=1}^n (I+m_i Z)$ where $m_i\in \{\pm 1\}$. The variance of the estimator $\nu$ is independent of the constant term $H-H_0$. Writing the variance from Eq. (11) for the state $\rho _{\mathrm {HF}}$ upon explicit removal of the constant term reads

$$\begin{aligned} {{\,\mathrm{Var}\,}}(\nu | \rho _\mathrm {HF}) = \sum _{Q \ne I^{\otimes n}} \sum _{R \ne I^{\otimes n}} f(Q,R,\beta ) \alpha _Q \alpha _R {{\,\mathrm{tr}\,}}(\rho _{\mathrm {HF}}QR) - {{\,\mathrm{tr}\,}}(\rho _{\mathrm {HF}} H_0 )^2. \end{aligned}$$

(13)

Our objective is to find probability distributions $\beta$ so as to minimise Eq. (13). The following proposition explicits the relevant cost function appropriate to this task.

Proposition 1

Given a reference product state $\rho _{\mathrm {HF}}$, represented by the logical basis element $\{m_i\}_{i=1}^n$, the variance associated with Algorithm 2 is minimised upon choosing $\beta$ so as to minimise

$$\begin{aligned} \mathrm {cost}(\beta ) = \sum _{(Q,R)\in {\mathcal {I}}_{Z^{\otimes n}}} \alpha _Q \alpha _R \prod _{i | Q_i=R_i\ne I} (\beta _i(Q_i))^{-1} \prod _{i | Q_i\ne R_i} m_i \end{aligned}$$

(14)

subject to $\beta _{i,P} \ge 0$ and $\beta _{i,X}+\beta _{i,Y}+\beta _{i,Z}=1$ for all i. In the above, the sum is taken over “influential pairs” : 

$$\begin{aligned} {\mathcal {I}}_{{Z^{{ \otimes n}} }} = \{ \left. {(Q,R)} \right| Q,R \ne I^{{ \otimes n}} and\,for\,all\,i,either\,Q_{i} = R_{i} ,or\,\{ Q_{i} ,R_{i} \} = \{ I,Z\} \} \end{aligned}$$

(15)

Proof

We must pay attention to only $\beta$-dependent terms in ${{\,\mathrm{Var}\,}}(\nu | \rho _\mathrm {HF})$. The simple structure of $\rho _{\mathrm {HF}}$ implies, for n-qubit non-identity Pauli operators Q, R,

$$\begin{aligned} f(Q, R, \beta ){{\,\mathrm{tr}\,}}(\rho _{\mathrm {HF}} Q R)&= \prod _{i=1}^n f_i(Q, R, \beta ) {{\,\mathrm{tr}\,}}\left( \frac{1}{2}(I+m_iZ)Q_iR_i \right) \\&= \prod _{i=1}^n f_i(Q, R, \beta )\delta _{Q_i,R_i} + m_i\left( \delta _{Q_i,Z}\delta _{R_i,I} + \delta _{Q_i,I}\delta _{R_i,Z} \right) \\&= \prod _{i=1}^n \delta _{Q_i,R_i} \left( \delta _{Q_i,I} + (1-\delta _{Q_i,I})(\beta _i(Q_i))^{-1} \right) \\&\quad + m_i\left( \delta _{Q_i,Z}\delta _{R_i,I} + \delta _{Q_i,I}\delta _{R_i,Z} \right) \end{aligned}$$

The preceding display is independent of $\beta$ whenever $(Q,R)\not \in {\mathcal {I}}_{Z^{\otimes n}}$. Hence the cost function captures precisely the component of the variance (when estimating the reference product state) which is dependent on the probability distributions $\beta$. $\square$

Some remarks are in order.

Remark 2

The cost function of Eq. (14) is not convex. If we however restrict to diagonal terms from the set of influential pairs, then we obtain the following alternative cost function, which we refer to as the diagonal cost function:

$$\begin{aligned} \mathrm {cost}_\mathrm {diag}(\beta ) = \sum _Q \alpha _Q^2 \prod _{i\in {{\,\mathrm{supp}\,}}(Q)} (\beta _i(Q_i))^{-1} \end{aligned}$$

(16)

This diagonal cost function is convex: For fixed Q, the function $-\log \beta _i(Q_i)$ is convex, hence so too is $\sum _{i\in {{\,\mathrm{supp}\,}}(Q)} (-\log (\beta _i(Q_i)))$. Exponentiating this result implies $\prod _{i\in {{\,\mathrm{supp}\,}}(Q)} \beta _i(Q_i)^{-1}$ is convex. The positive linear combination over Pauli operators Q preserves convexity. In this convex case we are assured that the minimised collection of distributions provides a global minimum (of the diagonal cost function).

This diagonal cost function makes no reference to the specific single-reference state, and therefore can be used to find $\beta _i$ which are independent of the underlying quantum state $\rho _\text {HF}$. In fact, the diagonal cost function can be derived from Eq. (11) when $\rho$ is the maximally mixed state. Since the diagonal cost function is convex, we may be confident that the values for $\beta$ found numerically are optimal with respect to the cost function. In the following section, the numerical experiments indicate surprisingly that the diagonal cost function leads to probability distributions which give very satisfying results irrespective of the diagonal cost function’s lack of reference to the ground state, or a state near the ground state. We explain this in Remark 4.

Remark 3

The diagonal cost function can be formulated in the language of geometric programming [24], while the original cost function is an example of signomial geometric programming. They can be numerically optimised using standard techniques such as iterative updates incorporating closed-form solutions obtained from Lagrange multipliers. See Appendix B for more details.

Remark 4

We provide a bound on the original cost function from that on the diagonal cost function. Set $\Gamma (Q,R) = |\alpha _Q|\,|\alpha _R|\, \prod _{i|Q_i = R_i \ne I} (\beta _i(Q_i))^{-1}$. The diagonal cost function is $\sum _{Q} \Gamma (Q,Q)$, while the original cost function is at most $\sum _{Q,R} \Gamma (Q,R)$, (the sum is over only influential pairs in the original cost function). Using that $2xy\le x^2+y^2$ for real x, y, the following inequality holds

$$\begin{aligned} \Gamma (Q,R) \le \frac{\Gamma (Q, Q) + \Gamma (R, R)}{2}. \end{aligned}$$

(17)

Summation over all pairs (Q, R) on both sides leads to

$$\begin{aligned} \sum _{Q, R} \Gamma (Q, R) \le |H_0| \sum _{Q} \Gamma (Q,Q) \end{aligned}$$

(18)

where $|H_0|$ is the number of traceless terms in the Hamiltonian.

It is perhaps less surprising than one might first expect that the diagonal cost function performs well for quantum chemistry systems. This is because of the structure of the problem at hand. For chemistry systems one has that Hamiltonian coefficients corresponding to integrals with fewer orbitals are larger than ones corresponding to many orbitals. This is because the overlapping spatial region between orbitals decreases with their number. Considering that in our cost function the Hamiltonian coefficients are squared, it is not surprising that coefficients corresponding to one-orbital integrals and two-orbital integrals dominate the total cost.

Remark 5

It is possible to obtain a rough confidence bound on the number of shots required to get an accurate estimate of ${{\,\mathrm{tr}\,}}(\rho H)$ given an unknown $\rho$ in the context of quantum chemistry. Recall Algorithm 3 samples the state $\rho$ a total of S times and returns an estimate $\nu =\frac{1}{S}\sum _{s}\nu ^{(s)}$. Consider an optimised $\beta ^*$ according to the diagonal cost function. Then the single-shot variance of the energy estimator $\nu ^{(s)}$, given $\rho$ and $\beta ^*$, may be bounded

$$\begin{aligned} \begin{aligned} {{\,\mathrm{Var}\,}}(\nu ^{(s)} | \rho , \beta ^*)&\le \sum _{Q,R} f(Q,R,\beta ^*) \alpha _Q \alpha _R {{\,\mathrm{tr}\,}}(\rho QR) \le \sum _{Q,R} f(Q,R,\beta ^*) |\alpha _Q| \, |\alpha _R| \\&\le \sum _{Q,R} \Gamma (Q,R) \le |H_0| \cdot \mathrm {cost}_\mathrm {diag}(\beta ^*) \end{aligned} \end{aligned}$$

(19)

where we have reintroduced the notation of the preceding remark and applied Eq. (18). Using Chebyshev’s inequality, we can bound the probability that our final estimate $\nu$ is worse than additive-error $\varepsilon$ from ${{\,\mathrm{tr}\,}}(\rho H)$

$$\begin{aligned} {\mathbb {P}}( |\nu - {{\,\mathrm{tr}\,}}(\rho H)| \ge \varepsilon ) \le \frac{1}{S\varepsilon ^2} |H_0| \cdot \mathrm {cost}_\mathrm {diag}(\beta ^*) \end{aligned}$$

(20)

and we recall that $|H_0|=O(n^4)$ for the quantum chemistry setting described in the following section.

4.2 Multi-reference optimisation

We finish this section by observing that the technique of optimising the probability distributions also works for multi-reference frame states such as fermionic Gaussian states, or perturbative solutions. Such reference states are important for quantum chemistry simulations far from equilibrium (unlike the Hartree–Fock reference state which is more appropriate near equilibrium). Specifically, consider a multi-reference state $\left| \psi \right\rangle _\text {MR}$, written in the logical basis

$$\begin{aligned} \left| \psi \right\rangle _\text {MR} = \sum _{k=1}^K \lambda _k \left| \psi ^{(k)}\right\rangle , \qquad \left| \psi ^{(k)}\right\rangle = \left| b_1^{(k)} \cdots b_n^{(k)} \right\rangle \end{aligned}$$

(21)

where $b_i^{(k)}\in \{0,1\}$ are associated with Z-eigenvalues $m_i^{(k)}=(-1)^{b_i^{(k)}}$ and $\lambda _k\in {\mathbb {C}}$ are amplitudes such that $\left| \psi \right\rangle _\text {MR}$ is normalised. The associated density now reads

$$\begin{aligned} \rho _\text {MR} = \sum _{k,\ell } \lambda _k \overline{\lambda _\ell } \rho ^{(k,\ell )}, \qquad \rho ^{(k,\ell )} = \otimes _{i=1}^n \left| b_i^{(k)}\right\rangle \left\langle b_i^{(\ell )}\right| \end{aligned}$$

(22)

In the following paragraphs, we calculate an appropriate cost function for this case.

Let us restrict ourselves to the single-qubit setting briefly: $\rho ^{(k,\ell )} = \left| b^{(k)}\right\rangle \left\langle b^{(\ell )}\right|$. There are two cases for $\rho ^{(k,\ell )}$ dependent on whether $b^{(k)}, b^{(\ell )}$ agree or not. If they agree then $\rho ^{(k,\ell )} = \frac{1}{2}(I + (-1)^{b^{(k)}}Z)$. If they disagree, then $\rho ^{(k,\ell )} = \frac{1}{2}(X + (-1)^{b^{(k)}}iY)$. In a similar way to the single-reference setting, we need to calculate $f(Q,R,\beta ) {{\,\mathrm{tr}\,}}(\rho ^{(k,\ell )}QR)$. This is best done by considering the two cases: We introduce the function g when $b^{(k)}= b^{(\ell )}$ and obtain

$$\begin{aligned}&f(Q,R,\beta ) {{\,\mathrm{tr}\,}}(\rho ^{(k,\ell )}QR)\\&\quad = \delta _{Q,R} \left( \delta _{Q,I} + (1-\delta _{Q,I})\beta _{Q}^{-1} \right) + (-1)^{b^{(k)}} \left( \delta _{Q,Z}\delta _{R,I} + \delta _{Q,I}\delta _{R,Z} \right) \\&\quad = g(Q,R,\beta , b^{(k)}); \end{aligned}$$

We introduce the function h when $b^{(k)}\ne b^{(\ell )}$ and obtain

$$\begin{aligned} f(Q,R,\beta ) {{\,\mathrm{tr}\,}}(\rho ^{(k,\ell )}QR)&= \left( \delta _{Q,X}\delta _{R,I} + \delta _{Q,I} \delta _{R,X} \right) +(-1)^{b^{(k)}} i \left( \delta _{Q,Y}\delta _{R,I} + \delta _{Q,I} \delta _{R,Y} \right) \\&= h(Q,R, b^{(k)}). \end{aligned}$$

We can now return to the multi-qubit setting to write down a cost function which ought be minimised:

$$\begin{aligned}&\mathrm {cost}_\text {multi-ref}(\beta )\nonumber \\&\quad = \sum _{k,\ell } \lambda _k \overline{\lambda _\ell } \sum _{Q,R} \alpha _Q \alpha _R \left( \prod _{i | b_i^{(k)} = b_i^{(\ell )}} g(Q_i,R_i,\beta _i, b_i^{(k)}) \prod _{i | b_i^{(k)} \ne b_i^{(\ell )}} h(Q_i,R_i, b_i^{(k)}) \right) \end{aligned}$$

(23)

We leave as future work a thorough investigation of cost functions associated with non-equilibrium quantum chemistry.

5 Numerical Experiments on Molecular Hamiltonians

In this section we test numerically the locally-biased classical shadows (LBCS) estimator defined in Algorithm 2 for molecular Hamiltonians. We consider six Hamiltonians corresponding to different molecules, represented in a minimal STO-3G basis, ranging from 4 to 16 spin orbitals. (The 8 qubit $\hbox {H}_2$ example uses a 6-31G basis.) We map the molecular Hamiltonians to qubit ones, using three encodings detailed in [25]. The result is qubit Hamiltonians defined on up to 16 qubits. The molecular Hamiltonians are defined in the molecular basis. In this basis, the Hartree–Fock state is a computational basis state. We choose the Hartree–Fock state as our single-reference state, and optimise the distributions $\beta$ according to Eqs. (14) and (16) separately. We call the optimisation procedure of the $\beta$ according to Eq. (16) diagonal. We then use the optimised $\beta ^*$ to compute the variance Eq. (11) on the ground state of the molecular Hamiltonians; the ground state and the ground energy are obtained by the Lanczos method for sparse matrices. Recall that, for a fixed accuracy with which one aims to estimate the energy, the variance is proportional to the number of preparations and measurements of the state one is required to perform. It may therefore be viewed as a measuring stick for the run-time of a VQE algorithm. We report the results in Table 1. In this table, we compare variances obtained with our LBCS estimator against other previously known observable estimators that do not increase circuit depth:

• An estimator based on $\ell ^1$ sampling of the Hamiltonian, detailed in [26, 27].

• An estimator which measures together collections of qubit-wise commuting Pauli operators. To find the collections of Pauli operators, we use a largest degree first (LDF) heuristic [28]. The collections are then sampled according to their Hamiltonian $\ell ^1$ weights.

• Classical shadows as given in [17], which corresponds to the case $\beta _i(P_i)=\frac{1}{3}$ for any qubit i and Pauli term $P_i\in \{X,Y,Z\}$.

Details of the first two estimators may be found in Appendix A.¹ For all the estimators, we report variances exactly computed on the ground states of the Hamiltonians considered.

Table 1 Variance for various estimators considered in this work

In all but one experiment of Table 1, we observe that the LBCS estimator outperforms the other estimators. The one case where the LDF decomposition provides a lower variance—$\hbox {H}_2$ on a minimal basis—should be considered a curiosity due to the small qubit count.

The two different cost functions used to optimise the $\beta$-distributions provide very similar variance. This is remarkable considering that the diagonal cost function defined in Eq. (16) is convex. For any given molecule, our numerical analysis indicated that the non-convex cost function Eq. (14) always converged to a single collection of distributions, irrespective of the initialised values for the distributions.

Next, we plot in Fig. 1 an optimised distribution $\beta ^*$. Specifically, we take the example of $\hbox {H}_2$O on 14 qubits in the Jordan–Wigner encoding. Due to the symmetry [25] where the first 7 qubits correspond to spin-up orbitals, and the last 7 qubits correspond to spin-down orbitals, we observe that $\beta _{i}^* = \beta _{i+7}^*$ for $i\in \{1,2,\dots , 7\}$. Note also that the probabilities are symmetric in X and Y (which is not the case for the Bravyi–Kitaev encoding).

Fig. 1

Probability distributions over the first 7 of 14 qubits for $\hbox {H}_2$O Hamiltonian using the Jordan–Wigner encoding. The probability distributions have been optimised according to Eq. (16)

Finally, we analyse the role played by the specific fermionic encoding used. For a restricted set of Hamiltonians, Table 2 reports variances for the three estimators: LDF grouping; classical shadows; and LBCS, with three different fermion-to-qubit encodings: Jordan–Wigner; parity; and Bravyi–Kitaev. Note that the variances for parity and Bravyi–Kitaev mappings are higher because those mappings generate Pauli distributions that tend to have more X and Y operators, as opposed to the linear tail of Z operators of the Jordan–Wigner, against which the distributions $\beta$ can be easily biased. We do not report $\ell ^1$ sampling in Table 2, as it is invariant under choice of encoding. Irrespective of the encoding, the locally biased classical shadows shows a reduction in variance over the LDF grouping whose collections are sampled according to their 1-norm.

Table 2 Variance for different estimators computed on the ground states of the molecules indicated

6 Conclusion

This article has considered the measurement problem associated with molecular energy estimation on quantum computers and has proposed a new algorithm for that problem. Investigating the principal subroutine present in classical shadows using random Pauli measurements, we are able to produce a non-uniform version of these shadows, termed locally-biased classical shadows. These locally biased classical shadows require probability distributions for each qubit. By solving a convex optimisation problem for a given molecular Hamiltonian, we find appropriate probability distributions for measuring states which are close to the true ground state of the molecular Hamiltonian. We benchmark the proposed algorithm on systems up to 16 qubits in size and observe significant and consistent improvement over Pauli grouping heuristic algorithms. To claim this improvement over Pauli grouping heuristic algorithms we have benchmarked our algorithm against the LDF heuristic. Note that Ref. [14] finds that other heuristics produce a number of qubit-wise commuting sets that only differ by 10% and are expected to offer similar performance to the LDF heuristic. Moreover standard Pauli grouping techniques are based on heuristically solving a computationally hard problem, whereas our method requires simply solving a convex optimisation problem whose number of variables is linear in the number of qubits.

Finally, the introduction of such a domain-specific cost function is, to the authors’ knowledge, novel. It is sufficiently general that applications of this idea will also be relevant in fields unrelated to quantum chemistry.

Appendices

Appendix A: Comparative Algorithms for Estimating Molecular Hamiltonians

This appendix provides details for the two algorithms against which we benchmark locally-biased classical shadows. Recall that we assume that the molecular Hamiltonian H acts on n-qubits and that a given state $\rho$ is provided and whose energy we aim to estimate. We write

$$\begin{aligned} H = \sum _{P \in \{I,X,Y,Z\}^{\otimes n}} \alpha _P P \end{aligned}$$

(24)

and denote by $H_0$ the traceless part of H. Denote by $\Vert \alpha \Vert _{\ell ^1}$ the $\ell ^1$-norm of the traceless coefficients, and associate with this norm the following $\ell ^1$-distribution $\gamma$ over the Pauli operators:

$$\begin{aligned} \Vert \alpha \Vert _{\ell ^1}&= \sum _{P\in \{I,X,Y,Z\}^{\otimes n}\backslash \{I^{\otimes n}\}} | \alpha _P |&\gamma (P)&= \frac{1}{\Vert \alpha \Vert _{\ell ^1}} |\alpha _P| \end{aligned}$$

(25)

We expose the dependence of the algorithms on the identity coefficient $\alpha _{I^{\otimes n}}$. This is because in the practical setting of molecular Hamiltonians considered in this text, the identity coefficient can be on the order of 10% of $\Vert \alpha \Vert _{\ell ^1}$. For the $\ell ^1$ sampling, it would be unwise to prepare $\rho$ only to subsequently measure no qubits. For the largest degree first setting, it would be unwise to arbitrarily associate the identity operator to one of the collections of qubit-wise commuting Pauli operators thereby associating the identity operator’s weight $|\alpha _{I^{\otimes n}}|$ to the corresponding collection’s weight and overly favouring the sampling of said collection.

Recall the notation from Sect. 2. Given a Pauli operator P, we let $\mu (P,i)\in \{\pm 1\}$ denote the eigenvalue measurement when qubit i is measured in the $P_i$ basis. For a subset $A\subseteq \{1,2,\dots , n\}$ we write $\mu (P,A) = \prod _{i\in A} \mu (P,i)$.

1.1 A.1. Ell-1 algorithm

This algorithm was the first algorithm proposed for estimating energies in the context of variational quantum algorithms [26]. The $\ell ^1$-norm of the traceless coefficients provides the probability distribution $\gamma$. We may use this probability distribution to select a Pauli operator P which dictates the Pauli basis in which to measure the state $\rho$, thereby providing an estimate for ${{\,\mathrm{tr}\,}}(\rho P)$. Algorithm 4 describes this procedure precisely.

For completeness, we record calculations for the expectation and variance of this estimator. Consider a single shot giving $\nu$. Let ${\mathbb {E}}_P$ denote the expected value over the distribution $\gamma (P)$ and let ${\mathbb {E}}_{\mu (P)}$ denote the expected value over the measurement outcomes for a fixed Pauli operator P. Without loss of generality, we may assume $\alpha _{I^{\otimes n}}=0$. Now ${\mathbb {E}}_{\mu (P)} \mu (P,{{\,\mathrm{supp}\,}}(P)) = {{\,\mathrm{tr}\,}}(\rho P)$ whence

$$\begin{aligned} {\mathbb {E}}(\nu ) = {\mathbb {E}}_P {\mathbb {E}}_{\mu (P)} \nu = {\mathbb {E}}_P \Vert \alpha \Vert _{\ell ^1} {{\,\mathrm{sgn}\,}}(\alpha _P) {{\,\mathrm{tr}\,}}(\rho P) = \sum _P \alpha _P {{\,\mathrm{tr}\,}}(\rho P) = {{\,\mathrm{tr}\,}}(\rho H). \end{aligned}$$

(26)

The variance (for a single sample) can also be calculated:

$$\begin{aligned} {{\,\mathrm{Var}\,}}(\nu ) = \sum _{P\ne I^{\otimes n}} ( \gamma _P \cdot \Vert \alpha \Vert _{\ell ^1}^2 ) - {{\,\mathrm{tr}\,}}(\rho H_0)^2 = \Vert \alpha \Vert _{\ell ^1}^2 - {{\,\mathrm{tr}\,}}(\rho H_0)^2. \end{aligned}$$

(27)

1.2 A.2. Largest degree first

Consider a Hamiltonian decomposed into K collections $\{C^{(k)}\}_{k=1}^{K}$ excluding the identity term: $H=\alpha _{I^{\otimes n}}I^{\otimes n} + \sum _{k=1}^K H_k$ where $H_k=\sum _{Q\in C^{(k)}}\alpha _Q Q$. (Recalling the notation $H_0$ for the traceless part of the Hamiltonian, we note that $H_0 = \sum _k H_k$.) Suppose that for each collection $C^{(k)}$, the Pauli terms commute qubit-wise: for all $Q,R \in C^{(k)}$ and all qubits i, we have $[Q_i,R_i]=0$. In this case, there exists a Pauli operator $P^{(k)}$ of weight n which commutes qubit-wise with each Pauli in $C^{(k)}$.

Consider also a probability distribution $\kappa$ over the collections $\{C^{(k)}\}_{k=1}^K$. Sampling from this distribution provides Algorithm 4.

Consider a single sample giving an estimator $\nu$. Similar to the $\ell ^1$ algorithm we observe that $\nu$ recovers ${{\,\mathrm{tr}\,}}(\rho H)$ in expectation. Specifically, for a fixed collection $C^{(k)}$ and hence a fixed full-weight Pauli operator $P^{(k)}$, let ${\mathbb {E}}_{\mu (P^{(k)})}$ denote the expected value over the measurement outcomes associated with $P^{(k)}$. Now ${\mathbb {E}}_{\mu (P^{(k)})} \mu (P^{(k)}, {{\,\mathrm{supp}\,}}(Q)) = {{\,\mathrm{tr}\,}}(\rho Q)$ whenever $Q\in C^{(k)}$ and if we let ${\mathbb {E}}_{C^{(k)}}$ denote the expected value over the distribution $\kappa (C^{(k)})$ we conclude

$$\begin{aligned} {\mathbb {E}}(\nu ) = {\mathbb {E}}_{C^{(k)}} {\mathbb {E}}_{\mu (P^{(k)})} \nu = {\mathbb {E}}_{C^{(k)}} \frac{1}{\kappa (C^{(k)})} \sum _{Q\in C^{(k)}} \alpha _Q {{\,\mathrm{tr}\,}}(\rho Q) = {{\,\mathrm{tr}\,}}(\rho H) \end{aligned}$$

(28)

Again, we have assumed without loss of generality that H is traceless.

The variance may be calculated as

$$\begin{aligned} {{\,\mathrm{Var}\,}}(\nu ) = \left( \sum _{k=1}^K \frac{1}{\kappa (C^{(k)})} \sum _{Q,R\in C^{(k)}} \alpha _Q \alpha _R \prod _{i\in {{\,\mathrm{supp}\,}}(QR)} {{\,\mathrm{tr}\,}}(\rho QR) \right) - {{\,\mathrm{tr}\,}}( \rho H_0 )^2 \end{aligned}$$

(29)

An alternative formula reads [3, Appendix A]

$$\begin{aligned} {{\,\mathrm{Var}\,}}(\nu ) = \sum _{k=1}^K \frac{1}{\kappa (C^{(k)}) } \sum _{Q,R\in C^{(k)}} \alpha _Q \alpha _R \left( {{\,\mathrm{tr}\,}}(\rho QR) - {{\,\mathrm{tr}\,}}(\rho Q) {{\,\mathrm{tr}\,}}(\rho R) \right) \end{aligned}$$

(30)

Our analysis uses the LDF heuristics in order to obtain such a decomposition. Various heuristics for building decompositions are investigated in [14] for systems up to 36 qubits. The heuristics give numbers of groups that differ by 10% and they conclude LDF is attractive due to its short runtime. For the LDF decomposition, we first construct a graph $G=(V,E)$ where:

• $v_Q \in V$ for all $Q\ne I^{\otimes n}$ such that $\alpha _Q\ne 0$;

• $e_{Q,R}\in E$ if $\{Q_i,R_i\}=0$ for some qubit i.

Second, the vertices of the graph are sorted in decreasing order of their degrees, and the smallest available colour is then progressively assigned to each ordered vertex. Colours correspond to collections in which Pauli operators commute qubit-wise. The LDF heuristics guarantee the number of colours of the graph is at most one plus the degree of the graph: $K \le 1 + \Delta (G)$. With this decomposition constructed, our analysis is done with the following choice for $\kappa$:

$$\begin{aligned} \kappa ( C^{(k)} )&= \frac{\Vert \alpha |_{C^{(k)}} \Vert _{\ell ^1}}{\Vert \alpha \Vert _{\ell ^1}}&\Vert \alpha |_{C^{(k)}} \Vert _{\ell ^1}&= \sum _{Q \in C^{(k)}} | \alpha _Q | \end{aligned}$$

(31)

Qiskit [29] provides an implementation of the decomposition procedure.²

Appendix B: Optimisation of Cost Functions

In Sect. 4 we introduced two cost functions. Specifically, a non-convex cost function in Eq. (14) which requires knowledge of the Hamiltonian H and an arbitrary computational basis state, and a convex “diagonal” cost function in Eq. (16) which requires knowledge of the Hamiltonian only.

We solve these optimisation problems using the method of iterative updates incorporating closed-form solutions obtained with Lagrange multipliers. Specifically given current values $\beta ^{(t)}(P)$ and update step-size $\Delta \in (0,1)$, we may update iteratively:

$$\begin{aligned} \beta ^{(t+1)}(P) = (1-\Delta )\,\beta ^{(t)}(P) + \Delta \,\beta ^\mathrm {closed}(P) \end{aligned}$$

(32)

where the closed-form equations (detailed below) are obtained by solving the optimization of the cost function with Lagrange multipliers to obtain conditions for all $\beta _i(P_i)$ which must hold at optimality. The closed-form equations for the diagonal cost function of Eq. (16) are

$$\begin{aligned} \beta _{i}(P_i) = \frac{ \sum _{Q | Q_i = P_i} \alpha _Q^2 \prod _{j \in {{\,\mathrm{supp}\,}}(Q)} \beta _j(Q_j)^{-1} }{ \sum _{Q | Q_i \ne I} \alpha _Q^2 \prod _{j \in {{\,\mathrm{supp}\,}}(Q)} \beta _j(Q_j)^{-1} } \end{aligned}$$

(33)

while for the original cost function of Eq. (14), they read

$$\begin{aligned} \beta _i(P_i) = \frac{ \sum _{ (Q,R) \in {\mathcal {I}}_{Z^{\otimes n}} | Q_i = R_i = P_i} \alpha _Q \alpha _R \prod _{j|Q_j = R_j \ne I} \beta _j(Q_j)^{-1} \prod _{j|Q_j \ne R_j} m_j }{ \sum _{ (Q,R) \in {\mathcal {I}}_{Z^{\otimes n}} | Q_i = R_i \ne I} \alpha _Q \alpha _R \prod _{j|Q_j = R_j \ne I} \beta _j(Q_j)^{-1} \prod _{j|Q_j \ne R_j} m_j }. \end{aligned}$$

(34)

We can confirm that if Eq. (32) converges for some $t = T$ and $\Delta \in (0,1)$, then the values $\beta ^{(T)}(P)$ at convergence are the closed-form equations. This is because by arranging the terms of the equation, we have

$$\begin{aligned} \left| \beta ^{(T+1)}(P) - \beta ^{(T)}(P)\right| = \Delta \left| \beta ^{(T)}(P) - \beta ^\mathrm {closed}(P)\right| , \end{aligned}$$

(35)

where the left-hand side of the above equation approaches zero at the convergence. Also, at every iterative update the constraints (that $\beta$ is a product probability distribution) are always satisfied whenever initialisation occurs with a random collection of probability distributions. Finally, we point out the use of the update step-size $\Delta$ in Eq. (32) was introduced in [30] where it is called smoothed updating.