Mean Curvature Flow in Null Hypersurfaces and the Detection of MOTS

Abstract

We study the mean curvature flow in 3-dimensional null hypersurfaces. In a spacetime a hypersurface is called null, if its induced metric is degenerate. The speed of the mean curvature flow of spacelike surfaces in a null hypersurface is the projection of the codimension-two mean curvature vector onto the null hypersurface. We impose fairly mild conditions on the null hypersurface. Then for an outer un-trapped initial surface, a condition which resembles the mean-convexity of a surface in Euclidean space, we prove that the mean curvature flow exists for all times and converges smoothly to a marginally outer trapped surface (MOTS). As an application we obtain the existence of a global foliation of the past of an outermost MOTS, provided the null hypersurface admits an un-trapped foliation asymptotically.

1 Introduction

Let (M, g) be a four dimensional, time-oriented Lorentzian manifold or spacetime with Levi-Civita connection D, where for convenience we write

$$\begin{aligned} \begin{aligned} \langle X,Y\rangle :=g(X,Y) \end{aligned} \end{aligned}$$

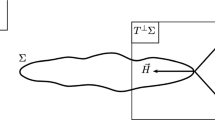
for vector fields X, Y of M. Let $\Sigma \subset M$ be an embedded spacelike 2-sphere. The second fundamental form of $\Sigma$ in M and the corresponding mean curvature vector are denoted by

$$\begin{aligned} \begin{aligned} \mathrm {II}\left( V,W\right) = (D_{V}W)^{\perp },\quad {H} = {{\,\mathrm{tr}\,}}_{\Sigma }\mathrm {II}, \end{aligned} \end{aligned}$$

for all sections $V,W\in \Gamma (T\Sigma )$. For a future directed null normal $l\in \Gamma (T^\perp \Sigma )$, the conditions

$$\begin{aligned} \begin{aligned} -\langle l,{H}\rangle > 0, \quad -\langle l,{H}\rangle <0 \end{aligned} \end{aligned}$$

on $\Sigma$ are called outer un-trapped, or outer trapped respectively. Those properties are referred to hold weakly, provided the respective weak inequality holds. If the space-time (M, g) is globally hyperbolic satisfying the null energy condition, then the famous singularity theorems of Hawking and Penrose imply (M, g) forms a singularity in the causal future of an outer trapped surface $\Sigma$. A marginally outer trapped surface, or MOTS, is identified by the condition

$$\begin{aligned} \begin{aligned} \langle l,{H}\rangle = 0. \end{aligned} \end{aligned}$$

If a MOTS bounds a family of trapped surfaces and (M, g) is asymptotically predictable, one concludes that a MOTS lies within the black-hole region of (M, g). Consequently, MOTSs are studied as ‘quasi-local versions’ of the event horizon of (M, g), the boundary of the black-hole region.

Our main motivation is to use a geometric flow in locating a MOTS. This idea goes back to work of Tod [30], where he suggested the mean curvature flow to find a MOTS inside a time-symmetric slice of spacetime. Time-symmetry indicates a Riemannian hypersurface fully decoupled (or totally geodesic) from the ambient spacetime geometry. Within such a slice, a MOTS is identified as a minimal surface. Given an initial boundary on which to initiate mean curvature flow, work by White [31] showed, provided this region encloses a minimal surface, that an outermost minimal surface will result in the limit of the flow. In the non time-symmetric case, whereby the Riemannian slice observes a non-trivial second fundamental form in spacetime, Tod also suggested the use of null mean curvature flow. Bourni–Moore [5] subsequently formulated a theory of weak solutions to the null mean curvature flow in this setting. Their approach similarly used a weak level set formulation as in the famous work of Huisken–Ilmanen [15] (in the time-symmetric case), and then Moore [22] (in the non-time symmetric case) to address inverse mean curvature flow. Governed by a scalar degenerate elliptic equation, Bourni-Moore were able to use elliptic regularization to establish existence of a weak solution to the null mean curvature flow. They observe convergence to a measure theoretic ‘generalized MOTS’ lying outside the outermost MOTS. Their solution also exhibits a blow-up at the outermost MOTS due to its strong association with a solution to Jang’s equation. In turn, the blow-up of solutions to Jang’s equation is a key property in characterising a MOTS as in the celebrated proof of the Positive Mass Theorem by Schoen–Yau [28, 29]. We also mention the work of Eichmair [11] where this blow-up was used to solve the Plateau problem for MOTSs. More specifically, one considers a region within a non time-symmetric slice bounded by an outer trapped region at one end and an outer un-trapped region at the other. Eichmair then developed a versatile technique to force and control a blow-up of Jang’s equation, subsequently showing the existence of a MOTS within this region.

In this paper we propose a new method to find MOTSs, namely by employing the mean curvature flow (MCF) in a null hypersurface of a spacetime. A null hypersurface is characterised by the property that the induced metric inherited from the spacetime is degenerate and more specifically, we will consider null hypersurfaces, which are foliated by spherical leaves. MCF has been widely studied as a flow of hypersurfaces in Riemannian and Lorentzian manifolds. If x denotes a time-dependent family of embeddings of a smooth manifold into a Riemannian or Lorentzian ambient space, MCF can concisely be written as

$$\begin{aligned} \begin{aligned} \dot{x} = \Delta x = {H}, \end{aligned} \end{aligned}$$

where $\Delta$ is the Laplace-Beltrami operator with respect to the metric induced by $x(t,\cdot )$ and $\dot{x} = \dot{x}(\cdot ,\xi )$ is the velocity of the curve $t\mapsto x(t,\xi )$, $\xi$ being an element of the embeddings’ common domain, which will be $\mathbb {S}^{2}$ in this paper. For any embedding, $\Delta x$ is perpendicular to the hypersurface and hence proportional to a chosen normal vector field. Then

$$\begin{aligned} \begin{aligned} \dot{x} = -\sigma H\nu , \end{aligned} \end{aligned}$$

where $\sigma = \langle \nu ,\nu \rangle$ is the signature of the ambient space and $H = |{H}|.$ This is one of the most important equations of geometric analysis and the literature is vast and exponentially growing. We do not give a very detailed account here. In the smooth setting it was pioneered by Huisken for convex hypersurfaces of the Euclidean space [14] and for entire graphs by Ecker–Huisken [9]. Huisken-Sinestrari have also developed surgery in the 2-convex setting [16]. Other important aspects of MCF relate to geometric pinching estimates [1, 6, 19], Harnack inequalities [13] and ancient solutions [4].

In the Lorentzian setting there are convergence results for spacelike entire graphs [8, 17]. In higher codimension the picture is much less developed and good results are usually only available under strong pinching conditions on the initial hypersurface, e.g. [2, 3].

To the best of our knowledge, MCF has never been studied as a flow within a null hypersurface $\mathcal {N}$ as we propose to do it here. The problems are obvious: The normal to any spacelike surface within $\mathcal {N}$ is a null vector and hence a representation of MCF in either of the above forms is impossible. Neither is there a Levi-Civita connection nor a unit normal vector field. We believe that the best way to write MCF in this setting is to take

$$\begin{aligned} \begin{aligned} \dot{x} = {{\,\mathrm{pr}\,}}_{T\mathcal {N}}H, \end{aligned} \end{aligned}$$

(1.1)

where ${{\,\mathrm{pr}\,}}_{T\mathcal {N}}$ is the skew-orthogonal projection of a vector onto $T\mathcal {N}$, see Section 2. About this approach there is good and bad news. The bad news is of geometric nature: We pick up classical “higher-codimension-problems”, such as the presence of torsion, that we have to deal with. The good news is of PDE-nature: Spacelike MCF in our null hypersurface is automatically graphical and the equation does not see the slope of the graphs, because the flow direction is a null vector. This makes things easier from a PDE point of view. To explain this further, note that graphical MCF in Euclidean (Lorentzian) space can be written as

$$\begin{aligned} \begin{aligned} \partial _{t}\omega = -\sigma H\sqrt{1\pm |\nabla \omega |^{2}}, \end{aligned} \end{aligned}$$

where $\omega$ is the graph function of the flow hypersurfaces. However, as we shall see later in Section 2, in a suitable gauge MCF in a null hypersurface is given by

$$\begin{aligned} \begin{aligned} \partial _{t}\omega = -H. \end{aligned} \end{aligned}$$

It is interesting to see how this flow somehow seems to “interpolate” between its Riemannian and Lorentzian relatives. It is important to note that this flow differs entirely from the previously mentioned null mean curvature flow by Bourni-Moore [5], as their flow is a variation of hypersurfaces in a Riemannian manifold.

In this paper we show that (1.1) is capable of doing the following: Given a null hypersurface $\mathcal {N}$ supporting a trapped surface or MOTS, we identify fairly generic constraints on $\mathcal {N}$ for which our mean curvature flow (1.1) from any outer un-trapped initial cross-section exists for all times and converges smoothly to a MOTS.

1.1 Main results

Under some sufficient conditions on a null hypersurface $\mathcal {N}$, we prove the long-time existence of the mean curvature flow for spacelike spherical cross-sections within $\mathcal {N}$ and show that it converges to a MOTS. To formulate the result, we go over notation very briefly. For a detailed description see Section 2. In the following theorem, R denotes the Riemann tensor as defined in (2.1) and G is the associated Einstein tensor. The past directed null vector k is part of a null basis $\{k,l\}\subset \Gamma (T^{\perp }\Sigma )$, $\Sigma \cong \mathbb {S}^2$, given by:

$$\begin{aligned} \begin{aligned} \langle l,l \rangle = 0,\quad \langle k,l \rangle =2,\quad \langle k,k \rangle =0. \end{aligned} \end{aligned}$$

(1.2)

If we also denote by k the unique null geodesic vector field extension throughout $\mathcal {N}$, then we may rescale to a vector field , for some $a\in C^\infty (\mathcal {N})$, $a>0$. The 2-tensor represents the second fundamental form of the null hypersurface with respect to , see (2.2) We take to be its traceless part. Finally,

for smooth vector fields V, W on M. Here is our main result.

Theorem 1.1

Let (M, g) be a 4-dimensional, time-oriented Lorentzian manifold, $\Sigma _{0}\subset M$ a weakly outer trapped two-sphere with respect to a future directed null normal section l, and let $\mathcal {N}$ be the null hypersurface generated by the past directed null partner k of l. Now consider , for $a\in C^\infty (\mathcal {N})$, $a>0$, satisfying the gauge condition:

(1.3)

whereby $\kappa = da(k)$. Then, if the null hypersurface $\Omega \subset \mathcal {N}$ generated by and $\Sigma _{0}$ admits an outer un-trapped cross-section $\Sigma _{\omega _{0}},$ the mean curvature flow

(1.4)

initiated at $\Sigma _{\omega _{0}}\subset \Omega$ exists for all times and converges smoothly to a MOTS.

The subscript $\omega _{0}$ to the initial hypersurface indicates that $\Sigma _{\omega _{0}}$ is given as the graph of a function $\omega _{0}$ on $\Sigma _{0}$, a property that is preserved throughout the flow. The flow hypersurfaces are then denoted by $\Sigma _{\omega _{t}}$, while $L_{\omega _{t}}$ is the unique null partner of with respect to $\Sigma _{\omega _{t}}$ as in (1.2). All tensor norms $|\cdot |$ in this and the following theorem are with respect to the induced metric on the background foliation of $\mathcal {N}$, see Section 2 for a detailed account.

The gauge condition (1.3) described in Theorem 1.1 translates to a family of ODE inequalities on the scaling $a\in C^\infty (\mathcal {N})$ along k for which a wealth of solutions exist. Associated to each solution is a neighbourhood of $\Sigma _0$ in $\mathcal {N}$ and the -directed one-sided part of that neighbourhood we call $\Omega$. In other-words, Theorem 1.1 indicates that the mean curvature flow exists and drives $\Sigma _{\omega _{0}}$ monotonically towards $\Sigma _{0}$ and into a MOTS, provided an outer un-trapped cross-section exists ‘within reach of $\Sigma _0$’ by one of these neighbourhoods. See Section 2 for an illustration of the situation.

For the 2-tensor K, representing the second fundamental form of $\mathcal {N}$ with respect to k, we can also observe a sufficient condition satisfying the gauge constraint of Theorem 1.1 as an energy type condition on specialised null structures. More specifically, in the case that $\mathcal {N}$ is a Null Cone, whereby ${{\,\mathrm{tr}\,}}K>0$ throughout $\mathcal {N}$:

Theorem 1.2

Let $\mathcal {N}$ be a Null Cone admitting a weakly outer trapped cross-section $\Sigma _0\subset \mathcal {N}$, and an outer un-trapped cross-section $\Sigma _{\omega _{0}}\subset \mathcal {N}$ to the timelike past of $\Sigma _0$. If the region bounded by $\Sigma _0,\Sigma _{\omega _{0}}$ satisfies

$$\begin{aligned} \begin{aligned} G(k,k)\ge \tfrac{5}{2}|\hat{K}|^2+2{{\,\mathrm{tr}\,}}K|\hat{K}|+2|{\hat{\alpha }}|, \end{aligned} \end{aligned}$$

(1.5)

whereby $\alpha (V,W) := \langle R_{kV}k,W \rangle$, then the mean curvature flow (1.4) initiated at $\Sigma _{\omega _{0}}\subset \mathcal {N}$ exists for all times and converges smoothly to a MOTS.

Remark 1.3

• (i) Note, in Schwarzschild space we have $G = {\hat{K}} = {\hat{\alpha }} = 0$. This can be viewed as the simplest setting of our theorem: The metric in so-called ingoing Eddington-Finkelstein coordinates reads

  $$\begin{aligned} \begin{aligned} g = -\left( 1-\frac{2M}{r}\right) dv^{2}+2dvdr+r^{2}\sigma , \end{aligned} \end{aligned}$$

  where $\sigma$ is the round metric on $\mathbb {S}^{2}$ and M is the mass. A standard null cone is $\Omega = \{v=v_{0}\}$ for some constant $v_{0}$. Then the slice $\Sigma _{0}=\{r = 2M\}$ is a MOTS, while the slices $\{r>2M\}$ are outer un-trapped. In fact, this MOTS is the strict outermost MOTS in the sense of Definition 5.1. See [25] or [26] for a detailed verification of these statements. Theorem 1.2 applies with any spacelike outer un-trapped graph over $\Sigma _{0}$.

• (ii) The assumption of $\Sigma _{0}$ being a topological two-sphere is not essential. We include this assumption because we formally rely on several calculations from [25], where it is a standing assumption throughout the paper. For convenience of the reader, we do not want to make any statements which can not easily be checked from the given references, so we stick to this assumption. However, we believe it is not necessary.

• (iii) Finally, we remark that energy condition like (1.3) and (1.5) are not uncommon to obtain gradient estimates for mean curvature (type) flows, see for example [10, 18].

We also obtain a past foliation of an outermost MOTS, provided $\mathcal {N}$ admits an asymptotically un-trapped foliation to the past of the MOTS. We refer to Section 5 for details. Briefly, we assume $\mathcal {N}\cong (\Lambda _-,\Lambda _+)\times \mathbb {S}^2$, where the interval $(\Lambda _-,\Lambda _+)$ is generated by the vector field k ($\Lambda _+=\infty$ included).

Theorem 1.4

Let M and $\mathcal {N}$ satisfy the conditions of Theorem 1.1, further we assume that $\mathcal {N}$ admits an outer un-trapped foliation in a neighbourhood of ${\Lambda }_+$. Then there exists a strict outermost MOTS $\Sigma _{out}\subset \mathcal {N}$ and a global foliation of $\mathcal {N}$ by outer un-trapped surfaces to the timelike past of $\Sigma _{out}$.

The paper is organized as follows. In Section 2 we introduce the underlying null geometry and the mean curvature flow equation in a detailed manner. In Section 3 we prove the required a priori estimates, which are estimates up to $C^{1}$ in view of the quasi-linearity of the equation. In Section 3 we complete the proof of Section 1.1, in Section 4 we prove Theorem 1.2, while in Section 5 we prove Theorem 1.4.

2 Setup

Let (M, g) be a four dimensional, time-oriented Lorentzian manifold with Levi-Civita connection D, the convention from [23] for the Riemann tensor

$$\begin{aligned} \begin{aligned} R_{XY}Z:= D_{[X,Y]}Z-[D_X,D_Y]Z \end{aligned} \end{aligned}$$

(2.1)

and Einstein tensor

$$\begin{aligned} \begin{aligned} G = {{\,\mathrm{Rc}\,}}- \tfrac{1}{2} S g, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {{\,\mathrm{Rc}\,}}(X,Y) = {{\,\mathrm{tr}\,}}_{g}\langle R_{X\cdot }Y,\cdot \rangle ,\quad S = {{\,\mathrm{tr}\,}}_{g}{{\,\mathrm{Rc}\,}}. \end{aligned} \end{aligned}$$

Let $\Sigma \hookrightarrow M$ be the embedding of a spacelike two-sphere. The second fundamental form of $\Sigma$ in M and the corresponding mean curvature vector are denoted by

$$\begin{aligned} \begin{aligned} \mathrm {II}\left( V,W\right) =(D_{V}W)^{\perp },\quad {H}={{\,\mathrm{tr}\,}}_{\Sigma }\mathrm {II}, \end{aligned} \end{aligned}$$

for all $V,W\in \Gamma (T\Sigma )$. We mostly follow the notation from [25].

2.1 Null geometry

We now briefly describe null hypersurfaces in (M, g). By definition, a null hypersurface $\mathcal {N}\subset M$ is a smooth hypersurface such that the induced metric $g|_{\mathcal {N}}$ is degenerate. We also assume $\mathcal {N}$ is orientable. We may therefore observe a global vector field , such that

for each $p\in \mathcal {N}$. In particular this gives . For $p\in \mathcal {N}$, the hypersurface structure of $\mathcal {N}$ also ensures a neighbourhood $\mathcal {U}$ of p in M and a smooth function $\upsilon \in C^\infty (\mathcal {U})$ such that

$$\begin{aligned} \begin{aligned} \mathcal {V}:=\mathcal {U}\cap \mathcal {N}= \{\upsilon =0\}. \end{aligned} \end{aligned}$$

Moreover, if $q\in \mathcal {V}$, we have $(D\upsilon )_q^\perp = T_q\mathcal {N}$, where we denote $D\upsilon :=\text {grad}(\upsilon )$. Consequently, the non-degeneracy of the ambient metric g enforces that

giving $\langle D\upsilon ,D\upsilon \rangle |_\mathcal {V} \equiv 0$. From the identity

$$\begin{aligned} \begin{aligned} D_{D\upsilon }D\upsilon = \tfrac{1}{2}D\langle D\upsilon ,D\upsilon \rangle \end{aligned} \end{aligned}$$

we conclude therefore that $T_q\mathcal {N}\subset (D_{D\upsilon }D\upsilon )^\perp _q$ giving

for some $\kappa \in C^\infty (\mathcal {N})$. It follows that integral curves along are pre-geodesic, and $\mathcal {N}$ is in-fact ruled by null geodesics. In the theory of general relativity, $\mathcal {N}$ represents the geometry of a given light-ray congruence in spacetime.

Now we introduce the second fundamental form of $\mathcal {N}$, for $X,Y\in \Gamma (T\mathcal {N})$:

(2.2)

This symmetric 2-tensor is defined up-to a scaling of . For $X,Y\in \Gamma (T\mathcal {N})$, $c\in C^\infty (\mathcal {N})$, we also observe the properties:

It follows that both the induced metric and the second fundamental form at $p\in \mathcal {N}$ are fully characterised ‘modulo ’. Equivalently, both the metric and second fundamental form on $\mathcal {N}$ at a point, $p\in \mathcal {N}$, are fully determined by their restrictions to any spacelike slice $\Sigma$ through p. Consequently, whenever convenient we use the rather small abuse of notation to denote both the induced metric of any spacelike submanifold $\Sigma \subset \mathcal {N}$ at p and $(g|_\mathcal {N})_p$, by $\gamma _p$. Similarly, we will simply denote by the restriction of to any spacelike $\Sigma \subset \mathcal {N}$ at p. We also notice the function

is independent of any spacelike slice $\Sigma$ through p, giving a well defined function . Finally, we bring to the attention of the reader that due to the symmetries of the Riemann curvature tensor, the same notational conventions (as for ) may be adopted for the 2-tensor

2.2 The background foliation

We will now assume a similar construction as in [21]. We may choose a past-pointing null geodesic vector field $k\in \Gamma (T\mathcal {N})$, such that $D_kk = 0$. We then assume the existence of a spacelike 2-sphere $\Sigma _0\subset \mathcal {N}$ and the property that any geodesic along k intersects $\Sigma _0$ precisely once. Consequently, $\mathcal {N}$ is ruled by geodesics of k, denoted $\beta _p(\lambda )$ for $p\in \Sigma _0$, whereby $\beta _p(0) = p$. We also observe

$$\begin{aligned} \begin{aligned} {\Lambda }_+:=\inf \{{\lambda }_+(p)|p\in \Sigma _0\}>0, \end{aligned} \end{aligned}$$

whereby ${\lambda }_+(p):=\sup \{\lambda |\beta _p(\lambda )\in \mathcal {N}\}$. Similarly,

$$\begin{aligned} \begin{aligned} {\Lambda }_-:=\sup \{{\lambda }_-(p)|p\in \Sigma _0\}<0, \end{aligned} \end{aligned}$$

whereby ${\lambda }_-(p):=\inf \{\lambda |\beta _p(\lambda )\in \mathcal {N}\}$. Standard ODE theory ensures the mapping

$$\begin{aligned} \begin{aligned} ({\Lambda }_-,{\Lambda }_+)\times \Sigma _0\rightarrow \mathcal {N}, \end{aligned} \end{aligned}$$

(2.3)

given by $(\lambda ,p)\rightarrow \beta _p(\lambda )$, is a smooth embedding onto an open subset of $\mathcal {N}$. This open subset depends on both our choice of $\Sigma _0$ and our geodesic generator k. In-fact, any rescaling $k\rightarrow a k$ for some $a\in C^\infty (\mathcal {N})$, $a>0$, yields integral curves that reparametrise the family $\{\beta _p\}_{p\in \Sigma _0}$. Any change in ‘base’ $\Sigma _0$ would induce parameter translations for the family $\{\beta _p\}_{p\in \Sigma _0}$. We will fix our choice of k and for convenience we will also assume $({\Lambda }_-,{\Lambda }_+)\times \mathbb {S}^2\cong \mathcal {N}$, by discarding all other points.

Throughout the paper we will consider a re-scaling of k, which we will again denote for some $a>0$, $a\in C^\infty (\mathcal {N})$. We conclude therefore that:

Integral curves of are denoted by for $p\in \Sigma _0$, whereby again. By an analogous analysis as above we get an embedding . We denote the null hypersurface associated to the image of by $\Omega$ and call it the null hypersurface generated by and $\Sigma _{0}$. We also obtain a canonical projection $\pi :\Omega \rightarrow \Sigma _0$ characterised by the property . The flow parameter extends to a coordinate function $s\in C^\infty (\Omega )$ such that , $s|_{\Sigma _0}=0$. The level sets

$$\begin{aligned} \begin{aligned} \Sigma _{s_0}:=\{s=s_0\}\subset \Omega \end{aligned} \end{aligned}$$

of the function s are diffeomorphic to $\Sigma _0$ under the projection $\pi$ and we refer to the foliation

as the background foliation of $\Omega$. We denote by $L_s\in \Gamma (T^{\perp }\Sigma _{s})$ the unique null partner of satisfying

We call a null basis for $T^{\perp }\Sigma _{s}$ and also say that $L_s$ complements in $\Gamma (T^\perp \Sigma _s)$. For geometric quantities along $\{\Sigma _s\}_s$, we write $\gamma _s$ for the induced metric

$$\begin{aligned} \begin{aligned} \chi _s(V,W)&= -\langle \mathrm {II}_s(W,V),L_s \rangle = \langle D_VL_s,W \rangle \end{aligned} \end{aligned}$$

for the second fundamental form and

for the torsion. By allowing any sections $V,W\in \Gamma (T\Omega )$ in these formulas, the tensors $\chi _s,\tau _s$ can naturally be extended to $\Omega$ and we denote these extensions by $\chi$ and $\tau$ respectively. We also drop the subscript from $\gamma _{s}$ and $L_{s}$ and simply write $\gamma$ and L instead. The symbol $\nabla$ denotes the Levi-Civita connection on $\Sigma _{s}$ and also the gradient of a function with respect to $\gamma _{s}$, while $\Delta$ denotes the Laplace operator. For a tensor T on a Riemannian manifold $(\Sigma ,\sigma )$ the tensor ${\hat{T}}$ denotes the traceless part of T, 

$$\begin{aligned} \begin{aligned} {\hat{T}}=T-\tfrac{1}{2} ({{\,\mathrm{tr}\,}}_{\sigma }T)\sigma . \end{aligned} \end{aligned}$$

Finally, we make a comment on norms of ambient quantities, in particular as arising in the main theorems. As the induced metric $\gamma = g_{\mathcal {N}}$ is degenerate, it does not induce a norm on tensors. However, for tensors annihilated by , e.g. and , we can define such norms with respect to the background foliation in the following sense:

(2.4)

where we identified $\mathcal {N}$ as in (2.3) and where coordinates are taken with respect to a local frame $(e_{i})$ for $\Sigma _{s}$. A similar definition applies to . Note that we use the summation convention throughout the paper.

2.3 Graphs in null hypersurfaces

Suppose that $\Sigma _{\omega }\subset \Omega$ is the embedding of a graphical spacelike surface,

$$\begin{aligned} \begin{aligned} \Sigma _{\omega }=\{(\omega (z),z):z\in \Sigma _{0}\} \end{aligned} \end{aligned}$$

for some function $\omega \in C^{\infty }(\Sigma _{0})$, , where the first component in $(\omega (z),z)$ denotes the flow parameter of the background foliation. We extend $\omega$ constantly along integral curves of to a function on $\Omega$. To list the induced geometric quantities of $\Sigma _{\omega }$, we write $L_{\omega }$, $\gamma _{\omega }$, , $\chi _\omega$ and $\tau _{\omega }$ for the null section complementing in $\Gamma (T^{\perp }\Sigma _{\omega })$, the induced metric, its Levi-Civita connection, the second fundamental form with respect to $L_{\omega }$, and the torsion with respect to . Note that due to the annihilating property of for and , the definition of the norm (2.4) does not depend on the cross-section, i.e. is the same on any such graph,

where we have already used our convention to drop the subscript from $\gamma _{s}$ and where indices for the terms on the right hand side are with respect to the local frame of $\Sigma _{\omega }$. For quantities defined solely on the graph, such as or , there is no ambiguity and we use the standard definition of norms, e.g.

2.4 Mean curvature flow

For $\Sigma _{\omega }$ as above the Gaussian formula is

and hence the correct definition for the mean curvature vector of $\Sigma _{\omega }$ in $\Omega$ is

For convenience, we simply denote ${{\,\mathrm{tr}\,}}\chi _\omega :={{\,\mathrm{tr}\,}}_{\gamma _\omega }\chi _\omega .$ Consequently, for $T^{*}>0$ the mean curvature flow of spacelike surfaces in $\Omega$ is a family

$$\begin{aligned} \begin{aligned} x:[0,T^{*})\times \mathbb {S}^{2}\rightarrow \Omega \end{aligned} \end{aligned}$$

of embeddings $x(t,\cdot )$ satisfying

(2.5)

Denote by $(t,\xi )$ elements of $[0,T^{*})\times \mathbb {S}^{2}$ and suppose all flow surfaces are given as graphs

$$\begin{aligned} \begin{aligned} x(t,\mathbb {S}^{2})=\Sigma _{\omega _{t}}=\{(\omega (t,z(x(t,\xi ))),z(x(t,\xi ))):\xi \in \mathbb {S}^{2}\}, \end{aligned} \end{aligned}$$

where z denotes the projection onto $\Sigma _{0}$, i.e. $z = \pi |_{\Sigma _{\omega _t}}$. Then differentiating

$$\begin{aligned} \begin{aligned} \omega (t,z(x(t,\xi )))=s(x(t,\xi )) \end{aligned} \end{aligned}$$

and using gives

$$\begin{aligned} \begin{aligned} \frac{\partial \omega }{\partial t}=-\frac{1}{2}{{\,\mathrm{tr}\,}}\chi _{\omega _t}. \end{aligned} \end{aligned}$$

(2.6)

The right hand side can be expressed in terms of $\omega$, see [25, Lemma 4.1.1]. Namely we have

where the right hand side is evaluated at $(\omega (t,z),z)$. This makes (2.6) a scalar parabolic equation associated to the mean curvature flow, where

On the other hand if we can prove that for a given function $\omega _{0}$, which describes a spacelike surface $x_{0}:\mathbb {S}^{2}\hookrightarrow \Sigma _{\omega _{0}}\subset \Omega$, we have a maximal solution $\omega$ of (2.6), then the surfaces $\Sigma _{t}$ given by

$$\begin{aligned} \begin{aligned} x(t,\xi )=(\omega (t,z(x_{0}(\xi ))),z(x_{0}(\xi ))) \end{aligned} \end{aligned}$$

solve mean curvature flow. Hence we may assume that $0<T^{*}\le \infty$ is the maximal time of smooth spacelike existence for both equations (Fig. 1).

Fig. 1

Mean curvature flow moves $\Sigma _{\omega _{0}}$ monotonically towards $\Sigma _{0}$, and it will find a MOTS in the region enclosed by those two surfaces

3 Estimates

To show that the graphical mean curvature flow exists for all times, we need gradient estimates for the function $\omega$, and hence we have to differentiate equation (2.6). In order to capture the geometric nature of the problem, it is favourable to express ${{\,\mathrm{tr}\,}}\chi _\omega$ in terms of geometric quantities on the hypersurface:

Lemma 3.1

For a graphical spacelike hypersurface of $\Omega$, there hold

• (i)
  

  (3.1)

  For each s, if we identify $\Sigma _s$ with $\Sigma _0$ under the induced diffeomorphism $\pi |_{\Sigma _s}$:

• (ii)
  

  (3.2)
• (iii)
  

Proof

For a tangent vector V of a cross section $\Sigma _{s}$ at $s=\omega (z)$ let

which defines an isomorphism of the tangent space of the cross section to that of the graph.

(i) The formula for $L_{\omega }$ can be checked from the conditions

For (ii) and (iii), by definition there holds

Hence

where in the last equality we used , which gives

We observe (ii) from the penultimate equality above. For (iii), note that for an orthonormal frame $(e_{i})$ of a cross section, the frame $(\tilde{e}_{i})$ is also orthonormal. Hence taking the trace of the final equality gives (iii). $\square$

We will also need the following famous propagation equations, known as the Raychaudhuri optical equations:

Lemma 3.2

For the foliation $\{\Sigma _s\}_s$ of $\Omega$ the following equations hold, where $\pounds$ denotes the Lie derivative:

Proof

For the first two equations, see, for example [25, Prop. 3.1, (7), (8)]. For the third:

where we have used [25, Prop. 3.1, (6)] and , where the latter follows from the symmetries of the Riemann tensor and the fact that is a null vector. $\square$

Along mean curvature flow, we need several evolution equations.

Lemma 3.3

Along the mean curvature flow (2.5) we have the following evolution equations.

• (i) The induced metrics

  $$\begin{aligned} \begin{aligned} \gamma _{\omega }=x^{*}\langle \cdot ,\cdot \rangle \end{aligned} \end{aligned}$$

  of the flow hypersurfaces evolve according to

  

• (ii) The vector $L_{\omega }$ evolves according to

  

• (iii) The function ${{\,\mathrm{tr}\,}}\chi _\omega$ evolves according to

  

  (3.3)

Proof

Fix a local coordinate frame $\partial _{i}$ on $\mathbb {S}^{2}$ and write

$$\begin{aligned} \begin{aligned} x_{i}=x_{*}(\partial _{i}), \end{aligned} \end{aligned}$$

then

$\square$

To calculate $D_{\dot{x}}L_{\omega }$, note that

$$\begin{aligned} \begin{aligned} 0=\langle L_{\omega },L_{\omega } \rangle =\langle D_{\dot{x}}L_{\omega },L_{\omega } \rangle , \end{aligned} \end{aligned}$$

from we get

and finally

For ${{\,\mathrm{tr}\,}}\chi _\omega$, recall its definition

$$\begin{aligned} \begin{aligned} {{\,\mathrm{tr}\,}}\chi _\omega ={{\,\mathrm{tr}\,}}_{\gamma _{\omega }}\langle D_{(\cdot )}L_{\omega },\cdot \rangle =\gamma _{\omega }^{ij}\langle D_{x_{i}}L_{\omega },x_{j} \rangle , \end{aligned} \end{aligned}$$

where coordinates to a tensor denote components with respect to the basis $(x_{1},x_{2})$. First we calculate

Hence

Corollary 3.4

Under the assumptions of Theorem 1.1, the mean curvature flow preserves positive ${{\,\mathrm{tr}\,}}\chi _\omega$ up to $T^{*}$.

Proof

This follows from the strong maximum principle applied to the evolution equation (3.3). $\square$

Now the goal is to deduce an estimate for the norm of the gradient

We first establish the $C^{0}$-estimates.

Proposition 3.5

Under the assumptions of Theorem 1.1, during the evolution the flow ranges in the fixed compact domain enclosed by $\Sigma _{0}$ and $\Sigma _{\omega _{0}}$.

Proof

This follows from the maximum principle applied to the evolution of the graph function

since $\Sigma _{0}$ has ${{\,\mathrm{tr}\,}}\chi \le 0$ and $\Sigma _{\omega _{t}}$ has ${{\,\mathrm{tr}\,}}\chi _{\omega _t}>0$. $\square$

We define the parabolic operator

In the following, $\mathcal {O}(y)$ denotes any function that is bounded up to order one, when $y\rightarrow \infty$, i.e. the estimate

$$\begin{aligned} \begin{aligned} \limsup _{|y|\rightarrow \infty }\frac{|\mathcal {O}(y)|}{|y|}\le C, \end{aligned} \end{aligned}$$

where C depends on the data of the problem (i.e. on $\Omega$ and $\Sigma _{0}$).

Lemma 3.6

Along (2.6) the quantity

satisfies the equation

Proof

We have to differentiate the PDE

(3.4)

covariantly with respect to $\gamma _{\omega } = x^{*}g$ in the variable $z\in \Sigma _{0}$. Pick a local coordinate frame $(\partial _{i})_{1\le i\le 2}$ for $\Sigma _{0}$ and denote by $(x_{i})$ the induced frame on the graph given by

We evaluate the terms in the following expression separately:

• (i) Firstly we have

  

  having used Lemma 3.2 and

  

  (3.5)

  in the penultimate equality.

• (ii) Secondly there is

  

  We notice that we deal with surfaces and hence the Ricci curvature is

  

  where is the Gauss curvature of the graph. Using [25, Prop. 2.1],

  

  We conclude with the help of (3.1), (3.2), the symmetries of the Riemann tensor, (3.5) and

  

  that

  

• (iii) Finally we have, locally extending $\tau$ to the covector bundle of M and using

  

Now we use

and

to deduce

The previous three steps provide all the terms coming from the right hand side of (3.4). For the left hand side we denote by $(\gamma _{\omega }^{ij})$ the inverse of $\langle x_{i},x_{j} \rangle$ and differentiate u in time:

Collecting the terms from items (i)-(iii), we get

giving the result. $\square$

Now we can turn to the $C^{1}$-estimates.

Proposition 3.7

Under the assumptions of Theorem 1.1, along the mean curvature flow starting from any embedded spacelike surface in the null hypersurface $\Omega$, the function

is uniformly bounded on $[0,T^{*})\times \Sigma _{0}$.

Proof

We have to control the right hand side in Lemma 3.6. First we deal with the term involving ${{\,\mathrm{tr}\,}}\chi _{\omega }$. We have

Since

we may complete the square on the second, third and forth terms above to conclude

where we have used Cauchy–Schwarz in the final estimate. Hence, under the assumptions of Theorem 1.1, and using Lemma 3.2,

In order to estimate u, we combine this evolution equation with that of $\omega$, which is

At points where $u>0$, define the auxiliary function

$$\begin{aligned} \begin{aligned} \phi = \log u + f(\omega ), \end{aligned} \end{aligned}$$

with f yet to be determined. Then

At maximal points of $\phi$ we have

and hence at such points

Denoting by $\mathcal {C}\subset \mathcal {N}$ the compact region of Proposition 3.5, we set

and with $\epsilon = \tfrac{1}{2} e^{-\lambda \max \omega _{0}}$ define

$$\begin{aligned} \begin{aligned} f(\omega ) = -\log (e^{-\lambda \omega }-\epsilon ) - \lambda \omega . \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} f' = \frac{\lambda e^{-\lambda \omega }}{e^{-\lambda \omega }-\epsilon } -\lambda ,\quad f''&= -\frac{\lambda ^{2}e^{-\lambda \omega }}{e^{-\lambda \omega }-\epsilon } + \frac{\lambda ^{2}e^{-2\lambda \omega }}{(e^{-\lambda \omega }-\epsilon )^{2}} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} f''&= -\lambda f'-\lambda ^{2} + f'^{2} + 2\lambda f'+\lambda ^{2} = f'^{2} + \lambda f'. \end{aligned} \end{aligned}$$

Hence

This estimate gives a contradiction, if u is too large. Hence u is uniformly bounded in terms of the data of the problem. $\square$

From quasi-linear regularity theory this bootstraps to estimates in $C^{\infty }$.

Proposition 3.8

Under the assumptions of Theorem 1.1, the mean curvature flow starting from any embedded spacelike outer un-trapped surface $\Sigma _{\omega _{0}}$ exists for all times and satisfies uniform estimates in any $C^{k}(\Sigma _{0})$ norm, where $\Sigma _{0}$ is understood to be equipped with its induced metric.

Proof

Due to the assumption, the functions $\omega (t,\cdot )$ are uniformly bounded independently of $t<T^{*}$. Since

the differential $d\omega$ is bounded with respect to the induced metric of $\Sigma _{s=\omega }$, which is in turn equivalent to the induced metric of $\Sigma _{0}$, since the surfaces $\Sigma _{\omega }$ range in a compact set of $\Omega$. Hence $\omega$ solves the quasi-linear equation

$$\begin{aligned} \begin{aligned} \frac{\partial \omega }{\partial t}(t,z)=-\tfrac{1}{2}{{\,\mathrm{tr}\,}}\chi _\omega (t,z), \end{aligned} \end{aligned}$$

to which parabolic regularity theory may be applied, [20, Ch. XII], to obtain $C^{1,\alpha }$ estimates for $\omega$. This is sufficient to start a bootstrap argument involving parabolic Schauder estimates to obtain the $C^{k}$-estimates, see [20], up to time $T^{*}$. The standard result on short-time existence, see for example [12, Thm. 2.5.7], implies that the flow can be continued beyond any finite time and hence we obtain $T^{*}=\infty$. $\square$

3.1 Completion of the proof of Theorem 1.1

The mean curvature flow starting from $\Sigma _{\omega _{0}}$ exists for all times, and the graph functions of its leaves $\Sigma _{\omega _{t}}$ are strictly decreasing due to

$$\begin{aligned} \begin{aligned} \frac{\partial \omega }{\partial t}(t,z)=-\tfrac{1}{2}{{\,\mathrm{tr}\,}}\chi _{\omega _t} \end{aligned} \end{aligned}$$

and the preservation of ${{\,\mathrm{tr}\,}}\chi _{\omega _t}>0$. Hence the pointwise limit

$$\begin{aligned} \begin{aligned} \omega _{\infty }(z)=\lim _{t\rightarrow \infty }\omega (t,z) \end{aligned} \end{aligned}$$

exists and the convergence takes place in the topology of $C^{\infty }$, due to the $C^{k}$-estimates from Proposition 3.8. Integration gives

$$\begin{aligned} \begin{aligned} \infty >|\omega _{\infty }(z)-\omega _{0}(z)|=\tfrac{1}{2}\int _{0}^{\infty }{{\,\mathrm{tr}\,}}\chi _{\omega }(t,z)~dt \end{aligned} \end{aligned}$$

and hence, due to the regularity estimates, the limit is a MOTS:

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }{{\,\mathrm{tr}\,}}\chi _{\omega }(t,\cdot )=0. \end{aligned} \end{aligned}$$

4 Null Cones

In this section we wish to prove Theorem 1.2 as our first application of Theorem 1.1 under the energy condition (1.5). First we need to specialise to a specific null geometry:

Definition 4.1

Let $\mathcal {N}$ be a null hypersurface as described in Section 2. If the second fundamental form of $\mathcal {N}$ associated to the vector field k satisfies the condition ${{\,\mathrm{tr}\,}}K>0,$ we say $\mathcal {N}$ is a Null Cone.

In general relativity the Einstein tensor G is coupled to the stress-energy tensor of matter as modelled by a spacetime (M, g). A somewhat weak consequence of the physical assumption of a non-negative energy density distribution within (M, g) is the so-called null convergence condition

$$\begin{aligned} \begin{aligned} G(k,k)\ge 0. \end{aligned} \end{aligned}$$

This condition gives rise to Null Cone structures in (M, g). Under fairly generic assumptions on $\mathcal {N}$, we support this claim with the following well known result:

Lemma 4.2

Suppose $\Lambda _+=\infty$, specifically $\mathcal {N}\cong (\Lambda _-,\infty )\times \mathbb {S}^2$, and satisfies the null convergence condition. Then ${{\,\mathrm{tr}\,}}K\ge 0$. If, in addition, the set $E:=\{p\in \mathcal {N}|{{\,\mathrm{tr}\,}}K(p)>0\}$ admits a surjection $\pi :E\rightarrow \Sigma _0$, then $\mathcal {N}=E$.

Proof

If we assume for a contradiction that ${{\,\mathrm{tr}\,}}K(p)<0$ for some $p\in \mathcal {N}$, then taking the geodesic $\beta _p(\lambda )$ associated to k, and applying Lemma 3.2 to the case (giving $\kappa \equiv 0$) we observe

$$\begin{aligned} \begin{aligned} \frac{d}{d\lambda }\frac{1}{{{\,\mathrm{tr}\,}}K} = \frac{1}{2}+\frac{|\hat{K}|^2+G(k,k)}{({{\,\mathrm{tr}\,}}K)^2}\ge \frac{1}{2}, \end{aligned} \end{aligned}$$

as long as ${{\,\mathrm{tr}\,}}K(\lambda )<0$. We conclude $\tfrac{1}{{{\,\mathrm{tr}\,}}K}(\lambda )\ge \tfrac{1}{2} \lambda +\tfrac{1}{{{\,\mathrm{tr}\,}}K}(p)$, so that $\tfrac{1}{{{\,\mathrm{tr}\,}}K}(\lambda )\rightarrow 0$ as $\lambda \rightarrow \lambda _\star ^-$ for some $\lambda _\star ^{-}>0$. Consequently, ${{\,\mathrm{tr}\,}}K(\lambda )\rightarrow -\infty$ as $\lambda \rightarrow \lambda _\star ^-$ contradicting the smoothness assumption of $\mathcal {N}$ under $\Lambda _+ = \infty$. It follows that ${{\,\mathrm{tr}\,}}K\ge 0$ throughout $\mathcal {N}$. If we take $p\in E$, we have for $\lambda \ge 0$

$$\begin{aligned} \begin{aligned} \frac{1}{{{\,\mathrm{tr}\,}}K}(\lambda ) \ge \tfrac{1}{2}\lambda +\frac{1}{{{\,\mathrm{tr}\,}}K}(p)>0, \end{aligned} \end{aligned}$$

which implies ${{\,\mathrm{tr}\,}}K(\lambda )>0$. Alternatively, for $\lambda \le 0$

$$\begin{aligned} \begin{aligned} \infty > \frac{1}{{{\,\mathrm{tr}\,}}K}(p) \ge -\tfrac{1}{2}\lambda +\frac{1}{{{\,\mathrm{tr}\,}}K}(\lambda ), \end{aligned} \end{aligned}$$

again implies ${{\,\mathrm{tr}\,}}K(\lambda )>0$. Since every $q\in \mathcal {N}$ admits a unique geodesic along k intersecting $\Sigma _0$, we conclude the same geodesic intersects the set E under our second hypothesis giving ${{\,\mathrm{tr}\,}}K(q)>0$. $\square$

A consequence of the above result is that any 2-sphere $\Sigma \subset M$ satisfying the outer un-trapped condition to the timelike past

$$\begin{aligned} \begin{aligned} -\langle k,{H} \rangle ={{\,\mathrm{tr}\,}}K>0, \end{aligned} \end{aligned}$$

for $k\in \Gamma (T^\perp \Sigma )$ a past-pointing null vector field, forms a Null Cone geometry if the congruence of null geodesics along k extend infinitely. Moreover, by the first variation of area formula, the variation of the area form dA on $\Sigma$ is

$$\begin{aligned} \begin{aligned} \delta _k(dA) = {{\,\mathrm{tr}\,}}KdA. \end{aligned} \end{aligned}$$

It follows that a Null Cone is foliated by 2-spheres with pointwise expanding area form along k, hence the name Null Cone. In physical spacetimes we observe that any infinite and shear-free Null Cone, i.e. satisfying $\hat{K}\equiv 0$, satisfies (1.5) as a consequence of the null convergence condition. We note that in the shear-free case also ${\hat{\alpha }}$ vanishes, see Lemma 3.2. Consequently, the mean curvature flow can be initiated from any outer un-trapped surface irrespective of it’s proximity to $\Sigma _0$ within a shear-free Null Cone.

4.1 Proof of Theorem 1.2

Our goal is to show the existence of a vector field satisfying the gauge condition of Theorem 1.1. This translates into showing the existence of $a\in C^\infty (\mathcal {C})$, $a>0$, for the region $\mathcal {C}$ bounded by $\Sigma _0$, and $\Sigma _{\omega _{0}}$ satisfying the gauge conditions of Theorem 1.1, and such that the integral curves along cover all of $\mathcal {C}$. For convenience, we will denote $\beta :=\tfrac{1}{2}{{\,\mathrm{tr}\,}}K$, and for a function f, $f':=df(k)$.

We start, for some $v_0\in C^\infty (\Sigma _0)$, $0<v_0<1$, by solving the ODEs

$$\begin{aligned} \begin{aligned} v' = \beta (1-v)^2,\quad v(0,p) = v_0(p). \end{aligned} \end{aligned}$$

From standard existence results, and a phase space analysis we observe:

$$\begin{aligned} \begin{aligned} 0<v(\lambda ,p)<1,\quad \lambda \in [0,\Lambda _+), \end{aligned} \end{aligned}$$

in-fact,

$$\begin{aligned} \begin{aligned} v(\lambda ,p)=\frac{v_0(p)+(1-v_0(p))\int _0^\lambda \beta (u,p)du}{1+(1-v_0(p))\int _0^\lambda \beta (u,p)du}. \end{aligned} \end{aligned}$$

Combining $0<v<1$ with (1.5) and then using Lemma 3.2 we have

$$\begin{aligned} \begin{aligned} \frac{v'}{\beta }&\ge (1-v)^2-\frac{v}{2\beta ^2}(|\hat{K}|^2+G(k,k)-4\beta |\hat{K}|)+\frac{v^2}{2\beta ^2}(\tfrac{7}{2}|\hat{K}|^2+2|\hat{\alpha }|)\\&=1-v+v^2-v\left( \tfrac{1}{\beta }\right) '+2|\hat{K}|\frac{v}{\beta }+\frac{v^{2}}{\beta ^{2}}(\tfrac{7}{4}|\hat{K}|^2+|\hat{\alpha }|), \end{aligned} \end{aligned}$$

giving

$$\begin{aligned} \begin{aligned} \frac{\beta ^{2}}{v^{2}}\left( \left( \frac{v}{\beta }\right) '-v^{2}+v-1\right)&\ge \tfrac{7}{4}|\hat{K}|^2+|\hat{\alpha }|+\beta |\hat{K}|+(2\tfrac{\beta }{v}-\beta )|\hat{K}|\\&\ge \tfrac{7}{4}|\hat{K}|^2+|\hat{\alpha }|+|2\tfrac{\beta }{v}-\beta ||\hat{K}|. \end{aligned} \end{aligned}$$

We claim that our desired $a(\lambda ,p)$ is given by solving the family of ODEs

$$\begin{aligned} \begin{aligned} (\log a)' = \beta v^{-1},\quad a(0,p) = 1. \end{aligned} \end{aligned}$$

The differential inequality above combined with Lemma 3.2 then gives

$$\begin{aligned} \begin{aligned}&\tfrac{1}{2}G(k,k)-\frac{d}{d\lambda }((\log a)'-\beta )-(\log a)'((\log a)'-\beta )\\&\quad \ge |2(\log a)'-\beta ||\hat{K}|+\frac{5}{4}|\hat{K}|^2+|\hat{\alpha }|. \end{aligned} \end{aligned}$$

Multiplying throughout by $2a^2$ and simplifying, we finally observe

since $\kappa = a'$, and , we’ve satisfied the gauge condition of Theorem 1.1. We also observe from the fact that $\infty >a(\lambda ,p)\ge 1$ throughout $\mathcal {C}$, that is globally defined throughout.

5 Existence of a Global Outer Un-trapped Foliation

In physical applications, where $\Omega$ admits an infinite asymptotically flat region, for example the study of the Penrose inequality [24] or mass in spacetimes [7], one observes a foliation of $\Omega$ by future un-trapped surfaces in a neighbourhood of infinity. In-fact, such foliations are plentiful in a neighbourhood of infinity (see for example, [21]). For $\Omega$ also admitting an outermost MOTS $\Sigma _{out}$, it is physically reasonable to also expect this future un-trapped foliation to extend all the way up-to $\Sigma _{out}\subset \Omega$ (see, for example [27]). More specifically, if $\Sigma _{out} := \{s=\omega (0,z)\}$, and $\sigma > 0$, we expect:

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \sigma }\omega (\sigma ,z)> 0,\quad {{\,\mathrm{tr}\,}}\chi _{\omega }(\sigma ,z) > 0. \end{aligned} \end{aligned}$$

In this section, we assume the existence of an un-trapped foliation in a neighbourhood of $\Lambda _+$ (note here $\Lambda _+ = \infty$ is a possibility) and apply Theorem 1.1 to show the existence of a global future un-trapped foliation to the timelike past of the MOTS of convergence. Moreover, also denoted $\Sigma _{out}\subset \Omega$, we show that this MOTS is indeed outermost.

Assuming the existence of a future un-trapped cross-section, we reparametrise our global coordinate chart on $\Omega$ so that a leaf $\Sigma _{\Lambda }$, for some $\Lambda \in (0,\Lambda _+)$, corresponds with this cross-section. We now also assume that all $\{\Sigma _s\}_{\Lambda \le s<\Lambda _+}$ are future un-trapped, in addition to the hypotheses of Theorem 1.1. Thus we may initiate mean curvature flow at $\tilde{\omega }(0,z) = \Lambda$ obtaining the smooth solution $\tilde{\omega }(t,z)$ for $t>0$. Here $\tilde{\omega }$ arises from the solution $\omega$ of (2.6), which arose from fixing the gauge according to the hypotheses of Theorem 1.1. It suffices therefore to show that the two families $\{\Sigma _s\}_{s> \Lambda }$ and $\{\Sigma _{\tilde{\omega }_t}\}_{t>0}$ can be ‘glued and smoothed’ at the boundary $\Sigma _\Lambda$ to form a global future un-trapped foliation. We achieve this is by smoothing the continuous function

$$\begin{aligned} \begin{aligned} v(\lambda ,z):={\left\{ \begin{array}{ll} \tilde{\omega }(\Lambda -\lambda ,z), &{} \text {for}~ \lambda <\Lambda \\ \lambda , &{} \text {for}~ \lambda \ge \Lambda . \end{array}\right. } \end{aligned} \end{aligned}$$

In order to do so, we adapt a standard mollifying procedure that we will now outline. With C chosen so that $\int \eta (s)ds = 1$, we start with the mollifier

$$\begin{aligned} \begin{aligned} \eta (s):={\left\{ \begin{array}{ll} Ce^{\frac{1}{s^2-1}}, &{} \text {for}~ |s|<1 \\ 0, &{} \text {for}~ |s|\ge 1 \end{array}\right. } \end{aligned} \end{aligned}$$

and define $\eta _\epsilon (s):=\tfrac{1}{\epsilon }\eta \left( \tfrac{s}{\epsilon }\right) .$ We mollify $v(\lambda ,z)$:

$$\begin{aligned} \begin{aligned} v_\epsilon (\lambda ,z): = \int \eta _\epsilon (\lambda -u)v(u,z)du. \end{aligned} \end{aligned}$$

It follows that

$$\begin{aligned} \partial _\lambda v_\epsilon (\lambda ,z)&= \int \partial _\lambda \eta _\epsilon (\lambda -u)v(u,z)du,\\ \partial ^\alpha _{z}v_{\epsilon }(\lambda ,z)&=\int \eta _\epsilon (\lambda -u)\partial ^\alpha _{z} v(u,z)du \end{aligned}$$

for any multi-index $\alpha$, and both functions above are smooth. Since

$$\begin{aligned} \begin{aligned} \partial ^\alpha _z v(\lambda ,z) = {\left\{ \begin{array}{ll} \partial _z^\alpha \tilde{\omega }(\Lambda -\lambda ,z), &{}\text {for}~\lambda <\Lambda \\ 0,&{}\text {for}~\lambda \ge \Lambda \end{array}\right. } \end{aligned} \end{aligned}$$

is continuous, standard results imply $\partial _z^\alpha v_\epsilon \rightarrow \partial _z^\alpha v$ uniformly as $\epsilon \rightarrow 0$ on $\mathcal {U}:=(\Lambda -\delta ,\Lambda +\delta )\times \mathbb {S}^2$ for some $\delta >0$. From our constraints on $\Omega$, we observe

$$\begin{aligned} \begin{aligned} {{\,\mathrm{tr}\,}}\chi _{v}(\lambda ,z)>4c>0 \end{aligned} \end{aligned}$$

for some $c>0$ throughout $\bar{\mathcal {U}}$. Define the partition of unity $\{\zeta _i\}_{1\le i\le 3}$ for $\mathbb {R}$,

$$\begin{aligned} \begin{aligned} \zeta _1(\lambda )&= {\left\{ \begin{array}{ll}1, &{} \lambda \le \Lambda -\delta \\ 0, &{} \lambda \ge \Lambda -\frac{1}{2}\delta , \end{array}\right. }\\ \zeta _2(\lambda )&= {\left\{ \begin{array}{ll} 1, &{} |\lambda -\Lambda |\le \frac{1}{2}\delta \\ 0, &{} |\lambda -\Lambda |\ge \delta \end{array}\right. }\\ \zeta _3(\lambda )&= \zeta _1(2\Lambda -\lambda ). \end{aligned} \end{aligned}$$

We may therefore construct the smooth function

$$\begin{aligned} \begin{aligned} \tilde{\omega }_\epsilon (\lambda ,z):=\zeta _1(\lambda )\tilde{\omega }(\Lambda -\lambda ,z)+\zeta _2(\lambda )v_{\epsilon }(\lambda ,z)+\zeta _3(\lambda )\lambda \end{aligned} \end{aligned}$$

and we observe that $\partial _z^\alpha \tilde{\omega }_\epsilon \rightarrow \partial _z^\alpha v$ uniformly on $\bar{\mathcal {U}}$ as $\epsilon \rightarrow 0$. From (3.2), we observe that ${{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}$ depends only upon $\partial _z^\alpha \tilde{\omega }_\epsilon$ for $|\alpha |\le 2$. Consequently,

$$\begin{aligned} \begin{aligned} {{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }_{\epsilon }}(\lambda ,z)\rightarrow {{\,\mathrm{tr}\,}}\chi _{v}(\lambda ,z) \end{aligned} \end{aligned}$$

uniformly as $\epsilon \rightarrow 0$ throughout $\bar{\mathcal {U}}$. We therefore conclude that $\epsilon _0>0$ exists such that ${{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }_{\epsilon }}(\lambda ,z)>c$ throughout $\bar{\mathcal {U}}$ for $\epsilon \le \epsilon _0$,

$$\begin{aligned} \begin{aligned} {{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }_{\epsilon }}(\lambda ,z) = {{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}(\Lambda -\lambda ,z)>0 \end{aligned} \end{aligned}$$

on $\lambda \le \Lambda -\delta$ and

$$\begin{aligned} \begin{aligned} {{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }_{\epsilon }}(\lambda ,z) = {{\,\mathrm{tr}\,}}\chi |_{\Sigma _\lambda }>0 \end{aligned} \end{aligned}$$

on $\lambda \ge \Lambda +\delta$. Finally, we wish to show $\partial _\lambda \tilde{\omega }_\epsilon >0$ for sufficiently small $\epsilon$. From the fact that

$$\begin{aligned} \begin{aligned} \tilde{\omega }_\epsilon (\lambda ,z)\equiv \tilde{\omega }(\Lambda -\lambda ,z) \end{aligned} \end{aligned}$$

for $\lambda \le \Lambda -\delta$, and $\tilde{\omega }_\epsilon \equiv \lambda$ for $\lambda \ge \Lambda +\delta$ it will suffice to show $\partial _\lambda \tilde{\omega }_\epsilon >0$ on $\bar{\mathcal {U}}$ for sufficiently small $\epsilon$. From a simple integration by parts:

$$\begin{aligned} \begin{aligned} \partial _\lambda v_\epsilon (\lambda ,z) = \int _{-\infty }^\Lambda \tfrac{1}{2}\eta _\epsilon (\lambda -u) {{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}(\Lambda -u,z)du+\int _\Lambda ^{\infty }\eta _\epsilon (\lambda -u)du>0, \end{aligned} \end{aligned}$$

leaving us only the sets

$$\begin{aligned} \begin{aligned} \mathcal {U}_{+}:=(\Lambda +\tfrac{1}{2}\delta ,\Lambda +\delta )\times \mathbb {S}^2,\,\,\,\mathcal {U}_-:=(\Lambda -\delta ,\Lambda -\tfrac{1}{2}\delta )\times \mathbb {S}^2 \end{aligned} \end{aligned}$$

to consider. On $\mathcal {U}_-$, we know $\zeta _1'+\zeta _2'\equiv 0$, so taking $\epsilon <\frac{1}{2}\delta$ we observe:

$$\begin{aligned} \begin{aligned} \partial _\lambda \tilde{\omega }_\epsilon (\lambda ,z)&= \zeta _1'(\lambda )\big (\tilde{\omega }(\Lambda -\lambda ,z)-v_\epsilon (\lambda ,z)\big )+\tfrac{1}{2}\zeta _1(\lambda ){{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}(\Lambda -\lambda ,z)\\&\quad +\zeta _2(\lambda )\partial _\lambda v_\epsilon (\lambda ,z)\\&=\zeta _1'(\lambda )\left( \int \eta _\epsilon (\lambda -u)\left( \tilde{\omega }(\Lambda -\lambda ,z)-\tilde{\omega }(\Lambda -u,z)\right) du\right) \\&\quad +\tfrac{1}{2}\zeta _2(\lambda )\int \eta _\epsilon (\lambda -u)\big ({{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}(\Lambda -u,z)-{{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}(\Lambda -\lambda ,z)\big )du\\&\quad +\tfrac{1}{2}{{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}(\Lambda -\lambda ,z). \end{aligned} \end{aligned}$$

We conclude

$$\begin{aligned} \begin{aligned} \partial _\lambda \tilde{\omega }_\epsilon (\lambda ,z)\rightarrow \tfrac{1}{2}{{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}(\Lambda -\lambda ,z) \end{aligned} \end{aligned}$$

uniformly as $\epsilon \rightarrow 0$. Moreover,

$$\begin{aligned} \begin{aligned} \tfrac{1}{2}{{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }}(\Lambda -\lambda ,z)>2c \end{aligned} \end{aligned}$$

giving $\partial _\lambda \tilde{\omega }_{\epsilon }>c$ for some $\epsilon <\min (\epsilon _0,\frac{1}{2}\delta )$. A similar argument shows $\partial _\lambda \tilde{\omega }_\epsilon \rightarrow 1$ uniformly as $\epsilon \rightarrow 0$ on the set $\mathcal {U}_+$. We conclude with some $\epsilon _1$, $\omega _{\epsilon _1}$ satisfies

$$\begin{aligned} \begin{aligned} \partial _\lambda \tilde{\omega }_{\epsilon _1}(\lambda ,z)>0,\quad {{\,\mathrm{tr}\,}}\chi _{\tilde{\omega }_{\epsilon _1}}(\lambda ,z)>0 \end{aligned} \end{aligned}$$

on $\Omega$, $\tilde{\omega }_{\epsilon _1}(\lambda ,z)= \tilde{\omega }(\Lambda -\lambda ,z)$ in a neighbourhood outside the MOTS of convergence for the mean curvature flow, and $\tilde{\omega }_{\epsilon _1}(\lambda ,z)= \lambda$ near $\Lambda _+$.

Definition 5.1

We say a cross-section $\Sigma _{out}\subset \Omega$ is a strict outermost MOTS if $\Sigma _{out}:=\{s=\omega _{out}(z)\}$ is a MOTS, and given any MOTS, $\Sigma :=\{s=\omega (z)\}$, it follows that $\omega _{out}\ge \omega$.

5.1 Completion of the proof of Theorem 1.4

Having established the existence of a global foliation by future un-trapped surfaces, we again for convenience reparametrise $\Omega$ so that the region

$$\begin{aligned} \bigcup _{s\ge 0}\Sigma _s\subset \Omega \end{aligned}$$

consists of future un-trapped leaves $\Sigma _s$, whereby $\Sigma _{out}:=\Sigma _0$ corresponds to the MOTS to which the mean curvature flow converges. From (3.2), we recall the quasi-linear elliptic equation for ${{\,\mathrm{tr}\,}}\chi _\omega$ associated to any graph $\Sigma _\omega :=\{s=\omega (z)\}$. From the fact that ${{\,\mathrm{tr}\,}}\chi _s>0$ for all $s> 0$, we conclude by the strong maximum principle that no graph $\Sigma _\omega$ can satisfy both $\omega (p) = \max {\omega }>0$ and ${{\,\mathrm{tr}\,}}\chi _\omega (p)=0$. Consequently, $\Sigma _{out}$ is a strict outermost MOTS.