Skip to main content
SpringerLink
Log in

Limit Distributions for Euclidean Random Permutations

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

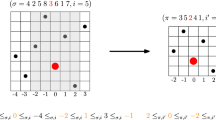
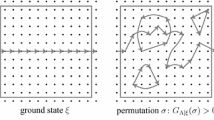
Abstract

We study the length of cycles in the model of spatial random permutations in Euclidean space. In this model, for given length L, density \(\rho \), dimension d and jump density \(\varphi \), one samples \(\rho L^d\) particles in a d-dimensional torus of side length L, and a permutation \(\pi \) of the particles, with probability density proportional to the product of values of \(\varphi \) at the differences between a particle and its image under \(\pi \). The distribution may be further weighted by a factor of \(\theta \) to the number of cycles in \(\pi \). Following Matsubara and Feynman, the emergence of macroscopic cycles in \(\pi \) at high density \(\rho \) has been related to the phenomenon of Bose–Einstein condensation. For each dimension \(d\ge 1\), we identify sub-critical, critical and super-critical regimes for \(\rho \) and find the limiting distribution of cycle lengths in these regimes. The results extend the work of Betz and Ueltschi. Our main technical tools are saddle-point and singularity analysis of suitable generating functions following the analysis by Bogachev and Zeindler of a related surrogate-spatial model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alon, G., Kozma, G.: The probability of long cycles in interchange processes. Duke Math. J. 162(9), 1567–1585 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Angel, O.: Random infinite permutations and the cyclic time random walk. In: DRW, pp. 9–16 (2003)

  3. Angel, O., Holroyd, A.E., Hutchcroft, T., Levy, A.: Mallows permutations as stable matchings. arXiv preprint arXiv:1802.07142 (2018)

  4. Angel, O., Hutchcroft, T.: Personal communication

  5. Barbour, A.D., Granovsky, B.L.: Random combinatorial structures: the convergent case. J. Comb. Theory Ser. A 109(2), 203–220 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  6. Benaych-Georges, F.: Cycles of random permutations with restricted cycle lengths. arXiv preprint arXiv:0712.1903 (2007)

  7. Berestycki, N.: Emergence of giant cycles and slowdown transition in random transpositions and \(k\)-cycles. Electron. J. Probab. 16, 152–173 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Betz, V., Ueltschi, D.: Spatial random permutations and infinite cycles. Commun. Math. Phys. 285(2), 469–501 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Betz, V., Ueltschi, D.: Spatial random permutations and Poisson–Dirichlet law of cycle lengths. Electron. J. Probab. 16, 1173–1192 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  10. Betz, V., Ueltschi, D.: Spatial random permutations with small cycle weights. Probab. Theory Relat. Fields 149(1), 191–222 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  11. Betz, V., Ueltschi, D., Velenik, Y.: Random permutations with cycle weights. Ann. Appl. Probab. 21(1), 312–331 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  12. Bhatnagar, N., Peled, R.: Lengths of monotone subsequences in a Mallows permutation. Probab. Theory Relat. Fields 161(3–4), 719–780 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Biane, P., Pitman, J., Yor, M.: Probability laws related to the Jacobi theta and Riemann zeta functions, and Brownian excursions. Bull. Am. Math. Soc. 38(4), 435–465 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  14. Biskup, M., Richthammer, T.: Gibbs measures on permutations over one-dimensional discrete point sets. Ann. Appl. Probab. 25(2), 898–929 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Björnberg, J.: Large cycles in random permutations related to the Heisenberg model. Electron. Commun. Probab. 20(55), 1–11 (2015)

    MathSciNet  MATH  Google Scholar 

  16. Bogachev, L.V., Zeindler, D.: Asymptotic statistics of cycles in surrogate-spatial permutations. Commun. Math. Phys. 334(1), 39–116 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. Borodin, A., Diaconis, P., Fulman, J.: On adding a list of numbers (and other one-dependent determinantal processes). Bull. Am. Math. Soc. 47(4), 639–670 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Braverman, M., Mossel, E.: Sorting from noisy information. arXiv preprint arXiv:0910.1191 (2009)

  19. Cipriani, A., Zeindler, D.: The limit shape of random permutations with polynomially growing cycle weights. Lat. Am. J. Probab. Math. Stat. 12(2), 971–999 (2015)

    MathSciNet  MATH  Google Scholar 

  20. Dereich, S., Mörters, P.: Cycle length distributions in random permutations with diverging cycle weights. Random Struct. Algorithms 46(4), 635–650 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. Diaconis, P., Shahshahani, M.: Generating a random permutation with random transpositions. Probab. Theory Relat. Fields 57(2), 159–179 (1981)

    MathSciNet  MATH  Google Scholar 

  22. Ercolani, N.M., Ueltschi, D.: Cycle structure of random permutations with cycle weights. Random Struct. Algorithms 44(1), 109–133 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  23. Feng, S.: The Poisson–Dirichlet Distribution and Related Topics: Models and Asymptotic Behaviors. Springer, Berlin (2010)

    Book  MATH  Google Scholar 

  24. Feynman, R.P.: Atomic theory of the \(\lambda \) transition in helium. Phys. Rev. 91(6), 1291 (1953)

    Article  ADS  MATH  Google Scholar 

  25. Gamelin, T.: Complex Analysis. Springer, Berlin (2003)

    Google Scholar 

  26. Gladkich, A., Peled, R.: On the cycle structure of Mallows permutations. Ann. Probab. 46(2), 1114–1169 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  27. Gnedin, A., Olshanski, G.: q-exchangeability via quasiinvariance. Ann. Probab. 38(6), 2103–2135 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  28. Gnedin, A., Olshanski, G.: The two-sided infinite extension of the Mallows model for random permutations. Adv. Appl. Math. 48(5), 615–639 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  29. Grafakos, L.: Classical and Modern Fourier Analysis. Prentice Hall, Englewood Cliffs (2004)

    MATH  Google Scholar 

  30. Hammond, A.: Infinite cycles in the random stirring model on trees. Bull. Inst. Math. Acad. Sin. (N.S.) 8(1), 85–104 (2013)

    MathSciNet  Google Scholar 

  31. Hammond, A.: Sharp phase transition in the random stirring model on trees. Probab. Theory Relat. Fields 161(3–4), 429–448 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  32. Henrici, P.: Applied and Computational Complex Analysis, Volume 2: Special Functions, Integral Transforms, Asymptotics, Continued Fractions, vol. 2. Wiley, New York (1991)

    MATH  Google Scholar 

  33. Koteckỳ, R., Miłoś, P., Ueltschi, D.: The random interchange process on the hypercube. Electron. Commun. Probab. 21(4), 1–9 (2016)

    MathSciNet  MATH  Google Scholar 

  34. Lugo, M.: Profiles of permutations. Electron. J. Comb. 16(1), R99 (2009)

    MathSciNet  MATH  Google Scholar 

  35. Mallows, C.L.: Non-null ranking models. I. Biometrika 44(1/2), 114–130 (1957)

    Article  MathSciNet  MATH  Google Scholar 

  36. Maples, K., Zeindler, D., Nikeghbali, A.: On the number of cycles in a random permutation. Electron. Commun. Probab. 17(20), 1–13 (2012)

    MathSciNet  MATH  Google Scholar 

  37. Matsubara, T.: Quantum-statistical theory of liquid helium. Prog. Theor. Phys. 6(5), 714–730 (1951)

    Article  ADS  MATH  Google Scholar 

  38. Mueller, C., Starr, S.: The length of the longest increasing subsequence of a random Mallows permutation. J. Theor. Probab. 26(2), 1–27 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  39. Mukherjee, S.: Fixed points and cycle structure of random permutations. Electron. J. Probab. 21, 40 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  40. Nikeghbali, A., Zeindler, D.: The generalized weighted probability measure on the symmetric group and the asymptotic behavior of the cycles. Ann. Inst. Henri Poincaré Probab. Stat. 49, 961–981 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  41. Polyakov, A.: Interaction of goldstone particles in two dimensions. Applications to ferromagnets and massive Yang–Mills fields. Phys. Lett. B 59(1), 79–81 (1975)

    Article  ADS  MathSciNet  Google Scholar 

  42. Schramm, O.: Compositions of random transpositions. Isr. J. Math. 147(1), 221–243 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  43. Starr, S.: Thermodynamic limit for the Mallows model on \(S_n\). J. Math. Phys. 50(9), 095208 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  44. Sütő, A.: Percolation transition in the Bose gas. J. Phys. A Math. Gen. 26(18), 4689–4710 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  45. Sütő, A.: Percolation transition in the Bose gas: II. J. Phys. A Math. Gen. 35(33), 6995 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  46. Timashov, A.N.: Random permutations with cycle lengths in a given finite set. Discrete Math. Appl. 18(1), 25–39 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  47. Tóth, B.: Improved lower bound on the thermodynamic pressure of the spin 1/2 Heisenberg ferromagnet. Lett. Math. Phys. 28(1), 75–84 (1993)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  48. Ueltschi, D.: Random loop representations for quantum spin systems. J. Math. Phys. 54(8), 083301 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  49. Yakymiv, A.L.: Random A-permutations: convergence to a Poisson process. Math. Notes 81(5–6), 840–846 (2007)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We thank Daniel Ueltschi for helpful advice and for referring us to the paper of Bogachev and Zeindler [16]. We thank Volker Betz, Gady Kozma, Mikhail Sodin, and Elad Zelingher for useful discussions. We thank Xiaolin Zeng for helpful comments on an earlier version of this work. We thank Omer Angel and Tom Hutchcroft for considering the validity of the statement (17) on the Mallows model and letting us know the conclusion of their calculations. We are grateful to two anonymous referees whose thoughtful comments helped to elucidate the presentation of the results.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Tel Aviv University, 69978, Tel Aviv, Israel

    Dor Elboim & Ron Peled

Authors
  1. Dor Elboim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ron Peled
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ron Peled.

Additional information

Communicated by H. Spohn

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Research of D.E. and R.P. supported by ISF Grant 861/15 and by ERC starting Grant 678520 (LocalOrder).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Elboim, D., Peled, R. Limit Distributions for Euclidean Random Permutations. Commun. Math. Phys. 369, 457–522 (2019). https://doi.org/10.1007/s00220-019-03421-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-019-03421-8

Search

Navigation