Stability of the Positive Mass Theorem for Graphical Hypersurfaces of Euclidean Space

Abstract

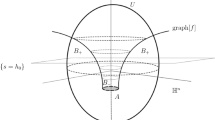
The rigidity of the positive mass theorem states that the only complete asymptotically flat manifold of nonnegative scalar curvature and zero mass is Euclidean space. We prove a corresponding stability theorem for spaces that can be realized as graphical hypersurfaces in ${\mathbb{R}^{n+1}}$. Specifically, for an asymptotically flat graphical hypersurface ${M^n\subset \mathbb{R}^{n+1}}$ of nonnegative scalar curvature (satisfying certain technical conditions), there is a horizontal hyperplane ${\Pi\subset \mathbb{R}^{n+1}}$ such that the flat distance between M and ${\Pi}$ in any ball of radius ${\rho}$ can be bounded purely in terms of n, ${\rho}$, and the mass of M. In particular, this means that if the masses of a sequence of such graphs approach zero, then the sequence weakly converges (in the sense of currents, after a suitable vertical normalization) to a flat plane in ${\mathbb{R}^{n+1}}$. This result generalizes some of the earlier findings of Lee and Sormani (J Reine Angew Math 686:187–220, 2014) and provides some evidence for a conjecture stated there.