Abstract
We consider a family of growth models defined using conformal maps in which the local growth rate is determined by \(|\Phi _n'|^{-\eta }\), where \(\Phi _n\) is the aggregate map for n particles. We establish a scaling limit result in which strong feedback in the growth rule leads to one-dimensional limits in the form of straight slits. More precisely, we exhibit a phase transition in the ancestral structure of the growing clusters: for \(\eta >1\), aggregating particles attach to their immediate predecessors with high probability, while for \(\eta <1\) almost surely this does not happen.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Conformal aggregation processes
Laplacian growth models describe processes where the local growth rate of a piece of the boundary of a growing compact cluster is determined by the Green’s function of the exterior of the cluster. Such growth processes can be used to model a range of physical phenomena, including ones involving aggregates of diffusing particles. Discrete versions can be formulated on a lattice in all dimensions: some famous examples of this type of growth process include diffusion-limited aggregation (DLA) [28], the Eden model [4], or the more general dielectric breakdown model (DBM) [22]. Despite considerable numerical evidence suggesting that the clusters that arise in these processes exhibit fractal features, very few rigorous results are known (for DLA, see [14]) and it remains a formidable challenge to rigorously analyze long-term behavior such as sharp growth rates of the clusters.
One objection that can be leveled at lattice-based models is that the underlying discrete spatial structure could potentially introduce anisotropies in the growing clusters that are not present in the physical setting of the plane or three-dimensional space. Indeed, large-scale simulations in two dimensions demonstrate anisotropy along the coordinate axes [6]. This fact provides one motivation for the study of off-lattice versions of aggregation processes. In the plane, such off-lattice models can be formulated in terms of iterated conformal mappings, providing access to complex analytic machinery. Clusters produced by these conformal growth processes are initially isotropic by construction, but simulations suggest that in many instances, anisotropic structures appear on timescales where the number of aggregated particles becomes large compared to the size of the individual constituent particles. Nevertheless, proving the existence of such small-particle limits, whether anisotropic or not, has proved elusive, similarly to the case of lattice-based models.
A fascinating feature of Laplacian growth models is competition between concentration and dispersion of particle arrivals on the cluster boundary. Protruding structures (“branches”) and their endpoints (“tips”) tend to attract relatively many arrivals, but they compete with each other as well as the remainder of the boundary. (Kesten’s discrete Beurling estimate gives an upper bound on the tip concentration in the case of DLA.) The degree to which tips are favored is determined by the exact choice of growth rule, and several models contain one or more parameters that affect concentration, dispersion, and competition [2, 8, 16, 22].
Previous and recent work on small-particle limits of conformal aggregation models [13, 23, 24, 27] has yielded growing disks, that is, smooth and isotropic shapes; the dispersion effect “wins” in the limit. In this paper, we study a particular instance of a conformal growth model, focusing instead on the concentration aspect of Laplacian growth and showing that anisotropic scaling limits arise in the presence of strong feedback in the growth rule. The scaling limits we exhibit are highly degenerate in the sense that growth, which is initially spread out, favors tips very strongly, and eventually collapses onto a single growing slit.
To state our results, we first describe the general class of processes our object of study fits into. Let \(\mathbf {c}>0\), and let \(f_{\mathbf {c}}\) denote the unique conformal map
having \(f_{\mathbf {c}}(z)=e^{\mathbf {c}}z+\mathcal {O}(1)\) at infinity, and sending the exterior disk \(\Delta \) to the complement of the closed unit disk with a slit of length \(d=d(\mathbf {c})\) attached to the unit circle \(\mathbb {T}\) at the point 1. The logarithmic capacity \(\mathbf {c}\) and the length d of the slit satisfy
in particular, \(d\asymp \mathbf {c}^{1/2}\) as \(\mathbf {c}\rightarrow 0\). In terms of aggregation, the closed unit disk can be viewed as a seed, while the slit represents an attached particle. Typically, we think of the particle as being small compared to the seed.
A general two-parameter framework to model random or deterministic aggregation, based on conformal maps, is given by the following construction. Pick a sequence \(\{\theta _k\}_{k=1}^{\infty }\) in \([-\,\pi , \pi )\), and let \(\{d_k\}_{k=1}^{\infty }\), or, equivalently, \(\{c_k\}_{k=1}^{\infty }\), be a sequence of non-negative numbers connected via (1). From the two numerical sequences \(\{\theta _k\}\) and \(\{c_k\}\), we obtain a sequence \(\{f_k\}_{k=1}^{\infty }\) of rotated and rescaled conformal maps, referred to as building blocks, via
On its own, each individual \(f_k\) grows a slit in the exterior disk, attached at \(e^{i\theta _k}\) and having logarithmic capacity \(c_k\). Finally, we set
Each \(\Phi _n\) is itself a conformal map sending the exterior disk onto the complement of a compact set \(K_n \subset \mathbb {C}\), that is,
The sets \(\{K_n\}_{n=1}^{\infty }\) are called clusters. They satisfy \(K_{n-1}\subset K_n\), and model a growing two-dimensional aggregate formed of n particles. At infinity, we have
where
is the total capacity of the nth cluster.
When modeling random aggregates formed via diffusion, one chooses the angles \(\{\theta _k\}\) to be i.i.d., and uniform in \([-\,\pi ,\pi )\). Due to the conformal invariance of harmonic measure, this has the effect of attaching the nth particle at a point chosen according to harmonic measure (seen from infinity) on the boundary of \(K_{n-1}\). This type of setup has been considered in a number of papers, see for instance [1, 8, 10, 12, 13, 17, 19, 23, 26, 27]; we shall only briefly mention models that are particularly pertinent to our study.
1.2 Aggregate Loewner evolution (ALE)
The main object of study in the present paper is a model we refer to as aggregate Loewner evolution, abbreviated \(\mathrm {ALE}(\alpha , \eta )\), with parameters \(\alpha \in \mathbb {R}\) and \(\eta \in \mathbb {R}\). In \(\mathrm {ALE}(\alpha , \eta )\), conformal maps \(\Phi _n\) are defined as in (2) as follows.
Initialize by setting \(\Phi _0(z)=z\) and letting \(\mathcal {F}_{0}\) be the trivial \(\sigma \)-algebra.
-
For \(k=1, 2, 3, \ldots \), we let \(\theta _k\) have distribution conditional on \(\mathcal {F}_{k-1}=\mathcal {F}(\theta _1,\ldots \theta _{k-1}; c_1, \ldots , c_{k-1})\) given by
$$\begin{aligned} h_k(\theta )=\frac{|\Phi _{k-1}'(e^{{\varvec{\sigma }}+i\theta })|^{-\eta }\text {d}\theta }{\int _{\mathbb {T}}|\Phi _{k-1}'(e^{{\varvec{\sigma }}+i\theta })|^{-\eta }\text {d}\theta }. \end{aligned}$$(4)Here, \({\varvec{\sigma }}>0\) is a regularization parameter, which ensures that the angle distributions are well defined even though \(\Phi '_{k-1}(e^{i\theta })\) has zeros and singularities on \(\mathbb {T}\). The parameter \({\varvec{\sigma }}\) is allowed to depend on the basic logarithmic capacity parameter \(\mathbf {c}\). Typically, we shall take
$$\begin{aligned} {\varvec{\sigma }}={\varvec{\sigma }}(\mathbf {c})=\mathbf {c}^{\gamma } \end{aligned}$$for some appropriate \(\gamma >0\).
-
Next, we define a sequence of logarithmic capacities for \(k=1, 2,3, \ldots \) by taking
$$\begin{aligned} c_k=\mathbf {c}|\Phi _{k-1}'(e^{{\varvec{\sigma }}+i\theta _k})|^{-\alpha }. \end{aligned}$$(5)
We note that \(\mathrm {ALE}(\alpha ,0)\) is the same model as the Hastings–Levitov \(\mathrm {HL}(\alpha )\) model studied in [3, 8, 13, 26], and in particular \(\mathrm {ALE}(0,0)\) coincides with the \(\mathrm {HL}(0)\) model studied in depth in [23, 27]. The Hastings–Levitov model was introduced as a conformal mapping model of dielectric breakdown (DBM) [22], a discrete model in which vertices are added to a growing cluster by drawing bonds from among the neighboring lattice points. At stage n of \(\mathrm {DBM}(\eta )\), a point is added to the cluster \(K_n\) by including a neighbor of \((j,k) \in K_n\) with probability
Here, summation is over lattice neighbors of \(K_n\) and the function \(\phi _n\) is discrete harmonic, and has \(\phi _n=0\) on \(K_n\) and \(\phi _n=1\) on some large external circle.
Off-lattice versions of \(\mathrm {DBM}\) involving non-uniform angle choices determined by the derivative of a conformal map have been considered by several authors. Hastings [7], and subsequently Mathiesen and Jensen [19], study a model that essentially corresponds to \(\mathrm {ALE}(2,\eta )\) modulo a slightly different parametrization in \(\eta \). (In fact, an alternative name for the growth model in this paper could have been \(\mathrm {DBM}(\alpha , \eta )\) or \(\mathrm {HL}(\alpha , \eta )\), but we have opted for a different terminology to avoid confusion with lattice models, and also to emphasize connections with the Loewner equation, see below.) Hastings argues that for large enough exponents, more precisely, for \(\eta \geqslant 3\) in our parametrization, the corresponding clusters become one-dimensional; he also points out that the behavior of the models depends strongly on the choice of regularization.
Another model that fits into this general framework is the Quantum Loewner Evolution model (\(\mathrm {QLE}(\gamma , \eta )\)) of Miller and Sheffield [20, 21] which is proposed as a scaling limit of DBM(\(\eta \)) on a \(\gamma \)-Liouville quantum gravity surface. In the \(\mathrm {QLE}\) construction, particles are attached according to a distribution which depends on the power of the derivative of the cluster map, as in (4), but with an additional term involving the Gaussian Free Field due to the presence of Liouville quantum gravity. In the construction of \(\mathrm {QLE}\), capacity increments are kept constant, as for \(\mathrm {ALE}(0,\eta )\). However, each particle in \(\mathrm {QLE}\) is constructed as an \(\mathrm {SLE}\) curve, rather than the straight slits used in \(\mathrm {ALE}\).
Common to all conformal mapping models of Laplacian growth is the difficulty that derivatives of conformal mappings do not remain bounded away from 0 or \(\infty \) as they approach the boundary and therefore the map \(\theta \mapsto |\Phi '_n(e^{i \theta })|^{-1}\) can be very badly behaved. For instance, even when \(n=1\), \(|\Phi '_n(e^{i \theta })|^{- \eta }\) is not integrable over \(\mathbb {T}\) for certain values of \(\eta \) and hence the \(\mathrm {ALE}(\alpha ,\eta )\) model would not be well defined if we were to use \(|\Phi '_n(e^{i \theta })|^{-\eta }\) as angle density. As mentioned above, for this reason we define the model via the regularization parameter \({\varvec{\sigma }}\) as in (4), and then let \({\varvec{\sigma }}\rightarrow 0\) together with the (pre-image) particle size, controlled by the parameter \(\mathbf {c}\). A similar difficulty arises from the dependence of the particle sizes on the derivatives of the conformal mappings. Although in this case the model is well-defined without the need for a regularization parameter in (5), it is no longer possible to guarantee that the resulting clusters have total capacity bounded above and below. Indeed, even with the presence of a regularization parameter, it is not clear that the total capacity remains bounded as \({\varvec{\sigma }}\rightarrow 0\). The exception is the \(\mathrm {ALE}(0,\eta )\) model: in light of (3), taking \(n\asymp \mathbf {c}^{-1}\) is a natural choice of time-scaling in \(\mathrm {ALE}(0,\eta )\) as with this choice the resulting clusters have total capacity bounded above and below. This in turn means that the total diameter of the clusters \(K_n\) remains bounded as a consequence of Koebe’s 1 / 4-theorem, see [25]. The fact that we have some a priori control over the global size of clusters is our main motivation for moving from studying \(\mathrm {HL}(\alpha )\) with \(\alpha \) large to \(\mathrm {ALE}(0,\eta )\) with \(\eta \) large. Simulations suggest that one-dimensional limits are present also in \(\mathrm {HL}(\alpha )\) for large \(\alpha \) but showing that this is the case seems technically more difficult.
In this paper, we mainly focus on \(\mathrm {ALE}(0,\eta )\) for \(\eta >1\), and show that the conformal maps \(\Phi _n\) converge to a randomly oriented single-slit map in the regime where \(n\asymp \mathbf {c}^{-1}\). This can be viewed as a rigorous version of Hastings’ investigation [7] of \(\mathrm {ALE}(2,\eta )\) for the \(\mathrm {ALE}(0,\eta )\) model. To obtain our convergence results, we exploit what is in a way the most extreme mechanism that could lead to a single-slit limit, namely that of aggregated particles becoming attached to their immediate predecessors. The main difficulties in the proof are that the angle densities induced by slit maps exhibit bad behavior even in the presence of regularization and have maxima and minima of different orders in the regularization parameter \({\varvec{\sigma }}\), making it hard to show convergence to a point mass. Furthermore, the feedback mechanism in (4) is sensitive so that a single “bad” angle can destroy the genealogical structure of the growing slit by leading to the creation of a new, competing tip further down the slit, which could lead to a splitting of growth into two branches.
2 Overview of Results
Clusters that are formed by successively composing slit maps come with a natural notion of ancestry for their constituent particles. We say that a particle j has parent 0 if it attaches directly to the unit disk and that the particle j has parent k if the jth particle is directly attached to the kth particle for \(j>k\). More precisely, suppose that \(\beta _{\mathbf {c}} \in (0, \pi )\) is defined by
so \(e^{\pm i\beta _{\mathbf {c}}}\) is mapped by the basic slit map to the base point of the slit i.e. \(f_{\mathbf {c}}(e^{ \pm i \beta _{\mathbf {c}}}) = 1\). Therefore particle j has parent 0 if \(|\Phi _{j}(e^{i (\theta _j \pm \beta _{\mathbf {c}})})|=1\) and particle j has parent \(k\geqslant 1\) if
where \(\Phi _{k,j}(z)=f_k \circ f_{k+1} \circ \cdots \circ f_j(z)\).
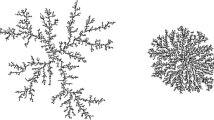
In the \(\mathrm {ALE}(0,\eta )\) model, each successive particle chooses its attachment point on the cluster according to the relative density of harmonic measure (as seen from infinity) raised to the power \(\eta \). As the highest concentration of harmonic measure occurs at the tips of slits, intuitively one would expect that for sufficiently large values of \(\eta \) each particle is likely to attach near the tip of the previous particle. In this paper we show that this indeed happens, and we identify the values of \(\eta \) for which the above event occurs with high probability in the small-particle limit, that is, we show that the probability tends to 1 as \(\mathbf {c}\rightarrow 0\). Figure 1 displays \(\mathrm {ALE}(0,\eta )\) clusters for different values of \(\eta \).
The limiting behavior of the model is quite sensitive to the rate at which \({\varvec{\sigma }}\rightarrow 0\) as \(\mathbf {c}\rightarrow 0\). Figure 2 shows how the angle sequences \(\{\theta _k\}\) in \(\mathrm {ALE}(0,4)\) are affected by the choice of exponent \(\gamma \) when regularizing by \({\varvec{\sigma }}=\mathbf {c}^{\gamma }\). This phenomenon is also observed by Hastings in [7] for a related model. In [13], which deals with slow-decaying \({\varvec{\sigma }}\) scaling limits in a strongly regularized version of \(\mathrm {HL}(\alpha )\), it is shown that the scaling limits of the clusters are disks for all values of \(\alpha \geqslant 0\), provided \({\varvec{\sigma }}\gg (\log \mathbf {c}^{-1})^{-1/2}\). By using similar techniques, combined with those developed in the paper [24], it is possible to prove that the corresponding scaling limits in \(\mathrm {ALE}(0,\eta )\) are again disks for all \(\eta \in \mathbb {R}\), provided \({\varvec{\sigma }}\gg (\log \mathbf {c}^{-1})^{-1}\). (In [24], which focusses on the case \(\eta \leqslant 1\), the stronger result is obtained that \(\mathrm {ALE}(0,\eta )\) clusters converge to disks for all \({\varvec{\sigma }}\gg \mathbf {c}^{\gamma }\) where \(\gamma = 1/3\) if \(\eta <1\) or 1/5 if \(\eta =1\), and a phase-transition is observed at \(\eta =1\) at the level of fluctuations). Together with the result in Theorem 1 stated below, this shows the existence of a transition in the macroscopic shape of the \(\mathrm {ALE}(0,\eta )\) clusters when \(\eta > 1\), from slits to disks as the regularization parameter \({\varvec{\sigma }}\) increases. Simulations suggest that there might be an intermediate regime where a suitable spatial rescaling, as in Fig. 2c, reveals stochastic features in the angle sequence \(\{\theta _n\}\). As we seek results in this paper which do not strongly depend on the choice of regularisation parameter, part of our objective is to identify the minimal value of \(\eta \) for which there exists some \(\sigma _0\) (dependent on \(\mathbf {c}\) and \(\eta \)) such that, provided \({\varvec{\sigma }}<\sigma _0\), with high probability each particle lands on the tip of the previous particle.
The following is the main result of the paper and shows that the \(\mathrm {ALE}(0,\eta )\) model exhibits a phase transition at \(\eta =1\) in the genealogy of the growing cluster in the small-particle limit. See Theorem 9 for a complete statement and proof; in particular we give sufficient conditions on \(\gamma \).
Theorem 1
(\(\mathrm {ALE}(0,\eta )\) model). For \(\mathrm {ALE}(0,\eta )\) with logarithmic capacity parameter \(\mathbf {c}\) and regularization parameter \({\varvec{\sigma }}\), let \(\Omega _{N}=\Omega _{N}^{\eta ,\mathbf {c}, {\varvec{\sigma }}}\) be the event defined by
For each \(\eta >1\), there exists some \(\gamma =\gamma (\eta )\) such that if \(\sigma _0=\mathbf {c}^\gamma \) and if \(N=n(T):=\lfloor T \mathbf {c}^{-1} \rfloor \) for some fixed \(T>0\), then
whereas if \(\eta <1\), then for any \(N >1\),
In the case when \(\eta >1\) and \({\varvec{\sigma }}<\sigma _0\), it follows that, for any \(r>1\) and \(T<\infty \),
and the cluster \(K_{n(t)}\) converges in the Hausdorff topology to a disk with slit of logarithmic capacity t attached at position \(z=e^{i\theta _1}\).
2.1 A related Markovian model
Observe that, for each k, we are free to specify the interval of length \(2 \pi \) in which to sample \(\theta _k\), and this choice does not have any effect on the maps \(\Phi _n\). It is convenient to choose to sample \(\theta _k\) from the interval \([\theta _{k-1}-\pi , \theta _{k-1}+\pi )\). In this case, we can express the event as
(Recall that, by definition, \(\beta _{\mathbf {c}} \in (0,\pi )\) and \(e^{\pm i\beta _{\mathbf {c}}}\) is mapped by the basic slit map to the base point of the slit i.e. \(f_{\mathbf {c}}(e^{ \pm i \beta _{\mathbf {c}}}) = 1\).) One of the main difficulties in analysing this event is that the distribution of \(\theta _k\) conditional on \(\mathcal {F}_{k-1}\) [as defined in (4)], depends non-trivially on the entire sequence \(\theta _1, \ldots , \theta _{k-1}\). In this subsection, we introduce an auxiliary model for random growth in the exterior unit disk in which the sequence of attachment angles is Markovian. The Markov model is relatively straightforward to analyze and exhibits an analogous phase transition to that described above. The remainder of the paper is concerned with examining how ALE\((0,\eta )\) and the Markov model relate to each other.
Set \(\Phi _0^*(z)=z\) and let \(\{\Phi ^*_n\}\) be conformal maps obtained through composing
where each \(f_k^*\) is a building block with \(c_k=\mathbf {c}\), and rotation angle \(\theta _k^*\) having conditional distribution with density
Here, we have set
and suppressed the dependence on \(\mathbf {c}\), \({\varvec{\sigma }}\) and \(\eta \) to ease notation.
In order for the measure above to be well-defined when \(\eta \geqslant 1\), we require \({\varvec{\sigma }}> 0\). In words, the density of the kth angle distribution in this model is obtained by replacing the complicated \((k-1)\)th cluster map of ALE by a simple slit map “centered” at \(\theta ^*_{k-1}\), and with deterministic logarithmic capacity \(\mathbf {c}(k-1)\).
For this model we obtain the following theorem: we again set \(n(t)=\lfloor t/\mathbf {c}\rfloor \), let \(K_{n(t)}^*\) denote the cluster associated with \(\Phi ^*_{n(t)}\), and define the event
Theorem 2
(Markov model). Set \(\sigma _0 = \mathbf {c}^{\gamma ^*}\) where
Then
Furthermore, when \(\eta > 1\) and \({\varvec{\sigma }}<\sigma _0\), for any \(r>1\) and \(T<\infty \),
and the cluster \(K^*_{n(t)}\) converges in the Hausdorff topology to a disk with slit of logarithmic capacity t attached at position \(z=e^{i\theta _1^*}\).
Remark
It can also be shown that \(\lim _{\mathbf {c}\rightarrow 0} \inf _{0<{\varvec{\sigma }}<\sigma _0} \mathbb {P}(\Omega _N^*) = 1\) when \(\eta =1\), provided \(\sigma _0 \rightarrow 0\) exponentially fast as \(\mathbf {c}\rightarrow 0\), but we omit the details here.
We give the relatively straight-forward proof of Theorem 2 in Sect. 5.1. Because of the Markovian nature of the auxiliary model, all that is needed are estimates on the derivative of the explicit slit map to control the densities (6), together with standard martingale arguments.
2.2 Overview of the proof of Theorem 1 and organization of the paper
The main idea for the proof of Theorem 1 is to show that the Markovian model of the previous section is a good approximation of the \(\mathrm {ALE}(0,\eta )\) process. In order to do this one approach would be to try to argue that \(|\Phi '_n(e^{{\varvec{\sigma }}+i\theta })|\) can be globally well approximated by \(|(f^{\theta _{n}}_{n \mathbf {c}})'(e^{{\varvec{\sigma }}+ i \theta })|\), where we use the notation
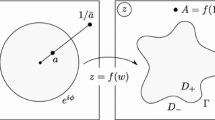
for the rotated slit maps. However, this seems difficult to make work to sufficient precision when evaluating the maps close to the boundary. Specifically, the map \(\Phi '_n(z)\) has zeros (respectively singularities) at each of the points on the boundary of the unit disk which are mapped to the tip (respectively to the base) of one of the slits corresponding to an individual particle. In contrast, for the map \((f^{\theta _{n}}_{n \mathbf {c}})'(z)\), the points corresponding to tips and bases of successive particles coincide and therefore the singularities and zeros corresponding to intermediate particles cancel each other out, leaving only a zero at the point mapped to the tip of the last particle and singularities at the two points which are mapped the base of the first particle (see Fig. 3).
Interactions between nearby tips can be subtle and are in general hard to analyze [2]. Our strategy is instead to establish two properties of the distribution function \(h_{n}(\theta )\).
-
The first is to show that near the tip of the last particle to arrive the derivatives of \(\Phi _n\) and \(f_{n\mathbf {c}}^{\theta _n}\) are in fact very close and so for very small values of \(\theta -\theta _n\), \(h_{n+1}(\theta )\) can be well approximated by \(h_{n+1}^*(\theta |\theta _n)\).
-
The second property is to show that \(h_{n+1}(\theta )\) concentrates the measure so close to \(\theta _{n}\) that even though the probability of attaching to earlier particles is higher than for the Markovian model, \(\Omega _N\) still occurs with high probability, provided we now require
$$\begin{aligned}\gamma > {\left\{ \begin{array}{ll} (\eta ^2+2\eta -1)/ [2(\eta -1)^2] &{}\hbox { if } 1< \eta< 3; \\ (2\eta +1)/[2(\eta -1)] &{}\hbox { if } 3 \leqslant \eta < 7; \\ 5/4 &{}\hbox { if } \eta \geqslant 7 \end{array}\right. } \end{aligned}$$when regularizing by \({\varvec{\sigma }}<\sigma _0=\mathbf {c}^{\gamma }\); see Fig. 4 for plots of the lower bounds on \(\gamma \) and \(\gamma ^*\).
We now give a brief overview of the structure of the paper. In Sect. 3 we provide some background information on the Loewner differential equation, which allows us to represent the aggregate maps \(\Phi _n\) as solutions corresponding to a \([-\,\pi , \pi )\)-valued driving process with equally spaced jump times and positions given by the random angles (4). In particular, we explain how convergence of an angle sequence \(\{\theta _k\}\) allows us to deduce convergence of the corresponding conformal maps \(\Phi _n\).
In Sect. 4 we obtain estimates on the derivative of the slit map used to construct the Markovian model. These estimates lead to moment bounds for \([-\,\pi , \pi )\)-valued random variables constructed from slit map derivatives. The arguments used are elementary in nature, and heavily use the explicit form of the slit map.
In Sect. 5, we first apply our slit map estimates to give a straight-forward proof of Theorem 2. Then we state the detailed estimates on Loewner derivatives at the tip and away from the approximate slit needed to show that \(h_n(\theta )\), the density function for the nth angle \(\theta _n\), has the required behaviour (deferring the proofs until the next Section). Similar arguments to those in the proof of Theorem 2 are used to establish Theorem 1, but since \(\{\theta _k\}\) does not have a Markovian structure, there are further terms to control. We also discuss some extensions of our results, valid for certain instances of the \(\mathrm {ALE}(\alpha ,\eta )\) model as well as related models.
Finally, Sect. 6 contains most of the technical machinery needed for the proof of Theorem 1. In this section, we obtain estimates on the distance between two solutions to the Loewner equation in terms of the distance between their respective driving functions, in the case where we know what one of the solutions is (in our application it is a slit map). These estimates, which we believe may be of independent interest, enable us to obtain much more precise estimates than exist for generic solutions. In particular, our estimates give very good approximations when the conformal mappings are quite close to the boundary, whereas generic estimates blow up in this region. We perform this analysis by using the reverse-time Loewner flow (12) to write the distance between the two solutions as the solution to an ordinary differential equation which we are able to linearize.
2.2.1 Notation
Many of the estimates presented in this paper, especially in Sect. 6, are more precise than what is strictly needed for the proof of our main theorem, in that we frequently keep track of the dependence of constants on parameters, and similar. We have opted to record detailed versions to enable potential further applications where such dependencies may be important. Generic constants, which may change from line to line, will mainly be denoted by the capital letters A and B.
Throughout, we use integer subscripts, or the letters j, k, and n, to denote building block maps, that is, rotated copies of a slit map aggregated to form the cluster maps \(\Phi _n\) and \(\Phi _n^*\). When we need to keep track of scaling, we use \(f_{\mathbf {c}k}\) (boldface subscript) to denote a slit map adding a single slit of logarithmic capacity \(\mathbf {c}k\) (\(k=1,2,\ldots \)) at the point 1. Finally, a generic single-slit map centered at 1 adding a slit of logarithmic capacity \(t>0\) will be denoted \(f_t\).
3 Loewner Flows
We shall make extensive use of Loewner techniques in this paper. Loewner equations describe the flow of families \(\{\Psi _t\}_{t\geqslant 0}\) of conformal maps of a reference domain in \(\mathbb {C}\cup \{\infty \}\) onto evolving domains in the plane in terms of measures on the boundary. We only give a very brief overview here, and refer the reader to [15] and the references therein for a discussion of Loewner theory.
3.1 Loewner’s equation
Let \(\{\mu _t\}_{t> 0}\) be a family of probability measures on the unit circle \(\mathbb {T}\), in this context referred to as driving measures, such that \(t\mapsto \Vert \mu _t\Vert \) is locally integrable. Then the Loewner partial differential equation for the exterior disk,
with initial condition
admits a unique solution \(\{\Psi _t\}_{t\geqslant 0}\) called a Loewner chain [1, 15]. Each \(\Psi _t(z)\) is a conformal map of the exterior disk onto a simply connected domain,
and at \(\infty \) we have the power series expansion \(\Psi _t(z)=e^{t}z+\mathcal {O}(1)\). The growing compact sets \(\{K_t\}_{t\geqslant 0}\) are called hulls, satisfy \(K_s\subsetneq K_t\) for \(s<t\), and have \(\mathrm {cap}(K_t)=e^t\) for \(t\geqslant 0\), where \(\text {cap}(K)\) denotes the capacity of a compact set \(K\subset \mathbb {C}\).
The limit functions appearing in Theorem 1 can be realized in terms of Loewner chains, and in fact have a very simple Loewner representation.
Example 1
(Growing a slit). Let \(\mu _{t}=\delta _1\), a point mass at \(\zeta =1\). Then (7) reads
With initial condition \(f_0(z)=z\), the solution has the explicit representation (viz. [18, p. 772])
The solution precisely consists of the slit maps \(f_t :\Delta \rightarrow \Delta {\setminus } (1,1+d(t)]\), where
This means that the growing hulls are \(K_t=\overline{\mathbb {D}}\cup (1,1+d(t)]\), the closed unit disk plus a radial slit emanating from \(\zeta =1\). We note that the somewhat complicated expression in (8) can be obtained by conjugating the simple formula for a slit map in the upper half-plane \(\mathbb {H}=\{z\in \mathbb {C}:\mathrm {Im}(z)>0\}\), namely
with suitable Möbius transformations.
In this paper, we are mainly concerned with the case \(\mu _t=\delta _{e^{i\xi _t}}\) for some function \(\xi _t:(0,T] \rightarrow \mathbb {R}\) and in that setting, we refer to \(\xi _t\) as a driving term.
The conformal maps arising in \(\mathrm {ALE}(\alpha , \eta )\) have the following simple Loewner representation. We first solve the Loewner equation with driving measure \(\mu _t=\delta _{e^{i \xi _t}}\), where
with \(C_k=\sum _{j=1}^{k}c_k\), and the angles \(\{\theta _k\}\) and logarithmic capacities \(\{c_k\}\) given by (4) and (5), respectively. Explicitly then, the Loewner problem associated with \(\mathrm {ALE}(\alpha , \eta )\) reads
To obtain the composite \(\mathrm {ALE}(\alpha , \eta )\)-maps \(\Phi _n\) described in Sect. 1, we evaluate the solution to (11) at \(t=\mathbf {c}n\); thus
The random driving function \(\xi _t\) can be viewed as a càdlàg jump process exhibiting a complicated dependence structure encoded through angles and capacity increments. When \(\alpha =0\), the dependence structure is only present in the distribution of the increments, as the jump times are deterministic, and equal to \(\mathbf {c}k\) for \(k=1,2,\ldots \). We emphasize that this is the main technical reason why the \(\mathrm {ALE}(0,\eta )\) model is easier to analyze then the general \(\mathrm {ALE}(\alpha ,\eta )\) model or the Hastings–Levitov model \(\mathrm {HL}(\alpha )\).
3.2 Reverse-time Loewner flow
The Loewner Eq. (11) is a first-order partial differential equation, and in the \(\mathrm {ALE}(\alpha , \eta )\) model, it gives rise to a non-linear PDE problem since the driving measures depend on the maps \(f_t\) via their derivatives. As is common in Loewner theory, we shall analyze solutions by passing to the backwards flow associated with (11): this essentially entails employing the method of characteristics to obtain an ordinary differential equation that describes the evolution at hand. See [1, 15] for detailed derivations and discussions.
Let \(T>0\) be fixed. The equation for the backward or reverse-time flow in the exterior disk is
where we define
Then, setting \(u_0(z)=z\), we obtain (see [15, Chapter 4])
where \(\Psi _t\) denotes the solution to the forward Eq. (11) with driving function \(\xi _t\). Note that this holds in general only at the special time T.
The main advantage of the backward flow is the fact that, for each z, (12) is now formally an ODE, simplifying the problem of analyzing and estimating the solution to the corresponding flow problem. Such analysis is carried out in Sect. 6 and will be crucial in the proof of Theorem 1.
3.3 Convergence of Loewner chains
Our strategy will be to argue that the driving function (10) arising in the \(\mathrm {ALE}\) process is close, in the regime where \(n\asymp \mathbf {c}^{-1}\), to the constant driving function \(\xi _t=\theta _1\). We would then like to argue that the resulting conformal maps are close. These kinds of continuity results have been established in several settings, see for instance [10, Proposition 3.1] and [12, Proposition 1], and [9] for a more systematic discussion.
Since the \(\mathrm {ALE}\) driving processes exhibit synchronous jumps, it is natural to measure distances between them in the uniform norm \(\Vert {\cdot }\Vert _ {\infty }\). For \(T>0\), we denote the space of piecewise continuous functions \(\xi :[0, T) \rightarrow \mathbb {R}\) endowed with this norm by \(D_T\). We consider the space \(\Sigma \) consisting of conformal maps \(f(z)=Cz+\mathcal {O}(1)\) as \(z\rightarrow \infty \), with \(C>0\) uniformly bounded, and we endow \(\Sigma \) with the topology of uniform convergence on compact subsets of \(\Delta \). We then view the conformal maps \(\Psi _t\), and hence the aggregate maps \(\Phi _n\), as random elements of \(\Sigma \).
The following result is well-known, but we give a proof for completeness. (With additional work, one could obtain estimates on rates of convergence. We do not pursue this direction here, however see Remark 3 after Lemma 11.)
Proposition 3
Let \(T>0\) be given. For \(j=1,2\) let \(\Psi _{t}^{(j)}, \, 0 \leqslant t \leqslant T,\) be the solution to the Loewner Eq. (7) with driving term \(\xi _{t}^{(j)}\). For every \(\varepsilon > 0\) there exists \(\delta =\delta (\varepsilon ,T)>0\) such that if \(\Vert e^{i\xi ^{(1)}}-e^{i\xi ^{(2)}}\Vert _{\infty } < \delta \), then
Proof
Fix \(s \in [0,T]\) and consider the reverse-time Loewner Eq. (12). We let \(u^{(j)}_{t}\) be the reverse flow driven by \(\xi ^{(j)}_{s-t}\) for \(0 \leqslant t \leqslant s\). Write \(W_{t}^{(j)} = e^{i\xi ^{(j)}_{s-t}}\). Taking the difference and differentiating \(H=u^{(1)}-u^{(2)}\) with respect to t gives
where
and
Since the flows move away from the unit circle, these expressions show that there is a constant A depending only on T such that if \(|z| \geqslant 1+\varepsilon \) then for all \(0 \leqslant t \leqslant s \leqslant T\),
Since \(H(0)=0\),
and consequently, for a different T-dependent A,
Hence we can take \(\delta < e^{-A/\varepsilon ^{2}}\varepsilon ^{3}/A\) and this is clearly uniform in \(0 \leqslant t \leqslant T\). \(\quad \square \)
Thus, we obtain convergence in law of conformal maps provided we can show convergence in law of driving processes. Note that in our main result we have convergence to a degenerate deterministic limit (modulo rotation). As is explained in [10, Section 4.2], we can strengthen the convergence that follows from Proposition 3 in this instance, and obtain convergence of \(K_n\) with respect to the Hausdorff metric in \(\Delta \).
4 Analysis of the Slit Map
In our arguments, we shall need effective bounds on the derivative \(f'_t(z)\) of the slit map, in order to estimate moments of angle sequences, among other things. An explicit formula for the slit map \(f_t:\Delta \rightarrow \Delta {\setminus }(1,1+d(t)]\) was given in (8), while the length d(t) of the growing slit is given by (9). We note that \(f_t(1)=1+d(t)\), and that one can compute that \(f_t(e^{i\beta _t})=f_t(e^{-i\beta _t})=1\) for
We shall refer to \(\exp (i\beta _t)\) and \(\exp (-\,i\beta _t)\) as the base points of the slit. In our scaling limit results, we will make use of the facts that
4.1 Pointwise estimates
We begin by obtaining bounds on the (spatial) derivative of the slit map \(f_t(z)\). To get a feeling for the overall behavior of these derivatives, it is instructive to first compute the derivative of the half-plane slit map,
From this formula, it is apparent that \(F_t'(z)\) has a zero at the point that is mapped to the tip of the slit, and square-root type singularities at points mapping to the base of the slit. We show that the slit map in the exterior disk exhibits the same type of local behavior.
Lemma 4
For all \(t>0\) and \(|z|>1\), we have
where \(H_t(z)\) is holomorphic in z, has \(\lim _{z\rightarrow \infty } H_t(z)=e^{t}\), and satisfies
Proof
Since the slit map \(f_t(z)\) solves the Loewner equation
we have
Differentiating the explicit expression (8) with respect to t, we find that
Inserting this into (16), we obtain
with
It remains to show that \(H_t(z)\) is bounded above and below. But this follows immediately upon writing \(H_t(z)=z^{-1}f_t(z)\), where \(f_t(z)\) is the slit map itself, and observing that \(1 \leqslant |f_t(z)|/|z| \leqslant (1+ d(t)) \vee e^t \leqslant 4e^t\). Finally, we verify that \(z_t=e^{i\beta _t}\) solves \((z+1)^2-4e^{-t}z=0\), and this leads to the factorization \((z+1)^2-4e^{-t}z=(z-e^{i\beta _t})(z-e^{-i\beta _t})\).
\(\square \)
Plots of \(\theta \mapsto |f'_t(e^{{\varvec{\sigma }}+i\theta })|\). Left: \({\varvec{\sigma }}=0.0001\) fixed, \(t=0.01\) (blue) and \(t=0.1\) (dashed). Right: \(t=0.01\) fixed, \({\varvec{\sigma }}=0.0001\) (blue) and \({\varvec{\sigma }}=0.02\) (dashed). Plot with \(t=0.01\) and \({\varvec{\sigma }}=0.2\) (black) shown in both pictures for comparison
Our analysis of the \(\mathrm {ALE}\) model will require local estimates on the derivative of the slit map. Representative graphs of how \(\theta \mapsto |f'_t(e^{{\varvec{\sigma }}+i\theta })|\) varies with t and \({\varvec{\sigma }}\) are shown in Fig. 5.
Lemma 5
Fix \(T>0\), let \(0<t\leqslant T\) and suppose \(|z|-1\leqslant d(t)\). Then the derivative of the slit map admits the following estimates, where \(A_1\) and \(A_2\) are non-zero constants depending only on T:
-
1.
(Near the tip) For \(|\arg z|<\frac{1}{2}\beta _t\),
$$\begin{aligned} A_1\frac{|z-1|}{d(t)}\leqslant |f'_{t}(z)|\leqslant A_2\frac{|z-1|}{d(t)}. \end{aligned}$$ -
2.
(Near the base) For \(|\arg z \pm \beta _t|\leqslant \frac{1}{2}\beta _t\),
$$\begin{aligned} A_1 \leqslant |f'_{t}(z)|\leqslant A_2 \frac{d(t)}{|z|-1}. \end{aligned}$$ -
3.
(Away from tip and base) For \(\frac{3}{2}\beta _t < |\arg z| \leqslant \pi \),
$$\begin{aligned} A_1 \leqslant |f'_{t}(z)|\leqslant A_2. \end{aligned}$$
Proof
We treat the case \(|\arg z|<\frac{1}{2}\beta _t\) first. In light of the global bounds on the function \(H_t(z)\) from Lemma 4, it suffices to estimate the square root expressions appearing in the denominator in (15). We have
If \(0<|z|-1\leqslant d(t)\) this yields
as claimed.
Near the base, the same reasoning as before shows that \(|z-1|\asymp d(t)\). On the other hand,
where the lower bound is attained when \(\arg (z)=\beta _t\). Combining these bounds leads to the claimed estimates for \(|\arg z \pm \beta _t|\leqslant \frac{\beta _t}{2}\).
On each fixed radius, the function \(v:\arg (z)\mapsto \left| \frac{z-1}{(z-e^{i\beta _t})^{1/2}(z-e^{-i\beta _t})^{1/2}}\right| \) is decreasing on \([\frac{3}{2}\beta _t,\pi ]\), with \(v(\pi )=(e^{\log |z|}+1)/((e^{\log |z|}+\cos \beta _t)^2+\sin ^2\beta _t)^{1/2}\geqslant 1\). So in order to obtain the last set of estimates, it suffices to note that v remains bounded above and below as \(\arg (z) \rightarrow \frac{3}{2}\beta _t\), by the same arguments as before. \(\quad \square \)
4.2 Moment computations
We now return to random growth models and present the moment bounds that will be needed in Sect. 5. As before, \({\varvec{\sigma }}>0\) is our regularization parameter, while \(\eta >0\) is a model parameter.
Define the normalization factor
Lemma 6
Fix \(T>0\) and \(\eta \geqslant 0\). There exist constants \(A_1\) and \(A_2\) depending only on T and \(\eta \) such that, for all \(0<t\leqslant T\), the total mass \(Z_t^*\) satisfies the following.
-
(\(\eta < 1\)) For all \({\varvec{\sigma }}> 0\),
$$\begin{aligned} A_1\leqslant Z^*_t\leqslant A_2. \end{aligned}$$(19)In particular, \(Z^*_t\) remains finite as \({\varvec{\sigma }}\rightarrow 0\).
-
(\(\eta >1\)) For all \(0<{\varvec{\sigma }}\leqslant t^{\frac{\eta }{2(\eta -1)}}\),
$$\begin{aligned} A_1d(t)^{\eta }{\varvec{\sigma }}^{-(\eta -1)}\leqslant Z^*_t\leqslant A_2d(t)^{\eta }{\varvec{\sigma }}^{-(\eta -1)}. \end{aligned}$$(20)In particular, \(Z^*_t\) diverges as \({\varvec{\sigma }}\rightarrow 0\) with \({\varvec{\sigma }}\ll t^{\frac{\eta }{2(\eta -1)}}\).
Moreover, for \(\eta >1\) and \(0<{\varvec{\sigma }}\leqslant t^{\frac{\eta }{2(\eta -1)}}\) we have the following estimates:
-
1.
(Near the tip) For \(|\theta |<\frac{\beta _t}{2}\),
$$\begin{aligned} A_1\frac{1}{{\varvec{\sigma }}}\left( 1+\left( \frac{\theta }{{\varvec{\sigma }}}\right) ^2\right) ^{-\eta /2}\leqslant \frac{1}{Z^*_t}|f'_{t}(e^{{\varvec{\sigma }}+i\theta })|^{-\eta }\leqslant A_2\frac{1}{{\varvec{\sigma }}}\left( 1+\left( \frac{\theta }{{\varvec{\sigma }}}\right) ^2\right) ^{-\eta /2}. \end{aligned}$$ -
2.
(Near the base) For \(|\theta -\beta _t|\leqslant \frac{1}{2}\beta _t\),
$$\begin{aligned} A_1{\varvec{\sigma }}^{2\eta -1}d(t)^{-2\eta }\leqslant \frac{1}{Z^*_t}|f'_{t}(e^{{\varvec{\sigma }}+i\theta })|^{-\eta }\leqslant A_2 {\varvec{\sigma }}^{\eta -1}d(t)^{-\eta }. \end{aligned}$$ -
3.
(Away from the tip and base) For \(\frac{3}{2}\beta _t < |\theta | \leqslant \pi \),
$$\begin{aligned} A_1{\varvec{\sigma }}^{\eta -1}d(t)^{-\eta }\leqslant \frac{1}{Z^*_t}|f'_{t}(e^{{\varvec{\sigma }}+i\theta })|^{-\eta }\leqslant A_2{\varvec{\sigma }}^{\eta -1}d(t)^{-\eta }. \end{aligned}$$
Proof
We begin by treating the case \(\eta <1\). In light of Lemma 5, non-trivial global bounds on \(Z_t^*\) from above and below follow immediately from the bounds on \(|f_t'(e^{{\varvec{\sigma }}+ is})|\) for \(|s|>\frac{3}{2}\beta _t\) provided the contribution from \((-\frac{\beta _t}{2}, \frac{\beta _t}{2})\) is finite. Hence it suffices to estimate the integral
where we have used that \(A_1<|e^{{\varvec{\sigma }}+is}-1|/({\varvec{\sigma }}^2+s^2)^{1/2}<A_2\) for \(s, {\varvec{\sigma }}\) small. Next, we note that
and the latter integral is bounded for \(0<t<T\) since \(\eta <1\).
We turn to the case \(\eta >1\). Since the integral \(\int |f_{t}'(e^{{\varvec{\sigma }}+is})|^{-\eta }\text {d}s\) now diverges as \({\varvec{\sigma }}\rightarrow 0\) due to the singularity at \(s=0\), it again suffices to estimate the contribution coming from \(|s|<\beta _t/2\) in order to establish (20). We have
after a change of variables. Since \(\int _0^{\infty }(1+u^2)^{-\eta /2}\text {d}u\) is now finite, the upper bound follows. Similar reasoning together with the assumption that \({\varvec{\sigma }}\leqslant t^{1/2}\) yields the lower bound on the integral. The estimates on the normalized derivative follow upon dividing through by \(Z_t^*\) in Lemma 5. \(\quad \square \)
We now turn to moment bounds for \(\eta >1\).
Lemma 7
For all \(\eta \) and \({\varvec{\sigma }}>0\),
Now suppose \(\eta >1\) and \({\varvec{\sigma }}\) satisfies the hypotheses of Lemma 6. Let \(x\in ({\varvec{\sigma }}, \frac{\beta _t}{2})\). Then, for \(1<\eta < 3\), we have
and for \(\eta =3\), we have
For \(\eta >3\), we have
Under the same assumptions as above, for \(1<\eta < 2\), we have
and for \(\eta =2\),
Finally, for \(\eta >2\),
Proof
The statement that \(\int \theta |f'_t(e^{{\varvec{\sigma }}+i\theta })|^{-\eta }\text {d}\theta =0\) follows immediately from symmetry of the function \(\theta \mapsto |f'_t(e^{{\varvec{\sigma }}+i\theta })|\) for each \({\varvec{\sigma }}\) and t.
We turn to second moments, and deal with the parameter range \(1<\eta \leqslant 3\) first. By Lemma 6,
Performing a change of variables, and assuming \(\eta < 3\), we obtain the integral
as claimed. An obvious modification of the argument leads to bounds for \(\eta =3\).
Finally, we treat the case \(\eta >3\) and show that the second moment decays like \({\varvec{\sigma }}^2\) independently of \(\eta \). It now suffices to examine
The integral on the right now converges since \(\eta >3\), and in fact
To get the lower bound, we use the assumption \(1<x/{\varvec{\sigma }}\) to bound the integral from below. The second assertion of the Lemma follows.
Analogous calculations lead to the quoted bounds on the first moments. \(\quad \square \)
5 Ancestral Lines and Convergence for \(\mathrm {ALE}\)
We now present a proof of our main convergence theorem, conditional on technical results proved in the final section of the paper, and discuss possible extensions of our results.
5.1 Convergence in the Markovian model
We first prove Theorem 2, which we restate for the reader’s convenience. Recall that \(K_{n(t)}^*\) is the cluster associated with \(\Phi ^*_{n(t)}\), and the event
Theorem 2
Set \(\sigma _0 = \mathbf {c}^{\gamma ^*}\) where
Then
Furthermore, when \(\eta > 1\) and \({\varvec{\sigma }}<\sigma _0\), for any \(r>1\) and \(T<\infty \),
and the cluster \(K^*_{n(t)}\) converges in the Hausdorff topology to a disk with slit of logarithmic capacity t attached at position \(z=e^{i\theta _1^*}\).
Proof
Since we can always rotate the clusters \(K_n^*\) by a fixed angle, without loss of generality, we assume that the initial angle \(\theta _1^*=0\). As explained in Sect. 2, we choose to sample \(\theta _k^*\) from the interval \([\theta _{k-1}^*-\pi , \theta _{k-1}^*+\pi )\). This means that we can write \(\theta _n^* = u_2+\cdots +u_n\) where the \(u_k\) are independent \([-\,\pi ,\pi )\)-valued random variables and \(u_k=\theta _k^*-\theta _{k-1}^*\) has symmetric distribution \(h_k^*(\theta |0)\).
First suppose \(\eta >1\). Then by (14) and Lemma 6 there exists some constant A (which may change from line to line), depending only on T and \(\eta \), such that for all \(k\leqslant N\),
and
Therefore
Hence, for \(\eta >1\),
as \(\mathbf {c}\rightarrow 0\).
Now suppose that \(\eta <1\) and \({\varvec{\sigma }}\rightarrow 0\) as \(\mathbf {c}\rightarrow 0\). Using Lemma 5 and setting \(|z|=e^{{\varvec{\sigma }}}\) in (17), and then letting \(\mathbf {c}\rightarrow 0\), we get
If \({\varvec{\sigma }}\) is bounded below, then \(h_k^*\) is uniformly bounded above and below, and \(\mathbb {P}(|u_k|\leqslant \beta _{\mathbf {c}})=2\int _0^{\beta _{\mathbf {c}}}h_k^*(\theta |0)d\theta \rightarrow 0\) since \(\beta _{\mathbf {c}}\rightarrow 0\) with \(\mathbf {c}\).
To show convergence of \(\Phi _{n(t)}^*(z)\) to \(f_t(z)\) for \(t<T\) when \(\eta >1\) and \({\varvec{\sigma }}<\sigma _0\), by Proposition 3 it is enough to show that \(\sup _{n \leqslant N}|\theta ^*_n| \rightarrow 0\) with high probability as \(\mathbf {c}\rightarrow 0\). To do this, we write
and note that \(M^*_n = \sum _{k=2}^n u_k \mathbf {1}_{\{|u_k| < \beta _{\mathbf {c}}/2\}}\) is a martingale. By the same argument as used to show \(\mathbb {P}((\Omega _N^*)^c) \rightarrow 0\),
Convergence of \(\sup _{n\leqslant N}|\theta ^*_n|\) to 0 follows from moment bounds in Lemma 7 together with standard martingale arguments (viz. the proof of Theorem 9). \(\quad \square \)
5.2 The ancestral lines and convergence theorem
We now return to the \(\mathrm {ALE}(0,\eta )\) process and show how the bounds obtained above, together with certain comparison results that will be proved in the next section, allow us to prove the analogue of Theorem 2 for the \(\Phi _n\) maps that generate \(\mathrm {ALE}(0,\eta )\) clusters.
Without loss of generality we may set \(\theta _1=0\). Let
denote the density functions conditional on \(\mathcal {F}_{k-1}\) associated with the angle sequence \(\{\theta _k\}\) of the \(\mathrm {ALE}(0, \eta )\)-model with model parameter \(\eta \in \mathbb {R}\), particle capacity parameter \(\mathbf {c}\in (0,1)\) and regularization parameter \({\varvec{\sigma }}\in (0,1)\). As usual, let \(\mathcal {F}_k\) be the \(\sigma \)-algebra generated by \(\theta _1, \ldots , \theta _k\).
We first state a precise estimate for how well \(|\Phi '_n(e^{{\varvec{\sigma }}+ i \theta })|\) can be approximated by \(|(f^{\theta _{n}}_{n \mathbf {c}})'(e^{{\varvec{\sigma }}+ i \theta })|\). In Sect. 2, we discussed how the intermediate particles are visible in the derivative of \(\Phi _n(z)\) in a way they are not in \(f_{n \mathbf {c}}^{\theta _n}(z)\) (see Fig. 3). The estimates below capture this discrepancy.
Lemma 8
Fix \(T>0\), let \(n \leqslant \lfloor T/\mathbf {c}\rfloor \) and set \(\varepsilon _n=(e^{\varvec{\sigma }}- 1) \vee \sup _{k\leqslant n} |\theta _k|\).
-
(i)
There exists some absolute constant \(A>1\), such that if \(|\theta -\theta _n|<\mathbf {c}^{1/2}\) and \(\varepsilon _n < A^{-1} \mathbf {c}^{1/2}\), then
$$\begin{aligned} \left| \left| \frac{\Phi '_n(e^{{\varvec{\sigma }}+ i \theta })}{(f^{\theta _{n}}_{n \mathbf {c}})'(e^{{\varvec{\sigma }}+ i \theta })} \right| - 1 \right| < A \varepsilon _n^2 \mathbf {c}^{-1}. \end{aligned}$$(22) -
(ii)
There exist absolute constants A and B only dependent on T, such that if \(\varepsilon _n \leqslant A^{-1} \mathbf {c}^{1/2}\), then
$$\begin{aligned} \left| \Phi '_n(e^{{\varvec{\sigma }}+ i \theta }) \right| \geqslant B^{-1} \varepsilon _n^{-1} {\varvec{\sigma }}(1 - \cos (\theta -\theta _n))^{1/2}. \end{aligned}$$
The proof of Lemma 8 relies on a refined analysis of solutions to the Loewner equation in the case where driving functions are uniformly close, and will be presented in Sect. 6 to avoid interrupting the flow of the proof of the main theorem below.
We now prove our main result. For fixed \(T>0\), set \(N=\lfloor T/\mathbf {c}\rfloor \). Recall the definition of \(\Omega _N\) from Sect. 2.
Theorem 9
Set \(\sigma _0 = \mathbf {c}^{\gamma }\) for
where
Then, for all \(T < \infty \),
Furthermore, when \(\eta > 1\) and \({\varvec{\sigma }}<\sigma _0\), for any \(r>1\) and \(T < \infty \),
and hence the cluster \(K_{n(t)}\) converges in the Hausdorff topology to a disk with slit of logarithmic capacity t attached at position 1.
Proof
Fix \(\eta >1\) and let
Observe that, since \({\varvec{\sigma }}< \sigma _0\), we have
Hence, using the fact that \(\gamma >\lambda +1/2\), and that \(A^{-1} \mathbf {c}^{1/2} \leqslant \beta _\mathbf {c}\leqslant A \mathbf {c}^{1/2}\), there exists some \(c_0 > 0\), dependent only on T and \(\eta \), such that if \(\mathbf {c}< c_0\), then \( \{ N_T=N \} \subseteq \Omega _N\). From now on assume that \(\mathbf {c}< c_0\). We shall prove that \(\mathbb {P}(N_T = N) \rightarrow 1\) as \(\mathbf {c}\rightarrow 0\). Once this has been done, it follows that if \(\eta >1\),
Exactly the same argument as Theorem 2 can then be used to show that
if \(\eta < 1\), and that when \(\eta > 1\) and \({\varvec{\sigma }}<\sigma _0\), for any \(r>1\) and \(T<\infty \),
and hence the cluster \(K_{n(t)}\) converges in the Hausdorff topology to a disk with slit of logarithmic capacity t attached at 1.
We turn to the proof. Suppose that \(n < N_T\). As before, using the fact that \({\varvec{\sigma }}< \sigma _0\), we have
where \(\varepsilon _n=(e^{{\varvec{\sigma }}}-1)\vee \sup _{k\leqslant n}|\theta _k|\) as in Lemma 8. Hence there exists some \(0< c_1 < c_0\), dependent only on T and \(\eta \), such that if \(\mathbf {c}< c_1\), then \(\varepsilon _n\) satisfies the conditions of Lemma 8. From now on assume that \(\mathbf {c}< c_1\). Then, by Lemma 8, there exists \(A_n\) such that, if \(|\theta -\theta _n| \leqslant \mathbf {c}^{1/2}\)
and furthermore \(A_n = A_\eta {\varvec{\sigma }}^2 \mathbf {c}^{-1} n^{2\lambda } (\log \mathbf {c}^{-1})^{12 \lambda }\) for \(A_{\eta }\) that depends only on \(\eta \) and T.
We begin by getting estimates on
We have
for some \(B'\) that depends only on \(\eta \) and T. Using the notation of Sect. 2, recall from Lemma 6 that there exist \(A', A''\) depending only on \(\eta \) and T such that
Hence,
for some \(B_\eta \) that depends only on \(\eta \) and T. Set \(B_n=B_\eta {\varvec{\sigma }}^{\eta -1} n^{(\lambda -1/2) \eta } \mathbf {c}^{-(2 \eta - 1)/2} (\log \mathbf {c}^{-1})^{6 \lambda \eta }\).
Observe that the choice of \(\gamma \) ensures that, provided \({\varvec{\sigma }}< \sigma _0\), we have \(N^{(1-\lambda ) \vee 0}A_N\rightarrow 0\) and \(NB_N \rightarrow 0\). We shall see that these conditions are sufficient to prove our result.
Now
Similarly, we can show that
Since \(A_n+B_n \rightarrow 0\) as \(\mathbf {c}\rightarrow 0\) there exists \(0<c_2 \leqslant c_1\), depending only on T and \(\eta \), such that \(A_n + B_n < 1/2\) provided \(\mathbf {c}< c_2\). Assume from now on that \(\mathbf {c}< c_2\). Hence, if \(|\theta -\theta _n| < \mathbf {c}^{1/2}\) then,
where \(\alpha _n = 7(A_n + B_n)\). Equivalently
As in the proof of Theorem 2, we choose to sample \(\theta _k\) from the interval \([\theta _{k-1}-\pi , \theta _{k-1}+\pi )\) and so we can write \(\theta _n = u_2+\cdots +u_n\) where the \(u_k\) are \([-\,\pi ,\pi )\)-valued random variables and, conditional on \(\mathcal {F}_{k-1}\), \(u_k=\theta _k-\theta _{k-1}\) has distribution function \(h_k(\theta +\theta _{k-1})\). We write
where
is a martingale.
We first show \(M_n\) is small with high probability. By Lemma 7,
for some constant A depending only on T and \(\eta \). Hence \(M_n\) is a martingale with quadratic variation
By Freedman’s version of Bernstein’s inequality, see [5, Proposition 1], we obtain that
as desired.
We next turn to the second term in (24). We use that
by the symmetry of \(h^*_k(\theta |0)\). Hence, again by Lemma 7,
for some constant A depending only on T and \(\eta \). Therefore, if \(1<\eta <2\),
and if \(\eta \geqslant 2\),
By our choice of \(\gamma \), there exists \(0<c_3 \leqslant c_2\), depending only on T and \(\eta \), such that
provided \(\mathbf {c}< c_3\). From now on assume that \(\mathbf {c}< c_3\).
Finally, we deal with the last term in (24). The same computation as was used to bound \(Z_n\) can be used to show that
We also have
Hence, putting these two bounds together,
since \({\varvec{\sigma }}< \sigma _0\).
But on the high probability event
we have
and hence \(N_T=N\). \(\quad \square \)
5.3 Modifications of the model
One criticism that can be levelled at the ALE\((0,\eta )\) model, from the point of view of modelling physical phenomena, is that the conformal mappings distort the sizes of particles as they are added to the growing cluster. Using the result proved above that the scaling limit of the ALE\((0,\eta )\) cluster is a growing slit, it can be shown that the size of the nth particle is approximately equal to \(d(\mathbf {c}n) - d(\mathbf {c}(n-1))\). Using the expression for d(t) in (9), we obtain
In particular, the first particle is of size approximately \(2 \mathbf {c}^{1/2}\), whereas all subsequent particles are strictly smaller.
A number of modifications to the model are possible which result in clusters where all of the particles are roughly the same size. The simplest modification (cf. [13]) is to recursively choose a deterministic sequence of capacities with \(c_1=\mathbf {c}\) and \(c_n\) satisfying
Another modification (see [7, 19]) is to take the logarithmic capacity of the nth particle to be
for some regularization parameter \(\tilde{{\varvec{\sigma }}}>0\), not necessarily equal to the angular regularization parameter \({\varvec{\sigma }}\). Closely related (see [1, 26]), is to choose logarithmic capacity \(c_n\) corresponding to slit length
In each of these modified models, the total capacity of the cluster no longer grows linearly in the number of particles and is potentially random. It is therefore necessary to modify the timescale in which to obtain scaling results. More precisely, given some fixed \(T>0\), let
and set \(N=n(T)\). The event \(\Omega _N\) can then be defined as before.
It is relatively straightforward to verify that the proof and conclusion of Theorem 9 still hold for these modified models (and further generalisations). We only state the modified result for \(\eta >1\), as the case \(\eta <1\) is identical to that for the Markov model, for any choice of logarithmic capacity sequence.
Corollary 10
For \(\eta >1\) and \(\mathbf {c}>0\), define \(\sigma _0\) as in Theorem 9 and take \({\varvec{\sigma }}<\sigma _0\). Consider a sequence of conformal mappings, constructed as in (2) from sequences \(\{\theta _k \}_{k=1}^{\infty }\) and \(\{c_k\}_{k=1}^\infty \), where (without loss of generality) \(\theta _1=0\) and, conditional on \(\mathcal {F}_{n-1} = \sigma (\theta _k, c_k: 1 \leqslant k \leqslant n-1)\), \(\theta _{n}\) are given by (4).
Provided there exists some constant \(A>0\), depending only on T and \(\eta \), such that
as \(\mathbf {c}\rightarrow 0\), it holds that \(\mathbb {P}(\Omega _N) \rightarrow 1\) as \(\mathbf {c}\rightarrow 0\). Furthermore, such a constant A exists for the three modifications defined above as well as for \(\mathrm {ALE}(\alpha ,\eta )\) for any \(\alpha >0\).
In this case, for any \(r>1\) and \(T<\infty \),
where \(\Psi _t\) is the solution to (11) corresponding to the modified model, and hence the cluster \(K_{t}\) converges in the Hausdorff topology to a disk with slit of logarithmic capacity t attached at position 1.
Note that, as we do not impose an upper bound on each logarithmic capacity \(c_k\), it is no longer necessarily the case that \(n(t)\rightarrow t\) as \(\mathbf {c}\rightarrow 0\). For his reason, we need to compare \(f_t\) with \(\Psi _t\), rather than \(\Phi _{n(t)}\) as in the previous result.
Proof
The proof consists of checking step by step that each inequality in the proofs of Lemma 8 and Theorem 9 still holds (possibly with new constants). The only changes are that we compare \(\Phi _n\) to
instead of \(f_{\mathbf {c}n}^{\theta _n}\) and we need to define
and then use the additional assumption in the statement of the corollary to show that \(N_T=N\) with high probability.
To show that the additional assumption holds for the modified models defined above, it is enough to show that, so long as \(n \leqslant N_T\), there exists some constant A (depending only on T and \(\eta \)), such that
But this follows by using the (analogous) estimates in Lemma 8 for the modified model and observing that there exists some constant \(A'\) (depending only on T) such that
whenever \(|\arg (z)| \leqslant \beta _t/2\) and \(t \leqslant T\). \(\quad \square \)
6 Estimates on Conformal Maps via Loewner’s Equation
We now obtain refined estimates on the distance between solutions to the Loewner equation in terms of the distance between their driving functions, in the special case when the driving functions are close to constant. These will enable us to prove Lemma 8. Generic estimates between conformal maps tend to blow up close to the boundary (as seen in, for example, Proposition 3). As we wish to compare \(|\Phi _n'(e^{{\varvec{\sigma }}+i\theta })|\) to \(|(f_{n\mathbf {c}}^{\theta _n})'(e^{{\varvec{\sigma }}+i\theta })|\) when \({\varvec{\sigma }}\) is typically much smaller than the difference between the respective driving functions, we need bespoke estimates which behave well close to the boundary.
Suppose \(\Psi ^j_t(z)\) is the solution to the Loewner Eq. (11) with driving function \(\xi ^j\), for \(j=0,1\). For fixed \(T>0\), let \(u_t^j(z)\) be the corresponding reverse-time Loewner flows defined in (12), so that \(\Psi ^j_T(z) = u^j_T(z)\) and \((\Psi ^j_T)'(z) = (u^j_T)'(z)\). In Sect. 6.1, we compare \(\Psi ^1_T(z)\) to \(\Psi ^0_T(z_0)\) under the assumption that \(\Psi ^0_T(z_0)\) (or, more precisely, \(u^0_t(z_0)\), for \(0 \leqslant t \leqslant T\)) is “known”. Specifically, we find conditions on \(\Vert \xi ^1-\xi ^0 \Vert _T = \sup _{t \leqslant T} |e^{i\xi ^1_t}-e^{i\xi ^0_t}|\) and \(|z-z_0|\), which depend on \(u^0_t(z_0)\) and \((u^0_t)'(z_0)\), under which \(|u^1_t(z)-u^0_t(z_0)|\) can be shown to be small.
In Sect. 6.2 we interpret this result when \(\xi ^0 \equiv 0\). This enables us to compare \(\Psi '_T(z)\) to \(f'_T(z)\) when \(\xi \), the driving function of \(\Psi \), is close to zero. Specifically, we obtain refined estimates in the case when \(\arg z\) is close to 0 and in the case when |z| is close to 1. We also obtain cruder estimates which apply in the intermediate regime between these two cases which are used in the proof of Lemma 8 to “glue” the two results together.
6.1 Analysis of the reverse-time Loewner flow
Define \(h: \Delta \times \mathbb {T}\rightarrow \mathbb {C}\) by
so, by (12),
Observe that
Since
using \((u_0^j)'(z)=1\), we therefore obtain
It is also convenient to write \(u_t^{j}(z)=r_t^{j}(z)e^{i \vartheta ^{j}_t(z)}\) where \(r_t^{j}(z) \geqslant 1\) and \(\vartheta ^{j}_t(z) \in \mathbb {R}\) with \(\vartheta ^{j}_0(z) \in (-\pi , \pi ]\). Substituting this into (12) and separating \(\mathrm {Re}[(u^{j}_t(z)e^{-i\xi ^j_{T-t}}+1)/(u^{j}_t(z)e^{-i\xi ^j_{T-t}}-1)]\) and \(\mathrm {Im}[(u^{j}_t(z)e^{-i\xi ^j_{T-t}}+1)/(u^{j}_t(z)e^{-i\xi ^j_{T-t}}-1)]\) we obtain the two differential equations
and
where we have suppressed the dependence on z to ease notation.
We observe that the right hand side of (27) is non-negative and maximised when \(\vartheta ^{j}_t-\xi ^j_{T-t}=0\). In this case, the differential equation
can be solved explicitly,
Noting that
we obtain the crude estimate
Lemma 11
Suppose \(z_0 \in {\Delta }\), \(T>0\) and \(\xi ^0:(0,T] \rightarrow \mathbb {R}\) are given and let
There exists some absolute constant A such that, for all \(|z| > 1\) satisfying
we have, for all \(0 \leqslant t \leqslant T\),
(where we interpret the left hand side as being equal to 0 if \(z=z_0\)) and
Furthermore, A can be chosen so that if, in addition, \(\xi ^1:(0,T] \rightarrow \mathbb {R}\) satisfies
then, for all \(0 \leqslant t \leqslant T\),
and
Lemma 11 can be interpreted as telling us that, provided \(u^0_t(z_0)\) stays away from \(e^{i \xi ^0_{T-t}}\), \(u_t^1(z)\) will be close to \(u_t^0(z_0)\) for sufficiently small \(|z-z_0|\) and \(\Vert \xi ^1-\xi ^0\Vert _T\). The conditions in (30) and (31) quantify precisely what is meant by ‘sufficiently small’.
Remark
-
1.
At first glance, Lemma 11 may not appear to be very illuminating. However, the key point is that all of the bounds have been expressed purely in terms of \(u^0_t(z_0)\) for \(0 \leqslant t \leqslant T\), which enables us to obtain good estimates in situations where we have good control over \(u^0_t(z_0)\). The benefit of this approach is demonstrated in Sect. 6.2. There, \(u^0_t(z_0)\) is taken to be the solution corresponding to a constant driver and so the relevant terms may be computed explicitly to yield simple expressions.
-
2.
The conditions (30) and (31) can be simplified by observing that by (27), for any \(g: [0,T] \rightarrow [0,\infty )\),
$$\begin{aligned} \int _0^t \frac{g(s) \text {d}s}{|u_s^0(z_0)e^{-i \xi ^0_{T-s}} -1|^2}\leqslant & {} \sup _{0 \leqslant s \leqslant t} g(s) \int _0^t \frac{\partial _s r^0_s}{r^0_s((r^0_s)^2 - 1)} \text {d}s\\= & {} \frac{1}{2} \sup _{0 \leqslant s \leqslant t} g(s) \log \frac{(|u^0_t(z_0)|^2-1)|z_0|^2}{|u^0_t(z_0)|^2 (|z_0|^2-1)}. \end{aligned}$$Therefore
$$\begin{aligned} \inf _{0 \leqslant t \leqslant T} \left( g(t)^{-1} \wedge \left( \int _0^t \frac{g(s) }{ |u_s^0(z_0)e^{-i \xi ^0_{T-s}} -1|^2} \text {d}s \right) ^{-1} \right) \end{aligned}$$can be replaced by
$$\begin{aligned} \inf _{0 \leqslant t \leqslant T} g(t)^{-1} \left( \frac{1}{2}\log \frac{|z_0|}{ |z_0|-1} \right) ^{-1}. \end{aligned}$$However, in the cases we are interested in, it is possible to eliminate the \(\log \) term by computing the integral explicitly.
-
3.
Although this result is most powerful when applied to specific choices of \(z_0\) and \(\xi ^0\), it can be used to provide generic estimates too.
Observe that, by (26) and the crude estimates on \(|u^0_t(z_0)|\) in (29),
$$\begin{aligned} \Lambda _t&\leqslant \int _0^t \exp \left( -s + \int _0^s \frac{2 |u_s^0(z_0)| \text {d}r}{|u^0_r(z_0) e^{-i \xi ^0_{T-r}} - 1|^2}\right) \frac{8 |z_0|e^s |u_s^0(z_0)|}{|u^0_s(z_0) e^{-i \xi ^0_{T-s}} - 1|^2} \text {d}s \\&= 4|z_0|\left( \exp \left( \int _0^t \frac{2 |u^0_s(z_0)| \text {d}s}{|u^0_s(z_0) e^{-i \xi ^0_{T-s}} - 1|^2} \right) - 1 \right) \end{aligned}$$and, by (27),
$$\begin{aligned} \int _0^t \frac{2 |u^0_s(z_0)| \text {d}t}{|u_s^0(z_0)e^{-i \xi ^0_{T-s}} -1|^2} = \int _0^t \frac{2 \partial _sr^{0}_s \text {d}s}{(r^{0}_s)^2-1} = \log \frac{(|u^0_t(z_0)|-1)(|z_0|+1)}{(|u^0_t(z_0)|+1)(|z_0|-1)}. \end{aligned}$$Hence it follows from (32) (taking \(z=z_0\)) that there exists some absolute constant A such that
$$\begin{aligned} |\Psi ^1_T(z) - \Psi ^0_T(z)| \leqslant A \Vert \xi ^1 - \xi ^0\Vert _T |(\Psi ^0_T)'(z)| |z| \frac{(|\Psi ^0_T(z)|-1)(|z|+1)}{(|\Psi ^0_T(z)|+1)(|z|-1)}. \end{aligned}$$By using standard distortion estimates to bound \(|(\Psi ^0_T)'(z)|\), there exists some (possibly different) absolute constant A such that
$$\begin{aligned} |\Psi ^1_T(z) - \Psi ^0_T(z)| \leqslant \frac{A e^T |z|\Vert \xi ^1 - \xi ^0\Vert _T}{(|z|-1)^2} \end{aligned}$$(cf Proposition 3).
Here we have used only generic information about the two flows. We note that this last estimate is not optimal, however, as we have taken worst-case bounds for both \(\Lambda _T\) and \(|(\Psi ^0_T)'(z)|\), whereas typically these two quantities are bad in different regions. Indeed, one expects the exponent 1 in the denominator as has been proved in the chordal setting. In fact, one can start from the setting of Proposition 3 to obtain an exponent \(1+\delta \) for \(\delta > 0\) arbitrarily small (see [9]). Alternatively, one can localise and use the half-plane case (see [11]). By following the latter approach near the tip of a slit map, one can obtain an estimate that also exploits information about the derivative but with a sub-power correction that we do not get here.
We emphasize that the case in which we apply this result is not the generic one. We have much information about \(|(u_t^0)'(z_0)|\) and the form of the estimates here allows us to use this information efficiently.
Proof
Set \(\delta ^j_t=u^j_t(z) - u^0_t(z_0)\) for \(j=0,1\). Then \(\delta ^j_t\) satisfies the ODE
We shall obtain the desired estimates by linearising this ODE and showing that, under assumptions (30) and (31), the higher order terms can be controlled.
Write
where, by direct computation,
Taking \(j=0\), we have
and hence, using (26) and that \((u^0_0)'(z_0)=1\),
Taking \(j=1\), we have
and hence, using (25),
Since
it follows immediately that
We next obtain bounds on \(H^j(t)\), under the assumption that \(t \leqslant T^j\), where
In what follows, we shall show that if we take \(A=25\) in assumption (30) then \(T^0=T\) and if we take it in (30) and (31) then \(T^1=T\). (Note that we have made no attempt to optimise the value of A.)
and
for all \(t \leqslant T^j\). Hence,
and so
Also
Hence, using the bounds above,
and so, by (33), \(T^0=T\) and the first statement in the lemma follows. Similarly
By (31), we have
It follows that \(T^1=T\) and hence
To obtain estimates on the derivative, we use that
where
As above,
and hence
Finally, we observe that, by the same arguments as above, under assumption (30) with \(A=25\), \(|u^0_t(z)|/|u^0_t(z_0)|\), \(|u^0_t (z) e^{-i \xi ^0_{T-t}}-1|/|u^0_t (z_0) e^{-i \xi ^0_{T-t}}-1|\) and \(|(u^0_t)'(z)|/|(u_t^0)'(z_0)|\) can be bounded above and below by strictly positive absolute constants and hence there exists some absolute constant \(A_1 \geqslant 1\) such that
for all \(0\leqslant t \leqslant T\), where
Hence, if assumption (31) holds with \(A=25(5/4)^3A_1\), then
and so we may set \(z=z_0\) in the computation above to get that
and
as required. \(\quad \square \)
6.2 Small driving functions
In this section, we explicitly evaluate \(u^0_t(z_0)\) and \((u^0_t)'(z_0)\) when \(\xi ^0 \equiv 0\) and either \(\arg z_0 = 0\) or \(|z_0|=1\). This enables us to compare \(\Psi _T(z)\) to the slit map \(f_T(z)\) when \(\xi \), the driving function of \(\Psi \), is close to zero. Since \(\xi ^0_{T-t}\) does not depend on T, \(u^0_t(z_0)=f_t(z_0)\) and \((u^0_t)'(z_0)=f'_t(z_0)\) for all \(t \geqslant 0\). We could therefore, in principle, just substitute the estimates from Sect. 4 into Lemma 11. However, instead we observe that in these two cases solving the pair of differential equations (27) and (28) reduces to solving a single ordinary differential equation, and we are able to obtain explicit solutions directly.
First suppose that \(z_0=r > 1\). Set \(u^0_t(z_0)=r^0_te^{i \vartheta ^0_t}\). From (28) it is immediate that \(\vartheta ^0_t=0\) for all \(t > 0\). Substituting this into (27) we get
Solving this gives
or
Observe that if \(r=1\), then \(r^0_t = d(t) + 1\).
Now suppose \(z_0=e^{i \theta }\) where \(|\theta | \in (0, \pi )\). Although \(u^0_t(z_0)\) is not explicitly defined when \(|z_0|=1\), \(u^0_t(z)\) for \(|z|>1\) can be continuously extended to the boundary of the unit disk in a well-defined way, so this is the interpretation we put on \(u^0_t(e^{i \theta })\).
From (27) it is immediate that \(r^0_t=1\) for all \(t \leqslant \inf \{ t > 0: u^0_t(e^{i \theta })=1\}\). Substituting this into (28) we get
Solving this gives
and hence
Corollary 12
Suppose \(\Psi _t(z)\) is the solution to the Loewner Eq. (11).
-
(i)
(Near the tip). There exists some absolute constant A such that, for all \(|z|>1\) and \(T>0\) satisfying \(\Vert \xi \Vert _T + |\arg z| \leqslant A^{-1} (|z|-1) / |z|\), we have
$$\begin{aligned} \left| \log \frac{|\Psi '_T(z)|}{|f_T'(z)|} \right| \leqslant \left( \frac{ A|z|(\Vert \xi \Vert _T + |\arg z|)}{|z|-1} \right) ^2. \end{aligned}$$ -
(ii)
(Away from the tip). There exists some absolute constant A such that, for all \(|z|>1\) and \(T>0\) satisfying
$$\begin{aligned} T \leqslant \log \frac{2}{1+\cos (\arg z)} \end{aligned}$$and
$$\begin{aligned} \Vert \xi \Vert _T + |z|-1 \leqslant A^{-1} e^{-T/2} \cot \frac{\arg z }{2} \tan \frac{\vartheta ^0_T}{2}\sqrt{1-\cos \vartheta ^0_T}, \end{aligned}$$where \(\vartheta ^0_t\) is defined as in (37) with \(\theta =\arg z\), we have
$$\begin{aligned} \left| \log \frac{|\Psi '_T(z)|}{\tan \frac{\arg z}{2} \cot \frac{\vartheta ^0_T}{2}} \right| \leqslant \frac{A\sqrt{e^T(e^T-1)}(\Vert \xi \Vert _T+|z|-1)}{1-\cos \vartheta ^0_T} \leqslant 1, \end{aligned}$$$$\begin{aligned} 1 - \cos (\arg \Psi _T(z)) \leqslant A (1-\cos \vartheta ^0_T), \end{aligned}$$and
$$\begin{aligned} |\Psi _T(z)| - 1 \geqslant A^{-1}(|z|-1)\tan \frac{\arg z}{2} \cot \frac{\vartheta ^0_T}{2}. \end{aligned}$$
Proof
-
(i)
Set \(z_0=|z|\) and define \(r^0_t\) as in (36), with \(r=|z|\). Using (35), we compute \(|(u^0_t)'(z_0)|\) and \(\Lambda _t\) from Lemma 11. By (26),
$$\begin{aligned} |(u^0_t)'(z_0)|&= e^t \exp \left( - \int _0^t \frac{2 \text {d}s}{(r^0_s - 1)^2}\right) \\&= e^t \exp \left( - \int _0^t \frac{2 \partial _sr^{0}_s }{r^0_s((r^0_s)^2 - 1)} \text {d}s\right) \\&= e^t \frac{(r^2-1)(r^0_t)^2}{((r^0_t)^2 - 1)r^2} \\&= \frac{(r-1)r^0_t(r^0_t+1)}{(r^0_t - 1)r(r+1)} \\&\leqslant e^t. \end{aligned}$$Therefore, again using (35),
$$\begin{aligned} \Lambda _t = \int _0^t \frac{(r^0_s - 1)r(r+1)}{(r-1)r^0_s(r^0_s+1)} \frac{2 (r^0_s)^2}{(r^0_s-1)^2} \text {d}s = \frac{2r(r_t^0-r)}{(r-1)(r_t^0+1)} \end{aligned}$$and so
$$\begin{aligned} |(u^0_t)'(z_0)| \Lambda _t = \frac{2r^0_t (r_t^0-r)}{(r^0_t - 1)(r+1)} \leqslant r^0_t. \end{aligned}$$Hence
$$\begin{aligned} \frac{|(u^0_t)'(z_0)| \Lambda _t + |u^0_t(z_0)|}{|u_t^0(z_0) -1|} \leqslant \frac{2r^0_t}{r^0_t-1} \leqslant \frac{2|z|}{|z|-1} \end{aligned}$$and
$$\begin{aligned} \int _0^t\frac{|(u^0_s)'(z_0)| \Lambda _s + |u^0_s(z_0)|}{|u_s^0(z_0) -1|^3} \text {d}s \leqslant \int _0^t \frac{2r^0_s}{(r^0_s-1)^3} \text {d}s \leqslant \frac{1}{|z|-1}. \end{aligned}$$Here we have used that \(r_t^0 \geqslant |z|\) for all \(0 \leqslant t \leqslant T\) in each of the final inequalities in the preceding two displays. Similarly
$$\begin{aligned} \frac{|(u^0_t)'(z_0)|}{|u_t^0(z_0) -1|} \leqslant \frac{1}{|z|-1} \end{aligned}$$and
$$\begin{aligned} \int _0^t \frac{|(u^0_s)'(z_0)|}{|u_s^0(z_0) -1|^3} \text {d}s \leqslant \frac{1}{2|z|(|z|^2-1)}. \end{aligned}$$By Lemma 11, using that \(r^0_t \leqslant 4|z|e^t\), we get
$$\begin{aligned} \left| \log \frac{\Psi '_T(z)}{f_T'(z)} \right| \leqslant \frac{A \Vert \xi \Vert _T}{|z|-1}. \end{aligned}$$By using that \(u^0_t(z_0)\) and hence \((u^0_t)'(z_0)\) are purely real, that
$$\begin{aligned} \left| \text {Re} \,(e^{i \xi _t}) - 1 \right| \leqslant \Vert \xi \Vert _T^2 \end{aligned}$$and that
$$\begin{aligned} \left| \text {Re} \,z - |z| \right| \leqslant |z| (\arg z)^2, \end{aligned}$$it is possible to repeat the computations in the proof of Lemma 11 for the real parts of \(u^1_t(z)\) and \(\log (u^1_t)'(z)\) to obtain the stronger bound
$$\begin{aligned} \left| \log \frac{|\Psi '_T(z)|}{|f_T'(z)|} \right| = \left| \text {Re} \,\log \frac{\Psi '_T(z)}{f_T'(z)} \right| \leqslant \left( \frac{ A|z|(\Vert \xi \Vert _T + |\arg z|)}{|z|-1} \right) ^2. \end{aligned}$$We omit the details as the argument is almost identical to that used in the proof of Lemma 11.
-
(ii)
Set \(z_0 = e^{i \arg z}\). If \(0 \leqslant t \leqslant T < \log \frac{2}{1 + \cos (\arg z)}\), then defining \(\vartheta ^0_t\) as in (37), with \(\theta =\arg z\),
$$\begin{aligned} |u_t^0(z_0) - 1|^2&= 2(1-\cos \vartheta ^0_t),\\ |(u^0_t)'(z_0)|&= \exp \left( \int _0^t \frac{\text {d}s}{1-\cos \vartheta ^0_s}\right) \\&= \exp \left( -\int _0^t \frac{ \partial _s\vartheta ^0_s }{\sin \vartheta ^0_s} \text {d}s \right) \\&= \tan \frac{\theta }{2} \cot \frac{\vartheta ^0_t}{2}, \end{aligned}$$and
$$\begin{aligned} \Lambda _t = \cot \frac{\theta }{2} \int _0^t \frac{\tan \frac{\vartheta ^0_t}{2}}{1-\cos \vartheta ^0_s} \text {d}s = 1-\cot \frac{\theta }{2} \tan \frac{\vartheta ^0_t}{2}. \end{aligned}$$By standard trigonometric identities, and using the explicit value of \(\vartheta ^0_t\) from (37),
$$\begin{aligned} \tan \frac{\theta }{2} \cot \frac{\vartheta ^0_t}{2} = \sqrt{\frac{(1-\cos \theta )(1+\cos \vartheta ^0_t)}{(1+\cos \theta )(1-\cos \vartheta ^0_t)}} = \sqrt{\frac{(1-\cos \theta )e^t}{1-\cos \vartheta ^0_t}} = \sqrt{1+\frac{2 (e^t-1)}{1-\cos \vartheta ^0_t}}. \end{aligned}$$(38)Hence
$$\begin{aligned} |(u^0_t)'(z_0)| \Lambda _t = \tan \frac{\theta }{2} \cot \frac{\vartheta ^0_t}{2} - 1, \end{aligned}$$$$\begin{aligned} \frac{|(u^0_t)'(z_0)| \Lambda _t + |u^0_t(z_0)|}{|u_t^0(z_0) -1|} = \frac{|(u^0_t)'(z_0)|}{|u_t^0(z_0) -1|} = \frac{\tan \frac{\theta }{2} \cot \frac{\vartheta ^0_t}{2}}{\sqrt{2(1-\cos \vartheta ^0_t)}} \end{aligned}$$and
$$\begin{aligned} \int _0^t\frac{|(u^0_s)'(z_0)|}{|u_s^0(z_0) -1|^3} \text {d}s&= 2^{-3/2}\tan \frac{\theta }{2} \int _0^t \frac{\cot \frac{\vartheta ^0_s}{2}}{(1-\cos \vartheta ^0_s)^{3/2}} \text {d}s \\&\leqslant \frac{\tan \frac{\theta }{2}}{2^{3/2}\sqrt{1 + \cos \theta }} \int _0^t \frac{\cot \frac{\vartheta ^0_s}{2} \sin \vartheta ^0_s }{(1-\cos \vartheta ^0_s)^{2}} \text {d}s \\&=\frac{\tan \frac{\theta }{2}}{2^{3/2}\sqrt{1 + \cos \theta }} \frac{\cos \vartheta ^0_t - \cos \theta }{(1-\cos \vartheta ^0_t)(1-\cos \theta )} \\&= \frac{e^{t/2}(1-e^{-t})\tan \frac{\theta }{2} \cot \frac{\vartheta ^0_t}{2}}{2^{3/2}(1 - \cos \theta )\sqrt{1-\cos \vartheta ^0_t}} \\&\leqslant \frac{e^{t/2}\tan \frac{\theta }{2} \cot \frac{\vartheta ^0_t}{2}}{4\sqrt{1-\cos \vartheta ^0_t}}, \end{aligned}$$where we used the upper bound on T in the final line. The first result follows directly from Lemma 11. For the second, as in the proof of Lemma 11,
$$\begin{aligned} 2 \left( 1-\cos (\arg |\Psi _T(z)| - \xi _0) \right)\leqslant & {} |u^1_T(z) e^{-i \xi _0} - 1|^2 \\\leqslant & {} 4|u^0_T(z_0) -1|^2 = 8 (1-\cos \vartheta ^0_T), \end{aligned}$$and the result follows by using the assumption on \(\Vert \xi \Vert _T\). For the final result, observe that, by (27) and Lemma 11 there exist absolute constants \(A_i\) such that
$$\begin{aligned}&\ \log \frac{|\Psi _T(z)|-1}{|z|-1} \\&\quad = \ \int _0^T \frac{|u^1_t(z)|(|u^1_t(z)| + 1)}{|u^1_t(z)e^{-i \xi _{T-t}}-1|^2} \text {d}t \\&\quad \geqslant \ \int _0^T \frac{2}{|u^0_t(z_0)-1|^2} \text {d}t - \int _0^T \left| \frac{2}{||u^1_t(z)e^{-i \xi _{T-t}}-1|^2} - \frac{2}{|u^0_t(z_0)-1|^2}\right| \text {d}t\\&\quad \geqslant \ \int _0^T \frac{\text {d}t}{1-\cos \vartheta ^0_t} - A_1 \int _0^T \frac{|u^1_t(z) - u^0_t(z_0)| + \Vert \xi \Vert _T}{|u^0_t(z_0)-1|^3}\text {d}t \\&\quad \geqslant \ \log \tan \frac{\theta }{2} \cot \frac{\vartheta ^0_T}{2} \\&\qquad - A_2 \left( \Vert \xi \Vert _T \int _0^T \frac{\Lambda _t|(u_t^0)'(z_0)| + |u_t^0(z_0)|}{ |u_t^0(z_0)e^{-i \xi ^0_{T-t}} -1|^3}\text {d}t + (|z|-1) \int _0^T \frac{|(u_t^0)'(z_0)| \text {d}t}{ |u_t^0(z_0)e^{-i \xi ^0_{T-t}} -1|^3} \right) \\&\quad \geqslant \ \log \tan \frac{\theta }{2} \cot \frac{\vartheta ^0_T}{2} - A_3. \end{aligned}$$Taking \(A>e^{A_3}\) gives the required result.\(\quad \square \)
Next, we extend Corollary 12 (ii) to give a lower bound on the derivative that holds for all values of T.
Lemma 13
Suppose \(\Psi _t(z)\) is the solution to the Loewner Eq. (11). There exists some absolute constant B such that, for all \(T>0\) and \(|z|>1\) satisfying
where A is the absolute constant from Corollary 12 (ii), we have
Proof
We first obtain a generic lower bound on \(|\Psi '_T(z)|\), without making any assumptions on the driving function \(\xi \) or initial value z. By (26)
Therefore, using the fact that \(|\Psi _T(z)|\geqslant |z|\),
Now suppose T satisfies the conditions of Corollary 12 (ii). Then
and hence the required result holds provided \(B \geqslant 3\sqrt{2}\).
If T does not satisfy the conditions from Corollary 12 (ii), then there exists some \(0<S_1 < T\) such that
By (38), this is equivalent to
We can write \(\Psi _T(z) = \Psi _{T-S_1}(\psi _{S_1}(z))\) where \(\psi _{S_1}\) is the solution to the Loewner equation for some driving function which is bounded by \(\Vert \xi \Vert _T\). Using the generic estimate above, the results of Corollary 12 (ii) applied to \(\psi _{S_1}(z)\), the identity in (38), and that \(| \Psi _T(z)| - 1 \leqslant 4|z| e^T\),
Taking the absolute constant \(B= 12 A^2\), gives the required result. \(\quad \square \)
Finally, we describe the radial and angular effect of the slit map \(f_t(z)\) near the tip for small values of t.
Lemma 14
There exists some absolute constant B such that, for all \(0<t<1\) and \(|z|>1\) with \(|\arg z| \leqslant t^{1/2}\), we have
Proof
By (27) and (28), \(|f_t(z)|\) is increasing in t and \(|\arg f_t(z)|\) is decreasing in t. Therefore, without loss, we may assume that \(|z|-1 \leqslant A^{-1}t^{1/2}\) and \((1-\cos (\arg z))^{1/2} \geqslant A (|z|-1)\) where A is the absolute constant from Corollary 12 (ii). (Here we have used that \(|\arg z| \asymp (1-\cos (\arg z))^{1/2}\)). It follows that \(|z|-1 \leqslant A^{-1}(1-\cos (\arg z))^{1/2}\) and so there exists some \(s \leqslant \log (2/(1+\cos (\arg z)))\) such that
where \(\vartheta ^0_s\) is defined as in (37) with \(\theta =\arg z\). Observe that, by Corollary 12 (ii),
Hence, again using (27) and that \(|\arg f_r(z)|\) is decreasing and \(|f_r(z)|\) increasing in r, we have for all \(s \leqslant r \leqslant t\) that
for some absolute constant \(A_1\). It follows that
and hence \(|f_t(z)| \geqslant 1+ d((t-s)/A_1)\). Since \(0<t<1\), it is straightforward to verify that
and so \(s \leqslant t/2\), Therefore \(|f_t(z)|-1 \geqslant d(t/(2A_1)) \geqslant B_1^{-1}t^{1/2}\) for some absolute constant \(B_1\).
and hence, integrating both sides,
It follows that there exists some absolute constant \(B \geqslant B_1\) such that \(|\arg f_t(z)| \leqslant B(|z|-1)\). \(\quad \square \)
We are now in a position to return to the \(\mathrm {ALE}(0,\eta )\) model and apply our results to prove Lemma 8, which we restate for convenience.
Lemma 8
Fix \(T>0\), let \(n \leqslant \lfloor T/\mathbf {c}\rfloor \) and set \(\varepsilon _n=(e^{\varvec{\sigma }}- 1) \vee \sup _{k\leqslant n} |\theta _k|\).
-
(i)
There exists some absolute constant \(A>1\), such that if \(|\theta -\theta _n|<\mathbf {c}^{1/2}\) and \(\varepsilon _n < A^{-1} \mathbf {c}^{1/2}\), then
$$\begin{aligned} \left| \left| \frac{\Phi '_n(e^{{\varvec{\sigma }}+ i \theta })}{(f^{\theta _{n}}_{n \mathbf {c}})'(e^{{\varvec{\sigma }}+ i \theta })} \right| - 1 \right| < A \varepsilon _n^2 \mathbf {c}^{-1}. \end{aligned}$$ -
(ii)
There exist absolute constants A and B only dependent on T, such that if \(\varepsilon _n \leqslant A^{-1} \mathbf {c}^{1/2}\), then
$$\begin{aligned} \left| \Phi '_n(e^{{\varvec{\sigma }}+ i \theta }) \right| \geqslant B^{-1} \varepsilon _n^{-1} {\varvec{\sigma }}(1 - \cos (\theta -\theta _n))^{1/2}. \end{aligned}$$
Proof
-
(i)
By the chain rule,
$$\begin{aligned} \frac{\Phi '_n(e^{{\varvec{\sigma }}+ i \theta })}{(f^{\theta _{n}}_{n \mathbf {c}})'(e^{{\varvec{\sigma }}+ i \theta })} = \frac{\Phi _{n-1}'(f^{\theta _n}_{\mathbf {c}}(e^{{\varvec{\sigma }}+ i \theta }))(f^{\theta _n}_{\mathbf {c}})'(e^{{\varvec{\sigma }}+ i \theta })}{(f^{\theta _n}_{(n-1)\mathbf {c}})'(f^{\theta _n}_{\mathbf {c}}(e^{{\varvec{\sigma }}+ i \theta })) (f^{\theta _n}_{\mathbf {c}})'(e^{{\varvec{\sigma }}+ i \theta })} = \frac{\Phi _{n-1}'(f^{\theta _n}_{\mathbf {c}}(e^{{\varvec{\sigma }}+ i \theta }))}{(f^{\theta _n}_{(n-1)\mathbf {c}})'(f^{\theta _n}_{\mathbf {c}}(e^{{\varvec{\sigma }}+ i \theta }))}. \end{aligned}$$Set
$$\begin{aligned}w=f^{\theta _n}_{\mathbf {c}}(e^{{\varvec{\sigma }}+ i\theta }) = e^{i \theta _n} f_\mathbf {c}(e^{{\varvec{\sigma }}+ i (\theta -\theta _n)}).\end{aligned}$$Then if \(|\theta -\theta _n| \leqslant \mathbf {c}^{1/2}\), by Lemma 14, we have \(|w|-1>B^{-1}\mathbf {c}^{1/2}\) and \(|\arg w - \theta _n| < B(e^{{\varvec{\sigma }}}-1)\) for some absolute constant B, and so
$$\begin{aligned} 2 \varepsilon _n + |\arg w - \theta _n| \leqslant (2B+B^2) \varepsilon _n \mathbf {c}^{-1/2} (|w|-1). \end{aligned}$$Since the conformal map \(e^{i \theta _n}\Phi _{n-1}(z e^{-i \theta _n})\) has driving function bounded by \(\sup _{k \leqslant n} |\theta _k - \theta _n| \leqslant 2 \varepsilon _n\), by Corollary 12 (i), there exists some constant A (different to that in the corollary), such that if \(\varepsilon _n < A^{-1} \mathbf {c}^{1/2}\), then
$$\begin{aligned} \left| \left| \frac{\Phi '_{n-1}(w)}{(f^{\theta _n}_{\mathbf {c}(n-1)})'(w)} \right| -1 \right| \leqslant A \varepsilon _n^2 \mathbf {c}^{-1}. \end{aligned}$$Observe that it is not possible to apply Corollary 12 (i) directly to \(\Phi _n\) in the argument above, as this result requires \((|z|-1)/|\arg z - \theta _n|\) to be bounded away from zero which is not the case here. This is where we use that \(\Phi _n\) evolves in discrete steps. Specifically, we invoke Lemma 14 to show that the single slit map \(f_{\mathbf {c}}^{\theta _n}\) maps z into a region in which the condition needed for Corollary 12 (i) holds.
-
(ii)
The result follows directly from Lemma 13.\(\quad \square \)
References
Carleson, L., Makarov, N.: Aggregation in the plane and Loewner’s equation. Commun. Math. Phys. 216, 583–607 (2001)
Carleson, L., Makarov, N.: Laplacian path models. Dedicated to the memory of Thomas H. Wolff. J. Anal. Math. 87, 103–150 (2002)
Davidovitch, B., Hentschel, H.G.E., Olami, Z., Procaccia, I., Sander, L.M., Somfai, E.: Diffusion limited aggregation and iterated conformal maps. Phys. Rev. E 87, 1366–1378 (1999)
Eden, M.: A two-dimensional growth process. In: 1961 Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, vol. IV, pp. 223–239 (1961)
Freedman, D.A.: On tail probabilities for martingales. Ann. Probab. 3, 100–118 (1975)
Grebenkov, D.S., Beliaev, D.: How anisotropy beats fractality in two-dimensional on-lattice DLA growth. Phys. Rev. E 96, 042159 (2017)
Hastings, M.B.: Growth exponents for 3.99 walkers. Phys. Rev. E 64, 046104 (2001)
Hastings, M.B., Levitov, L.S.: Laplacian growth as one-dimensional turbulence. Phys. D 116, 244–252 (1998)
Johansson Viklund, F.: Convergence rates for loop-erased random walk and other Loewner curves. Ann. Probab. 43, 119–165 (2015)
Johansson, F., Sola, A.: Rescaled Lévy–Loewner hulls and random growth. Bull. Sci. Math. 133, 238–256 (2009)
Johansson Viklund, F., Rohde, S., Wong, C.: On the continuity of \({{\rm SLE}}(\kappa )\) in \(\kappa \). Probab. Theory Relat. Fields 159, 413–433 (2014)
Johansson Viklund, F., Sola, A., Turner, A.: Scaling limits of anisotropic Hastings–Levitov clusters. Ann. Inst. Henri Poincaré Probab. Stat. 48, 235–257 (2012)
Johansson Viklund, F., Sola, A., Turner, A.: Small-particle limits in a regularized Laplacian random growth model. Commun. Math. Phys. 334, 331–366 (2015)
Kesten, H.: Hitting probabilities of random walks on \(\mathbb{Z}^d\). Stoch. Process. Appl. 25, 165–184 (1987)
Lawler, G.F.: Conformally Invariant Processes in the Plane, Mathematical Surveys and Monographs, vol. 114. American Mathematical Society, Providence (2005)
Lawler, G.F.: The Laplacian-\(b\) walk and the Schramm–Loewner evolution. Ill. J. Math. 50, 701–746 (2006)
Makarov, N.G.: Fine structure of harmonic measure. St Petersburg Math. J. 10, 217–268 (1999)
Marshall, D.E., Rohde, S.: The Loewner differential equation and slit mappings. J. Am. Math. Soc. 18, 763–778 (2005)
Mathiesen, J., Jensen, M.H.: Tip splittings and phase transition in the dielectric breakdown model: mapping to the diffusion-limited aggregation model. Phys. Rev. Lett. 88, 235505 (2002)
Miller, J., Sheffield, S.: Quantum Loewner evolution. Duke Math. J. 165, 3241–3378 (2016)
Miller, J., Sheffield, S.: Liouville quantum gravity and the Brownian map I: the \({{\rm QLE}}(8/3, 0)\) metric. Preprint available at arXiv:1507.00719
Niemeyer, L., Pietronero, L., Wiesmann, H.J.: Fractal dimension of dielectric breakdown. Phys. Rev. Lett. 52, 1033–1036 (1984)
Norris, J., Turner, A.: Hastings–Levitov aggregation in the small-particle limit. Commun. Math. Phys. 316, 809–841 (2012)
Norris, J., Silvestri, V., Turner, A.: Scaling limits for planar aggregation with subcritical fluctuations. Preprint available at arXiv:1902.01376
Pommerenke, Ch.: Boundary Behaviour of Conformal Maps. Springer, Berlin (1992)
Rohde, S., Zinsmeister, M.: Some remarks on Laplacian growth. Topol. Appl. 152, 26–43 (2005)
Silvestri, V.: Fluctuation results for Hastings–Levitov planar growth. Probab. Theory Relat. Fields 167, 417–460 (2017)
Witten Jr., T.A., Sander, L.M.: Diffusion-limited aggregation: a kinetic critical phenomenon. Phys. Rev. Lett. 47, 1400–1403 (1981)
Acknowledgements
We would like to thank the Isaac Newton Institute for Mathematical Sciences (Cambridge, UK) for support and hospitality during the programme “Random Geometry” where work on this paper was initiated. This work was supported by EPSRC Grant No. EP/K032208/1. AS thanks the members of the Statistical Laboratory, University of Cambridge, for their hospitality during visits in the summers of 2016 and 2017. FV acknowledges generous support from the Knut and Alice Wallenberg Foundation, the Swedish Research Council, and the Gustafsson Foundation. We are grateful to James Norris for numerous discussions and useful remarks, and for pointing out an error in an earlier version of our manuscript. Thanks go to Vittoria Silvestri for extensive comments on a draft of this paper. Finally, we thank two anonymous referees for a careful reading of our paper, and for incisive and detailed suggestions on how to improve the presentation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H. Duminil-Copin.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sola, A., Turner, A. & Viklund, F. One-Dimensional Scaling Limits in a Planar Laplacian Random Growth Model. Commun. Math. Phys. 371, 285–329 (2019). https://doi.org/10.1007/s00220-019-03460-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-019-03460-1