1 Introduction

Different noncovalent interactions have been extensively studied in the recent years. One type of these interactions is halogen bond which plays a significant role in different fields such as crystal engineering [1,2,3,4,5], biomolecular systems [6,7,8], organic catalysis [9, 10] or optoelectronics [11, 12]. Halogen bond is an attractive interaction between the positively charged fragment of the electrostatic surface (σ-hole) on the halogen atom (Cl, Br, I) and the electron-rich center (e.g., electron lone pair from nitrogen atom) [13, 14]. This interaction is described in the literature as R-X···Y where R is a moiety covalently bonded with halogen atom (X), and Y is a donor of electron density [15]. Halogen bond is explained by the theory of σ-hole proposed by Politzer and co-workers [16,17,18]. The strength of σ-hole can be determined by V s,max [19] parameter, and it increases with an increase in polarizability and the size of the halogen atom. It also depends on electron-withdrawing properties of the group attached to the halogen [20]. The other factors affecting the quality of this interaction are: the most negative values of the electrostatic potential (V s,min) of the σ-hole acceptor, charge transfer from electron lone pair into the σ*(R-X) antibonding orbital of the σ-hole donor [21,22,23] and dispersion forces [24, 25].

It was shown in the literature that the interaction energy (ΔE) in many complexes correlates with the most positive values of the electrostatic potential (V s,max) of the electron acceptor (σ-hole donor) [24, 26,27,28]. The bigger the value of V s,max, the bigger the absolute value of the interaction energy. Analogous correlation was found between the ΔE and the most negative values of the electrostatic potential (V s,min) of the electron donors (σ-hole acceptor) [16, 28, 29].

Recently, Scheiner et al. reported that the trend of V s,min was opposite to the pattern of binding energies for the chalcogen-bonded complexes of SF4 with alkylamines [30]. These authors investigated also complexes of SF4 with heteroaromatic amines, and they did not find any correlation between the values of the ΔE and V s,min. Finally, they concluded that “V s,min is a poor indicator of binding strength” in the investigated complexes [30].

In our recent paper on the chalcogen-bonded complexes between ammonia derivatives and the CS2 molecule, we found that in the chloramine complexes, the interaction energies were ordered according to the V s,min values of the electrostatic potential [31].

The main purpose of the present work is to discuss the nature of correlations between the values of the interaction energies and the V s,min (as well as the other properties) of chlorinated and methylated amines in the halogen-bonded complexes with F3CCl.

2 Computational methods

The optimized geometries and vibrational harmonic frequencies were calculated for the following bases: NH3, NH2Cl, NHCl2, NCl3, NH2CH3, NH(CH3)2, N(CH3)3 and for their complexes with F3CCl. Vibrational frequency calculations confirmed that the optimized structures correspond to the minima on the potential energy surfaces. The BLYP-D3 method [32] with the Def2TZVPP basis set [33, 34] was used in the calculations. This functional was recommended by Hobza et al. for the complexes stabilized by noncovalent interactions [35].

The interaction energies between the molecules were determined at the BLYP-D3/Def2TZVPP and CCSD(T)/cc-pVTZ levels of theory. The interaction energies were corrected for the basis set superposition error (BSSE) computed by the CP method [36].

The electron density of the investigated complexes was analyzed by the Atoms in Molecules (AIM) methodology [37] to characterize the intermolecular interactions. The presence of an AIM bond critical point (BCP) between the centers of the monomers in the complexes indicates the attractive interaction between them.

For the isolated molecules, the critical points on the electrostatic potential surface (V s,max and V s,min) were computed using the WFA (Wavefunction Analysis) Program [38, 39]. A natural bond orbital (NBO) analysis has been performed for the isolated molecules as well as for their complexes [40, 41]. The calculations were carried out with the Gaussian 09 [42].

3 Results and discussion

3.1 Structures of complexes and interaction energies

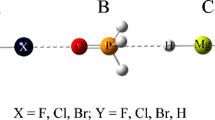
The DFT optimized structures of F3CCl complexes with ammonia and its chlorinated and methylated derivatives are illustrated in Fig. 1. Selected intermolecular parameters are presented in Table 1. As follows from this table, in all the complexes the intermolecular N⋯Cl distances are smaller than the sum of the corresponding van der Waals radii (3.30 Å). In chlorinated amine complexes, the N⋯Cl distance increases with the increasing number of the chlorine substituents. In the case of the methylated amine complexes, the corresponding distance decreases in the order of increasing number of the methyl groups. As follows from the results collected in Table 1, the N⋯Cl–C angles are almost linear.

Fig. 1
figure 1

Optimized structures of the complexes discussed in this work

Full size image
Table 1 Intermolecular parameters (distances in Å, angles in degrees) in the F3CCl complexes with chlorinated and methylated amines calculated at the BLYP-D3/Def2TZVPP level of theory
Full size table

The interaction energies (ΔE) calculated at the BLYP-D3/Def2TZVPP and CCSD(T)/cc-pVTZ levels of theory are collected in Table 2. In these complexes, the values of ΔE vary from − 1.56 to − 4.81 kcal mol−1. These values are in the same order of magnitude as the values of the ΔE calculated for the chalcogen-bonded complexes of CS2 with chlorinated or methylated amines [31].

Table 2 Interaction energies (ΔE, kcal mol−1) of the halogen-bonded complexes calculated at the BLYP-D3/Def2TZVPP (I) and CCSD(T)/cc-pVTZ (II) levels of theory
Full size table

As follows from the data collected in Table 2, in chloramine complexes the absolute values of the ΔE decrease in the order NH3 > NH2Cl > NHCl2 > NCl3. The opposite trend is observed in the methylated amine complexes, where the values of the |ΔE| increase with the number of the methyl groups, in the following order NH3 < NH2CH3 < NH(CH3)2 < N(CH3)3.

3.2 Electrostatic potential

Figure 2 illustrates the calculated molecular electrostatic potentials (MEPs) of isolated F3CCl and NH3. The values of the minima (V s,min) on MEPs of ammonia and its derivatives as well as the most positive electrostatic potentials (V s,max) of F3CCl (σ-hole) are collected in Table 3. It was demonstrated in our previous paper [31] that the substitution of one H atom of ammonia by the Cl atom results in a decrease in the value of |V s,min| by about 10 kcal mol−1, while the substitution of one H atom by the CH3 group lowers the corresponding values by 2–3 kcal mol−1. According to the results presented in Table 3, the calculated value of V s,max for F3CCl is 18.8 kcal mol−1.

Fig. 2
figure 2

Molecular electrostatic potentials (MEPs) of isolated F3CCl and NH3 molecules on the 0.001 a.u. contour of the electron density computed at the BLYP-D3/Def2TZVPP level. Color ranges, in kcal mol−1, are: red greater than 15, yellow between 8 and 15, green between 0 and 8, blue less than 0 (negative)

Full size image
Table 3 Molecular electrostatic potentials extrema (in kcal mol−1) on ammonia nitrogen atom (V s,min) of isolated amines and on Cl atom of CF3Cl (V s,max) on the 0.001 a.u. contour of the electrostatic density calculated at the BLYP-D3/Def2TZVPP level of theory
Full size table

It has been shown for several halogen- or chalcogen-bonded complexes that the interaction energies correlate with the V s,max on a σ-hole donor. The bigger the V s,max, the bigger the values of the |ΔE| [24, 26,27,28]. Similar effect was obtained for the complexes studied in this work.

It was reported that the ΔE can be correlated with the most negative values of the electrostatic potential (V s,min) of an electron donor (σ-hole acceptor). The bigger the absolute value of V s,min, the bigger the absolute value of the interaction energy [16, 28, 29]. Politzer et al. [16] performed calculations for SiF4 and SiCl4 complexes with two different Lewis bases NH3 and HCN. They found that the ammonia complexes are distinctly more stable (more negative ΔE) than those of HCN. They explained this fact as a consequence of considerably more negative potential of NH3 (V s,min = − 46.3 kcal/mole) than that calculated for HCN (V s,min = − 32.9 kcal/mole). In our earlier work [29] on the halogen-bonded complexes between carbonyl bases and molecular chlorine, it was found that the ΔE correlates with the V s,min with a correlation coefficient (R 2) of 0.916.

As illustrated in Fig. 3, the positive correlation between the ΔE and the V s,min of ammonia and its chlorinated derivatives is consistent with this observation. This correlation is linear and can be written as:

$$ \Delta E = 0.051V_{{s,{ \rm min }}} {-} \, 1.019\quad \left( {R^{2} = 0.952} \right) $$
(1)
Fig. 3
figure 3

ΔE (kcal mol−1) as a function of V s,min (kcal mol−1) for chloramine complexes with F3CCl studied in this work

Full size image

In the case of the CS2 complexes with chloramines, a similar correlation was found [31].

However, in the case of the methylated amine complexes studied in this work the opposite trend (negative correlation) has been found. As shown in Fig. 4, the values of the interaction energies ΔE correlate inversely with V s,min. This correlation is also linear and can be written as:

Fig. 4
figure 4

ΔE (kcal mol−1) as a function of V s,min (kcal mol−1) for methylated amine complexes with F3CCl studied in this work

Full size image
$$ \Delta E = -\, 0.189V_{{s,{ \rm min }}} {-}10.395\quad \left( {R^{2} = 0.940} \right) $$
(2)

The question arises what is the origin of this peculiar characteristic of methylated amine complexes with F3CCl?

3.3 AIM analysis

The presence of the bond critical points (BCPs) between the atoms indicates the attractive bonding interactions. The results of the Atoms in Molecules (AIM) analysis of the selected BCPs are collected in Table 4. As follows from this table, in chlorinated amine complexes the values of electron density (ρ) and Laplacian of electron density (Δ2 ρ) slightly decrease with the number of chlorine atoms, while the opposite trend is observed with respect to the methylated amine complexes. The AIM analysis has revealed that all the complexes are stabilized by only one interaction, namely the Cl···N halogen bond. Figure 5 demonstrates the existence of one BCP between the interacting subunits, in the F3CCl···NCl3 and F3CCl⋯N(CH3)3 complexes.

Table 4 Bond critical points (BCP) properties: electron density ρ, Laplacian of electron density ∇2 ρ (both in atomic units) and total electron energy (H, kcal mol−1). Calculations were performed at the BLYP-D3/Def2TZVPP level
Full size table
Fig. 5
figure 5

Contour line diagram of the Laplacian of the electron density of the F3CCl⋯NCl3 and F3CCl⋯N(CH3)3 complexes (in the plane passing through the N, Cl and C atoms). The solid (blue) lines represent the positive values of the Laplacian, while the dashed (red) lines represent the negative values. Small green points represent the bond critical points (BCP). Calculations were performed at the BLYP-D3/Def2TZVPP level

Full size image

According to the Popelier’s criteria for the hydrogen bonds, the electron density at the BCP ranges from 0.002 to 0.035 au, and the Laplacian of the electron density ranges from 0.024 to 0.139 au [43, 44]. All of the complexes investigated in this work fulfill these criteria.

3.4 NBO analysis

3.4.1 Isolated amines

In our previous paper on the chalcogen-bonded complexes of CS2, the variations of charges on the N atom in isolated chlorinated and methylated amines were discussed [31]. It was shown that the substitution of the H atom(s) in ammonia by the chlorine atom(s) or the methyl group(s) decreases the absolute values of the negative charge on the nitrogen atom. Therefore, in isolated amines both the Cl and CH3 substituents act as the electron-withdrawing groups.

The natural charges calculated on the nitrogen atom q(N) in isolated amines were reported in the paper [31]. Comparison of these data and the values of the minima on MEPs of ammonia and its derivatives clearly shows that the values of the V s,min and q(N) are linearly correlated with according to the following equations:

$$ V_{{s,{ \hbox{min} }}} = 43.634 \, q(N) + 6.447\quad \left( {R^{2} = \, 0.977} \right) \quad {\text{for}}\;{\text{chlorinated}}\;{\text{amines}} $$
(3)
$$ V_{{s,{ \hbox{min} }}} = 13.606 \, q(N)\,{-}\,24.180\quad \left( {R^{2} = \, 0.973} \right)\quad \text{ for}\;{\text{methylated}}\;{\text{amines}} $$
(4)

A decrease in the absolute values of the negative charge on the nitrogen atom in chloramines is expected from a larger electronegativity of Cl, in comparison with N atom. However, for the methyl substituents the explanation is different.

In this case, a decrease in the |q(N)| is caused by the negative hyperconjugation (a lone pair effect), which is an intramolecular stabilizing interaction between lone pair orbital on N and adjacent antibonding σ*(CH) orbital(s) [31, 45,46,47]. When a carbon atom of the methyl group is attached to an amine nitrogen and a C–H bond is anti-coplanar to the nitrogen lone pair LP(N), a transfer of the electron density from the LP(N) into the sigma antibonding σ*(C–H)trans orbital occurs. This leads to a weakening and elongation of the anti-coplanar C–H bond, in comparison with the other two C–H bonds of the methyl group. Moreover, the C–H stretching frequency of this particular bond is redshifted, by about 100–150 cm−1. This phenomenon is observed in IR spectroscopy and is also known as the Bohlmann effect [48]. A classic negative hyperconjugation is illustrated in Fig. 6.

Fig. 6
figure 6

Negative hyperconjugation between LP(N) and σ*(C–H)trans orbitals in isolated methylamine

Full size image

We have examined the occupancy of the LP(N) and the characteristic features of C–H bonds: the occupancy of σ*(C–H) orbitals, C–H distances, C–H stretching frequencies and second-order interaction energies between selected orbitals in the isolated methylated amines and their complexes with F3CCl. Table 5 collects the results obtained for the isolated methylated amines.

Table 5 LP(N) and σ*(C–H) occupancies (in me), C–H bond lengths (R in Å), C–H stretching frequencies (ν in cm−1) and the sum of E 2 interaction energies between selected orbitals (in kcal mol−1) in isolated methylated amines. The calculations were performed at the BLYP-D3/Def2TZVPP level of theory
Full size table

In the isolated ammonia molecule, the occupancy of the LP(N) orbital is 1997 me. As follows from Table 5, this occupancy decreases upon substitution by about − 50 me per each of the methyl groups. These changes are accompanied by an increase in the occupancy on the Σσ*(C–H)trans orbital. An increase in the occupancy on the other Σσ*(C–H)other orbitals is much smaller. One should remember that in the case of Σσ*(C–H)other the number of the components in a sum is twice bigger than that of the Σσ*(C–H)trans orbitals. As follows from Table 5, the total occupancy of Σσ*(C–H)trans and Σσ*(C–H)other is comparable to the decrease in the occupancy on the LP(N).

The anti-coplanar (trans) C–H bond is longer than the other two C–H bonds of the methyl group, by 0.009, 0.012 and 0.015 Å, in NH2CH3, NH(CH3)2 and N(CH3)3, respectively. The corresponding C–H stretching frequencies are redshifted by 101, 126 and 154 cm−1, respectively.

In the last two rows of Table 5, the second-order interaction energies between LP(N) and antibonding σ*(CH) orbitals are listed. The sum of ΣE 2 (LP(N) → σ*(CH)trans) values increases in the order NH2CH3 < NH(CH3)2 < N(CH3)3. It should be noted that these values are significantly larger than those of ΣE2 (LP(N) → σ*(CH)other).

All of these results indicate that the negative hyperconjugation increases in the order methylamine < dimethylamine < trimethylamine. This effect can also explain a decrease in the absolute values of V s,min in the order: methylamine > dimethylamine > trimethylamine.

3.4.2 Amine complexes with F3CCl

It was reported for the methylated amine complexes with H+ that the more alkyl groups were connected with N, the more stable was the cation [49]. Experimental gas-phase basicities, defined as ΔG, for the protonation reaction of NH3, NH2CH3, NH(CH3)2 and N(CH3)3 are − 196, − 206, − 213 and − 217 kcal mol−1, respectively [49]. It is worth mentioning that the lone pair effect (negative hyperconjugation) was studied in the hydrogen-bonded complexes between phenol derivatives and trimethylated amines [50].

In this work, we have shown that the absolute values of the interaction energy (ΔE) of the F3CCl complexes with methylated amines increase in the order methylamine < dimethylamine < trimethylamine (see Table 2), and these results are consistent with those reported in the literature [49].

In our previous studies on the chalcogen-bonded complexes between CS2 and ammonia derivatives, it was demonstrated that these complexes were stabilized by a charge transfer (CT) from the LP(N) to the σ*(CS) orbital [31]. A similar effect has been found for the complexes studied in the present work. The NBO analysis has revealed that upon complexation the CT from the LP(N) of the ammonia derivatives to the σ*(CCl) orbital occurs. Table 6 lists the values of second-order interaction energies (E 2) between LP(N) and antibonding σ*(C–Cl) orbital and the values of the CT taking place from the amines to the F3CCl molecule.

Table 6 Interaction energy (E 2) between lone electron pair on nitrogen atom and antibonding σ*(C–Cl) orbital (kcal mol−1) and charge transfer (CT, in me) in the studied complexes
Full size table

As follows from Table 6, for the chlorinated amine complexes, both the E 2 and CT values decrease with the number of the chlorine atoms. The opposite trend is observed in the case of the methylated amine complexes, where the values of E 2 and CT increase with the number of the methyl groups. It should be stressed that the values of E 2 and CT perfectly correlate with the ΔE. The correlation coefficients (R 2) between the ΔE and CT are equal to 0.999 and 0.998 for chloramine and methylated amines complexes, respectively.

$$ \Delta E = -\, 0.058 \, CT{-}1.485\quad \left( {R^{2} = 0.999} \right)\quad {\text{for}}\;{\text{chlorinated}}\;{\text{amine}}\;{\text{complexes}} $$
(5)
$$ \Delta E = - \,0.071 \, CT{-}1.148\quad \left( {R^{2} = \, 0.998} \right)\quad {\text{for}}\;{\text{methylated}}\;{\text{amine}}\;{\text{complexes}} $$
(6)

In the case of the chloramine complexes, the situation is clear. The smaller are the values of |q(N)| (or |V s,min|) in isolated chloramines, the smaller are the values of E 2, CT and |ΔE| in complexes with F3CCl. In the methylated amine complexes, the relationship is reverse; the smaller are the values of |q(N)| (or |V s,min|) in isolated methylated amines, the larger are E 2, CT and |ΔE| in their complexes with F3CCl.

Again the question arises: How can we explain these correlations in the methylated amine complexes? To answer this question, we have investigated the changes in negative hyperconjugation in these molecules caused by complexation. In Table 7, the calculated data for methylated amine complexes are collected. The changes caused by complexation are given in parentheses.

Table 7 LP(N) and σ*(C–H) occupancies (in me), C–H bond length (R in Å), C–H stretching frequencies (ν in cm−1) and E 2 interaction energies between selected orbitals (in kcal mol−1) in the investigated complexes
Full size table

As follows from the results collected in this table, in all complexes the occupancy of the LP(N) orbital decreases upon complexation. Surprisingly, the calculated values of these changes are similar in all methylated amine complexes and range between − 35 and − 33 me. As follows from the data given in Table 6, the values of CT are larger than the changes of the occupancy of the LP(N) orbitals by 4, 11 and 18 me for methylamine, dimethylamine and trimethylamine complexes, respectively. As listed in Table 7, upon complexation with F3CCl the occupancy of the Σσ*(C–H)trans orbital decreases with the number of the substituting methyl groups by − 3, − 8 and − 15 me, respectively.

Thus, it seems that a decrease in electron density (ED) on the N atom due to a charge transfer from LP(N) to σ*(C–Cl) is partly compensated by a back donation of electron density from the antibonding σ*(CH)trans orbitals to LP(N), i.e., a weakening (or hampering) of the negative hyperconjugation effect, as illustrated in Fig. 7.

Fig. 7
figure 7

Charge transfer between LP(N) and σ*(C–Cl) orbitals and a simultaneous weakening of negative hyperconjugation between LP(N) and σ*(C–H)trans orbitals

Full size image

The weakening of negative hyperconjugation is also confirmed by a decrease in the ΣE 2 LP(N) → σ*(CH)trans values by − 0.57, − 1.13 and − 1.67 kcal mol−1 in methylamine, dimethylamine and trimethylamine complexes, respectively. Moreover, the corresponding C–H bonds are contracted by − 0.002 or − 0.003 Å, and the C–H stretching frequencies are blueshifted by 23 or 26 cm−1.

Based on the presented results, it can be concluded that the formation of halogen-bonded complexes between methylated amines and F3CCl leads to an increase in the CT from LP(N) to σ*(C–Cl) in the order methylamine < dimethylamine < trimethylamine. This causes an increase in the |ΔE| in the same order. Simultaneously, the weakening of the transfer of the electron density from the LP(N) to σ*(CH)trans orbitals takes place. The largest weakening of the negative hyperconjugation has been found in the most stable (the largest |ΔE|) trimethylamine complex (with the smallest value of the |V s,min|), while the smallest weakening of the negative hyperconjugation has been found in the less stable (the smallest |ΔE|) methylamine complex (with the largest value of the |V s,min|).

This indicates that the weakening of the negative hyperconjugation is probably responsible for the inverse correlation (negative correlation) between ΔE and V s,min in the complexes of methylated amines.

4 Conclusions

  1. 1.

    For the investigated halogen-bonded complexes, the interaction energies (ΔE) calculated at the CCSD(T)/cc-pVTZ level range between − 0.90 and − 2.57 kcal mol−1. The calculated at the BLYP-D3/Def2TZVPP level ΔE vary from − 1.56 to − 4.81 kcal mol−1.

  2. 2.

    In the case of the chlorinated amine complexes, the linear correlation between ΔE and V s,min was found with positive correlation coefficients R 2 of 0.952. The inverse (negative) correlation was observed for the methylated amines (V s,min was decreasing with increasing ΔE), with a correlation coefficient of 0.940.

  3. 3.

    In all the complexes studied in this work, the AIM analysis reveals the presence of only one attractive interaction confirmed by a BCP between the N and Cl atoms.

  4. 4.

    In the isolated methylated amines, the decrease in the occupancy of the LP(N) is caused by the charge transfer from LP(N) to the antibonding σ*(CH) orbitals of the methyl group(s). This stabilizing intramolecular interaction is called negative hyperconjugation.

  5. 5.

    The NBO analysis has revealed that upon complexation of chlorinated and methylated amines with F3CCl the CT from the LP(N) to the σ*(CCl) orbital occurs. This CT stabilizes the complexes.

  6. 6.

    In the halogen-bonded complexes of F3CCl with methylated amines, the occupancy of the LP(N) orbital results from two effects: the CT from LP(N) to σ*(CCl) antibonding orbital and the weakening (or hampering) of the negative hyperconjugation LP(N) → σ*(CH)trans. The former effect leads to a decrease in electron density (ED) on the LP(N) orbital, while the latter effect causes an increase in ED on the LP(N) orbital. The largest weakening of the negative hyperconjugation has been found in the most stable (the largest |ΔE|) trimethylamine complex. It should be noted that the isolated trimethylamine has the smallest value of |V s,min|. On the contrary, the smallest weakening is noted in the less stable (the smallest |ΔE|) methylamine complex (where NH2CH3 has the largest value of |V s,min|). These effects can explain the inverse (negative) correlation) between ΔE and V s,min.