Abstract
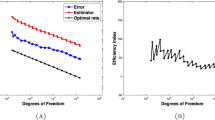
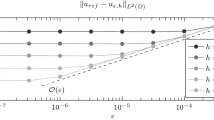
The adaptive algorithm for the obstacle problem presented in this paper relies on the jump residual contributions of a standard explicit residual-based a posteriori error estimator. Each cycle of the adaptive loop consists of the steps ‘SOLVE’, ‘ESTIMATE’, ‘MARK’, and ‘REFINE’. The techniques from the unrestricted variational problem are modified for the convergence analysis to overcome the lack of Galerkin orthogonality. We establish R-linear convergence of the part of the energy above its minimal value, if there is appropriate control of the data oscillations. Surprisingly, the adaptive mesh-refinement algorithm is the same as in the unconstrained case of a linear PDE—in fact, there is no modification near the discrete free boundary necessary for R-linear convergence. The arguments are presented for a model obstacle problem with an affine obstacle χ and homogeneous Dirichlet boundary conditions. The proof of the discrete local efficiency is more involved than in the unconstrained case. Numerical results are given to illustrate the performance of the error estimator.
Similar content being viewed by others
References
Ainsworth M. and Oden J.T. (2000). A Posteriori Error Estimation in Finite Element Analysis. Wiley, Chichester
Ainsworth M., Oden J.T. and Lee C.Y. (1993). Local a posteriori error estimators for variational inequalities. Numer. Methods Partial Differ. Equ. 9: 23–33
Babuška I. and Strouboulis T. (2001). The Finite Element Method and its Reliability. Clarendon, Oxford
Bangerth, W., Rannacher, R.: Adaptive Finite Element Methods for Differential Equations. Lectures in Mathematics. ETH-Zürich. Birkhäuser, Basel (2003)
Bartels S. and Carstensen C. (2004). Averaging techniques yield reliable a posteriori finite element error control for obstacle problems. Numer. Math. 99: 225–249
Binev P., Dahmen W. and DeVore R. (2004). Adaptive finite element methods with convergence rates. Numer. Math. 97: 219–268
Braess D. (2005). A posteriori error estimators for obstacle problems—another look. Numer. Math. 101: 415–421
Carstensen C. (2004). Some remarks on the history and future of averaging techniques in finite element error analysis. ZAMM 84: 3–21
Carstensen C. (2005). A unifying theory of a posteriori finite element error control. Numer. Math. 100: 617–637
Carstensen C. (2006). Reliable and efficient averaging techniques as universal tool for a posteriori finite element error control on unstructured grids. Int. J. Numer. Anal. Model. 3: 333–347
Carstensen C. and Hoppe R.H.W. (2005). Convergence analysis of an adaptive edge finite element method for the 2D eddy current equations. J. Numer. Math. 13: 19–32
Carstensen C. and Hoppe R.H.W. (2006). Error reduction and convergence for an adaptive mixed finite element method. Math. Comp. 75: 1033–1042
Carstensen C. and Hoppe R.H.W. (2006). Convergence analysis of an adaptive nonconforming finite element method. Numer. Math. 103: 251–266
Carstensen C. and Verfürth R. (1999). Edge residuals dominate a posteriori error estimates for low order finite element methods. SIAM J. Numer. Anal. 36: 1571–1587
Chen Z. and Nochetto R. (2000). Residual type a posteriori error estimates for elliptic obstacle problems. Numer. Math. 84: 527–548
Dörfler W. (1996). A convergent adaptive algorithm for Poisson’s equation. SIAM J. Numer. Anal. 33: 1106–1124
Eriksson K., Estep D., Hansbo P. and Johnson C. (1995). Computational Differential Equations. Cambridge University Press, Cambridge
Glowinski R., Lions J.L. and Trémolières R. (1981). Numerical Analysis of Variational Inequalities. North-Holland, Amsterdam
Hackbusch W. and Mittelmann H.D. (1983). On multi-grid methods for variational inequalities. Numer. Math. 42: 65–76
Hoppe R.H.W. (1987). Multigrid algorithms for variational inequalities. SIAM J. Numer. Anal. 24: 1046–1065
Hoppe R.H.W. and Kornhuber R. (1994). Adaptive multilevel methods for obstacle problems. SIAM J. Numer. Anal. 31: 301–323
Johnson C. (1992). Adaptive finite element methods for the obstacle problem. Math. Models Methods Appl. Sci. 2: 483–487
Kinderlehrer D. and Stampacchia G. (1980). An Introduction to Variational Inequalities. Academic, New York
Kornhuber R. (1997). Adaptive Monotone Multigrid Methods for Nonlinear Variational Problems. Teubner, Stuttgart
Morin P., Nochetto R.H. and Siebert K.G. (2000). Data oscillation and convergence of adaptive FEM. SIAM J. Numer. Anal. 38: 466–488
Neittaanmäki P. and Repin S. (2004). Reliable Methods for Mathematical Modelling. Error Control and A Posteriori Estimates. Elsevier, New York
Nochetto R.H., Siebert K.G. and Veeser A. (2003). Pointwise a posteriori error control for elliptic obstacle problems. Numer. Math. 95: 163–195
Nochetto R.H., Siebert K.G. and Veeser A. (2005). Fully localized a posteriori error estimators and barrier sets for contact problems. SIAM J. Numer. Anal. 42: 2118–2135
Ortega J.M. and Rheinboldt W.C. (2000). Iterative Solution of Nonlinear Equations in Several Variables. SIAM, Philadelphia
Stevenson, R.: Optimality of a standard adaptive finite element method. Preprint. Department of Mathematics, University of Utrecht (2005)
Suttmeier F.T. (2005). On a direct approach to adaptive FE-discretisations for elliptic variational inequalities. J. Numer. Math. 13: 73–80
Veeser A. (2001). Efficient and reliable a posteriori error estimators for elliptic obstacle problems. SIAM J. Numer. Anal. 39: 146–167
Veeser A. (2002). Convergent adaptive finite elements for the nonlinear Laplacian. Numer. Math. 92: 743–770
Verfürth R. (1996). A Review of A Posteriori Estimation and Adaptive Mesh-Refinement Techniques. Wiley-Teubner, New York
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Braess, D., Carstensen, C. & Hoppe, R.H.W. Convergence analysis of a conforming adaptive finite element method for an obstacle problem. Numer. Math. 107, 455–471 (2007). https://doi.org/10.1007/s00211-007-0098-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-007-0098-6