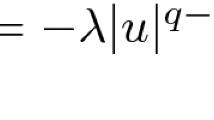The nonlinear Schrödinger equation in the half-space

Abstract

The present paper is concerned with the half-space Dirichlet problem

where $\mathbb {R}^{N}_{+}:= \{\,x \in \mathbb {R}^N: x_N > 0\, \}$ for some $N \ge 1$ and $p > 1$, $c > 0$ are constants. We analyse the existence, non-existence and multiplicity of bounded positive solutions to ($P_c$). We prove that the existence and multiplicity of bounded positive solutions to ($P_c$) depend in a striking way on the value of $c > 0$ and also on the dimension N. We find an explicit number ${c_p}\in (1,\sqrt{e})$, depending only on p, which determines the threshold between existence and non-existence. In particular, in dimensions $N \ge 2$, we prove that, for $0< c < {c_p}$, problem ($P_c$) admits infinitely many bounded positive solutions, whereas, for $c > {c_p}$, there are no bounded positive solutions to ($P_c$).

1 Introduction

Due to its relevance within several models arising in physics and biology, the nonlinear stationary Schrödinger equation

$$\begin{aligned} -\Delta v + v = |v|^{p-1} v, \quad in \mathbb {R}^N, \end{aligned}$$

(1.1)

received extensive attention in the last four decades. In particular, let us mention that the study of solitary wave solutions for the (focusing) NLS

$$\begin{aligned} i \partial _t \varphi + \Delta \varphi + |\varphi |^{p-1}\varphi = 0, \quad (t,x) \in \mathbb {R}\times \mathbb {R}^N, \end{aligned}$$

is reduced to problem (1.1) via a time-harmonic ansatz. For classic existence and multiplicity results, we refer the reader e.g. to the seminal papers [2, 3, 6, 8, 9, 30, 31] and the monographs [32, 34]. We also recall the fundamental works [16, 24] where the radial symmetry and uniqueness, up to translations, of positive solutions to (1.1) satisfying the decay condition

$$\begin{aligned} v(x) \rightarrow 0, \qquad \text {as} |x| \rightarrow \infty , \end{aligned}$$

(1.2)

are proved in the case $1< p < 2^*-1$. Here and in the following $2^*$ denotes the critical Sobolev exponent, i.e. $2^*= \frac{2N}{N-2}$ for $N \ge 3$ and $2^* =2^*-1 = \infty$ for $N=1,2$. In particular, these results imply the uniqueness, up to translations, of positive finite energy solutions $u \in H^1(\mathbb {R}^N)$. In contrast, for $N \ge 2$, (1.1) admits an abundance of sign-changing finite energy solutions satisfying (1.2), see e.g. [2, 3, 27, 28] and the references therein. Moreover, more recent geometric constructions of different solution shapes highlight the rich structure of the set of positive solutions which do not satisfy the decay assumption (1.2), see e.g. [1, 11, 26, 28] and the references therein.

Whereas it seems impossible to provide an exhaustive list of references for the full space problem (1.1), much less is known regarding the half-space Dirichlet problem

$$\begin{aligned} \left\{ \begin{aligned} -\Delta v + v&= |v|^{p-1} v, \quad&in \mathbb {R}^{N}_{+},\\ v&= c,&\quad on \partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

(1.3)

where $\mathbb {R}^{N}_{+}:= \{ x \in \mathbb {R}^N: x_N > 0\}$ for some $N \ge 1$ and $c \ge 0$ is a constant. In the case $c=0$, general nonexistence results are available for (1.3). More precisely, the non-existence of finite energy solutions $u \in H_0^1(\mathbb {R}^{N}_{+})$ to (1.3) in the case $c=0$ follows from [14, Theorem I.1], while [4, Corollary 1.3] yields, in particular, the non-existence of positive solutions to (1.3) with $c=0$ and the the decay property

$$\begin{aligned} \lim _{x_N \rightarrow \infty } v(x',x_N) = 0, \qquad \text {uniformly in}\, x' \in \mathbb {R}^{N-1}. \end{aligned}$$

(1.4)

The aim of the present paper is to analyse the existence, non-existence and multiplicity of bounded positive solutions v to the problem (1.3)–(1.4) in the case $c>0$, for which we are not aware of any previous result in general dimensions N. As we shall see below, the multiplicity of positive solutions depends in a striking way on the value $c > 0$ and, somewhat surprisingly, also on the dimension N. Let us stress that we cannot expect the existence of finite energy solutions $u \in H^1(\mathbb {R}^{N}_{+})$ to (1.3) in the case $N \ge 2$. Actually, we cannot expect solutions to (1.3) belonging to $L^p(\mathbb {R}^{N}_{+})$ for any $1 \le p < \infty$. The one-dimensional decay condition (1.4) therefore seems natural.

The consideration of inhomogeneous Dirichlet boundary conditions as in (1.3) is to some extend motivated by recent works on pattern formation in biological and chemical models. For instance, in [23], the authors numerically show that, for different types of reaction-diffusion systems, the pattern formation can be isolated away from the boundary using this type of boundary conditions. Moreover, within a rigorous analysis of some of these models in an asymptotically small diffusivity ratio, one may expect that the equation of the limiting profile is precisely (1.3) with $c > 0$. This is indeed the case for the Gierer–Meinhardt system considered in [19]. As one can observe in [19, Sect. 2], the homoclinic solution $w_0 (\, \cdot +t_{c,p})$ (see (1.6) and (1.7) below) plays a key role in the construction of multi-spike patterns for this model.

Not surprisingly, problem (1.3) is completely understood in the case $N=1$. This is due to the fact that the one-dimensional equation

$$\begin{aligned} -w'' + w = w^p, \end{aligned}$$

(1.5)

admits a first integral, and from this one can easily deduce that, for $1<p< \infty$, (1.5) admits, up to sign and translation, a unique global non trivial solution satisfying $w(t) \rightarrow 0$ as $t \rightarrow \pm \infty$. See e.g. [8, Theorem 5], [34, Theorem 3.16] and [22, Theorem 1.2] where, in addition, the Mountain-Pass characterization of this unique solution is established. By direct computations, one can verify that this solution is precisely given by

$$\begin{aligned} \begin{aligned}&t \mapsto w_0(t) = {c_p}\left[ \cosh \left( \frac{p-1}{2} t \right) \right] ^{-\frac{2}{p-1}}, \\&\text {with}\qquad {c_p}: = \left( \frac{p+1}{2} \right) ^{\frac{1}{p-1}} = w_0(0) = \sup _{t \in \mathbb {R}} w_0(t). \end{aligned} \end{aligned}$$

(1.6)

As we shall see below, the value ${c_p}$ will be of key importance also for the higher dimensional version of (1.3). The following complete characterization of the one dimensional case is an immediate consequence of these facts.

Proposition 1.1

Let $N =1$, $p>1$ and $c>0$. Then:

• (i) If $0< c < {c_p}$, problem (1.3)–(1.4) admits exactly two positive solutions given by $t \mapsto w_0(t + t_{c,p})$ and $t \mapsto w_0(t - t_{c,p})$, where

  $$\begin{aligned} t_{c,p}:= \frac{2}{p-1} \ln \left( \sqrt{\frac{p+1}{2c^{p-1}}} + \sqrt{\frac{p+1}{2c^{p-1}}-1}\right) . \end{aligned}$$

  (1.7)

• (ii) If $c = {c_p}$, the function $w_0$ is the unique positive solution to (1.3)–(1.4).

• (iii) If $c > {c_p}$, problem (1.3)–(1.4) does not admit solutions.

Our main results concern dimensions $N \ge 2$. In this case, problem (1.3)–(1.4) is invariant under translations and rotations parallel to the boundary $\partial \mathbb {R}^N_+ = \mathbb {R}^{N-1}$. In particular, if $N \ge 2$ and v is a positive solution to (1.3)–(1.4), then the functions $x \mapsto v(x' + \tau ,x_N)$, $\tau \in \mathbb {R}^{N-1}$ are also solutions to (1.3)–(1.4), where, here and in the following, we write $x = (x',x_N)$ for $x \in \mathbb {R}^N_{+}$ with $x' \in \mathbb {R}^{N-1}$. In the following, we call two solutions geometrically distinct if they do not belong to the same orbit of solutions under translations and rotations in $\mathbb {R}^{N-1}$.

Our first main result reads as follows.

Theorem 1.2

Let $N \ge 2$, $p > 1$ and $c > 0$. Then:

• (i) If $0< c < {c_p}$, there exist at least three geometrically distinct bounded positive solutions to (1.3)–(1.4).

• (ii) If $c > {c_p}$, there are no bounded positive solutions to (1.3)–(1.4).

Remark 1.1

• (a) By a bounded positive solution to (1.3)–(1.4), we mean a positive function $v \in C^2(\mathbb {R}^{N}_{+}) \cap C(\overline{\mathbb {R}^{N}_{+}}) \cap L^{\infty }(\mathbb {R}^{N}_{+})$ satisfying (1.3) in the pointwise sense and such that (1.4) holds.

• (b) The nonexistence part (ii) of Theorem 1.2 is proved with a variant of the sliding method based on a comparison with $x_N$-translates of the function $x \mapsto w_0(x_N)$. We shall comment on this in more detail further below.

• (c) As we have indicated above already, Theorem 1.2 (i) highlights the rich structure of solutions to (1.3)–(1.4) in the case $N \ge 2$, $0< c< {c_p}$, which is in striking contrast to the case $N =1$. Indeed, Theorem 1.2 (i) yields, in addition to the two one-dimensional profile solutions $x \mapsto w_0(x_N + t_{c,p})$ and $x \mapsto w_0(x_N - t_{c,p})$ at least one further geometrically distinct solution which is not merely a function of the $x_N$-variable. Hence, by the remarks above, this one solution gives rise to an infinite number of positive solutions via translations parallel to the boundary $\partial \mathbb {R}^N_+ = \mathbb {R}^{N-1}$. In Corollary 1.4 below, we shall derive more precise lower estimates on the number of geometrically distinct solutions depending on the exponent p and the dimension N.

• (d) It suffices to prove Theorem 1.2 (i) in the case $N=2$ since every positive solution v to (1.3)–(1.4) in the case $N=2$ gives rise to a corresponding solution $\tilde{v}$ to (1.3)–(1.4) in general dimension $N \ge 3$ by simply setting $\tilde{v}(x) = v(x_{1},x_{N})$.

• (e) It remains as an interesting open question whether the function $x \mapsto w_0(x_N)$ is the unique bounded positive solution to (1.3)–(1.4) in the case $c={c_p}$. At first glance, it seems natural to establish such a uniqueness result also with the help of a sliding argument as mentioned in (b) above, but additional difficulties appear in the case $c= {c_p}$, and non-uniqueness remains a possibility for now.

The following result provides some information on the shape of the solutions we construct.

Theorem 1.3

Let $N \ge 2$, $1< p < 2^*-1$ and $0< c < {c_p}$. Then there exists a positive solution to (1.3)–(1.4) of the form

$$\begin{aligned} x \mapsto w_0\left( x_N + t_{c,p}\right) + u(x), \end{aligned}$$

(1.8)

with a nonnegative function $u \in H^1_0(\mathbb {R}^N_+) {\setminus } \{0\}$.

By the remarks above and since all exponents $p<\infty$ are subcritical in the case $N=2$, Theorem 1.3 implies Theorem 1.2 (i) in the case $N=2$ and therefore for all $N \ge 2$. It also allows us to distinguish different solution orbits under translations and rotations in $\mathbb {R}^{N-1}$.

Corollary 1.4

Let $N \ge 3$, $1< p < \frac{M+2}{M-2}$ for some $M \in \{3,\dots ,N\}$ and $0< c < {c_p}$. Then problem (1.3)–(1.4) admits at least $M+1$ geometrically distinct positive solutions.

This result is a rather immediate corollary of Theorem 1.3. Indeed, under the given assumptions, for every dimension ${\widetilde{N}} \in \{2,3,\dots ,M\}$, Theorem 1.3 yields the existence of a solution to (1.3)–(1.4) of the form

$$\begin{aligned} x \mapsto w_0\left( x_{\widetilde{N}} + t_{c,p}\right) + u\left( x_1,\dots ,x_{{\widetilde{N}}-1},x_{\widetilde{N}}\right) \end{aligned}$$

with a nonnegative $u \in H^1_0(\mathbb {R}^{{\widetilde{N}}}_+) {\setminus } \{0\}$. Clearly, these $M-1$ solutions are geometrically distinct, and they are also geometrically distinct from the two one-dimensional profile solutions.

It is natural to guess that the change of the solution set when passing from $c>{c_p}$ to $c<{c_p}$ is a bifurcation phenomenon. More precisely, one may guess that the solutions constructed in Theorem 1.3 have the property that $u = u_c \rightarrow 0 \in H^1_0(\mathbb {R}^N_+)$ as $c \nearrow {c_p}$ for the functions u in the ansatz (1.8). This remains an open question, and the answer could even depend on the value of p. We note that standard results from bifurcation theory do not apply here since the linearized problem

$$\begin{aligned} \left\{ \begin{aligned} -\Delta v + v - p |w_0(x_N)|^{p-1} v&= 0 \quad&in \mathbb {R}^{N}_{+}, \\ v&= 0&\quad on \partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

at the parameter value $c = c_p$ has purely essential spectrum due to its invariance with respect to translations in directions parallel to the boundary $\partial \mathbb {R}^N_+ = \mathbb {R}^{N-1}$. Bifurcation from the essential spectrum has been observed successfully in other contexts (see e.g. the survey paper [33] and the references therein), but there is still no general functional analytic framework which provides sufficient abstract conditions.

We now give some ideas of the proof of Theorem 1.3. For this we fix $c \in (0,{c_p})$ and define the functions

$$\begin{aligned} t \mapsto z_c(t):= w_0\left( t + t_{c,p}\right) \qquad and \qquad t \mapsto \widetilde{z}_c(t):= w_0\left( t -t_{c,p}\right) , \end{aligned}$$

where $t_{c,p}$ is given in (1.7). We recall that $z_c$ and $\widetilde{z}_c$ are the unique positive solutions to (1.5) such that $z_c(0) = \widetilde{z}_c(0) = c$. Moreover, we define $u_c: \overline{\mathbb {R}^{N}_{+}} \rightarrow \mathbb {R}$ and $\widetilde{u}_c : \overline{\mathbb {R}^{N}_{+}} \rightarrow \mathbb {R}$ as

$$\begin{aligned} u_c(x) := z_c(x_N) \quad and \quad \widetilde{u}_c(x):= \widetilde{z}_c(x_N), \end{aligned}$$

(1.9)

and we directly notice that $u_c$ and $\widetilde{u}_c$ are both solutions to (1.3)–(1.4). Furthermore, it follows that

$$\begin{aligned} u_c(x) = O\left( e^{-x_N}\right) \quad and \quad \widetilde{u}_c(x) = O\left( e^{-x_N}\right) , \quad as x_N \rightarrow \infty . \end{aligned}$$

(1.10)

Proving Theorem 1.3 now amounts to find a nonnegative solution $u \in H_0^1(\mathbb {R}^{N}_{+}) {\setminus } \{0\}$ to the non-autonomous Schrödinger type equation

$$\begin{aligned} -\Delta u + u = f(x,u), \quad u \in H_0^1(\mathbb {R}^{N}_{+}), \end{aligned}$$

(1.11)

with

$$\begin{aligned} f(x,s):= |u_c(x)+s|^{\,p-1}\left( u_c(x)+s\right) - \left( u_c(x)\right) ^{\,p}, \end{aligned}$$

(1.12)

because in this case $v = u_c + u$ is of the form (1.8), solves (1.3) and it is easy to see that also satisfies (1.4). Since we are interested in finding non-negative solutions to (1.11), we truncate the nonlinearity and define

$$\begin{aligned} g(x,s):= \left( u_c(x)+s^+\right) ^{\,p} - (u_c(x))^{\,p} = \left\{ \begin{aligned}&f(x,s), \quad&if s \ge 0,\\&0,&if s \le 0, \end{aligned} \right. \end{aligned}$$

(1.13)

with f given in (1.12). We then consider the auxiliary problem

$$\begin{aligned} -\Delta u + u = g(x,u), \quad u \in H_0^1(\mathbb {R}^{N}_{+}). \end{aligned}$$

(1.14)

Considering $u^{-} \in H_0^1(\mathbb {R}^{N}_{+})$ as test function in (1.14), one can easily check that every solution to (1.14) is non-negative and so, that every solution to (1.14) is a non-negative solution to (1.11). It might be worth pointing out that the one-dimensional function $\widetilde{u}:= \widetilde{u}_c - u_c \in C^2(\mathbb {R}^{N}_{+})$ is a positive solution to the equation in (1.14) and also satisfies $\widetilde{u} = 0$ on $\partial \mathbb {R}^{N}_{+}$. However, $\widetilde{u} \not \in H_0^1(\mathbb {R}^{N}_{+})$ since it only depends on the $x_N$ variable. Hence, $\widetilde{u}$ is not a solution to (1.14).

We shall look for a non-trivial solution to (1.14) as a critical point of the associated functional

$$\begin{aligned} E: H_0^1(\mathbb {R}^{N}_{+}) \rightarrow \mathbb {R},\qquad E(u) = \frac{1}{2} \int _{\mathbb {R}^{N}_{+}} \left( |\nabla u|^2 + u^2\right) dx - \int _{\mathbb {R}^{N}_{+}} G(x,u) dx, \end{aligned}$$

(1.15)

where

$$\begin{aligned} G(x,u):= \int _0^u g(x,s) ds = \frac{1}{p+1}\left( \left( u_c+u^{+}\right) ^{p+1}-u_c^{p+1} - (p+1) u_c^p u^{+} \right) . \end{aligned}$$

(1.16)

More precisely, we are going to prove the existence of a non-trivial critical point of mountain pass type. This requires new and subtle estimates. The key difficulties in the variational approach are the non-standard shape of the nonlinearity g in (1.14) and the lack of compactness due to the unboundedness of $\mathbb {R}^{N}_{+}$. To overcome these difficulties, we need new estimates within the analysis of Cerami sequences and for comparing the mountain pass energy value for E with the corresponding one of the limit energy functional

$$\begin{aligned} E_\infty : H^1(\mathbb {R}^N) \rightarrow \mathbb {R}, \qquad E_{\infty }(u) = \frac{1}{2}\int _{\mathbb {R}^N} \left( |\nabla u|^2 + u^2\right) \,dx - \frac{1}{p+1} \int _{\mathbb {R}^N} |u|^{\,p+1} dx. \end{aligned}$$

(1.17)

In particular, we shall use the asymptotic decay properties of the unique positive radial solution to (1.1) in order to build suitable test functions.

We wish to mention two further open problems at this stage. First, one may ask whether Theorem 1.3 extends to the critical case $N \ge 3$, $p=2^*-1$. In this case, the mountain pass geometry of the functional E remains, but the lack of compactness is more severe as it is not only caused by the unboundedness of $\mathbb {R}^N_+$ but also by possible point concentration of bounded Cerami sequences. Indeed, while the limit energy functional $E_\infty$ in (1.17) does not admit critical points in the case $p=2^*$ by Pohozaev’s identity (see e.g. [34, Corollary B.4]), rescaling bounded Cerami sequences around possible concentration points leads to critical points of the Yamabe functional $u \mapsto \frac{1}{2}\int _{\mathbb {R}^N} |\nabla u|^2 \,dx - \frac{1}{2^*} \int _{\mathbb {R}^N} |u|^{2^*} dx$. It therefore seems natural to build test functions from translated and concentrated instantons $x \mapsto [N(N-2)\varepsilon ^2]^{\frac{N-2}{4}} \bigl (\varepsilon ^2+|x-x_*|^2\bigr )^{-\frac{N-2}{2}}$ in order to estimate the mountain pass energy. However, since our estimates rely on the precise exponential decay rate of the unique positive radial solution to (1.1) as given in (4.6), they do not apply to instantons. Hence the case $p=2^*$ remains a problem for future research.

The second open problem concerns the existence of solutions of the form $x \mapsto w_0(x_N - t_{c,p}) + u(x)$ with $u \in H^1_0(\mathbb {R}^N_+) {\setminus } \{0\}$. In this case, $u_c$ has to be replaced by $\widetilde{u}_c$ in the definition of the nonlinearity G in (1.16). One may observe that the mountain pass geometry is lost in this case, and the presence of essential spectrum leads to additional difficulties which seem hard to deal with.

We now comment on the proofs of the non-existence part (ii) of Theorem 1.2. We argue by contradiction and use a suitable modification of the so-called sliding method introduced by H. Berestycki and L. Nirenberg and further developed by H. Berestycki, L. Caffarelli and L. Nirenberg among others. Specifically, our proofs are inspired by [15, Sect. 2] and [7, Sect. 4].

We finally comment on the boundedness of positive solutions to (1.3)–(1.4). As stated in the following proposition, all the positive solutions to (1.3)–(1.4) are bounded in the case where $1< p < 2^{*}-1$. Hence, the fact that we are considering bounded solutions is not a restriction in this case.

Proposition 1.5

Let $N \ge 2$, $1< p < 2^*-1$ and $c > 0$. Any positive $v \in C^2(\mathbb {R}^{N}_{+}) \cap C(\overline{\mathbb {R}^{N}_{+}})$-solution to (1.3)–(1.4) belongs to $L^{\infty }(\mathbb {R}^{N}_{+})$.

The proof of Proposition 1.5 follows by a rather standard blow up argument based on the doubling lemma by P. Poláčik, P. Quittner and P. Souplet in [29]. For the convenience of the reader, we include the proof in Sect. 5 below.

1.1 Organization of the paper

In Sect. 2, we collect estimates related to the nonlinearity g in (1.13) and the functional E associated with (1.14). With the help of these estimates, we establish the mountain pass geometry of E in Sect. 3, and we show that Cerami sequences at nontrivial energy levels are bounded and admit nontrivial weak limits after suitable translation. In Sect. 4, we then prove a key energy estimate which shows that, in dimensions $N \ge 2$, the mountain pass energy of the functional E is strictly smaller than the corresponding one for the limit energy functional $E_\infty$ given in (1.17). With the help of this energy estimate, we then complete the proof of Theorem 1.3 in Sect. 5. Finally, we give the proof of Theorem 1.2 (ii) in Sect. 6.

1.2 Notation

For $1\le p<\infty ,$ we let $\Vert \cdot \Vert _{L^p(\mathbb {R}^{N}_{+})}$ denote the standard norm on the usual Lebesgue space $L^p(\mathbb {R}^{N}_{+})$. The Sobolev space $H_0^1(\mathbb {R}^{N}_{+})$ is endowed with the standard norm

$$\begin{aligned} \Vert u\Vert ^2 = \int _{\mathbb {R}^{N}_{+}} \left( \,|\nabla u|^2 + |u|^2 \right) \, dx. \end{aligned}$$

Also, for a function v, we define $v^{+} := \max \{v,0\}$ and $v^{-}:= \max \{-v,0\}$ and we write $x = (x',x_N)$ for $x \in \mathbb {R}^{N}_{+}$ with $x' \in \mathbb {R}^{N-1}$. We denote by $'\rightarrow '$, respectively by $'\rightharpoonup '$, the strong convergence, respectively the weak convergence in corresponding space and denote by $B_R(x)$ the open ball in $\mathbb {R}^N$ of center x and radius $R>0.$ Also, we shall denote by $C_i>0$ different constants which may vary from line to line but are not essential to the analysis of the problem. Finally, at various places, we have to distinguish the cases $p \le 2$ and $p>2$. For this it is convenient to introduce the special constant

$$\begin{aligned} 1_{\{p>2\}}:= \left\{ \begin{aligned}&0,&\quad p \le 2,\\&1,&\quad p > 2. \end{aligned} \right. \end{aligned}$$

2 Preliminaries

In this section we collect some estimates related to the transformed nonlinearity g defined in (1.13), its primitive G and the functional E defined in (1.15). For this we fix, throughout Sects. 2–5, $c \in (0,{c_p})$, $p \in (1,2^{*}-1)$, and we let $u_c$ be given in (1.9). We recall that we have the uniform estimate

$$\begin{aligned} 0 \le u_c \le c_p \qquad \text {in } \mathbb {R}^{N}_{+}. \end{aligned}$$

(2.1)

We start with an elementary inequality for nonnegative real numbers which will be used in the energy estimates in Sect. 4 below.

Lemma 2.1

For every $q > 2$ there exists $\kappa _q>0$ with

$$\begin{aligned} (a+b)^q - a^q-b^q \ge qa^{q-1}b +\kappa _q a b^{q-1} \qquad \text {for all}\, a,b \ge 0. \end{aligned}$$

(2.2)

Remark 2.1

If $q \ge 3$, then (2.2) holds in symmetric form with $\kappa _q = q$, see e.g. [20, Theorem 1]. If $q \in (2,3)$, it is easy to see that one has to choose $\kappa _q < q$.

Proof

We first note that, since $q-1>1$, we have, by convexity of the function $\tau \mapsto (1+\tau )^{q-1}$,

$$\begin{aligned} (s+t)^{q-1}-\left( s^{q-1}+t^{q-1}\right)= & {} s^{q-1}\left[ \left( 1+\frac{t}{s}\right) ^{q-1}- \left( 1+\left( \frac{t}{s}\right) ^{q-1}\right) \right] \nonumber \\\ge & {} s^{q-1}\left( (q-1)\frac{t}{s} - \left( \frac{t}{s}\right) ^{q-1}\right) \nonumber \\= & {} (q-1)ts^{q-2} - t^{q-1} \end{aligned}$$

(2.3)

for $s \ge t >0$. Now, to prove the claim, it suffices to consider $a,b>0$, since the inequality holds trivially if $a=0$ or $b=0$. Moreover, it suffices to prove that the inequality holds for $b \ge a>0$ with some $\kappa _q \in (0,q]$, since then it also follows for arbitrary $a,b >0$. For fixed $a>0$, we consider the function

$$\begin{aligned} \ell : [0,\infty ) \rightarrow \mathbb {R}, \qquad \ell (t)= (a+t)^q - a^q-t^q - qa^{q-1}t \end{aligned}$$

Then we have $\ell (0)=0$ and

$$\begin{aligned} \ell '(t)= q \left[ (a+t)^{q-1}-\left( a^{q-1}+t^{q-1}\right) \right] \end{aligned}$$

Consequently, by (2.3) we have, for $b \ge a$,

$$\begin{aligned} \ell (b)=&\int _0^a \ell '(t)\,dt+ \int _a^b \ell '(t)\,dt \ge q \left[ \int _0^a \left( (q-1)ta^{q-2} - t^{q-1}\right) dt\right. \\&\left. \,+ \int _a^b \left( (q-1)a t^{q-2} - a^{q-1}\right) dt\right] \\ =&\, qa \left( \kappa _{q,1} a^{q-1} + b^{q-1} - a^{q-2}b \right) \\&\text {with}\, \qquad \kappa _{q,1} :=\,\frac{q-1}{2}-\frac{1}{q} >0. \end{aligned}$$

Since, by Young’s inequality,

$$\begin{aligned} a^{q-2}b \le \frac{q-2}{q-1}a^{q-1} + \frac{1}{q-1}b^{q-1}, \end{aligned}$$

we deduce that

$$\begin{aligned} \ell (b) \ge qa \left[ \left( \kappa _{q,1}-\frac{q-2}{q-1}\right) a^{q-1} + \frac{q-2}{q-1} b^{q-1}\right] . \end{aligned}$$

If $\kappa _{q,1} \ge \frac{q-2}{q-1}$, we conclude that $\ell (b) \ge \frac{q(q-2)}{q-1} a b^{q-1}$. On the other hand, if $0< \kappa _{q,1} < \frac{q-2}{q-1}$, we use again that $b \ge a$ and conclude that

$$\begin{aligned} \ell (b) \ge qa \left[ \left( \kappa _{q,1}-\frac{q-2}{q-1}\right) b^{q-1} + \frac{q-2}{q-1} b^{q-1}\right] = q \kappa _{q,1} a b^{q-1}. \end{aligned}$$

Hence, (2.2) holds for $b \ge a >0$ with $\kappa _q = q \min \{ \frac{q-2}{q-1}, \kappa _{q,1}\} \in (0,q)$. The proof is finished. $\square$

Next we provide basic but important estimates for the nonlinearity g defined in (1.13) and its primitive G.

Lemma 2.2

• (i) For $(x,s) \in \mathbb {R}^{N}_{+}\times \mathbb {R}$ we have

  $$\begin{aligned} 0 \le g(x,s)- s^+ p u_c(x)^{p-1} \le C_{1,p}\, \left[ s^+\right] ^{\,p} + 1_{\left\{ p>2\right\} }C_{2,p}\, \left[ s^+\right] ^2, \end{aligned}$$

  (2.4)

  and

  $$\begin{aligned} 0 \le G(x,s)- \frac{p}{2}\left[ s^+\right] ^2 u_c(x)^{p-1} \le \frac{C_{1,p}}{p+1}\left[ s^+\right] ^{p+1} + 1_{\left\{ p>2\right\} }\frac{C_{2,p}}{3} \left[ s^+\right] ^3, \end{aligned}$$

  (2.5)

  with $C_{1,p}:= 1+2^{p-3} p(p-1)$ and $C_{2,p}:=p(p-1)2^{p-3}{c_p}^{p-2}$.

• (ii) Let

  $$\begin{aligned} H(x,s) := \frac{1}{2}g(x,s)s -G(x,s)\qquad \text {for}\, x \in \mathbb {R}^{N}_{+}, s \in \mathbb {R}. \end{aligned}$$

  Then we have

  $$\begin{aligned} H(x,s)\ge & {} \max \left\{ \,0\,,\, \frac{p-1}{2(p+1)}\, \left[ s^+\right] ^{p+1} - u_c(x)^{p-1} D_{1,p}\left[ s^+\right] ^2\right. \nonumber \\&\left. - u_c(x)\, 1_{\{p>2\}} D_{2,p} \left[ s^{+}\right] ^p \right\} \end{aligned}$$

  (2.6)

  with $D_{1,p}:= \frac{p(p-1)}{p+1}\bigl (1+2^{p-2}\bigr )$ and $D_{2,p}:= \frac{p2^{p-2}}{p+1}$.

  Moreover, the function $H(x,\cdot )$ is non-decreasing in s for every $x \in \mathbb {R}^{N}_{+}$.

Remark 2.2

The constants $C_{i,p}$ and $D_{i,p}$, $i = 1,2$, are not optimal. However, this choice simplifies the presentation. Moreover, they do not play an important role in our proofs below.

Proof of Lemma 2.2

(i) Since $g(\cdot ,s) \equiv 0$ and $G(\cdot ,s) \equiv 0$ for $s \le 0$, it suffices to consider $s > 0$. Fix $x \in \mathbb {R}^{N}_{+}$. Since $g(x,\cdot )$ is of class $C^1$ on $(0,\infty )$, we have

$$\begin{aligned}&g(x,s)=\left( u_c(x)+s\right) ^{p}-u_c(x)^p\\&\quad = s p u_c(x)^{p-1}+ p\int _0^s \left[ \left( u_c(x)+\tau \right) ^{p-1}-u_c(x)^{p-1}\right] \,d\tau , \qquad \text {for}\,s > 0.\nonumber \end{aligned}$$

(2.7)

We now distinguish two cases. If $p \in (1,2]$, we have

$$\begin{aligned} 0 \le (a +\tau )^{p-1} - a^{p-1} \le \tau ^{p-1} \qquad \text {for}\, \tau >0,\, a \ge 0, \end{aligned}$$

and therefore, if $p \in (1,2]$,

$$\begin{aligned} 0 \le g(x,s) - s p u_c(x)^{p-1} \le p \int _0^s \tau ^{p-1}\,d\tau \le s^p, \qquad \text {for}\, s \ge 0. \end{aligned}$$

(2.8)

If $p>2$, we have

$$\begin{aligned} 0 \le (a +\tau )^{p-1} - a^{p-1} \le (p-1)\tau (a+\tau )^{p-2}, \qquad \text {for}\, \tau >0,\, a \ge 0, \end{aligned}$$

by the convexity of the function $a \mapsto (a +\tau )^{p-1}$ and therefore, using also (2.1),

$$\begin{aligned} 0&\le g(x,s) - s p u_c(x)^{p-1} \le p\int _0^s \left[ \left( u_c(x)+\tau \right) ^{p-1}-u_c(x)^{p-1}\right] \,d\tau \\&\le p (p-1)\int _0^s \tau (u_c(x)+\tau )^{p-2}\,d\tau \le \frac{p(p-1)}{2}s^2 \left( u_c(x)+s\right) ^{p-2}\\&\le \frac{p(p-1)}{2}s^2 \left( {c_p}+s\right) ^{p-2}. \end{aligned}$$

Note also that, since $p > 2$,

$$\begin{aligned} ({c_p}+s)^{p-2} \le \left( 2 \max \{{c_p},s\}\right) ^{p-2} \le (2{c_p})^{p-2} + (2s)^{p-2}, \qquad \text {for}\, s \ge 0. \end{aligned}$$

(2.9)

Consequently, if $p > 2$,

$$\begin{aligned} 0 \le g(x,s) - s p u_c(x)^{p-1} \le 2^{p-3} p(p-1)s^p + p(p-1)2^{p-3}{c_p}^{p-2} s^2, \qquad \text {for}\, s \ge 0. \end{aligned}$$

(2.10)

Now (2.4) follows by combining (2.8) and (2.10). Moreover, (2.5) follows by integrating (2.4).

(ii) We first note that $H(x,s) \equiv 0$ for all $s \le 0$. Thus, we just have to prove the result for $s > 0$. Directly observe that, for all $x \in \mathbb {R}^{N}_{+}$, we have $H(x,\cdot ) \in C^1(\mathbb {R})$ and

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial s} H(x,s)&= \frac{p}{2}\left( u_c(x)+s\right) ^{p-1}s + \frac{1}{2} \left( u_c(x)+s\right) ^p - \frac{1}{2} u_c^p(x)- \left( u_c(x)+s\right) ^p + u_c^p(x) \\&= \frac{1}{2} \left[ p \left( u_c(x)+s\right) ^{p-1} s - \left( u_c(x)+s\right) ^p+ u_c^p(x) \right] \qquad \text {for}\, (x,s) \in \mathbb {R}^{N}_{+}\times (0,+\infty ). \end{aligned} \end{aligned}$$

On the other hand, since $p>1$, we have, by the mean value theorem,

$$\begin{aligned} \left( u_c(x)+s\right) ^p - u_c^p(x) \le p \left( u_c(x)+s\right) ^{p-1} s \qquad \text {for}\, (x,s) \in \mathbb {R}^{N}_{+}\times (0,+\infty ). \end{aligned}$$

Hence $\frac{\partial }{\partial s} H(x,s) \ge 0$ for all $s > 0$, so the function $H(x,\cdot )$ is non-decrasing in $s \in [0,\infty )$. This also implies that $H(x,s) \ge 0$ for $s \ge 0$. It thus remains to prove (2.6) for $s \ge 0$. For this we first note that

$$\begin{aligned} H(x,s) =\frac{g(x,s)s}{2}-G(x,s)&= \frac{1}{2}\left( \left( u_c(x)+s\right) ^p - u_c(x)^p\right) s\\&\quad - \frac{1}{p+1}\left( \left( u_c(x)+s\right) ^{p+1} - u_c(x)^{p+1} - (p+1) u_c(x)^{p}s \right) \\&= \left( \frac{1}{2}-\frac{1}{p+1}\right) \left( \left( u_c(x)+s\right) ^p - u_c(x)^p\right) s\\&\quad - \frac{1}{p+1}\left( \left( u_c(x)+s\right) ^{p} - u_c(x)^{p} - p u_c(x)^{p-1}s \right) u_c(x)\\&\ge \frac{p-1}{2(p+1)}\,s^{p+1} - \frac{1}{p+1}u_c(x) \left( g(x,s)- s p u_c(x)^{p-1}\right) . \end{aligned}$$

It therefore remains to show that

$$\begin{aligned} u_c(x) \left( g(x,s)- s p u_c^{p-1}(x)\right)\le & {} (p+1) \left( u_c^{p-1}(x)\, D_{1,p} s^2\right. \nonumber \\&\left. + u_c(x)\, 1_{\{p> 2\}} D_{2,p} s^p \right) , \quad for s > 0.\nonumber \\ \end{aligned}$$

(2.11)

By (2.7) and integration by parts we have

$$\begin{aligned} u_c(x) \left( g(x,s)- s p u_c^{p-1}(x)\right)&= p u_c(x)\int _0^s \left[ \left( u_c(x)+\tau \right) ^{p-1}-u_c(x)^{p-1}\right] \,d\tau \nonumber \\&= p(p-1) u_c(x) \int _0^s (s-\tau ) \left[ \left( u_c(x)+\tau \right) ^{p-2}\right] \,d\tau . \end{aligned}$$

(2.12)

If $p \in (1,2]$, we have $(u_c(x)+\tau )^{p-2} \le u_c(x)^{p-2}$ for $\tau >0$ and therefore

$$\begin{aligned}&u_c(x) \left( g(x,s)- s p u_c(x)^{p-1}\right) \nonumber \\&\le p(p-1) u_c^{p-1}(x) \int _0^s (s-\tau ) \,d\tau \le p(p-1) u_c^{p-1}(x)s^2. \end{aligned}$$

(2.13)

If $p >2$, arguing as (2.9), we have

$$\begin{aligned} \left( u_c(x)+\tau \right) ^{p-2} \le 2^{p-2} \left( u_c^{p-2}(x) + \tau ^{p-2} \right) ,\qquad \text {for}\, \tau \ge 0, \end{aligned}$$

and therefore (2.12) yields

$$\begin{aligned}&u_c(x) \left( g(x,s)- s p u_c(x)^{p-1}\right) \le 2^{p-2} p(p-1) u_c(x) \int _0^s (s-\tau )\left[ u_c^{p-2}(x) + \tau ^{p-2}\right] \,d\tau \nonumber \\&\quad = 2^{p-2} p(p-1) u_c(x) \left( u_c^{p-2}(x) \int _0^s (s-\tau ) d\tau + \int _0^s (s-\tau ) \tau ^{p-2} d\tau \right) \nonumber \\&\quad \le 2^{p-2} p (p-1) u_c^{p-1}(x)\, s^2 + 2^{p-2} p u_c(x)\, s^p, \quad for s > 0. \end{aligned}$$

(2.14)

Now (2.11) follows by combining (2.13) and (2.14). The proof is finished. $\square$

Remark 2.3

• (a) From the growth estimates given in Lemma 2.2 (i) and the fact that g is continuous, it follows in a standard way that the functional E is well-defined on $H_0^1(\mathbb {R}^{N}_{+})$ and of class $C^1$.

• (b) Part (ii) of Lemma 2.2 will be useful in the analysis of Cerami sequences of the functional E, see Sect. 3 below.

Next, we consider the quadratic form $q_c: H_0^1(\mathbb {R}^{N}_{+}) \rightarrow \mathbb {R}$ given by

$$\begin{aligned} q_{c}(u) := \int _{\mathbb {R}^{N}_{+}} \left( |\nabla u|^2 + V_c(x) u^2\right) \,dx, \end{aligned}$$

(2.15)

with

$$\begin{aligned} V_c(x) := 1 - p u_c^{p-1}\left( x_N\right) \, \in \, L^{\infty }(\mathbb {R}^{N}_{+}). \end{aligned}$$

(2.16)

As we show in the following lemma, $q_{c}$ is positive definite on $H^1_0(\mathbb {R}^N_+)$.

Proposition 2.3

We have

$$\begin{aligned} \widetilde{q}_c := \inf _{u \in H^1_0\left( \mathbb {R}^N_+\right) {\setminus } \{0\}} \frac{q_{c}(u)}{\Vert u\Vert ^2}>0. \end{aligned}$$

(2.17)

Remark 2.4

• (a) Recall that we are using the shortened notation $\Vert u\Vert ^2 = \int _{\mathbb {R}^{N}_{+}} \big (|\nabla u|^2 + |u|^2\big )\, dx$.

• (b) From Proposition 2.3 it follows that $(q_c(\cdot ))^{1/2}$ is an equivalent norm to $\Vert \cdot \Vert$ in $H_0^1(\mathbb {R}^{N}_{+})$.

Proof of Lemma 2.2

Since $V_{c} \in L^\infty (\mathbb {R}^N_+)$, it suffices to show there exists $C>0$ such that

$$\begin{aligned} q_{c}(u) \ge C \Vert u\Vert _{L^2(\mathbb {R}^N_+)}^2 \qquad \text {for all}\, u \in H^1_0\left( \mathbb {R}^N_+\right) . \end{aligned}$$

(2.18)

Indeed, if (2.18) holds, then for $\delta \in (0,1)$ we have

$$\begin{aligned} q_{c}(u)&\ge \delta q_{c}(u)+ (1-\delta )C \Vert u\Vert ^2_{L^2\left( \mathbb {R}^N_+\right) } \ge \delta \Vert u\Vert ^2 + \left[ (1-\delta )C\right. \\&\left. \quad - \delta \left( 1 +\Vert V_{c}\Vert _{L^\infty \left( \mathbb {R}^N_+\right) }\right) \right] \,\Vert u\Vert ^2_{L^2\left( \mathbb {R}^N_+\right) }. \end{aligned}$$

Choosing $\delta$ sufficiently small, we have $(1-\delta )C - \delta \bigl (1 +\Vert V_{c}\Vert _{L^\infty (\mathbb {R}^N_+)}\bigr )\ge 0$ and therefore (2.17) holds with $\widetilde{q}_c \ge \delta$.

To show (2.18), we first consider the case $N= 1$. Arguing by contradiction, we assume that

$$\begin{aligned} \lambda := \inf \left\{ q_{c}(u): u \in H_0^1\left( \mathbb {R}_{+}\right) and \Vert u\Vert _{L^2\left( \mathbb {R}_{+}\right) } = 1 \right\} \le 0, \end{aligned}$$

(note that $\lambda >-\infty$ since $V_{c} \in L^\infty (\mathbb {R}_+)$). Then, there exists a sequence $(u_n)_n$ such that $\Vert u_n\Vert _{L^2(\mathbb {R}_+)}= 1$ for all $n \in \mathbb {N}$ and $q_{c}(u_n) \rightarrow \lambda$ as $n \rightarrow \infty$. Hence, $(u_n)_n$ is a bounded sequence in $H_0^1(\mathbb {R}_+)$, and thus $u_n \rightharpoonup u_*$ weakly in $H_0^1(\mathbb {R}_+)$ after passing to a subsequence. Moreover, with $v_n:= u_n- u_*$, we have $v_n \rightharpoonup 0$ in $H_0^1(\mathbb {R}_+)$ and therefore $v_n \rightarrow 0$ in $L^2_{loc}(\mathbb {R}_{+})$. Since $V_{c}(t) \rightarrow 1$ as $t \rightarrow \infty$, this implies that

$$\begin{aligned} q_{c}\left( v_n\right) \ge \int _{\mathbb {R}_+}V_{c}(t) v_n^2\,dt \ge \Vert v_n\Vert _{L^2\left( \mathbb {R}_{+}\right) }^2 + o(1), \qquad \text {as}\, n \rightarrow \infty , \end{aligned}$$

and therefore

$$\begin{aligned} \lambda + o(1)&= q_{c}(u_n)= q_{c}(u_*) + q_{c}(v_n)+ o(1) \\&\ge \lambda \Vert u_*\Vert _{L^2(\mathbb {R}_{+})}^2 + \Vert v_n\Vert _{L^2\left( \mathbb {R}_{+}\right) }^2+o(1)\\&= \lambda \left( \Vert u_*\Vert _{L^2\left( \mathbb {R}_{+}\right) }^2+ \Vert v_n\Vert _{L^2\left( \mathbb {R}_{+}\right) }^2\right) \\&\quad + (1-\lambda )\Vert v_n\Vert _{L^2\left( \mathbb {R}_{+}\right) }^2 + o(1)\\&= \lambda + (1-\lambda )\Vert v_n\Vert _{L^2\left( \mathbb {R}_{+}\right) }^2 +o(1) \end{aligned}$$

It thus follows that $v_n \rightarrow 0$ in $L^2(\mathbb {R}_{+})$ and hence $u_n \rightarrow u_*$ in $L^2(\mathbb {R}_+)$, which yields that $\Vert u_*\Vert _{L^2}=1$. Moreover, by weak lower semicontinuity of $q_{c}$ and the definition of $\lambda$, it follows that $q_{c}(u_*)=\lambda$, so $u_*$ is a constrained minimizer for $q_{c}$. A standard argument (based on replacing $u_*$ by $|u_*|$) shows that $u_* \in H_{0}^1(\mathbb {R}_+)$ is a positive or negative solution of

$$\begin{aligned} -u_*'' + V_{c}(t)u_* = \lambda u_* \quad \text {in}\, \mathbb {R}_+, \qquad u_*(0)=0. \end{aligned}$$

Without loss of generality, we may assume that $u_*$ is positive, which implies that $u_*'(0)>0$. We also recall that $w_*:= -u_{c}'$ satisfies

$$\begin{aligned} -w_*'' + V_{c}(t)w_* = 0 \quad \text {in}\, \mathbb {R}_+, \qquad w_*>0 \quad \text {in}\, \overline{\mathbb {R}_+}. \end{aligned}$$

Consequently, we have

$$\begin{aligned} 0 \le - \lambda \int _{\mathbb {R}^+}w_* u_* \,dx = \int _{\mathbb {R}^+} \left( w_* u_*'' - u_* w_*''\right) \,dx =- w_*(0) u_*'(0)<0, \end{aligned}$$

a contradiction. Hence, we conclude that (2.18) holds in the case $N=1$. To show (2.18) for general $N\ge 2$, we remark that, by density, we only have to show it for $u \in C^\infty _c(\mathbb {R}^N_+)$. For any such function we then have, writing $x = (x',t) \in \mathbb {R}^N_+$ with $x' \in \mathbb {R}^{N-1}$, $t>0$:

$$\begin{aligned} q_{c}(u)&\ge \int _{\mathbb {R}^N_+}\left( |\partial _t u|^2 + V_{c} u^2\right) \,dx \\&= \int _{\mathbb {R}^{N-1}} \int _{\mathbb {R}_+}\left( |\partial _t u(x',t)|^2 + V_c u^2(x',t)\right) \,dt dx' \\&\ge C \int _{\mathbb {R}^{N-1}} \int _{\mathbb {R}_+}u^2(x',t)\,dt dx' = C \Vert u\Vert ^2_{L^2\left( \mathbb {R}^N_+\right) }. \end{aligned}$$

Here we have used the result in the case $N=1$ and the fact that $u(x', \cdot ) \in C^\infty _c(\mathbb {R}_+) \subset H^1_0(\mathbb {R}_+)$ for every $x' \in \mathbb {R}^{N-1}$. We thus have proved (2.18) for general $N \ge 1$, and the proof is complete. $\square$

Having at hand Proposition 2.3, we prove a lower estimate on the functional E given in (1.15) that will be useful at several points below.

Corollary 2.4

We have

$$\begin{aligned} E(u) \ge \frac{\widetilde{q}_c}{2} \Vert u\Vert ^2 - \frac{C_{1,p}}{p+1} \Vert u\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} - 1_{\{p>2\}} \frac{C_{2,p}}{3} \Vert u\Vert _{L^{3}(\mathbb {R}^{N}_{+})}^{3}\qquad \text {for all}\, u \in H_0^1(\mathbb {R}^{N}_{+}). \end{aligned}$$

with $\widetilde{q}_c$ given in (2.17) and $C_{1,p},C_{2,p}$ given in Lemma 2.2 (i).

Proof

For all $u \in H_0^1(\mathbb {R}^{N}_{+})$, we have, by (2.5) and Proposition 2.3,

$$\begin{aligned} E(u)&= \frac{1}{2} \Vert u\Vert ^2 - \int _{\mathbb {R}^{N}_{+}} G(x,u) dx \\&\ge \frac{1}{2}\Vert u\Vert ^2 - \frac{1}{2} \int _{\mathbb {R}^{N}_{+}} p u_c^{p-1} \left( u^+\right) ^2 dx -\frac{C_{1,p}}{p+1} \Vert u^+\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} - 1_{\{p>2\}}\frac{C_{2,p}}{3} \Vert u^+\Vert _{L^{3}(\mathbb {R}^{N}_{+})}^{3}\\&\ge \frac{1}{2}q_c(u) -\frac{C_{1,p}}{p+1} \Vert u\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} - 1_{\{p>2\}}\frac{C_{2,p}}{3} \Vert u\Vert _{L^{3}(\mathbb {R}^{N}_{+})}^{3}\\&\ge \frac{\widetilde{q}_c}{2}\Vert u\Vert ^2 - \frac{C_{1,p}}{p+1}\Vert u\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} - 1_{\{p>2\}}\frac{C_{2,p}}{3} \Vert u\Vert _{L^{3}(\mathbb {R}^{N}_{+})}^{3}. \end{aligned}$$

$\square$

3 Mountain-pass geometry and boundedness of the Cerami sequences

This section is devoted to show that the functional E has a Mountain-pass geometry and that, for any $d \in \mathbb {R}$, the Cerami sequences for E and level d are bounded. We keep using the notation of the introduction and of Sect. 2, which depends on the fixed quantities $c \in (0,{c_p})$ and $p \in (1,2^{*}-1)$. We begin by proving that the functional E has indeed a Mountain-pass geometry.

Lemma 3.1

The functional E has the following properties.

• (i) $E(0) = 0$.

• (ii) There exist $\rho _0 > 0$ and $\delta _0 > 0$ such that $E(u) \ge \delta _{0}$ for all $u \in H_0^1(\mathbb {R}^{N}_{+})$ such that $\Vert u\Vert = \rho _0$.

• (iii) There exists $\psi \in H_0^1(\mathbb {R}^{N}_{+})$ such that $\Vert \psi \Vert > \rho _0$ and $E(\psi ) < 0$.

Proof

Since (i) is obvious, we concentrate on proving (ii) and (iii). We first prove (ii). Let $u \in H_0^1(\mathbb {R}^{N}_{+})$ with $\Vert u\Vert = \rho _0$. By Corollary 2.4, we have

$$\begin{aligned} E(u) \ge \frac{\widetilde{q}_c}{2}\rho _0^2 - \frac{C_{1,p}}{p+1} \Vert u\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} - 1_{\{p>2\}}\frac{C_{2,p}}{3} \Vert u\Vert _{L^3(\mathbb {R}^{N}_{+})}^3. \end{aligned}$$

Applying then Sobolev embeddings, we deduce that

$$\begin{aligned} E(u) \ge \frac{\widetilde{q}_c}{2}\rho _0^2 - C \left( \rho _0^{p+1} + 1_{\{p>2\}} \rho _0^3 \right) , \end{aligned}$$

with a constant $C>0$. Since $p>1$, Claim (ii) follows by taking $\rho _0$ sufficiently small. It then remains to prove (iii). Let $\varphi \in C_c^{\infty }(\mathbb {R}^{N}_{+})$ with $\varphi \gneqq 0$ and $\psi := t \varphi$ with $t \in (0,+\infty )$. Directly observe that

$$\begin{aligned} E(\psi ) = \frac{t^2}{2} \Vert \varphi \Vert ^2 + t \int _{\mathbb {R}^{N}_{+}} u_c^p \varphi dx - \frac{1}{p+1} \int _{\mathbb {R}^{N}_{+}} \left( (u_c+t\varphi )^{p+1} - u_c^{p+1}\right) dx \end{aligned}$$

Then, since

$$\begin{aligned} \int _{\mathbb {R}^{N}_{+}} \left( \left( u_c+t\varphi \right) ^{p+1}-u_c^{p+1} \right) dx \ge t^{p+1} \Vert \varphi \Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1}, \end{aligned}$$

we have that

$$\begin{aligned} E(\psi ) \le \frac{t^2}{2}\Vert \varphi \Vert ^2+tc^p\Vert \varphi \Vert _{L^1(\mathbb {R}^{N}_{+})} - \frac{t^{p+1}}{p+1} \Vert \varphi \Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1}. \end{aligned}$$

Claim (iii) follows taking t sufficiently large and thus the proof is complete. $\square$

We now prove the boundedness of Cerami sequences of the functional E.

Proposition 3.2

Cerami sequences for E at any level $d \in \mathbb {R}$ are bounded.

Remark 3.1

• (a) Recall that $(\varphi _n)_n \subset H_0^1(\mathbb {R}^{N}_{+})$ is a Cerami sequence for E at level $d \in \mathbb {R}$ if

  $$\begin{aligned} E(\varphi _n) \rightarrow d \quad and \quad \left( 1+\Vert \varphi _n\Vert \right) \Vert E'(\varphi _n)\Vert _{H^{-1}(\mathbb {R}^{N}_{+})} \rightarrow 0. \end{aligned}$$

• (b) The proof of Proposition 3.2 is inspired by [21, Sect. 3]. However, since our problem is not invariant under translations in $\mathbb {R}^N$ and our nonlinearity g has a non-standard shape, several difficulties appear.

Proof of Proposition 3.2

Let $d \in \mathbb {R}$ be an arbitrary but fixed constant and let $(u_n)_n \subset H_0^1(\mathbb {R}^{N}_{+})$ be a Cerami sequence for E at level $d \in \mathbb {R}$. First of all, observe that

$$\begin{aligned} \Vert u_n^{-}\Vert ^2 = - \langle E'(u_n), u_n^{-}\rangle \rightarrow 0, \quad as n \rightarrow \infty . \end{aligned}$$

In particular, we deduce that $(u_n^{-})_n$ is bounded. It then remains to prove that $(u_n^{+})_n$ is bounded. We assume by contradiction that $\Vert u_n\Vert \rightarrow \infty$ and we set $v_n:= u_n\,/\,\Vert u_n\Vert$ for all $n \in \mathbb {N}$. Since $(v_n)_n$ and $(u_n^{-})_n$ are bounded, up to a subsequence if necessary, we have

$$\begin{aligned} v_n \rightharpoonup v in H_0^1(\mathbb {R}^{N}_{+}), \quad v_n \rightarrow v in L^q_{loc}(\mathbb {R}^{N}_{+}) \quad \text {for}\, 1 \le q < 2^{*} \quad and \quad v_n \rightarrow v \;a.e. in \, \mathbb {R}^{N}_{+}, \end{aligned}$$

(3.1)

for some $v \in H_0^1(\mathbb {R}^{N}_{+})$ with $v \ge 0$. We have now two possible cases:

• $\underline{\mathbf{Case 1 (Vanishing) }}$: For all $R > 0$, it follows that

  $$\begin{aligned} \lim _{n \rightarrow \infty } \sup _{y \in \mathbb {R}^{N}_{+}} \int _{B_R(y)\cap \mathbb {R}^{N}_{+}} v_n^2 dx = 0. \end{aligned}$$

  (3.2)

• $\underline{\mathbf{Case 2 (Non-vanishing) }}$: There exist $R> 0,\ \delta > 0$ and a sequence of points $(y^n)_n \subset \mathbb {R}^{N}_{+}$ such that

  $$\begin{aligned} \lim _{n \rightarrow \infty } \int _{B_R(y^n) \cap \mathbb {R}^{N}_{+}} v_n^2 dx \ge \delta . \end{aligned}$$

  (3.3)

We shall prove that none of these cases may happen. This will prove the boundedness of the sequence Cerami sequence $(u_n)_n$.

• $\underline{\mathbf{Case 1 (Vanishing) }}$: First of all, observe that, by (3.2) and Lions’ Lemma [25, Lemma I.1], $v_n \rightarrow 0$ in $L^q(\mathbb {R}^{N}_{+})$ for all $2< q < 2^{*}$, and so, by uniqueness of the limit we have $v \equiv 0$. We define then the sequence $(z_n)_n \subset H_0^1(\mathbb {R}^{N}_{+})$ by $z_n := t_n u_n$ with $t_n \in [0,1]$ satisfying

  $$\begin{aligned} E(z_n) = \max _{t \in [0,1]} E(tu_n), \end{aligned}$$

  (if, for $n \in \mathbb {N}$, $t_n$ is not unique, we choose the smallest value) and we split the proof in the vanishing case (Case 1) into three steps.

• Step 1.1: $\lim _{n \rightarrow \infty } E(z_n) = + \infty$.

We argue by contradiction. Suppose there exists $M < +\infty$ such that

$$\begin{aligned} \liminf _{n \rightarrow \infty } E(z_n) \le M, \end{aligned}$$

and define $(k_n)_n \subset H_0^1(\mathbb {R}^{N}_{+})$ as

$$\begin{aligned} k_n := \left( \frac{4M}{\widetilde{q}_c}\right) ^{\frac{1}{2}}v_n = \left( \frac{4M}{\widetilde{q}_c}\right) ^{\frac{1}{2}} \frac{1}{\Vert u_n\Vert } u_n, \qquad \text {for all}\,\, n \in \mathbb {N}, \end{aligned}$$

where $\widetilde{q}_c > 0$ is the constant given by Proposition 2.3. First, observe that

$$\begin{aligned} k_n \rightharpoonup 0 in H_0^1(\mathbb {R}^{N}_{+}), \quad k_n \rightarrow 0 in L^q(\mathbb {R}^{N}_{+}),\ \ \text {for}\, 2< q < 2^{*}, \quad and \quad k_n \rightarrow 0 a.e. in \mathbb {R}^{N}_{+}. \end{aligned}$$

(3.4)

Then, by Corollary 2.4 and (3.4), we obtain that

$$\begin{aligned} E(k_n) \ge \frac{\widetilde{q}_c}{2} \Vert k_n\Vert ^2 - C\left( \Vert k_n\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} + 1_{\{p>2\}} \Vert k_n\Vert _{L^3(\mathbb {R}^{N}_{+})}^3 \right) = 2M + o(1). \end{aligned}$$

(3.5)

Taking M bigger if necessary, we have that, for all $n \in \mathbb {N}$ large enough,

$$\begin{aligned} E(k_n) > \frac{3}{2}M. \end{aligned}$$

On the other hand, observe that, for $n \in \mathbb {N}$ large enough, $\left( \frac{4M}{\widetilde{q}_c}\right) ^{\frac{1}{2}} \frac{1}{\Vert u_n\Vert } \in [0,1].$ Hence, we have that

$$\begin{aligned} \frac{3}{2}M \le \liminf _{n \rightarrow \infty } E\left( k_n\right) \le \liminf _{n \rightarrow \infty } E\left( z_n\right) \le M, \end{aligned}$$

which is a contradiction. Thus, the Step 1.1 follows.

• $\mathbf{Step} 2.1:$ $\langle E'(z_n), z_n \rangle = 0$ for all $n \in \mathbb {N}$ large enough.

  By Step 1.1 we know that $E(z_n) \rightarrow \infty$ as $n \rightarrow \infty$. On the other hand, $E(0) = 0$ and $E(u_n) \rightarrow d$ as $n \rightarrow \infty$. Hence, for $n \in \mathbb {N}$ large enough, $t_n \in (0,1)$ and so, by the definition of $z_n$, the Step 2.1 follows.

• Step 3.1: Conclusion $\underline{\mathbf{Case 1 }}$.

  Observe that, by Step 2.1, for all $n \in \mathbb {N}$ large enough,

  $$\begin{aligned} E\left( z_n\right) = E\left( z_n\right) - \frac{1}{2}\langle E'\left( z_n\right) ,z_n \rangle = \int _{\mathbb {R}^{N}_{+}}H\left( x,z_n\right) dx, \end{aligned}$$

  where H is given in Lemma 2.2 (ii). By Step 1.1, we have that

  $$\begin{aligned} \lim _{n \rightarrow \infty } \int _{\mathbb {R}^{N}_{+}}H\left( x,z_n\right) dx = +\infty . \end{aligned}$$

  (3.6)

  On the other hand, since $(u_n)_n$ is a Cerami sequence,

  $$\begin{aligned} d+o(1) = E(u_n)-\frac{1}{2}\langle E'(u_n), u_n \rangle = \int _{\mathbb {R}^{N}_{+}} H\left( x,u_n\right) dx. \end{aligned}$$

  Then, using the definition of $z_n$ and the fact that H(x, s) is non-decreasing in s by Lemma 2.2 (ii), we obtain

  $$\begin{aligned} \int _{\mathbb {R}^{N}_{+}} H\left( x,z_n\right) dx \le \int _{\mathbb {R}^{N}_{+}} H\left( x,u_n\right) dx = d+o(1), \end{aligned}$$

  which clearly contradicts (3.6). Hence, Case 1 (vanishing) cannot happen.

• $\underline{\mathbf{Case 2 (Non-vanishing) }}$: We split the proof into two steps.

• Step 1.2: There exists $M > 0$ such that $y^n_{N}:= \mathrm{dist}(y^n,\partial \mathbb {R}^{N}_{+}) \le M$ for all $n \in \mathbb {N}$.

We assume by contradiction that $y^n_{N} \rightarrow +\infty$ as $n \rightarrow +\infty$. Then, for all $n \in \mathbb {N}$, we introduce $w_n:= v_n( \cdot + y^n)$ and observe that

$$\begin{aligned} w_n \rightharpoonup w in H^1(\mathbb {R}^N), \quad w_n \rightarrow w in L^q_{loc}(\mathbb {R}^N) \;\text {for}\, 1 \le q < 2^{*}, \quad and \quad w_n \rightarrow w a.e. in \mathbb {R}^N, \end{aligned}$$

(3.7)

for some $w \in H^1(\mathbb {R}^N)$ with $w \not \equiv 0$ (by (3.3)) and $w \ge 0$. Now, observe that, since $(u_n)_n$ is a Cerami sequence, Lemma 2.2 (ii) implies that

$$\begin{aligned} o(1)&= \frac{1}{\Vert u_n\Vert ^{p+1}}\left( E\left( u_n\right) - \frac{1}{2} \langle E'\left( u_n\right) ,u_n \rangle \right) \\&= \frac{1}{\Vert u_n\Vert ^{p+1}} \int _{\mathbb {R}^{N}_{+}} H\left( x,u_n(x)\right) \,dx\\&\ge \frac{1}{\Vert u_n\Vert ^{p+1}}\left[ \frac{p-1}{2(p+1)} \Vert u_n^+\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1}\right. \\&\left. \quad - \int _{\mathbb {R}^{N}_{+}} \left( u_c^{p-1}(x) D_{1,p}\left[ u_n^+\right] ^{2} + u_c(x) \, 1_{\{p>2\}} D_{2,p}\left[ u_n^+\right] ^{p}\right) dx\right] \\&\ge \frac{1}{\Vert u_n\Vert ^{p+1}}\left[ \frac{p-1}{2(p+1)}\Vert u_n^+\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1}\right. \\&\left. \quad - \max \{ {c_p}^{p-1}, {c_p}\} \left( D_{1,p}\Vert u_n^+\Vert _{L^{2}(\mathbb {R}^{N}_{+})}^{2} +1_{\{p>2\}} D_{2,p}\Vert u_n^+\Vert _{L^p(\mathbb {R}^{N}_{+})}^{p}\right) \right] \\&\ge \frac{p-1}{2(p+1)}\Vert v_n^+\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1}\\&\quad - \frac{C}{\Vert u_n\Vert ^{p+1}} \left( \Vert u_n\Vert ^{2} +1_{\{p>2\}}\Vert u_n\Vert ^{p} \right) \ge \frac{p-1}{2(p+1)} \Vert v_n^+\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} +o(1), \end{aligned}$$

where $C>0$ is a constant independent of n. Here we also used Sobolev embeddings and the fact that $\Vert u_n\Vert \rightarrow \infty$ as $n \rightarrow \infty$. Since $p>1$, we thus conclude by Fatou’s Lemma that

$$\begin{aligned} 0 =\lim _{n \rightarrow \infty } \Vert v_n^+\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1}= \liminf _{n \rightarrow \infty } \int _{\{x_N \ge -y^n_{N}\}} (w_n^{+})^{p+1} dx \ge \int _{\mathbb {R}^N} (w^{+})^p dx. \end{aligned}$$

Hence $w = w^+ \equiv 0$, which clearly is a contradiction. Thus, Step 1.2 follows.

• Step 2.2: Conclusion $\underline{\mathbf{Case 2 }}$.

  By Step 1.2 we know there exists $M > 0$ such that $y^n_{N} \le M$ for all $n \in \mathbb {N}$. We then define, for all $n \in \mathbb {N}$, $\widetilde{w}_n:= v_n( \cdot + \xi _n)$, where $\xi _n = (y^n_{1}, \ldots , y^n_{N-1},0)$. Again by (3.3), we have

  $$\begin{aligned}&\widetilde{w}_n \rightharpoonup \widetilde{w} in H_0^1(\mathbb {R}^{N}_{+}), \quad \widetilde{w}_n \rightarrow \widetilde{w} in L^q_{loc}(\mathbb {R}^{N}_{+})\; \text {for}\, 1 \le q < 2^{*}, \quad and \quad \nonumber \\&\widetilde{w}_n \rightarrow \widetilde{w} a.e. in \mathbb {R}^{N}_{+}, \end{aligned}$$

  (3.8)

  for some $\widetilde{w} \in H_0^1(\mathbb {R}^{N}_{+})$ with $\widetilde{w} \not \equiv 0$ and $\widetilde{w} \ge 0$. For $n \in \mathbb {N}$, let $\varphi _n:= \widetilde{w}(\cdot - \xi _n) \in H^1_0(\mathbb {R}^{N}_{+})$. Since $(u_n)_n$ is a Cerami sequence with $\Vert u_n\Vert \rightarrow \infty$ as $n \rightarrow \infty$, we have

  $$\begin{aligned} \begin{aligned} o(1)&= \frac{\langle E'(u_n),\varphi _n \rangle }{\Vert u_n\Vert }\\&= \frac{1}{\Vert u_n\Vert }\int _{\mathbb {R}^{N}_{+}} \left( \nabla u_n \nabla \varphi _n + u_n \varphi _n - g(x,u_n)\varphi _n \right) dx \\&= \int _{\mathbb {R}^{N}_{+}} \bigl ( \nabla v_n \nabla \varphi _n + v_n\varphi _n\bigr )dx\\\&\quad - \int _{\mathbb {R}^{N}_{+}} \left( \frac{(u_c+u_n^{+})^p-u_c^p}{\Vert u_n\Vert }\right) \, \varphi _n dx\\&=\int _{\mathbb {R}^{N}_{+}} \left( \nabla \widetilde{w}_n \nabla \widetilde{w} + \widetilde{w}_n \widetilde{w} \right) dx\\&\quad - \int _{\mathbb {R}^{N}_{+}} \left( \frac{(u_c+\Vert u_n\Vert \widetilde{w}_n^{+})^p-u_c^p}{\Vert u_n\Vert }\right) \, \widetilde{w} dx\\&=\Vert \widetilde{w}\Vert ^2 + o(1)- \int _{\mathbb {R}^{N}_{+}} \Bigl ( \frac{(u_c+\Vert u_n\Vert \widetilde{w}_n^{+})^p-u_c^p}{\Vert u_n\Vert }\Bigr )\, \widetilde{w} dx.\\ \end{aligned} \end{aligned}$$

  On the other hand, since $p>1$, we have that

  $$\begin{aligned} \liminf _{n \rightarrow \infty } \frac{\left( u_c+\Vert u_n\Vert \widetilde{w}_n^{+}\right) ^p-u_c^p}{\Vert u_n\Vert \widetilde{w}_n^{+}} \, \widetilde{w}_n^{+} \widetilde{w} = + \infty , \quad a.e. in \, \{\widetilde{w}>0\} \end{aligned}$$

  and therefore, since $\widetilde{w} \ge 0$ and $\widetilde{w} \not \equiv 0$,

  $$\begin{aligned}&\liminf _{n \rightarrow \infty } \int _{\mathbb {R}^{N}_{+}} \left( \frac{\left( u_c+u_n^{+}\left( \cdot + \xi _n\right) \right) ^p - u_c^p}{\Vert u_n\Vert }\right) \, \widetilde{w}dx\\&\quad = \liminf _{n \rightarrow \infty } \int _{\{\widetilde{w}>0\}} \left( \frac{\left( u_c+u_n^{+}(\cdot + \xi _n)\right) ^p - u_c^p}{\Vert u_n\Vert }\right) \, \widetilde{w}dx = + \infty \end{aligned}$$

  by Fatou’s Lemma. This yields a contradiction. Hence, Case 2 (non-vanishing) cannot happen either and thus the result follows. $\square$

Lemma 3.3

Let $(u_n)_n$ be a Cerami sequence for E at level $d \in \mathbb {R}{\setminus } \{0\}$. Then, there exist $R > 0$, $\delta > 0$ and a sequence of points $(y^n)_n \subset \mathbb {R}^{N}_{+}$ such that

$$\begin{aligned} \liminf _{n \rightarrow \infty } \int _{B_R\left( y^n\right) \cap \mathbb {R}^{N}_{+}} u_n^2\, dx \ge \delta . \end{aligned}$$

Proof

We assume by contradiction that, for all $R > 0$,

$$\begin{aligned} \liminf _{n \rightarrow \infty } \sup _{y \in \mathbb {R}^{N}_{+}} \int _{B_R(y) \cap \mathbb {R}^{N}_{+}} u_n^2 dx = 0. \end{aligned}$$

Then, by Lions’ [25, Lemma I.1], we have that $u_n \rightarrow 0$ in $L^q(\mathbb {R}^{N}_{+})$ for all $2< q < 2^{*}$. Now, since $(u_n)_n$ is a Cerami sequence, using Lemma 2.2 (i), we get

$$\begin{aligned} o(1)&= \langle E'(u_n), u_n \rangle = \Vert u_n\Vert ^2 - \int _{\mathbb {R}^{N}_{+}}g(x,u_n(x))u_n\,dx \\&\ge \Vert u_n\Vert ^2 - \int _{\mathbb {R}^{N}_{+}} p u_c^{p-1} (u_n^{+})^2 dx - C_{1,p}\Vert u_n^+\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} - 1_{\{p>2\}} C_{2,p} \Vert u_n^+\Vert _{L^3(\mathbb {R}^{N}_{+})}^3 \\&\ge q_c(u_n) - C_{1,p}\Vert u_n\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} - 1_{\{p>2\}} C_{2,p} \Vert u_n\Vert _{L^3(\mathbb {R}^{N}_{+})}^3 \\&\ge \widetilde{q}_c \Vert u_n\Vert ^2 - C_{1,p}\Vert u_n\Vert _{L^{p+1}(\mathbb {R}^{N}_{+})}^{p+1} - 1_{\{p>2\}} C_{2,p} \Vert u_n\Vert _{L^3(\mathbb {R}^{N}_{+})}^3. \end{aligned}$$

Hence, since $u_n \rightarrow 0$ in $L^{q}(\mathbb {R}^{N}_{+})$ for all $2< q < 2^*$, we deduce that $\Vert u_n\Vert \rightarrow 0$. Since E is continuous, this implies that $E(u_n) \rightarrow 0$ as $n \rightarrow \infty$, contradicting our assumption that $d \not = 0$. The proof is finished.

4 Energy estimates

We keep using the notation of the introduction and of Sect. 2, which depends on the fixed quantities $c \in (0,{c_p})$ and $p \in (1,2^{*}-1)$. Moreover, we will assume $N \ge 2$ throughout this section, which will be of key importance in order to derive the energy estimates we need. The mountain pass value associated to (1.14) is given by

$$\begin{aligned} b := \inf _{\gamma \in \Gamma } \max _{t \in [0,1]} E(\gamma (t)), \end{aligned}$$

(4.1)

where

$$\begin{aligned} \Gamma := \left\{ \gamma \in C\left( [0,1], H_0^1(\mathbb {R}^{N}_{+})\right) : \gamma (0) = 0,\ E(\gamma (1)) < 0\, \right\} . \end{aligned}$$

We note that $b > 0$ by Lemma 3.1. We also note that the functional E (given in (1.15)) can be written as

$$\begin{aligned} E(u)= & {} E_{\infty }^{+}(u)\nonumber \\- & {} \frac{1}{p+1} \int _{\mathbb {R}^{N}_{+}} \left( \left( u_c+u^{+}\right) ^{p+1}-u_c^{p+1}-\left( u^{+}\right) ^{p+1}-(p+1)u_c^p u^{+} \right) dx,\qquad \quad \end{aligned}$$

(4.2)

where $E_{\infty }^{+}: H_0^1(\mathbb {R}^{N}_{+}) \rightarrow \mathbb {R}$ is given by

$$\begin{aligned} E_{\infty }^{+}(u) = \frac{1}{2}\Vert u\Vert ^2-\frac{1}{p+1} \int _{\mathbb {R}^{N}_{+}}\left( u^{+}\right) ^{p+1} dx. \end{aligned}$$

Now, we introduce the auxiliary (limit) problem

$$\begin{aligned} -\Delta u + u = |u|^{p-1}u, \quad u \in H^1(\mathbb {R}^N), \end{aligned}$$

(4.3)

and its associated energy $E_{\infty }: H^1(\mathbb {R}^N) \rightarrow \mathbb {R}$ given by

$$\begin{aligned} E_{\infty }(u) = \frac{1}{2}\int _{\mathbb {R}^N} \left( |\nabla u|^2 + u^2\right) \,dx - \frac{1}{p+1} \int _{\mathbb {R}^N} |u|^{\,p+1} dx. \end{aligned}$$

(4.4)

Also, we define

$$\begin{aligned} b_{\infty }:= \inf _{\mathcal {K}_{\infty }}E_{\infty }, \quad \text { where } \quad \mathcal {K}_{\infty }:= \left\{ u \in H^1(\mathbb {R}^N) {\setminus } \{0\}: E_{\infty }'(u) = 0 \right\} . \end{aligned}$$

(4.5)

According to [8, Theorem 1], [6, Théorème 1] and [16, Theorem 2], there exists a ground-state solution $\psi \in C^2(\mathbb {R}^N)$ to (4.3) which is positive, radially symmetric, and such that

$$\begin{aligned} \psi (x) \le C_{GS} |x|^{-\frac{N-1}{2}} e^{-|x|} \quad and \quad |\nabla \psi (x)| \le C_{GS} |x|^{-\frac{N-1}{2}} e^{-|x|}, \qquad as \quad |x| \rightarrow \infty , \end{aligned}$$

(4.6)

for some $C_{GS} > 0$ depending only on N and p. Moreover,

$$\begin{aligned} \psi \,\text {is strictly decreasing in the radial variable.} \end{aligned}$$

(4.7)

Let us also emphasize that

$$\begin{aligned} 0 < b_{\infty }= & {} E_\infty (\psi )= \left( \frac{1}{2}-\frac{1}{p+1} \right) \Vert \psi \Vert _{L^{p+1}(\mathbb {R}^N)}^{p+1} = \frac{p-1}{2(p+1)} \Vert \psi \Vert _{L^{p+1}(\mathbb {R}^N)}^{p+1}\nonumber \\= & {} \frac{p-1}{2(p+1)} \inf _{u \in {{\mathcal K}}_{\infty }}\Vert u\Vert _{L^{p+1}(\mathbb {R}^N)}^{p+1}. \end{aligned}$$

(4.8)

The aim of this section is to show, based on the assumption $N \ge 2$, that

$$\begin{aligned} b < b_{\infty }. \end{aligned}$$

(4.9)

This strict inequality will be crucial to prove the existence result to (1.14) contained in Sect. 5. To this end, let us recall that $u_c(x) \sim e^{-x_N}$ as $x_N \rightarrow \infty$. More precisely, it follows from (1.6) and the definition of $u_c$ that

$$\begin{aligned} m_{c,1}\, e^{-x_N}\le & {} u_c(x) \le m_{c,2}\, e^{-x_N}, \quad \text {for}\, x \in \mathbb {R}^{N}_{+}, \quad \text {with}\nonumber \\ m_{c,1}:= & {} {c_p}e^{-t_{c,p}}, \quad m_{c,2} := {c_p}2^{\frac{2}{p-1}} e^{-t_{c,p}}. \end{aligned}$$

(4.10)

Moreover, for $r > 0$, we introduce the function

$$\begin{aligned} x \mapsto \psi _r(x):= \left( \psi \left( x- r e_N\right) - \varepsilon _r\right) ^{+}, \end{aligned}$$

where $e_N = (0, \ldots ,0,1)$ is the N-th coordinate vector and $\varepsilon _r>0$ is uniquely defined by (4.7) and the property that

$$\begin{aligned} \psi > \varepsilon _r \qquad \text {in}\, B_r(0)\qquad \text {and}\qquad \psi \le \varepsilon _r \qquad \text {in}\, \mathbb {R}^N {\setminus } B_r(0). \end{aligned}$$

We note that, as a consequence of (4.6), we have

$$\begin{aligned} \varepsilon _r \le C_{GS} r^{-\frac{N-1}{2}} e^{-r} \end{aligned}$$

(4.11)

We also note that $\psi _r \in H_0^1(\mathbb {R}^{N}_{+})$ for every $r \ge 0$.

The rest of the section is devoted to prove the following result from which (4.9) immediately follows.

Proposition 4.1

There exists $R>0$ and $k>0$ with the following properties:

• (i) $E(t\psi _r) < b_{\infty }$ for all $r \ge R,\, t \in [0,k]$.

• (ii) $E(k \psi _r) < 0$ for all $r \ge R$.

We split the proof of this proposition into several lemmas.

Lemma 4.2

There exists $C_1 > 0$ with

$$\begin{aligned} E_{\infty }^{+} (t\psi _r) \le b_{\infty } + C_1 e^{-r} r^{-\frac{N-1}{2}} t^{p+1} \qquad \text {for all}\,\, t,r >0. \end{aligned}$$

(4.12)

Proof

Let $t,r>0$. Directly observe that, by the definition of $\psi _r$,

$$\begin{aligned} E_{\infty }^{+}\left( t\psi _r\right)= & {} \frac{t^2}{2} \Vert \psi _r\Vert ^2 - \frac{t^{p+1}}{p+1} \int _{\mathbb {R}^{N}_{+}} \psi _r^{p+1} dx\nonumber \\= & {} \frac{t^2}{2} \int _{B_r(0)} \left( |\nabla \psi |^2 + \left( \psi - \varepsilon _r\right) ^2 \right) \, dx - \frac{t^{p+1}}{p+1} \int _{B_r(0)} \left( \psi - \varepsilon _r\right) ^{p+1} dx.\nonumber \\ \end{aligned}$$

(4.13)

On the other hand, since $\psi$ is a solution to (4.3) and $(\psi -\varepsilon _r)^{+} \in H^1(\mathbb {R}^N)$, using $(\psi -\varepsilon _r)^{+}$ as test function in (4.3), we obtain that

$$\begin{aligned} \begin{aligned} \int _{B_r(0)} | \nabla \psi |^2 dx&= \int _{\mathbb {R}^N} \nabla \psi \nabla \left( \psi -\varepsilon _r\right) ^{+} dx \\&= \int _{\mathbb {R}^N} \left( - \psi \left( \psi - \varepsilon _r\right) ^{+} + \psi ^p \left( \psi - \varepsilon _r\right) ^{+} \right) dx\\&= \int _{B_r(0)} \left( - \psi (\psi - \varepsilon _r) + \psi ^p (\psi - \varepsilon _r) \right) dx. \end{aligned} \end{aligned}$$

Substituting the above identity into (4.13) and using the mean value theorem, we find that

$$\begin{aligned} E_{\infty }^{+}\left( t\psi _r\right)&= \frac{t^2}{2} \int _{B_r(0)} \left( -\psi \left( \psi -\varepsilon _r\right) + \psi ^p \left( \psi -\varepsilon _r\right) + \left( \psi -\varepsilon _r\right) ^2 \right) dx\\&\quad - \frac{t^{p+1}}{p+1} \int _{B_r(0)} \left( \psi -\varepsilon _r\right) ^{p+1} dx \\&= - \frac{\varepsilon _r t^2}{2} \int _{B_r(0)} \left( \psi -\varepsilon _r\right) dx\\&\quad + \frac{1}{p+1} \int _{B_r(0)} \left( \psi -\varepsilon _r\right) \left[ \frac{p+1}{2} t^2 \psi ^p - t^{p+1} \left( \psi -\varepsilon _r\right) ^p \right] dx \\&\le \frac{1}{p+1} \int _{B_r(0)} \left( \psi -\varepsilon _r\right) \left[ \frac{p+1}{2} t^2 \psi ^p - t^{p+1} (\psi -\varepsilon _r)^p \right] dx \\&= \frac{1}{p+1} \left( \frac{p+1}{2}t^2-t^{p+1} \right) \int _{B_r(0)} \left( \psi -\varepsilon _r\right) \psi ^p dx\\&\quad + \frac{t^{p+1}}{p+1} \int _{B_r(0)} \left( \psi -\varepsilon _r\right) \left[ \psi ^p - \left( \psi -\varepsilon _r\right) ^p \right] dx\\&\le \frac{p-1}{2(p+1)} \int _{B_r(0)} \left( \psi -\varepsilon _r\right) \psi ^p dx + \frac{\varepsilon _r\,p\, t^{\,p+1}}{p+1} \int _{B_r(0)} \left( \psi -\varepsilon _r\right) \psi ^{p-1} dx \\&\le \frac{p-1}{2(p+1)} \int _{\mathbb {R}^N} \psi ^{\,p+1} dx + \frac{\varepsilon _r\,p\, t^{\,p+1}}{p+1} \int _{\mathbb {R}^N} \left( \psi -\varepsilon _r\right) ^{+} \psi ^{p-1} dx. \end{aligned}$$

Using (4.8) and (4.11), we deduce that

$$\begin{aligned} E_{\infty }^{+}\left( t\psi _r\right)\le & {} b_{\infty } + \frac{\varepsilon _r\,p\, t^{\,p+1}}{p+1} \int _{\mathbb {R}^N} \left( \psi -\varepsilon _r\right) ^{+} \psi ^{p-1} dx \le b_{\infty }\\&+ \frac{p}{p+1}C_{GS} r^{-\frac{N-1}{2}} e^{-r} t^{p+1} \int _{\mathbb {R}^N} \psi ^p dx. \end{aligned}$$

Hence (4.12) holds with $C_1 = \frac{p C_{GS}}{p+1} \int _{\mathbb {R}^N} \psi ^p dx$. $\square$

Lemma 4.3

There exists ${R'}\ge 1$ and $C_2 > 0$ with

$$\begin{aligned} E_{\infty }^{+}\left( t\psi _r\right) - E\left( t \psi _r\right) \ge C_2 e^{-r}\, t^{\,p} \qquad \text {for all}\, t >0, r \ge {R'}. \end{aligned}$$

(4.14)

Proof

Let $t >0$ be arbitrary but fixed. Using Lemma 2.1 with $q = p+1$, $\kappa := \kappa _{q}>0$, the identity (4.2), the lower bound in (4.10) and the mean value theorem, we deduce that, for all $r \ge 1$,

$$\begin{aligned} E_{\infty }^{+}\left( t\psi _r\right) - E\left( t\psi _r\right)&= \frac{1}{p+1} \int _{\mathbb {R}^{N}_{+}} \left( \left( u_c+t\psi _r\right) ^{p+1}-u_c^{p+1}\right. \\&\left. \quad - \left( t\psi _r\right) ^{p+1} -(p+1)u_c^p t \psi _r \right) dx \ge \kappa t^p \int _{\mathbb {R}^{N}_{+}} u_c \psi _r^p dx\\&= \kappa t^p \int _{\mathbb {R}^{N}_{+}} u_c\left( \left( \psi \left( \cdot -re_N\right) - \varepsilon _r\right) ^{+}\right) ^p dx\\&= \kappa t^p \int _{B_r(0)} u_c\left( \cdot +re_N\right) \left( \psi - \varepsilon _r\right) ^p dx\\&\ge \kappa t^p \int _{B_r(0)} u_c\left( \cdot +re_N\right) \left( \psi ^p -\varepsilon _r p \psi ^{p-1}\right) \, dx\\&\ge \kappa t^p \left( \int _{B_r^-(0)} u_c\left( \cdot +re_N \right) \psi ^p dx - \varepsilon _r p c_p \int _{\mathbb {R}^N} \psi ^{p-1} dx\right) \\&\ge \kappa t^p \left( m_{c,1}e^{-r} \int _{B_r^{\,-}(0)} \psi ^p dx\right. \\&\left. \quad - p c_p C_{GS} r^{-\frac{N-1}{2}} e^{-r} \int _{\mathbb {R}^N} \psi ^{p-1} dx\right) \\&\ge \kappa t^p e^{-r} \left( \frac{m_{c,1}}{2} \int _{B_r(0)} \psi ^p dx - p c_p C_{GS} r^{-\frac{N-1}{2}} \int _{\mathbb {R}^N} \psi ^{p-1} dx\right) \\&\ge \kappa t^p e^{-r} \left( \frac{m_{c,1}}{2} \int _{B_1(0)} \psi ^p dx - p c_p C_{GS} r^{-\frac{N-1}{2}} \int _{\mathbb {R}^N} \psi ^{p-1} dx\right) \end{aligned}$$

where we have set $B_r^{\,-}(0):= \{x \in B_r(0)\,:\, x_N \le 0\}$. Since $N \ge 2$, we may choose ${R'} \ge 1$ sufficiently large to guarantee that

$$\begin{aligned} p c_p C_{GS} r^{-\frac{N-1}{2}} \int _{\mathbb {R}^N} \psi ^{p-1} dx \le \frac{m_{c,1}}{4} \int _{B_1(0)} \psi ^p dx, \qquad \text {for}\,\, r \ge {R'}, \end{aligned}$$

and therefore

$$\begin{aligned} E_{\infty }^{+}(t\psi _r) - E(t\psi _r) \ge C_2 e^{-r}\, t^{\,p}, \quad \text {for}\, r \ge {R'}, \quad \text {with}\quad C_2:= \frac{\kappa m_{c,1}}{4} \int _{B_1(0)} \psi ^p dx. \end{aligned}$$

Hence the claim follows. $\square$

Lemma 4.4

Let ${R'}\ge 1$ be given as in Lemma 4.3. Then there exist $k > 0$ with $E(k\psi _r) < 0$ for all $r \ge {R'}$.

Proof

Let $k >0$. For $r \ge {R'} \ge 1$ we have, by Lemma 4.3 and since the map $r \mapsto \varepsilon _r$ is strictly decreasing by (4.7),

$$\begin{aligned} E(k \psi _r)&\le E_{\infty }^+(k\psi _r) = \frac{k^2}{2} \Vert \psi _r\Vert ^2 - \frac{k^{p+1}}{p+1} \int _{\mathbb {R}^{N}_{+}} \psi _r^{p+1} dx\\&\le \frac{k^2}{2} \Vert \psi \Vert _{H^1(\mathbb {R}^N)}^2 - \frac{k^{p+1}}{p+1} \int _{B_r(0)} \left( \psi - \varepsilon _r \right) ^{p+1} dx \\&\le \frac{k^2}{2} \Vert \psi \Vert _{H^1(\mathbb {R}^N)}^2 - \frac{k^{p+1}}{p+1} \int _{B_1(0)} \left( \psi - \varepsilon _1 \right) ^{p+1} dx \end{aligned}$$

Since $\int _{B_1(0)} \big (\psi - \varepsilon _1 \big )^{p+1} dx >0$ by (4.7), we may choose

$$\begin{aligned} k> \left( \frac{(p+1)\Vert \psi \Vert _{H^1(\mathbb {R}^N)}^2}{2 \int _{B_1(0)} \left( \psi - \varepsilon _1 \right) ^{p+1} dx}\right) ^{\frac{1}{p-1}} \end{aligned}$$

which implies that $E(k \psi _r) < 0$ for $r \ge {R'}$, as claimed. $\square$

Proof of Proposition 4.1

Let ${R'}\ge 1$ be given by Lemma 4.3, and let $k>0$ be given by Lemma 4.4. For $r \ge {R'}$ and $t \in [0,k]$ we then have, by Lemmas 4.2 and 4.3,

$$\begin{aligned} E\left( t \psi _r\right)= & {} E_{\infty }^{+}\left( t \psi _r\right) - \left( E_{\infty }^{+}\left( t\psi _r\right) -E\left( t\psi _r\right) \right) \le b_{\infty } + e^{-r} \left( t^{p+1} C_1 r^{-\frac{N-1}{2}} - t^p C_2 \right) \\\le & {} b_{\infty } + e^{-r} t^p \left( k C_1 r^{-\frac{N-1}{2}} - C_2 \right) . \end{aligned}$$

Since $N \ge 2$, we may fix $R \ge R'$ with the property that $k C_1 r^{-\frac{N-1}{2}} \le \frac{C_2}{2}$ for $r \ge R$, which implies that

$$\begin{aligned} E\left( t \psi _r\right) \le b_{\infty } - \frac{C_2}{2} e^{-r} t^p < b_\infty \quad \text {for}\, t \in (0,k], r \ge R. \end{aligned}$$

Since also $E(0)= 0 < b_{\infty }$, we thus obtain that $E(t \psi _r) < b_{\infty }$ for $t \in [0,k]$, $r \ge R$. Moreover, by Lemma 4.4 we have $E(k\psi _r) < 0$ for all $r \ge R$ since $R \ge R'$. The proof is finished. $\square$

5 The existence result

We keep using the notation of the introduction and of Sect. 2, which depends on the fixed quantities $c \in (0,{c_p})$ and $p \in (1,2^{*}-1)$. Moreover, we will assume $N \ge 2$ throughout this section, which will allow us to prove the existence of a non-trivial solution to (1.14). This will conclude the proof of Theorem 1.3.

Theorem 5.1

Let $N \ge 2$. Then there exists a non-trivial solution $u \in H_0^1(\mathbb {R}^{N}_{+})$ to (1.14) which, in particular, is a positive solution to (1.11).

The strategy of the proof is as follows: using the strict inequality (4.9), we will manage to prove the existence of a Cerami sequence whose weak limit is non trivial and thus we will obtain a non trivial solution to (1.14).

Proof of Theorem 5.1

Since the functional E has a mountain pass geometry (see Lemma 3.1), there exists a Cerami sequence for E at the corresponding mountain pass level b defined in (4.1) (see e.g. [10] or [13, Theorem 6, Sect. 1, Chapter IV]), i.e. there exists $(u_n)_n \subset H_0^1(\mathbb {R}^{N}_{+})$ such that

$$\begin{aligned} E(u_n) \rightarrow b \quad and \quad \left( 1+\Vert u_n\Vert \right) \Vert E'\left( u_n\right) \Vert _{H^{-1}(\mathbb {R}^{N}_{+})} \rightarrow 0, \quad as n \rightarrow \infty . \end{aligned}$$

By Proposition 3.2 we know that $(u_n)_n$ is bounded in $H_0^1(\mathbb {R}^{N}_{+})$. Moreover,

$$\begin{aligned} \Vert u_n^-\Vert ^2 = \langle E'(u_n),u_n^- \rangle \rightarrow 0 \qquad \text {as}\, n \rightarrow \infty . \end{aligned}$$

(5.1)

Let $(y^n)_n \subset \mathbb {R}^{N}_{+}$ be the sequence of points obtained in Lemma 3.3 applied to $(u_n)_n$, i.e., we have

$$\begin{aligned} \liminf _{n \rightarrow \infty } \int _{B_R(y^n) \cap \mathbb {R}^{N}_{+}} u_n^2\, dx \ge \delta \qquad \text {for some}\, \delta >0. \end{aligned}$$

(5.2)

We split the argument into two steps.

Step 1: There exists $M > 0$ such that $y^n_{N} = \mathrm{dist}(y^n, \partial \mathbb {R}^{N}_{+}) \le M$ for all $n \in \mathbb {N}$.

We assume by contradiction that

$$\begin{aligned} \lim _{n \rightarrow \infty } y^n_{N} = + \infty . \end{aligned}$$

(5.3)

Then, let us define, for all $n \in \mathbb {N}$, $w_n := u_n (\cdot + y^n)$. By Lemma 3.3 and (5.1), it follows that

$$\begin{aligned}&w_n \rightharpoonup w in H^1(\mathbb {R}^N), \quad w_n \rightarrow w in L^q_{loc}(\mathbb {R}^N)\ \;\text {for}\, 1 \le q < 2^{*}, \quad and \nonumber \\&\quad w_n \rightarrow w a.e. in \mathbb {R}^N, \end{aligned}$$

(5.4)

for some $w \in H^1(\mathbb {R}^N)$ with $w \ge 0$, $w \not \equiv 0$. We also observe that

$$\begin{aligned} b + o(1)&= E(u_n) - \frac{1}{2} \langle E'(u_n), u_n \rangle = \int _{\mathbb {R}^{N}_{+}} H(x,u_n(x))\,dx\nonumber \\&=\int _{ \{x_N \ge -y^n_{N} \}} H\left( x+y_n,w_n^{+}(x)\right) dx, \qquad \text {as}\, n \rightarrow \infty , \end{aligned}$$

(5.5)

with the function H defined in Lemma 2.2 (ii). Next, we note that

$$\begin{aligned} H\left( x+y_n,w_n^{+}(x)\right) \ge 0, \qquad \text {for}\, x \in \{x_N \ge -y^n_{N} \}, \end{aligned}$$

and

$$\begin{aligned} \liminf _{n \rightarrow \infty } H(x+y_n,w_n^{+}(x))&\ge \liminf _{n \rightarrow \infty }\,\left( \frac{p-1}{2(p+1)}\,\left[ w_n^+(x)\right] ^{p+1} - u_c\left( x+y_n\right) ^{p-1} D_{1,p} \left[ w_n^+(x)\right] ^2\right. \\&\quad \left. - u_c\left( x+y_n\right) 1_{\{p > 2\}} D_{2,p} \left[ w_n^+(x)\right] ^p \right) \\&\quad = \frac{p-1}{2(p+1)}\,\left[ w^+(x)\right] ^{p+1}\\&\quad = \frac{p-1}{2(p+1)}\,w^{p+1}(x), \qquad \text {for}\, x \in \{x_N \ge -y^n_{N} \}, \end{aligned}$$

by Lemma 2.2 (ii) and (4.10). Thus, (5.5) and Fatou’s Lemma imply that

$$\begin{aligned} \frac{p-1}{2(p+1)}\Vert w\Vert _{L^{p+1}(\mathbb {R}^N)}^{p+1} \le b. \end{aligned}$$

(5.6)

Next we claim that $w \in {\mathcal K}_\infty$, i.e., w is a nontrivial solution of (4.3). To see this, we fix an arbitrary $\varphi \in C_c^{\infty }(\mathbb {R}^N)$, and we show that

$$\begin{aligned} \int _{\mathbb {R}^N} \left( \nabla w \nabla \varphi + w \varphi \right) dx = \int _{\mathbb {R}^N} \left( w^{+}\right) ^{\,p} \varphi \, dx. \end{aligned}$$

(5.7)

Since (5.3) holds, we have that $\mathrm{supp}(\varphi ) \subset \{x_N \ge -y^n_{N}\}$ for $n \in \mathbb {N}$ sufficiently large. Hence, for $n\in \mathbb {N}$ large enough, we have that

$$\begin{aligned} \begin{aligned} o(1)&= \langle E'(u_n), \varphi (\cdot - y^n) \rangle \\&= \int _{\{x_N \ge - y^n_{N}\}} \left( \nabla w_n \nabla \varphi + w_n \varphi \right) dx\\&\quad - \int _{\{x_N \ge - y^n_{N}\}} \left( u_c(\cdot +y^n)+w_n^{+}\right) ^p \varphi dx - \int _{\{x_N \ge - y^n_{N}\}} u_c^p\left( \cdot +y^n\right) \varphi dx \\&= \int _{\mathbb {R}^N} \left( \nabla w_n \nabla \varphi + w_n \varphi \right) dx\\&\quad - \int _{\mathbb {R}^N} \left( u_c(\cdot +y^n)+w_n^{+}\right) ^p \varphi dx + o(1)\\&= \int _{\mathbb {R}^N} \left( \nabla w_n \nabla \varphi + w_n \varphi \right) dx - \int _{\mathbb {R}^N} (w_n^{+})^p \varphi dx\\&\quad - \int _{\mathbb {R}^N} \left( \left( u_c\left( \cdot +y^n\right) +w_n^{+}\right) ^p - (w_n^{+})^p \right) \varphi dx + o(1) \\&= \int _{\mathbb {R}^N} \left( \nabla w_n \nabla \varphi + w_n \varphi \right) dx - \int _{\mathbb {R}^N} \left( w_n^{+}\right) ^p \varphi dx + o(1) \\&= \int _{\mathbb {R}^N} \left( \nabla w \nabla \varphi + w \varphi \right) dx - \int _{\mathbb {R}^N} (w^{+})^{\,p} \varphi \, dx + o(1), \qquad \text {as}\,\, n \rightarrow \infty . \end{aligned}\nonumber \\ \end{aligned}$$

(5.8)

Hence (5.7) follows, and therefore $w \in {\mathcal K}_\infty$. Together with (4.8) and (5.6) it then follows that $b \ge b_{\infty }$, but this contradicts (4.9). Hence, (5.3) cannot happen and Step 1 follows.

Step 2: Conclusion.

Let us define, for all $n \in \mathbb {N}$, $v_n:= u_n( \cdot + \xi _n)$ with $\xi _n:= (y^n_{1}, \ldots , y^n_{{N-1}}, 0)$ and observe that, after passing to a subsequence

$$\begin{aligned} v_n \rightharpoonup v in H_0^1(\mathbb {R}^{N}_{+}), \quad v_n \rightarrow v in L_{loc}^q(\mathbb {R}^{N}_{+}) for 1 \le q < 2^{*} \quad and \quad v_n \rightarrow v a.e. in \mathbb {R}^{N}_{+}, \end{aligned}$$

(5.9)

for some $v \in H_0^1(\mathbb {R}^{N}_{+})$. Also, note that $(v_n)_n \subset H_0^1(\mathbb {R}^{N}_{+})$ is a Cerami sequence for E at level b. Hence, if $v \not \equiv 0$, we will have that v is a non-trivial solution to (1.14). Since $v_n \rightarrow v$ in $L^q_{loc}(\mathbb {R}^{N}_{+})$ and $y^n_{N} \le M$ for all $n \in \mathbb {N}$, the lower integral bound (5.2) implies that $v \not \equiv 0$, and the result follows. $\square$

Proof of Theorem 1.3

(Completed) Let $u \in H_0^1(\mathbb {R}^{N}_{+})$ be the non-negative and non-trivial solution to (1.11) obtained in Theorem 5.1. By standard elliptic regularity we have that $u \in C^2(\mathbb {R}^{N}_{+}) \cap C(\overline{\mathbb {R}^{N}_{+}}) \cap L^{\infty }(\mathbb {R}^{N}_{+})$ and $v := u_c + u$ is a bounded positive solution to (1.3)–(1.4) of the form (1.8). $\square$

Remark 5.1

As explained in the introduction, Theorem 1.2 (i) and Corollary 1.4 are direct consequences of Theorem 1.3.

In the remaining of this section we prove Proposition 1.5. Let us first state a technical lemma due to Poláčik, Quittner and Souplet that will be key to prove this result.

Lemma 5.2

(Particular case of [29, Lemma 5.1]) Let (X, d) be a complete metric space and let $M: X \rightarrow (0,+\infty )$ be continuous. For any $\delta < \sup _{X} M$ and any $k > 0$ there exists $y \in X$ such that

• $M(y) \ge \delta$.

• $M(z) \le 2 M(y)$ for all $z \in X$ with $d(z,y) \le \frac{k}{M(y)}$.

The following proof is inspired by [12, Lemma 2.5].

Proof of Proposition 1.5

We assume by contradiction that there exists $v \in C^2(\mathbb {R}^{N}_{+}) \cap C(\overline{\mathbb {R}^{N}_{+}})$ unbounded solving (1.3)–(1.4). By Lemma 5.2 applied with $X= \overline{\mathbb {R}^{N}_{+}}$ and $M = v^{\frac{p-1}{2}}$, there exits a sequence $(y^k)_k \subset \mathbb {R}^{N}_{+}$ such that

$$\begin{aligned}&M(y^k) \rightarrow \infty , \quad as \ k \rightarrow \infty , \end{aligned}$$

(5.10)

$$\begin{aligned}&M(z) \le 2 M(y^k), \quad for all z \in \mathbb {R}^{N}_{+}\ with \ d(z,y^k) \le \frac{k}{M(y^k)}\ and all \,\, k \in \mathbb {N}. \end{aligned}$$

(5.11)

Note that, without loss of generality, we can suppose that $M(y^k) \ge 1$ for all $k \in \mathbb {N}$. We then define, for all $k \in \mathbb {N}$, $d_k:= y_N^k M(y^k)$, the half-space $H_k := \big \{x \in \mathbb {R}^{N}_{+}: x_N > - d_k \big \}$ and

$$\begin{aligned} v^k: H_k \rightarrow \mathbb {R}^{N}_{+}\quad given by \quad v^k(z):= \frac{1}{v(y^k)} v\big ( y^k + \frac{z}{M(y^k)} \big )\,. \end{aligned}$$

Note that, for all $k \in \mathbb {N}$, $v^k$ is a positive solution to

$$\begin{aligned} \left\{ \begin{aligned} -\Delta v^k + \frac{1}{M^2(y^k)} v^k&= (v^k)^p,&\quad in H_k,\\ v^k&= \frac{c}{M^{\frac{2}{p-1}}(y^k)},&on \partial H_k, \end{aligned} \right. \end{aligned}$$

(5.12)

and, by its definition and (5.11), it satisfies

$$\begin{aligned} v^k(0) = 1 \quad and \quad v^k(z) \le 2^{\frac{2}{q-1}} \quad for all z \in H_k \cap B_k(0). \end{aligned}$$

(5.13)

We now consider two cases separately.

Case 1: $d_k \rightarrow \infty \$ as $\ k \rightarrow \infty$.

Using standard $L^q$ estimates (see e.g. [18, Chapter 9]), (5.12) and (5.13), we get (taking a subsequence if necessary) that $(v^k)_k$ is locally $W^{2,q}$-bounded in $\mathbb {R}^N$ for arbitrarily large $q < +\infty$. Hence, up to a subsequence, $v^k \rightarrow \overline{v}$ in $C_{loc}^{1}(\mathbb {R}^N)$, where $\overline{v} \in C^1(\mathbb {R}^N)$ is a non-trivial positive solution to

$$\begin{aligned} \Delta \overline{v} + \overline{v}^p = 0, \quad in \mathbb {R}^N. \end{aligned}$$

(5.14)

By (5.13) we infer that $\overline{v}$ is bounded in $\mathbb {R}^N$ with $\overline{v}(0)=1$. Hence $\overline{v} \in C^2(\mathbb {R}^N)$ by standard elliptic regularity. Then, since by [17, Theorem 1.2] we know that the only $C^2(\mathbb {R}^N)$ non-negative solution to (5.14) is $\overline{v} \equiv 0$, we obtain a contradiction and deduce that Case 1 cannot happen.

Case 2: $d_k \rightarrow d \ge 0\$ as $\ k \rightarrow \infty$.

Let us define, for all $k \in \mathbb {N}$,

$$\begin{aligned} w^k: \mathbb {R}^{N}_{+}\rightarrow \mathbb {R}\quad as \quad w^k(z) = v^k \left( z-d_k e_N\right) , \end{aligned}$$

(5.15)

where $e_N := (0, \ldots ,0,1)$ is the N-th coordinate vector. Note that, for all $k \in \mathbb {N}$, $w^k$ is a positive solution to

$$\begin{aligned} \left\{ \begin{aligned} -\Delta w^k + \frac{1}{M^2(y^k)} w^k&= (w^k)^p,&\quad in \mathbb {R}^{N}_{+},\\ w^k&= \frac{c}{M^{\frac{2}{p-1}}(y^k)},&on \partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

(5.16)

and satisfies

$$\begin{aligned} w^k\left( d_k e_N\right) = 1 \quad and \quad w^k(z) \le 2^{\frac{2}{p-1}} \quad for all z \in \overline{\mathbb {R}^{N}_{+}} \cap B_k\left( d_k e_N\right) . \end{aligned}$$

(5.17)

Now, arguing as in the proof of [18, Theorem 9.13] (with auxiliary functions $\varphi ^k = w^k - c\, M^{-\frac{2}{p-1}}(y^k)$) and taking into account (5.16) and (5.17), we get (taking a subsequence if necessary) that $(w^k)_k$ is locally $W^{2,q}$-bounded in $\overline{\mathbb {R}^{N}_{+}}$ for arbitrarily large $q < +\infty$ and therefore also locally $C^{1,\beta }$-bounded in $\overline{\mathbb {R}^{N}_{+}}$ for all $\beta \in (0,1)$. In particular, $|\nabla w^k|$ remains bounded pointwise independently of k in a neighbourhood of the origin. Taking into account (5.10), the boundary conditions in (5.16) and (5.17), we infer that $d = \lim _{k \rightarrow \infty } d_k > 0$. Hence, up to a subsequence, $w^k \rightarrow \overline{w}$ in $C^{1}_{loc}(\mathbb {R}^{N}_{+})$ with $\overline{w} \in C^1(\mathbb {R}^{N}_{+})$ a non-trivial positive solution to

$$\begin{aligned} \left\{ \begin{aligned} \Delta \overline{w} + \overline{w}^p&= 0,&\quad in \mathbb {R}^{N}_{+},\\ \overline{w}&= 0,&\quad on \partial \mathbb {R}^{N}_{+}. \end{aligned} \right. \end{aligned}$$

(5.18)

By (5.17) we have that $\overline{w}$ is bounded with $\overline{w}(d e_N)=1$. Hence $\overline{w} \in C^2(\mathbb {R}^N) \cap C(\overline{\mathbb {R}^{N}_{+}})$ by standard elliptic regularity. Then, since by [17, Theorem 1.3] we know that the only $C^2(\mathbb {R}^{N}_{+}) \cap C(\overline{\mathbb {R}^{N}_{+}})$ non-negative solution to (5.18) is $\overline{w} \equiv 0$ , we obtain a contradiction and deduce that Case 2 cannot happen either. Hence, the result follows. $\square$

6 The non-existence result

In this section we prove Part (ii) of Theorem 1.2, which is concerned with the non-existence of bounded positive solutions to (1.3)–(1.4) in the case $c > {c_p}$. Recall that

$$\begin{aligned} w_0(t) = {c_p}\left[ \cosh \left( \frac{p-1}{2} t \right) \right] ^{-\frac{2}{p-1}}, \end{aligned}$$

is the unique even non-trivial positive solution to (1.5). Throughout this section, we will use the following notation. We define $v_0: \mathbb {R}^N\rightarrow \mathbb {R}$ as

$$\begin{aligned} v_0(x) = w_0\left( x_N\right) , \qquad \text {for}\, x \in \mathbb {R}^N. \end{aligned}$$

(6.1)

Also, recall that for a bounded positive solution to (1.3)–(1.4), we mean a function $v \in C^2(\mathbb {R}^{N}_{+}) \cap C(\overline{\mathbb {R}^{N}_{+}}) \cap L^{\infty }(\mathbb {R}^{N}_{+})$, positive, satisfying (1.3) in the pointwise sense and such that (1.4) holds.

Theorem 6.1

For $N \ge 1$, $p > 1$ and $c > {c_p}$, there are no bounded positive solutions to (1.3)–(1.4).

Proof

Let us fix an arbitrary $c > {c_p}$. We assume by contradiction that there exists a bounded positive solution v to (1.3)–(1.4) and we define, for all $t \in \mathbb {R}$, $v_t:= v_0 (\cdot + te_N)$ where $v_0$ is given in (6.1) and $e_N = (0,\ldots ,0,1)$ is the N-th coordinate vector. We split the proof into three steps.

Step 1: There exists $t_0 > 0$ such that $v > v_t$ in $\overline{\mathbb {R}^{N}_{+}}$ for all $t \ge t_0$.

First of all, fixed an arbitrary $x \in \overline{\mathbb {R}^{N}_{+}}$, observe that

$$\begin{aligned} v_t(x) \rightarrow 0, \quad as t \rightarrow \infty , \quad and \quad v_{t_1}(x) > v_{t_2}(x), \quad for all 0< t_1 < t_2. \end{aligned}$$

Hence, there exists $t_0 > 0$ such that, for all $t \ge t_0$,

$$\begin{aligned} v_t \le \left( \frac{1}{2p}\right) ^{\frac{1}{p-1}} \quad in \,\, \overline{\mathbb {R}^{N}_{+}}. \end{aligned}$$

(6.2)

We fix $t_0 > 0$ such that (6.2) holds and we are going to prove the Step 1 for this $t_0$. To that end, we fix an arbitrary $t \ge t_0 > 0$. First, we are going to prove that $v \ge v_t$ in $\overline{\mathbb {R}^{N}_{+}}$. Since $c > {c_p}\ge \max _{x \in \mathbb {R}} v_t(x)$, we have that

$$\begin{aligned} \left\{ \begin{aligned} -\Delta (v-v_t) + (v-v_t)&= |v|^{p-1} v-|v_t|^{p-1} v_t, \quad&in \,\, \mathbb {R}^{N}_{+},\\ v-v_t&> 0,&\quad on \,\, \partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

(6.3)

or equivalently

$$\begin{aligned} \left\{ \begin{aligned} -\Delta (v-v_t) + c_t(x)(v-v_t)&= 0, \quad&in \,\, \mathbb {R}^{N}_{+},\\ v-v_t&> 0,&\quad on \,\, \partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

(6.4)

where

$$\begin{aligned} c_t(x):= \left\{ \begin{aligned}&1 - \frac{(v(x))^p - (v_t(x))^p}{v(x)-v_t(x)},&\quad if \,\, v(x) - v_t(x) \ne 0,\\&1,&\qquad if \,\, v(x)-v_t(x) = 0. \end{aligned} \right. \end{aligned}$$

(6.5)

We assume by contradiction that

$$\begin{aligned} \left\{ x \in \mathbb {R}^{N}_{+}: v(x) < v_t(x)\right\} \ne \emptyset . \end{aligned}$$

(6.6)

Then, using the mean value theorem and (6.2), we deduce that, for all $x \in \{x \in \mathbb {R}^{N}_{+}: v(x) < v_t(x) \}$,

$$\begin{aligned} c_t(x) \ge 1-p (v_t(x))^{p-1} \ge \frac{1}{2}. \end{aligned}$$

(6.7)

Hence, in each connected component D of $\{x \in \mathbb {R}^{N}_{+}: v(x) < v_t(x)\}$ we have that

$$\begin{aligned} \left\{ \begin{aligned} -\Delta (v-v_t) + c_t(x)(v-v_t)&= 0, \quad&in \,\, D,\\ v-v_t&= 0,&\quad on \,\, \partial D, \end{aligned} \right. \end{aligned}$$

(6.8)

with $c_t$ satisfying (6.7). Then, applying the weak maximum principle [5, Lemma 2.1], we obtain that $v \ge v_t$ in $\overline{D}$ which contradicts the fact that $D \subset \{x \in \mathbb {R}^{N}_{+}: v(x) < v_t(x) \}$. Hence, we conclude that $\{x \in \mathbb {R}^{N}_{+}: v(x) < v_t(x) \} = \emptyset$ and so, that $v \ge v_t$ in $\mathbb {R}^{N}_{+}$. Having this at hand and substituting in (6.3), we deduce that

$$\begin{aligned} \left\{ \begin{aligned} -\Delta (v-v_t) + (v-v_t)&\ge 0, \quad&in \,\, \mathbb {R}^{N}_{+},\\ v-v_t&> 0,&\quad on \,\, \partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

(6.9)

and so, the Step 1 follows from the strong maximum principle and the fact that $t \ge t_0$ is arbitrary.

Step 2: $v > v_t$ in $\overline{\mathbb {R}^{N}_{+}}$ for all $t \in \mathbb {R}$.

Note that, if we prove that $v \ge v_t$ in $\mathbb {R}^{N}_{+}$ for all $t \in \mathbb {R}$, then the claim follows from the Strong Maximum principle. Also, by the Step 1, we know that

$$\begin{aligned} \left\{ \, t \in \mathbb {R}: v \ge v_s in \mathbb {R}^{N}_{+} for all s \ge t\, \right\} \ne \emptyset . \end{aligned}$$

Hence, we can define

$$\begin{aligned} t_{\star } := \inf \left\{ \, t \in \mathbb {R}: v \ge v_s in \mathbb {R}^{N}_{+} for all s \ge t\, \right\} \in \left[ -\infty , t_0\right] . \end{aligned}$$

(6.10)

We argue by contradiction and suppose that $t_{\star } > - \infty$. First note that, by continuity, $v \ge v_{t_{\star }}$ in $\mathbb {R}^{N}_{+}$. Also, $t_{\star } > - \infty$ implies the existence of $M > 0$ such that

$$\begin{aligned} v_{t}(x',x_N) \le \left( \frac{1}{2p}\right) ^{\frac{1}{p-1}}, \quad for all t \in [t_{\star }-1, t_{\star }],\ x' \in \mathbb {R}^{N-1} and \ x_N \ge M. \end{aligned}$$

(6.11)

We now consider separately two cases.

Case 1: $\inf _{x \in \mathbb {R}^{N-1} \times [0,M]}\big (v-v_{t_{\star }}\big ) =: \delta _M > 0$.

First, taking into account that $\Vert w_0'\Vert _{L^{\infty }(\mathbb {R})} \le {c_p}$, we infer that, for all $t \le t_{\star }$ and $x \in \mathbb {R}^{N-1} \times [0,M]$,

$$\begin{aligned} \begin{aligned} v(x',x_N) - v_t(x',x_N)&= v(x',x_N) - v_{t_{\star }}(x',x_N) + \big (v_{t_{\star }}(x',x_N) - v_t(x',x_N) \big ) \\&\ge \delta _M - \big | w_0(x_N+ t_{\star }) - w_0(x_N+t) \big | \\&\ge \delta _M - c_p |t_{\star }-t|. \end{aligned} \end{aligned}$$

Hence, there exists $\eta _0 \in (0,1)$ such that, for all $t_{\star } \ge t \ge t_{\star }-\eta _0$,

$$\begin{aligned} v\left( x',x_N\right) - v_t\left( x',x_N\right) > 0, \quad for all x' \in \mathbb {R}^{N-1}\ and \ x_N \in [0,M]. \end{aligned}$$

(6.12)

In particular, if we define $\Sigma _M:= \{ x \in \mathbb {R}^N: x_N > M\}$, we have

$$\begin{aligned} v - v_t > 0, \quad on \partial \Sigma _M, \quad for all \,\, t \in \left[ t_{\star } - \eta _0, t_{\star }\right] . \end{aligned}$$

Next, we are going to prove that, for all $t \in [t_{\star }- \eta _0, t_{\star }]$, it follows $v \ge v_t$ in $\Sigma _M$. To that end, we fix an arbitrary $t \in [t_{\star }- \eta _0, t_{\star }]$. Arguing as in Step 1, we have that

$$\begin{aligned} \left\{ \begin{aligned} -\Delta (v-v_t) + c_t(x)(v-v_t)&= 0, \quad&in \Sigma _M,\\ v-v_t&> 0,&\quad on \partial \Sigma _M, \end{aligned} \right. \end{aligned}$$

(6.13)

where

$$\begin{aligned} c_t(x):= \left\{ \begin{aligned}&1 - \frac{(v(x))^p - (v_t(x))^p}{v(x)-v_t(x)},&\quad if v(x) - v_t(x) \ne 0,\\&1,&\qquad if v(x)-v_t(x) = 0. \end{aligned} \right. \end{aligned}$$

(6.14)

We assume by contradiction that

$$\begin{aligned} \left\{ x \in \Sigma _M: v(x) < v_t(x) \right\} \ne \emptyset . \end{aligned}$$

(6.15)

Then, using the mean value theorem and (6.11), we deduce that, for all $x \in \{x \in \Sigma _M: v(x) < v_t(x) \}$,

$$\begin{aligned} c_t(x) \ge 1-p (v_t(x))^{p-1} \ge \frac{1}{2}. \end{aligned}$$

(6.16)

Hence, in each connected component D of $\{x \in \Sigma _M: v(x) < v_t(x)\}$ we have that

$$\begin{aligned} \left\{ \begin{aligned} -\Delta (v-v_t) + c_t(x)(v-v_t)&= 0, \quad&in D,\\ v-v_t&= 0,&\quad on \partial D, \end{aligned} \right. \end{aligned}$$

(6.17)

with $c_t$ satisfying (6.16). Then, applying the weak maximum principle [5, Lemma 2.1], we obtain that $v \ge v_t$ in $\overline{D}$ which contradicts the fact that $D \subset \{x \in \Sigma _M: v(x) < v_t(x) \}$. Hence, we conclude that $\{x \in \Sigma _M: v(x) < v_t(x) \} = \emptyset$ and so, that $v \ge v_t$ in $\Sigma _M$. Taking into account (6.12), we infer that, for all $\eta \in [0,\eta _0]$, $v \ge v_{t_{\star }-\eta }$ in $\mathbb {R}^{N}_{+}$. This is in contradiction with the definition of $t_{\star }$. Hence, Case 1 cannot happen.

Case 2: $\inf _{x \in \mathbb {R}^{N-1} \times [0,M]} \big ( v - v_{t_{\star }} \big ) = 0$.

In this case there exists a sequence of points $(x^n)_n \subset \mathbb {R}^{N-1} \times [0,M]$ such that

$$\begin{aligned} v\left( x^n\right) - v_{t_{\star }}(x^n) \rightarrow 0, \quad as n \rightarrow \infty . \end{aligned}$$

(6.18)

Up to a subsequence, it follows that $x_N^n \rightarrow \overline{x}_N$ for some $\overline{x}_N \in [0,M]$. We define then

$$\begin{aligned} v^n(x) = v\left( x' + \left( x^n\right) ', x_N\right) \,, \quad for all \,\,n \in \mathbb {N}, \end{aligned}$$

and, for all $n \in \mathbb {N}$, we have $v^n \ge v_{t_{\star }}$ in $\mathbb {R}^{N}_{+}$ and

$$\begin{aligned} \left\{ \begin{aligned} -\Delta v^n + v^n&= (v^n)^p, \quad&in \,\, \mathbb {R}^{N}_{+},\\ v^n&= c,&on \,\, \partial \mathbb {R}^{N}_{+}. \end{aligned} \right. \end{aligned}$$

Moreover, for all $n \in \mathbb {N}$, it follows that

$$\begin{aligned} \left\{ \begin{aligned} -\Delta \left( v^n-v_{t_{\star }}\right) + (v^n-v_{t_{\star }})&\ge 0, \quad&in \,\, \mathbb {R}^{N}_{+},\\ v^n - v_{t_{\star }}&> 0,&on \,\,\partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

and so, by the Strong Maximum principle, we have that

$$\begin{aligned} v^n - v_{t_{\star }} > 0, \quad in \,\,\overline{\mathbb {R}^{N}_{+}}, \quad for all \,\, n \in \mathbb {N}. \end{aligned}$$

Now, arguing as in [15, Proof of Theorem 2.1, Step 1], we deduce that the sequence $(v^n)_n$ admits a subsequence, still denoted by $(v^n)_n$, converging to a function $\overline{v}$ in $C_{loc}^{2}(\mathbb {R}^{N}_{+})$. This function $\overline{v}$ still solves

$$\begin{aligned} \left\{ \begin{aligned} -\Delta \overline{v} + \overline{v}&= \overline{v}^p, \quad&in \mathbb {R}^{N}_{+},\\ \,\,\overline{v}&= c,&on \,\, \partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

and satisfies $\overline{v} \ge v_{t_{\star }}, in \mathbb {R}^{N}_{+}$, and

$$\begin{aligned} \overline{v}\left( 0',\overline{x}_N\right) = v_{t_{\star }}\left( 0',\overline{x}_N\right) . \end{aligned}$$

(6.19)

Note that (6.19) and $\overline{v} = c > c_p \ge v_{t_{\star }}$ on $\partial \mathbb {R}^{N}_{+}$ imply $\overline{x}_N > 0$. Since $\overline{v} \ge v_{t_{\star }}$ in $\mathbb {R}^{N}_{+}$, we have

$$\begin{aligned} \left\{ \begin{aligned} -\Delta \left( \overline{v}-v_{t_{\star }}\right) + \left( \overline{v} -v_{t_{\star }}\right)&\ge 0, \quad&in \mathbb {R}^{N}_{+},\\ \overline{v}-v_{t_{\star }}&> 0,&on \partial \mathbb {R}^{N}_{+}, \end{aligned} \right. \end{aligned}$$

Hence, by the Strong Maximum principle, it follows that $\overline{v} > v_{t_{\star }}$ in $\mathbb {R}^{N}_{+}$ which gives a contradiction with (6.19). Case 2 cannot happen either and hence the Step 2 follows.

Step 3: Conclusion.

Observe that $v > v_t$ in $\mathbb {R}^{N}_{+}$ for all $t \in \mathbb {R}$ implies that $v \ge v_0(0) = {c_p}$ in $\mathbb {R}^{N}_{+}$. This gives a contradiction with (1.4) and so the proof is complete. $\square$