Abstract
This paper studies an economy inhabited by overlapping generations of households and investors, with the only difference between the two being that households derive utility from housing services, whereas investors do not. Tight collateral constraint limits the borrowing capacity of households and drives the equilibrium interest rate level down to the housing price growth rate, which makes housing attractive as a store of value for investors. A housing bubble arises in an equilibrium in which investors hold houses for resale purposes only and without the expectation of receiving a dividend either in terms of utility or in terms of rent. Pension reform that reduces the contribution rate may increase the supply of credit and create the housing bubble. Empirical findings from China are consistent with theoretical predictions.











Similar content being viewed by others
Notes
With a positive growth rate, the model economy has two stationary equilibria with an interest rate that is either above or below the growth rate. (If the growth rate is zero, there is only one equilibrium with a positive interest rate.) In the bubbly equilibrium, the growth rate of the bubble is equal to the interest rate, and the size of the bubble cannot grow more rapidly than the economy does. Therefore, only the lower interest rate is possible in the bubbly equilibrium. Moreover, positive dividends (either in terms of rent or in terms of utility) rule out negative equilibrium interest rate. Hence, the growth rate of the bubble must be positive and lower than the growth rate, which implies that the size of the bubble as a proportion of the economy approaches zero in the stationary equilibrium.
The definition of housing bubble used in this paper is different from the traditional definition of bubbles. Asset bubbles are usually defined as the difference between the fundamental and market values of assets, and it is often assumed that bubbles are intrinsically valueless, e.g., Tirole (1985). The two definitions are not always equivalent, and bubbles can be attached to assets that are intrinsically valuable. See Arce and Lopez-Salido (2011) for the case that housing price is lower than the fundamental value, i.e., the discounted value of utility flows generated by the housing assets, in the bubbly equilibrium. Miao and Wang (2011) study bubbles in stocks’ prices whose payoffs are endogenously determined by investment and affected by bubbles. Our paper shares some similarities with Miao and Wang (2011). Both studies investigate bubbles on assets that are intrinsically valuable. In our paper, housing assets provide utility flows to a subgroup of population. In Miao and Wang (2011), bubbles are attached to productive assets, which can be used as a collateral. Both papers consider the impact of credit constraint on asset bubbles. However, our model abstracts from credit constraint to investment, and housing asset is not an input to production. Therefore, two models have different implications of asset bubbles on investment.
For example, in Samuelson (1958) and Tirole (1985), the market friction comes from the market incompleteness of OLG structure. In Farhi and Tirole (2012), the market friction comes from the borrowing constraint. See Brunnermeier and Oehmke (2013) for other frictions, such as informational frictions and heterogeneous beliefs.
The constrained dynamic efficiency is a weaker notion of efficiency than the dynamic efficiency. An allocation is constrained dynamically efficient if there is no other resource feasible allocation that increases the lifetime utility of some agents without reducing that of another, which satisfies the collateral constraint. For its definitions in other model environment, see Farhi and Tirole (2012) and Kunieda (2008). I should thank one anonymous referee for pointing out this. In Tirole (1985), the source of dynamic inefficiency is inherited from standard overlapping generation model with production à la Diamond (1965). In this paper, the constrained dynamic inefficiency is caused by the presence of collateral constraint.
See Brunnermeier and Oehmke (2013) for other forms of bubbles.
The borrowing constraint in the infinite-horizon models essentially shortens the life span of households and makes an infinitely lived household’s behavior similar to that of a sequence of finitely lived households without altruism.
The reasons we consider the pension reform in the policy experiment are twofolded. The first reason is its empirical relevance to China. The second reason is that the pension wealth (including PAYG pension wealth as well as fully funded pension wealth) and housing wealth are the two largest components in households’ balance sheet. Therefore, they are the most important stores of value for average households.
The discount factor for households should be \(\beta \left( 1-\zeta \right) \), not \(\beta \). The reason that I did not assume a different utility function for investors, e.g., \(u_{h}\left( c_{h,t}^{t},c_{h,t+1}^{t},h_{h,t+1}^{t}\right) =\ln c_{h,t}^{t}+\beta \ln c_{h,t+1}^{t}+\gamma \ln h_{h,t+1}^{t}\), is that the current utility form in Eq. 2 can greatly simplify the analytical expressions in equilibrium. It would not affect the qualitative results.
Section 2 includes the production sector and endogenous wage rate. Since I introduce pay-as-you-go social security in the model, the old will receive positive pension benefit. Hence, I can normalize the labor income of the elderly to zero without loss of generality.
If \(\theta =0\), borrowing-constrained households can buy infinite amount of housing without violating the borrowing constraint. If \(\theta =1\), this endowment economy becomes autarky, and the equilibrium interest rate is not well defined.
We can define \(\tilde{y}_{t}^{t} \equiv \frac{y_{t}^{t} }{\left( 1+g\right) ^{t}}\), \(\tilde{c}_{s,t}^{t} \equiv \frac{c_{s,t}^{t}}{ \left( 1+g\right) ^{t}}\), \(\tilde{c}_{s,t}^{t-1} \equiv \frac{c_{s,t}^{t-1}}{ \left( 1+n\right) \left( 1+g\right) ^{t}}\), \(\tilde{a}_{s,t+1}^{t} \equiv \frac{a_{s,t+1}^{t}}{\left( 1+g\right) ^{t}}\), \(\tilde{p}_{t} \equiv \frac{ p_{t}}{\left( 1+n\right) ^{t}\left( 1+g\right) ^{t}}\), \(\tilde{R}_{t+1} \equiv \frac{R_{t+1}}{\left( 1+n\right) \left( 1+g\right) }\), \(\tilde{h} _{s,t+1}^{t} \equiv h_{s,t+1}^{t}\left( 1+n\right) ^{t}\), \(\tilde{H}_{t+1} \equiv H_{t+1}\), \(\tilde{\varphi } \equiv \frac{\varphi }{\left( 1+n\right) \left( 1+g\right) }\), \(s=i,h\).
This paper does not model the collapse of the bubble. In the benchmark model, the current young investors are willing to hold empty housing assets because they expect that the future young generations will purchase housing assets from them. We can introduce the crash of bubble following Caballero and Krishnamurthy (2006). Suppose we introduce another useless asset, say fiat money, as an alternative store of value for investors in this economy. The fiat money may also be valued by investors and becomes a pure bubble using the definition of Arce and Lopez-Salido (2011). After the introduction of fiat money, there could be multiple stationary equilibria. The conjecture is that investors only purchase fiat money as a store of value in one equilibrium and only purchase housing as a store of value in the other equilibrium. Hence, housing price crash is possible when there is a coordination failure among investors. Under this assumption, the expected housing price growth rate will be higher than the interest rate before the bubble crashes. This is because the risk-averse investors need to be compensated for the housing price risks.
Obviously, the collapse of housing bubble implies welfare losses for those who hold the assets and welfare gains for the future young generation who will purchase the assets.
On one hand, tighter collateral constraint reduces total borrowing from households, which pushes the housing prices down. On the other hand, interest rate becomes smaller due to the general equilibrium effect which tends to raise housing prices by allowing households to pay less interest on their mortgages.
We can normalize all economic variables by their growth rate along the balanced growth path. Denote \(\tilde{y}_{t}^{t} \equiv \frac{y_{t}^{t}}{ \left( 1+g\right) ^{t}}\), \(\tilde{s,c}_{t}^{t} \equiv \frac{c_{s,t}^{t}}{\left( 1+g\right) ^{t}}\), \(\tilde{c}_{s,t}^{t-1} \equiv \frac{c_{s,t}^{t-1}}{\left( 1+n\right) \left( 1+g\right) ^{t}}\), \(\tilde{a}_{s,t+1}^{t} \equiv \frac{ a_{s,t+1}^{t}}{\left( 1+g\right) ^{t}}\), \(\tilde{k}_{t+1} \equiv \frac{k_{t+1}}{ \left( 1+g\right) ^{t}\left( 1+n\right) ^{t}}\), \(\tilde{p}_{t} \equiv \frac{ p_{t}}{\left( 1+n\right) ^{t}\left( 1+g\right) ^{t}} \), \(\tilde{R}_{t+1} \equiv \frac{R_{t+1}}{\left( 1+n\right) \left( 1+g\right) } \), \(\tilde{h} _{s,t+1}^{t} \equiv h_{s,t+1}^{t}\left( 1+n\right) ^{t}\), \(\tilde{H}_{t+1} \equiv H_{t+1}\), \(\tilde{\varphi } \equiv \frac{\varphi }{\left( 1+n\right) \left( 1+g\right) }\), \(s=i,h\).
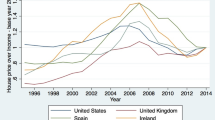
The average selling price does not take into account the quality changes in the housing market. Unfortunately, there is no official constant-quality housing price index for China.
The urban home ownership rate increases from less than 30 to 70 % during 1994–1999, a period when the housing reform takes place. Before the housing reform, it is the state-owned enterprises (SOE) that are responsible for providing employee housing to workers, with a little or no charge for rents. The government liberalizes the housing market in 1994 by selling the public housing to the current employee in state-owned enterprises at heavily subsidized price. Newly employed workers in SOE and workers in the private sectors have to purchase houses that are provided by private real estate developers. The transition into the new housing system ends around 1999, after which no SOE are allowed to provide employee housing to their workers. At the end of the year 2010, the home ownership rate of urban households in China is 89.3 %. 40.1 % of them own privatized houses which previously are owned by the government or state-owned enterprises. 38 % of households have bought houses that are provided at a market price.
A vacant house or apartment is a unit that has been sold but is not occupied by anybody. The vacancy rate is defined as the proportion of vacant units in total housing units.
22 % of urban households own more than one apartment. Among them, only 25 % households rent their apartments out.
See Song et al. (2012) for the detailed descriptions of China’s pension system.
The average real return on Shanghai stock market index is only 2 % from 2000 to 2009.
The 35 cities are Beijing (BJ), Tianjing (TJ), Shijiazhuang (SJZ), Taiyuan (TY), Huhehaote (HHHT), Shenyang (SY), Changchun (CC), Haerbing (HEB), Shanghai (SH), Nanjing (NJ), Hangzhou (HZ), Hefei (HF), Fuzhou (FZ), Nanchang (NC), Jinan (JN), Zhengzhou (ZZ), Wuhan (WH), Changsha (CS), Nanning(NN), Haikou (HK), Chongqing (CQ), Chengdu (CD), Guiyang (GY), Kunming(KM), Xian(XA), Lanzhou (LZ), Xining (XN), Yinchuan (YC), Wulumuqi (WLMQ), Dalian (DL), Qingdao (QD), Ningbo (NB), Xiamen (XM), Shengzhen (SZ), and Guangzhou (GZ).
The simple OLS univariate regression has a coefficient \(-\)7.06, which is significant at 1 % confidence level. The adjusted R-squared is 0.33.
The simple OLS univariate regression has a coefficient \(-\)2.64, which is also significant at 1 % confidence level. The adjusted R-square is 0.31.
One standard deviation of contribution rate in the sample is 6.4 percentage points. One standard deviation of investment-to-GDP ratio is 14 percentage points. Strictly speaking, we only identify the correlation rather the causality in the regression. Future works require finding valid instruments to control the endogeneity issues of explanatory variables, such as investment-to-GDP ratio and the contribution rate.
The other solution \(R<1\) cannot be an equilibrium interest rate.
References
Aiyagari, S.R., McGrattan, E.R.: The optimum quantity of debt. J. Monet. Econ. 42(3), 447–469 (1998)
Arce, A., Lopez-Salido, D.: Housing bubbles. Am. Econ. J. Macroecon. 3(1), 212–241 (2011)
Bai, C.E., Hsieh, C.T., Qian, Y.: The Return to Capital in China. Brookings Papers on Economic Activity 37(2), 61–102 (2006)
Bewley, T.: The Optimum Quantity of Money. Discussion Papers 383, Northwestern University, Center for Mathematical Studies in Economics and Management Science (1979)
Brock, W.: An Integration of Stochastic Growth Theory and the Theory of Finance. Report, Center for Mathematical Studies in Business and Economics, University of Chicago (1978)
Brock, W.A.: Asset Prices in a Production Economy (NBER Chapters). The Economics of Information and Uncertainty, pp. 1–46. National Bureau of Economic Research Inc, New York (1982)
Brunnermeier, M.K., Oehmke, M.: Bubbles, Financial Crises, and Systemic Risk. Elsevier, Amsterdam (2013)
Caballero, R.J., Krishnamurthy, A.: Bubbles and capital flow volatility: Causes and risk management. J. Monet. Econ. 53(1), 35–53 (2006)
Caballero, R.J., Farhi, E., Gourinchas, P.O.: An equilibrium model of global imbalances and low interest rates. Am. Econ. Rev. 98(1), 358–93 (2008)
Chen, K., Wen, Y.: The Great Housing Boom of China (2014). http://research.stlouisfed.org/wp/more/2014-022
Cozzi, G.: A note on heterogeneity, inefficiency, and indeterminacy with Ricardian preferences. J. Econ. Theory 97(1), 191–202 (2001)
Diamond, P.A.: National debt in a neoclassical growth model. Am. Econ. Rev. 55(5), 1126–1150 (1965)
Farhi, E., Tirole, J.: Bubbly liquidity. Rev. Econ. Stud. 79(2), 678–706 (2012)
Grossman, G.M., Yanagawa, N.: Asset bubbles and endogenous growth. J. Monet. Econ. 31(1), 3–19 (1993)
Hellwig, C., Lorenzoni, G.: Bubbles and self-enforcing debt. Econometrica 77(4), 1137–1164 (2009)
Hirano, T., Yanagawa, N.: Asset Bubbles, Endogenous Growth, and Financial Frictions. CARF F-Series CARF-F-223, Center for Advanced Research in Finance, Faculty of Economics, The University of Tokyo (2010)
Kiyotaki, N., Moore, J. Liquidity, business cycles, and monetary policy. Working Paper 17934, National Bureau of Economic Research. doi:10.3386/w17934 (2012)
Kocherlakota, N.: Bursting bubbles: Consequences and cures. Unpublished manuscript, Federal Reserve Bank of Minneapolis (2009)
Kocherlakota, N.R.: Bubbles and constraints on debt accumulation. J. Econ. Theory 57(1), 245–256 (1992)
Kunieda, T.: Asset bubbles and borrowing constraints. J. Math. Econ. 44(2):112–131, the Conferences at Lawrence, Lisbon, New Haven, Rio de Janeiro and Taipei (2008)
Martin, A., Ventura, J.: Economic growth with bubbles. Am. Econ. Rev. 102(6), 3033–58 (2012)
Miao, J., Wang, P.: Bubbles and credit constraints. SSRN 1779485 (2011)
Miao, J., Wang, P.: Sectoral bubbles, misallocation, and endogenous growth. J. Math. Econ. 53, 153–163 (2014). Special Section: Economic Theory of Bubbles (I)
Miao, J., Wang, P., Zhou, J.: Housing Bubbles and Policy Analysis, Working Paper, Boston University and HKUST (2014)
Olivier, J.: Growth-enhancing bubbles. Int. Econ. Rev. 41(1), 133–151 (2000)
Samuelson, P.A.: An exact consumption-loan model of interest with or without the social contrivance of money. J. Polit. Econ. 66, 467 (1958)
Santos, M.S., Woodford, M.: Rational asset pricing bubbles. Econometrica 65(1), 19–57 (1997)
Scheinkman, J.: Notes on asset pricing. Tech. rep (1977)
Song, Z., Storesletten, K., Zilibotti, F.: Growing like China. Am. Econ. Rev. 101(1), 196–233 (2011)
Song, Z.M., Storesletten, K., Wang, Y., Zilibotti, F.: Sharing High Growth Across Generations: Pensions and Demographic Transition in China. CEPR Discussion Papers 9156, C.E.P.R. Discussion Papers (2012)
Tirole, J.: On the possibility of speculation under rational expectations. Econometrica 50(5), 1163–1181 (1982)
Tirole, J.: Asset bubbles and overlapping generations. Econometrica 53(6), 1499–1528 (1985)
Ventura, J.: Bubbles and capital flows. Working Paper 9304, National Bureau of Economic Research, doi:10.3386/w9304 (2002)
Wallace, N.: The overlapping-generations model of fiat money. Tech. rep (1978)
Wang, P., Wen, Y.: Speculative bubbles and financial crises. Am. Econ. J. Macroecon. 4(3), 184–221 (2012)
Weil, P.: Confidence and the real value of money in an overlapping generations economy. Q. J. Econ. 102(1), 1–22 (1987). doi:10.2307/1884677
Wu, J., Gyourko, J., Deng, Y.: Evaluating conditions in major chinese housing markets. Reg. Sci. Urban Econ. 42(3), 531–543 (2012)
Acknowledgments
I received helpful comments from Kjetil Storesletten, Johnathan Heathcote, Christopher Phelan, Pengfei Wang, Kaiji Chen, and seminar participants at Federal Reserve Bank of Minneapolis, University of Queensland, the 24th NBER EASE conference, the 2014 CCE at Tsinghua University, Guanghua School of Management, Peking University, and University of International Business and Economics, China. I thank the editor and three anonymous referees for suggestions. I also thank Li Chao for excellent research assistance. All errors are my own.
Author information
Authors and Affiliations
Corresponding author
Mathematical appendix
Mathematical appendix
1.1 Proof of Proposition 1
The Lagrangian function is
The FOCs become
where
The lifetime budget constraint for the investors is
-
1.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}>0,\) i.e., the borrowing constraint of the investors is not binding; \(h_{i,t+1}^{t}>0\), i.e., the unconstrained investors hold positive amount of housing. Therefore, \(\mu _{1}=\nu _{1}=0\). Plug them into the FOCs
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}= & {} 0 \end{aligned}$$The following equality holds \(R_{t+1}=\frac{p_{t+1}}{p_{t}}\), and the optimal consumption rules are
$$\begin{aligned} c_{i,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ c_{i,t+1}^{t}= & {} \frac{\beta R_{t+1}}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \end{aligned}$$The allocation between the loans and housing assets is indeterminate. The total saving is determined by
$$\begin{aligned} a_{i,t+1}^{t}+p_{t}h_{i,t+1}^{t}=\left( 1-\tau _{t}\right) y_{t}^{t}-c_{i,t}^{t} \end{aligned}$$ -
2.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}>0\), i.e., the borrowing constraint of investor is not binding; \(h_{i,t+1}^{t}=0\), i.e., the investor holds zero amount of housing. Therefore, \(\mu _{1}=0,\nu _{1}\ge 0. \) Plug them into the FOCs,
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\nu _{1}= & {} 0 \end{aligned}$$Hence, \(R_{t+1}\ge \frac{p_{t+1}}{p_{t}}\)
-
(a)
If \(\nu _{1}=0,\) then we go back to case 1
-
(b)
If \(\nu _{1}>0,\) then \(R_{t+1}>\frac{p_{t+1}}{p_{t}}.\) The purchase of housing is less attractive than lending to the others.
$$\begin{aligned} a_{i,t+1}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-c_{i,t}^{t} \\ h_{i,t+1}^{t}= & {} 0 \end{aligned}$$
-
(a)
-
3.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}=0\), i.e., the borrowing constraint of the investors is binding; \(h_{i,t+1}^{t}>0\), i.e., the constrained investors hold positive amount of housing. Therefore, \(\mu _{1}\ge 0,\nu _{1}=0.\)
-
(a)
If \(\mu _{1}=v_{1}=0,\) we go back to case 1. If \(\mu _{1}>0,\nu _{1}=0\), then
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}> & {} R_{t+1} \\ \frac{\lambda _{1}}{\lambda _{2}}> & {} \frac{p_{t+1}}{p_{t}} \\ \frac{\lambda _{1}}{\lambda _{2}}= & {} \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}} \end{aligned}$$Suppose \(\frac{p_{t+1}}{p_{t}}<R_{t+1}<\frac{\lambda _{1}}{\lambda _{2}},\) then \(R_{t+1}<\frac{\lambda _{1}}{\lambda _{2}}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}<\frac{p_{t+1}-\left( 1-\theta \right) p_{t+1}}{\theta p_{t}}=\frac{p_{t+1}}{p_{t}}\), a contradiction! Therefore,
$$\begin{aligned} R_{t+1}<\frac{p_{t+1}}{p_{t}}<\frac{\lambda _{1}}{\lambda _{2}}=\frac{ p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}} \end{aligned}$$Let \(\gamma _{i,t}\equiv \frac{\lambda _{1}}{\lambda _{2}}=\frac{ p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}.\) Rewrite the budget constraints as
$$\begin{aligned} c_{i,t}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-\theta p_{t}h_{i,t+1}^{t} \\ c_{i,t+1}^{t}= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\theta \gamma _{i,t}p_{t}h_{i,t+1}^{t} \end{aligned}$$Solve for \(p_{t}h_{i,t+1}^{t}\)
$$\begin{aligned} p_{t}h_{i,t+1}^{t}=\frac{\beta \gamma _{i,t}\left( 1-\tau \right) -\tau \left( 1+n\right) \left( 1+g\right) }{\theta \gamma _{i,t}\left( 1+\beta \right) } y_{t}^{t} \end{aligned}$$Therefore,
$$\begin{aligned} c_{i,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{i,t}}\right] y_{t}^{t} \\ c_{i,t+1}^{t}= & {} \frac{\beta \gamma _{i,t}}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{i,t}}\right] y_{t}^{t} \\ a_{i,t+1}^{t}= & {} -\left( 1-\theta \right) p_{t}h_{i,t+1}^{t} \\ p_{t}h_{i,t+1}^{t}= & {} \frac{\beta \gamma _{i,t}\left( 1-\tau \right) -\tau \left( 1+n\right) \left( 1+g\right) }{\theta \gamma _{i,t}\left( 1+\beta \right) }y_{t}^{t} \end{aligned}$$
-
(a)
-
4.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}=0\), i.e., the borrowing constraint of the investors is binding; \(h_{i,t+1}^{t}=0\), i.e., the investors hold zero amount of housing
$$\begin{aligned} c_{i,t}^{t}= & {} \left( 1-\tau \right) y_{t}^{t} \\ c_{i,t+1}^{t}= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t} \end{aligned}$$Then, \(\mu _{1},v_{1}\ge 0.\)
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}+\mu _{1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{1}\left( 1-\theta \right) p_{t}+\nu _{1}= & {} 0 \end{aligned}$$-
(a)
If \(\mu _{1},\nu _{1}>0,\) either investors have too little endowment when they are young and do not want to save
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}>\frac{p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{\theta p_{t}}>\frac{p_{t+1}}{p_{t}}>R_{t+1} \end{aligned}$$or investors’ borrowing cost is too large
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}>R_{t+1}>\frac{p_{t+1}}{p_{t}}>\frac{ p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{\theta p_{t}} \end{aligned}$$In this article, I assume the young has enough endowment and wants to save. Therefore, I rule out the case \(\frac{\lambda _{1}}{\lambda _{2}}>\frac{ p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{\theta p_{t}}>\frac{p_{t+1}}{ p_{t}}>R_{t+1}.\)
-
(b)
If \(\mu _{1}>0,v_{1}=0,\) we go back to case 3
-
(c)
If \(\mu _{1}=0,\nu _{1}>0,\) we go back to case 2
-
(d)
If \(\mu _{1}=0,v_{1}=0,\) we go back to case 1
-
(a)
1.2 Proof of Proposition 2
The Lagrangian function is
The FOCs become
where
and the lifetime budget constraint is given by
-
1.
\(a_{h,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{h,t+1}^{t}>0,\) i.e., the borrowing constraint of the households is not binding. Therefore, \(\mu _{1}=0.\) Hence,
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}=R_{t+1}=\frac{p_{t+1}+\frac{\zeta }{1-\zeta } \frac{c_{h,t+1}^{t}}{h_{h,t+1}^{t}}}{p_{t}} \end{aligned}$$The optimal decision rules are
$$\begin{aligned} c_{h,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ c_{h,t+1}^{t}= & {} \frac{\beta \left( 1-\zeta \right) R_{t+1}}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ p_{t}h_{h,t+1}^{t}= & {} \frac{1}{1-\frac{p_{t+1}}{p_{t}R_{t+1}}}\frac{\beta \zeta }{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{ R_{t+1}}\right] y_{t}^{t} \\ a_{h,t+1}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-p_{t}h_{h,t+1}^{t}-c_{h,t}^{t} \end{aligned}$$ -
2.
\(a_{h,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{h,t+1}^{t}=0,\) i.e., the borrowing constraint of the households is binding. Therefore, \(\mu _{1}\ge 0 \)
-
(a)
If \(\mu _{1}=0,\) then we go back to case 1.
-
(b)
If \(\mu _{1}>0\)
$$\begin{aligned} \displaystyle -\lambda _{1}+\lambda _{2}R_{t+1}+\mu _{1}&=0 \\ \displaystyle \frac{\beta \zeta }{h_{h,t+1}^{t}}-\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{1}\left( 1-\theta \right) p_{t}&=0 \end{aligned}$$Hence, the condition for \(R_{t+1}\) is given by
$$\begin{aligned} R_{t+1}<\frac{\lambda _{1}}{\lambda _{2}} \end{aligned}$$Let \(\frac{\lambda _{1}}{\lambda _{2}}\equiv \gamma _{h,t}\), then from the budget constraint
$$\begin{aligned} c_{h,t}^{t}=\left( 1-\tau \right) y_{t}^{t}-\theta p_{t}h_{h,t+1}^{t} \end{aligned}$$and
$$\begin{aligned} c_{h,t+1}^{t}=\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) h_{h,t+1}^{t} \end{aligned}$$From the FOC w.r.t. \(h_{h,t+1}^{t},\) we have
$$\begin{aligned} \frac{\beta \zeta }{h_{h,t+1}^{t}}-\lambda _{1}\theta p_{t}+\lambda _{2}\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) =0 \end{aligned}$$Use the expression for \(\lambda _{1},\lambda _{2},\) we have
$$\begin{aligned} 1= & {} \lambda _{1}\left( 1-\tau \right) y_{t}^{t}-\lambda _{1}\theta p_{t}h_{h,t+1}^{t} \\ \beta \left( 1-\zeta \right)= & {} \lambda _{2}\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\lambda _{2}\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) h_{h,t+1}^{t} \\ \beta \zeta= & {} \lambda _{1}\theta p_{t}h_{h,t+1}^{t}-\lambda _{2}\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) h_{h,t+1}^{t} \end{aligned}$$Therefore,
$$\begin{aligned} 1+\beta =\lambda _{1}\left( 1-\tau \right) y_{t}^{t}+\lambda _{2}\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t} \end{aligned}$$Note that
$$\begin{aligned} 1+\beta&=\frac{\left( 1-\tau \right) y_{t}^{t}}{\left( 1-\tau \right) y_{t}^{t}-\theta p_{t}h_{t+1}^{t}} \\&\quad +\beta \left( 1-\zeta \right) \frac{\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}}{\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) h_{h,t+1}^{t}} \end{aligned}$$This is a quadratic equation for \(p_{t}h_{h,t+1}^{t}.\) Let
$$\begin{aligned} x= & {} p_{t}h_{h,t+1}^{t} \\ \varphi= & {} \frac{p_{t+1}}{p_{t}}-\left( 1-\theta \right) R_{t+1} \\ a= & {} \left( 1-\tau \right) y_{t}^{t} \\ b= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t} \end{aligned}$$Then,
$$\begin{aligned} 1+\beta =\frac{a}{a-\theta x}+\frac{\beta \left( 1-\zeta \right) b}{ b+\varphi x} \end{aligned}$$Positive consumption in both periods requires that
$$\begin{aligned} a-\theta x> & {} 0 \\ b+\varphi x> & {} 0 \end{aligned}$$which is equivalent to
$$\begin{aligned} x< & {} \frac{a}{\theta }\quad \text { if }\varphi >0 \\ x< & {} \min \left( \frac{a}{\theta },-\frac{b}{\varphi }\right) \quad \text { if } \varphi <0 \end{aligned}$$The above equation can be written as:
$$\begin{aligned} \left( 1+\beta \right) \left( a-\theta x\right) \left( b+\varphi x\right) -a\left( b+\varphi x\right) -\beta \left( 1-\zeta \right) b\left( a-\theta x\right) =0 \end{aligned}$$Let
$$\begin{aligned} \varPi \left( x\right)= & {} \left( 1+\beta \right) \left( a-\theta x\right) \left( b+\varphi x\right) -a\left( b+\varphi x\right) -\beta \left( 1-\zeta \right) b\left( a-\theta x\right) \\= & {} -\theta \varphi \left( 1+\beta \right) x^{2}+\left( a\varphi \beta -b\theta \left( 1+\beta \zeta \right) \right) x+\beta \zeta ab \end{aligned}$$
-
i.
If \(\varphi >0,\) because \(\varPi \left( 0\right) =\beta \zeta ab>0,\) it has one positive solution. The positive solution must satisfy \(x<\frac{a}{\theta }\) because
$$\begin{aligned} \varPi \left( \frac{a}{\theta }\right)= & {} -\theta \varphi \left( 1+\beta \right) \frac{a^{2}}{\theta ^{2}}+\left( a\varphi \beta -b\theta \left( 1+\beta \zeta \right) \right) \frac{a}{\theta }+\beta \zeta ab \\= & {} -\frac{\varphi a^{2}}{\theta }-ab<0 \end{aligned}$$The positive solution is the relative larger solution, which is given by
$$\begin{aligned} p_{t}h_{h,t+1}^{t}=x=\frac{-\varPsi _{t}-\varPhi _{t}}{-2\theta \varphi \left( 1+\beta \right) }= \frac{\varPsi _{t}+\varPhi _{t}}{2\theta \varphi \left( 1+\beta \right) } \end{aligned}$$where \(\varPsi _{t}=a\varphi \beta -b\theta \left( 1+\beta \zeta \right) ,\varPhi _{t}=\sqrt{\varPsi _{t}^{2}+4ab\theta \beta \zeta \varphi \left( \beta +1\right) }.\)
-
ii.
If \(\varphi <0,\) there are two positive solutions or two negative solutions because the product of two solutions is equal to
$$\begin{aligned} \frac{\beta \zeta ab}{-\theta \varphi \left( 1+\beta \right) x^{2}}>0 \end{aligned}$$If there are two positive solutions, the sum of two solutions has to satisfy
$$\begin{aligned} \frac{\left( a\varphi \beta -b\theta \left( 1+\beta \zeta \right) \right) }{ \theta \varphi \left( 1+\beta \right) }>0 \end{aligned}$$because \(\varphi <0,\) it implies that \(a\varphi \beta -b\theta \left( 1+\beta \zeta \right) <0.\)
-
A.
If \(\frac{-\varphi }{b}>\frac{\theta }{a},\) then \(x<\min \left( \frac{a }{\theta },-\frac{b}{\varphi }\right) =-\frac{b}{\varphi }\)
$$\begin{aligned} \varPi \left( -\frac{b}{\varphi }\right)= & {} -\theta \varphi \left( 1+\beta \right) b^{2}\frac{1}{\varphi ^{2}}-\left( a\varphi \beta -b\theta -\beta \zeta b\theta \right) \frac{b}{\varphi }+\beta \zeta ab \\= & {} b\theta \left( 1-\zeta \right) \beta \left( \frac{b}{-\varphi }-\frac{a}{ \theta }\right) <0 \end{aligned}$$Therefore, only the smaller solution satisfies \(x<-\frac{b}{\varphi }\). The unique solution is given by
$$\begin{aligned} x=\frac{-\varPsi _{t}-\varPhi _{t}}{-2\theta \varphi \left( 1+\beta \right) }= \frac{\varPsi _{t}+\varPhi _{t}}{2\theta \varphi \left( 1+\beta \right) } \end{aligned}$$ -
B.
If \(\frac{-\varphi }{b}<\frac{\theta }{a},\) then \(x<\min \left( \frac{a }{\theta },-\frac{b}{\varphi }\right) =\frac{a}{\theta }\)
$$\begin{aligned} \varPi \left( \frac{a}{\theta }\right) =\frac{a^{2}b}{\theta }\left( \frac{ -\varphi }{b}-\frac{\theta }{a}\right) <0 \end{aligned}$$Therefore, only the smaller solution satisfies \(x<\frac{a}{\theta }\). The unique solution is given by
$$\begin{aligned} x=\frac{-\varPsi _{t}-\varPhi _{t}}{-2\theta \varphi \left( 1+\beta \right) }= \frac{\varPsi _{t}+\varPhi _{t}}{2\theta \varphi \left( 1+\beta \right) } \end{aligned}$$
In the end, we can define \(\gamma _{h,t}\)
$$\begin{aligned} \gamma _{h,t}\equiv \frac{\lambda _{1}}{\lambda _{2}}=\frac{c_{h,t+1}^{t}}{\beta \left( 1-\zeta \right) c_{h,t}^{t}}=\frac{b+\varphi x}{\beta \left( 1-\zeta \right) \left( a-\theta x\right) } \end{aligned}$$and
$$\begin{aligned} c_{h,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{h,t}}\right] y_{t}^{t} \\ c_{h,t+1}^{t}= & {} \frac{\beta \left( 1-\zeta \right) \gamma _{h,t}}{1+\beta } \left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{h,t}} \right] y_{t}^{t} \\ p_{t}h_{h,t+1}^{t}= & {} \frac{\varPsi _{t}+\varPhi _{t}}{2\theta \varphi \left( 1+\beta \right) }. \end{aligned}$$ -
(a)
1.3 Proof of Lemma 1
We start first by looking the saving function of the unconstrained investor. Investors are not constrained if and only if \(R_{t+1}>\frac{p_{t+1}}{p_{t}}\). From Proposition 1, we can write down the saving function of an unconstrained investor as
It is obvious to see that the saving function of the unconstrained investor is a decreasing function of interest rate. Investor is borrowing-constrained if and only if \(R_{t+1}<\frac{p_{t+1}}{p_{t}}\). From Proposition 1, we can write down the saving function of an constrained investor as
where \(\gamma _{i,t+1}\equiv \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t} }{\theta p_{t}}>0\) Lower interest rate increases \(\gamma _{i,t}\) and implies more borrowing, or equivalently, less saving. Hence, the credit supply of investors is always a decreasing function of interest rate.
For the unconstrained households, its credit demand is given by \(-a_{h,t+1}^{t}= c^{t}_{h,t}+p_{t}h^{t}_{h,t+1}-\left( 1-\tau \right) y_{t}^{t}\). From Proposition 2, we know that both \(c^{t}_{h,t}\) and \(p_{t}h^t_{h,t+1}\) are decreasing function of interest rate. When the household is borrowing-constrained, the credit demand function becomes complicated.
Differentiate \(p_{t}h_{h,t+1}^{t}\) directly w.r.t. \(\varphi \) Then,
Note that \(\varPsi _{t}=a\varphi \beta -b\theta \left( 1+\beta \zeta \right) \) and \( \frac{d}{d\varphi }\varPsi _{t}=a\beta \)
because of
We have \(\frac{\partial p_{t}h_{h,t+1}^{t}}{\partial \varphi }>0,\frac{\partial p_{t}h_{h,t+1}^{t}}{\partial R}<0 \). The credit demand of constrained household is an decreasing function of interest rate.
1.4 Proof of Lemma 2
The stationary equilibrium is defined as the competitive general equilibrium in which all individual allocations and prices are time-invariant. We need to further assume that \(H_{t}=\bar{H}\) in the stationary equilibrium to get constant housing price. Denote the constant housing price by \(p^{*}.\) Obviously, we have \(p^{*}>0\). Otherwise, workers would purchase infinite amount of houses. Suppose the equilibrium gross interest \(R^{*}<1\). The gross return of housing for the investors is 1, which is higher than the gross return \(R^{*}\) on consumption loans. From the previous decision rules, the borrowing constraint for both types of households would be binding. The total borrowing of workers is positive, and the total borrowing of investors is nonnegative. Therefore, the market for credit cannot clear at \(R^{*}<1\). Equilibrium interest rate has to be higher, and \(R^{*}<1 \) cannot be a equilibrium interest rate. Note that if \(\theta =1\), both investors and households cannot borrow in the equilibrium. Therefore, the economy becomes autarky, and the interest rate is not well defined. We rule out this case by requiring that \(\theta <1\).
1.5 Proof of Proposition 3
Proposition 3 characterizes the uniqueness of stationary equilibrium. It states that the allocation of housing assets in this economy depends on the tightness of collateral constraint. We provide some intuition here (please see the appendix for the proof). We have shown that the optimal demand and supply of credit are continuous. Lemma 1 proves that the demand of credit from households is monotonically decreasing in the interest rate, and the supply of credit from investors is a monotonically increasing function of interest rate. From Lemma 2, there exists a unique stationary equilibrium with \(R^{*}\ge 1.\) Households always borrow from investors in the model because they consume housing services. Investors will not be borrowing-constrained when \(R^{*}\ge 1.\) They supply credit in the market. \(\theta \) will only affect the optimal decision of households, who are the demand side of credit market. As the borrowing constraint becomes tighter (higher \(\theta \)), households are going to be borrowing-constrained first. High \(\theta \) reduces the borrowing limit of constrained households. If \(\theta \) is high enough, the total borrowing from households become less than the total credit supply from investors. Interest rate has to be lower in order to clear the consumption loan market. Therefore, tighter borrowing constraint reduces the credit demand from households and drives the equilibrium interest rate down. When the gross interest rate drops to one, housing assets become attractive as an alternative saving mean to the investors. The credit market clearing condition requires that the extra supply of credit coming from investors to be invested in the housing assets, which are the only alternative assets in this economy. Therefore, there are two threshold levels for collateral constraint, denoted by \(\theta _{L}\) and \( \theta _{H}\) and three different cases which we analyze one by one.
-
1.
Unconstrained households and unconstrained investors without housing. In the stationary equilibrium, \(y_{t}^{t}=y,\) \(H_{t}=H.\) The equilibrium prices \(\left( p_{1}^{*},R_{1}^{*}\right) \) are determined by
$$\begin{aligned} H= & {} \omega \frac{1}{p_{1}}\frac{R_{1}}{R_{1}-1}\frac{\beta \zeta }{1+\beta } \left( 1-\tau +\frac{\tau }{R_{1}}\right) y \\ 0= & {} 1-\tau -\frac{1}{1+\beta }\left( 1-\tau +\frac{\tau }{R_{1}}\right) \left( 1+\omega \frac{\beta \zeta R_{1}}{R_{1}-1}\right) \end{aligned}$$The second equation determines a unique \(R_{1}^{*}>1\).Footnote 26 Hence, housing price can be determined by
$$\begin{aligned} p_{1}^{*}=\omega \frac{y}{H}\frac{R_{1}^{*}}{R_{1}^{*}-1}\frac{ \beta \zeta }{1+\beta }\left( 1-\tau +\frac{\tau }{R_{1}^{*}}\right) \end{aligned}$$Note that \(\theta \) cannot affect either \(p_{1}^{*}\) or \(R_{1}^{*}.\) Now, we can solve for the first threshold \(\theta _{L}\) when households is borrowing-constrained
$$\begin{aligned} \left( 1-\tau \right) -\frac{1}{1+\beta }\left( 1-\tau +\frac{\tau }{ R_{1}^{*}}\right) =\theta _{L}\frac{R_{1}^{*}}{R_{1}^{*}-1}\frac{ \beta \zeta }{1+\beta }\left( 1-\tau +\frac{\tau }{R_{1}^{*}}\right) \end{aligned}$$Using the credit market clearing condition, we have \(\theta _{L}=\omega .\) Therefore, \(\frac{\partial \theta _{L}}{\partial \omega }=1.\) The intuition is that more households will increase the equilibrium interest rate. When the interest rate becomes higher, households will reduce the consumption and housing expenditure. They will be borrowing-constrained under a stricter borrowing constraint.
-
2.
Constrained households and unconstrained investors without housing. The equilibrium prices \(\left( p_{2}^{*},R_{2}^{*}\right) \) are determined by
$$\begin{aligned}&\displaystyle \omega \frac{1}{p_{2}}\frac{\varPsi +\varPhi }{2\theta \varphi \left( \beta +1\right) } =H \\&\displaystyle \left( 1-\omega \right) \left[ 1-\tau -\frac{1}{1+\beta }\left( 1-\tau + \frac{\tau }{R_{2}}\right) \right] y-\omega \left( 1-\theta \right) \frac{ \varPsi +\varPhi }{2\theta \varphi \left( \beta +1\right) } =0 \end{aligned}$$The two equations imply two implicit functions \(p_{2}^{*}\left( R_{2}^{*},\theta \right) \) and \(R_{2}^{*}\left( \theta \right) \!.\) The effect of \(\theta \) on equilibrium housing price is given by
$$\begin{aligned} \frac{dp_{2}^{*}\left( R_{2}^{*},\theta \right) }{d\theta }=\frac{ \partial p_{2}^{*}\left( R_{2}^{*},\theta \right) }{\partial R_{2}^{*}}\frac{dR_{2}^{*}}{d\theta }+\frac{\partial p_{2}^{*}\left( R_{2}^{*},\theta \right) }{\partial \theta } \end{aligned}$$On one hand, tighter credit constraint reduces the housing demand, which tends to reduce the price. However, tighter credit constraint also reduces interest rate, which in turn encourages housing consumption. Hence, the total effect is indeterminate.
-
3.
Constrained households and unconstrained investors with empty housing. When \(R_{3}^{*}=\frac{p_{t+1}}{p_{t}}=1,\) the market clearing conditions become
$$\begin{aligned}&\displaystyle \omega \frac{1}{p_{3}}\frac{\varPsi +\varPhi }{2\theta \varphi \left( \beta +1\right) }+\left( 1-\omega \right) \frac{I}{p_{3}} =H \\&\displaystyle \left( 1-\omega \right) \left[ \left( 1-\tau \right) y-\frac{1}{1+\beta }y-I \right] -\omega \left( 1-\theta \right) \frac{\varPsi +\varPhi }{2\theta \varphi \left( \beta +1\right) } =0 \end{aligned}$$where I denotes the investor’s purchase of housing assets. Combine the two conditions and note that \(\varphi =\theta \) when \(R=1.\)
$$\begin{aligned} \left( 1-\omega \right) \left( 1-\tau -\frac{1}{1+\beta }\right) y+\omega \frac{\varPsi +\varPhi }{2\theta \left( \beta +1\right) }=p_{3}H \end{aligned}$$which suggests that \(p_{3}^{*}\) is independent of \(\theta \) since \( \left( \varPsi +\varPhi \right) /\theta \) does not depend on \(\theta .\) The total amount of savings is invested in housing assets. The threshold \(\theta _{H}\) for investors to hold housing assets is determined by
$$\begin{aligned} \left( 1-\omega \right) \left( 1-\tau -\frac{1}{1+\beta }\right) y-\omega \left( \frac{1-\theta _{H}}{\theta _{H}}\right) \frac{\varPsi +\varPhi }{2\theta _{H}\left( \beta +1\right) }=0 \end{aligned}$$It is also true that \(\frac{\partial \theta _{H}}{\partial \omega }>0.\) This is because high \(\omega \) implies fewer credit supply from investors. The collateral constraint has to be higher to clear the credit market.
1.6 Proof of Proposition 1
Suppose there is a useless asset called paper. In case 3, it has positive value in the equilibrium. This is because investor has excess supply of credit in the market, which can be invested in the paper. Since the equilibrium interest rate is 1, the price of paper remains constant in the equilibrium. The size of the paper bubble is given by
This is called pure bubble. However, the bubble can also take the form of housing assets. If the investors purchase the housing assets I instead, then
which means bubble can shift from paper market to the housing market. If we define the bubble as the case in which investors hold houses for resale purposes only and not with the expectation of receiving a dividend either in terms of utility or in terms of rent, then the case 3 satisfies this definition because we rule out the rental market. The next question is whether there is bubble for households? The answer is no. First of all, we define the fundamental value of housing assets to households, and then, we show that under properly adjusted interest rate, the housing price is equal to its fundamental value for households in all three cases.
-
1.
Unconstrained households and unconstrained investors without housing. The fundamental value of housing is defined as
$$\begin{aligned} p_{t}^{F}= & {} \frac{p_{t+1}+\frac{\zeta }{1-\zeta }\frac{c_{h,t+1}^{t}}{ h_{h,t+1}^{t}}}{R_{t+1}} \\= & {} \sum _{\tau =0}^{\infty }\frac{1}{R_{t+1}\ldots R_{t+\tau }}\frac{\zeta }{ 1-\zeta }\frac{c_{h,t+\tau +1}^{t+\tau }}{h_{h,t+\tau +1}^{t+\tau }} +\lim _{T\rightarrow \infty }p_{t+T}\frac{1}{R_{t+1}\ldots R_{t+T-1}} \end{aligned}$$Using the first-order condition of households
$$\begin{aligned} p_{t}^{F}&=\sum _{\tau =0}^{\infty }\frac{1}{R_{t+1}\ldots R_{t+\tau }}\left( p_{t+\tau }R_{t+\tau }-p_{t+\tau +1}\right)&\quad +\lim _{T\rightarrow \infty }p_{t+T}\frac{1}{R_{t+1}\ldots R_{t+T-1}} \end{aligned}$$In the stationary equilibrium, \(R_{1}^{*}>1,\lim _{T\rightarrow \infty }p_{1}^{*}\frac{1}{\left( R_{1}^{*}\right) ^{T}}=0\)
$$\begin{aligned} p^{F}=\sum _{\tau =0}^{\infty }\frac{1}{\left( R_{1}^{*}\right) ^{\tau +1}}\left( p_{1}^{*}R_{1}^{*}-p_{1}^{*}\right) =p_{1}^{*}\sum _{\tau =0}^{\infty }\frac{R_{1}^{*}-1}{\left( R_{1}^{*}\right) ^{\tau +1}}=p_{1}^{*} \end{aligned}$$ -
2.
Constrained households and unconstrained investors without housing. The fundamental value of housing can be defined as
$$\begin{aligned} p_{t}^{F}= & {} \frac{p_{t+1}+\frac{\zeta }{1-\zeta }\frac{c_{h,t+1}^{t}}{ h_{h,t+1}^{t}}}{\hat{R}_{t}} \\= & {} \sum _{\tau =0}^{\infty }\frac{1}{\hat{R}_{t}\ldots \hat{R}_{t+\tau }} \frac{\zeta }{1-\zeta }\frac{c_{h,t+\tau +1}^{t+\tau }}{h_{h,t+\tau +1}^{t+\tau } }+\lim _{T\rightarrow \infty }p_{t+T}\frac{1}{\hat{R}_{t}\ldots \hat{R}_{t+T-1}} \end{aligned}$$where \(\hat{R}_{t}=\theta \frac{\lambda _{1}}{\lambda _{2}}+\left( 1-\theta \right) R_{t+1}.\) This measures the effective interest rate that households face. It takes into account the shadow value of borrowing constraint. If the borrowing constraint is not binding, \(\lambda _{1}/\lambda _{2}=R_{t+1}=\hat{R} _{t}.\) If the borrowing constraint is binding, the effect interest rate is a weighted average of \(\lambda _{1}/\lambda _{2}\) and \(R_{t+1}.\) Therefore, \( R_{t+1}<\hat{R}_{t}<\lambda _{1}/\lambda _{2}.\) Using the first-order condition of constrained households
$$\begin{aligned} p_{t}^{F}\!\!=\!\!\sum _{\tau =0}^{\infty }\frac{1}{\hat{R}_{t}\ldots \hat{R} _{t+\tau }}\frac{\lambda _{1}p_{t}\!-\!\lambda _{2}p_{t+1}-\mu _{1}\left( 1\!-\!\theta \right) p_{t}}{\lambda _{2}}+\!\lim _{T\rightarrow \infty }p_{t+T} \frac{1}{\hat{R}_{t}\ldots \hat{R}_{t+T-1}} \end{aligned}$$In the stationary equilibrium, \(\hat{R}_{2}^{*}=\theta \frac{\lambda _{1} }{\lambda _{2}}+\left( 1-\theta \right) R_{2}^{*}>1,\lim _{T\rightarrow \infty }p_{2}^{*}\frac{1}{\left( \hat{R}_{2}^{*}\right) ^{T}}=0\)
$$\begin{aligned} p^{F}= & {} \sum _{\tau =0}^{\infty }\frac{1}{\left( \hat{R}_{2}^{*}\right) ^{\tau +1}}\frac{\lambda _{1}p_{2}^{*}-\lambda _{2}p_{2}^{*}-\left( \lambda _{1}-\lambda _{2}R_{2}^{*}\right) \left( 1-\theta \right) p_{2}^{*}}{\lambda _{2}} \\= & {} p_{2}^{*}\sum _{\tau =0}^{\infty }\frac{1}{\left( \hat{R} _{2}^{*}\right) ^{\tau +1}}\left( \frac{\lambda _{1}}{\lambda _{2}} \theta +R_{2}^{*}\left( 1-\theta \right) -1\right) \\= & {} p_{2}^{*}\sum _{\tau =0}^{\infty }\frac{\hat{R}_{2}^{*}-1}{ \left( \hat{R}_{2}^{*}\right) ^{\tau +1}}=p_{2}^{*} \end{aligned}$$ -
3.
Constrained households and unconstrained investors with empty housing. The fundamental value of housing can be defined as
$$\begin{aligned} p_{t}^{F}= & {} \frac{p_{t+1}+\frac{\zeta }{1-\zeta }\frac{c_{h,t+1}^{t}}{ h_{h,t+1}^{t}}}{\hat{R}_{t}} \\= & {} \sum _{\tau =0}^{\infty }\frac{1}{\hat{R}_{t}\ldots \hat{R}_{t+\tau }} \frac{\zeta }{1-\zeta }\frac{c_{h,t+\tau +1}^{t+\tau }}{h_{h,t+\tau +1}^{t+\tau } }+\lim _{T\rightarrow \infty }p_{t+T}\frac{1}{\hat{R}_{t}\ldots \hat{R}_{t+T-1}} \end{aligned}$$where \(\hat{R}_{3}=\theta \frac{\lambda _{1}}{\lambda _{2}}+1-\theta .\) Using the first-order condition of households,
$$\begin{aligned} p_{t}^{F}= & {} \sum _{\tau =0}^{\infty }\frac{1}{\hat{R}_{t}\ldots \hat{R} _{t+\tau }}\frac{\lambda _{1}p_{t}-\lambda _{2}p_{t+1}-\left( \lambda _{1}-\lambda _{2}R_{t+1}\right) \left( 1-\theta \right) p_{t}}{\lambda _{2}}\\&+\lim _{T\rightarrow \infty }p_{t+T}\frac{1}{\hat{R}_{t}\ldots \hat{R}_{t+T-1}} \end{aligned}$$In the stationary equilibrium, \(p_{t}=p_{3}^{*},\) \(\hat{R}_{3}^{*}>1,\lim _{T\rightarrow \infty }p_{3}^{*}\frac{1}{\left( \hat{R} _{3}^{*}\right) ^{T}}=0\)
$$\begin{aligned} p^{F}=p_{3}^{*}\sum _{\tau =0}^{\infty }\frac{\hat{R}_{3}^{*}-1}{\left( \hat{R}_{3}^{*}\right) ^{\tau }}=p_{3}^{*} \end{aligned}$$
1.7 Proof of Proposition 4
When \(\tau =0,\) the total supply of credit by investors becomes \(\left( 1-\omega \right) \frac{\beta }{1+\beta }y.\) The total credit demand from constrained households becomes \(\omega \frac{1-\theta }{\theta }\frac{\beta }{\beta +1}y.\) Note that both the supply and demand do not depend on interest rate. Therefore, bubble will arise iff
which is equivalent to \(\theta >\theta _{L}=\omega .\) Therefore, if the economy stays at the case 1 of stationary equilibrium, where both investors and households are unconstrained, then the removal of pension system will not trigger a bubble equilibrium. If the economy stays at case 2 of stationary equilibrium, we have
In the bubble equilibrium, the housing wealth-to-GDP ratio is \(\frac{\beta }{ 1+\beta }\). If \(\tau >\frac{\theta -\omega }{1-\omega },\) then
1.8 Model extension
1.8.1 Investor’s problem
The Lagrangian function is
The FOCs become
where
The lifetime budget constraint for the investors is
-
1.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}>0,\) \( h_{i,t+1}^{t}-h_{i,t+1}^{R}>0,\) \(h_{i,t+1}^{t}>0,h_{i,t+1}^{R}>0,\) Then, \(\mu _{1}=\mu _{2}=\nu _{1}=\nu _{2}=0.\) Plug them into the FOCs
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}= & {} 0 \\ \lambda _{1}p_{t}^{r}-\lambda _{2}\delta _{r}p_{t+1}= & {} 0 \end{aligned}$$The following equality holds
$$\begin{aligned} R_{t+1}=\frac{p_{t+1}}{p_{t}}=\frac{\delta _{r}p_{t+1}}{p_{t}^{r}}=\frac{ \left( 1-\delta _{r}\right) p_{t+1}}{p_{t}-p_{t}^{r}} \end{aligned}$$, and the optimal consumption rules are
$$\begin{aligned} c_{i,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ c_{i,t+1}^{t}= & {} \frac{\beta R_{t+1}}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \end{aligned}$$and the private credit, housing assets, and rental housing are jointly determined by
$$\begin{aligned} a_{i,t+1}^{t}+p_{t}h_{i,t+1}^{t}-p_{t}^{r}h_{i,t+1}^{R}=\left( 1-\tau \right) y_{t}^{t}-c_{i,t}^{t} \end{aligned}$$Note that
$$\begin{aligned} \frac{\delta _{r}p_{t+1}}{p_{t}^{r}}=R_{t+1}=\frac{p_{t+1}}{p_{t}}=\frac{ \left( 1-\delta _{r}\right) p_{t+1}}{p_{t}-p_{t}^{r}} \end{aligned}$$Then,
$$\begin{aligned} R_{t+1}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}=\frac{ \left( 1-\delta _{r}\right) p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{ \theta p_{t}-p_{t}^{r}} \end{aligned}$$ -
2.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}>0,h_{i,t+1}^{t}-h_{i,t+1}^{R}>0,h_{i,t+1}^{t}>0, h_{i,t+1}^{R}=0,\) then \(\mu _{1}=\mu _{2}=\nu _{1}=0,\) \(\nu _{2}\ge 0.\) Plug them into the FOCs,
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}= & {} 0 \\ \lambda _{1}p_{t}^{r}-\lambda _{2}\delta _{r}p_{t+1}+\nu _{2}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} R_{t+1}=\frac{p_{t+1}}{p_{t}}\le \frac{\delta _{r}p_{t+1}}{p_{t}^{r}} \end{aligned}$$-
(a)
If \(\mu _{1}=\mu _{2}=\nu _{1}=\nu _{2}=0,\) then we go back to the case 1.
-
(b)
If \(\mu _{1}=\mu _{2}=\nu _{1}=0,\nu _{2}>0,\) then
$$\begin{aligned} \frac{\delta _{r}p_{t+1}}{p_{t}^{r}}>R_{t+1}=\frac{p_{t+1}}{p_{t}}>\frac{ p_{t+1}\left( 1-\delta _{r}\right) }{p_{t}-p_{t}^{r}} \end{aligned}$$and
$$\begin{aligned} a_{i,t+1}^{t}+p_{t}h_{i,t+1}^{t}=\left( 1-\tau \right) y_{t}^{t}-c_{i,t}^{t} \end{aligned}$$Under this case, it is also true that
$$\begin{aligned} R_{t+1}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}>\frac{ \left( 1-\delta _{r}\right) p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{ \theta p_{t}-p_{t}^{r}} \end{aligned}$$
-
(a)
-
3.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}>0,h_{t+1}^{t}-h_{i,t+1}^{R}=0,\) \(h_{i,t+1}^{t}>0,h_{i,t+1}^{R}>0,\) then \(\mu _{1}=\nu _{1}=\nu _{2}=0,\mu _{2}\ge 0.\) Plug them into the FOCs,
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{2}= & {} 0 \\ \lambda _{1}p_{t}^{r}-\lambda _{2}\delta _{r}p_{t+1}-\mu _{2}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} R_{t+1}\ge & {} \frac{p_{t+1}}{p_{t}} \\ R_{t+1}\ge & {} \frac{\delta _{r}p_{t+1}}{p_{t}^{r}} \\ R_{t+1}= & {} \frac{p_{t+1}\left( 1-\delta _{r}\right) }{p_{t}-p_{t}^{r}} \end{aligned}$$-
(a)
If \(\mu _{1}=\mu _{2}=\nu _{1}=\nu _{2}=0,\) then we go back to the case 1.
-
(b)
If \(\mu _{1}=\nu _{1}=\nu _{2}=0,\mu _{2}>0,\) then
$$\begin{aligned} R_{t+1}=\frac{p_{t+1}\left( 1-\delta _{r}\right) }{p_{t}-p_{t}^{r}}>\frac{ p_{t+1}}{p_{t}}>\frac{\delta _{r}p_{t+1}}{p_{t}^{r}} \end{aligned}$$and
$$\begin{aligned} a_{i,t+1}^{t}+\left( p_{t}-p_{t}^{r}\right) h_{i,t+1}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-c_{i,t}^{t} \\ h_{i,t+1}^{R}= & {} h_{i,t+1}^{t} \end{aligned}$$In this case, it is also true that
$$\begin{aligned} R_{t+1}=\frac{\left( 1-\delta _{r}\right) p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{\theta p_{t}-p_{t}^{r}}>\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}} \end{aligned}$$
-
(a)
-
4.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}>0,h_{i,t+1}^{t}=h_{i,t+1}^{R}=0,\) then \(\mu _{1}=0,\mu _{2}\ge 0,\nu _{1}\ge 0,\nu _{2}\ge 0.\) Plug them into the FOCs,
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{2}+\nu _{1}= & {} 0 \\ \lambda _{1}p_{t}^{r}-\lambda _{2}\delta _{r}p_{t+1}-\mu _{2}+\nu _{2}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} R_{t+1}\ge & {} \frac{p_{t+1}}{p_{t}} \\ R_{t+1}\ge & {} \frac{\left( 1-\delta _{r}\right) p_{t+1}}{p_{t}-p_{t}^{r}} \end{aligned}$$-
(a)
If \(\mu _{1}=\mu _{2}=\nu _{1}=\nu _{2}=0,\) then we go back to case 1
-
(b)
If \(\mu _{1}=\mu _{2}=\nu _{1}=0,\nu _{2}>0,\) then we go back to case 2
-
(c)
If \(\mu _{1}=\nu _{1}=\nu _{2}=0,\mu _{2}>0,\) then we go back to case 3
-
(d)
If \(\mu _{1}=0,\mu _{2}+\nu _{1}>0,\nu _{1}+\nu _{2}>0,\) then \(R_{t+1}> \frac{p_{t+1}}{p_{t}}\) and \(R_{t+1}>\frac{\left( 1-\delta _{r}\right) p_{t+1}}{ p_{t}-p_{t}^{r}}.\)
$$\begin{aligned} a_{i,t+1}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-c_{i,t}^{t} \\ h_{i,t+1}^{R}= & {} h_{i,t+1}^{t}=0 \end{aligned}$$It is also true that
$$\begin{aligned} R_{t+1}> & {} \frac{\left( 1-\delta _{r}\right) p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{\theta p_{t}-p_{t}^{r}} \\ R_{t+1}> & {} \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}} \end{aligned}$$
-
(a)
-
5.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}=0,h_{i,t+1}^{t}-h_{i,t+1}^{R}>0, h_{i,t+1}^{t}>0,h_{i,t+1}^{R}>0,\) then \(\mu _{1}\ge 0,\mu _{2}=\nu _{1}=\nu _{2}=0.\) Plug them into the FOCs,
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}+\mu _{1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{1}\left( 1-\theta \right) p_{t}= & {} 0 \\ \lambda _{1}p_{t}^{r}-\lambda _{2}\delta _{r}p_{t+1}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}\ge & {} R_{t+1} \\ \frac{\lambda _{1}}{\lambda _{2}}\ge & {} \frac{p_{t+1}}{p_{t}} \\ \frac{\lambda _{1}}{\lambda _{2}}= & {} \frac{\delta _{r}p_{t+1}}{p_{t}^{r}} \end{aligned}$$Discussion:
-
(a)
If \(\mu _{1}=\mu _{2}=\nu _{1}=\nu _{2}=0,\) then we go back to case 1.
-
(b)
If \(\mu _{1}>0,\mu _{2}=\nu _{1}=\nu _{2}=0,\) then
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}} \end{aligned}$$Use the equation \(\frac{\lambda _{1}}{\lambda _{2}}=\frac{\delta _{r}p_{t+1} }{p_{t}^{r}}\) then we have an expression for \(R_{t+1}\)
$$\begin{aligned} R_{t+1}=\frac{\frac{p_{t+1}}{p_{t}}-\theta \frac{\delta _{r}p_{t+1}}{p_{t}^{r}} }{1-\theta }<\frac{p_{t+1}}{p_{t}} \end{aligned}$$It follows that
$$\begin{aligned} R_{t+1},\frac{p_{t+1}\left( 1-\delta _{r}\right) }{p_{t}-p_{t}^{r}}<\frac{ p_{t+1}}{p_{t}}<\frac{\lambda _{1}}{\lambda _{2}}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}=\frac{\delta _{r}p_{t+1}}{ p_{t}^{r}} \end{aligned}$$First of all, this suggests that the borrowing cost is smaller than the intertemporal rate of substitution Therefore, the investors must be borrowing-constrained. Secondly, the investors are indifferent between constrained-borrow-to-empty and constrained-borrow-to-rent, i.e.,
$$\begin{aligned} \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}=\frac{\left( 1-\delta _{r}\right) p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$Let \(x\equiv \left( p_{t}h_{i,t+1}^{t}-\frac{p_{t}^{r}}{\theta } h_{i,t+1}^{R}\right) \) and \(\gamma _{i,t}\equiv \frac{\lambda _{1}}{\lambda _{2}} =\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}.\) Rewrite the budget constraints as
$$\begin{aligned} c_{i,t}^{t}+\theta p_{t}h_{i,t+1}^{t}= & {} \left( 1-\tau \right) y_{t}+p_{t}^{r}h_{i,t+1}^{R} \\ c_{i,t+1}^{t}= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\left( p_{t}h_{i,t+1}^{t}-\frac{p_{t}^{r}}{\theta }h_{i,t+1}^{R}\right) \theta \gamma _{i,t} \end{aligned}$$Then,
$$\begin{aligned} c_{i,t}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-\theta x \\ c_{i,t+1}^{t}= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\theta \gamma _{i,t}x \end{aligned}$$Solve for x
$$\begin{aligned} x=\frac{\beta \gamma _{i,t}\left( 1-\tau \right) y_{t}^{t}-\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}}{\theta \gamma _{i,t}\left( \beta +1\right) } \end{aligned}$$Therefore,
$$\begin{aligned} c_{i,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{i,t}}\right] y_{t}^{t} \\ c_{i,t+1}^{t}= & {} \frac{\beta \gamma _{i,t}}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{i,t}}\right] y_{t}^{t} \\ a_{i,t+1}^{t}= & {} -\left( 1-\theta \right) p_{t}h_{i,t+1}^{t} \\ p_{t}h_{i,t+1}^{t}-\frac{p_{t}^{r}h_{i,t+1}^{R}}{\theta }= & {} \frac{\beta \gamma _{i,t}\left( 1-\tau \right) -\tau \left( 1+n\right) \left( 1+g\right) }{\theta \gamma _{i,t}\left( \beta +1\right) }y_{t}^{t} \end{aligned}$$
-
(a)
-
6.
\(a_{t+1}^{t}+\left( 1-\theta \right) p_{t}h_{t+1}^{t}=0,\) \( h_{t+1}^{t}-h_{t+1}^{R}>0,h_{t+1}^{t}>0,h_{t+1}^{R}=0,\) then \(\mu _{1},\nu _{2}\ge 0,\mu _{2}=\nu _{1}=0.\) Plug them into the FOCs,
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}+\mu _{1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{1}\left( 1-\theta \right) p_{t}= & {} 0 \\ \lambda _{1}p_{t}^{r}-\lambda _{2}\delta _{r}p_{t+1}+\nu _{2}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}\ge & {} R_{t+1} \\ \frac{\lambda _{1}}{\lambda _{2}}\ge & {} \frac{p_{t+1}}{p_{t}} \\ \frac{\lambda _{1}}{\lambda _{2}}\le & {} \frac{\delta _{r}p_{t+1}}{p_{t}^{r}} \end{aligned}$$-
(a)
If \(\mu _{1}=\mu _{2}=\nu _{1}=\nu _{2}=0,\) then we go back to case 1
-
(b)
If \(\mu _{1}>0,\mu _{2}=\nu _{1}=\nu _{2}=0,\) then we go back to case 5
-
(c)
If \(\mu _{1}=\mu _{2}=\nu _{1}=0,\nu _{2}>0,\) then we go back to case 2
-
(d)
If \(\mu _{1}>0,\nu _{2}>0,\mu _{2}=\nu _{1}=0,\) then
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}} \end{aligned}$$Use the condition that \(\frac{\lambda _{1}}{\lambda _{2}}<\frac{\delta _{r}p_{t+1}}{p_{t}^{r}}\), and the following inequality for \(R_{t+1}\) holds
$$\begin{aligned} R_{t+1}>\frac{\frac{p_{t+1}}{p_{t}}-\theta \frac{\delta _{r}p_{t+1}}{p_{t}^{r}} }{1-\theta } \end{aligned}$$It turns out that \(\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}>\frac{p_{t+1}}{p_{t}}\) implies \(\frac{p_{t+1}}{p_{t}}>R_{t+1}.\) Therefore, it follows that
$$\begin{aligned} R_{t+1},\frac{p_{t+1}\left( 1-\delta _{r}\right) }{p_{t}-p_{t}^{r}}<\frac{ p_{t+1}}{p_{t}}<\frac{\lambda _{1}}{\lambda _{2}}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}<\frac{\delta _{r}p_{t+1}}{ p_{t}^{r}} \end{aligned}$$First of all, this suggests that the borrowing cost is smaller than the intertemporal rate of substitution Therefore, the investors must be borrowing-constrained. Secondly, the investors prefer the constrained-borrow-to-empty to the constrained-borrow-to-rent, i.e.,
$$\begin{aligned} \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}}>\frac{\left( 1-\delta _{r}\right) p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$Let \(x\equiv p_{t}h_{t+1}^{t}\) and \(\gamma _{i,t}\equiv \frac{ \lambda _{1}}{\lambda _{2}}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t} }{\theta p_{t}}.\) Use the fact that
$$\begin{aligned}&c_{i,t}^{t} =\left( 1-\tau \right) y_{t}^{t}-\theta p_{t}h_{i,t+1}^{t} \\&\quad c_{i,t+1}^{t} =\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}-R_{t+1}\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}+p_{t+1}h_{i,t+1}^{t} \end{aligned}$$Then,
$$\begin{aligned} c_{i,t}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-\theta x \\ c_{i,t+1}^{t}= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\theta \gamma _{i,t}x \end{aligned}$$Solve for x
$$\begin{aligned} x=\frac{\beta \gamma _{i,t}\left( 1-\tau \right) -\tau \left( 1+n\right) \left( 1+g\right) }{\theta \gamma _{i,t}\left( \beta +1\right) }y_{t}^{t} \end{aligned}$$Therefore,
$$\begin{aligned} c_{i,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{i,t}}\right] y_{t}^{t} \\ c_{i,t+1}^{t}= & {} \frac{\beta \gamma _{i,t}}{1+\beta }\left[ \left( 1-\tau \right) +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{i,t}}\right] y_{i,t}^{t} \\ a_{i,t+1}^{t}= & {} -\left( 1-\theta \right) p_{t}h_{i,t+1}^{t} \\ p_{t}h_{i,t+1}^{t}= & {} \frac{\beta \gamma _{i,t}\left( 1-\tau \right) -\tau \left( 1+n\right) \left( 1+g\right) }{\theta \gamma _{i,t}\left( \beta +1\right) }y_{t}^{t} \\ h_{i,t+1}^{R}= & {} 0 \end{aligned}$$
-
(a)
-
7.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}=0,\) i.e., the borrowing constraint of the investors is binding \(h_{i,t+1}^{t}-h_{i,t+1}^{R}=0,\) i.e., the investors rent all the houses out \(h_{i,t+1}^{t}>0,h_{i,t+1}^{R}>0,\) i.e., the investors hold positive amount of housing Therefore, \(\mu _{1},\mu _{2}\ge 0,\) \(\nu _{1}=\nu _{2}=0.\) Plug them into the FOCs,
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}+\mu _{1}= & {} 0 \\ -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{1}\left( 1-\theta \right) p_{t}+\mu _{2}= & {} 0 \\ \lambda _{1}p_{t}^{r}-\lambda _{2}\delta _{r}p_{t+1}-\mu _{2}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}\ge & {} R_{t+1} \\ \frac{\lambda _{1}}{\lambda _{2}}\ge & {} \frac{p_{t+1}}{p_{t}} \\ \frac{\lambda _{1}}{\lambda _{2}}\ge & {} \frac{\delta _{r}p_{t+1}}{p_{t}^{r}} \end{aligned}$$Use the fact that
$$\begin{aligned}&\displaystyle -\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\left( \lambda _{1}-\lambda _{2}R_{t+1}\right) \left( 1-\theta \right) p_{t}+\mu _{2} =0 \\&\displaystyle \lambda _{1}p_{t}^{r}-\lambda _{2}\delta _{r}p_{t+1}-\mu _{2} =0 \end{aligned}$$Solve for \(\frac{\lambda _{1}}{\lambda _{2}}\)
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}=\frac{\left( 1-\delta _{r}\right) p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$-
(a)
If \(\mu _{1}=0,\mu _{2}=0,\nu _{1}=\nu _{2}=0\), then we go back to case 1.
-
(b)
If \(\mu _{1}>0,\mu _{2}=0,\nu _{1}=\nu _{2}=0\), then we go back to case 5.
-
(c)
If \(\mu _{1}=0,\mu _{2}>0,\nu _{1}=\nu _{2}=0\), then we go back to case 3.
-
(d)
If \(\mu _{1}>0,\mu _{2}>0,\nu _{1}=\nu _{2}=0\), then we have
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}> & {} R_{t+1} \\ \frac{\lambda _{1}}{\lambda _{2}}> & {} \frac{p_{t+1}}{p_{t}} \\ \frac{\lambda _{1}}{\lambda _{2}}> & {} \frac{\delta _{r}p_{t+1}}{p_{t}^{r}} \end{aligned}$$Use the expression \(\frac{\lambda _{1}}{\lambda _{2}}=\frac{\left( 1-\delta _{r}\right) p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{\theta p_{t}-p_{t}^{r}},\) the above three inequalities imply
$$\begin{aligned} R_{t+1}< & {} \frac{\left( 1-\delta _{r}\right) p_{t+1}}{p_{t}-p_{t}^{r}} \\ R_{t+1}< & {} \frac{\frac{p_{t+1}}{p_{t}}-\theta \frac{\delta _{r}p_{t+1}}{ p_{t}^{r}}}{1-\theta } \end{aligned}$$where I use the assumption \(\theta p_{t}-p_{t}^{r}>0.\) Therefore,
$$\begin{aligned} \frac{\left( 1-\delta _{r}\right) p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t} }{\theta p_{t}-p_{t}^{r}}=\frac{\lambda _{1}}{\lambda _{2}}>\frac{\delta _{r}p_{t+1}}{p_{t}^{r}},\frac{p_{t+1}}{p_{t}},R_{t+1} \end{aligned}$$It is also true that
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}> & {} \frac{p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}}{\theta p_{t}} \\ \frac{\lambda _{1}}{\lambda _{2}}> & {} \frac{p_{t+1}\left( 1-\delta _{r}\right) }{p_{t}-p_{t}^{r}} \end{aligned}$$Recall that
$$\begin{aligned} c_{i,t}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}+p_{t}^{r}h_{i,t+1}^{R}-\theta p_{t}h_{i,t+1}^{t} \\ c_{i,t+1}^{t}= & {} \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+R_{t+1}a_{i,t+1}^{t}+p_{t+1}h_{i,t+1}^{t}-\delta _{r}p_{t+1}h_{i,t+1}^{R} \end{aligned}$$Let \(x\equiv \left( p_{t}-\frac{p_{t}^{r}}{\theta }\right) h_{i,t+1}^{t},\gamma _{i,t}\equiv \frac{\lambda _{1}}{\lambda _{2}}=\frac{\left( 1-\delta _{r}\right) \frac{p_{t+1}}{p_{t}}-R_{t+1}\left( 1-\theta \right) }{ \theta -\frac{p_{t}^{r}}{p_{t}}}.\) Then, the above budget constraint becomes
$$\begin{aligned} c_{i,t}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-\theta x \\ c_{i,t+1}^{t}= & {} \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\theta \gamma _{i,t}x \end{aligned}$$Solve for x
$$\begin{aligned} x=\frac{\beta \gamma _{i,t}\left( 1-\tau \right) y_{t}^{t}-\tau _{t+1}y_{t+1}^{t}}{\theta \gamma _{i,t}\left( \beta +1\right) } \end{aligned}$$Therefore,
$$\begin{aligned} \left( p_{t}-\frac{p_{t}^{r}}{\theta }\right) h_{i,t+1}^{t}= & {} \frac{\beta \gamma _{i,t}\left( 1-\tau \right) y_{t}^{t}-\left( 1+n\right) \left( 1+g\right) y_{t}^{t}}{\theta \gamma _{i,t}\left( \beta +1\right) } \\ h_{i,t+1}^{t}= & {} h_{t+1}^{R} \\ c_{i,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{i,t}}\right] y_{t}^{t} \\ c_{i,t+1}^{t}= & {} \frac{\beta \gamma _{i,t}}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{i,t}}\right] y_{t}^{t} \end{aligned}$$
-
(a)
-
8.
\(a_{i,t+1}^{t}+\left( 1-\theta \right) p_{t}h_{i,t+1}^{t}=0,h_{t+1}^{t}-h_{i,t+1}^{R}=0, h_{i,t+1}^{t}=h_{i,t+1}^{R}=0,\) then \(\mu _{1},\mu _{2},v_{1},v_{2}\ge 0.\)
$$\begin{aligned} c_{i,t}^{t}= & {} \left( 1-\tau \right) y_{t}^{t} \\ c_{i,t+1}^{t}= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t} \end{aligned}$$
1.8.2 Household’s problem
The Lagrangian function is
The FOCs become
where
and the lifetime budget constraint is given by
-
1.
\(a_{h,t+1}^{t}+\left( 1-\theta \right) p_{t} h_{h,t+1}^{t}>0,h_{h,t+1}^{t}>0, h_{h,t+1}^{r}>0,\) then \(\mu _{1}=\nu _{1}=\nu _{2}=0\)
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{r}+h _{h,t+1}^{t}}-\lambda _{1}p_{t}+\lambda _{2}p_{t+1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{r}+h _{h,t+1}^{t}}-\lambda _{1}p_{t}^{r}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}=R_{t+1}=\frac{p_{t+1}}{p_{t}-p_{t}^{r}}= \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$The optimal decision rules are
$$\begin{aligned} c_{h,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ c_{h,t+1}^{t}= & {} \frac{\beta \left( 1-\zeta \right) R_{t+1}}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ h_{h,t+1}^{r}+h_{h,t+1}^{t}= & {} \frac{\beta \zeta }{p_{t}^{r}}c_{h,t}^{t} \\ \left( p_{t}-p_{t}^{r}\right) h_{h,t+1}^{t}+a_{h,t+1}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-\left( 1+\beta \zeta \right) c_{h,t}^{t} \end{aligned}$$ -
2.
\(a_{h,t+1}^{t}+\left( 1-\theta \right) p_{t} h_{h,t+1}^{t}>0,h_{h,t+1}^{t}>0, h_{h,t+1}^{r}=0,\) then \(\mu _{1}=\nu _{1}=0,\nu _{2}\ge 0.\) If \(\mu _{1}=\nu _{1}=\nu _{2}=0,\) then we go back to case 1. If \(\mu _{1}=\nu _{1}=0,\nu _{2}>0,\)
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{t}}-\lambda _{1}p_{t}+\lambda _{2}p_{t+1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{t}}-\lambda _{1}p_{t}^{r}+\nu _{2}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}=R_{t+1}<\frac{p_{t+1}}{p_{t}-p_{t}^{r}}< \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$This suggests that if the rental price is high enough, i.e., \( p_{t}^{r}>p_{t}-\frac{p_{t+1}}{R_{t+1}}\), unconstrained workers will choose to own houses. The optimal policy rules are
$$\begin{aligned} c_{h,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ c_{h,t+1}^{t}= & {} \frac{\beta \left( 1-\zeta \right) R_{t+1}}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ h_{h,t+1}^{t}= & {} \frac{\beta \zeta }{p_{t}-\frac{p_{t+1}}{ R_{t+1}}}c_{h,t}^{t} \\ a_{h,t+1}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-\frac{ \left( 1+\beta \zeta \right) p_{t}-\frac{p_{t+1}}{R_{t+1}}}{p_{t}-\frac{p_{t+1} }{R_{t+1}}}c_{h,t}^{t} \end{aligned}$$ -
3.
\(a_{h,t+1}^{t}+\left( 1-\theta \right) p_{t} h_{h,t+1}^{t}>0,\) \(h_{h,t+1}^{t}=0, h_{h,t+1}^{r}>0,\) then \(\mu _{1}=0,\nu _{1}\ge 0,\nu _{2}=0. \)If \(\mu _{1}=\nu _{1}=\nu _{2}=0,\) then we go back to case 1. If \(\mu _{1}=\nu _{2}=0,\nu _{1}>0\)
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{r}+h _{h,t+1}^{t}}-\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\nu _{1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{r}+h _{h,t+1}^{t}}-\lambda _{1}p_{t}^{r}= & {} 0 \end{aligned}$$Hence,
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}=R_{t+1}>\frac{p_{t+1}}{p_{t}-p_{t}^{r}}> \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$The optimal policy rules are
$$\begin{aligned} c_{h,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ c_{h,t+1}^{t}= & {} \frac{\beta }{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \\ p_{t}^{r}h_{h,t+1}^{r}= & {} \frac{\beta \zeta }{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{R_{t+1}}\right] y_{t}^{t} \end{aligned}$$ -
4.
\(a_{h,t+1}^{t}+\left( 1-\theta \right) p_{t} h_{h,t+1}^{t}=0,\) \(h_{h,t+1}^{t}>0, h_{h,t+1}^{r}>0,\) then \(\mu _{1}\ge 0,\nu _{1}=\nu _{2}=0.\) If \(\mu _{1}=\nu _{1}=\nu _{2}=0,\) then we go back to case 1. If \(\mu _{1}>0,\nu _{1}=0,\nu _{2}=0\)
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}+\mu _{1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{r}+h _{h,t+1}^{t}}-\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{1}\left( 1-\theta \right) p_{t}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{r}+h _{h,t+1}^{t}}-\lambda _{1}p_{t}^{r}= & {} 0 \end{aligned}$$Hence, the condition for \(R_{t+1}\) is
$$\begin{aligned} R_{t+1}<\frac{p_{t+1}}{p_{t}-p_{t}^{r}}<\frac{\lambda _{1}}{\lambda _{2}}= \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$Because
$$\begin{aligned} c_{h,t}^{t}= & {} \left( 1-\tau \right) y_{t}^{t}-\theta p_{t}h _{h,t+1}^{t}+p_{t}^{r}h_{h,t+1}^{t}-p_{t}^{r}\left( h_{h,t+1}^{t}+h_{h,t+1}^{r}\right) \\ c_{h,t+1}^{t}= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) h _{h,t+1}^{t} \end{aligned}$$Then, we have
$$\begin{aligned} 1+\beta \zeta =\lambda _{1}\left( 1-\tau \right) y_{t}^{t}-\lambda _{1} h_{h,t+1}^{t}\left( \theta p_{t}-p_{t}^{r}\right) \end{aligned}$$and
$$\begin{aligned} \beta \left( 1-\zeta \right) =\lambda _{2}\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\lambda _{2}\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) h_{h,t+1}^{t} \end{aligned}$$Combine the above two equations and let \(\frac{\lambda _{1}}{\lambda _{2}} \equiv \gamma _{h,t},\) then we have
$$\begin{aligned} \left( 1+\beta \right) c_{t}^{t}=\frac{\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}}{\gamma _{h,t}}+\left( 1-\tau \right) y_{t}^{t} \end{aligned}$$If we know \(\gamma _{h,t},\) then we can express \( c_{h,t}^{t},c_{h,t+1}^{t},h_{h,t+1}^{t}\) in terms of \(\gamma _{h,t}\)
$$\begin{aligned} 1+\beta&=\frac{\left( 1-\tau \right) y_{t}^{t}}{\left( 1-\tau \right) y_{t}^{t}-\theta p_{t}h_{h,t+1}^{t}-p_{t}^{r}h_{h,t+1}^{r}} \\&\quad +\beta \left( 1-\zeta \right) \frac{\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}}{\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) h_{h,t+1}^{t}} \end{aligned}$$Use \(\frac{1+\beta \zeta }{\left( 1-\tau \right) y_{t}^{t}-\left( \theta p_{t}-p_{t}^{r}\right) h_{h,t+1}^{t}}=\lambda _{1}=\frac{1}{c_{h,t}^{t}},\) the above equation can be simplified into
$$\begin{aligned} 1+\beta= & {} \frac{\left( 1-\tau \right) \left( 1+\beta \zeta \right) y_{t}^{t} }{\left( 1-\tau \right) y_{t}^{t}-\left( \theta p_{t}-p_{t}^{r}\right) h_{h,t+1}^{t}} \\&+\beta \left( 1-\zeta \right) \frac{\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}}{\tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}+\left( p_{t+1}-R_{t+1}\left( 1-\theta \right) p_{t}\right) h_{h,t+1}^{t}} \end{aligned}$$This is a quadratic equation for \(p_{t}h_{h,t+1}^{t}.\) Let
$$\begin{aligned} x= & {} p_{t}h_{h,t+1}^{t} \\ \hat{\theta }= & {} \theta -\frac{p_{t}^{r}}{p_{t}} \\ \varphi= & {} \frac{p_{t+1}}{p_{t}}-\left( 1-\theta \right) R_{t+1} \\ a= & {} \left( 1-\tau \right) y_{t}^{t} \\ b= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t}\\ 1+\beta= & {} \frac{\left( 1+\beta \zeta \right) a}{a-\hat{\theta }x}+\frac{\beta \left( 1-\zeta \right) b}{b+\varphi x} \end{aligned}$$with one solution is zero, the other solution is
$$\begin{aligned} x=\frac{a\varphi \beta \left( 1-\zeta \right) -b\hat{\theta }\left( 1+\beta \zeta \right) }{\hat{\theta }\varphi \left( 1+\beta \right) } \end{aligned}$$We can still define \(\gamma _{h,t}\)
$$\begin{aligned} \gamma _{h,t}= & {} \frac{\lambda _{1}}{\lambda _{2}}=\frac{c_{h,t+1}^{t}}{\beta \left( 1-\zeta \right) c_{h,t}^{t}}=\frac{\left( b+\varphi x\right) \left( 1+\beta \zeta \right) }{\beta \left( 1-\zeta \right) \left( a-\hat{\theta } x\right) } \\= & {} \frac{\varphi }{\hat{\theta }}=\frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$which gives
$$\begin{aligned} c_{h,t}^{t}= & {} \frac{1}{1+\beta }\left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{h,t}}\right] y_{t}^{t} \\ c_{h,t+1}^{t}= & {} \frac{\beta \left( 1-\zeta \right) \gamma _{h,t}}{1+\beta } \left[ 1-\tau +\frac{\tau \left( 1+n\right) \left( 1+g\right) }{\gamma _{h,t}} \right] y_{t}^{t} \\ p_{t}h_{h,t+1}^{t}= & {} \frac{p_{t}}{\theta p_{t}-p_{t}^{r}} \left[ \left( 1-\tau \right) y_{t}^{t}-\left( 1+\beta \zeta \right) c_{h,t}^{t} \right] \\ h_{h,t+1}^{r}= & {} \frac{\left( 1-\tau \right) y_{t}^{t}-\theta p_{t}h_{h,t+1}^{t}-c_{h,t}^{t}}{p_{t}^{r}} \\ a_{h,t+1}^{t}= & {} -\left( 1-\theta \right) p_{t} h_{h,t+1}^{t} \end{aligned}$$ -
5.
\(a_{h,t+1}^{t}+\left( 1-\theta \right) p_{t} h_{h,t+1}^{t}=0,\) \(h_{h,t+1}^{t}>0, h_{h,t+1}^{r}=0,\) then \(\mu _{1}\ge 0,\nu _{1}=0,\nu _{2}\ge 0.\)If \(\mu _{1}=\nu _{1}=\nu _{2}=0,\) then we go back to case 1. If \(\mu _{1}=0,\nu _{1}=0,\nu _{2}>0,\) then we go back to case 2. If \(\mu _{1}>0,\nu _{1}=0,\nu _{2}=0,\) then we go back to case 4. If \(\mu _{1}>0,\nu _{1}=0,\nu _{2}>0,\) then the solution is the same as the benchmark model without rental market.
-
6.
\(a_{h,t+1}^{t}+\left( 1-\theta \right) p_{t} h_{h,t+1}^{t}=0,\) \(h_{h,t+1}^{t}=0, h_{h,t+1}^{r}>0,\) then \(\mu _{1}\ge 0,\nu _{1}\ge 0,\nu _{2}=0.\) If \(\mu _{1}=\nu _{1}=\nu _{2}=0,\) then we go back to case 1. If \( \mu _{1}>0,\nu _{1}=0,\nu _{2}=0,\) then we go back to case 4. If \(\mu _{1}=0,\nu _{1}>0,\nu _{2}=0,\) then we go back to case 3. If \(\mu _{1}>0,\nu _{1}>0,\nu _{2}=0,\) then
$$\begin{aligned} -\lambda _{1}+\lambda _{2}R_{t+1}+\mu _{1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{r}}-\lambda _{1}p_{t}+\lambda _{2}p_{t+1}+\mu _{1}\left( 1-\theta \right) p_{t}+\nu _{1}= & {} 0 \\ \frac{\beta \zeta }{h_{h,t+1}^{r}}-\lambda _{1}p_{t}^{r}= & {} 0 \end{aligned}$$Either
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}>R_{t+1}>\frac{p_{t+1}}{p_{t}}>\frac{ p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}} \end{aligned}$$or
$$\begin{aligned} \frac{\lambda _{1}}{\lambda _{2}}> & {} \frac{p_{t+1}-\left( 1-\theta \right) R_{t+1}p_{t}}{\theta p_{t}-p_{t}^{r}}>\frac{p_{t+1}}{p_{t}}>R_{t+1}\\ a_{h,t+1}^{t}= & {} 0 \\ h_{h,t+1}^{t}= & {} 0 \\ c_{h,t+1}^{t}= & {} \tau \left( 1+n\right) \left( 1+g\right) y_{t}^{t} \\ c_{h,t}^{t}= & {} \frac{1}{1+\beta \zeta }\left( 1-\tau \right) y_{t}^{t} \\ p_{t}^{r}h_{h,t+1}^{r}= & {} \frac{\beta \zeta }{1+\beta \zeta } \left( 1-\tau \right) y_{t}^{t} \end{aligned}$$
1.9 Proof of Lemma 3
Suppose households are not borrowing-constrained. The Focs of households become
Suppose \(h_{t+1}^{r}>0,\) then \(v_{2}=0,\)
Therefore,
This suggests that investors would not hold housing assets because the return of investment in housing assets is strictly less than the return on consumption loans. Hence, \(h_{h,t+1}^{r}=0\) if households are borrowing-constrained. This is a contradiction. Therefore, \(h_{h,t+1}^{r}=0\) if households are unconstrained.
1.10 Proof of Proposition 5
Since our point of interest is to see whether frictional rental market can resolve the problem of vacant houses and prevent the rise of bubbles, I assume \(\theta >\theta _{L}=\omega ,\) such that there exists a bubble after the pension reform when \(\delta _{r}=0.\) From Lemma 10, we know that investors will hold housing assets only if households are borrowing-constrained. Therefore, I only consider the equilibrium where households are borrowing-constrained and investors lend to households.
When there is a housing bubble, \(R^{*}=1.\) For the investors to be indifferent between holding empty houses and renting them out, it must be \( p^{r}=\delta _{r}p.\) For the households to rent positive amount of housing, the necessary condition is
which is obviously satisfied when \(R^{*}=1.\) The demand function for rental housing is given by
If \(\delta _{r}\ge \theta \zeta ,\) then \(p^{r}h_{h}^{r}<0\). Households demand zero rental housing if the rental market friction \(\delta _{r}\ge \theta \zeta \).
Housing bubble can still exist even with active rental market. The credit supply is given by
where \( h_{i}\ge h^{R} \). Let us suppose \(h_{i}=h_{i}^{R}+h_{i}^{B},\) where \(h_{i}^{B}\) is the amount of vacant houses.
The credit demand function can be written as
The credit market clearing condition requires that \(\int a_{i}\mathrm{d}\mu _{i}+\int a_{h}d\mu _{h}=0 \). Hence,
where the second equality comes from the market clearing condition for rental market, \(\int h_{i}^{R}\mathrm{d}\mu _{i}=\int h_{h}^{r}\mathrm{d}\mu _{h}.\) If \(\delta _{r}>\omega \zeta ,\) then \(p\int h_{i}^{B}\mathrm{d}\mu _{i}>0\), i.e., there are empty housing held by investors even through the rental market is active.
1.11 Proof of Proposition 6
In the equilibrium, if \(R_{t+1}\equiv \left( 1+n\right) \left( 1+g\right) \), then \( \frac{K_{t}}{A_{t}L_{t}} =\left( \frac{n+g+\delta }{\alpha }\right) ^{\frac{1 }{\alpha -1}} \). We know that this is the lowest equilibrium interest rate. Hence, \( K_{t+1}=\left( \frac{n+g+\delta }{\alpha }\right) ^{\frac{1}{\alpha -1}} A_{t+1}L_{t+1}\) is maximum asset demand the production sector can absorb. If there exists bubble in the equilibrium, then the following condition holds
Because \(K_{t+1}=\frac{K_{t}}{A_{t}L_{t}} A_{t+1}L_{t+1}\), the above condition can be simplified as
which implies
1.12 Proof of Proposition 7
We know that households are constrained, and investor holds housing assets close to the neighborhood of new stationary equilibrium. From the financial market constraint, we can show that \( K_{t+1}=\left( 1-\omega \right) L_{t}a_{i,t+1}+\omega L_{t}a_{h,t+1} \). Because
Plug them to the expression for \(K_{t+1},\) we have
Hence, \( p_{t}H+K_{t+1}=L_{t}\frac{\beta }{1+\beta }w_{t} \). Because
then
where \(p_{t}=\tilde{p}_{t}A_{t}L_{t}\), \(K_{t+1}=\tilde{k} _{t+1}A_{t+1}L_{t+1}.\)
When investor holds housing assets, we know that \(p_{t+1}/p_{t}=R_{t+1},\) or equivalently,
Therefore, those two equations determine an autonomous system of \(\left( \tilde{p}_{t},\tilde{k}_{t}\right) \) with \(\tilde{p}_{t}>0\) and \(\tilde{k} _{t}>0.\) The phase diagram is shown by Fig. 12. Note that \(\tilde{p}_{t}=0\) cannot be a stationary equilibrium price because households will demand infinite amount.
Rights and permissions
About this article
Cite this article
Zhao, B. Rational housing bubble. Econ Theory 60, 141–201 (2015). https://doi.org/10.1007/s00199-015-0889-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-015-0889-4