Automated VLBI scheduling using AI-based parameter optimization

Abstract

Within this work, a new geodetic very long baseline interferometry (VLBI) scheduling approach inspired by evolutionary processes based on selection, crossover and mutation is presented. It mimics the biological concept “surviving of the fittest” to iteratively explore the scheduling parameter space looking for the best solution. Besides providing high-quality results, one main benefit of the proposed approach is that it enables the generation of fully automated and individually optimized schedules. Moreover, it generates schedules based on transparent rules, well-defined scientific goals and by making decisions based on Monte Carlo simulations. The improvements in terms of precision of geodetic parameters are discussed for various observing programs organized by the International VLBI Service for Geodesy and Astrometry (IVS), such as the OHG, R1, and T2 programs. In the case of schedules with a difficult telescope network, an improvement in the precision of the geodetic parameters up to 15% could be identified, as well as an increase in the number of observations of up to 10% compared to classical scheduling approaches. Due to the high quality of the produced schedules and the reduced workload for the schedulers, various IVS observing programs are already making use of the evolutionary parameter selection, such as the AUA, INT2, INT3, INT9, OHG, T2 and VGOS-B program.

1 Introduction

Very long baseline interferometry (VLBI) (Sovers et al. 1998; Schuh and Böhm 2013) is, together with the global navigation satellite system (GNSS), satellite laser ranging (SLR), and Doppler orbitography and radiopositioning integrated by satellite (DORIS), one of the geometric space geodetic techniques. By measuring the difference in arrival time from signals of extra-galactic radio sources, it plays an important role in a broad range of applications. For example, VLBI is used in the determination of terrestrial reference frames (Altamimi et al. 2016), in particular of its scale, and determines the celestial reference frame in radio frequencies (Fey et al. 2015; Charlot et al. 2020). Furthermore, it is the only technique capable of determining the full set of earth orientation parameters (EOPs) (Petit and Luzum 2010), which are critical for positioning and navigation in space and on Earth.

Due to its observing principle, VLBI observations need to be coordinated between telescopes. When multiple telescopes observe the same radio source simultaneously, this is called a scan. Within a scan, each pair of telescopes forms one baseline and provides one observation. For sustainable resource management, international collaborations such as the International VLBI Service for Geodesy and Astronomy (IVS) (Nothnagel et al. 2017) organize VLBI experiments, so-called sessions. In general, VLBI sessions can be divided into two groups:

• 24-h long experiments with about ten globally distributed telescopes. These sessions are typically used to determine station and source coordinates, as well as EOPs and geophysical parameters.

• 1-h long so-called intensive experiments with mostly two, but sometimes up to five telescopes. These sessions are performed solely to measure the Earth rotation angle expressed through dUT1 (Petit and Luzum 2010).

For each session, an observing schedule is generated and distributed to the telescopes. This schedule is of utmost importance since it directly determines which observations are available for analysis.

Over the last years, substantial work has been conducted to improve the observation schedules for geodetic VLBI. Most of this work was related to intensive sessions. Uunila et al. (2012) highlighted the importance of observations near the corners of the mutually visible sky between telescopes participating in intensive sessions. This was later confirmed by Baver and Gipson (2015). A different scheduling approach was demonstrated by Leek et al. (2015), who studied the use of so-called impact factors for intensive scheduling with a special emphasis on twin-telescopes. Recently, a new approach was presented by Corbin et al. (2020) based on linear programming. Additionally, many studies were investigating the impact of different source lists on intensive scheduling and the relation between sky-coverage and source brightness, see Baver and Gipson (2014), Gipson and Baver (2016), Baver and Gipson (2020).

For 24-h sessions, recent research focused on improving schedules for the next-generation VLBI network, the VLBI global observing system (VGOS) (Petrachenko et al. 2012; Niell et al. 2018). Sun et al. (2014) demonstrated the usefulness of a source-based scheduling approach for VGOS, while (Schartner and Böhm 2020) demonstrated that a combination of different optimization criteria will lead to substantial improvement.

Additionally, a paper by McCallum et al. (2017) investigated a so-called star scheduling mode for legacy 24-h sessions, which was used to optimize the observations of weak radio sources in the southern hemisphere by evaluating only observations between a sensitive telescope and multiple weak telescopes.

An alternative automated scheduling strategy was proposed by Lovell et al. (2016) and Iles et al. (2018) in particular for the Australian AuScope VLBI array (Lovell et al. 2013). In contrast to classical scheduling, this approach, called “dynamic scheduling”, does not generate the full schedule in advance of the session. Instead, the schedule is generated and distributed in small blocks in near real time. Via a web-interface, stations can dynamically drop in and out of the session leading to higher flexibility.

Within this work, we are demonstrating a new, general VLBI scheduling approach that can be used for both 24-h and intensive sessions. This approach is based on optimizing scheduling via large-scale Monte Carlo simulations (Metropolis and Ulam 1949) in comparison with evolutionary algorithms (Jong 2006; Eiben and Smith 2015). Besides providing high-quality schedules, one main benefit of this approach is that it is self-learning and can thus be used for all types of sessions, enabling fully automated scheduling with every session being individually optimized. Due to the flexibility of the approach, the reduced workload through the automation, combined with the high quality of the results, it is now used to schedule multiple official IVS observing programs, such as AUA, INT2, INT3, INT9, OHG, T2 and VGOS-B.

In the following sections, we will describe the scheduling approach that is used (Sect. 2.1) as well as the evolutionary algorithm used to optimize the schedule (Sect. 2.2). In Sect. 3.1, the best set of hyperparameters is identified and later used to evaluate the algorithm. At first, a specific and difficult VLBI session, namely OHG127, is analysed in detail (Sect. 3.2), followed by a general evaluation based on all OHG sessions in the years 2019 and 2020 (Sect. 3.3). Furthermore, R1 sessions (3.4) from October 2020 until December 2020, as well as all T2 sessions from 2019 and 2020 (3.5), are evaluated by using the evolutionary algorithm. Additionally, the potential and limitations of the algorithm are briefly discussed for intensive sessions (3.6). Besides producing high-quality schedules, the main benefit of the proposed algorithm is that it can run fully automated. This fact and the resulting advantage in terms of reduced human-bias are further discussed in Sect. 4. Finally, Sect. 5 summarizes the results.

2 Method

2.1 Scheduling approach

Recent studies by Schartner and Böhm (2020), Schartner et al. (2020) have demonstrated the benefit of optimizing every schedule individually based on a combination of optimization criteria such as sky-coverage, number of observations, number of scans, and mitigation of idle time. This approach is now applied to various official IVS observing programs, such as AUA, INT2, INT3, INT9, OHG, T2, VGOS-B and parts of the EU-VGOS program as well as multiple non-IVS observing programs. The general idea is that the different network geometries, observing rates, scientific purposes, and available sources of each VLBI session require a different balance between these optimization criteria to produce the best result. The optimal balance can be found based on large-scale Monte Carlo simulations. For this purpose, a new VLBI scheduling software, VieSched++ (Schartner and Böhm 2019), was developed that can be used to test different balances of optimization criteria in scheduling based on simulations.

To understand the concept of the proposed algorithm, it is necessary to discuss the generation of a geodetic VLBI schedule first. A schedule is generated scan-by-scan. For every scheduled scan, the scheduling software is evaluating all possible radio sources and thus all possible scans that could potentially be observed based on the previously mentioned optimization criteria opt. Internally, a score per optimization criterion $\mathrm{{score}}_{\mathrm{{opt}}}$ is assigned to each potential scan. These optimization criteria scores are further combined using so-called weight-factors $\omega _{\mathrm{{opt}}}$ to calculate a total score per potential scan based on Eq. 1.

$$\begin{aligned} \mathrm{{score}} = \sum _{\mathrm{{opt}}} \left( \omega _{\mathrm{{opt}}} \cdot \mathrm{{score}}_{\mathrm{{opt}}} \right) \end{aligned}$$

(1)

The potential scan with the highest total score is selected and assigned to the final schedule. After a scan is fixed, the process is repeated until all scans are selected and the schedule is finished. Thus, the weight-factors $\omega _{\mathrm{{opt}}}$ determine how much an optimization-criterion contributes to the decision which scan should be scheduled. Therefore, it is important to pick reasonable values for these weight factors to find a good balance of all optimization-criteria.

Besides the weighted sum of the individual scores from the optimization criteria, additional parameters can influence the calculation of the total score and thus the scan selection. Most importantly, it is possible to assign every station sta a certain weight $\omega _{\mathrm{{sta}}}$. Increasing the station weight is regularly done to incorporate telescopes more prominently into the schedule, in case they would be otherwise scheduled with few scans only. Therefore, Eq. 1 is extended with the product over all individual station weights.

$$\begin{aligned} \mathrm{{score}} = \sum _{\mathrm{{opt}}} \left( \omega _{\mathrm{{opt}}} \cdot \mathrm{{score}}_{\mathrm{{opt}}} \right) \cdot \prod _{\mathrm{{sta}}} \omega _{\mathrm{{sta}}} \end{aligned}$$

(2)

More information about how the scores per optimization criteria $\mathrm{{score}}_{\mathrm{{opt}}}$ are calculated as well as a full discussion on the scan selection can be found in Schartner and Böhm (2019).

Within this work, the scheduling is performed as sophisticated as possible to yield realistic results. This means that subnetting and fillin-modes are enabled (see Gipson (2016) for more details), as well as iterative source selection with a recursive scan selection (Schartner and Böhm 2019). Additionally, down time due to simultaneous intensive sessions is applied.

2.1.1 24-hour sessions

The proposed optimization of the 24-h sessions is based on the four most important optimization criteria and their corresponding weight-factors $\omega$

• improvement in sky coverage $\omega _{\mathrm{{sky}}}$

• the number of observations per scan $\omega _{\mathrm{{obs}}}$

• the duration of each scan $\omega _{\mathrm{{dur}}}$

• the mitigation of long idle time $\omega _{\mathrm{{idle}}}$

and the individual weights of the stations $\omega _{\mathrm{{sta}}}$. These are the primary parameters that are optimized by the evolutionary algorithm described in Sect. 2.2. Thus, for a VLBI session with 10 telescopes, the dimension of the parameter space is $4+10=14$ with four dimensions representing the weight-factors $\omega _{\mathrm{{opt}}}$ and the rest from the station weights $\omega _{\mathrm{{sta}}}$. Using a classical multi-scheduling (MS) approach (Schartner and Böhm 2019) with only 4 tested values per parameter and a grid-wise combination of these values would lead to $\approx 4^{14}$ (more than 200 million) schedules that would need to be evaluated and is thus not feasible. In contrast, by defining the number of schedules to be generated and by randomly picking the values of the parameters, only a very sparse sampling of the parameter space would be achieved.

This is where the evolutionary algorithm comes into play. Instead of doing a grid-wise combination or a pure random selection, it iteratively adjusts the parameter values and thus avoids areas in the parameter space that would likely lead to poor schedules based on its previous experience with close-by parameter values. Therefore, the total number of schedules that need to be evaluated to achieve a good and dense sampling of the most promising areas in the parameter space is significantly less.

2.1.2 Intensive sessions

Intensive schedules are typically generated in a way that all telescopes are always observing the same radio source together. Therefore, only two optimization criteria are relevant, namely $\omega _{\mathrm{{sky}}}$ and $\omega _{\mathrm{{dur}}}$ since the number of observations per scan is constant and there will be no long idle times. For the same reason, there is no need to assign individual weights to the stations since their impact would be the same for all scans.

However, following the suggestions of Uunila et al. (2012) and Baver and Gipson (2015), observations of sources located at the corners of the mutually visible sky are beneficial for estimating dUT1, the primary parameter derived from intensive sessions. In VieSched++, it is possible to set a time cadence in which these observations should be enforced. The software will start by observing one source located at one corner and after $t_{c}$ s, it will be forced to observe a source located at the second corner and so on. For the intensive scheduling setup, the two weight-factors $\omega _{\mathrm{{sky}}}$ and $\omega _{\mathrm{{dur}}}$ and the corner switch cadence $t_{c}$ are the primary scheduling parameters that are optimized via the evolutionary algorithm. Thus, the dimension of the parameter space is only $2+1=3$.

Fig. 1

Flowchart of the proposed ES strategy including a simplified graphical visualization

2.2 Evolutionary algorithm

Evolutionary algorithms (EA) are a subsection of evolutionary computation and thus belong to the field of artificial intelligence (Fogel 2006; Eiben and Smith 2015). They are inspired by biological concepts such as the concept of natural selection (Darwin 1859). Thus, they simulate evolution to explore the solutions for complex real-world problems based on an incrementally changing system Vikhar (2016).

For optimizing geodetic VLBI scheduling, an EA based on selection, mutation, and crossover was chosen following the concept of evolution strategy (ES) summarized in Fogel (2006). Closely related to ES are the so-called genetic algorithms (Mitchell 1996). In geodesy, genetic algorithms are regularly used to solve optimization problems (Saleh and Chelouah 2004; Baselga and García-Asenjo 2008; Coulot et al. 2009; Asgarimehr and Hossainali 2015). In practice, there is not always a clear distinction between an evolutionary strategy and a genetic algorithm. Within this work, we are mostly following Fogel (2006) and Eiben and Smith (2015) with respect to the nomenclature that is used.

The aim of the ES is to optimize scheduling parameters, resulting in a schedule with high precision for the estimated geodetic parameters. Figure 1 visualizes the concept of the ES.

In short, the scheduling parameters that will be optimized are defining the n-dimensional parameter space to be exploited. Every point in this parameter space represents one schedule, represented by an n-dimensional vector $\mathbf {p}$. By starting with a random selection of several instances of $\mathbf {p}$, the corresponding schedules can be generated, simulated and analysed, see Sect. 2.2.1. As noted, the quality of the schedules is mostly determined by the precision of the estimated geodetic parameters, quantified through a fitness function, further described in Sect. 2.2.2. Based on the fitness function, the best parameter vectors are selected. The selected parameter vectors are further combined and adjusted as discussed in Sects. 2.2.3 and 2.2.4 to form new parameter vectors. Based on the new parameter vectors, new schedules are generated and evaluated and the whole process starts over again.

2.2.1 Initialization

First, an initial starting population of $m_0$ n-dimensional parameter vectors

$$\begin{aligned} \mathbf {p}_{i,g_0} = \begin{pmatrix} v_1 &{} v_2 &{} v_3 &{} \dots &{} v_n \\ \end{pmatrix}^\top \end{aligned}$$

(3)

(called individuals) is generated with $i \in [0,m_0)$ referring to one particular parameter vector within this population and $g_0$ standing for the initial generation. Within the context of ES, the parameter vector $\mathbf {p}$ represents the genes of the individuals, while the individual values v their genetic code. The initial genetic codes are selected using random values with some restrictions: As discussed in Sect. 2.1, parts of the scheduling parameters are the weight-factors of the optimization criteria $\omega _{\mathrm{{opt}}}$ and the individual station weights $\omega _{\mathrm{{sta}}}$. Both of these groups of parameters are multiplicative effects for determining the score of a scan during the scan selection algorithm (see Sect. 2.1). Thus, only the relative ratio between the parameters within one group is of importance, see Schartner and Böhm (2019) and in particular Schartner et al. (2020) for a detailed discussion on this topic.

The parameter space and thus the parameter space vector $\mathbf {p}$ can be divided into two parts, a sub-space for the weight-factors with the corresponding sub-parameter vector $\mathbf {p}_{\mathrm{{opt}}}$ and a sub-space for the individual station weights with the corresponding sub-parameter vector $\mathbf {p}_{\mathrm{{sta}}}$.

$$\begin{aligned} \mathbf {p} = \begin{pmatrix} \mathbf {p}_{\mathrm{{opt}}} \\ \mathbf {p}_{\mathrm{{sta}}} \end{pmatrix} \end{aligned}$$

(4)

Since only the relative ratio between the parameters within one group is of importance, the parameter vectors of each sub-space can be scaled to arbitrary length without changing the scheduling result. Thus, all parameters listed in Eq. 5 will lead to identical schedules.

$$\begin{aligned} \mathbf {p}_{\mathrm{{opt}}}= & {} \begin{pmatrix} \omega _{\mathrm{{sky}}} \\ \omega _{\mathrm{{obs}}} \\ \omega _{\mathrm{{dur}}} \\ \omega _{\mathrm{{idle}}} \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} \equiv \begin{pmatrix} 2 \\ 4 \\ 6 \\ 8 \end{pmatrix} \equiv \frac{1}{\Vert \mathbf {p}_{\mathrm{{opt}}}\Vert _2} \cdot \mathbf {p}_{\mathrm{{opt}}}\nonumber \\= & {} \begin{pmatrix} 0.1826 \\ 0.3651 \\ 0.5477 \\ 0.7303 \end{pmatrix} \end{aligned}$$

(5)

The same is valid for $\mathbf {p}_{\mathrm{{sta}}}$. By scaling all instances of the sub-parameter vectors to the same length, the possible sub-parameter space reduces to the surface of a n-sphere.

Although the parameter scaling does not necessarily have to be done based on two individual sub-parameter spaces but rather could also be done at once for all dimensions, there is significant benefit for splitting it up. For example, the length of the sub-parameter vectors can be chosen individually, this allows for an easy interpretation of the result. In practice, the length of the sub-parameter vector $\mathbf {p}_{\mathrm{{opt}}}$ is typically set to one to directly see the ratio between the different optimization criteria. In contrast, the length of the sub-parameter vector $\mathbf {p}_{\mathrm{{sta}}}$ is typically set to $n_{\mathrm{{sta}}}$. Therefore, if all stations have equal weight, their weight-value is 1.00. This definition is also consistent with other scheduling packages such as skedGipson (2016), where the default station weight is also set to 1.00.

After the genes from the individuals of the initial population are initialized, the scheduling process can start. As already noted, every $\mathbf {p}_i$ represents the input parameters used to generate one schedule. Every schedule is further simulated 1000 times, using state-of-the-art simulation approaches. The simulations consist of three parts: simulation of clock drifts as a sum of random walk and integration random walk (Herring et al. 1990), simulation of the tropospheric effects where temporal and spatial correlation is taken into account as discussed in Nilsson et al. (2007), and white noise. Based on the simulations, the mean formal errors and repeatability values of the estimated geodetic parameters can be determined to calculate the fitness function.

So far, the ES is conceptually identical to a classical MS approach with random initialization. The innovation starts after the initial population is computed. Thus, the ES can be seen as an extension of the classical MS approach.

2.2.2 Selection

From the current $g_j$ and previous ($g_0$ until $g_{j-1}$) generations, a certain amount of individuals are selected to serve as parents for the offspring. Thus, it is allowed that the same individual serves as a parent in multiple future generations. The selection of the parents can be done based on the best performing individuals, randomly, or as a mixture of both (Fogel 2006). To quantify the best performing individuals, a fitness function f is calculated based on the mean formal errors mfe and repeatabilities rep of the simulated EOP (XPO, YPO, dUT1, NUTX, NUTY) and the 3d-station coordinate vector $sta = \sqrt{\delta _x^2 + \delta _y^2 + \delta _z^2}$. In the following, we call the EOP and/or station coordinates, depending on the goal of the VLBI session, the “target parameters” $\mathbf {x}$ of the session. Additionally, other metrics might also be added to the target parameters. For example, in many cases, a high number of observations is a good indicator for a good geodetic result. Thus, it makes sense to also add the number of observations ($\#\mathrm{{obs}}$) to the target parameters of the session.

$$\begin{aligned} \mathbf {x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \\ \end{pmatrix} = \begin{pmatrix} x_{\#\mathrm{{obs}}} \\ x_{XPO} \\ x_{YPO} \\ \vdots \\ x_{sta_{n_{\mathrm{{sta}}}}} \\ \end{pmatrix} \end{aligned}$$

(6)

The definition of the fitness function is not straightforward for the following reasons. In most geodetic VLBI sessions, multiple geodetic parameters are of interest (e.g. EOP and station coordinates). Additionally, the sensitivity of the individual geodetic parameters might be different based on the network geometry (e.g. the network might be more sensitive to dUT1 in comparison with polar motion). Thus, a simple average over all parameters is problematic and might favour some parameters, which is unintended. For example, consider the case of a network, where the range of polar motion sensitivity is between 50 and 150 $\mu$as, while the range of 3d-station coordinate accuracy is between 5 and 10 mm. One needs to find a way to properly compare these values.

Furthermore, some schedules might be generated that are exceptionally bad and produce outlier values. Thus, the fitness function needs to be—at least to some degree—invariant to outliers.

Finally, the simulations provide access to two metrics, the mean formal errors and the repeatabilities. In case of perfect simulations, these two metrics should be identical. However, due to imperfections in the simulations and due to the simplifications applied during parameter estimation, they are not completely identical and can both be used to quantify the scheduling performance.

To overcome these problems, the values of the target parameter $x_i$ (e.g. dUT1 or $\#\mathrm{{obs}}$) over all individuals are first scaled, in order to provide values between zero and one to solve the issue of the different parameter value ranges between the target parameters. The scaling is done linearly, between the best achieved value $x_{i,0}$ (the highest number of observations or the lowest mfe, rep that were achieved) and the $75\%$ quantile $x_{i,.75}$ of the worst achieved value (the lowest number of observations or the highest mfe, rep). Thus, the scaled target parameter values $x_{i,s}$ are calculated based on Eq. (7) leading to one for the best value ($x_i = x_{i,0}$) 400 and zero for the 25% of the worst values ($x_i > x_{i,.75}$).

$$\begin{aligned} x_{i,s} = {\left\{ \begin{array}{ll} x_i \le x_{i,.75} &{} 1-\frac{x_i - x_{i,0}}{x_{i,.75} - x_{i,0}} \\ x_i > x_{i,.75} &{} 0 \end{array}\right. } \end{aligned}$$

(7)

We will again note here that the best achieved value might be the highest value (in case of $\#\mathrm{{obs}}$) or the lowest value (in case of the simulated geodetic parameter precision). By using the $75\%$ quantile instead of the worst present value, the scaling is invariant to $<25\%$ outlier values providing bad values. Exceptionally good values are included in the scaling since finding parameters leading to good values is the main goal of the ES and in practice, this has been proven to be the right approach.

Next, the fitness function is computed as a weighted sum based on all scaled target parameters $x_{i,s}$. The weights $\omega$ are defined based on the scientific goal of the session.

$$\begin{aligned} f= & {} \varvec{\omega }^\top \cdot \mathbf {x} = \begin{pmatrix} \omega _1 \\ \omega _2 \\ \omega _3 \\ \vdots \\ \omega _n \\ \end{pmatrix}^\top \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \\ \end{pmatrix}\nonumber \\&\quad = \begin{pmatrix} \omega _{\#\mathrm{{obs}}} \\ \omega _{XPO} \\ \omega _{YPO} \\ \vdots \\ \omega _{sta_{n_{sta}}} \\ \end{pmatrix}^\top \cdot \begin{pmatrix} x_{\#\mathrm{{obs}}} \\ x_{XPO} \\ x_{YPO} \\ \vdots \\ x_{sta_{n_{sta}}} \\ \end{pmatrix} \end{aligned}$$

(8)

Finally, for a better interpretability of the result, f is scaled between zero (worst fitness) and one (best fitness) over all individuals—the higher the fitness, the better the scheduling parameters. The fitness function is once calculated based on the mean formal errors $f(\mathrm{{mfe}})$ and once calculated based on the repeatabilities $f(\mathrm{{rep}})$. They are further combined with a $70\%$ ratio for the $f(\mathrm{{rep}})$ and a $30\%$ ratio for the $f(\mathrm{{mfe}})$.

$$\begin{aligned} f = 0.7 \cdot f(\mathrm{{rep}}) + 0.3 \cdot f(\mathrm{{mfe}}) \end{aligned}$$

(9)

The 70/30 ratio was chosen based on experience in scheduling and based on simulations of real experiments.

As noted before, the selection of the parents for the offspring can be done based on the fitness of the individuals, by selecting a percentage of $n_{\mathrm{{best}}}$ individuals. However, one problem of ES is a phenomena called “genetic drift” Yu and Gen (2010) that might cause the algorithm to converge towards a wrong solution. Also, it might happen that the algorithm keeps stuck in a local minima. To overcome this problem, a selection of $n_{\mathrm{{rand}}}$ random individuals is selected to serve as parents for the offspring in addition to the best performing ones. The inclusion of randomly picked parents helps to mitigating genetic drifts since they lead to a higher genetic variance during crossover and mutation as can be seen in Sects. 2.2.3 and 2.2.4 and they help to overcome local minima in the fitness function. However, this comes at the cost of a slower learning rate.

2.2.3 Crossover

Based on the selected parents, $m_{i+1}$ offspring individuals $\mathbf {p}_{i,g_{j+1}}$ are formed for the next generation $g_{j+1}$. Every offspring is calculated based on a number of $n_{\mathrm{{par}}}$ parents $\hat{\mathbf {p}}$, where $n_{\mathrm{{par}}}$ can be defined as a hyperparameter as shown in Sect. 3.1. The initial genetic code of the offspring is the average over the genetic codes of the parents.

$$\begin{aligned} \mathbf {p}_{g+1} = \frac{1}{n_{\mathrm{{par}}}} \cdot \sum ^{n_{\mathrm{{par}}}} \hat{\mathbf {p}}. \end{aligned}$$

(10)

2.2.4 Mutation

Finally, for every offspring, a normal distribution mutation is performed. The reason for the mutation is, again, to increase the variability of the genetic codes in order to overcome local minima and to better explore the solution landscape. The mutation is controlled by two hyperparamters, a mutation factor $\delta$ and a minimum mutation factor $\delta _{\mathrm{{min}}}$. The amount of mutation is calculated based on the differences in the genetic code from the parents. For every element $v_k$ with $k \in [1,n]$ in the parameter vectors

$$\begin{aligned} \mathbf {p} = \begin{pmatrix} v_1 &{} v_2 &{} v_3 &{} \dots &{} v_n \\ \end{pmatrix}^\top \end{aligned}$$

(11)

the corresponding minimum and maximum values from the parent vectors, $v_{k,\mathrm{{min}}}$ and $v_{k,\mathrm{{max}}}$, are taken to calculate the value range r.

$$\begin{aligned} r_k = v_{k,\mathrm{{max}}} - v_{k,\mathrm{{min}}} \end{aligned}$$

(12)

Next, the minimum required mutation range $r_{\mathrm{{min}}}$ is calculated based on the initial genetic code in the offspring parameter vector, see Sect. 2.2.3.

$$\begin{aligned} r_{k,\mathrm{{min}}} = v_k \cdot \delta _{\mathrm{{min}}} \end{aligned}$$

(13)

The final mutation range $r_{\mathrm{{mut}}}$ is the maximum between $r_k$ and $r_{k,\mathrm{{min}}}$.

$$\begin{aligned} r_{k,\mathrm{{mut}}} = \max {\left\{ r_k,\;r_{k,\mathrm{{min}}}\right\} } \end{aligned}$$

(14)

Finally, the mutated value $v_{k,\mathrm{{mut}}}$ of each element from the offspring parameter vector can be calculated using

$$\begin{aligned} v_{k,\mathrm{{mut}}} = r_{k,\mathrm{{mut}}} \cdot \delta \cdot {\mathcal {N}}(0,1) \end{aligned}$$

(15)

where ${\mathcal {N}}(0,1)$ stands for a normally distributed random value with mean zero and variance one.

2.2.5 Iteration

The newly generated offspring individuals are populating the next generation of parameter vectors $\mathbf {p}_{i,g_{j+1}}$. Based on the genetic code of every newly generated offspring, a new schedule is generated, simulated, analysed and evaluated and the whole process repeats. This continues until a maximum number of generations are reached or until a termination criterion is fulfilled. In case proper hyperparameters are selected, the algorithm converges after some iterations.

3 Results

3.1 Hyperparameter tuning and comparison with classical multi-scheduling approach

The following hyperparameters can be used to set up the evolutionary scheduling algorithm:

• n number of generations

• $m_0$ number of individuals in the initial population

• $m_j$ number of individuals for generation $j>0$

• $n_{\mathrm{{best}}}$ number of parents selected based on fitness function (expressed via a percentage of $m_j$)

• $n_{\mathrm{{rand}}}$ number of parents selected randomly (expressed via a percentage of $m_j$)

• $n_{\mathrm{{par}}}$ number of parents used during crossover

• $\delta$ mutation factor

• $\delta _{\mathrm{{min}}}$ minimum mutation range.

The parameters n, $m_0$, and $m_j$ define how many individuals will be generated and thus mainly determine the total run time. The parameters $n_{\mathrm{{best}}}$, $n_{\mathrm{{rand}}}$, and $n_{\mathrm{{par}}}$ define how the crossover is performed. Finally, the parameters $\delta$ and $\delta _{\mathrm{{min}}}$ determine how the mutation is done.

The selection of appropriate hyperparameters was first done for a typical R1 session setup with eight stations as shown in Fig. 2 and later evaluated for intensive sessions.

Fig. 2

Station network used to define a good set of hyperparameters

For this test, the fitness function was defined using 1.00 for $\omega _{\#\mathrm{{obs}}}$, $\frac{1}{8}$ for the $\omega _{\mathrm{{sta}}_i}$, and 0.2 each of the five $\omega _{\mathrm{{EOP}}}$. Thus, the total number of observations, the simulated EOP precision and the simulated station coordinate precision contribute to an equal amount to the fitness of the individuals.

The hyperparameter tuning was done iteratively. First, the algorithm was tested based on randomly selected values to get an understanding of which parameter values provide reasonable results. From this investigation, $m_0$ was fixed to 256, $m_j$ was fixed to 128 and n was fixed to 10 ($g_0$–$g_9$), leading to a total of 1408 schedules. During the initial tests, this has been proven to be a good compromise between computational cost and parameter space sampling. Next, based on the initial tests, a grid-wise combination of $n_{\mathrm{{best}}}=\{5\%$, $10\%$, $15\%$, $20\%$, $25\%\}$, $n_{\mathrm{{rand}}} = \{0\%$, $2.5\%$, $5\%$, $7.5\%$, $10\%\}$ and $\delta = \{0.3$, 0.4, 0.5, 0.6, $0.7\}$ was investigated. From this search, the values $n_{\mathrm{{best}}}=20$, $n_{\mathrm{{rand}}}=5$ and $\delta =0.4$ were found to perform well. In general, the $\delta$ parameter had the biggest impact on the result. Slight changes of $n_{\mathrm{{best}}}$ and $n_{\mathrm{{rand}}}$ did not have a significant impact, for example, $n_{\mathrm{{best}}}=10$, $n_{\mathrm{{rand}}}=2.5$ and $\delta =0.4$ also led to good results.

Fig. 3

Parameter evolution for $n=10$, $m_0=256$, $m_j=128$, $n_{\mathrm{{best}}}=20\%$, $n_{\mathrm{{rand}}}=5\%$, $n_{\mathrm{{par}}}=2$, $\delta =0.4$, and $\delta _{\mathrm{{min}}}=5\%$. The abscissa lists the individuals. Red lines mark new generations. The fitness is color-coded

From a biological point of view, the obvious candidate for the number of parents $n_{\mathrm{{par}}}$ is two. However, for a related algorithm, called genetic algorithm (Mitchell 1996), experiments with multi-parent setups have been proven to be beneficial in some cases, see Eiben et al. (1994) and Ting (2005) for example.

Within this study setup, the ES was tested with $n_{\mathrm{{par}}} = \{1,\;2,\; 3\}$ and again by using different $\delta$ values since it was expected that the number of parents influences the best selection of the mutation factor as well. However, based on this investigation, two parents have been proven to be the optimal number. Using only one parent and trying to provide the genetic variation solely using $\delta _{\mathrm{{min}}}$ also did not provide good results.

In general, investigations of $\delta _{\mathrm{{min}}}$ did not show any noteworthy impact on the result. Setting this parameter to $5\%$ provided a good result overall.

In practice, the selection of hyperparameters was found to be not critical for generating optimal schedules. Slight changes in the hyperparameters do not influence on the quality of the generated schedule but rather how fast the algorithm converges. However, by selecting very different hyperparameters as the ones proposed here, it might happen that the solution does not converge at all (especially when selecting a very high value for $\delta$) or it does not converge to a minima in time (especially when selecting a very low value for $\delta$). However, the proposed values should work fine for all session types and can serve as a starting point for further hyperparameter tuning.

Figure 3 visualizes the evolution of the genetic code for a good set of hyperparameters. This set of hyperparameters is further used within this work.

Note, that Fig. 3 visualizes the evolution of a 12-dimensional parameter space as 12 individual plots. Thus, cross-connections between individual parameters cannot be depicted properly. It can be seen that the fitness of the individuals increases over time. By comparing the evolution of the four weight factors, one can see that especially $\omega _{\mathrm{{dur}}}$ is converging towards a relatively large value of around 0.39, followed by $\omega _{\#\mathrm{{obs}}}$ with a weight of 0.28. The weights $\omega _{\mathrm{{sky}}}$ and $\omega _{\mathrm{{idle}}}$ converged towards 0.20 and 0.13, respectively. Thus, the optimal weight of $\omega _{\mathrm{{dur}}}$ is three times larger than $\omega _{\mathrm{{idle}}}$.

By comparing the individual station weights, at first, it seems like that the differences are not very big. However, one has to keep in mind that Fig. 3 is only a simplified visualization of a 12-dimensional parameter space.

It is very important to note that the individual station weights do not reflect how important a station is for achieving good geodetic results. The station weights only reflect how much attention a station needs during the scheduling generation. It is easily possible that the most important station for achieving good geodetic results is already incorporated well into the schedule using an average weight of 1.00.

In general, interpretation of individual station weights has been proven to be difficult, mostly due to the very complex interactions between network geometry, telescope parameters such as sensitivity and slew speed, source distribution and requirements for good geodetic results. However, trends can be identified in the station weights as well. By looking at the actual numbers, one can see that in the final generation, the highest weights belong to WETTZELL with 1.16, followed by AGGO with 1.12. The high weight of AGGO is not surprising, since AGGO is the least sensitive telescope in this network and additionally is in a remote location and thus needs special attention during scheduling. The high weight of WETTZELL might be explained by the central location of the telescopes. If WETTZELL participates in a scan, many other telescopes can participate as well. The lowest weights were found for HARTRAO (0.83) and FORTLEZA (0.90). Thus, the highest station weight is about $40\%$ higher compared to the lowest one. The low weight of FORTLEZA might be a direct result of the high weight of AGGO. In case that AGGO is participating in a scan, it is very likely that FORTLEZA can also observe the same scan since it is more sensitive than AGGO and in a similar location. Thus, a high weight of AGGO is sufficient to properly incorporate FORTLEZA into the schedule. However, as already noted, interpreting individual station weights is rather difficult due to the complex interactions and probably multiple combinations of weights exist that lead to schedules of similar quality.

One very important detail in the context of optimizing geodetic scheduling is that only the best performing individual is of interest since the parameters stored in the genetic code of this individual will be used for the scheduling of the session. Thus, a full convergence of all parameters is not necessarily required. It is sufficient to produce one individual with very high fitness. However, since the mutation and crossover steps are based on randomness (e.g. for the parent selection and the amount of mutation), it is difficult to predict when and how such an individual will be generated. Since the average fitness rises from generation to generation, the likelihood of producing a very fit individual increases over time.

Figure 4 depicts the evolution of fitness as a function of the individuals, comparing the ES with a classical multi-scheduling (MS) approach with an identical computation cost.

Fig. 4

Fitness as a function of individuals. Gray up-pointing triangles depict fitness of individuals generated by the ES. Red lines delimit different generations of the ES. The dashed black line depicts the average fitness from individuals of the ES in this generation. The solid black line depicts the maximum fitness from individuals of the ES in this generation. Green down-pointing triangles depict the fitness of individuals generated by a classical MS approach

As already noted, the ES can be seen as an extension to the classical MS approach. In fact, the first 256 schedules, the initial population ($g_0$), are generated based on a classical MS approach and thus are identical to the first 256 schedules of the MS. The ES starts with generation $g_1$ where the individuals are generated as described in Sect. 2.2.

Figure 4 further confirms that the ES increases the quality of the schedules significantly. In the initial population ($g_0$) of the ES, most individuals had a fitness of 0.00. The reason for this is the scaling of the target parameters based on the best and the 75% quantile, as explained in Sect. 2.2.2. In the initial population, the mean formal errors and repeatability values of most geodetic parameters fell above the $75\%$ quantile resulting in a fitness of zero.

The average fitness of the following generations increased up to $g_7$, while, in this particular example, an individual in $g_4$ already reached a very high maximum fitness; thus, it would have been sufficient to compute fewer generations. In the last generation, the maximum fitness was decreasing again. This could happen due to the randomness of the crossover and mutation process for the generation of the new offspring. However, it is uncritical for several reasons. As explained in Sect. 2.2.2, individuals can serve as parents in all following generations. Thus, the high performing individuals of previous generations will serve as parents in the following generations as well. Thus, the maximum fitness of even more following generations is very likely to increase again. Lastly, the best schedule is selected based on the best performing individual from all generations, not only based on the individuals of the last generation. In this case, the best performing individual was found in $g_8$.

The fitness of individuals generated by the MS approach did not increase over time since every individual is randomly initialized. Most individuals of the MS approach have a fitness of zero, because they are scaled identical to the individuals of the ES for a fair comparisons. The MS approach also managed to generate individuals that reach a reasonable high fitness of almost 0.8. However, if we keep in mind that the parameter initialization of the initial generation is done randomly, one can conclude that this happens based on pure luck and is not reliably the case.

The evolution of the genetic code for a typical intensive sessions with just a three-dimensional parameter space (see Sect. 2.1.2) is visualized in Fig. 5. Figure 5 is derived by using similar hyperparameters as identified earlier. Since the parameter space has way fewer dimensions as in case of a 24-h session, the initial population size $m_0$ was set to 64, while the population size of the following generations $m_j$ was set to 32.

Fig. 5

Parameter evolution for $n=10$, $m_0=64$, $m_j=32$, $n_{best}=20\%$, $n_{rand}=5\%$, $n_{par}=2$, $\delta =0.4$, and $\delta _{min}=5\%$. The abscissa lists the individuals. Red lines delimit different generations. The fitness is color-coded

In this example, a representative intensive session (namely I20310) was selected as a test subject. It is a 1-h long session with KOKEE and WETTZELL and thus a good example of a typical IVS intensive session.

As depicted in Fig. 5, the weight factors converge towards extreme values. The duration weight factor $\omega _{\mathrm{{dur}}}$ converged towards 0.9, while the sky-coverage weight factor converged towards 0.1. This highlights that the algorithm is able to find optimal parameters even if the optima lie in extreme positions. It also conveys that genetic drifts leading to a convergence towards the average parameter value is not a problem in this case. The value for the corner switch cadence $t_c$ converged towards 1500 s. It is noisier compared to the weight factors, indicating that there exists not only one dedicated best value but a range of equally good values.

3.2 Session OHG127

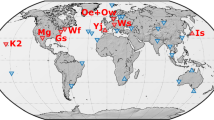
The ES is first evaluated based on an tricky-to-schedule OHG session, namely OHG127. The difficulty in scheduling the OHG sessions is related to the station network. Figure 6 depicts the station network for session OHG127.

Fig. 6

Station network for session OHG127

Many telescopes are in remote locations, mostly in the southern hemisphere, and they suffer from poor sensitivity (see Table 1).

Table 1 OHG127 telescope sensitivity. Telescopes marked with an asterisk mean that an elevation-dependent SEFD model exists and the listed values correspond to the minimum SEFD

This is especially problematic in comparison with the very low recording rate of 128 Mbps and the lack of good sources that are available on the southern hemisphere. To record a usable observation, the signal-to-noise ratio (SNR) in the observed bands should be reasonably high. When generating a schedule, typically an SNR of 20 for X-band and 15 for S-band is aimed for. The SNR is related to the station sensitivities, expressed through the system equivalent flux density (SEFD) of the two telescopes, the source flux density F, the recording rate rec, the integration time sec, and a constant efficiency factor $\eta$.

$$\begin{aligned} \mathrm{{SNR}} = \eta \frac{F}{\sqrt{\mathrm{{SEFD}}_1 \cdot \mathrm{{SEFD}}_2}} \sqrt{\mathrm{{rec}} \cdot \mathrm{{sec}}} \end{aligned}$$

(16)

Thus, when observing with telescopes of a high SEFD in combination with a low recording rate, the simple solution would be to focus on bright sources only (high F) or to increase the integration time (high sec). However, both options come with their own problems. When focussing on a small selection of bright sources, systematic effects due to source structure might affect the solution significantly. Additionally, the result is more strongly affected by possible issues in the source flux models. A further side-effect is that the sky-coverage of the telescopes decreases, leading to problems in resolving tropospheric time delays—one of the major error sources in geodetic VLBI (Schuh and Böhm 2013). On the other hand, it is also not possible to increase the integration time without bounds, for example, due to the loss in coherence of the troposphere during correlation.

In practice, it is necessary to generate a schedule with good sky-coverage and many sources despite the listed problems. Therefore, scheduling these sessions requires much fine-tuning to make sure that all stations are properly incorporated into the schedule. In OHG127, the network is composed of eight telescopes, seven of which are located on the southern hemisphere.

Figure 7 depicts the evolution of the fitness by using the same hyperparameters as listed in Sect. 3.1. To reflect the goal of the OHG session, the fitness function was defined with a weight of 1.00 for $\#\mathrm{{obs}}$ and $\frac{1}{n_{\mathrm{{sta}}}}$ for the individual station weights. The weights of the EOP were set to 0.00 since EOP estimates are not a primary goal of the OHG observing program.

Fig. 7

Fitness as a function of individuals for OHG127. Red lines delimit different generations. The dashed black line depicts the average fitness in this generation. The solid black line depicts the maximum fitness in this generation

It can be seen that the average fitness improves from generation to generation; thus, the ES manages to improve the quality of the average schedule over time. However, as already noted, in the context of scheduling, it is sufficient to find one single schedule for a particular session that performs very well. Therefore, the maximum fitness within each generation is more important than the average fitness and thus determines the success of the ES. It can be seen that, although most individuals in the first generation have only modest fitness (the average is just slightly above 0.00), some individuals managed to reach a fitness of up to 0.4. This is based on pure luck, since the parameter initialization of the initial population is done randomly. In the following generations, more and more individuals manage to reach very high fitness values. Here, the fittest individual was present in $g_6$ although the highest average fitness was achieved by generation $g_9$.

The fitness function itself is an abstract quantification for the scheduling performance. Therefore, Fig. 8 depicts the relative improvement in the precision of the geodetic parameters. For comparison reasons, the relative improvement is calculated between the schedule based on the fittest individual in the initial population (classical MS approach) and the schedule based on the fittest individual over all generations (new ES approach). It is to note, that in this comparison, the ES comes with a significantly higher computation cost since more schedules are generated. However, as we will show in the following, the higher computation cost is worth the improvement. Additionally, the higher computation cost can be counter-weighted by the fact that it is possible to run the algorithm fully automated by a cron job as discussed in Sect. 4. Finally, the ES manages to find optimal solutions faster than the MS approach that is solely based on random initialization of individuals.

Fig. 8

Ratio in percent between the precision/#obs of the best schedule generated using a classical MS approach (initial population) and the precision/#obs of best schedule generated using ES for OHG127 schedule. Improvements are highlighted in blue, while degradations are depicted in red

Table 2 Optimal parameters found by the ES for session OHG127

Fig. 9

Average and maximum fitness of all OHG sessions in 2019 and 2020. The abscissa lists the generations. Solid lines represent the average fitness of a generation, while dashed lines represent the maximum fitness of a single individual inside a generation

For this particular session, the precision of most geodetic parameters shows a better mean formal error and a better repeatability based on the Monte Carlo simulations. Additionally, the best performing schedule has $7\%$ more observations by using the ES instead of the general MS approach. For this session, on average, the improvement in terms of mean formal errors of the station coordinates is $7\%$ and for the repeatabilities is $8\%$, compared to the results from the classical MS approach. The only exception is station FORTLEZA, where a degradation of the precision can be seen. Additionally, the repeatabilities of the polar motion and nutation parameter in y-direction and the coordinate repeatability of YARRA12M got slightly worse. The degradation of some parameters can be explained by the fact that different geodetic products require different observations (e.g. east-west baselines for dUT1, north-south baselines for polar motion). In practice, it is impossible to fulfill all these requirements in one session. Furthermore, the ES did not try to optimize the polar motion and nutation precision at all since we set its weight to zero in the fitness function.

Table 2 lists the parameters of the fittest individual.

Similar as in Section (3.1), $\omega _{\mathrm{{dur}}}$ was identified as the most important weight factor with a value of 0.47. For the individual station weights, this time SYOWA got the highest weight of 1.33, followed by YARRA12M and O‘Higgins, both with a weight of 1.10. Surprisingly, Station KOKEE only received a weight of 0.64. Although this weight is very small compared to the rest of the stations, the telescope is well integrated in the resulting schedule nevertheless. There are 181 scans with 476 observations scheduled with KOKEE, while the average number of scans and observations per station is 181 and 511 respectively. This, again, highlights the difficulty in interpreting individual station weights.

3.3 OHG observing program

To further confirm the improvement, all OHG sessions of the year 2019 and 2020 were investigated. In total, these are 12 sessions (OHG117–OHG128). Figure 9 depicts the evolution of the average and maximum fitness of the OHG sessions.

From this plot, it can be seen that for all sessions, the average fitness increased considerably over the generations. More importantly, the maximum fitness increased as well. Although for some sessions, relatively high fitness was already achieved at $g_2$, the maximum fitness of other sessions increased until $g_7$. In some cases, it seems like the fitness was still rising even at the last generation; thus, it should make sense to increase the number of generations that will be computed for these sessions. Finally, Fig. 10 depicts the average parameter improvement over all 12 OHG sessions scheduled in 2019 and 2020. Since the station network changed between sessions, some parameters were estimated more often than others. The numbers above the abscissa depict how often the parameters were estimated.

Fig. 10

Average improvement of all (12) OHG sessions in 2019 and 2020. The number above the abscissa depicts how often this parameter was estimated within the 12 investigated OHG sessions. Improvements are highlighted in blue, while degradations are depicted in red

Fig. 11

Average improvement of all R1 session from October until December 2020 compared with a traditional MS approach. The number above the abscissa lists in how many sessions this parameter was estimated within the 14 investigated R1 sessions. Improvements are highlighted in blue, while degradations are depicted in red

It can be seen that, on average, all parameters benefit from the ES. This is important, because it proves that the ES will not lead to a degradation of some parameters over time. On average and weighted by the number a station did participate in a session, the improvement in the mean formal errors is $8\%$ for the station coordinates and $6\%$ for the EOPs compared to the classical MS approach (initial population). The repeatabilities got improved by $7\%$ for the station coordinates and $4\%$ for the EOPs. The maximum improvement for the station coordinates was found for SYOWA (mfe: $14\%$, rep: $10\%$). Furthermore, the number of observations rose by an average of $10\%$. These findings confirm the results presented in Sect. 3.2.

3.4 R1 observing program

The R1 and R4 observing programs are indisputably the most important 24-h sessions within the IVS. They are observed every week, typically Mondays for the R1 and Thursdays for the R4 program. Here, only the improvement in the R1 program will be discussed since both observing programs are similar in terms of network geometry and observing rate. The R1 sessions are observed using a 256 or 512 Mbps recording rate. Generally, the network is composed of globally distributed geodetic VLBI stations. Therefore, scheduling R1 sessions is simpler and does not suffer from the same problems as, for example, OHG sessions.

In the following, the R1 sessions from October 2020 until December 2020 (R1967–R1979) will be discussed. For the R1 observing program, the fitness function was defined with a weight of 0.5 for $\#\mathrm{{obs}}$, 0.1 for XPO and YPO, 0.3 for dUT1, NUTX and NUTY, and $\frac{1}{n_{\mathrm{{sta}}}}$ for the individual station weights. Thus, the fitness function covers all parameters and is therefore very general. As discussed in Sect. 3.2, it is hard to account for all the different requirements of these parameters during scheduling, leading to difficulties to receive good improvement for all geodetic parameters. Figure 11 depicts the average relative improvements of the 13 investigated R1 sessions.

Although the improvement is small, almost all parameters benefit from the ES approach. In addition, the number of observations was increased by $3\%$. In this case, the main problem is the very general definition of the fitness function combined with the different requirements of the target geodetic parameters. Thus, it is not possible for the ES to improve the solution any further. However, it can also be seen that in this case, the ES does not lead to worse solutions, in fact, the parameter precision was improved by $2\%$ with up to $8\%$ for single stations. In contrast, the maximum degradation in precision is only $0.7\%$ for the repeatability of the nutation parameter in x-direction.

3.5 T2 observing program

To conclude the investigations of 24-h sessions, the T2 observing program was studied. Within the IVS observing programs, the T2 program plays a special role since they make use of the biggest station networks with up to 20+ stations. Additionally, telescopes participate that usually do not observe many geodetic VLBI sessions. Similar to OHG sessions, in T2 sessions many low-sensitive stations are present, which is especially critical since the recording rate is only 128 Mbps. Thus, the T2 sessions are especially tricky to schedule. Still, the T2 observing program has a well-defined scientific goal. They aim to provide highly accurate station coordinates. To reflect this goal, the fitness function was defined with a weight of 0.5 for $\#\mathrm{{obs}}$ and $\frac{1}{n}$ for the individual station weights and zero for the EOP.

Figure 12 depicts the average relative improvements of all T2 sessions scheduled in 2019 and 2020. In total, these are 14 sessions (T2130–T2143).

Fig. 12

Average improvement of all T2 sessions in 2019 and 2020 compared with a traditional MS approach. The number above the abscissa depicts how often this parameter was estimated within the 14 investigated T2 sessions. Improvements are highlighted in blue, while degradations are depicted in red

It can be seen that most parameters benefit by the ES. The highest improvement was achieved for the station coordinates of KOKEE (mfe: $9\%$, rep: $21\%$). However, this has to be interpreted with caution, since KOKEE did only participate in one session. The biggest reliable improvement was achieved for station O’Higgins Sowie (mfe: $11\%$, rep: $9\%$). Although the improvement is relatively small for many parameters, most of them benefit by the ES approach. On average and weighted by the number a station did participate in a session, the improvement is $2\%$ for the station coordinates and also $2\%$ for the EOPs. In addition, the accuracy of only a few parameters degenerates compared to a traditional MS approach.

3.6 Intensive sessions

For an intensive session, the need of a ES for parameter optimization is smaller since the parameter space has fewer dimensions and the generation and simulation of millions of intensive sessions is relatively inexpensive in terms of computation resources. Therefore, it should be noted that it is possible to scan the parameter space with thousands of random individuals in few seconds using a classical MS approach as well.

However, given the same setup as described in Fig. 5, compared with a fitness function that is only determined by $\#\mathrm{{obs}}$ and the repeatability of dUT1 with equal weights, the repeatability of dUT1 is reduced from 14.35 to ${13.45}{\mu \mathrm{{as}}}$, while the mean formal error of this schedule was reduced from 9.63 to ${9.02}{\mu \mathrm{{as}}}$. However, as already noted, in practice, the same could have been achieved by simply generating thousand schedules without ES and picking the best from there.

Although the benefit of the ES is not that significant for intensive sessions and similar results could be achieved by a classical MS approach, it also does not lessen the result. In fact, the result is at least as good as by using the classical approach, and it converges faster to an optimum and works well for intensives with more than two telescopes.

Fig. 13

Individual station weights $\omega _{sta} \ne 1.00$ selected by schedulers for R1 and R4 sessions in 2019

4 Automation

Arguably, one of the main benefits of the ES is that the algorithm works well for all types of schedules without human interaction. It only needs information about which hyperparameters to use, which parameters should be optimized and what the goal of the session is to properly define a fitness function. The hyperparameters can be defined a priori. In practice, the values provided within this work (see Sect. 3.1) have been proven to work well in all cases and no additional hyperparameter tuning per session is necessary. The goal of the session and thus the fitness function can also be defined a priori for every observing program. Thus, this approach makes it possible to fully automate geodetic VLBI scheduling.

In the past, geodetic VLBI scheduling has been a time-consuming and iterative process. Every schedule was individually generated by hand. In case the responsible person decided that a telescope was not properly included in the schedule, its weight was increased by some amount. In reality, the sessions within one observation program were mostly generated using the exact same scheduling parameters, no matter how the telescope networks looked like or if there were changes in the observing mode. In case a station was clearly not properly included in the session, its weight was increased. For practical reasons, the individual station weights were often set to integer values, as can be seen in Fig. 13. Here, the individual station weights of all R1 and R4 sessions in 2019 that are available at the IVS BKG data server¹ are visualized.

A station weight of 1.0 is not visualized because this is the case for the majority of stations. In more than half of the remaining cases, a weight of 2.0 was chosen. For the rest, the weight was set to either 3.0 or 4.0. Although increasing the station weight is a good approach to properly include difficult telescopes into the schedule, using integer values only for the station weights is a very crude approach and is also likely human-biased. In contrast, the ES works fully automatically and is able to fine-tune the weighting a lot better, is not human-biased and is fully transparent since it selects the station weights based on large-scale Monte Carlo simulations and a properly defined session goal.

It is to note that the proposed ES rarely uses a weight $>1.5$, while in the R1 and R4 sessions, the manually selected weights are two, three and four. However, the ES changes the weights of all stations and often reduces the weight to be $<1.0$ to produce a higher relative change in the individual station weights. Additionally, the R1 and R4 sessions are scheduled by using a different software package (sked) that implements different scheduling approaches and algorithms. Thus, it might not be applicable to compare sked-station weights directly with VieSched++-station weights.

Since June 2020, VieSched++ runs as a daily “cron job” on a server at BKG in Wettzell.² Here, for 24-h sessions, the four weight factors listed in Sect. 2.1.1, the individual station weights and the number of observations are determined by the ES for most observing programs. Additionally, for every observing program, a distinct set of geodetic parameters and their corresponding weights are defined as the target parameters, to reflect the goal of the observing program.

For the intensive sessions, the three parameters listed in (Sect. 2.1.2) are explored by the ES and the fitness function is only based on dUT1 and the number of observations.

After an initial test phase, the resulting schedules have been proven to be of high quality. Currently, the schedules for the IVS observing programs INT2, INT3, INT9, AUA, OHG, T2 and VGOS-B as well as other non-IVS observing programs such as the southern hemisphere intensive sessions and intensive sessions between Wettzell, AGGO and partly O’Higgins, are automatically generated and sent to the station operators. Additionally, schedules for other IVS observing programs, such as INT1, R1, R4 and VGOS sessions, are generated for test purposes only without submitting them to the IVS schedule distribution server.

5 Conclusion

In this work, we present a new approach to individually optimize geodetic VLBI schedules using a general approach that can be fully automated. It is based on the concept of an evolutionary strategy (ES), meaning that the algorithm mimics evolutionary processes based on selection, crossover and mutation to iteratively find optimal scheduling parameters for any given session, based on a well-defined geodetic goal. Due to the high quality of the resulting schedule, this approach is currently used for the scheduling of various IVS observing programs. Besides discussing the ES in detail and providing good hyperparameters, we highlighted the benefits of the ES algorithm over a classical multi-scheduling (MS) approach. This was evaluated based on the OHG, R1 and T2 observing program. For intensive sessions, the benefit is less significant since a classical MS approach can also sample the parameter space sufficiently. For the 24-h sessions, improvements can be seen throughout most parameters. The biggest improvement was seen for the OHG sessions, which are very difficult to schedule. Here, the ES yields on average 10% more observations and an average improvement in station coordinate mean formal errors and repeatabilities of 7% and 8%, respectively, with up to 14% for individual stations. For the T2 observing program, individual stations such as O’Higgins experienced an average improvement of 11% for the mean formal errors and 9% based on the repeatabilities of the coordinate precision. For the R1 observing program, the improvement is on average smaller but still up to 8% for individual stations. Additionally, the number of observations could be increased by an average of 3%. However, this improvement is paid by an increased computation cost. Within this work, we showed that this increased computation cost is worth the effort. Moreover, the additional computation cost can be compensated by the fact that the whole algorithm can run fully automated, as it is demonstrated by the IVS DACH observations center. Thus, it saves significant workload and reduces the human-bias in generating schedules.

It is to note that this work is solely based on simulations. In reality, other factors, such as inaccurate source structure models, source flux density values, and nominal station system equivalent flux densities (SEFDs) used in scheduling might lead to a significant mismatch between the simulated and real precision of geodetic parameters.

Within this work, we investigated an optimization of scheduling based on weight factors and individual station weights. Experiments with different types of parameters, such as the parameters defining the interaction between observations for the sky-coverage saturation, source weights, or parameters defining minimum/maximum slew distances/times per station could be investigated in future. Furthermore, the quality of the source coordinate precision could be incorporated in the fitness function as well.

The complete automation of VLBI scheduling opens up the possibility to automate related operational tasks as well. For example, it would be possible to generate a plan for the source selection over all geodetic VLBI observations or to automate scheduling quality control. A plan for the source selection would be very beneficial to counteract the current trend in VLBI observations, where most scans are observing a very limited amount of sources. It would also be beneficial for imaging purposes and for astrometry. However, this is left as a subject for a different study.