Quantifying errors in GNSS antenna calibrations

Abstract

We evaluated the performance of GNSS absolute antenna calibrations and its impact on accurate positioning with a new assessment method that combines inter-antenna differentials and laser tracker measurements. We thus separated the calibration method contributions from those attainable by various geometric constraints and produced corrections for the calibrations. We investigated antennas calibrated by two IGS-approved institutions and in the worst case found the calibration’s contribution to the vertical component being in excess of 1 cm on the ionosphere-free frequency combination L3. In relation to nearby objects, we gauge the $1\sigma$ accuracies of our method to determine the antenna phase centers within $\pm \,0.38$ mm on L1 and within $\pm \,0.62$ mm on L3, the latter applicable to global frame determinations where atmospheric influence cannot be neglected. In addition to antenna calibration corrections, the results can be used with an equivalent tracker combination to determine the phase centers of as-installed individual receiver antennas at system critical sites to the same level without compromising the permanent installations.

1 Introduction

In a geodetic system where VLBI provides connection to the celestial reference frame and SLR to the center of the terrestrial frame, GNSS ground stations play a key role in the implementation on the observational level (Plag and Pearlman 2009; United Nations 2015; Altamimi et al. 2016). The space geodesy focus lies in the location of the antenna, and particularly its phase center, i.e., the mathematically best fitted non-physical point that relates the incoming electromagnetic signals’ time of arrival to the tangible structure. In other fields of interest, the calibration tables and diagrams used to characterize antennas are dedicated to establish gain characteristics in different directions (e.g., ARRL 2015). As far as we know, the location objective is unique to geodesy which might explain why GNSS antenna calibration is still a field in continual development (Tranquilla and Colpitts 1989; Wübbena et al. 1996; Schupler and Clark 2001; Akrour et al. 2005; Bányai 2005; Wübbena et al. 2006; Aerts and Moore 2013; Baire et al. 2014; IGS AWG 2017).

From early observations with uncalibrated GPS antennas at the still operative CIGNET stations (Schenewerk 1991) via relative methods (Mader 1999) to the current asserted absolute calibrations (AC) of antennas in the IGS network, the observational vertical error has decreased from 10 cm to an order claimed less than 1 cm (Schmid at al 2005). To reduce the vertical error by another order of magnitude and meet climate change monitoring requirements on the geodetic system of 1 mm accuracy (Plag and Pearlman 2009; NRC 2010), reliable determinations of the antenna phase center offsets (PCO) and variations (PCV) combined as phase center corrections (PCC) with respect to the tangible structure are instrumental. These PCCs are currently rather weakly constrained by independent methods, and the lack of on-site phase center model tests in particular is a primary source of systematic errors and biases in GNSS processing (Dilssner et al. 2008; Gross and Herring 2017; Johansson et al. 2019). The IGS currently approves AC tables generated with two different principles—robotic vis-à-vis anechoic chamber, compared in (Görres et al. 2006)—from four service providers (IGS AWG 2017), but the methods have been shown to produce different results at an order of 2 mm in the horizontal and 5 mm in the vertical components (Baire et al. 2014). This difference obviously does not match the reference frame requirements and IGS lacks established procedures to prove equivalence between the calibrations (cf. CIPM 2003). To conform the terminology, JCGM (2012) defined calibration as an

where also the included terms are explicitly defined. Adhering to this, it is clear that the conditions are an essential part of the operation, and also that the provided uncertainties should be made with respect to measurement standards and not only as a distribution around an arbitrarily estimated mean. Referring to the condition aspect, it is implicit that the validity of the calibration deteriorates the more the calibration differs from the conditions of use to a level where the calibration results eventually become irrelevant, and also that this deterioration is accelerated if the measurement uncertainties aren’t well understood in all parts of the operation.

Fig. 1

Differences between the $M_1$ and $M_2$ AC tables for the broadcast frequencies L1 and L2 for three duplicate antenna pairs displayed as polar plots. #1–#4 are choke ring antennas, #5–#6 are rover antennas, $\varDelta ^\otimes \! C_{\mathrm {L}1}^{M12}$ in the top row and $\varDelta ^\otimes \! C_{\mathrm {L}2}^{M12}$ below

Applied to a GNSS realm, an important condition is the antenna phase patterns, which result from interactions with the surrounding electromagnetic near field, i.e., the reactive and radiative/Fresnel regions where the distance (r) from the phase center expressed in observation wavelengths ($\lambda$) typically is $r<\lambda$. A good practice is therefore to keep even mildly disturbing objects in the far field, i.e., $r\gg 2\lambda$. To achieve and provide a geodetic reference frame which is accurate to 1 mm and not only precise, the calibration method characteristics of the L1 and L2 frequencies need to be explored and understood in detail. According to a rule of thumb, individual uncorrelated errors should be less than one third of this value, i.e., $\le 0.3$ mm, which is a looser constraint than the 0.1 mm requirement on local ties set out in Plag and Pearlman (2009). The calibration method’s influence on the AC tables was acknowledged in Wübbena et al. (2006), but the electromagnetic interaction between the antennas and the near-field surroundings, as well as the transfer function from calibration to deployment, remains to be quantified.

As the discrepancy between different calibration methods exceeds metrologically traceable measurement method uncertainties (JCGM 2008) between physically manifested antenna reference points (ARP) by at least two orders of magnitude and antennas are deployed in totally different environments to where they were calibrated, the AC tables need to be used with precaution for the most demanding applications. It is therefore of great importance to develop an on-site traceable antenna calibration method that can be utilized for system critical reference antennas when they are installed in their final position (Baire et al. 2014; Gross and Herring 2017).

In this paper, we present an assessment that utilizes a combination of inter-antenna differentials and high-precision geometric measurements to determine the unbiased phase center offset from the geometric ARP. To achieve this objective, we examine the AC tables for antennas calibrated by two IGS-approved service providers and examine the differences between their results. We then show how geometric constraints and the similarity between duplicate antennas, i.e., of same design and similar characteristics, can be combined to quantify the error function ($\varepsilon$) of the AC tables with independent means. In the subsequent step, we connect the vector between the electromagnetic phase centers to the physical structure of the antennas using laser tracker measurements and thus quantify the AC table error functions in two parallel investigations of the service providers’ results. Having characterized the AC table errors, we determine the extent to which these alias as tropospheric delay and antenna height/reference frame scale errors in the geodetic analysis. Finally, we validate the assessment by reprocessing the data with the obtained correction factors.

Fig. 2

Mean and standard deviation of the $\varDelta ^\otimes \!C_{\mathrm {L}1}^{M12}$ differences for L1 in the AC tables. Antennas #1–#6 are grouped from left to right in the $5^{\circ }$ elevation lanes. The differences between the methods’ results are close to 0 mm for #1, #2 and #3 and are elevation dependent with high internal correlation between #5 and #6

Fig. 3

Mean and standard deviation of the $\varDelta ^\otimes \! C_{\mathrm {L}2}^{M12}$ differences between $M_1$ and $M_2$ for L2 AC tables, #1–#6 grouped from left to right in the elevation lanes. The general correlation features correspond to those in Fig. 2 but with loss of method equality for #1–#4 at L2

Fig. 4

Variations in #1’s AC tables for the two methods $M_1$ (black) and $M_2$ (red); L1 at the top, L2 at the bottom. The AC table values are presented as 72 individual lines that connect the elevation values in each azimuth. The left column displays the AC table values and the right column the variation around the mean for all $5^{\circ }\times 5^{\circ }$ cells

2 Examination of AC table differences

In two separate projects (SIB60 2017; Johansson et al. 2019), we have had six antenna samples in three pairs of duplicates individually calibrated with both robotic and anechoic chamber methods by two different service providers who applied one method each on their premises. From the service providers, we were supplied with ARP-referenced calibration table values ($^\otimes \!C$) in azimuth ($\alpha$) and elevation ($\epsilon$) but found these to be different to a level that raises doubt of their validity. Although neither of the providers is accredited, we expected to get the AC table measurement uncertainties in accordance with ISO/IEC 17025 (ISO 2017 and earlier eds.) but to no avail.

Recognizing that systematic errors result from a combination of the procedures and the hardware applied by each service provider, it is impossible to make an a posteriori separation between these two categories from the AC tables. ’Service provider’ and ’method’ could therefore be used interchangeably in our investigation, but as the assessment outlined in Sect. 3 is general and does not provide any information on robotic or chamber calibrations per se, we decouple the providers and the robotic chamber principles from the investigation and relate to them generically as ’methods’ ($M_i$).

In Fig. 1, we display the differences $\varDelta ^\otimes \!C_{\mathrm {L}j}^{M12}(\alpha , \epsilon )=^\otimes \!C_{\mathrm {L}j}^{M2}(\alpha , \epsilon )-~^\otimes \!C_{\mathrm {L}j}^{M1}(\alpha , \epsilon )$ between $M_1$ and $M_2$ at frequency (L) for the duplicate antenna pairs #1–2, #3–4 and #5–6 to illustrate the differences between the AC tables; antennas #1–4 are classic reference station choke ring antennas JNSCR_C146-22-1, #5–6 are surveying/rover antennas LEIAS10 (NGS 2017).

To facilitate a quantitative evaluation of the method differences, we present the elevation dependence of $\varDelta ^\otimes \!C_{\lambda }^{M12}(\alpha , \epsilon )$ in Figs. 2 and 3. In Fig. 2, we notice that the difference between the methods at L1 is close to zero and almost identical for the choke ring antennas (particularly for #1, #2 and #3) and that the difference between the methods is elevation dependent for the rover antennas. In Fig. 3, we observe that the difference between the methods at L2 differs from zero with internally repeatable patterns for similar antennas, indicating larger differences between the methods at L2, and an elevation dependence for both antenna types. From this, we conclude that the differences between the methods in our AC tables are reproducible and to a high degree dependent of elevation, frequency, and antenna design. We identify the similarity between antennas as a key component in the assessment method presented in this study and focus on the #1 and #2 duplicates, using #1 as the individual showcase.

To this end, we present the $5^{\circ }\times 5^{\circ }$ AC table contents for #1 in Fig. 4, with the delivered values ($~\!^\otimes \!C_{\mathrm {L}j}^{Mi}$) and the distributions ($~\!^\otimes \!s_{\mathrm {L}j}^{Mi}$) the latter here extracted and centered around the individually computed mean $~\!^\otimes \!{\bar{C}}^{Mi}_{\mathrm {L}j}(\epsilon )$ at each elevation. The offset between the two methods at the same frequency—particularly visible between $^\otimes \!C_{\mathrm {L1}}^{M1}$ and $^\otimes \!C_{\mathrm {L1}}^{M2}$ in the top left panel—depends on different definitions of the PCCs, which are handled later in the processing and therefore have no actual impact on the results; the calibration values (C) used from here on are adjusted to zero offset in the zenith.

Fig. 5

AC table differences between $M_1$ and $M_2$ for antenna #1, individual lines connect the elevation values with the same azimuths. $\varDelta C_{\mathrm {L}1}^{M12}$ (red) are generally within 1 mm agreement, whereas $\varDelta C_{\mathrm {L2}}^{M12}$ (green) approach 5 mm

The adjusted differences $\varDelta C_{\mathrm {L}j}^{M12} = C_{\mathrm {L}j}^{M2}- C_{\mathrm {L}j}^{M1}$ are shown in Fig. 5. Considering that

$$\begin{aligned} |\varDelta C_{\mathrm {L1}}^{M12}|\ge & {} 0.3~\mathrm {mm} \quad ,\quad \epsilon< 65^{\circ }; \mathrm {and}\\ |\varDelta C_{\mathrm {L2}}^{M12}|\ge & {} 0.3~\mathrm {mm} \quad ,\quad \epsilon < 80^{\circ }; \qquad \end{aligned}$$

neither $\varDelta C_{\mathrm {L1}}^{M12}$ nor $\varDelta C_{\mathrm {L2}}^{M12}$ satisfies the rule of thumb objective to be less than one third of the targeted 1 mm between the methods for any practical purposes. Nevertheless,

$$\begin{aligned} |\varDelta C_{\mathrm {L1}}^{M12}|\le 1~\mathrm {mm}\qquad ~, \quad \epsilon\ge & {} 15^{\circ }; \mathrm {and}\\ |\varDelta C_{\mathrm {L2}}^{M12}|< 4.5~\mathrm {mm}\quad , \quad \epsilon\ge & {} 25^{\circ }; \qquad \end{aligned}$$

indicate better agreement on L1 than on L2, and from comparing the tables it appears as if the L1 results fulfill the 3 mm requirement set out by Ray and Altamimi (2005).

We note that it is impossible to draw any conclusions on the accuracy of either method from this AC table examination as the differences only relate the methods to each other. Furthermore, with both service providers making tacit claims of zero uncertainty, an attempt to retrieve a realistic estimate of the true value is futile. However, thriving on the similarities between selected antenna samples, we outline a differential analysis to examine the calibration methods’ contribution to the errors in position estimates.

Fig. 6

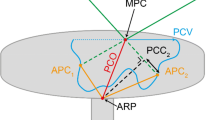
Illustration of the assessment that separates the calibration error function $\varepsilon$ from the true antenna pattern $T_a$. Top: Duplicate antennas oriented at different inclinations $\varPsi _i$ are positioned with geometrical constraints $\varDelta x$, $\varDelta y$, $\varDelta z$ between the ARPs. Satellite signals (parallel red arrows) are received at the antenna phase centers in the antenna-oriented elevation $\epsilon _i$ with the resulting phase wind-up $\tilde{\varPhi _i}$ and a small time shift $\varDelta t {\dot{\rho }}$ (intentionally omitted in the diagram). Middle: The observations are used to create an elevation-dependent error map with respect to the true pattern $T_a$, which is displayed as a baseline but in itself has variations that are not discernible in this diagram. Every observation adds information to the error map at the positions where the signals are received in the two separate antenna oriented frames. The polar plot relates only to angles with respect to the phase center point, not the antenna dimensions. Bottom: The errors with respect to $T_a$ are added at two positions in the elevation error-oriented projection

3 Isolating calibration method errors using external constraints

Between two antennas separated sufficiently to be in each others receiving far field, say $r>20 \lambda$, the observed phase difference ($\varDelta \varPhi _{raw}$) to any particular satellite can be expressed

$$\begin{aligned} \varDelta \varPhi _{raw}=\varDelta ^{Atm}+G+T_2-T_1+\tau +N\lambda +\nu \end{aligned}$$

(1)

with the sum of the neutral and dispersive atmospheric differences ($\varDelta ^{Atm}$), the geometric conditions of the setup (G), the individual true antenna patterns ($T_a$), the intrinsic clock and hardware errors ($\tau$), a phase integer (N), and the noise components of the observations ($\nu$).

Whereas atmospheric differences at short distances can be approximated by a deterministic function of the height difference ($\varDelta H$) and the elevation angle, i.e., $\varDelta ^{Atm}(\varDelta H, \epsilon )$, G is characterized by the projections on the baseline in the direction of the propagating wave, the phase wind-up (${\tilde{\varPhi }}_a$) resulting from different orientations ($\varPsi _a$) with respect to the vertical and satellite direction, the satellite trajectory induced Doppler correction ($\varDelta t{\dot{\rho }}$) and the atmospheric difference, and may be expressed

$$\begin{aligned} G = f( \varDelta x,\varDelta y,\varDelta z,{\tilde{\varPhi }}_{1}(\varPsi _1),{\tilde{\varPhi }}_{2}(\varPsi _2),\varDelta t{\dot{\rho }},\varDelta ^{Atm}(\varDelta H, \epsilon )) \end{aligned}$$

(2)

Identifying the terms of G that can be determined independently of the phase solution ($G_\bot$) reduces the uncertainties involved in determining $\varDelta \varPhi _{raw}$ and consequentially also $\varDelta T$. The purely geometric components in G, i.e., $\varDelta x, \varDelta y, \varDelta z, \varPsi _i$ and $\varDelta ^{Atm}$, can be determined accurately with, e.g., a laser tracker and an inclination sensor, whereas $G_\bot ({\tilde{\varPhi }}_i)$ and $G_\bot (\varDelta t {\dot{\rho }})$ can be gauged accurately from code measurements and orbital data (Wu et al. 1993). In this work, we have represented the antenna orientations $\varPsi _i$ as a set of Euler angles.

For any method M, the calibration values $C_{aM}(\alpha ,\epsilon )$ in the antenna-oriented reference frame are associated with method errors ($\varepsilon _{aM}(\alpha , \epsilon )$) with respect to the true value $T_a(\alpha ,\epsilon )$

$$\begin{aligned} \varepsilon _{aM}(\alpha ,\epsilon )=C_{aM}(\alpha ,\epsilon )- T_a(\alpha ,\epsilon ) \end{aligned}$$

(3)

Utilizing that the phase patterns of duplicate antennas are both largely azimuth independent and near identical between selected individuals, we generalize an elevation-dependent method error ($\varepsilon _M(\epsilon )$)

$$\begin{aligned} \varepsilon _{aM}(\alpha ,\epsilon )\approx \varepsilon _{aM}(\epsilon )\approx \varepsilon _{M}(\epsilon ) \end{aligned}$$

(4)

By deliberately orienting the antennas differently with respect to the satellites, we can force the received signals into different apparent elevation angles in the individual frames, as illustrated in the top part of Fig. 6. Applying the externally determined $G_{\bot }$ from which the N integers are determined unambiguously, we use Eq. 4 and substitute Eqs. 3 into Eq. 1 to express the difference between the calibrated phase observations ($\varDelta \varPhi _C$)

$$\begin{aligned} \varDelta \varPhi _C= & {} \varDelta \varPhi _{raw}-(C_{2M}(\alpha _2,\epsilon _2) - (C_{1M}(\alpha _1,\epsilon _1) +G_{\bot }+N) \nonumber \\ \end{aligned}$$

(5)

$$\begin{aligned}= & {} \varepsilon _{M}(\epsilon _2)-\varepsilon _{M}(\epsilon _1)+\tau +\nu \end{aligned}$$

(6)

This difference can therefore also be expressed as the difference between the calibration method’s error at different elevation angles as observed by two duplicate antenna samples, plus clock/hardware and noise.

As the AC tables provide $C_{aM}$ at discrete grid points in azimuth and elevation, the side lobes of $\varepsilon _M (\epsilon )$ are distributed to preset equiangular elevation cells $(E_j,E_{j+1})$ through an ordinary moment equation with the fraction (f) so that

$$\begin{aligned} \varepsilon _M(\epsilon )=f\varepsilon _{Ej}+(1-f)\varepsilon _{Ej+1} \,. \end{aligned}$$

(7)

With a $5 ^{\circ }$ cell separation, the method error for a satellite observed at $\epsilon _1=41 ^{\circ }$ and $\epsilon _2=28 ^{\circ }$ is then distributed with 0.8 weight in $E_{40 ^{\circ }}$ and 0.2 weight in the $E_{45 ^{\circ }}$ due to antenna 1, and with 0.4 weight in $E_{25 ^{\circ }}$ and 0.6 weight in $E_{30 ^{\circ }}$ due to antenna 2. From the table cells {0$^{\circ }$, 5$^{\circ }$, $\ldots$, 90$^{\circ }$} we construct a sparse elevation design matrix (${\mathbf {H}}_{\epsilon ti}$) for the $n_i$ commonly observed satellites at epoch $t_i$. The matrix has two, three, or four nonzero elements on each row, depending on whether the apparent elevation angles at the two antennas for a satellite are located in the same cell, adjacent cells, or isolated cells. Labeling the combination of antennas and satellites in Eq. 7 with ($f_a^S$) yields a structure of the matrix as follows:

(8)

Operating on the antenna differentials, we lock observations to the zenith observation cell, i.e., $\varepsilon _{90^{\circ }}=0$. This corresponds to removing the rightmost column of ${\mathbf {H}}_{\epsilon i}$, yielding an $[n_{i}\times 18]$ matrix to produce an error table for elevations at every $5 ^{\circ }$ over $0-85 ^{\circ }$.

Table 1 Laser tracker inclinometer constraints on Euler angle orientations (Tait–Bryan)

The clock and hardware errors $\tau$ are identical for all observations in an epoch, but differ between epochs. We construct a corresponding set of $[n_{i}\times 1]$ clock phase design matrices (${\mathbf {H}}_{\tau i}$) for $i=1$, ..., m

$$\begin{aligned} {\mathbf {H}}_{\tau i}= \begin{pmatrix} 1&\cdots&1 \end{pmatrix} ^\top \end{aligned}$$

(9)

and concatenate the ${\mathbf {H}}_{\epsilon i}$ and ${\mathbf {H}}_{\tau i}$ blocks to complete the design matrices

$$\begin{aligned} {\mathbf {H}}_{\epsilon }= \begin{pmatrix} {\mathbf {H}}_{\epsilon 1} \\ {\mathbf {H}}_{\epsilon 2} \\ \vdots \\ {\mathbf {H}}_{\epsilon m} \\ \end{pmatrix} \qquad \mathrm {and} \qquad {\mathbf {H}}_{\tau } = \begin{pmatrix} {\mathbf {H}}_{\tau 1} &{} 0 &{} \cdots &{} 0 \\ 0 &{} {\mathbf {H}}_{\tau 2} &{} &{}0 \\ \vdots &{} &{} \ddots &{}\vdots \\ 0 &{} 0&{} \cdots &{}{\mathbf {H}}_{\tau m} \\ \end{pmatrix}.\nonumber \\ \end{aligned}$$

(10)

It is then possible to solve

$$\begin{aligned} \varDelta {\varvec{\varPhi }} = \begin{bmatrix} {\mathbf {H}}_{\epsilon } \quad {\mathbf {H}}_{\tau } \end{bmatrix} \cdot \begin{bmatrix} {\mathbf {X}} \end{bmatrix} \end{aligned}$$

(11)

for the regression vector ${\mathbf {X}}$ of $\varepsilon _{j}$ and $\tau _{i}$

$$\begin{aligned} {\mathbf {X}} = \begin{pmatrix} \varepsilon _{0^{\circ }}&\cdots&\varepsilon _{85^{\circ }}&\tau _{1}&\cdots&\tau _{m} \end{pmatrix} ^\top \end{aligned}$$

(12)

in a least squares sense, where an elevation-dependent function of the noise standard deviation ($\sigma _\nu$) can be derived from the post-fit residuals. Weighing data by $1/\sigma ^2_\nu (\epsilon )$ yield a weight matrix (${\mathbf {W}}$) which is diagonal provided that the noise terms are uncorrelated. We solve these separately for various combinations of methods M and frequencies $\lambda$, including the individual weight matrices and write

$$\begin{aligned} \widehat{{\mathbf {X}}}_{M,\lambda } = \begin{pmatrix} {\mathbf {H}} ^\top {{W}}\!_{M,\lambda } {{\mathbf {H}}} \end{pmatrix} ^{-1}{\mathbf {H}} ^\top {W}\!_{M,\lambda } \varDelta {\varvec{\varPhi }}_{M,\lambda } \end{aligned}$$

(13)

where ${\mathbf {H}}=\begin{bmatrix} {\mathbf {H}}_{\epsilon } \quad {\mathbf {H}}_{\tau } \end{bmatrix}$. The weighted least squares solutions also provide the noise-related uncertainties ($u_{M,\lambda \nu }$) of the estimates as the square root of the main diagonal of the error covariance ($\mathrm {Cov}_{M,\lambda }$) where

$$\begin{aligned} \mathrm {Cov}_{M,\lambda }= \begin{pmatrix}{\mathbf {H}} ^\top \mathbf {W\!}_{M,\lambda } {\mathbf {H}} \end{pmatrix} ^{-1}. \end{aligned}$$

(14)

4 Antenna setup and externally measured constraints

The duplicate antennas #1 and #2 were mounted on surveying tribrachs on wooden tripods to reduce the amount of perturbing material in the electromagnetic near field. The antennas were then tilted with the tripod heads and aligned preliminary with a magnetic compass, declination 3.4$^{\circ }$ E imposing only minor influence. The geometric parameters $G_{\bot }$ to constitute the constraints for the analysis were measured with a combination of a laser tracker and an inclinometer (Leica Geosystems 2003, 2005) to provide accurate measurements and relations to the local plumb line.

The measurements were then used to relate the individual antenna-fixed (E, N, U) orientations to the local frame using Tait–Bryan Euler angles (Table 1) and the tracker measurements to determine the baseline vector between the ARPs (Table 2). As a mean of aiding the determination of the baseline vector, a subset of the GNSS observation data were processed several times with small changes in the azimuth angle of the vector. The standard deviations of the residuals were calculated, and from the minima displayed in Fig. 7 the azimuth of the baseline vector was found to be $90.297^{\circ }$. The azimuth angles of all minima in Fig. 7 deviate from this value on a $0.005^{\circ }$ level, corresponding to the 0.63 mm North component uncertainty on the baseline displayed in Table 2.

Table 2 Laser tracker constraints on the baseline between ARPs, including rotation

Fig. 7

Baseline orientation angle iterations from GNSS L1 and L2 data for the two methods. Zero offset corresponds to the chosen value for the vector azimuth: $90.297^{\circ }$

Fig. 8

Uncertainties $u_{G\bot }$ of the calibration error estimates $\varepsilon$ due to uncertainties in the east, north and up directions individually, and in combination with the Euler angles. The Euler angle effects are barely discernible at this resolution, but are included in the “All” containers where the uncertainties are added in quadrature

5 GNSS observations and calibration table corrections

We performed GNSS observations for one week and a posteriori chose a two-minute sample interval to ascertain uncorrelated noise in the satellite observations. With the geometric constraints known to the accuracy of Tabs. 1, 2 and Fig. 7, we used the individual AC tables introduced in Sect. 2 to determine the differences between GNSS processing and the geometrically determined phase centers, utilizing the method described in Sect. 3. While signals are broadcast at the L1 and L2 frequencies, the ionosphere-free L3 is a synthetic frequency combination of L1 and L2 and cannot be calibrated in itself. Nevertheless; L3 is essential for long baselines and orbit determinations, and the errors that propagate into these solutions are equally important to monitor, and the effects on L3 are treated with the same pertinence as the broadcast frequencies.

In a set of simulations, we varied the geometrical parameters in the processing to assess the sensitivity of the AC table error estimates to the uncertainties in these parameters. To this end, we used the uncertainties of Tabs. 1 and 2 to assess the $\varepsilon$ uncertainties in the east, north and up directions, as well as to the Euler angles. The results are presented in Fig. 8, where all components are added in quadrature, forming a total uncertainty due to the geometry ($u_{G\bot }$). The domination of the East component in the uncertainty is a consequence of the main tilt directions of the antennas, one to the east and the other to the west.

We also show the GNSS observation uncertainties ($u_{M,\lambda \nu }$) in Fig. 9, extracted from the square root of Eq. 14, for a more detailed picture of the method uncertainties at different elevations and frequencies. The higher noise level of L3 compared to those of the broadcast frequencies is a direct consequence of the quadratic adding of the contributing components. In practice, $u_{M1,\lambda \nu }$ and $u_{M2,\lambda \nu }$ turn out identical at the 0.01 mm level, and we therefore present them interchangeably here as $u_{\lambda \nu }$ without loss of information.

Fig. 9

Uncertainties $u_{\lambda \nu }$ of the calibration error estimates for $M_1$ and $M_2$ at L1 (red), L2 (green), and L3 (blue). $u_{M1,\lambda \nu }$ and $u_{M2,\lambda \nu }$ are identical at the 0.01 mm level and are therefore presented here as $u_{\lambda \nu }$

Fig. 10

Uncertainties $u_C$ of the method error estimates due to the stochastic variations in individual calibration results at L1 (red), L2 (green), and L3 (blue). The scatter in the calibration difference results for antennas #1, 2 and 3 (e.g., visible as a spread of the results in Figs. 2 and  3 for these antennas) was used to derive values for these uncertainties. Lacking information of the originating uncertainties in $M_1$ and $M_2$, we presume that the two methods contribute equally to the scatter and consider $u_{CM1,\lambda }$ and $u_{CM2,\lambda }$ identical

We aim to estimate the systematic method errors in the $M_1$ and $M_2$ calibration of the choke ring antennas #1 and #2. Their respective AC tables contain a calibration scatter, which needs to be quantified in order to derive relevant uncertainty measures for the method errors. We use the AC table differences for antennas #1, #2, and #3 to derive the typical calibration scatter ($u_C$) and presume that both service providers contribute equally to this uncertainty. The scatter is presented in Fig. 10, where we used the data from #1–3 in the analysis, but excluded #4 as the AC table differences for this antenna deviate significantly from the other antennas and we cannot be certain of the origin of this deviation.

Fig. 11

Errors of the assessed calibration method $M_1$ compared to traceable measurements. Results are from one week’s error mapping at L1 (red), L2 (green), and L3 (blue). The underlying observations are the same as in Fig. 12

Fig. 12

Errors of the assessed calibration method $M_2$ compared to traceable measurements. Results are from one week’s error mapping at L1 (red), L2 (green), and L3 (blue). The underlying observations are the same as in Fig. 11

With access to the uncertainties of the geometric constraints, the GNSS observations and the calibration scatter, we use the sum of variances to get a more complete view of the total uncertainties ( $u_{\lambda }$) in the combination

$$\begin{aligned} u_{\lambda }= \root \of {u_{G\bot }^{2}+u_{\lambda \nu }^{2}+2u_{C}^2} \end{aligned}$$

(15)

where $u_{C}^2$ appears twice to account for the contribution of both antennas. In Figs. 11 and 12, we display the AC table errors coupled with the combined uncertainties, $\varepsilon _{Mi\mathrm {L}j}\pm u_{\mathrm {L}j}$, using the geometric measurements as ground truth and all uncertainties transferred to the AC table error functions. One should notice in this case that $\varepsilon _{\mathrm {L3}}$ is a combination of $\varepsilon _{\mathrm {L1}}$ and $\varepsilon _{\mathrm {L2}}$ with opposite signs, which results in constructive or destructive interference of the errors present in the delivered AC tables depending on how the broadcast errors interact. Examining the results, we notice that for all practical purposes

$$\begin{aligned}&|\varepsilon _{\mathrm {L1}}^{M1}|< {\left\{ \begin{array}{ll} 0.1~\mathrm {mm} ~ , \quad \epsilon \ge 45^{\circ }\\ 0.3~\mathrm {mm}~,\quad \epsilon \ge 10^{\circ }\end{array}\right. } \ |\varepsilon _{\mathrm {L1}}^{M2}|> 0.3~\mathrm {mm}~ , \quad \epsilon< 60^{\circ };\\&|\varepsilon _{\mathrm {L2}}^{M1}|>\quad 1~\mathrm {mm} \quad , \quad \epsilon< 50^{\circ }\quad \quad |\varepsilon _{\mathrm {L2}}^{M2}|> 1~\mathrm {mm} \quad , \quad \epsilon< 55^{\circ };\\&|\varepsilon _{\mathrm {L3}}^{M1}|>\quad 3~\mathrm {mm}\quad ,\quad \epsilon< 25^{\circ }\qquad |\varepsilon _{\mathrm {L3}}^{M2}|> 3~\mathrm {mm} \quad ,\quad \epsilon < 55^{\circ }; \end{aligned}$$

which means that only $C_{\mathrm {L1}}^{M1}$ is up to our estimate of the required system standards, but that the specifications set forth in Plag and Pearlman (2009) have not been met. As expected from the examination of the AC tables in Sect. 2, the $\varepsilon _{\mathrm {L1}}$ errors are smaller than the $\varepsilon _{\mathrm {L2}}$. We also notice the sign of the derivatives in broad terms and find that

$$\begin{aligned} \varepsilon _{\mathrm {L1}}^{\prime M1}= & {} ~~~ 0,\quad \epsilon> 10^{\circ }\qquad \qquad \!\!\!\!\!\!\! \varepsilon _{\mathrm {L1}}^{\prime M2} = {\left\{ \begin{array}{ll} +,\quad \epsilon< 40^{\circ }\\ -,\quad \epsilon> 40^{\circ }\end{array}\right. }\!\!\!\!;\\ \varepsilon _{\mathrm {L2}}^{\prime M1}= & {} ~~~ - ,\quad \! \epsilon>10^{\circ }\qquad \quad \!\!\! \varepsilon _{\mathrm {L2}}^{\prime M2} = {\left\{ \begin{array}{ll} -, \quad \epsilon< 30^{\circ }\\ +, \quad \epsilon> 30^{\circ }\end{array}\right. }\!\!\!\!;\\ \varepsilon _{\mathrm {L3}}^{\prime M1}= & {} {\left\{ \begin{array}{ll} +,\quad \!\epsilon< 35^{\circ }\\ 0,\quad \,\epsilon> 35^{\circ }\end{array}\right. } \quad \varepsilon _{\mathrm {L3}}^{\prime M2} = {\left\{ \begin{array}{ll} +,\quad \epsilon < 40^{\circ }\\ -,\quad \epsilon > 40^{\circ }\end{array}\right. }\!\!\!\!;\quad \end{aligned}$$

the effects of which is examined more closely in Sect. 6.

Fig. 13

AC table errors’ contribution in $\varDelta ^\theta$, $\varDelta ^\upsilon$ and $\varDelta ^\kappa$ estimates at L3. The identified calibration errors in $M_1$ (black) and $M_2$ (red) are fitted with an unweighted (dash dot) and a $\sin \epsilon$ (dash) mapping function, respectively

6 Effects on parameter estimation in GNSS processing

As mentioned in Sect. 1, PCCs have only been weakly constrained with respect to current demands, and AC errors on the order of Figs. 11 and 12 have therefore unknowingly been incorporated in the GNSS processing. In an unconstrained Eq. 1, the errors propagate to the final solutions where they are distributed among the estimated parameters much as in communicating vessels. Depending on their general behavior, these parameters can in broad terms be categorized as

(16)

where the power sets (${\mathbb {P}}$) represent general generic terms for groups of similarly perturbing phenomena. More specifically, error components that are large at low elevations alias as troposphere parameters $(\varDelta ^\theta$) those that increase near zenith alias as height $\varDelta ^\upsilon$, whereas those that are insensitive to elevation alias as clock errors $\varDelta ^\kappa$ which shifts the observations uniformly along the $\varPhi$-axis in Figs. 11 and 12. Large errors in $\varDelta ^\kappa$ are an inherited property accounted for in the system design and essentially allowed to run free. We explore the effect of the calibration errors and fit the residuals

$$\begin{aligned} r_{\mathrm {L}j}^{Mi}(\epsilon )=-\varepsilon _{\mathrm {L}j}^{Mi}(\epsilon ) \end{aligned}$$

(17)

with a parameter combination that satisfies Eq. 16. We investigate two scenarios:

to evaluate the end effect of using $C_{M}(\epsilon )$ instead of $T_{M}(\epsilon )$ and we apply both uniformly weighted and $\sin \epsilon$-weighted observations to estimate the $\varDelta _M^\theta$ and $\varDelta _M^\upsilon$ contributions that inevitably affect the geodetic analysis. The L3 results are shown in Fig. 13, where the $M_1$ fit is achieved by a set of rather moderate parameters, whereas the corresponding $M_2$ fit needs rather high values of both $\varDelta ^\theta _{M2}$ and $\varDelta ^\upsilon _{M2}$ to fit the data at both low and high elevations. The full parameter evaluation is presented in Table 3, where the results reveal that both $M_1$ and $M_2$ are probably sufficient for L1 on short baselines, whereas the L3 results indicate that both methods are significant error contributors in reference frame determinations. This is particularly true for $M_2$, whose contribution at L3 is an order of magnitude larger than the 1 mm frame objective and even worse with respect to the anticipated acceptable calibration contribution 0.3 mm.

Table 3 AC method contributions to the L1 and L3 analytic solutions for equal weight and $\sin \epsilon$ weight functions

7 Discussion

The outlined assessment method is in all essence independent of the antenna designs employed in the evaluation and should be transferable also to other types of antennas within the width of the uncertainty bands. However, as is shown in Sect. 2, the AC table differences vary considerably between antenna designs, and our results can therefore not be transferred to other antennas the way they would have been for methods with inter-model reproducible errors—the a priori knowledge of the uncertainties in the AC tables is simply too poor and we cannot assume that the antenna interactions with the surroundings at the service provider premises are invariable. Nevertheless, assuming that the applied AC tables are representative for our antennas and that no changes have been made at the service providers’ facilities, our results should be applicable to the AC tables delivered for JNSCR_C146-22-1 and similar choke ring antennas.

To verify that our method has not redistributed the parameters unjustly, we compare the differences in the estimates for the two methods with the a priori known differences in the calibration tables and display these in Fig. 14. In the graph, we present the calculated uncertainties of the differences in the estimated models as

$$\begin{aligned} u_\delta = \sqrt{ u_{\delta \nu }^2 + 2u_{C} } \end{aligned}$$

(18)

The noise-related uncertainty of the estimation difference ($u_{\delta \nu }$) is only about one sixth of the uncertainty, $u_{\nu }$, presented in Fig. 9, as a consequence of using the same set of observations in the processing for both methods. The geometrical component, $u_{G\bot }$, is identical for both methods, and its contribution cancels in the difference. The estimation differences, with accompanying uncertainties, describe fairly well the calibration table differences for antennas #1–3, while antenna #4 deviates as discussed earlier.

Fig. 14

Model inversion of the observation data compared to AC table differences. Solid, colored lines represent our observed method differences at each frequency L1 (red), L2 (green), and L3 (blue). Black lines represent the differences between the two supplied AC tables, L3 being calculated from L1 and L2

Finally, we formed the corrected AC tables (${\hat{T}}_a(\alpha , \epsilon )$) from the estimated method errors by reversing Eq. 3

$$\begin{aligned} {\hat{T}}_a(\alpha ,\epsilon )=C_{aM}(\alpha ,\epsilon )-\varepsilon _{M}(\epsilon ) \end{aligned}$$

(19)

and conducted a verification rerun of the original satellite data using ${\hat{T}}_a(\alpha ,\epsilon )$ instead of $C_{aM}(\alpha ,\epsilon )$. Since identical data were used in forming the correction models and in the verification, the newly derived errors (${\hat{\varepsilon }}$) should ideally become zero. As shown in Fig. 15, this holds true for ${\hat{\varepsilon }}_{\mathrm {L}1}$ and ${\hat{\varepsilon }}_{\mathrm {L}2}$, which both are $<1 \mathrm {\mu m}$, with ${\hat{\varepsilon }}_{\mathrm {L}3}$ being slightly larger but typically below 0.1 mm. We have sought the root cause for the correlated patterns in ${\hat{\varepsilon }}_{M1\mathrm {L}3}$ and ${\hat{\varepsilon }}_{M2\mathrm {L}3}$, but fail to explain how these originate without any trace in the broadcast frequencies and anticipate the cause to be imperfections in the iterative creation of the weight matrix ${\mathbf {W}}$ in Eq. 13.

Fig. 15

Error functions ${\hat{\varepsilon }}$ from a rerun of the original observation data, using the obtained ${\hat{T}}_a(\alpha ,\epsilon )$ tables at frequencies L1, L2, and L3 for $M_1$ and $M_2$; to compare with Figs. 11 and 12. L1 and L2 (red and green, respectively) are overlaid in the diagram, as ${\hat{\varepsilon }}_{L1, L2}\rightarrow 0$

Broadly categorizing uncertainties as being of geometric or electromagnetic character, we briefly mention some factors and dependencies worth addressing and characterizing in focused investigations ahead. First, we notice that a comprehensive correction for a full hemisphere can be obtained by introducing a $\varDelta \alpha$ shift in the characterization with the same method generics as those applied here. Due to the non-polar GNSS orbits, all cells were not occupied with direct observations in our stationary set up, something that could be amended with common antenna rotations if considered necessary. Full characterizations are redundant in local assessments such as the one we performed, where the GNSS orbits affect the assessed antennas and an adjacent deployed CORS antenna; similarly, for a complete correction table in azimuth and elevation, a full characterization would be necessary.

Secondly, as already noted, the uncertainty in baseline length dominates the current $u_{G\bot }$. We used the laser tracker with a probe configuration as generally fit for purpose, and with all data collected at the end of the analysis it is possible, but not certain, that a different setup could have improved the situation slightly. However, with the orientation fitting procedure in Sect. 4, the length is likely to be the dominant source regardless of orientation (at least as long as the antennas are tilted in the direction of the baseline).

Thirdly, we speculate that a smaller $\varDelta \varPsi$ could reduce $u_{\lambda }$. While an angular shift between the antennas is needed to evaluate the differentials, we concede to have been influenced by the $5 ^{\circ }$ equi-angular separation between the cells in the original AC tables and tilted the tribrach heads as far as we possibly could during the campaign—in an evolution we are likely to employ a smaller $\varDelta \varPsi$, and it is possible that an optimal angle can be found.

For electromagnetic-related uncertainties, the assessment errors introduced by the approximations in Eq. 4 would obviously be reduced by using perfect antenna duplicates, but evaluations of the differences between individual antennas are not meaningful without metrologically traceable uncertainties in the AC tables. Looking at perturbations caused by the antenna positions and rotations with respect to the tribrach heads and outgoing antenna cables, respectively, these remain to be investigated for more comprehensive investigations of the uncertainties in our measurements. As long as such objects are kept inside the cylinders extending downwards from the antenna ground planes, we expect their influence on the results to be negligible. Ultimately, the minimal required angle separation between the calibration table cells depends on the GNSS observation repeatability in each cell and the accuracy in the determination of the $G_\bot$ components—we believe that the $5 ^{\circ }$ equiangular separation is adequate for contemporary applications.

We also note that once a reference antenna has been well characterized, it is no longer restricted to its duplicate, but can be used in combination with any antenna. Taking all of the above into account, differential measurements that relate the phase center positions of already deployed antennas to their physical structure are ready to be made without affecting on-site installations. Such measurements could provide a metrologically traceable on-site antenna calibration that satisfies (JCGM 2012; Baire et al. 2014; Gross and Herring 2017) with unbiased results at the uncertainty levels of Figs. 11 and  12. This, thus, promises to reduce systematic GNSS errors to a level which satisfy the requirements on a reference consistent frame (Ray and Altamimi 2005; Altamimi et al. 2016).

8 Conclusion

GNSS antennas are an essential part of bringing a unified geodetic observation system on the observation level to fruition. However, the absolute antenna calibrations currently approved by IGS disagree on a level which exceeds the observation system requirements, and the delivered tables do not fulfill JCGM (2012) calibration standards in terms of traceability to the related SI unit, sufficient control of uncertainties, or proven degree of equivalence. As a consequence, the AC tables have so far been allowed to differ to an extent that exceeds the reference frame requirements without any means of control.

Utilizing the similarities between duplicate GNSS antennas, we have developed an assessment method based on geometric laser tracker constraints and antenna differentials to quantify the systematic errors in existing AC tables. We applied this method in an elevation-oriented evaluation and found two IGS-approved service providers’ AC contributions to the L3 vertical for JNSCR_C146-22-1 choke ring antennas be of order 1 mm and 1 cm, respectively.

Stating the benchmark values for $30 ^{\circ }$ elevation, we gauge our assessment method being able to determine GNSS antenna phase centers accurately within $\pm 0.38$ mm on L1 and within $\pm 0.62$ mm on L3. Although larger than the 0.1 mm requirement set out in Plag and Pearlman (2009), we consider this sufficient to satisfy the overall 1 mm system objective as well as the 3 mm set out by Ray and Altamimi (2005).

As this can be done without compromising the characteristics of the existing installations, we advocate that a combination of well characterized reference antennas and commensurate geometric instruments is ready to be deployed at system critical sites to determine the actual phase center positions of existing GNSS antennas in the global frame.