Bayesian approach for network adjustment for gravity survey campaign: methodology and model test

Abstract

The drift rate of relative gravimeters differs from time to time and from meter to meter. Furthermore, it is inefficient to estimate the drift rate by returning them frequently to the base station or stations with known gravity values during gravity survey campaigns for a large region. Unlike the conventional gravity adjustment procedure, which employs a linear drift model, we assumed that the variation of drift rate is a smooth function of lapsed time. Using this assumption, we proposed a new gravity data adjustment method by means of objective Bayesian statistical inference. Some hyper-parameters were used as trade-offs to balance the fitted residuals of gravity differences between station pairs and the smoothness of the temporal variation of the drift rate. We employed Akaike’s Bayesian information criterion (ABIC) to estimate these hyper-parameters. A comparison between results from applying the classical and the Bayesian adjustment methods to some simulated datasets showed that the new method is more robust and adaptive for solving problems caused by irregular nonlinear meter drift. The new adjustment method is capable of determining the time-varying drift rate function of any specific gravimeter and optimizing the weight constraints for every gravimeter used in a gravity survey. We also carried out an error analysis for the inverted gravity value at each station based on the marginal distribution. Finally, we used this approach to process actual gravity survey campaign data from an observation network in North China.

1 Introduction

Gravity survey campaign data generally refer to the gravity observed repeatedly at fixed stations with the same routes and similar time schedules. For each campaign, the less time needed to finish the entire loop of stations, the more acceptable the observation results are. During the campaign, it is assumed that the gravity does not change at the same location. A continental-scale gravity network has been established on the Chinese mainland. Gravity survey campaigns using this network require many observational teams working together in the scheduled period. The regional gravity variations detected by this terrestrial gravity network have been successfully used to study geoscience problems, including groundwater change (Kennedy et al. 2014), surface vertical deformation (Ballu et al. 2003), tectonic events (Lambert et al. 2006; Van Camp et al. 2016), and earthquakes (Chen et al. 1979, 2016; Kuo et al. 1993, 1999; Zhu et al. 2010).

In a time-lapse terrestrial gravity survey, the whole network is traveled with a fixed time interval (1/2 or 1 year) to measure gravity variation, which is at a scale of a few tens of microgals, at each station during the period between these two observations. The distance between two adjacent gravity stations is about several tens of kilometers, and road vehicles are used to travel between stations. The time interval between gravity measurements at two adjacent stations is about few hours. Realistically, only about ten measurements can be taken per day. For improving survey productivity, portable relative gravimeters are widely used.

Since their invention in the early 1960s, relative gravimeters have come to be used in terrestrial gravity surveys all over the world. These gravimeters mainly employ zero-length springs as the core gravitational sensor. Because the drift of the zero-length spring is typically low and can be predicted with a linear fitting in a short time period, the observations by the high-precision microgravity meters are processed by the technique of gravity network adjustment (Crossley et al. 2013). Currently, the absolute gravimeters (FG-5 and A10 made by Micro-G, Inc.) are the best alternative approach for the terrestrial gravity measurement. However, they are still much more expensive and more time-consuming to use in the field compared with relative gravimeters, although their accuracy is much higher. In contrast, relative gravimeters, which are equipped with spring sensors, are economical and portable, and they do not have specific environmental requirements. These reasons make them still irreplaceable for the foreseeable future.

Drift is one of the inherent features of all kinds of relative gravimeters. It is the phenomenon that the gravity measurement varies with the passage of time. The drift rate should be frequently estimated by repeating measurements at the base station or stations with known precise gravity values throughout the entire survey period. The estimation error of instrument drift rate will significantly affect the accuracy of network adjustment. In general, the gravity survey campaign refers to sets of in situ gravity measurements at a stable station at fixed time intervals year after year. The campaign time of a gravity survey often spans weeks or months. The drift rate cannot be modeled with a simple linear function if the campaign time is more than 24 h. The repeatability of ± 0.005 mGal is often requested for the high-precision microgravity and time-lapse gravity research. But a regional survey may only require a repeatability of ± 0.050 mGal. Since many factors can affect the drift rate of the gravimeter, such as the spring age, temperature inside the instrument, and transportation, using repeated observations is a practical approach for estimating the drift rate. However, the need to frequently return to the base station obviously reduces the efficiency of the survey. Moreover, loop errors at the base station, tares, offset, and outliers are also potential causes of errors in gravity data.

All relative gravimeters that use spring sensors, including Scintrex CG5/6, Locaost-Romberg model D/G, and ZLS Burris, have a complicated drift feature, especially for nonlinear long-term drift. Besides adding more absolute gravity observations and increasing the number of loops in the survey network, which are time-consuming and expensive, an economical and efficient way to obtain more accurate estimation of gravity is improving the network adjustment methods. Currently, most of gravity network adjustment methods cannot provide the adaptive drift rate inversion and the weight on strict optimization for multiple gravimeters. It is one of the key limitations on the improvement of gravity estimation accuracy.

Gravity survey campaigns have been carried out many years on the Chinese mainland. To accomplish a continental-scale terrestrial gravity survey, thousands of stations need to be observed every year by means of tens of relative gravimeters. The key aim of gravity surveys is to acquire high-accuracy gravity changes with a magnitude of tens of microgals. The network adjustment is essential and necessary for processing the relative gravity survey data, which calculates least-squares solutions (optimal estimates of gravity values) from the redundant observations based on the assumptions of linear drift. Some improvements of the classical adjustment method have been proposed for some particular applications (Hwang et al. 2002; Kennedy et al. 2016). However, how to fit nonlinear drift and balance the accuracy and productivity of gravity surveys is rarely discussed.

In this paper, we proposed a new approach for adjusting gravity survey data using objective Bayesian analysis and minimizing Akaike’s Bayesian information criterion (ABIC) (Sakamoto et al. 1988; Malinverno 2000; Mitsuhata 2004). The origin of the ABIC was in weather data analysis (Akaike 1977, 1980), and it has been widely used for the problems of estimating parameters of seismicity models (Ogata et al. 1993), 3D tomography (Inoue et al. 1990), and geodetic data inversion (Fukahata et al. 2004, 2008; Murata 1993; Nawa et al. 1997). For example, the BAYTAP-G is one representative example of the application of ABIC to analyzing the earth tide in a continuous relative gravity data at a fixed station (Tamura et al. 1991).

In this study, we rewrote the network adjustment equations by introducing new trade-off parameters that balance the residual of gravity survey campaign data and the drift rate of the relative gravimeter. This new method was tested with some synthetic datasets that were prepared with different drift models based on an actual gravity observation network. A comprehensive analysis of the fitting residuals and the accuracy of adjustment was carried out. The gravity survey route and time schedule at each station all came from actual gravity field work. We also performed a sensitive analysis for the uncertainty parameters of earth tide factor (TF) and atmospheric admittance (AA). At last, we evaluated this method by applying it to two observation datasets and compared the adjustment results to the absolute gravity observation.

2 Observations from the gravity survey campaigns and nonlinear drift of relative gravimeters

The accuracy of gravity variation data is a primary demand for many potential studies. It depends to a great degree on the gravity data processing method. In practice, the variation of the drift rate of relative gravimeters has been regarded as the primary error source.

Generally, to reduce the effects of drift rate variation and offsets, the relative gravity difference (GD) between adjacent station pairs is used instead of the actual gravity measurements obtained at each station as the input information for the adjustment. Another advantage of using GD is that, for station pairs with a relatively short elapsed time between observations, common-mode signals can be removed automatically (Kennedy et al. 2016).

2.1 Observation data

For ground-based relative gravity measurement, the observation equation can be written as (Torge 2001):

$$ x_{e\left( k \right)} - x_{s\left( k \right)} + v \times \Delta t_{k} + \varepsilon_{k} = y_{k} , $$

(1)

where $y_{k}$ is the $k$-th observed value of GD; $s\left( k \right)$ and $e\left( k \right)$ are the starting and ending station numbers corresponding to the $k$ th observed GD, respectively; $x_{s\left( k \right)}$ and $x_{e\left( k \right)}$ represent the true gravity values at the $s\left( k \right)$-th and $e\left( k \right)$-th stations, respectively; $v$ is the meter drift rate; $\Delta t_{k}$ is the travel time for observing $y_{k}$ between the $s\left( k \right)$-th and $e\left( k \right)$-th stations; and $\varepsilon_{k}$ is the observation error for $y_{k}$. In Eq. (1), the unknown gravity values, $x_{i} , i = 1, 2, \ldots ,N,$ and $v$ need to be estimated. Technically, if we have more than two observations at the same segment between two stations, say, $i$ and $j$ (i.e., unordered pair $\left\{ {i,j} \right\}$ appears in all the unordered pairs $\left\{ {s\left( k \right), e\left( k \right)} \right\}, k = 1, 2, \ldots , K$, twice or more), the unknown values of $\Delta x_{ij} = x_{j} - x_{i}$ and $v$ can be estimated. In general, the least-squares network adjustment method is used to process these redundant relative gravity measurements.

2.2 Drift

Even though different relative gravimeters have different drift features, the cumulative drift of a relative gravimeter in time, or in other words, the measured gravity change at the same location due to drift, can still be approximated by a polynomial of degree $a$

$$ D\left( t \right) \approx \mathop \sum \limits_{p = 1}^{a} v_{p} \left( {t - t_{0} } \right)^{p} , $$

(2)

where $v_{p}$ is the drift rate at the $p$-th order and $t_{0}$ is the travel start time. When $a = 1$, Eq. (2) is a linear drift model. The adopted value of $a$ depends on the gravimeter characteristics, but it rarely exceeds 2. Also, if the estimate of the drift rate has some minor error, an error in the measured gravity values is introduced by

$$ \varepsilon_{d} \approx \left( {\bar{v} - v_{t} } \right) \times \Delta t, $$

(3)

where $\bar{v}$ is the estimated drift rate and $v_{t}$ is the true value of the drift rate during the travel time $\Delta {\text{t}}$. Therefore, shortening travel time benefits the adjustment. By experience, the drift rate of all spring-type relative gravimeters has a low-frequency temporal variation distinct from the stochastic noise. Also, the drift features of most commercial ground-based relative gravimeters, including Scintrex CG5, Lacoste-Romberg model G, and ZLS Burris, may potentially change with the age of the instrument (Crossley et al. 2013).

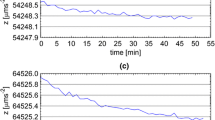
Figure 1 shows the time-series data recorded by a CG5 gravimeter (No. 1098) at an observation basement in Beijing. These data are continuously recorded in the basement with good observation conditions at a sampling rate of once per minute. The effect of the earth tide has been eliminated theoretically. The common drift rate of a gravimeter is about 1.43 mGal/day. If a linear drift model is fit to the temporal variation of the drift in these 25 h, the residuals of the gravity signals after eliminating the linear drift are about ± 10 μGal (Fig. 1a). Nonlinear gravity variation remains in the residuals, indicating that the drift rate varies with time. The magnified plot (inset) shows the stochastic noise signals over a stable time interval, which have small variations over a range of about 5 μGal. Besides the instrument itself, the noise level also depends on the environmental interference and site conditions. However, the long-term drift of a gravimeter is more complicated.

Fig. 1

Short-term and long-term real drift features of the relative gravity instrument. a A 25 h’ continuous record by CG-5 gravimeter (No 1098). b Fitting a linear drift model to 55 days’ records. c Fitting a piecewise linear model to 55 days’ records. In (a), the solid blue line shows the continuing gravity after removing the tidal effect. The solid black line is the fitted drift values by the linear model. The black scatter dots are the fitted residuals. In (b), the meanings of the solid blue and black lines and the black scatter dots are the same in (a). The solid red line is the fitted drift by a second-order drift model. In (c), the blue solid step line is the fitted drift rate by the piecewise linear model. The black scatter dots are the fitting residuals

Figure 1b shows a continuous record of gravity reductions over 55 days by the same CG5 gravimeters, from which we can see the high-ordered drift. If a second-order drift model is employed to fit these 55 days of time-series data, the gravity residual is about ± 150 μGal and significantly related to the temporal variance of the meter drift rate. Moreover, if a segmental linearization is applied to fit the gravity records for each day, the residual gravity variation decreases to about ± 10 μGal with a few outliers, as shown Fig. 1c. The residual this time basically contains the internal noise of the instrument with obviously random characteristics. However, the range of estimated drift rate increased to 0.3 mGal/day. In this case, we can see that the gravimeter’s long-term and short-term drift rates obviously differ from the observation noise.

Instrumental drift can be influenced by many factors. Apparently, the drift can be decomposed into linear and nonlinear components. The nonlinear drift is possibly caused by the spring age, temperature, transportation, and tilt (Reudink et al. 2014). Since the drift can be always approximated by a linear function over a short time period for any gravimeter in good condition, the piecewise linear model is suitable to estimate the drift rate of gravimeter. We cannot find an obvious statistical feature in Fig. 2a, but if we plot the second-order differences of the daily drift rate as a histogram, a Gaussian distribution can fit them nicely, as shown in Fig. 2b. In the next section, our adjustment model and related algorithm are designed based on this feature.

Fig. 2

Histograms of (a) fitted drift rate per day and (b) difference of drift rate per day. The histogram of fitted drift rate per day in Fig. 1c is shown in Fig. 2a

Redundant observations at each station are necessary in the relative gravity survey campaigns to eliminate the effects of instrumental drift and observational noise. Figure 3 shows two types of commonly used field survey schemes, with each letter denoting a station. Figure 3a shows the triple-time survey scheme, and Fig. 3b the double-time survey scheme. These redundant measurements help us to reduce uncertainty. During the survey campaign, an average of one or two gravity observations can be made each hour. To improve efficiency, the double-time gravity survey is carried out using two gravimeters. For the continental-scale campaign, the triple-time survey with three gravimeters is generally adopted to ensure the accuracy of gravity survey data, because the average distance between adjacent survey stations is hundreds of km. The balance between accuracy and efficiency should be carefully considered. In this paper, we proposed an alternative approach to estimate the temporal variation of the drift rate by using redundant measurements and employing the ABIC approach for the estimation of trade-off hyper-parameters.

Fig. 3

Two kinds of field survey schemes for the relative gravity observation

3 Methodology

In this section, we introduce a new adjustment method for estimating gravity values in the case of long-term gravity survey campaigns with multiple gravimeters. The method mainly focuses on the processing of temporal variation of the drift rate and stochastic noise. The input consists of relative GD data with noises of unknown variance and absolute gravity data with errors of known variance. We assume that the effects caused by the earth tide, ocean tide, air pressure, and polar motion are reduced before the network adjustment. Transient processes including precipitation, surface deformation, and temperature fluctuations at the stations during the campaign are not taken into account for the time being.

3.1 Basic definitions and notation

First, we write out the observation equations used in this study by revisiting the conventional gravity network adjustment strategy for the relative gravity data. We start from the observation equation for the relative gravity survey. This survey generally uses the GD between two adjacent stations as the input to determine an optimal gravity value at each station. In practice, the overall gravity survey needs to be synchronously carried out by several teams using tens of gravimeters. To improve observation accuracy, at least two gravimeters are used for synchronous observation at each station. Since the gravimeters may differ in observation performance, this can be quantified with the variance of the errors of corresponding relative gravity observations for each gravimeter. The observation equation gives the relationship between the input gravity differences and the unknown gravity value written as follows:

$$ y_{k} = x_{e\left( k \right)} - x_{s\left( k \right)} + d_{q\left( k \right)} \left( {t_{k}^{\left( e \right)} } \right) - d_{q\left( k \right)} \left( {t_{k}^{\left( s \right)} } \right) + \varepsilon_{k} ,\quad k = 1,2, \ldots , K, $$

(4)

where $y_{k}$ is the $k$-th observed value of GD from the $s\left( k \right)$-th station to the $e\left( k \right)$-th station; $s\left( k \right)$ and $e\left( k \right)$ are the starting and ending station numbers corresponding to the $k$-th observed GD, respectively; $q\left( k \right)$ is the gravimeter by which $y_{k}$ is obtained; $x_{s\left( k \right)}$ and $x_{e\left( k \right)}$ are the true gravity values at the $s\left( k \right)$-th and $e\left( k \right)$-th stations, respectively; $d_{q\left( k \right)} \left( {t_{k}^{\left( s \right)} } \right)$ and $d_{q\left( k \right)} \left( {t_{k}^{\left( e \right)} } \right)$ are the meter drifts at the observation times at the starting and ending stations, respectively; and $\varepsilon_{k}$ is the observation error for $y_{k}$, which is independently distributed as Gaussian random variables with mean of 0 and variance of $\sigma_{q\left( k \right)}^{2}$.

Another basic equation is

$$ g_{k} = x_{w\left( k \right)} + \varepsilon_{k}^{\left( a \right)} ,\quad k = 1, 2, \ldots , K_{g} , $$

(5)

where $g_{k}$ is the $k$-th observed value of absolute gravity at station $w\left( k \right)$ and $\varepsilon_{k}^{\left( a \right)}$ is the observation error for $g_{k}$, assumed to be independently and identically distributed according to a Gaussian distribution with a mean of 0 and a known variance $\sigma_{\text{g}}^{2}$.

We adopt the following notation throughout this article. The numbers of observed stations, relative gravimeters, absolute gravity observations, and GD observations are $N, P, K_{g}$, and $K,$ respectively, and $K > N$ based on the redundant observations. The number of drift rate estimates is $M$.

3.1.1 Data vector definitions

The vectors of the observed GDs, gravity values at the station, estimated drift rates, and absolute gravity values are denoted by $\varvec{y},\varvec{x},\varvec{v},\,{\text{and}}\,\varvec{g}$, respectively. The gravity data vectors are expressed as follows:

$$ \varvec{x} = \left[ {x_{1} ,x_{2} , \ldots ,x_{N} } \right]^{\text{T}} $$

is the vector of gravity values at all the stations,

$$ \varvec{g} = \left[ {g_{1} ,g_{2} , \ldots ,g_{{K_{g} }} } \right]^{\text{T}} $$

is the vector of observed absolute gravity values, and

$$ \varvec{y} = \left[ {y_{1} ,y_{2} , \ldots ,y_{K} } \right]^{\text{T}} $$

is the vector of observed GD values. When multiple gravimeters are employed, we also use

$$ \varvec{y}_{i} = \left[ {y_{i1} ,y_{i2} , \ldots ,y_{{iK_{i} }} } \right]^{\text{T}} $$

to denote the vector of GD values observed by gravimeter $i$, and thus, by arranging GD values obtained by using the same gravimeter in the same group,

$$ \varvec{y} = \left[ {\varvec{y}_{1}^{\text{T}} ,\varvec{y}_{2}^{\text{T}} , \ldots ,\varvec{y}_{P}^{\text{T}} } \right]^{\text{T}} . $$

The vector of the drift rates for all the gravimeters is

$$ \varvec{v} = \left[ {\varvec{v}_{1}^{\text{T}} ,\varvec{v}_{2}^{\text{T}} , \ldots ,\varvec{v}_{1}^{\text{T}} } \right]^{\text{T}} . $$

For the linear drift model, $\varvec{v}_{i} = \left[ {v_{i} } \right]$ and when $M$ time intervals are used for estimating the nonlinear drift model for gravimeter $i$, $\varvec{v}_{i} = \left[ {v_{i1} , v_{i2} , \ldots , v_{iM} } \right]^{\text{T}} .$

If P gravimeters are used in the survey, the total number of GDs can be calculated by $\mathop \sum \nolimits_{i = 1}^{P} {\text{size}}\left( {\varvec{y}_{i} } \right) = K_{1} + K_{2} + \cdots + K_{p} = K$,where $K_{i} ,i = 1, 2, \ldots ,P,$ are the numbers of GD observations by each gravimeter.

3.1.2 Matrix definitions

The matrices of relative gravity observation configurations, observed durations of each GD, smoothness for drift rate variations, and absolute gravity observation configuration are denoted by ${\mathbf{A}},\varvec{ }{\mathbf{D}},\varvec{ }{\mathbf{B}},$ and ${\mathbf{G}}$, respectively.

The variances of observational noises, drift rate variations, and absolute gravity observations are denoted by $\sigma^{2} , \sigma_{b}^{2} ,$ and $\sigma_{g}^{2}$, respectively. The weighted diagonal matrix of relative gravimeters, drift rate variation, and absolute gravity are denoted by ${\mathbf{W}}, {\mathbf{W}}_{\varvec{b}} ,\varvec{ }$ and $\varvec{ }{\mathbf{W}}_{\varvec{g}}$, respectively. In this case, ${\mathbf{W}}_{g}$ with respect to the absolute gravity or basement station needs to be known before adjustment.

If there are $P$ relative gravimeters in total, the variances of each observation value and the drift rate for the $i$-th gravimeter are, respectively, denoted by $\sigma_{i}^{2}$ and $\sigma_{bi}^{2}$, where $i = 1, 2, \ldots ,P$. The corresponding matrices for the relative gravity observation configuration, observed durations of each GD, smoothness for drift rate variations, weights of relative gravimeters, weights of drift rate variations, and weights for absolute gravity are denoted by ${\mathbf{A}}_{\varvec{i}} ,\varvec{ }{\mathbf{D}}_{i} ,\varvec{ }{\mathbf{B}}_{i} , {\mathbf{W}}_{i} ,\varvec{ }$ and ${\mathbf{W}}_{{\varvec{b}i}}$, respectively. Please see Appendix A for a summary of this notation.

3.2 Gravity network adjustment with linear drift model

In gravity surveys, the GD data need to be adjusted because of the existence of observation noise and gravimeter drift. The absolute gravity observations can be used to establish the network datum and improve the precision of adjustment. Network adjustment, which combines the absolute gravity and redundant relative gravity observations, generally determines an optimal gravity value for each station by a least-squares criterion (Torge 1989).

3.2.1 Basic equations

In the classical adjustment method, we suppose that the observation noise is stochastic, following a normal distribution, and the gravimeter drift is a linear function. When only one gravimeter is used, the basic equations for the network adjustment can be written as

$$\begin{aligned} \varepsilon_{k} & = y_{k} - \left[ {x_{e\left( k \right)} - x_{s\left( k \right)} + d_{q\left( k \right)} \left( {t_{k}^{\left( e \right)} } \right) - d_{q\left( k \right)} \left( {t_{k}^{\left( s \right)} } \right)} \right] \\ &\quad \sim {\text{Normal}}\left( {0,\sigma_{q\left( k \right)}^{2} } \right),\quad k = 1, 2, \ldots ,K, \end{aligned} $$

(6)

$$ \varepsilon_{j}^{\left( g \right)} = g_{j} - x_{v\left( j \right)} \sim {\text{Normal}}\left( {0,\sigma_{g}^{2} } \right),\quad j = 1,2, \ldots ,K_{g} . $$

(7)

For the linear drift model,$d_{q\left( k \right)} \left( {t_{k}^{\left( e \right)} } \right) - d_{q\left( k \right)} \left( {t_{k}^{\left( s \right)} } \right) = v_{q\left( k \right)} \left( {t_{k}^{\left( e \right)} - t_{k}^{\left( s \right)} } \right)$, we can write Eqs. (6) and (7) in the matrix/vector format,

$$ {\mathbf{A}}\varvec{x} + {\mathbf{D}}\varvec{v} - \varvec{y}\sim{\text{Normal}}\left( {\tilde{0},{\mathbf{W}}^{ - 1} } \right) $$

(8)

$$ {\mathbf{G}}\varvec{x} - \varvec{g}\sim{\text{Normal}}\left( {0,{\mathbf{W}}_{g}^{ - 1} } \right), $$

(9)

or combine them into one equation:

$$ {\mathbf{S}}\varvec{X} - \varvec{Y} \sim {\text{Normal }}\left( {\tilde{0}, {\tilde{\mathbf{W}}}^{ - 1} } \right) $$

(10)

where

$$ {\mathbf{S}} = \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{D}} \\ {\mathbf{G}} & 0 \\ \end{array} } \right],\quad \varvec{X} = \left( {\begin{array}{*{20}c} \varvec{x} \\ \varvec{v} \\ \end{array} } \right),\quad \varvec{Y} = \left( {\begin{array}{*{20}c} \varvec{y} \\ \varvec{g} \\ \end{array} } \right), \quad {\tilde{\mathbf{W}}} = \left[ {\begin{array}{*{20}c} {\mathbf{W}} & 0 \\ 0 & {{\mathbf{W}}_{g} } \\ \end{array} } \right] $$

and $\tilde{\varvec{v}} = \left[ {v_{1} ,v_{2} , \ldots ,v_{P} } \right]^{\text{T}}$ consists of the unknown drift rates for each gravimeter (see Appendix B for the structure of these matrices).

3.2.2 Likelihood function

Since the probability density functions (PDFs) for the observation errors $\varepsilon_{k} ,k = 1,2, \ldots K,$ of the GD values are the normal densities $\varphi \left( { \cdot |0, \sigma_{q\left( k \right)}^{2} } \right)$, and for the observation errors $\varepsilon_{j}^{\left( g \right)} ,j = 1,2, \ldots ,k_{g} ,$ of the absolute gravity observations are $\varphi \left( { \cdot |0, \sigma_{g}^{2} } \right)$, the likelihood function, which is the joint PDF combining the relative and absolute gravity observations, can be written as

$$ L = \mathop \prod \limits_{k = 1}^{K} \varphi \left( {\varepsilon_{k} | 0, \sigma_{q\left( k \right)}^{2} } \right) \cdot \mathop \prod \limits_{j = 1}^{{K_{g} }} \varphi \left( {\varepsilon_{j}^{\left( g \right)} | 0,\sigma_{g}^{2} } \right). $$

(11)

Considering Eqs. (8) and (9), the joint likelihood can be written as

$$ \begin{aligned} L & = \mathop \prod \limits_{i = 1}^{P} \left[ {{ \det }\left( {2\pi {\mathbf{W}}_{i}^{ - 1} } \right)} \right]^{ - 1/2}\\ &\qquad { \exp }\left[ { - \frac{1}{2}\left( {{\mathbf{A}}_{i} \varvec{x} + {\mathbf{D}}_{i} v_{i} - \varvec{y}_{i} } \right)^{\text{T}} {\mathbf{W}}_{i} \left( {{\mathbf{A}}_{i} \varvec{x} + {\mathbf{D}}_{i} v_{i} - \varvec{y}_{i} } \right)} \right] \\ & \qquad \cdot \left[ {{ \det }\left( {2\pi {\mathbf{W}}_{g}^{ - 1} } \right)} \right]^{ - 1/2} { \exp }\left[ { - \frac{1}{2}\left( {{\mathbf{G}}\varvec{x} - \varvec{g}} \right)^{T} {\mathbf{W}}_{g} \left( {{\mathbf{G}}\varvec{x} - \varvec{g}} \right)} \right] \\ \end{aligned} $$

(12)

or in short,

$$ L = \left[ {{ \det }\left( {2\pi {\tilde{\mathbf{W}}}^{ - 1} } \right)} \right]^{ - 1/2} { \exp }\left[ { - \frac{1}{2}\left( {{\mathbf{S}}X - Y} \right)^{T} {\tilde{\mathbf{W}}}\left( {{\mathbf{S}}X - Y} \right)} \right] $$

In the above, matrix ${\mathbf{A}}$ exactly relates to the gravity survey routes.

3.2.3 Solution for gravity values

If all the covariance matrices are given, the least-squares network adjustment is equivalent to solving the following general linear equation system.

$$ {\mathbf{S}}^{T} {\tilde{\mathbf{W}}\mathbf{S}}\varvec{X} = {\mathbf{S}}^{T} {\tilde{\mathbf{W}}}\varvec{Y} $$

(13)

and the estimates of the gravity values and drift rates are given by

$$ \hat{\varvec{X}} = \left( {{\mathbf{S}}^{T} {\tilde{\mathbf{W}}\mathbf{S}}} \right)^{ - 1} {\mathbf{S}}^{T} {\tilde{\mathbf{W}}}Y. $$

(14)

However, if the weighted matrix, Eq. (11), is unknown before adjustment, maximum likelihood estimation (MLE) can be used. The logarithmic form of likelihood, Eq. (12), can be written as

$$\begin{aligned} - 2\log L & = \left( {K + N_{g} } \right)\log \left( {2\pi } \right) + \mathop \sum \limits_{i = 1}^{P} K_{i} { \log }(\sigma_{i}^{2} )\\ &\quad + N_{g} \log \left( {\sigma_{g}^{2} } \right) + \mathop \sum \limits_{i = 1}^{P} \frac{{{\mathbf{A}}_{i} \varvec{x} + {\mathbf{D}}_{i} d_{i} - \varvec{y}_{\varvec{i}}^{2} }}{{\sigma_{i}^{2} }} + \frac{{{\mathbf{G}}\varvec{x} - \varvec{g}^{2} }}{{\sigma_{g}^{2} }}. \end{aligned} $$

(15)

Since the variance of observed GD measured by gravimeter $i$ is in the form of

$$ \hat{\sigma }_{i}^{2} = \frac{{{\mathbf{A}}_{i} \varvec{x} + {\mathbf{D}}_{i} v_{i} - \varvec{y}_{i}^{2} }}{{K_{i} }}, i = 1, 2, \ldots , P $$

(16)

the likelihood in Eq. (15) can be rewritten as

$$\begin{aligned} - 2\log L & = \left( {K + N_{g} } \right)\log \left( {2\pi } \right) + \mathop \sum \limits_{i = 1}^{P} K_{i} { \log }\left( {\hat{\sigma }_{\text{i}}^{2} } \right)\\ &\qquad + N_{g} \log \left( {\sigma_{g}^{2} } \right) + K + N_{g} . \end{aligned} $$

(17)

The errors of the estimates from the network adjustment can be written as

$$ {\varvec{\Sigma}} = {\text{diag}}\left( {{\mathbf{S}}^{T} {\tilde{\mathbf{W}}\mathbf{S}}} \right)^{ - 1} . $$

(18)

The residual gravity vector can be obtained in the form of

$$ \varvec{R} = \varvec{Y} - {\mathbf{S}}\hat{\varvec{X}}. $$

(19)

In summary, by investigating the traditional gravity observation network adjustment method in the framework of statistical multivariate Gaussian models, an approach for estimating the optimal weighted coefficient related to relative gravimeter by means of minimizing Eq. (17) with the MLE method is proposed naturally.

3.3 Bayesian gravity adjustment with nonlinear drift model

In the above model, the variation of gravimeter drift is assumed to be linear, that is, over the entire campaign period, the drift rate of each gravimeter is expressed as a single value $\varvec{v}_{i} = v_{i} , i = 1,2, \ldots , P$. In fact, most relative gravimeters have drift rates that change with time during the gravity survey campaign. In this paper, we introduced a new nonlinear model to incorporate the nonlinear drift variation for a relative gravimeter.

3.3.1 Smoothness prior for instrument drift

According to our knowledge of the drift rate of the spring-type gravimeter, we assume that the variation of the drift rate is smooth. In practice, the drift rate for one gravimeter can be regarded as a constant over a short time interval. If we divide the whole survey duration into T intervals, and denote the drift rate in the $j$-th period $\left( {j = 1,2, \ldots ,T} \right)$ by $v_{ij}$, the drift rate vector can be written in the form of $\varvec{v}_{i} = \left[ {v_{i1} ,v_{i2} , \ldots ,v_{iT} } \right]^{\text{T}}$.

This a priori assumption can be expressed by the following model:

$$ {\mathbf{B}}\varvec{v}_{i} \sim{\text{Normal}}\left( {0,{\mathbf{W}}_{bi}^{ - 1} } \right), $$

(20)

where ${\mathbf{B}}$ is the smoothing operator and ${\mathbf{W}}_{bi} = {\text{diag}}\left[ {\frac{1}{{\sigma_{bi}^{2} }}, \frac{1}{{\sigma_{bi}^{2} }}, \cdots , \frac{1}{{\sigma_{bi}^{2} }}} \right]_{{M_{i} }}$. In this paper, we use the second-order differential operator, that is,

$$ {\mathbf{B}} = \left[ {\begin{array}{*{20}c} 1 & { - 2} & 1 & {} & {} & {} \\ {} & 1 & { - 2} & 1 & {} & {} \\ {} & {} & \ddots & \ddots & \ddots & {} \\ {} & {} & {} & 1 & { - 2} & 1 \\ \end{array} } \right]. $$

(21)

Hereby, we estimate the optimal value of $\sigma_{b,i}^{2}$ for each gravimeter $i$ by employing the empirical Bayesian method together with other trade-off parameters.

3.3.2 Posterior distribution and ABIC

By the Bayesian theorem, the posterior likelihood is in the form of

$$ \begin{aligned} {\text{Posterior}} & = \frac{{\smallint L\left( {\varvec{y} |\varvec{v}} \right)\pi \left( \varvec{v} \right){\text{d}}\varvec{v}}}{{\smallint \pi \left( \varvec{v} \right){\text{d}}\varvec{v}}} \\ & = \frac{{\smallint \cdots \smallint L(\varvec{y}|\varvec{v})\mathop \prod \nolimits_{i = 1}^{P} { \exp }\left( { - \frac{1}{{2\sigma_{bi}^{2} }}{\mathbf{B}}\varvec{v}_{i}^{2} } \right){\text{d}}\varvec{v}_{1} \cdots {\text{d}}\varvec{v}_{P} }}{{\smallint \cdots \smallint \mathop \prod \nolimits_{i = 1}^{P} { \exp }\left( { - \frac{1}{{2\sigma_{bi}^{2} }}{\mathbf{B}}\varvec{v}_{i}^{2} } \right){\text{d}}\varvec{v}_{1} \cdots d\varvec{v}_{\text{P}} }} , \\ \end{aligned} $$

(22)

where $L(\varvec{y}|\varvec{v})$ is the likelihood function from Eq. (11) and

$$ \pi \left( \varvec{v} \right) = \mathop \prod \limits_{i = 1}^{P} \exp \left( { - \frac{1}{{2\sigma_{bi}^{2} }}\left| {\left| {{\mathbf{B}}\varvec{v}_{i} } \right|} \right|^{2} } \right) $$

is the PDF for the a priori distribution of the drift rates of all the gravimeters used, without knowing the normalizing factor. The Bayesian estimation on the goodness of fit of the model can be given by the ABIC. The optimal function is supposed as

$$ {\text{ABIC}} = - \,2{ \hbox{max} }\left[ {\text{Posterior}} \right] + 2\left( {{\text{No}}.\,{\text{of}}\,{\text{hyperparameters}}} \right). $$

(23)

Here, by substituting the integral result of Eq. (22), Eq. (23) can be rewritten as

$$ \begin{aligned} {\text{ABIC}} & = \log { \det }\left({\begin{array}{*{20}c} {\mathbf{W}} & 0 \\ 0 & {{\mathbf{W}}_{g} } \\ \end{array} } \right)^{ - 1} + \log { \det }{\bar{\mathbf{S}}}^{T} {\bar{\mathbf{W}}}{\bar{\mathbf{S}}} \\ &\quad - \log { \det }^+\left( {2\pi {\mathbf{B}}^{T} {\mathbf{W}}_{B} {\mathbf{B}}} \right) + \log \hbox{min} \left[ {U\left( \varvec{X} \right)} \right] \\ &\quad +2\,\left( {{\text{No}}.\,{\text{of}}\,{\text{hyperparameters}}} \right) , \\\end{aligned} $$

(24)

where ${ \det }^+ (\cdot)$ is the product of all nonzero eigenvalues of nonnegative definite matrix “${\cdot}$”, and

$$ U\left( \varvec{X} \right) = \left( {{\bar{\mathbf{S}}}\varvec{X} - \bar{\varvec{Y}}} \right)^{T} {\bar{\mathbf{W}}}\left( {{\bar{\mathbf{S}}}\varvec{X} - \bar{\varvec{Y}}} \right) . $$

(25)

Please see Appendix B for the meanings of the notations in the above equations.

In this model, hyper-parameters $\theta = \left\{ {\sigma_{1}^{2} ,\sigma_{2}^{2} , \ldots ,\sigma_{p}^{2} ,\sigma_{b1}^{2} ,\sigma_{b2}^{2} , \ldots ,\sigma_{bP}^{2} } \right\}$, including the $2P$ unknown variances, need to be estimated by minimizing the ABIC. If the number of hyper-parameters is small, the direct searching method with a multiplier step can be used for finding the minimum ABIC (Tamura et al. 1991). But in this case, the number of hyper-parameters depends on the number of gravimeters and days in the survey campaign. Thus, a high-dimensional space searching problem has to be faced. The nonlinear optimization methods need to be used for speeding up the minimization of the ABIC. Therefore, we employ the Nelder–Mead simplex nonlinear optimization method (Nelder et al. 1965; see, Wright 1996, for a review) in this study.

3.3.3 Solution of gravity vector

The estimated gravity values vector can be given as

$$ \hat{\varvec{X}} = \left( {{\bar{\mathbf{S}}}^{T} {{\bar{\mathbf{W}}}{\bar{\mathbf{W}}}}} \right)^{ - 1} {\bar{\mathbf{S}}}^{T} {\bar{\mathbf{W}}}\bar{\varvec{Y}}. $$

(26)

The error estimation by the network adjustment can be written as

$$ \varSigma = {\text{diag}}\left( {{\bar{\mathbf{S}}}^{T} {\bar{\mathbf{W}}}{\bar{S}}} \right)^{ - 1} , $$

(27)

and the residual vector for the observations can be obtained by

$$ \varvec{R} = \bar{\varvec{Y}} - {\bar{\mathbf{S}}}\hat{\varvec{X}}. $$

(28)

4 Model tests for the simulated data

In this section, we use a practical network of gravimeters northwest of Beijing, China, and simulate the observation data according to a practical measurement scheme. The simulated gravity data can help us to understand the efficiency of Bayesian adjustment. Gaussian white noise and the instrument drift rate were generated to evaluate the capability of our adjustment theory. In the following tests, the observations between two adjacent stations are the input data for the adjustment. Five tests on simulation datasets were designed, including (1) investigating how to select the optimal weight constraints related to multiple gravimeters in the combined adjustment by means of MLE method, (2) verifying the validity of the Bayesian adjustment for the stochastic nonlinear drift rate model, (3) extending the Bayesian adjustment method to the case of multiple gravimeters, and (4) analyzing the sensitivity of input prior parameters in the adjustment.

In all the simulations, an actual observation route and time scheme were used. Such a survey campaign generally takes about 16 days. The intervals between the observations at two successive stations range from 0.3 to 4 h, with an average of about 0.7 h. In the simulation, the gravity values at all stations are known, the drift models are predefined, and noises with different features were added to the known gravity value at each station. In the synthetic model data, the simulated time spans between gravity observations cause meter drift and stochastic noise is added to the observation values at each station. The variation of random noise in the simulated time-lapse gravity data was controlled within a level similar to that of an actual CG5 m. We also simulated and added the gravity variation derived by the theory earth tide and air pressure related to specific times and locations based on recordings from an actual field gravity survey campaign. In total, 202 GD observation values, which form up to eight loops, were simulated for each gravimeter, and these were used to estimate the gravity values at the 91 stations.

4.1 Case 1: Comparison between optimally and equally weighted adjustment methods for linear drift model with instrument-dependent observational noise

In this case, we mainly aimed to compare the results from the equally weighted and optimally weighted adjustment constraints. The records from two gravimeters were simulated. The standard deviation (SD) of the white noise in the input GD with meters 1 and 2 at all stations was 11.63 μGal and 4.21 μGal (Table 1), respectively. The initial SD estimation of both GD values as input was 10 μGal. The rates of the linear instrumental drifts, which were added to the gravity observation, are listed in Table 1. The adjustment results for the optimally weighted approach (Sect. 3.2) are shown in Table 1. The SD of residual GD after adjustment was equal to the prior estimation by the MLE.

Table 1 Results from optimally weighted by the conventional linear drift adjustment model in Case 1

The residuals of GDs from the two adjustment models are shown in Fig. 4. In the case of the equally weighted adjustment, the weights do not match the SDs of the GD residuals. But the optimally weighted adjustment could estimate the appropriate weights in this case. The GD residuals after adjustment show clearly that the optimally weighted adjustment can recover the noise level that was added to the input. The differences between the adjustment results and actual gravity values at 91 stations are also summarized in Table 2, and they indicate that the optimally weighted adjustment results are more robust than those of the equally weighted approach.

Fig. 4

Comparison in GD residuals with two gravimeter problems between the equally weighted and optimally weighted conventional adjustment methods in case 1. The points to the left of the red lines represent the residuals of GD by gravimeter No. 1 after adjustment, and the points to the right by gravimeter No. 2. a The adjustment with equal weights, b the adjustment with optimal weight. The GD indices are grouped by the observing instruments

Table 2 Difference between the adjustment and real gravity values at all stations for Case 1 (Unit: μGal)

This adjustment needs to be applied to a large-scale gravity network, where tens of gravimeters are generally used for measurement in the same time period. The adjustment results are more accurate if the optimal weighting is applied based on the likelihood function proposed in this paper to estimate the optimally weighted values. The minimized process for searching the optimal weights is shown in Fig. 5.

Fig. 5

Filled contour image for the negative log-likelihood with the two weights for case 1

4.2 Case 2: Nonlinear drift rate model

In this case, records from gravimeters with nonlinear drift rates were simulated. The purpose is to compare the adjustment results between linear and stochastic drift rate models. For simplification, only the problem of adjusting one gravimeter is discussed. Two datasets with different nonlinear drift rate models were simulated for the experiment. The temporal variations of the simulated drift rates are shown in Fig. 6. The SD of the observed noise with models 1 and 2 was the same 3 μGal at all stations.

Fig. 6

Estimated nonlinear drift rates for (a) model 1 and (b) model 2 in Case 2 from the Bayesian adjustment method. The solid black lines show the temporal variations of the drift rates during the survey days. The dotted blue lines show the inversed variation of the drift rate. The gray areas, which contain the dashed line segments, represent the estimated standard deviation of inversed drift rates

In this case, a duration of 16 days was used for the entire gravity survey campaign. Bayesian and classical adjustments were applied and compared. The smoothness of nonlinear drift rates can be estimated by the Bayesian approach (minimizing the ABIC) as shown in Fig. 6.

The GD residuals can be used to validate adjustment methods. Figure 7 shows the GD residuals in chronological sequence. It is easy to see in Fig. 7a, c that non-stochastic trends can be found in the processing of the GD residuals, indicating that the hypothesis behind the linear drift model is not suitable in this case and that the nonlinear drift rate model should be considered. The GD residuals obtained using the Bayesian adjustment are plotted in Fig. 7b, d. The true standard deviation of the input noise for the GDs is about 4.2 μGal, and the estimated SD of GD from the Bayesian adjustment is about 4.1 μGal. These results verified that the Bayesian adjustment gives suitable posterior estimation.

Fig. 7

GD residuals from fitting the classical (a, b) and Bayesian adjustment (c, d) methods. a and c are results from fitting model 1. b and d are results from fitting model 2. BAY and CLS indicate the Bayesian and classical adjustments, respectively

The ABIC value as a function of hyper-parameters $\sigma^{2}$ and $\sigma_{b}^{2}$ is shown in the contour image in Fig. 8. Since searching the minimum value of ABIC is time-consuming, we employed the simplex method (Lagarias et al. 1998) to boost the speed of adjustment. The minimum ABIC value is equal to − 1004.1, as shown in Fig. 8. The trade-off between the two hyper-parameters, $\sigma^{2}$ and $\sigma_{b}^{2}$, balanced the smoothness of the variation of the drift rate and the variance of GD residuals.

Fig. 8

Contours of the ABIC values in the Bayesian adjustment with the nonlinear drift rate (model 2) for Case 2

4.3 Case 3: Multi-gravimeter adjustment using Bayesian adjustment method

In this case, we simulated a dataset in which two gravimeters are used to test the Bayesian adjustment algorithm. Practically, double gravimeters are used in a gravity survey campaign to reduce the effects by the offset change, tares, outliers, and other random or system errors caused by instruments and environments. This simulation model with double gravimeters is designed for testing the potential advantages and efficiency of the Bayesian adjustment.

The nonlinear variations of the drift rates are shown in Fig. 9. In this case, the nonlinear drift features of the two gravimeters are obviously different. The SD noises added to the recordings for meters 1 and 2 were 9.1 μGal and 4.3 μGal, respectively. If the Bayesian adjustment is employed, four hyper-parameters need to be estimated. For comparison, we applied both the classical and Bayesian adjustment methods to estimate the gravity values for all 91 stations. The results are shown in Fig. 10. It is clear that the results from the Bayesian adjustment method are better than those from the classical method. The SDs of GD residuals of Bayesian adjustment for meters 1 and 2 are 8.7 and 4.2 μGal, respectively, while for the classical adjustment, they are 7.0 and 8.8 μGal, respectively. The optimal SD given by the classical method is smaller than that given by the Bayesian results, but the Bayesian method gives a value closer to the SD of actual noise. Because the drift rate of meter 1 changed little, the estimated drift rate of meter 1 was over-fitted on the basis of linear drift rate model. However, the larger drift rate variation in meter 2 cannot be illustrated if using the linear drift rate and the classical adjustment because the SD of 8.8 μGal is far from its true value of 4.3 μGal.

Fig. 9

Estimates of the nonlinear drift rates of the two gravimeters in Case 3. The red and blues lines are the simulated and inverted drift rates for gravimeters 1 and 2, respectively. The solid lines show the variation of the drift rates used in the simulation. The dotted lines show the inverted results

Fig. 10

Difference between results from two adjustments and true gravity values in the simulation for all 91 stations in Case 3. The red solid lines indicate the true gravity values

Comparing the adjustment results to the true gravity values at all stations (Fig. 10), we can see that the Bayesian adjustment is still better than the classical method with the optimal weight classical adjustment method in case 3. The details are summarized in Table 3.

Table 3 Comparison between results from two adjustments and true gravity values in the simulation for all the stations in Case 3 (Unit: μGal)

4.4 Case 4: Sensitivity analysis for adjustment of input parameters

In cases 1–3, the uncertainties caused by the reductions of the tide and air loading are considered. To reduce such effects, two suitable parameters, generally called earth TF and AA, need to be used. In this section, we employ a sensitivity analysis approach to evaluate the potential effects caused by the uncertainty in a priori parameters.

Significant daily gravity changes are caused by tidal forces acting on the solid earth and oceans, and they range up to 0.3 mGal peak to peak (Hinze et al. 2013). The ocean tide loading is generally less than 10% of the solid earth tide. The value of TF generally varies over time and space owing to the fact that the actual earth is not a rigid body. The regional tidal factors can be estimated by the long-term continuous gravity observations, such as for 1 year or longer. The TF value can be approximated as 1.16 because its value is 1.1562 in the two-degree preliminary reference earth model (Dehant et al. 1999). An accurate TF value is often used to generate a time series of tidal gravity variation at a specific spatiotemporal location. But the TF value is likely to change, due to various factors, including the solid earth model, ocean tide loading model, and latitude dependence. The general variation is possibly about 2% (Hinze et al. 2013).

However, only the non-tidal gravity signal is of interest in a gravity survey campaign, and data are insufficient to estimate the TF. Therefore, the TF value needs be given as an a priori parameter before the gravity adjustment.

In addition, the atmosphere also affects gravity variation, which adds up to 10% of the TF over a wide frequency range, from minutes to seasonal periods (Crossley et al. 2013). A scalar admittance as a good approximation relates observed gravity to local pressure variation. A nominal AA value widely used is -0.3 μGal/hPa. The relationship includes the attraction of the atmosphere above the gravimeter and loading from air masses that elastically deform the crust (Warburton and Goodkind 1977). The AA value may change between − 0.27 and − 0.43 μGal/hPa using different local-zone models (Merriam 1992). A frequency-dependent admittance is also proposed and seen as a better approximation. The resulting difference between the two alternative approaches is not significant at the 0.5-μGal level (Hinderer et al. 2007). In general, the simple AA value is enough to remove the atmospheric effects, and the AA correction is straightforward.

In this case, a sensitivity analysis of the simulated gravity response with respect to the a priori model parameters was carried out. The sensitivity runs were performed using the simulated data. Sensitivities are reported as scaled sensitivities (SS) (Hill 1998):

$$ SS = \left( {\Delta e/e} \right)/\left( {\Delta p/p} \right), $$

where $e$ is the root-mean-square error (RMSE) of the gravity value in the specific a priori parameters, ∆e is the change of RMSE, p is the parameter value in the reference run, and ∆p is the parameter change.

First, 5% and 10% errors of TF were applied to tidal correction before the network adjustment. The periodic earth tide signal was mixed with the gravity time-series data. The smoothed feature was more similar to the nonlinear drift gravity variation, so it can be an error source that affects the accuracy of the adjustment. Second, 5 and 10% errors of AA were applied to the atmospheric effects correction before the network adjustment.

In this case, we employed the nonlinear drift model with noise for recordings from one gravimeter. The RMSE of residual GD after adjustment was 4.13 μGal using the exact a priori parameters. From the SS variation with different a priori parameter errors (Table 4), the 10% AA uncertainty only made the RMSE variation less than 0.01 μGal. The uncertainties related to the TF could affect the RMSE variation up to 0.8 μGal. It is clear that the results are more sensitive to TF than to AA, and the Bayesian adjustment results are stable because of the small variation of SS values. For the 10% uncertainties with respect to the TF and AA, the sensitivity is not significant.

Table 4 Sensitivity test of uncertainty in prior parameters in Case 4

But the SS values are also related to the noise level in the observed gravity data. If the noise feature can be estimated in the actual gravity survey campaign, we can select the appropriate method to estimate the a priori parameters by means of the sensitivity test. The corrections related to the controlled uncertainty of a priori parameters should be applied to reduce their effect on gravity before the gravity network adjustment processing.

5 Processing actual gravity survey data

In this section, we apply the Bayesian adjustment algorithm to two gravity observation datasets from North China.

5.1 Example 1

The first observation network, which has 95 stations, 103 segments and eight circuits, is shown in Fig. 11a. The field observation for this network is performed twice annually. The gravity survey campaign for our first dataset was carried out in September 2014, and a total of 412 measurements were obtained for gravity variations using dual gravimeters over 16 days.

Fig. 11

a Route map of gravity survey campaign in the Beijing region and differences between gravities at each station estimated by the linear and nonlinear drift rate models in the survey during September 2014. b GD residuals from the Bayesian adjustment method with two gravimeters. c Same as (b) but from the classical adjustment method. d Histograms of GD residuals in (b) and (c). e Estimated drift rates of two gravimeters, Nos 1099 and 1097, and their error bands. In (a), the triangles mark the locations of cities in this area. In (b) and (c), the data series left to the vertical red straight lines are the GD residuals for gravimeter No. 1099 after adjustment and the data series to the right are for gravimeter No. 1097

We applied both the Bayesian and the classical adjustment approaches to this dataset. The spatial differences between the linear and nonlinear drift rate models for adjustment are shown in the geometrical route map in Fig. 11a. Results showed the existence of gravity differences of a few tens of microgals. Significant differences between the two approaches appear in regions close to the edge of the network in Fig. 11a.

The fitting residuals for the actual GDs are plotted as Fig. 11b and 11c, and a histogram of the residuals is shown in Fig. 11d. It is obvious that the residuals from the Bayesian method are smaller and more like stochastic noise than those from the classical method. If using a simplistic linear drift model to estimate the gravity values, the residuals in Fig. 11c do not satisfy the assumptions of stochastic noise; rather, they show a systematic trend with time.

Thus, the existence of nonlinear drift in the actual gravity survey data has been demonstrated. Figure 11e shows the estimated temporal changes of the drift rates using the Bayesian adjustment approach with the related uncertainties. The variations of the drift rates are nonlinear and different from each other. The variation pattern of actual drift rates is similar to the simulated cases. Therefore, the Bayesian adjustment is effective and robust for the practical case.

5.2 Example 2

The second dataset is from a large-scale gravity survey campaign in a network containing 155 stations, 181 segments and 20 circuits (Fig. 12), carried out during the period from August 4 to September 25, 2015. Three gravimeters (CG-5 #1097, #1098, and #1099) were used for this survey. In total, 780 measurements of gravity differences between adjacent stations were observed over 53 days.

Fig. 12

Differences between estimated gravity values by the linear and nonlinear drift rate models at each station in the extended observation network when different absolute gravity stations are using the base observations: a BJT, b ZJK, c DX and d BJT & DX

In this case, the network contains three absolute gravity stations (BJT, ZJK, and DX). The detailed configuration and results for the absolute gravity measurement are shown in Table 5. For evaluating the effectiveness of the Bayesian adjustment method, we designed the following experiment: Only one or two absolute gravity values were used for adjustment, and the absolute gravity values at the other stations were compared with their corresponding values obtained using the two adjustment methods.

Table 5 Absolute gravity stations

We sequentially used the absolute gravity values from the BJT, ZJK, and DX stations in the adjustment, and the other two absolute gravity values were used to validate these adjustments. The results, given in Table 6, show that the Bayesian adjustment method produced results better than those of the conventional method. When both absolute gravity values from the BJT and DX stations were used in the adjustment, the Bayesian approach (last three rows in Table 6) still produced better estimates than did the conventional method. The spatial differences between the linear and nonlinear drift rate models for adjustment are shown in the geometrical route map in Fig. 12. The figure shows the existence of gravity differences of a few tens of microgals. Again, significant differences between the two approaches are visible in regions close to the edge of network in Fig. 12. Gravity values at stations along the same path in Fig. 12 potentially were measured on the same day. If using a linear drift rate model or classical adjustment method to deal with this network, systematic biases might be resulted from periods when the drift rate of the gravimeter changes.

Table 6 Adjustment result when using different absolute gravity stations as known (unit: μGal)

6 Conclusions

Relative gravimeters have been widely used in terrestrial gravity measurement. Designing and using a suitable model to estimate the nonlinear drift of relative gravimeters is a key point of gravity data adjustment. The drift and noise are the two main causes of errors and can be estimated by using redundant gravity observations, including adding more absolute gravity observations and increasing the number of loops in the survey network, with suitable data processing methods. To deal with the drift problem, we presented a novel approach for gravity campaign data processing, based on the Bayesian analysis theory. The basic assumption is that the variation of instrument drift rate is smooth over the entire campaign period for any relative gravity meters that are in good conditions. Such a prior constraint of the smoothness for the drift rate has been introduced to replace and to improve the linear drift model. On the basis of the “principle of parsimony,” appropriate unknown hyper-parameters were used to estimate the model using ABIC to balance the fitting residuals and the smoothness of the drift rate. Our Bayesian adjustment approach gives a good trade-off to avoid over-fitting problems.

In our results from model testing and error analysis, this new Bayesian approach for the network gravity adjustment was shown to be effective and straightforward for estimating the temporally complicated variation of meter drift rate. Particularly, if only linear drift exists in the relative gravity measurement, then there is little difference between this approach and the classical adjustment method. The testing results also showed that the Bayesian adjustment method is robust and adaptive for solving a similar problem for irregular drift rates. The new approach balances the survey productivity and the accuracy of gravity measurement and is especially powerful when returning to a base station takes more than 24 h in long-distance gravity surveys, when the gravimeter has a high-ordered drift rate, and when the environment or transportation is complex during the campaign.

In our experience, the computational load was affordable and could be handled by the majority of modern personal computers. A potential difficulty with this approach is that the dimensionality could increase dramatically if a large number of different gravimeters are used in the same survey campaign. The Nelder–Mead simplex nonlinear optimization method used in this work is more effective than other direct searching methods to optimize the joint likelihood function. Parallel computational techniques will be used to improve the computational efficiency in future work.

In summary, the objective Bayesian approach is suitable and powerful for reducing the effects of meter drift and stochastic noise in terrestrial gravity surveys performed in a large-scale and complicated network.

Appendices

Appendix A: List of notations

Notation	Description
Integers
$P$	Number of gravimeters used in the survey
$N$	Number of gravity stations
$K, K_{i}$	Total number of GD values and number of GD values observed by gravimeter $i$
$M, M_{i}$	Total length of the drift rate vector for all the gravimeters and length of the drift rate vector for gravimeter $i$
$K_{g}$	Number of absolute gravity observations
Matrices	(See Appendix B for details)
${\mathbf{A}}$	The configuration related to the observed sequences between two adjacent gravity stations for the entire survey
${\mathbf{A}}_{i}$	The configuration related to the observed sequences between two adjacent gravity stations for gravimeter $i$
${\mathbf{D}}$	The configuration for all the durations between the two adjacent gravity observations used to estimate the drift
${\mathbf{D}}_{\varvec{i}}$	The configuration for all the durations between the two adjacent gravity observations for Gravimeter $i$
${\mathbf{G}}$	The configuration related to the absolute gravity observations
${\mathbf{B}}$	The smoothness configuration matrix for drift rate variation for all the gravimeters. The second-order model used in this paper
${\mathbf{B}}_{i}$	The smoothness configuration for drift rate variation for Gravimeter $i$. The second-order model used in this paper
${\mathbf{S}}, {\bar{\mathbf{S}}}$	The combination related to the observed configurations
${\mathbf{W}}_{i}$	The weight diagonal matrix of relative gravimeter $i$, composed of the reciprocal of each relative gravimeter variance $\sigma_{i}^{2}$
${\mathbf{W}}$	The weight matrix of all relative gravimeters, ${\mathbf{W}} = {\text{diag }}\left[ {{\mathbf{W}}_{1} , {\mathbf{W}}_{2} , \ldots ,{\mathbf{W}}_{P} } \right]$
${\mathbf{W}}_{\varvec{g}}$	The weight diagonal matrix of absolute gravity, which has been given before adjustment, composed of the reciprocal of each absolute gravimeter variance $\sigma_{g}^{2}$
${\mathbf{W}}_{{\varvec{b}i}}$	The weight diagonal matrix of variations of drift rates for gravimeter $i$, composed of the reciprocals of the variances $\sigma_b^2$ for variations of each drift rate.
${\mathbf{W}}_{\varvec{b}}$	The weight matrix of the variations of drift rates for all the gravimeters, ${\mathbf{W}}_{\varvec{b}} = {\text{diag }}\left[ {{\mathbf{W}}_{b1} , {\mathbf{W}}_{b2} , \ldots ,{\mathbf{W}}_{bP} } \right]$
${\tilde{\mathbf{W}}},\varvec{ }{\bar{\mathbf{W}}}$	The combined matrix related to all the weighted diagonal matrices for the conventional and the Bayesian adjustment methods
$*^{\varvec{T}}$	The transposition of matrix*
Vectors
$\varvec{y}$	The GD vector from the observation, which has been given before adjustment
$\varvec{x}$	The gravity value vector at all stations, which will be estimated by adjustment
$\varvec{v}$	The drift rate vector for all relative gravimeters, which will be estimated by adjustment
$\varvec{g}$	The known absolute gravity values, which has been given before adjustment
$\varvec{X} = \left( {\begin{array}{*{20}c} \varvec{x} \\ \varvec{v} \\ \end{array} } \right)$	Combined vector of $\varvec{x}$ and $\varvec{v}$
$\varvec{Y} = \left( {\begin{array}{*{20}c} \varvec{y} \\ \varvec{g} \\ \end{array} } \right)$ $\bar{\varvec{Y}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} \varvec{y} \\ \varvec{g} \\ \end{array} } \\ {\tilde{0}} \\ \end{array} } \right)$	Combined vectors of $\varvec{y}$ and $\varvec{g}$ Combined vectors of $\varvec{y}$ and $\varvec{g}$ and zeros

Appendix B: The structure of Matrices

In Eq. (10) in Sect. 3.2, for the conventional adjustment model, matrices ${\mathbf{A}}$ and ${\mathbf{G}}$ are the relative and absolute gravity observation configurations, respectively. ${\mathbf{D}}$ consists of the durations for observing each GD. These matrices can be defined by:

$$ \begin{aligned} & {\mathbf{A}} = \left[ {\xi_{kj} } \right]_{K \times N} ,\quad \xi_{ij} = \left\{ {\begin{array}{*{20}l} { - 1, } \hfill & {{\text{if}}\,s\left( k \right) = j} \hfill \\ {1, } \hfill & {{\text{if}}\,e\left( k \right) = j} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.;\quad {\mathbf{G}} = \left[ {\eta_{ij} } \right]_{{K_{g} \times N}} ,\\ &\quad \eta_{ij} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\,v\left( i \right) = j} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ & {\mathbf{D}} = \left[ {\delta_{kj} } \right]_{K \times P} ,\quad \delta_{ij} = \left\{ {\begin{array}{*{20}l} {t_{k}^{\left( e \right)} - t_{k}^{\left( s \right)} ,} \hfill & {{\text{if}}\,q\left( k \right) = j} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(B.1)

The weight matrices have a diagonal form:

$$\begin{aligned} & {\mathbf{W}} = {\text{diag}}\left[ {\frac{1}{{\sigma_{q\left( 1 \right)}^{2} }},\frac{1}{{\sigma_{q\left( 2 \right)}^{2} }}, \ldots ,\frac{1}{{\sigma_{q\left( K \right)}^{2} }}} \right] ,\\ & {\mathbf{W}}_{g} = {\text{diag}}\left[ {\frac{1}{{\sigma_{g}^{2} }},\frac{1}{{\sigma_{g}^{2} }}, \ldots ,\frac{1}{{\sigma_{g}^{2} }}} \right]_{{K_{g} }} ; \end{aligned} $$

(B.2)

If we re-order the elements of the above matrices by grouping them according to the used instrument, then

$$ \begin{aligned} & \varvec{y} = \left[ {\varvec{y}_{1}^{\text{T}} ,\varvec{y}_{2}^{\text{T}} , \ldots ,\varvec{y}_{P}^{\text{T}} } \right]^{\text{T}} \\ & {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {\left[ {{\mathbf{A}}_{1} } \right]_{{K_{1} \times N}} } \\ {\left[ {{\mathbf{A}}_{2} } \right]_{{K_{2} \times N}} } \\ \cdots \\ {\left[ {{\mathbf{A}}_{P} } \right]_{{K_{P} \times N}} } \\ \end{array} } \right],\quad {\mathbf{D}} = \left[ {\begin{array}{*{20}l} {\left[ {{\mathbf{D}}_{1} } \right]_{{K_{1} \times 1}} } \hfill & 0 \hfill & \cdots \hfill & 0 \hfill \\ 0 \hfill & {\left[ {{\mathbf{D}}_{2} } \right]_{{K_{2} \times 1}} } \hfill & \cdots \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & {\left[ {{\mathbf{D}}_{p} } \right]_{{K_{p} \times 1}} } \hfill \\ \end{array} } \right] \\ & {\bar{\mathbf{W}}} = \left[ {\begin{array}{*{20}c} {\left[ {{\mathbf{W}}_{1} } \right]_{{K_{1} \times K_{1} }} } & 0 & \cdots & 0 & 0 \\ 0 & {\left[ {{\mathbf{W}}_{2} } \right]_{{K_{2} \times K_{2} }} } & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & {\left[ {{\mathbf{W}}_{p} } \right]_{{K_{p} \times K_{p} }} } & 0 \\ 0 & 0 & \cdots & 0 & {\left[ {{\mathbf{W}}_{g} } \right]_{{N_{g} \times N_{g} }} } \\ \end{array} } \right] \\ & {\mathbf{W}}_{i} = \left[ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{i}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{i}^{2} }$}}} & 0 & \cdots & 0 \\ 0 & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{i}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{i}^{2} }$}}} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{i}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{i}^{2} }$}}} \\ \end{array} } \right]_{{K_{i} \times K_{i} }} ,i = 1,2, \ldots p; \\ & {\mathbf{W}}_{g} = \left[ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{g}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{g}^{2} }$}}} & 0 & \cdots & 0 \\ 0 & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{g}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{g}^{2} }$}}} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{g}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{g}^{2} }$}}} \\ \end{array} } \right]_{{N_{g} \times N_{g} }} \\ \end{aligned} $$

(B.3)

In Sect. 3.3, for the Bayesian adjustment model, the matrices in Eqs. (24) and (25) are written in detail as:

$$ \begin{aligned} & {\bar{\mathbf{W}}} = \left( {\begin{array}{*{20}c} {\mathbf{W}} & 0 & 0 \\ 0 & {{\mathbf{W}}_{g} } & 0 \\ 0 & 0 & {{\mathbf{W}}_{b} } \\ \end{array} } \right)\quad {\text{and}}\quad {\bar{\mathbf{S}}} = \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{D}} \\ {\mathbf{G}} & 0 \\ 0 & {\mathbf{B}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{A}}_{1} } & {{\mathbf{D}}_{1} } & 0 & \cdots & 0 \\ {{\mathbf{A}}_{2} } & 0 & {{\mathbf{D}}_{2} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{\mathbf{A}}_{P} } & 0 & 0 & \cdots & {{\mathbf{D}}_{P} } \\ {\mathbf{G}} & 0 & 0 & \cdots & 0 \\ 0 & {{\mathbf{B}}_{1} } & 0 & \cdots & 0 \\ 0 & 0 & {{\mathbf{B}}_{2} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & {{\mathbf{B}}_{P} } \\ \end{array} } \right], \\ & {\mathbf{W}}_{b} = \left[ {\begin{array}{*{20}c} {\left[ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{b1}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{b1}^{2} }$}}} \right]_{{{\text{T}} \times {\text{T}}}} } & 0 & \cdots & 0 \\ 0 & {\left[ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{b2}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{b2}^{2} }$}}} \right]_{{{\text{T}} \times {\text{T}}}} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {\left[ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma_{bP}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{bP}^{2} }$}}} \right]_{{{\text{T}} \times {\text{T}}}} } \\ \end{array} } \right] \\ \end{aligned} $$

(B.4)