Calibration of the clock-phase biases of GNSS networks: the closure-ambiguity approach

Abstract

In global navigation satellite systems (GNSS), the problem of retrieving clock-phase biases from network data has a basic rank defect. We analyse the different ways of removing this rank defect, and define a particular strategy for obtaining these phase biases in a standard form. The minimum-constrained problem to be solved in the least-squares (LS) sense depends on some integer vector which can be fixed in an arbitrary manner. We propose to solve the problem via an undifferenced approach based on the notion of closure ambiguity. We present a theoretical justification of this closure-ambiguity approach (CAA), and the main elements for a practical implementation. The links with other methods are also established. We analyse all those methods in a unified interpretative framework, and derive functional relations between the corresponding solutions and our CAA solution. This could be interesting for many GNSS applications like real-time kinematic PPP for instance. To compare the methods providing LS estimates of clock-phase biases, we define a particular solution playing the role of reference solution. For this solution, when a phase bias is estimated for the first time, its fractional part is confined to the one-cycle width interval centred on zero; the integer-ambiguity set is modified accordingly. Our theoretical study is illustrated with some simple and generic examples; it could have applications in data processing of most GNSS networks, and particularly global networks using GPS, Glonass, Galileo, or BeiDou/Compass satellites.

Appendices

Appendix A: Elementary notions on GNSS graphs

In this appendix, we present some preliminary notions of algebraic graph theory; these elementary notions are used throughout the paper. Further details about the functional spaces and the operators involved in the GNSS problems can be found in Sect. 3. We first define the notions of GNSS grid and GNSS graph (Sect. ). We then introduce the concepts of spanning tree and loop (Sect. ).

1.1 A.1 GNSS grid and graph

For our present purpose (see Sects. 2.1 and 2.2 in particular), we consider a typical situation in which the network has $n_\mathrm{r}$ receivers ${\mathrm{r}}_i$ and $n_\mathrm{s}$ satellites $\mathrm{s}_j$. (We recall that ‘satellite’ should be here understood as ‘satellite transmitter;’ see Sect. 1.) The ‘network grid’ $G_\mathrm{o}$ then includes $n_\mathrm{r}$ rows, $n_\mathrm{s}$ columns, and $n_\mathrm{r} n_\mathrm{s}$ points; see Fig. 7. A function such as $N(i,j)$ for example takes its values on some points $(i,j)$ of that grid. Those points form a subgrid denoted by ${G}$.

In the example presented in Fig. 7, the points $(i,j)$ of ${G}$ are displayed as large dots in the upper part of this figure. Those points correspond to the ‘edges’ $({\mathrm{r}}_i , \mathrm{s}_j)$ of the graph associated with the GNSS network; this graph is displayed in the lower part of Fig. 7; $\mathcal{E }$ denotes the set of its edges; $n_\mathrm{e}$ is their number. The receivers and the satellites involved in the definition of these edges define the ‘vertices’ of this graph; $\mathcal{V }$ denotes the set of its vertices, and $n_\mathrm{v}$ their number: $n_\mathrm{v}= n_\mathrm{r} + n_\mathrm{s}$. A graph such as $\mathcal{G }$ is therefore defined by the pair $(\mathcal{V }, \mathcal{E })$: $\mathcal{G }\equiv \mathcal{G }(\mathcal{V }, \mathcal{E })$. We now assume that $\mathcal{G }$ is connected: given any two vertices of $\mathcal{V }$, there exists a path of edges of $\mathcal{E }$ connecting these vertices (see, e.g., Biggs 1996).

Fig. 7

Subgrid ${G}$ and graph $\mathcal{G }$. In the example described here, the network grid $G_\mathrm{o}$ includes twelve points ($n_\mathrm{r} =3$, $n_\mathrm{s} = 4$), while its subgrid ${G}$ includes nine points only; these points are shown as large dots. The corresponding graph $\mathcal{G }$ includes seven vertices and nine edges: $n_\mathrm{v}= n_\mathrm{r} + n_\mathrm{s} =7$, $n_\mathrm{e} = 9$; ${\mathrm{r}}_1$ does not see $\mathrm{s}_2$, ${\mathrm{r}}_2$ does not see $\mathrm{s}_3$, and ${\mathrm{r}}_3$ does not see $\mathrm{s}_1$

1.2 A.2 GNSS spanning tree and loops

As illustrated in Fig. 8, a spanning tree of a connected graph $\mathcal{G }\equiv \mathcal{G }(\mathcal{V }, \mathcal{E })$ is a subgraph $\mathcal{G }_\mathrm{st} \equiv \mathcal{G }_\mathrm{st}(\mathcal{V }, \mathcal{E }_\mathrm{st})$ formed by $n_\mathrm{v}$ vertices and $n_\mathrm{v} - 1$ edges, with no ‘cycle’ in it. Here, ‘cycle’ is used in the sense defined in algebraic graph theory (see, e.g., Biggs 1996). In the GNSS community, to avoid any confusion with the usual notion of wave cycle, the term of ‘loop’ can be substituted for that of ‘cycle.’ In this context, the number of loops defined through a given fixed (but arbitrary) spanning tree is the number of edges of $\mathcal{E }$ that do not lie in $\mathcal{E }_\mathrm{st} \,$. These edges, $\mathrm{c}(\ell ) {\displaystyle {} \mathop {=}^\mathrm{\scriptscriptstyle def}{}}({\mathrm{r}}_{i_\ell } , \,\mathrm{s}_{j_\ell })$, are said to be ‘(loop-)closure edges’ (see Fig. 8). Their number is denoted by $n_\mathrm{c}$:

$$\begin{aligned} n_\mathrm{c} = n_\mathrm{e} - n_\mathrm{st} \end{aligned}$$

(84)

where

$$\begin{aligned} n_\mathrm{st} {\displaystyle {} \mathop {=}^\mathrm{\scriptscriptstyle def}{}}n_\mathrm{v} - 1 = n_\mathrm{r} + n_\mathrm{s} - 1 \end{aligned}$$

(85)

Many spanning trees of the same graph can be constructed. Here, we are going to present the Kruskal algorithm which is often used in algebraic graph theory (see Biggs 1996). The first step of this algorithm consists in ordering the edges of $\mathcal{E }$, thus generating a sequence of the form $\{ ({\mathrm{r}}_{i_q}, \,\mathrm{s}_{j_q}) : \; q =1, \ldots , n_\mathrm{e} \}$. The spanning tree is then obtained as follows. Set $q =0$, $n_\mathrm{st}= 0$, and $\mathcal{E }_\mathrm{st} = \emptyset$ (the empty set). Then,

• (i) if $n_\mathrm{st} = n_\mathrm{v} - 1$, terminate the process; otherwise, set $q := q+1$;

• (ii) when the vertices of edge $({\mathrm{r}}_{i_q}, \mathrm{s}_{j_q})$ are not connected via edges of $\mathcal{E }_\mathrm{st}$, set ${\mathcal{E }_\mathrm{st}} := {\mathcal{E }_\mathrm{st}} \cup \{ (\mathrm{r}_{i_q}, \mathrm{s}_{j_q}) \}$, $n_\mathrm{st} := n_\mathrm{st} + 1$; then go to step (i).

By construction, the spanning tree thus found depends on how the edges are ordered in the first step. The subgrid of ${G}$ corresponding to the edges of $\mathcal{G }_\mathrm{st}$ is denoted by ${G}_\mathrm{st}$; ${G}_\mathrm{c}$ is that corresponding to the closure edges:

$$\begin{aligned} {G}_\mathrm{c} {\displaystyle {} \mathop {=}^\mathrm{\scriptscriptstyle def}{}}\{(i,j) \in {G}: (i,j) \notin {G}_\mathrm{st} \} \end{aligned}$$

(86)

Clearly, ${G}_\mathrm{c}$ includes $n_\mathrm{c}$ loop-closure points; see Eq. (84) and Fig. 8.

To illustrate the action of the Kruskal algorithm, let us consider the graph $\mathcal{G }$ of Fig. 7. To build a spanning tree of $\mathcal{G }$ from its grid ${G}$, let us order the edges of $\mathcal{G }$ by scanning ${G}$ from left to right and top to bottom. The algorithm examines the edges of $G$ in that order and adds them to the current version of $\mathcal{E }_\mathrm{st}$ when condition (ii) holds. In this example, this is the case for the first five edges; the vertices $\mathrm{s}_1, \,\mathrm{s}_3, \,\mathrm{s}_4, \,{\mathrm{r}}_1, \,{\mathrm{r}}_2$ are thus connected. The sixth edge, $({\mathrm{r}}_2, \,\mathrm{s}_4)$, therefore includes two vertices already connected. This edge is therefore the first closure edge: $\mathrm{c}(1) = ({\mathrm{r}}_2, \,\mathrm{s}_4)$. The next edge, $({\mathrm{r}}_3, \mathrm{s}_2)$, is added to $\mathcal{E }_\mathrm{st}$ since it corresponds to the first connection of $\mathrm{s}_2$ with the edges of the current version of $\mathcal{E }_\mathrm{st}$. All the vertices of $\mathcal{G }$ are then connected. The remaining edges are therefore closure edges: $\mathrm{c}(2) = ({\mathrm{r}}_3,\, \mathrm{s}_3)$, $\mathrm{c}(3) = ({\mathrm{r}}_3, \,\mathrm{s}_4)$. The $\mathcal{G }_\mathrm{st}$-edge set thus obtained is the following (see Fig. 8):

$$\begin{aligned} \mathcal{E }_\mathrm{st} := \big \{ ({\mathrm{r}}_1, \mathrm{s}_1), ({\mathrm{r}}_1, \mathrm{s}_3), ({\mathrm{r}}_1, \mathrm{s}_4), ({\mathrm{r}}_2, \mathrm{s}_1), ({\mathrm{r}}_2, \mathrm{s}_2), ({\mathrm{r}}_3, \mathrm{s}_2) \big \} \end{aligned}$$

Note that this procedure does not provide the edge path of $\mathcal{E }_\mathrm{st}$ that links the vertices of the closure edge under consideration. Clearly, closure paths are not needed to be known for the construction of $\mathcal{G }_\mathrm{st}$. In simple cases such as that of Fig. 8, such a path can visually be obtained by moving on grid ${G}$ horizontally and vertically, in alternate manner from the selected closure-edge point; see the related telescoping sums introduced in Sect. 3.3. If need be, the edges paths can be obtained automatically in an algebraic manner; see Sect. 3.4.

Fig. 8

GNSS spanning tree and loops. Here, the edges of the selected spanning tree $\mathcal{G }_\mathrm{st}$ of the graph $\mathcal{G }$ introduced in Fig. 7 are shown as thick lines. The points of the corresponding subgrid ${G}_\mathrm{st}$ are shown as large dots. The remaining points of ${G}$ (the small dots of ${G}$) correspond to the (loop-)closure edges (the thin edges of $\mathcal{G }$). We then have one loop of order four, and 2 loops of order six: $({\mathrm{r}}_2 , \,\mathrm{s}_4, \,{\mathrm{r}}_1, \,\mathrm{s}_1)$, $({\mathrm{r}}_3, \,\mathrm{s}_3, \,{\mathrm{r}}_1, \,\mathrm{s}_1, \,{\mathrm{r}}_2, \,\mathrm{s}_2) \,$ and $\,({\mathrm{r}}_3, \,\mathrm{s}_4, \,{\mathrm{r}}_1, \,\mathrm{s}_1, \,{\mathrm{r}}_2, \,\mathrm{s}_2)$. In ${G}$, these orders are shown as small numbers

Appendix B: The S-system approach

In this appendix, we give a survey of the general framework of the S-system approach; for further details and related applications, see Baarda (1973), Teunissen (1984), de Jonge (1998), Teunissen and Odijk (2003).

Denoting by $\mathfrak{E }$ a Euclidean space of dimension $\text{ n }$, we consider some linear operator $\mathcal{A }$ from $\mathfrak{E }$ into $\mathbb{R }^\mathrm{m}$ with $\text{ m } \ge \text{ n }$ for example. The problem to be solved in a sense to be defined is governed by a relation of the form

$$\begin{aligned} \mathcal{A }\xi = \gamma \end{aligned}$$

(87)

The components of $\xi$ are the unknown parameters of the problem, whereas $\gamma$ is the data vector. In many situations encountered in practice, $\mathcal{A }$ is not of full rank; its null space (i.e., its kernel) is not reduced to $\{0\}$:

$$\begin{aligned} \mathrm{n}_0 {\displaystyle {} \mathop {=}^\mathrm{\scriptscriptstyle def}{}}\dim (\ker \mathcal{A }) \ge 1 \end{aligned}$$

(88)

In the S-system approach, this rank defect is removed via an appropriate reduction and redefinition of the unknown parameters. Those new parameters are the ‘estimable functions of parameters’ of some minimum- constrained problem thus defined (see, e.g., de Jonge 1998). We now give a geometrical interpretation of the S-system principle.

Let us choose some subspace $\mathfrak{F }$ of $\mathfrak{E }$ of dimension $\text{ n } - \text{ n }_0$ such that $\mathfrak{F }\cap \ker \mathcal{A }= \{0\}$; $\mathfrak{E }$ can then be regarded as the direct sum of $\mathfrak{F }$ and $\ker \mathcal{A }$ (see Fig. 9):

$$\begin{aligned} \mathfrak{E }= \mathfrak{F }\oplus \ker \mathcal{A } \end{aligned}$$

(89)

The ‘estimable functional variable’ is then defined as the oblique projection of $\xi$ on $\mathfrak{F }$ along $\ker \mathcal{A }$: $\mathcal{S }\xi$.

The oblique projection (operator) $\mathcal{S }$ is the $\mathcal{S }$-transfor-mation of the S-system method (see, e.g., de Jonge 1998).

Fig. 9

S-system principle. In this geometrical representation, $\mathfrak{E }$ is a Euclidean space of dimension $\mathrm{n}$. The unknown functional variable $\xi$ is a vector of $\mathfrak{E }$. The null space of the operator $\mathcal{A }$ involved in Eq. (87) is of dimension $\mathrm{n}_0$: $\dim (\ker \mathcal{A }) = \mathrm{n}_0$; $\mathfrak{F }$ is a subspace of $\mathfrak{E }$ of dimension $\mathrm{n} - \mathrm{n}_0$ such that $\mathfrak{F }\,\cap \,\ker \mathcal{A }= \{0\}$; $\mathfrak{E }$ can then be regarded as the direct sum $\mathfrak{F }\,\,\oplus \,\, \ker \mathcal{A }$. In the S-system approach, the ‘estimable functional variable’ is then defined as the oblique projection of $\xi$ on $\mathfrak{F }$ along $\ker \mathcal{A }$: $\mathcal{S }\xi$

We now show how the S-system approach can provide the matrix of $\mathcal{S }$ in the standard basis of $\mathfrak{E }$. The estimable functional variable $\mathcal{S }\xi$, which basically depends on the choice of $\mathfrak{F }$, can thus be explicitly defined.

According to its definition,

$$\begin{aligned} \mathcal{S }\xi = \xi - \eta \end{aligned}$$

(90)

where $\eta$ is the vector of $\ker \mathcal{A }$ such that $\xi - \eta$ lies in $\mathfrak{F }$; see Fig. 9. Denoting by $[W]$ a matrix whose column vectors form a basis of $\ker \mathcal{A }$, we have

$$\begin{aligned}{}[\eta ] = [W] [\zeta ] \end{aligned}$$

(91)

where $\zeta$ is some vector of $\mathbb{R }^{\mathrm{n}_0}$. Clearly, the entries of $[\eta ]$, $[W]$ and $[\zeta ]$ are expressed in the standard basis of $\mathfrak{E }$. Let $[S_\bot ]$ now be a matrix whose column vectors form a basis of $\mathfrak{F }^\bot \!$, the orthogonal complement of $\mathfrak{F }$ in $\mathfrak{E }$. As $\xi - \eta$ is orthogonal to all the vectors of $\mathfrak{F }^\bot$, we have (in particular) $[S_\bot ]^\mathrm{T} \bigl ( [\xi ] - [W ][\zeta ] \bigr ) = 0$, i.e.,

$$\begin{aligned}{}[S_\bot ]^\mathrm{T}[W ][\zeta ] = [S_\bot ]^\mathrm{T} [\xi ] \end{aligned}$$

(92)

As shown further on, $[S_\bot ]^\mathrm{T}[W ]$ is invertible. It then follows that $[\zeta ] = ( [S_\bot ]^\mathrm{T}[W ])^{-1} [S_\bot ]^\mathrm{T} [\xi ]$, hence from Eqs. (90) and (91),

$$\begin{aligned}{}[\mathcal{S }] = [I] - [W ] \, \bigl ( [S_\bot ]^\mathrm{T}[W ] \bigr )^{-1} [S_\bot ]^\mathrm{T} \end{aligned}$$

(93)

where $[I]$ is the identity matrix on $\mathfrak{E }$.

We now show that the $\mathrm{n}_0$-by-$\mathrm{n}_0$ matrix $[M_0] {\displaystyle {} \mathop {=}^\mathrm{\scriptscriptstyle def}{}}[S_\bot ]^\mathrm{T}[W ]$ is invertible.

Proof

Let $\xi _\bot$ be the projection of some vector $\eta$ of $\ker \mathcal{A }$ on $\mathfrak{F }^\bot$; see Fig. 9. By considering the case where $\xi = \xi _\bot$, Eq. (92) yields $[M_0][\zeta ] = [S_\bot ]^\mathrm{T} [\xi _\bot ]$. The condition $[M_0] [\zeta ] = 0$ implies $[S_\bot ]^\mathrm{T} [\xi _\bot ] = 0$, hence $\xi _\bot = 0$. As a result, $\eta$ then lies in $\mathfrak{F }$. As $\mathfrak{F }\cap \ker \mathcal{A }= \{0 \}$, it follows that $\eta = 0$, hence $\zeta = 0$. The null space of $[M_0]$ is therefore reduced to $\{0\}$; but $[M_0]$ is an $\text{ n }_0$-by-$\text{ n }_0$ matrix; $[M_0]$ is therefore invertible. $\square$

Remark

In the S-system approach as it is implemented by de Jonge (1998) for example, one chooses some basis for $\mathfrak{F }$. The corresponding matrix is denoted by $S$; $\mathfrak{F }$ is then regarded as the range of $S$; $[S_\bot ]^\mathrm{T}\xi$ is called the ‘$S$-basis.’ Note that $[S_\bot ]$ is then denoted by $S^\bot$.

Appendix C: QR implementation

In this appendix, we show how the float version of Eq. (81) can be solved in the LS sense via recursive QR factorization. Here, for simplicity, we will assume that the elementary orthogonal transformations involved in that factorization are Givens rotations; see Eqs. (2.3.10) to (2.3.13) in Björck (1996).

In the CAA, the number of entries of ${\varvec{v}}$, $n_\mathrm{c}$, is a non-decreasing function of $k$; see Sect. 6.3. In Sect. , we consider the case where $n_\mathrm{c}$ is constant; the cases where at some epochs $k$, $n_\mathrm{c}$ increases is dealt with in Sect. . In that QR framework, we finally describe in Sect.  the construction of the matrices ${\varvec{A}}_k$, ${\varvec{B}}_k$ and ${\varvec{b}}_k$ involved in Eq. (81).

1.1 C.1 Recursive QR factorization

As shown in this section, the float version of the following equation (Eq. 81) can be solved in the LS sense via recursive QR factorization:

Throughout this section, $n_\mathrm{c}$ is assumed to be fixed; for related notions, see Sect. 6.3 of Björck (1996), Golub and Loan (1989), Bierman (1977).

1.1.1 C.1.1 Initialization: epoch 1

At epoch 1, the problem is to minimize the functional (see the first line of Eq. 81)

$$\begin{aligned} f_1({\varvec{w}}_1,{\varvec{v}}) {\displaystyle {} \mathop {=}^\mathrm{\scriptscriptstyle def}{}}\Vert ({\varvec{B}}_1 {\varvec{w}}_1 + {\varvec{A}}_1 {\varvec{v}}) - {\varvec{b}}_1 \Vert ^2 _{\mathbb{R }^{n_{\mathrm{e}1}}} \end{aligned}$$

The LS solution $(\hat{{\varvec{w}}}_1 , \hat{{\varvec{v}}})$ is then obtained via two QR factorizations (see Fig. 10).

Fig. 10

QR factorization at epoch 1. The principle of the recursive QR method is sketched here for the first epoch with the input block matrices ${\varvec{B}}_1 \,$, ${\varvec{A}}_1$ and the data column matrix ${\varvec{b}}_1$. The initialization process is performed in two steps: ${\varvec{K}}_1\,$, $({\varvec{L}}_1\, , {\varvec{L}}^{\prime }_1)$, $({\varvec{c}}_1^{}\,, {\varvec{c}}^{\prime }_1)$ are built in the first step (see text for ${\varvec{L}}^{\prime }_1$), whereas ${\varvec{R}}_1\,$, $({\varvec{d}}_1^{}\,, {\varvec{d}}^{\prime }_1)$ are built in the second one; for the LS solution thereby obtained at epoch 1, see text

1. QR factorization of ${\varvec{B}}_1$: the Givens rotations of this step are those required for finding the upper-triangular matrix ${\varvec{K}}_{1}$. The modified version of ${\varvec{A}}_1$ thus obtained includes an upper block ${\varvec{L}}_1$ and a lower block ${\varvec{L}}^{\prime }_1$. Likewise, the modified version of ${\varvec{b}}_1$ includes two column submatrices: ${\varvec{c}}_1$ and ${\varvec{c}}^{\prime }_1$.

2. QR factorization of ${\varvec{L}}^{\prime }_1$: the Givens rotations of that step yield the upper-triangular matrix ${\varvec{R}}_1$. The lower part of ${\varvec{L}}^{\prime }_1$ is reduced to $\mathbf{0}$; ${\varvec{c}}^{\prime }_1$ then yields $({\varvec{d}}_1^{}\, , {\varvec{d}}^{\prime }_1)$; see Fig. 10. Note that ${\varvec{K}}_{1}$, ${\varvec{L}}_1$ and ${\varvec{c}}_1$ are not affected by those rotations.

At the end of this initialization stage, we thus have

$$\begin{aligned} f_1({\varvec{w}}_1 ,{\varvec{v}})&=\Vert ({\varvec{K}}_{1} {\varvec{w}}_1 - ({\varvec{c}}_1 - {\varvec{L}}_1 {\varvec{v}}) \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{b}1}}}} \\&\quad + \Vert {\varvec{R}}_1 {\varvec{v}} - {\varvec{d}}_1 \Vert ^2_{\mathbb{R }^{n_{_\mathrm{c}}}} \\&\quad + \Vert {\varvec{d}}^{\prime }_1 \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{e}1}} - n_{_{\mathrm{b}1}} - n_{_\mathrm{c}}}} \end{aligned}$$

The float solution in ${\varvec{v}}$ at epoch 1 is therefore given by the formula $\hat{{\varvec{v}}} = {\varvec{R}}_1^{-1} {\varvec{d}}_1$, hence $\hat{{\varvec{w}}}_1 = {\varvec{K}}_{1}^{-1} ({\varvec{c}}_1 - {\varvec{L}}_1 \hat{{\varvec{v}}})$. These solutions can therefore be computed by back substitution. Note that $\Vert {\varvec{d}}^{\prime }_1 \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{e}1} }- n_{_{\mathrm{b}1}} - n_{_{\mathrm{c}}}}}$ is the square of the LS residual norm at epoch 1.

1.1.2 C.1.2 Next epoch: epoch 2

The functional to be minimized is then $f_1({\varvec{w}}_1 ,{\varvec{v}}) + f_2({\varvec{w}}_2 ,{\varvec{v}})$ where

$$\begin{aligned} f_2({\varvec{w}}_2,{\varvec{v}}) {\displaystyle {} \mathop {=}^\mathrm{\scriptscriptstyle def}{}}\Vert ({\varvec{B}}_2 {\varvec{w}}_2 + {\varvec{A}}_2 {\varvec{v}}) - {\varvec{b}}_2 \Vert ^2 _{\mathbb{R }^{n_{_{\mathrm{e}2}}}} \end{aligned}$$

As sketched in Fig. 11, the LS solution $(\hat{{\varvec{w}}}_1 , \hat{{\varvec{w}}}_2 , \hat{{\varvec{v}}})$ is again obtained via two QR factorizations. The first step of epoch 2 is similar to that of epoch 1; the second one is different.

1. QR factorization of ${\varvec{B}}_2$

One thus obtains the upper-triangular matrix ${\varvec{K}}_{ 2}$; see Fig. 11. The modified version of ${\varvec{A}}_2$ then includes an upper block ${\varvec{L}}_2$ and a lower block ${\varvec{L}}^{\prime }_2$. Likewise, the modified version of ${\varvec{b}}_2$ includes two column submatrices: ${\varvec{c}}_2$ and ${\varvec{c}}^{\prime }_2$.

2. QR factorization of $\Bigl [ \begin{array}{c} {\varvec{R}}_1 \\ {\varvec{L}}^{\prime }_2 \\ \end{array}\Bigr ]$:

The Givens rotations of the second step then operate on $({\varvec{R}}_1^{}\, , {\varvec{L}}^{\prime }_2)$ and $({\varvec{d}}_1^{}\,, {\varvec{c}}^{\prime }_2)$ so as to transform ${\varvec{L}}^{\prime }_2$ into a zero-block matrix. One thus gets ${\varvec{R}}_2$ and $({\varvec{d}}_2^{}\,, {\varvec{d}}^{\prime }_2)$.

At the end of this stage, we thus have

$$\begin{aligned} f_1({\varvec{w}}_1,{\varvec{v}}) + f_2({\varvec{w}}_2,{\varvec{v}})&= \Vert ({\varvec{K}}_{1} {\varvec{w}}_1 - ({\varvec{c}}_1 -{\varvec{L}}_1 {\varvec{v}}) \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{b}1}}}} \\&\quad + \Vert {\varvec{R}}_2 {\varvec{v}} - {\varvec{d}}_2 \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{c}}}}} \\&\quad + \Vert {\varvec{d}}^{\prime }_1 \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{e}1}} - n_{_{\mathrm{b}1}} - n_{_{\mathrm{c}}}}}\\&\quad + \Vert ({\varvec{K}}_2 {\varvec{w}}_2 - ({\varvec{c}}_2 - {\varvec{L}}_2 {\varvec{v}}) \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{b}2}}}} \\&\quad + \Vert {\varvec{d}}^{\prime }_2 \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{e}2}} - n_{_{\mathrm{b}2}}}} \end{aligned}$$

The float solution in ${\varvec{v}}$ at epoch 2 is therefore given by the formula $\hat{{\varvec{v}}} = {\varvec{R}}_2^{-1} {\varvec{d}}_2$, hence the LS solutions in ${\varvec{w}}_1$ and ${\varvec{w}}_2$:

$$\begin{aligned} \hat{{\varvec{w}}}_1 = {\varvec{K}}_{ 1}^{-1} ({\varvec{c}}_1 - {\varvec{L}}_1 \hat{{\varvec{v}}}) , \quad \hat{{\varvec{w}}}_2 = {\varvec{K}}_{ 2}^{-1} ({\varvec{c}}_2 - {\varvec{L}}_2 \hat{{\varvec{v}}}) \end{aligned}$$

The square of the LS residual norm at epoch 2 is then equal to $\Vert {\varvec{d}}^{\prime }_1 \Vert ^2 _{\mathbb{R }^{n_{_{\mathrm{e}1}} - n_{_{\mathrm{b}1}} - n_{_{\mathrm{c}}}}} + \Vert {\varvec{d}}^{\prime }_2 \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{e}2}} - n_{_{\mathrm{b}2}}}}$.

Fig. 11

QR factorization at epochs 1 and 2. The principle of the recursive QR method is sketched here for the first two epochs: epoch 1 with the input block matrices ${\varvec{B}}_1 \,$, ${\varvec{A}}_1$ and the data column matrix ${\varvec{b}}_1$; epoch 2 with the input block matrices ${\varvec{B}}_2 \,$, ${\varvec{A}}_2$ and the data column matrix ${\varvec{b}}_2$. The initialization process is performed in two steps as described in Fig. 10. At epoch 2, one first builds ${\varvec{K}}_2 \,$, $({\varvec{L}}_2^{}\, , {\varvec{L}}^{\prime }_2)$, $({\varvec{c}}_2^{}\,, {\varvec{c}}^{\prime }_2)$ like at epoch 1, and then ${\varvec{R}}_2$, $({\varvec{d}}_2^{}\,, {\varvec{d}}^{\prime }_2)$; for the LS solution thereby obtained at epoch 2, see text

1.1.3 C.1.3 Next epochs

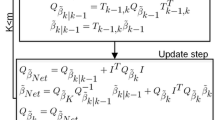
In summary, one thus operates, recursively, with the key structure shown in Fig. 12: ${\varvec{K}}_{ k}$, $({\varvec{L}}_k^{}\,, {\varvec{L}}^{\prime }_k)$ and $({\varvec{c}}_k^{}\,, {\varvec{c}}^{\prime }_k)$ are computed from ${\varvec{B}}_k$, ${\varvec{A}}_k$ and ${\varvec{b}}_k$, the quantities ${\varvec{R}}_k$ and $({\varvec{d}}_k^{}\,, {\varvec{d}}^{\prime }_k)$ being then computed from $({\varvec{R}}_{k-1}^{}\,, {\varvec{L}}^{\prime }_k)$ and $({\varvec{d}}_{k-1}^{}\,,\, {\varvec{c}}^{\prime }_\kappa )$. The generalization is straightforward; we then have

$$\begin{aligned} \sum _{\kappa =1}^{k} f_\kappa ({\varvec{w}}_1,{\varvec{v}})&= \Vert ({\varvec{K}}_{ 1} {\varvec{w}}_1 - ({\varvec{c}}_1 -{\varvec{L}}_1 {\varvec{v}}) \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{b}1}}}} \\&+ \Vert {\varvec{R}}_k {\varvec{v}} - {\varvec{d}}_k \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{c}}}}}\\&+ \Vert {\varvec{d}}^{\prime }_1 \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{e}1}} - n_{_{\mathrm{b}1}} - n_{_{\mathrm{c}}}}}\\&+ \Vert ({\varvec{K}}_2 {\varvec{w}}_2 - ({\varvec{c}}_2 - {\varvec{L}}_2 {\varvec{v}}) \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{b}2}}}} \\&+ \Vert {\varvec{d}}^{\prime }_2 \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{e}2}} - n_{_{\mathrm{b}2}}}} \\&\quad \vdots \\&+ \Vert ({\varvec{K}}_{k} {\varvec{w}}_k - ({\varvec{c}}_k - {\varvec{L}}_k {\varvec{v}}) \Vert ^2_{\mathbb{R }^{n_{_{\mathrm{b}k}}}} \\&+ \Vert {\varvec{d}}^{\prime }_k \Vert ^2 _{\mathbb{R }^{n_{_{\mathrm{e} k}} -n_{_{\mathrm{b}k}}}} \end{aligned}$$

The float solution in ${\varvec{v}}$ at epoch $k$ is therefore given by the formula

$$\begin{aligned} \hat{{\varvec{v}}} = {\varvec{R}}_k^{-1} {\varvec{d}}_k \end{aligned}$$

(94)

hence the LS solutions in ${\varvec{w}}_1, \ldots , {\varvec{w}}_k$:

$$\begin{aligned} \hat{{\varvec{w}}}_\kappa = {\varvec{K}}_{ \kappa }^{-1} ({\varvec{c}}_\kappa - {\varvec{L}}_\kappa \hat{{\varvec{v}}})\quad (\kappa = 1, \ldots , k) \end{aligned}$$

(95)

The solution of the corresponding NLP problem is therefore defined as follows:

$$\begin{aligned} \check{{\varvec{v}}} = \mathop {\mathrm{argmin}}_{{\varvec{v}} \in {\mathbb{Z }}^{n_{\mathrm{c}}}} \Vert {\varvec{R}}_k({\varvec{v}} - \hat{{\varvec{v}}}) \Vert ^2_{\mathbb{R }^{n_{\mathrm{c}}}} \end{aligned}$$

(96)

Indeed, ${\varvec{R}}_k {\varvec{v}} - {\varvec{d}}_k = {\varvec{R}}_k({\varvec{v}} - \hat{{\varvec{v}}})$. The phase biases $\check{{\varvec{w}}}_\kappa$ are then given by the relations

$$\begin{aligned} \check{{\varvec{w}}}_\kappa = {\varvec{K}}_{ \kappa }^{-1} ({\varvec{c}}_\kappa - {\varvec{L}}_\kappa \check{{\varvec{v}}}) (\kappa = 1, \ldots , k) \end{aligned}$$

(97)

Their variance-covariance matrix is equal to ${\varvec{K}}_{ \kappa }^{-1} [{\varvec{K}}_{ \kappa }^{-1}]^\mathrm{T}$.

1.2 C.2 Handling new components of the closure-ambiguity variable

We now consider the case where $\mathcal{L }_{\mathrm{c}, k}$ includes $n_{\mathrm{c}}^{\mathrm{a}}$ new closure edges (see Sect. 6.3); superscript a stands for added. One then proceeds in three steps:

• 1. $n_{\mathrm{c}}^{\mathrm{a}}$ closure-ambiguity entries are added at the top of column matrix ${\varvec{v}}$;

• 2. as specified in Sect. , $n_{\mathrm{c}}^{\mathrm{a}}$ columns are added on the right-hand side of ${\varvec{B}}_k$;

• 3. as shown in Fig. 13, to build ${\varvec{R}}_k$, the last $n_{\mathrm{c}}^{\mathrm{a}}$ lines of ${\varvec{K}}$ and ${\varvec{L}}$ obtained through the first QR step are added at the top of ${\varvec{R}}$. Matrices ${\varvec{d}}_k$, ${\varvec{K}}_{ k}$, ${\varvec{L}}_k$ and ${\varvec{c}}_k$ are then updated accordingly.

Fig. 12

Recursive QR triangular structure. According to the principle of the recursive QR method sketched in Fig. 11, the calculation of ${\varvec{R}}_{k+1}$ and ${\varvec{d}}_{k+1}$ requires to have kept in memory the upper-triangular matrix ${\varvec{R}}_k$ and the column matrix ${\varvec{d}}_k$; see text

Fig. 13

Handling new components of the closure-ambiguity variable. When new entries of ${\varvec{v}}$ appear at epoch $k$, the first columns of ${\varvec{A}}_k$ are processed as the last columns of ${\varvec{B}}_k$ (see Fig. 11). The recursive QR operation then yields the quantities ${\varvec{K}}$, ${\varvec{L}}$, ${\varvec{c}}$, ${\varvec{R}}$ and ${\varvec{d}}$. To get ${\varvec{K}}_{k}$, ${\varvec{L}}_k$, ${\varvec{c}}_k$, ${\varvec{R}}_k$ and ${\varvec{d}}_k$, one then proceeds as illustrated here

1.3 C.3 Construction of matrices ${{\varvec{B}}}_k, {{\varvec{A}}}_k$ and ${{\varvec{b}}}_k$

We first consider the case where the variance-covariance matrix ${{\varvec{V}}}_k$ of the data involved in the definition of $b_k$ is the identity: ${{\varvec{V}}}_k = {\varvec{I}}$. Denoting by $\mathbf{b}_k$ the column matrix whose entries are the values of $b_k$ on the edges of the observational graph $\mathcal{H }_k$ (see Sect. 1), we then have ${\varvec{b}}_k = \mathbf{b}_k$. To build ${\varvec{B}}_k = \mathbf{B}_k$ and ${\varvec{A}}_k = \mathbf{A}_k$, we then distinguish the cases where at epoch $k$, $n_\mathrm{c}$ does not increase (Sect. ), or increases (Sect. ). The case ${{\varvec{V}}}_k \ne {\varvec{I}}$ is dealt with in Sect. .

1.3.1 C.3.1 Case where $n_\mathrm{c}$ does not increase

Matrix $\mathbf{B}_k$, whose number of columns is $n_{\mathrm{b}k}$, is built from the characteristic function $H_k$ of $\mathcal{H }_k$; see Fig. 1. The $p$th line of $\mathbf{B}_k$ corresponds to the $p$th edge $({\mathrm{r}}_i, \mathrm{s}_j)$ on which $H_k(i,j) = 1$. All the matrix elements of that line are zero, except (one or) two of them (see Eq. 6 and the definition of $\varpi _{\mathrm{s}k}$ in Sect. 6.2):

$$\begin{aligned} \mathbf{B}_k^{p, i-1} = 1 \,(\text{ for } i > 1 ), \quad \mathbf{B}_k^{p, \,n_\mathrm{r} - 1 + \varpi _{\mathrm{s}k} (j)} = -1 \end{aligned}$$

Matrix $\mathbf{A}_k$ has $n_\mathrm{c}$ columns: the number of elements of $\mathcal{L }_{\mathrm{c}, k}$; see Sect 6.3 and Fig. 5. According to the action of $\mathcal{R }_k^\mathrm{e}$, the entries of the column associated with some closure edge $({\mathrm{r}}_i, \mathrm{s}_j)$ are then all zero, except that corresponding to the line associated with that edge if $H_k(i,j) = 1$; that entry is then set equal to unity. The lines of $\mathbf{A}_k$ are of course sorted as the lines of $\mathbf{B}_k$.

1.3.2 C.3.2 Case where $n_\mathrm{c}$ increases

We here consider the case where $n_{\mathrm{c}}^{\mathrm{a}}$ new closure edge(s) appear(s) in $\mathcal{L }_{\mathrm{c}, k}$ at some epoch $k > 1$: $n_\mathrm{c}:= n_\mathrm{c}+ n_{\mathrm{c}}^{\mathrm{a}}$; see Sect 6.3.

Matrix $\mathbf{B}_k^{p, q}$ is defined as in Sect. , but $n_{\mathrm{c}}^{\mathrm{a}}$ columns are then added on its right-hand side. (For example, at epoch 2 of Fig. 5, $\mathbf{B}_2$ has four additional columns.) The entries of the column of $\mathbf{B}_k$ associated with some new closure edge $(\mathrm{r}_i, \mathrm{s}_j)$ are all zero, except that corresponding to the line associated with that edge; that entry is set equal to unity.

Matrix $\mathbf{A}_k$ is then built as in Sect. , except for the new closure-edges, since they are then taken into account in the augmented definition of $\mathbf{B}_k$.

1.3.3 C.3.3 Case where ${{\varvec{V}}}_{\!k}$ is not the identity

We here consider the general case where the variance-covariance matrix ${{\varvec{V}}}_{\!k}$ is to be taken into account. In the QR implementation under consideration, the inverse of ${{\varvec{V}}}_{\!k}$ is then factorized in the form

$$\begin{aligned} {{\varvec{V}}}_k^{-1} = {{\varvec{U}}}_k^\mathrm{T} {{\varvec{U}}}_k \end{aligned}$$

(98)

where ${{\varvec{U}}}_k$ is an upper-triangular matrix. As

$$\begin{aligned}&(\mathbf{B}_k {\varvec{w}}_k + \mathbf{A}_k {\varvec{v}} - \mathbf{b}_k) ^\mathrm{T} \,{{\varvec{V}}}_k^{-1} \, (\mathbf{B}_k {\varvec{w}}_k + \mathbf{A}_k {\varvec{v}} - \mathbf{b}_k) \\&\quad = \Vert {{\varvec{U}}}_k (\mathbf{B}_k {\varvec{w}}_k + \mathbf{A}_k {\varvec{v}} - \mathbf{b}_k) \Vert ^2_{\mathbb{R }^{n_{\mathrm{e}k}}} \end{aligned}$$

matrices ${\varvec{B}}_k$, ${\varvec{A}}_k$ and ${\varvec{b}}_k$ are then given by the relations

$$\begin{aligned} {\varvec{B}}_k = {{\varvec{U}}}_k \mathbf{B}_k, \quad {\varvec{A}}_k = {{\varvec{U}}}_k \mathbf{A}_k, \quad {\varvec{b}}_k = {{\varvec{U}}}_k \mathbf{b}_k \end{aligned}$$

(99)

The problem is then to solve Eq. (81) in the Euclidean LS sense.