Between-satellite ambiguity resolution based on preliminary GNSS orbit and clock information using a globally applied ambiguity clustering strategy

Abstract

The use of undifferenced (UD) processing schemes of GNSS measurements is becoming more and more popular for the generation of global network solutions (GNSS orbits and clock products) within the GNSS community. As opposed to classical processing schemes, which are based on a two-step approach where the orbits (generally, the contributions to the observation geometry) are estimated in a double-difference (DD) scheme while leaving the estimation of the corresponding clock information (and other linear terms) to a second, independent UD procedure where the orbits are introduced as known, the newer designs combine both parts into a single, compact processing scheme. Although this offers a higher flexibility, some challenges arise from the handling of the many parameters, as well as from the implementation of robust ambiguity resolution (AR) strategies. The latter could lead to a prohibitive computational time for a growing size of the network due to the large amount of ambiguity parameters. To overcome that issue, we propose a new UD-AR strategy that adapts the DD-AR approach. This is accomplished by carefully inspecting the real-valued ambiguities in a stand-alone step, where the DD-AR information is explicitly considered through the use of ambiguity clusters. As a result, the preliminary satellite orbits and clock corrections are modified to become consistent with the integer-cycle property of the carrier phase ambiguities, allowing to resolve them as integer numbers in a computationally inexpensive station-wise parallelization. This strategy is introduced and explained in detail. Moreover, it is shown that the GPS and Galileo solutions generated by this procedure are at a competitive level compared to classical DD-based solutions.

Introduction

New ambiguity resolution (AR) algorithms can still enhance the flexibility and capabilities of the currently adopted GNSS processing schemes. This is especially true for the generation of global network solutions, for which the analysis centers (ACs) of the International GNSS Service (IGS, Johnston et al. 2017) have created their own schemes to process undifferenced (UD) GNSS measurements, complementing, or even replacing, the legacy double-difference (DD) approaches. Unlike these latter approaches, the undifferenced schemes give direct access to clock corrections, as well as other linear terms, where the phase biases (Håkansson et al. 2017) are of special interest in enabling precise point positioning (PPP) with ambiguity resolution (altogether, PPP-AR) for single-receiver users.

It can be distinguished between two main strategies for the UD processing schemes proposed so far: On the one hand, some strategies rely on the availability of a priori geometry solutions (typically based on DD approaches) which are already compatible with the integer-cycle property of the carrier phase ambiguities to estimate satellite clock corrections and other associated biases in a dedicated processing (Geng et al. 2012; Duan et al. 2021; Schaer et al. 2021). On the other hand, other strategies jointly estimate the various contributions of the GNSS observation model under a common processing (Loyer et al. 2012; Strasser et al. 2019). Whereas the former strategies easily unveil the integer nature of the between-satellite ambiguities after neatly calibrating phase biases at the cost of a twofold processing scheme, the latter ones are challenged by a more complex AR stage, which must deal with potential errors absorbed by the real-valued ambiguities. In this case, the direct use of robust AR algorithms leads to a prohibitive computational burden for a sizable network owe to the huge number (more than 10,000) of ambiguity parameters. Aiming at taking the greatest advantage of both approaches, we propose a novel between-satellite AR strategy to solve the global network GNSS problem overcoming the restriction due to the network size. To achieve this, the adopted architecture eliminates the receiver-dependent parameters (including ambiguities) in a station-wise parallelization, being later efficiently recovered after a back-substitution step. By carefully inspecting the resulting real-valued between-satellite ambiguities, some auxiliary global parameters are estimated to compensate for the coupling between them and the preliminary satellite information (orbits and clock corrections), allowing to resolve the integer numbers of the between-satellite ambiguities in an inexpensive station-wise parallelization, also establishing a direct link to PPP-AR. This strategy builds on the concept of ambiguity cluster, which uses the advantages of the DD-AR.

In Ge et al. (2005), the DD-AR information is integrated into a UD processing scheme by using the resolved DD ambiguities as tight constraints during the least-squares adjustment, which is still computationally expensive for large networks. Likewise, some authors have explored methods based on real-valued ambiguity inspection (Ge et al. 2008; Laurichesse et al. 2009). The presented approach, however, further extends them, increasing their robustness.

From the many different GNSS groups active in this field, a huge number of PPP-AR enabling products are available that are actually equivalent under certain transformations, as proved in Teunissen and Khodabandeh (2015). In the frame of this work, we use the integer recovery clock (IRC) model presented in Laurichesse et al. (2009) and Loyer et al. (2012) (in analogy to the decoupled satellite clock model, or DSC model, Collins 2008; Collins et al. 2008), which is characterized by lumping together clock corrections and narrow-lane phase biases.

Besides this introduction, our article consists of five additional sections. The following section introduces the design of the proposed UD processing scheme. Afterward, a detailed description of the AR method is given. The fourth section describes some metrics that are relevant for quality control purposes. Next, the performance of the newly generated GPS and Galileo solutions is evaluated by comparing these products against classical DD-based solutions. A final section is devoted to the conclusions. Accompanying this paper, it is also provided an electronic supplement addressing some technical aspects which are relevant for the practical implementation of the presented AR strategy.

Undifferenced, station-wise processing architecture

The proposed scheme comprises four different stages: preprocessing, computation of global parameters, computation of receiver-dependent parameters and ambiguity resolution. The associated flowchart is displayed in Fig. 1. It is to be clarified that global parameters enclose satellite orbits and clock corrections, earth rotation parameters (ERP) and station coordinates (defining a global earth-fixed reference frame; Altamimi and Gross 2017). Likewise, receiver-dependent parameters include receiver clock corrections, ambiguities and tropospheric delays.

Fig. 1

Flowchart for the processing scheme

The preprocessing aims at cleaning the observations and includes several steps. Firstly, code-only solutions are iteratively generated and their residuals analyzed to exclude outliers. The code biases (treated as Observable Specific Biases, OSBs, Villiger et al. 2019) are also determined here as a by-product. Afterward, the phase data are analyzed using several iterations too, not only to clean the observations, but also to define the set of ambiguity parameters (i.e., cycle-slip detection). The preprocessing concludes after resolving as integer numbers the wide-lane (WL) ambiguities of the Hatch–Melbourne–Wubbena linear combination (Hatch 1982; Melbourne 1985; Wübbena 1985). This observation is geometry- and ionospheric-free, and because of this relative simplicity, resolving its ambiguities is a moderate effort exercise. Although the concept presented hereafter is also applicable to them, their explicit treatment has thus been omitted for brevity, and the reader is referred to Schaer et al. (2021), which is the reference followed in the frame of this work.

All in all, the ionospheric-free GNSS observation model that will be used in the sequel (from the second to the last block in Fig. 1) reads as (Subirana et al. 2013):

$${P}_{k}^{i}={\rho }_{k}^{i}+c\left({\tau }_{k}-{\tau }^{i}\right)+{T}_{k}^{i}$$

$${L}_{k}^{i}={\rho }_{k}^{i}+c\left({\tau }_{k}-{\tau }^{i}\right)+{T}_{k}^{i}+\lambda \left({N}_{k}^{i}+{b}_{k}+{b}^{i}\right)$$

(1)

where ${P}_{k}^{i}$ and ${L}_{k}^{i}$, respectively, refer to smooth code (Dach et al. 2015, Sect. 6.2.5) and phase observations transmitted by satellite $i$ and received by station $k$. The range (${\rho }_{k}^{i}$), clock corrections (${\tau }_{k}$ and ${\tau }^{i}$) and tropospheric delays (${T}_{k}^{i}$) are common to both observation types, whereas the ambiguity term (${N}_{k}^{i}$) and associated narrow-lane (NL) phase biases (${b}_{k}$ and ${b}^{i}$; sign convention in agreement with Schaer 2016) are specific aggregates of the phase measurements. The constants $c$ and $\lambda$ are the speed of light in vacuum and the NL wavelength, which depends on the corresponding ionospheric-free linear combination frequencies. Note that ${N}_{k}^{i}$ can be identified with the integer ambiguity of the carrier phase observation tracked at the first frequency of the corresponding GNSS system. It should converge to an integer number as long as its associated WL ambiguity has been previously removed from the observations. Otherwise, AR should not be even tried. Of course, Eqs. (1) are reconstructed in full agreement with the latest conventions and geophysical a priori models (Kouba 2009; Petit and Luzum 2010; Rebischung and Schmid 2016), as well as using a recent parameterization for the GNSS orbital dynamics (Arnold et al. 2015; Sidorov et al. 2020).

As can be seen from (1), there is a one-to-one correlation between ambiguity and bias terms: If the ambiguities are not resolved, their estimated real values will absorb the phase biases, i.e., ${N}_{k}^{i}+{b}_{k}+{b}^{i}\to {B}_{k}^{i}$, provided that no ambiguity datum is enabled. However, if the ambiguities are resolved as integer numbers, the phase biases have to be accounted for. It is customary to resolve between-satellite ambiguities instead of undifferenced ones, and consequently, at least one reference real-valued ambiguity parameter per station has to be estimated, being lumped with ${b}_{k}$. Furthermore, the ${b}^{i}$ parameters have a magnitude in the order of the NL wavelength (~ 10 cm) because of its own construction: The code observations weakly constrain the ambiguities, which, in turn, align phase and code measurements at a certain level. If they were absorbed by the satellite clock corrections, the code observations would be distorted by the same amount, which would be scarcely sensed due to their precision, leaving the remaining parameters unaltered. This is the basis for IRC (Laurichesse et al. 2009), also experimentally confirmed in Schaer et al. (2021). The final consequence is that no (NL) phase bias parameters are explicitly estimated.

The core of the processing is based on a station-wise architecture, i.e., single stations are independently processed as far as possible, uniformly distributing the computational resources while alleviating the computational effort for large networks. Therefore, the first step to compute the global parameters is the station-wise elimination of the receiver-dependent parameters, where resolved between-satellite ambiguities are considered as known after the first processing loop iteration. Once all the station-dependent normal equations (NEQs) are generated, they are stacked and inverted. This inversion is carried out along with a reduction of the clock parameters by sequentially splitting the stacked NEQ into smaller NEQs, each one containing 3-h-clock batches. Substituting the previously generated global solution allows to readily estimate the remaining receiver-dependent parameters during another station-wise parallelization (third block in Fig. 1).

In case of additional iterations are still pending, it is important that the ambiguities are estimated as real numbers during the computation of receiver-dependent parameters, since their fractional parts will be the input for the subsequent ambiguity resolution stage. In this step, between-satellite ambiguities are station-wise resolved (PPP-AR using the sigma strategy; Dach et al. 2015, Sect. 8.3.3) after the refinement of orbits and clock corrections. This refinement, pale blue highlighted in Fig. 1, is the cornerstone of this processing scheme, making the preliminary satellite products consistent with the integer-cycle property of the carrier phase ambiguities.

The proposed scheme is initialized with satellite broadcast information to jointly process about 300 stations (more than 200 of which containing GPS and Galileo data) at a 5-min sampling with a 5° cutoff angle. The selected ionospheric-free signals are GPS L1/L2 and Galileo E1/E5a. Moreover, the processing is performed in daily batches and two iterations with AR are performed. The interested reader may find a comprehensive insight into the latest processing standards applied in Dach et al. (2021).

Inspection of real-valued ambiguities

Schaer et al. (2021) show that the agreement between integer-cycle-conform products is below 10 ps in standard deviation (StD) for the between-satellite signal-in-space (SIS, Montenbruck et al. 2018) range differences for an ideal station located at the center of the Earth. This quantity is readily computed for the between-satellite pair $i,j$ as ${\mathrm{SIS}}_{AB}^{ij}={\rho }_{AB}^{ij}-c{\uptau }_{AB}^{ij}+{\mathrm{BIA}}_{AB}^{ij}$, where the labels $A$ and $B$ appoint to each of the compared products. Note that $\left( \cdot \right)_{AB}^{ij} : = \left( \cdot \right)_{A}^{i} - \left( \cdot \right)_{A}^{j} - \left( \cdot \right)_{B}^{i} + \left( \cdot \right)_{B}^{j}$. The bias term, denoted by ${\mathrm{BIA}}_{AB}^{ij}$, can be decomposed in terms of WL and NL integer jumps, and NL phase bias differences. This decomposition is paramount if independent integer-cycle-conform products are to be combined (Banville et al. 2020). For the sake of simplicity, here we remove it as a constant mean value. Although the resulting comparison represents a rigorous equivalence relation, we will simply refer to it as clock comparison.

The blue line in Fig. 2 depicts the aforementioned comparison between the preliminary UD-based solution (i.e., unresolved ambiguities; second block, first iteration in Fig. 1) and the CODE (Center for Orbit Determination in Europe) Final products (consistent with the integer-cycle property) for the between-satellite pair G26/G29 on 2021/050 (year/day of year). Far from a stability of 10 ps (~ 0.03 NL cycles), the preliminary products may exhibit a drift with deviations larger than 1 NL cycle in the course of one day, which precludes between-satellite AR. Superimposed to it, the red lines indicate the real-valued between-satellite ambiguities associated with the UD-based solution (which result from third block, first iteration in Fig. 1), which have been shifted by integer jumps to better accommodate the clock comparison. Typically, each red line corresponds to the observations from a single station and satellite pass. As can be seen, there is a clear correlation between the ambiguities and the clock differences. This indicates that the unresolved ambiguities could be used to remove the drift the preliminary products are suffering. The goal of this section is to define a systematic and rigorous way to accomplish this.

Fig. 2

Between-satellite (G26/G29) clock comparison between the preliminary UD-based solution and the CODE Final products on 2021/050. The thin horizontal red lines indicate the corresponding between-satellite real-valued ambiguities

Ambiguity parameterization

To mathematically quantify the coupling between the different parameters of the phase observation model, i.e., the second equation in (1), let us start writing its linearized observed-minus-computed between-satellite version in units of NL cycles:

$${L}_{k}^{ij}=\left({\varvec{e}}_{k}^{i}\cdot {\varvec{x}}^{i}-{\varvec{e}}_{k}^{j}\cdot {\varvec{x}}^{j}\right)-\left({\tau }^{i}-{\tau }^{j}\right)+\left({b}^{i}-{b}^{j}\right)+{T}_{k}^{ij}+{\varvec{e}}_{k}^{ij}\cdot {\varvec{x}}_{k}+{N}_{k}^{ij}$$

(2)

where ${\varvec{e}}_{k}^{i}$ stands for the line-of-sight pointing from station $k$ to satellite $i$, and ${\varvec{x}}^{i}$ and ${\varvec{x}}_{k}$ are corrections over the a priori orbit and station coordinates, respectively. Note that ${\left(\cdot \right)}^{ij}:={\left(\cdot \right)}^{i}-{\left(\cdot \right)}^{j}$. This observation can be reconstructed using either the preliminary ($\mathrm{PRE}$) estimates or the integer-cycle-conform ($\mathrm{ICC}$) estimates, and therefore, the following equality holds within the noise of the phase observations:

$${\left[\left({{\varvec{e}}}_{k}^{i}\cdot {{\varvec{x}}}^{i}-{{\varvec{e}}}_{k}^{j}\cdot {{\varvec{x}}}^{j}\right)-\left({\tau }^{i}-{\tau }^{j}\right)+{T}_{k}^{ij}+{{\varvec{e}}}_{k}^{ij}\cdot {{\varvec{x}}}_{k}+{B}_{k}^{ij}\right]}_{\mathrm{PRE}}=$$

$${\left[\left({{\varvec{e}}}_{k}^{i}\cdot {{\varvec{x}}}^{i}-{{\varvec{e}}}_{k}^{j}\cdot {{\varvec{x}}}^{j}\right)-\left({\tau }^{i}-{\tau }^{j}\right)+\left({b}^{i}-{b}^{j}\right)+{T}_{k}^{ij}+{{\varvec{e}}}_{k}^{ij}\cdot {{\varvec{x}}}_{k}+{N}_{k}^{ij}\right]}_{\mathrm{ICC}}$$

(3)

Recall that ${N}_{k}^{i}+{b}_{k}+{b}^{i}\to {B}_{k}^{i}$. Regrouping terms, it yields

$${B}_{k}^{ij}-{N}_{k}^{ij}=\delta {N}_{k}^{ij}=\left({{\varvec{e}}}_{k}^{i}\cdot \delta {{\varvec{x}}}^{i}-{{\varvec{e}}}_{k}^{j}\cdot \delta {{\varvec{x}}}^{j}\right)-\left({\delta \tau }^{i}-{\delta \tau }^{j}\right)+{\delta T}_{k}^{ij}+{{\varvec{e}}}_{k}^{ij}\cdot {\delta {\varvec{x}}}_{k}+\left({b}^{i}-{b}^{j}\right)$$

(4)

where the $\delta$ represents the difference between the $\mathrm{PRE}$ and $\mathrm{ICC}$ realizations of the corresponding parameter.

In the following, we use the $\delta {N}_{k}^{ij}$ quantities as “observations” in a subsequent least-squares adjustment where the right-hand side terms are estimated as corrections for the preliminary solution. A direct implementation is, however, impossible since these observations are the (known) real-valued between-satellite ambiguities shifted by an unknown number of NL cycles. To overcome this issue, we may form ambiguity clusters. As will be detailed in the next subsection, their main outcome is the redefinition of the $\delta {N}_{k}^{ij}$ terms in such a way that they are not individually shifted, but the shift is common for a set of observations. This is,$\delta {N}_{k}^{ij}\to \delta {N}_{k}^{ij}-{B}_{\alpha }^{ij}$, where the new realization of $\delta {N}_{k}^{ij}$ is unambiguously known and ${B}_{\alpha }^{ij}$ is an unknown shift unique for every cluster  (Greek letters, in this case $\alpha$, designate ambiguity clusters). The unknown shifts, referred to as cluster biases, can be initially interpreted as between-satellite ambiguities and will be estimated as part of the least-squares adjustment.

The model (4) is further simplified with:

• We address the ambiguity resolution problem from a global point of view, neglecting the receiver-dependent parameters (i.e., $\delta {T}_{k}^{ij}$ and $\delta {{\varvec{x}}}_{k}$).

• The time-dependent orbit and clock corrections ($\delta {{\varvec{x}}}^{i}$ and $\delta {\tau }^{i}$, respectively) are averaged over the time interval stretched by the observations $\delta {N}_{k}^{ij}$.

• The orbit and clock corrections are characterized by a sum of polynomials, whose coefficients are the sought parameters.

Altogether, the simplified model eventually reads as

$$\delta {N}_{k}^{ij}=\overline{{{\varvec{e}} }_{k}^{i}\cdot \delta {{\varvec{x}}}^{i}}-\overline{{\mathbf{e} }_{k}^{j}\cdot \delta {{\varvec{x}}}^{j}}-\left(\overline{{\delta \tau }^{i}}-\overline{{\delta \tau }^{j}}\right)+{B}_{\alpha }^{ij}$$

(5)

where the horizontal upper bars indicate temporal average of the corresponding contribution. In this equation, the phase biases, ${b}^{i}$ and ${b}^{j}$, are assumed to be absorbed by the clock corrections, which require a dedicated datum (e.g., a zero-mean condition) to give access to “absolute” satellite-specific information. There is another rank defect between cluster biases (${B}_{\alpha }^{ij}$) and clock corrections that can be overcome by fixing $n-1$ (with $n$ equal to the number of satellites) ${B}_{\alpha }^{ij}$ parameters to zero, implying that they can now be interpreted as DD ambiguities (Teunissen and Khodabandeh 2015) and, as such, should converge to integer numbers. On the other hand, the radial component of the orbit corrections should be loosely constrained to mitigate the numerical instability resulting from their high correlation with the clock corrections.

The model (5) can be seen as a kinematic approach that refines satellite orbits and clock corrections without requiring any a priori model. However, $\delta {\varvec{x}}^{i}$ and $\delta {\tau }^{i}$ compensate general error sources and, hence, do not have a real physical interpretation. The only important aspect for a successful between-satellite AR is that, when those corrections are applied over the preliminary solution (fixed during the station-wise AR step; final block in Fig. 1), it eventually resembles an integer-cycle-conform solution.

One between-satellite observation, $\delta {N}_{k}^{ij}$, is obtained from two overlapping undifferenced real-valued ambiguities belonging to the same station, whose difference and common overlap represent, respectively, the observation value and the observation time interval. The between-satellite pairs $i,j$ are selected from the linearly independent combinations that maximize the overall coverage. Afterward, in order to complement potentially poorly observed periods, additional between-satellite pairs will be included following the same criterion. The new pairs will be appended into the set of observations until a predefined redundancy level is satisfied, which is defined as the number of occurrences of one satellite in the set of between-satellite combinations. Since no correlations between observations are considered, the larger the level of redundancy, the better. However, an exponentially increasing number of observations would compromise the computational performance of the method. Therefore, as a trade-off solution, a redundancy level of four occurrences per satellite is assumed in the frame of this work.

Although no correlations are considered, specific variances are used to weight the observations. Being ${\sigma }^{{i}^{2}}$ the variance associated with the undifferenced ambiguity of satellite $i$ for a particular station and $\Delta {T}^{i}$ its temporal length, the variance for a between-satellite combination is defined as

$${\sigma }^{{ij}^{2}}=\frac{\Delta {T}^{i}{\sigma }^{{i}^{2}}+\Delta {T}^{j}{\sigma }^{{j}^{2}}}{\Delta {T}^{ij}}$$

(6)

where $\Delta {T}^{ij}$ represents the satellites common tracked time. Note that a rejection criterion could be considered as well for those observations stretching time intervals shorter than a user-defined length (e.g., 1 h). Eventually, it has to be emphasized that the model (5) should be separately used for different GNSS systems (i.e., independent runs for GPS and Galileo).

Ambiguity clustering

Ambiguity clusters are used to easily integrate the DD-AR information into the model (5). Let us recover the definition of the observations from (4):

$$\delta {N}_{k}^{ij}={B}_{k}^{ij}-{N}_{k}^{ij}$$

(7)

Without loss of generality, these observations can be initialized as the fractional part of the real-valued between-satellite ambiguities. Now, let us take two observations from two different stations (i.e., $\delta {N}_{1}^{ij}$ and $\delta {N}_{2}^{ij}$) and let us focus on a specific property of the definition: If the DD ambiguity formed by them meets the ambiguity resolution criteria (defined below), the rounding operation (denoted by $\lfloor \cdot \rceil$) shall return an exact zero, i.e.,

$$\lfloor \delta N_{2}^{ij} - \delta N_{1}^{ij} \rceil= \lfloor B_{2}^{ij} - B_{1}^{ij}\rceil - \left( {N_{2}^{ij} - N_{1}^{ij} } \right) = 0$$

(8)

If this outcome is other than zero, either $\delta {N}_{1}^{ij}$ or $\delta {N}_{2}^{ij}$ has to be redefined accordingly. For instance, in the case that it returns 1,

$$\delta {N}_{1}^{ij}+1\to \delta {N}_{1}^{ij}$$

(9)

After this redefinition, a two-ambiguity cluster has been created. Additionally, since it is only required to preserve the underlying DD ambiguity, any common shift (i.e., the cluster bias) applied over both observations represents a valid transformation. Of course, the more the number of between-satellite ambiguities per cluster, the better. This is achieved by combining clusters. To exemplify this idea, let us consider two ambiguity clusters, namely $\alpha$ and $\beta$, each composed by three observations with the following numerical values:

$$\begin{gathered} \delta N_{1\alpha }^{ij} = 0.3\,\,\,\,\delta N_{2\alpha }^{ij} = 0.4\,\,\,\,\delta N_{3\alpha }^{ij} = 0.5 \hfill \\ \delta N_{3\beta }^{ij} = \, - \,0.5\,\,\,\,\delta N_{4\beta }^{ij} \, = \, - \,0.4\,\,\,\,\delta N_{5\beta }^{ij} = \, - \,0.3 \hfill \\ \end{gathered}$$

(10)

It can be seen that the two clusters are overlapping, because each cluster contains its own realization of the observation $\delta {N}_{3}^{ij}$. This allows to merge them by properly shifting the ambiguities of, e.g., the cluster $\beta$:

$$\beta +\left(\delta {N}_{3\alpha }^{ij}-\delta {N}_{3\beta }^{ij}\right)\to \alpha$$

(11)

leading to one single $\alpha$ cluster:

$$\begin{gathered} \delta N_{1\alpha }^{ij} = 0.3\,\,\,\,\delta N_{2\alpha }^{ij} = 0.4\,\,\,\,\delta N_{3\alpha }^{ij} = 0.5 \hfill \\ \delta N_{4\alpha }^{ij} = 0.6\,\,\,\,\delta N_{5\alpha }^{ij} = 0.7 \hfill \\ \end{gathered}$$

(12)

Note that the combination of clusters results in a set of observations whose fractional parts are not necessarily bounded by − 0.5 and 0.5 NL cycles.

A basic cluster associated with a particular pivot observation can be defined as the cluster containing all those observations that, when double-differentiated w.r.t. the former one, satisfy the AR criteria for a fixed between-satellite pair (the pivot observation is part of the basic cluster, too). The adopted processing scheme (recall Fig. 1) disregards the inter-station correlations, which may become vital in undifferenced global ambiguity resolution. Fortunately, the experience with DD-based solutions demonstrates that the error sources potentially absorbed by the ambiguity parameters partially vanish when forming regional baselines (Dach et al. 2015, Sect. 8.5). For such cases, this allows to correctly resolve DD ambiguities by simply rounding their real-valued estimates. Then, we may establish robust AR criteria obeying three physical-driven rules:

• 1. The absolute value of the fractional part associated with the DD ambiguity shall be lower than a predefined threshold (e.g., 0.1 NL cycles).

• 2. The maximum baseline length between the station associated with the pivot observation and any other station belonging to the basic cluster shall not exceed a predefined distance (e.g., 4000 km).

• 3. The overlapping factor between the pivot observation and any other observation belonging to the basic cluster shall not be lower than a predefined ratio (e.g., 0.5). This ratio is computed as the overlapping time over the total time span covered by both between-satellite ambiguities.

These basic clusters, which contain the DD-AR information, constitute the most elemental unit that, after sequential combinations, conforms the global ambiguity clusters.

Figure 3 sketches some cluster interrelations that become very useful when constructing the general clusters:

• We address those clusters as disconnected clusters if they are fully independent, and hence, one cluster bias needs to be estimated for each cluster.

• We address those clusters as overlapping clusters if they share at least one common observation. These clusters shall be combined.

• We address those clusters as neighboring clusters if at least one observation in cluster $\alpha$ is in the vicinity of at least one observation in cluster $\beta$. Such a vicinity occurs if those (at least) two observations fulfill the AR criteria, in which case both clusters must be combined.

Fig. 3

Abstract representation of cluster interrelations

Figure 4 shows the temporal distribution (top) of some observations along with the geographical distribution for those with shaded background (bottom). The selected between-satellite pair is G06/G17 on 2021/050. As can be seen, these observations are grouped in several ambiguity clusters, which are represented by different colors. The generic black color has been designated for those containing five observations or fewer. A drift can be easily seen, ranging up to one NL cycle once the pink and green clusters are dragged downwards, which is accomplished by the estimation of cluster biases in (5). It is interesting to note that each cluster is homogeneously spaced in different regions of the globe and isolated from the others. This is a consequence mainly (but not exclusively) induced by the maximum baseline length rule. On the other hand, the use of ambiguity clusters allows to use those ${B}_{\alpha }^{ij}$ parameters performing best (e.g., in terms of ambiguity cluster density) to define the ambiguity datum.

Fig. 4

Between-satellite (G06/G17) ambiguity clusters on 2021/050. Each cluster is represented by a different color. The top panel displays the temporal distribution of the observations $\delta {N}_{k}^{ij}$ associated with each cluster. The bottom panel shows, on the other hand, the corresponding tracking stations (i.e., geographical distribution) for the temporal period with gray background

Mixed-integer model property

The model (5) features as a mixed-integer GNSS model (Teunissen 2017), since $\delta {x}_{(p)}^{i}, \delta {\tau }^{i}\in {\mathbb{R}}$ and ${B}_{\alpha }^{ij}\in {\mathbb{Z}}$ (where $\delta {x}_{(p)}^{i}$ stands for the $p$-component of $\delta {\varvec{x}}^{i}$). To make full profit of this property, it is convenient to use an integer estimator. Integer rounding, integer bootstrapping and integer least-squares (ILS, whose most widespread algorithm implementation is least-squares ambiguity decorrelation adjustment, or, simply, LAMBDA; Teunissen 1995b; Chang et al. 2005) are the most commonly used integer estimators in increasing robustness (and complexity).

Figure 5 shows the correlations between the ${B}_{\alpha }^{ij}$ parameters for a GPS run on 2021/050 from two different views: The left-hand side panel depicts such correlations for the entire set of parameters, whereas the right panel displays them only for relatively high densely populated clusters, i.e., clusters containing at least five observations. As shown, the correlations are not negligible, and thus, the integer rounding could benefit from resolving the cluster biases in a nearly decorrelated space after applying the so-called $Z$-transformation (Teunissen 1995a). Additionally, it illustrates that the stronger correlations occur on the set of dense clusters. Should it be small enough, then this set qualifies for ILS. Indeed, this is confirmed in Table 1. This table contains the percentage of observations, as well as the number of clusters which hold when discriminating them by their size (defined as observations per cluster, obs/clust) for a case study on 2021/050. If we do not consider clusters that are smaller than 5 obs/clust, a total of 233 and 204 ${B}_{\alpha }^{ij}$ parameters remain, which is an affordable amount that LAMBDA may deal with for this problem, while retaining the 95% and 91% of the GPS and Galileo observations, respectively. All in all, the strategy to resolve the cluster biases is twofold:

• 1. For those cluster biases whose associated cluster size is larger or equal than a predefined value (e.g., 5 obs/clust), their integer resolution is performed by using the LAMBDA algorithm.

• 2. The remaining cluster biases are recomputed to account for the ones previously resolved, and afterward, they are rounded to the nearest integer as long as their fractional part is below a predefined threshold (e.g., 0.2 NL cycles). The process finishes when no more cluster biases can be resolved.

Fig. 5

Correlations between ${B}_{\alpha }^{ij}$ parameters. On the left-hand side, the panel contains the entire set of parameters, whereas the right panel contains only those related to densely populated ambiguity clusters (≥ 5 obs/clust)

Table 1 Accumulated percentage of observations and number of clusters for different cluster size levels on 2021/050

Quality control and metrics

There is a direct connection between the overall AR performance of the processing scheme and those unresolved cluster biases. However, they belong to their own single-ambiguity cluster as inferred from the aggressive transition between the last two rows of Table 1, and since this implies one ${B}_{\alpha }^{ij}$ parameter and one $\delta {N}_{k}^{ij}$ observation, their presence does not degrade the least-squares adjustment. Conveniently, we thus define the residuals (${\varvec{\epsilon}}$) as:

$${\varvec{\epsilon}}=\varvec{y}-\mathbf{A}_x\varvec{x}_x-\mathbf{A}_{\tau}\varvec{x}_{\tau}-\mathbf{A}_{B}\lfloor\varvec{x}_{B}\rceil$$

(13)

where $\varvec{y}$, ${\varvec{x}}_{x}$, ${\varvec{x}}_{\tau }$ and ${\varvec{x}}_{B}$ are the vectors containing the observations, the estimated orbit corrections, the estimated clock corrections and the estimated cluster biases, respectively. ${\mathbf{A}}_{x}$, ${\mathbf{A}}_{\tau }$ and ${\mathbf{A}}_{B}$ are the corresponding parts of the design matrix. Since these residuals are actually between-satellite residuals, we have generated satellite-dependent errors at epoch $t$ (${\varvec{e}}_{t}$) as

$${\varvec{e}}_{t}=\mathrm{diag}{\left({\left[{{\mathbf{D}}}_{t}^{\top}{{\varvec{\Sigma}}}_{t}^{-1}{{\mathbf{D}}}_{t}\right]}^{-1}\right)}^\frac{1}{2}$$

(14)

The rows of the matrix ${{\mathbf{D}}}_{t}$ contain the between-satellite differences of each $i,j$ pair participating at epoch $t$ (with a final row including a zero-mean-like condition), and ${{\varvec{\Sigma}}}_{t}$ is a covariance-like diagonal matrix whose $k$ (diagonal) component is computed as (note that every different $i,j$ pair is mapped into one and the same $k$ index)

$$d_k=N_r\frac{N_{t,max}}{N_t^{ij}}\left(\mathrm{m}_t^{ij}[\varvec{\epsilon}]^2+\mathrm{IQR}_t^{ij}[\varvec{\epsilon}]^2\right)$$

(15)

with ${N}_{r}$, ${N}_t^{ij}$ and ${N}_{t,max}$ being the predefined redundancy level, the total number of $i,j$ observations at $t$ and the maximum number of observations for any $i,j$ pair at $t$, respectively. $\mathrm{m}_t^{ij}[\cdot]$ and $\mathrm{IQR}_t^{ij}[\cdot]$ are the median and inter-quartile range (IQR) operators applied over all the elements belonging to the $i,j$ pair at $t$. This empirical normalization of the residuals is useful to detect epoch- and satellite-dependent anomalous events.

The AR metrics described hitherto focus on the satellite side. Nonetheless, the station counterpart provides a wealth of quality indicators and can be used to analyze the overall AR performance, e.g., by looking into the AR residuals (fractional parts of the resolved ambiguities) or the AR rates (with the resolved WL ambiguities as reference).

In Table 2, we summarize some AR quality metrics for a 122-day-long reprocessing (from 2021/031 to 2021/152, both included), including GPS and Galileo satellite systems, during the first and second processing loop iterations. Distinction is made between the satellite and station sides. For the satellites, the rows stand for mean percentage of daily unresolved cluster biases and the maximum, mean daily StD for the residuals and the maximum, and median daily IQR for the residuals and the maximum, respectively. In contrast, for the stations, the rows contain mean AR daily residuals and the maximum, and mean AR daily rates and the minimum. The numerical values show that the extreme cases do barely deviate from the mean. The worst case is linked to the AR rates for the first iteration, with a minimum of roughly 80% (for day 2021/102; the complete series shows that this is really not a standard case), which is about 7% and 9% below the average for GPS and Galileo, respectively. This inferior performance vanishes during the second iteration. In general, the transition between iterations is almost nonexistent on the satellite side, despite using a much more stringent parameterization during the second iteration (as noted in the electronic supplement, only constant biases for the clock corrections are estimated). The StD and IQR are in the order of 0.06 and 0.04 NL cycles for both GPS and Galileo. On the station side, however, a small improvement is noticed between the iterations, from about 0.05 to 0.04 NL cycles in terms of mean AR residuals, and an increment of 1% in AR rates, which are in the order of 88–90% for both GNSS systems.

Table 2 AR metrics for a reprocessing of 122 days using the proposed undifferenced scheme. The residuals are in units of NL cycles

Results

This section evaluates the performance of the results generated from the proposed UD processing scheme and AR strategy by means of comparisons against two reference solutions based on classical DD approaches. One of them relies on a controlled, tailored test case, whereas the other comes from the CODE MGEX (Multi-GNSS Extension; Montenbruck et al. 2017; Prange et al. 2020) production line.

UD-based against DD-based solutions: controlled test case

From March 23 to April 6, 2021, fifteen daily DD-based solutions have been generated following the standard procedures adopted by the CODE AC, i.e., a twofold strategy: Generation of geometry using DD observations, followed by the computation of clock corrections and associated biases through a UD processing scheme where the geometry is held fixed. To preserve to the extent possible the consistency with the corresponding UD-based solutions, the same screening has been used as well as the same a priori models and even the same ambiguity parameterization, for which the UD ambiguities have been converted into baseline ones. The fundamental differencing theorem (Wells 1987) states that both solutions will be identical, provided that every reduced (during differentiation) observation also reduces the number of parameters. This assumption is, however, not fully met as the baseline measurements demand equal observation windows between two stations, which generally leads to the rejection of some additional measurements at the boundaries of the satellite tracks.

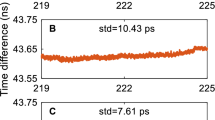
Figure 6 compares the UD- and DD-based clock corrections for the GPS (left axis) and Galileo (right axis) satellites. The cloud of points is at the ~ 6 ps level in StD for both systems, illustrating that the UD- and DD-based solutions may be considered as equivalent in terms of AR.

Fig. 6

UD- vs. DD-based clock comparisons for the GPS (left axis) and Galileo (right axis) satellites

The corresponding orbit comparisons are given in Fig. 7. An excellent agreement between both solutions can be seen at the level of 1.6 and 2.1 cm in (3D) RMS for GPS and Galileo, respectively. The satellite G11, which shows larger differences, is unhealthy and, hence, very poorly observed during this period, especially affecting the generation of baselines for the DD-based solution. The satellites E11, E12 and E19 are also showing larger differences than the majority of the Galileo satellites, although remain at an acceptable averaged level of about 3 cm.

Fig. 7

UD- vs. DD-based orbit comparisons for a 15-day trial interval (March 23 to April 7, 2021)

UD-based solution against CODE MGEX products

In order to better agree the setup of the CODE MGEX solutions, long-arc UD-based products have been derived from stacking three individual daily NEQs for a total of 120 days (from February to May, 2021). The resulting orbit comparisons are depicted in the upper panel of Fig. 8. The agreement between both processing lines is outstanding, with an average RMS of 1.8 and 2 cm for GPS and Galileo, respectively. It can be seen that there is an outlier on April 12 for GPS. A closer inspection of that day reveals that it is caused by the unhealthy satellite G24. On the other hand, the lower panel of Fig. 8 compares the clock corrections by means of daily StD statistics. As these comparisons represent the most sensitive metric to spot inconsistencies in AR, they have been inspected in more detail. For a period of 120 days, about 6720 GPS and Galileo (56 satellites) solutions have been compared, of which:

• A total of 19 daily satellite solutions are missing in the UD-based series w.r.t. the CODE MGEX one as they were excluded during the preprocessing stage.

• A total of 13 daily satellite clock comparisons are omitted from Fig. 8 as they contain discontinuities (see the electronic supplement) distorting the statistics.

• A total of 19 degraded daily satellite clock comparisons are omitted from Fig. 8. The problem has been found on the MGEX side.

• 2 entire days (2021/065 and 2021/121) with general poor performance are excluded from Fig. 8. The problem has been found on the MGEX side.

Fig. 8

Comparisons between UD-based solutions and CODE MGEX products for a period of 120 days. The top panel corresponds to the daily RMS of the orbit differences. The bottom panel shows the daily StD of the clock comparisons

In general, the clock agreement is at the level of 6 and 7 ps in StD for GPS and Galileo, respectively, which reflects an exceptionally good AR equivalence. Unfortunately, there is an outlier on May 6. A detailed analysis of this day is given on the upper panel of Fig. 9. As can be seen, the satellite E11 (highlighted in red) exhibits suspicious variations that usually entail a damaged AR. This satellite experiences an eclipse period at noon on this day (pale red shaded in the figure), which, according to Banville et al. (2020), may induce diverging clock estimates due to attitude mismodeling. Moreover, the AR satellite errors (denoted as ${\varvec{e}}_{t}$ in the preceding section) are depicted on the lower panel of Fig. 9. They hint that, indeed, something probably got wrong with AR from the end of the eclipse to the lapse of the clock transition for this satellite.

Fig. 9

On the top panel, the detailed clock comparison between the UD-based solution and the MGEX products is shown. The bottom panel depicts the AR errors resulting from the first processing loop iteration and computed with (13–15). The E11 eclipse period is pale red shaded

Finally, the orbit midnight misclosures for both the UD-based solutions and the CODE MGEX products are summarized in Table 3 by using median and IQR statistics satellite by satellite. It is worth noting that the new UD-based solution is systematically superior to the DD-based MGEX products, reducing the overall median from 7.8 to 5.4 mm and from 10.0 to 6.4 mm for GPS and Galileo, respectively.

Table 3 Midnight orbit misclosures statistics for a period of 120 days (February–May, 2021). All the entries are in mm

Conclusions

A GNSS processing scheme based on undifferenced observations has been designed and implemented to generate global GNSS solutions without the need to have precise a priori information at hand. To overcome the restriction resulting from the huge number of ambiguity parameters (more than 10,000) during the AR stage, we have developed a novel between-satellite AR strategy.

The proposed AR strategy is based on a mixed-integer model that rigorously inspects the between-satellite real-valued ambiguities in a stand-alone step. The DD-AR information is explicitly considered through the use of ambiguity clusters. These clusters complement the model by reducing the number of integer parameters down to ~ 200, which is of utmost importance because it allows LAMBDA to be used at a global scale. Additionally, the detailed view offered by this method can be exploited to define a more robust datum for the integer parameters and to characterize other phenomena such as apparent phase jumps (see electronic supplement). On the other hand, the resulting metrics may also reveal relevant information about the quality of the AR performance, supporting the identification of potential anomalies. As an ultimate result, the preliminary solution (orbits and clock information) is modified to become compatible with the integer-cycle property of the carrier phase ambiguities, enabling between-satellite AR in an inexpensive station-wise sense.

The performance of the newly generated UD-based products for GPS and Galileo has been evaluated by means of comparisons against two independent DD-based solutions, one of which derives from a controlled test case where the same network, screening and parameterization as for the undifferenced processing scheme have been preserved, whereas the other comes from the official CODE MGEX production line. The findings show that the UD-based solution is at a competitive level, with a StD statistic of 6–7 ps for the clock comparisons, and orbit comparisons in the order of 1.5–2 cm in (3D) RMS. The new solutions are also apparently superior in internal consistency, measured as orbit midnight misclosures over a period of 120 days, with median statistics at the level of 5.4 and 6.4 mm for GPS and Galileo, respectively.