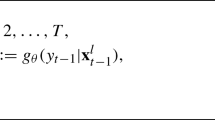Abstract
Motivated by a certain type of infinite-patch metapopulation model, we propose an extension to the popular Poisson INAR(1) model, where the innovations are assumed to be serially dependent in such a way that their mean is increased if the current population is large. We shall recognize that this new model forms a bridge between the Poisson INAR(1) model and the INARCH(1) model. We analyze the stochastic properties of the observations and innovations from an extended Poisson INAR(1) process, and we consider the problem of model identification and parameter estimation. A real-data example about iceberg counts shows how to benefit from the new model.





Similar content being viewed by others
Notes
Note that the extended Poisson INAR(1) model differs from the CINAR(1) model of Triebsch (2008), where the innovations \(\epsilon _t\) stem from an INARCH(1) process on their own. While the first is observation driven according to the classification by Cox (1981), see Definition 1, the latter is parameter driven.
Note that reparametrization (20) is also advantageous for numerical optimization, since it allows to work with box constraints.
References
Al-Osh MA, Alzaid AA (1987) First-order integer-valued autoregressive (INAR(1)) process. J Time Ser Anal 8(3):261–275
Alzaid AA, Al-Osh MA (1988) First-order integer-valued autoregressive process: distributional and regression properties. Stat Neerl 42(1):53–61
Bradley RC (2005) Basic properties of strong mixing conditions. A survey and some open questions. Probab Surv 2:107–144
Bu R, McCabe B, Hadri K (2008) Maximum likelihood estimation of higher-order integer-valued autoregressive processes. J Time Ser Anal 29(6):973–994
Buckley F, Pollett P (2010) Limit theorems for discrete-time metapopulation models. Probab Surv 7:53–83
Cox DR (1981) Statistical analysis of time series: some recent developments. Scand J Stat 8:93–115
Feller W (1968) An introduction to probability theory and its applications, vol I, 3rd edn. Wiley, New Jersey
Freeland RK, McCabe BPM (2004) Analysis of low count time series data by Poisson autoregression. J Time Ser Anal 25(5):701–722
Frey S, Sandas P (2009) The impact of iceberg orders in limit order books. CFR working paper 09–06
Grunwald GK, Hyndman RJ, Tedesco L (1997) A unified view of linear AR(1) models. Research report, Department of Statistics, University of Melbourne
Grunwald GK, Hyndman RJ, Tedesco L, Tweedie RL (2000) Non-Gaussian conditional linear AR(1) models. Aust NZ J Stat 42(4):479–495
Heathcote CR (1966) Corrections and comments of the paper “A branching process allowing immigration”. J R Stat Soc Ser B 28(1):213–217
Heyde CC, Seneta E (1972) Estimation theory for growth and immigration rates in a multiplicative process. J Appl Probab 9(2):235–258
Ibragimov I (1962) Some limit theorems for stationary processes. Theory Probab Appl 7(4):349–382
Johnson NL, Kotz S, Balakrishnan N (1997) Discrete multivariate distributions. Wiley, Hoboken
Johnson NL, Kemp AW, Kotz S (2005) Univariate discrete distributions, 3rd edn. Wiley, Hoboken
Jung RC, Tremayne AR (2003) Testing for serial dependence in time series models of counts. J Time Ser Anal 24(1):65–84
Jung RC, Tremayne AR (2011a) Useful models for time series of counts or simply wrong ones? AStA Adv Stat Anal 95(1):59–91
Jung RC, Tremayne AR (2011b) Convolution-closed models for count time series with applications. J Time Ser Anal 32:268–280
Katz RW (1981) On some criteria for estimating the order of a Markov chain. Technometrics 23(3):243–249
Klimko LA, Nelson PI (1978) On conditional least squares estimation for stochastic processes. Ann Stat 6(3):629–642
Latour A (1998) Existence and stochastic structure of a non-negative integer-valued autoregressive process. J Time Ser Anal 19(4):439–455
McKenzie E (1985) Some simple models for discrete variate time series. Water Resour Bull 21(4):645–650
Monteiro M, Scotto MG, Pereira I (2012) Integer-valued self-exciting threshold autoregressive processes. Commun Stat Theory Methods 41(15):2717–2737
Nummelin E, Tweedie RL (1978) Geometric ergodicity and \(R\)-positivity for general Markov chains. Ann Probab 6(3):404–420
Pakes AG (1971) Branching processes with immigration. J Appl Probab 8(1):32–42
Seneta E (1968) The stationary distribution of a branching process allowing immigration: a remark on the critical case. J R Stat Soc Ser B 30(1):176–179
Steutel FW, van Harn K (1979) Discrete analogues of self-decomposability and stability. Ann Probab 7(5):893–899
Sun J, McCabe BPM (2013) Score statistics for testing serial dependence in count data. J Time Ser Anal 34(3):315–329
Triebsch LK (2008) New Integer-valued Autoregressive and Regression Models with State-dependent Parameters. Doctoral dissertation, TU Kaiserslautern, Verlag Dr. Hut, Munich
Tsay RS (1992) Model checking via parametric bootstraps in time series analysis. J R Stat Soc Ser C 41(1):1–15
Wei CZ, Winnicki J (1990) Estimation of the means in the branching process with immigration. Ann Stat 18(4):1757–1773
Weiß CH (2008) Thinning operations for modelling time series of counts—a survey. AStA Adv Stat Anal 92(3):319–341
Weiß CH (2010a) The INARCH(1) model for overdispersed time series of counts. Commun Stat Simul Comput 39(6):1269–1291
Weiß CH (2010b) INARCH(1) processes: higher-order moments and jumps. Stat Probab Lett 80(23–24):1771–1780
Weiß CH (2012) Process capability analysis for serially dependent processes of Poisson counts. J Stat Comput Simul 82(3):383–404
Weiß CH, Pollett PK (2014) Binomial autoregressive processes with density dependent thinning. J Time Ser Anal 35(2):115–132
Winnicki J (1991) Estimation of the variances in the branching process with immigration. Probab Theory Relat Fields 88(1):77–106
Zhu F, Wang D (2011) Estimation and testing for a Poisson autoregressive model. Metrika 73:211–230
Acknowledgments
The author thanks the two referees for highly useful comments on an earlier draft of this article. The iceberg order data of Section 4.2 were kindly made available to the author by the Deutsche Börse. Prof. Dr. Joachim Grammig, University of Tübingen, is to be thanked for processing of it to make it amenable to data analysis. I am also very grateful to Prof. Dr. Robert Jung, University of Hohenheim, for his kind support to get access to the data, and for valuable comments on an earlier draft of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Proofs
Proofs
1.1 Proof of Proposition 2
Since \((X_t)_{\mathbb N_0}\) is a homogeneous Markov chain with strictly positive 1-step transition probabilities, \((X_t)_{\mathbb N_0}\) is also irreducible and aperiodic. Furthermore, it is distributed as a BPI, so we can apply the theorem in Heathcote (1966). It remains to check two conditions:
-
The mean related to the individual offspring, i.e., the mean of \(Y\) according to our notations in Sect. 2, must be smaller than 1 (subcritical case). From Proposition 1, we obtain that \(E[Y]=\rho +a\), so \(E[Y]<1\) iff the condition \(\rho +a<1\) holds.
-
The immigration in (4) is described by the i.i.d. random variables \(\nu _t\sim {\text {Po}}(b)\). Now consider the quantity \(\sum _{n=1}^{\infty }\ {\textstyle \frac{1}{n}}\cdot P(\nu _t\ge n)\), i.e., the expectation \(E[H(\nu _t)]\), where \(H(n) := \sum _{k=1}^n \frac{1}{k}\) for \(n\in \mathbb N\) and \(H(0):=0\) denote the harmonic numbers. Since \(H(\nu _t)\le \nu _t\), and since \(E[\nu _t] = b<\infty \), also \(E[H(\nu _t)]<\infty \) holds.
So the existence of a stationary marginal distribution follows, and together with the irreducibility and aperiodicity, it follows that \((X_t)_{\mathbb N_0}\) is an ergodic Markov chain (Feller 1968, p. 394). Note that this stationarity result could also be derived by applying Proposition 3.1 in Latour (1998), because binomial-Poisson thinning is an instance of the generalized thinning concept considered by Latour (1998).
With similar arguments as for Heathcote (1966), we now apply Theorem 1 in Pakes (1971). \((X_t)_{\mathbb N_0}\) is not only distributed as a subcritical BPI, the corresponding offspring also has a finite variance, i.e., \(V[Y]<\infty \). Hence, \((X_t)_{\mathbb N_0}\) satisfies all conditions being required in Sect. 2 of Pakes (1971), so Theorem 1 in Pakes (1971) implies geometric ergodicity. From Theorem 1 of Nummelin and Tweedie (1978) and Theorem 3.7 in Bradley (2005), we conclude that a stationary extended Poisson INAR(1) process is also \(\beta \)-mixing (and thus \(\alpha \)-mixing) with exponentially decreasing weights.
1.2 Proofs of Sect. 3.1
Let \(f(x) := a\cdot x+b\). Formula (5) about conditional mean and variance follows from
respectively. For computing the variance, we used the conditional independence of \(\rho \circ X_{t-1}\) and \(\epsilon _t\), given \(X_{t-1}\). From formula (5) and the stationarity assumption, we obtain the marginal mean and variance as given in formula (6) by solving
The expression (7) for the pgf is shown analogously:
Recursions (8) and (9) for higher-order moments follow from
To compute the second and third moments of \(X_t\), we first require the first few moments of the binomial and the Poisson distribution:
Now we apply formula (9) to obtain
This confirms formula (6) about the variance. Analogously,
from which we obtain an expression for \(\mu _{3,X}\). After tedious algebra, we find an expression for the third central moment:
Next, we derive an expression for the autocovariance function. For \(k\ge 1\), we obtain by applying formula (5) and by conditioning that
Finally, the proof of formula (11) is done by induction, with this formula being true for \(k=1\) according to the expression for \(E[X_t\ |\ X_{t-1},\ldots ]\) in formula (5).
1.3 Proofs of Sect. 3.2
Since \(E[\epsilon _t | X_{t-1},\ldots ] = V[\epsilon _t | X_{t-1},\ldots ] = a\cdot X_{t-1}+b\), we obtain
In particular, this result shows that \(V[\epsilon _t] = E[\epsilon _t] + a^2\cdot \sigma _X^2\), so the proof of formula (12) is complete. Similarly, we prove formula (13) via
Next, we consider the covariance between \(X_t\) and \(\epsilon _{t-j}\) with \(j\in \mathbb N_0\). First, using the conditional independence between \(\rho \circ X_{t-1}\) and \(\epsilon _{t}\) given \(X_{t-1}\), we have
Secondly, for \(j\ge 1\) and using formula (5),
So through conditioning on \(X_{t-1},\ldots , \epsilon _{t-1},\ldots \), we obtain for \(j\ge 1\) that
1.4 Proofs of Sect. 4.1
The score functions (17) to (19) can be derived in analogy to Sect. 3 in Freeland and McCabe (2004). Since
it is essential to discuss the first-order partial derivatives of the transition probabilities \(P_{{\varvec{\theta }}}(k|l)\) according to (3). Let us start with the derivative in \(\rho \). Since (Freeland and McCabe 2004, p. 716)
and since
we can express
So (17) follows. Differentiating with respect to \(a\), we have
So (18) follows, since
Finally, we have
and hence
in analogy to Proposition 2 in Freeland and McCabe (2004). This completes the proof of (19).
1.5 Proofs of Sect. 5.1
To compute the derivative \(\frac{\partial }{\partial \tau }\,\ell \big ((1-\tau )\xi ,\ \tau \xi ,\ b\big )\), we proceed in analogy to the proof of formulae (17) and (18), but by also applying the chain rule. Since \(\frac{\partial \rho }{\partial \tau } = -\xi \) and \(\frac{\partial a}{\partial \tau } = \xi \), we obtain
Hence, it follows that
from which we obtain the formula for the score function \(S_{\tau ;T}(\xi ,b)\).
For the sake of readability, let us now use the abbreviation \(g(X_t,X_{t-1})\) for the summands of \(S_{\tau ;\, T}(\xi ,b)\). Under the null of a Poisson INAR(1) model, it follows from Proposition 2 in Freeland and McCabe (2004) that
and
Hence, the conditional mean of \(g(X_t,X_{t-1})\) becomes
As a result,
Finally, the process of \(g(X_t,X_{t-1})\) is \(\alpha \)-mixing with exponentially decreasing weights, see Proposition 2, such that Theorem 1.7 of Ibragimov (1962) is applicable, which gives the stated asymptotic normality with \(\sigma ^2=E\big [g(X_1,X_{0})^2\big ]+ 2\,\sum _{k=1}^{\infty }\ E\big [g(X_1,X_{0})\,g(X_{k+1},X_{k})\big ]\). Using the above result \(E\big [g(X_t,X_{t-1})| X_{t-1}, \ldots \big ]=0\), it follows that
So the proof of Proposition 3 is complete.
Rights and permissions
About this article
Cite this article
Weiß, C.H. A Poisson INAR(1) model with serially dependent innovations. Metrika 78, 829–851 (2015). https://doi.org/10.1007/s00184-015-0529-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00184-015-0529-9