Abstract
This paper provides an underlying reason for why recent Bayesian trend-cycle decompositions of US real GDP differ despite using identical unobserved components models. We stress that a pitfall in estimating unobserved components models accounts for the divergence in the empirical conclusions. Our results also show that the decline in the long-run growth rate of real GDP has been slow and gradual rather than abrupt during the post-World War II period.




Similar content being viewed by others
Notes
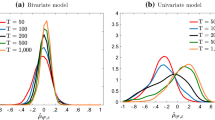
Kim and Kim (2018) demonstrate that classical maximum likelihood and Bayesian estimation methods produce starkly different trend-cycle decompositions of real GDP in a finite sample.
Morley et al. (2003) theoretically and empirically show that a UC model and its equivalent ARIMA model should produce identical trend-cycle decompositions.
The posterior moments are defined as \({{\bar{\mu }}} = {{\bar{\varOmega }}_{\mu }}({{\underline{\varOmega }}_{\mu }}^{-1} \underline{\mu } + \sigma ^{-2}_u {X^*}'{Y^*})\), \({{\bar{\varOmega }}_{\mu }} = ({{\underline{\varOmega }}_{\mu }^{-1}} + \sigma ^{-2}_u {X^*}'{X^*})^{-1}\), where \(\{\underline{\mu },{\underline{\varOmega }}_{\mu } \}\) is the set of prior mean and variance for \(\mu \). The data matrices \(\{X^*,Y^*\}\) are constructed by vertically stacking \(\{X_t^*,Y_t^*\}\), where \(Y_t^* = X_t^*\mu + u_{t}\), \(Y_t^* = x_t - x_{t-1}\), and \(X_t^* = 1\).
They sample \(\phi \) using the normal distribution with mean \({\bar{\phi }} = {{\bar{\varOmega }}_{\phi }}({{\underline{\varOmega }}_{\phi }}^{-1} \underline{\phi } + \sigma ^{-2}_e {{\hat{X}}}'{{\hat{Y}}})\) and covariance matrix \({{\bar{\varOmega }}_{\phi }} = ({{\underline{\varOmega }}_{\phi }^{-1}} + \sigma ^{-2}_e {{\hat{X}}}'{{\hat{X}}})^{-1}\), where \(\{ \underline{\phi }, {\underline{\varOmega }}_{\phi }\}\) are the prior mean and covariance matrix, respectively. The data matrices \(\{{\hat{X}},{\hat{Y}}\}\) are constructed by vertically stacking \(\{{\hat{X}}_t,{\hat{Y}}_t\}\), where \({\hat{Y}}_t = {\hat{X}}_t\phi + e_{t}\), \({\hat{Y}}_t = z_t\), and \({\hat{X}}_t = [z_{t-1} \ z_{t-2}]\).
Luo and Startz (2014) and Huang and Luo (2018) do estimate the correlation parameter \(\rho \) for their UC models. However, when driving the posterior distributions of \(\mu \) and \(\phi \) from which posterior samples are drawn, they do not consider \(\rho \). More detailed expositions of their Gibbs sampling algorithms are provided in the appendices of Luo and Startz (2014) and Huang and Luo (2018).
Here, we follow the model specification proposed by Chib (1998). The Bayesian algorithm to estimate the regime indicator variable is provided in “Appendix.”
The Bayes factor, which is a ratio of two marginal likelihood values, is sensitive to prior distributions. Specifically, the Bayes factor is not well defined for improper diffuse priors. We employ the WAIC because its performance for model selection is stable and reliable regardless of prior distributions.
References
Antolin-Diaz J, Drechsel T, Petrella I (2017) Tracking the slowdown in long-run gdp growth. Rev Econ Stat 99(2):343–356
Chib S (1998) Estimation and comparison of multiple change-point models. J Econom 86(2):221–241
Christiano LJ (1992) Searching for a break in gnp. J Bus Econ Stat 10(3):237–250
Durbin J, Koopman SJ (2002) A simple and efficient simulation smoother for state space time series analysis. Biometrika 89(3):603–616
Eo Y, Kim CJ (2016) Markov-switching models with evolving regime-specific parameters: Are postwar booms or recessions all alike? Rev Econ Stat 98(5):940–949
Grant AL, Chan JC (2017) A bayesian model comparison for trend-cycle decompositions of output. J Money Credit Bank 49(2–3):525–552
Hamilton JD (1989) A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57:357–384
Huang Y-F, Luo S (2018) Potential output and inflation dynamics after the Great Recession. Empir Econ 55(2):495–517
Kim CJ, Kim J (2018) Trend-cycle decompositions of real GDP revisited: classical and Bayesian perspectives on an unsolved puzzle. SSRN: https://ssrn.com/abstract=2883438 or https://doi.org/10.2139/ssrn.2883438
Luo S, Startz R (2014) Is it one break or ongoing permanent shocks that explains us real gdp? J Monet Econ 66:155–163
Morley JC, Nelson CR, Zivot E (2003) Why are the beveridge-nelson and unobserved-components decompositions of gdp so different? Rev Econ Stat 85(2):235–243
Perron P (1989) The great crash, the oil price shock, and the unit root hypothesis. Econometrica 57:1361–1401
Perron P, Wada T (2009) Let’s take a break: trends and cycles in us real gdp. J Monet Econ 56(6):749–765
Stock JH, Watson MW, Blinder AS, Sims CA (2012) Disentangling the channels of the 2007–2009 recession/comments and discussion. Brookings papers on economic activity p 81
Wang J, Zivot E (2000) A bayesian time series model of multiple structural changes in level, trend, and variance. J Bus Econ Stat 18(3):374–386
Watanabe S (2010) Asymptotic equivalence of bayes cross validation and widely applicable information criterion in singular learning theory. J Mach Learn Res 11:3571–3594
Zellner A, Ando T (2010) A direct monte carlo approach for bayesian analysis of the seemingly unrelated regression model. J Econom 159(1):33–45
Zivot E, Andrews DWK (2002) Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. J Bus Econ Stat 20(1):25–44
Acknowledgements
We are grateful to two anonymous referees and the coordinating editor for helpful suggestions and constructive comments that greatly improved the paper.
Author information
Authors and Affiliations
Corresponding author
Appendix: Posterior simulation for latent state variables
Appendix: Posterior simulation for latent state variables
To recover the Markovian property of the unobserved state variables, we cast the UC model in Eqs. (1), (2), and (3) as a state-space representation as follows:
where
In the above representation, the transition densities associated with Eq. (A.2) are degenerated because of the reduced rank covariance matrix of \(G\epsilon _t\). We employ the disturbance smoothing sampler by Durbin and Koopman (2002) to circumvent the degeneracy problem and to sample the continuous latent variables \(x_{1:T}\) and \(z_{1:T}\) conditional on \(s_{1:T}\). Since in this “Appendix” we focus on quantifying the uncertainty in break points, we do not provide detailed expositions for the smoothing algorithm here.
Unlike Wang and Zivot (2000), we suggest a simple alternative method of estimating the break date and constructing a corresponding Bayesian credible set using the smoothing algorithm of Hamilton (1989). The proposed algorithm is a multi-move sampler that samples the whole sequence of \(s_t\) through one-time forward–backward recursion. Consequently, the proposed method has a good mixing property. The target distribution in sampling \(s_{1:T}\) is given by:
where \(s_{t+1:T}= \{s_{t+1}, s_{t+2}, \ldots ,s_T\}\). For the sake of notational simplicity, the model parameter \(\theta \) is abbreviated throughout the derivation. The conditional density at time t is further decomposed as follows:
In the last line, we drop the density of \(\beta _k\) for \(k = t+1,t+2,\ldots ,T\) because it is irrelevant conditional on \(\beta _{t}\). The evaluation of the filtering density \(f(s_t\vert \beta _{1:t})\) for \(t = 1,\ldots ,T\) is performed by Hamilton (1989)’s filtering algorithm. In the prediction step, given \(f(s_{t-1}\vert \beta _{1:t-1})\), the joint density for \(s_t\) and \(s_{t-1}\) is obtained by \(f(s_t,s_{t-1}\vert \beta _{1:t-1}) = f(s_t\vert s_{t-1}) f(s_{t-1}\vert \beta _{1:t-1})\), where \(f(s_t\vert s_{t-1})\) is the transition probability in Eq. (12) or (13). In the updating step, we compute the density of \(s_t\) conditional on \(\beta _{1:t}\) as follows:
where \(f(s_t \vert \beta _{1:t-1}) = \sum _{s_{t-1}} f(s_t,s_{t-1}\vert \beta _{1:t-1})\). We obtain \(f(\beta _{t}\vert \beta _{1:t-1})\) by integrating out \(s_t\) as \(f(\beta _{t}\vert \beta _{1:t-1}) = \sum _{s_t} f(\beta _t \vert s_t, \beta _{1:t-1})f(s_t \vert \beta _{1:t-1})\). Therefore, it is simple to obtain \(f(s_t\vert \beta _{1:t})\) for \(t=1,\ldots ,T\) by iterating the prediction and the updating steps. Based on Eq. (A.4), \(s_t\) is drawn from the following posterior distribution:
moving backward in time for \(t = T,T-1,\ldots ,1\) and for \(i=1,2\).
Rights and permissions
About this article
Cite this article
Kim, J., Chon, S. Why are Bayesian trend-cycle decompositions of US real GDP so different?. Empir Econ 58, 1339–1354 (2020). https://doi.org/10.1007/s00181-018-1554-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-018-1554-0