FDM technology and the effect of printing parameters on the tensile strength of ABS parts

Abstract

The effect of printing speed on the tensile strength of acrylonitrile butadiene styrene (ABS) samples fabricated using the fused deposition modelling (FDM) process is addressed in this research. The mechanical performance of FDM-ABS products was evaluated using four different printing speeds (10, 30, 50, and 70 mm/s). A numerical model was developed to simulate the experimental campaign by coupling two computational codes, Abaqus and Digimat. In addition, this article attempts to investigate the impacts of printing parameters on ASTM D638 ABS specimens. A 3D thermomechanical model was implemented to simulate the printing process and evaluate the printed part quality by analysing residual stress, temperature gradient and warpage. Several parts printed in Digimat were analysed and compared numerically. The parametric study allowed us to quantify the effect of 3D printing parameters such as printing speed, printing direction, and the chosen discretisation (layer by layer or filament) on residual stresses, deflection, warpage, and resulting mechanical behaviour.

1 Introduction

The rapidly developing digital manufacturing process [1] known as additive manufacturing (AM)or 3D printing entails constructing a three-dimensional object by superimposing layers [2,3,4]. Today, 3D printing is required in most industries [5,6,7]. Due to its many benefits, trustworthy outcomes, design, materials, and manufacturing techniques, 3D printing now plays a significant role in the aircraft and aerospace industry [8]. AM makes it possible to quickly have functioning parts with complex shapes, increasing reliability, and lowering costs. AM can also create pieces with a lattice structure, which reduces an aircraft’s weight and improves fuel economy [9]. Airbus has decreased the number of parts for a hydraulic tank from 126 elements to a single 3D printed portion, which is one of the accomplishments of 3D printing [10].

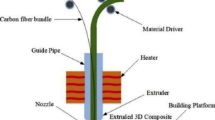
Similarly, GE Aviation reduces 855 pieces to a dozen 3D-printed parts, increasing energy efficiency and decreasing weight [11]. Thanks to additive manufacturing, producing lighter, more robust, and more efficient features in a shorter time is crucial for the automobile sector [12]. BMW was one of the first companies in 25 years to use 3D printing technology in manufacturing. In 2020, BMW will open an additive manufacturing campus with more than 80 employees. It has established its credibility in this industry by developing the sporty i8 Roadster vehicle [13]. Ferrari also produces items using additive manufacturing. Therefore, the business has developed new, hollow-structured 3D-printed pedals that are harder and lighter than the previous model [13]. In regards to the development of 3D printing in the medical field [14], a study was conducted by Tarfaoui et al. [15] to ascertain the capacity of AM to offer unique advantages to humanity in the medical supply sector (for instance, it is advised to use filaments (PLA, PETG) with low porosity and that provide the possibility to be sterilised without damage (withstand high temperatures) for the printing of the COVID-19 mask). The COVID-19 pandemic’s effects on the global additive manufacturing sector and the merits and drawbacks of 3D printing, in general, were also discussed [16, 17]. The most popular approach is fused deposition modelling (FDM) technology [18] because it is straightforward, readily available, and reasonably priced. This method is most frequently used to create polymer-based materials [19]. For design projects, working prototypes, manufacturing tools, and low-volume single-use products, FDM is ideal. The FDM method’s basic idea is introduced by first dividing 3D CAD data into layers. The data is then sent to a machine that uses a manufacturing platform to construct the part layer-by-layer. For each cross-section, thin thermoplastic wire and carrier material coils are employed. The unwinding material is progressively extruded via two heated nozzles, resembling a hot glue gun. The extrusion nozzles are precisely positioned on the layer above the carrier and thermoplastic materials. As the build platform descends, the extrusion nozzle moves in a horizontal X-Y plane, layer by layer, building the part [20, 21]. The completed part is taken off the build platform, its support material is removed, and the raw FDM pieces with distinct layer lines are left behind. Numerous industries use the FDM method [22], including aerospace, automotive, and medical. Choosing the suitable material to print a given object is becoming increasingly difficult.

Mummel et al. [23] studied the effects of several 3D printing process parameters on the hardness and tensile strength of PLA polymer. The results showed an increase in Young’s modulus and tensile strength for the edge-oriented samples: 1.896 ± 0.044 GPa and 49.12 ± 0.78 MPa, respectively. In addition, a proportional relationship between hardness and tensile strength was noticed when varying the print orientation parameters. Parham et al. [24] studied the effect of printing speed on the tensile and fracture strength of ABS specimens, using four printing speeds of 10, 30, 50, and 70 mm/s. The results showed that samples made at a printing speed of 70 mm/s have the highest elongation and ductility. On the other hand, specimens made at a printing speed of 30 mm/s have the lowest ductility and elongation. Moreover, the sample made with a printing speed of 70 mm/s represents the best resistance to breakage. ABS is a popular thermoplastic material in 3D printing due to its remarkable strength, durability, and chemical resistance. It can withstand high impact and heat and has excellent dimensional stability, which makes it an excellent choice for creating complex designs. Compared to PLA, ABS is more temperature-resistant, but it emits harmful fumes when heated. Therefore, it is essential to use it in a well-ventilated area. However, ABS requires higher printing temperatures, making it more challenging to work with. As a result, it is often used for advanced 3D printing projects, including the production of mechanical device parts, prototypes, and everyday items that require durability. The validity of the numerical program developed for ABS has been confirmed through experimental results, adding to its appeal as a reliable 3D printing material.

Most materials used in 3D printing technology are polymers and composite-based polymers [25]. These polymers can be synthetic resins or biomaterials. The new 3D printing technology uses polymers that come in various forms, such as liquid and thermoplastic mixtures [26]. One of the solutions to increase the performances of the materials realised by 3D printing would be doping by nanofillers. Indeed, according to research by Tarfaoui et al. [27], carbon nanotube (CNT) additives impact the elastic behaviour of textile-based composites. Different volume fractions of CNT were used (0.5%, 1%, 2%, and 4%). The experiment results show that the composite’s mechanical performance improves up to 2% of CNT additives, but the material’s strength significantly declines above this point.

Zhong et al. [28] evaluated the glass fibre-reinforced ABS Matrix. Experimental studies evaluated the processability of glass fibre-reinforced ABS matrix composites with three different amounts of glass fibre used as filler filaments in FDM. The results proved that glass fibres could improve ABS filaments’ tensile strength and surface stiffness. Hao et al. [29] investigated composites based on thermoset polymers reinforced with continuous carbon fibres using FDM 3D printing technology. The tests have shown an increase in the mechanical performance of thermoset composites compared to thermoplastic composites. The authors show that the obtained reinforced thermoset composites’ tensile strength and modulus of elasticity were 792.8 MPa and 161.4 GPa, respectively. In addition, the flexural strength and modulus of elasticity were 202.0 MPa and 143.9 GPa, respectively. Nachtane et al. [30] used split Hopkinson pressure bars in an experimental investigation to examine the effect of infill density (20%, 50%, and 100%) on the dynamic behaviour of 3D printed CF-PEKK composite under cyclic uniaxial compression. The ability of the material to absorb a mechanical shock wave was evaluated with the increase of infill density and the number of impact cycles in compression.

The present study addresses the challenges associated with finite element modelling (FEM) in 3D printing, including modelling accuracy, material characterization, modelling boundary conditions, meshing, computational resources, coupling between two computer codes (Abaqus and Digimat), and the effect of print settings (printing speed, printing direction, and chosen discretization). The originality of this work lies in its comprehensive investigation of these challenges and the development of new methodologies and approaches to address them. By considering the impact of coupling between two computer codes and print settings on the accuracy of FEM predictions, this study provides valuable insights into the accurate prediction of the behaviour of printed structures under various printing conditions.

In this paper, after reviewing the work and experimental results obtained by Parham et al. [24] on the 3D printing of ABS, we have focused on their numerical modelling. First, we numerically studied the effect of printing speed (10, 30, 50, and 70 mm/s) on the tensile and fracture behaviour of ABS samples produced by the FDM technique. The printing speed has a direct effect on the behaviour of the material. The faster the printing speed, the more likely there is to be over-extrusion, stringing, and other problems with the material. Additionally, faster printing speeds can cause warping, curling, and other dimensional issues. Therefore, it is important to adjust the printing speed appropriately to ensure the best possible result with the material. After validating the numerical model, one then numerically enriched the results obtained experimentally by Parham et al. using both Abaqus and Digimat software and a parametric study. The latter allowed us to quantify the effect of 3D printing parameters such as printing speed, printing direction, and the chosen discretisation (layer by layer or filament) on residual stresses, deflection, warpage, and resulting mechanical behaviour. A cost estimate for the present printing setup was created during the costing process. The price of the printing medium (ABS) must be considered. Thus, various data are required, including the material’s cost, the portion’s mass, and the substrate’s mass.

2 Recap of experimental study

Parham et al. employed a 3D printing method, particularly fused deposition modelling (FDM), to create ABS specimens at various printing speeds (10, 30, 50, and 70 mm/s). To choose the suitable/optimal speed for the 3D printing of this material, they studied the effect of printing speed (10, 30, 50, and 70 mm/s) on the behaviour law of ABS. The geometry and dimensions of the tensile specimens are shown in Fig. 1. Table 1 shows the printing parameters used in this study.

Fig. 1

Geometry and dimensions of the tensile specimens [24]

Table 1 Constant building parameters for manufacturing the test specimens [24]

Tensile tests were conducted using a SATAM STM-150 universal testing machine at a displacement speed of 1 mm/min, and the displacement and deformation were measured using the digital image correlation (DIC) technique (Fig. 2).

Fig. 2

Characterisation of the mechanical properties of FDM-ABS specimens: (a) Printed tensile specimen and (b) tensile testing configuration [24]

The stress-strain curves for ABS parts printed using the FDM technique at various printing speeds are shown in Fig. 3 (Table 2). At a printing speed of 10 mm/s, the specimen with the greatest tensile strength was produced. The specimen made at a speed of 30 mm/s has the lowest value in elongation at failure, while the specimen made at a speed of 70 mm/s exhibits the maximum value. Table 3 summarises the properties of ABS thermoplastic as determined by a tensile test, where E stands for the Young modulus, ν is the Poisson’s ratio, σ_y is the yield strength, σ_u is the ultimate strength, ε_elastic is the elastic deformation, and ε_plastic is the plastic deformation.

Fig. 3

Representative true stress. True strain curves for the manufactured tensile specimens with different printing speeds

Table 2 Mechanical properties of ABS material

Table 3 Average tensile properties of the tested FDM-ABS specimens [24]

3 FEA: constitutive mechanical and thermal models

3.1 Mechanical analysis

The constitutive equation that determines the mechanical behaviour of FDM printed parts must be defined to use the FEA model to forecast the thermomechanical behaviour of those parts. Hooke’s law, which establishes the correlation between stress and strain, describes the linear elasticity of polymers. This relationship is described as follows in 3D:

$$\left(\begin{array}{c}{\varepsilon}_{11}\\ {}{\varepsilon}_{22}\\ {}{\varepsilon}_{33}\\ {}{\gamma}_{12}\\ {}{\gamma}_{23}\\ {}{\gamma}_{31}\end{array}\right)=\left(\begin{array}{cccccc}{S}_{11}& {S}_{12}& {S}_{13}& {S}_{14}& {S}_{15}& {S}_{16}\\ {}& {S}_{22}& {S}_{23}& {S}_{24}& {S}_{25}& {S}_{26}\\ {}& & {S}_{33}& {S}_{34}& {S}_{35}& {S}_{36}\\ {}& & & {S}_{44}& {S}_{45}& {S}_{46}\\ {}& & & & {S}_{55}& {S}_{56}\\ {}& & & & & {S}_{66}\end{array}\right).\left(\begin{array}{c}{\sigma}_{11}\\ {}{\sigma}_{22}\\ {}{\sigma}_{33}\\ {}{\tau}_{12}\\ {}{\tau}_{23}\\ {}{\tau}_{31}\end{array}\right)$$

(1)

where ε is the deformation, γ is the shearing strain, τ is the shearing stress, and σ is the normal stress. By using the standard engineering constants, Eq. (1) expresses the constitutive law in terms of Young’s modulus, Poisson’s ratio, and shear modulus:

$$\left(\begin{array}{c}{\varepsilon}_{11}\\ {}{\varepsilon}_{22}\\ {}{\varepsilon}_{33}\\ {}{\gamma}_{12}\\ {}{\gamma}_{23}\\ {}{\gamma}_{31}\end{array}\right)=\left(\begin{array}{cccccc}1/{E}_{11}& -{\vartheta}_{12}/{E}_{11}& -{\vartheta}_{13}/{E}_{11}& 0& 0& 0\\ {}& 1/{E}_{22}& -{\vartheta}_{23}/{E}_{22}& 0& 0& 0\\ {}& & 1/{E}_{33}& 0& 0& 0\\ {}& & & 1/{G}_{23}& 0& 0\\ {}& & & & 1/{G}_{13}& 0\\ {}& & & & & 1/{G}_{12}\end{array}\right).\left(\begin{array}{c}{\sigma}_{11}\\ {}{\sigma}_{22}\\ {}{\sigma}_{33}\\ {}{\tau}_{12}\\ {}{\tau}_{23}\\ {}{\tau}_{31}\end{array}\right)$$

(2)

By inverting the stiffness matrix, the compliance matrix is created, and we are left with:

$$\left(\begin{array}{c}{\sigma}_{11}\\ {}{\sigma}_{22}\\ {}{\sigma}_{33}\\ {}{\tau}_{12}\\ {}{\tau}_{23}\\ {}{\tau}_{31}\end{array}\right)=\left(\begin{array}{cccccc}{C}_{11}& {C}_{12}& {C}_{13}& {C}_{14}& {C}_{15}& {C}_{16}\\ {}& {C}_{22}& {C}_{23}& {C}_{24}& {C}_{25}& {C}_{26}\\ {}& & {C}_{33}& {C}_{34}& {C}_{35}& {C}_{36}\\ {}& & & {C}_{44}& {C}_{45}& {C}_{46}\\ {}& & & & {C}_{55}& {C}_{56}\\ {}& & & & & {C}_{66}\end{array}\right).\left(\begin{array}{c}{\varepsilon}_{11}\\ {}{\varepsilon}_{22}\\ {}{\varepsilon}_{33}\\ {}{\gamma}_{12}\\ {}{\gamma}_{23}\\ {}{\gamma}_{31}\end{array}\right)$$

(3)

where

$${C}_{11}=\frac{\left({S}_{22}\cdot {S}_{33}-{S}_{23}^2\right)}{S},{C}_{22}=\frac{\left({S}_{11}\cdot {S}_{33}-{S}_{13}^2\right)}{S},{C}_{33}=\frac{\left({S}_{11}\cdot {S}_{22}-{S}_{12}^2\right)}{S}$$

(4)

$${C}_{12}=\frac{\left({S}_{23}\cdot {S}_{13}-{S}_{12}\cdot {S}_{33}\right)}{S},{C}_{13}=\frac{\left({S}_{12}\cdot {S}_{23}-{S}_{22}\cdot {S}_{13}\right)}{S},{C}_{23}=\frac{\left({S}_{12}\cdot {S}_{13}-{S}_{11}\cdot {S}_{23}\right)}{S}$$

(5)

$${C}_{44}=\frac{1}{{\textrm{S}}_{44}},{C}_{55}=\frac{1}{S_{55}},{C}_{66}=\frac{1}{S_{66}}$$

(6)

$$S={S}_{11}{S}_{22}{S}_{33}+2{S}_{12}{S}_{23}{S}_{13}-{S}_{13}^2{S}_{22}-{S}_{23}^2{S}_{11}-{S}_{13}^2{S}_{33}$$

(7)

In the case of polymers, the substance is thought to exhibit anisotropic behaviour, and the stress-strain behaviour can be expressed using the following Cartesian coordinates:

$${\varepsilon}_{11}=\frac{1}{E}\left[{\sigma}_{11}\vartheta \left({\sigma}_{22}+{\sigma}_{33}\right)\right]+{\alpha}_e\Delta T$$

(8)

$${\varepsilon}_{22}=\frac{1}{E}\left[{\sigma}_{22}\vartheta \left({\sigma}_{11}+{\sigma}_{33}\right)\right]+{\alpha}_e\Delta T$$

(9)

$${\varepsilon}_{33}=\frac{1}{E}\left[{\sigma}_{33}\vartheta \left({\sigma}_{11}+{\sigma}_{22}\right)\right]+{\alpha}_e\Delta T$$

(10)

$${\varepsilon}_{xy}=\frac{1+\vartheta }{E}{\sigma}_{xy},{\varepsilon}_{xz}=\frac{1+\vartheta }{E}{\sigma}_{xz},{\varepsilon}_{yz}=\frac{1+\vartheta }{E}{\sigma}_{yz}$$

(11)

where α_e is the coefficient of thermal expansion. The thermal stain can be found as:

$${\varepsilon}_{th}={\alpha}_e\Delta T$$

(12)

The real stress and the Von Mises Stress can be determined as follows:

$${\sigma}_{eff}=\sqrt{\sigma_{11}^2+{\sigma}_{22}^2+{\sigma}_{33}^2}+2\vartheta \left({\sigma}_{11}{\sigma}_{22}+{\sigma}_{11}{\sigma}_{33}+{\sigma}_{22}{\sigma}_{33}\right)$$

(13)

$${\sigma}_{\textrm{Mises}}=\sqrt{\frac{1}{2}\left[{\left({\sigma}_{11}^2-{\sigma}_{22}^2\right)}^2+{\left({\sigma}_{22}^2-{\sigma}_{33}^2\right)}^2+{\left({\sigma}_{33}^2-{\sigma}_{11}^2\right)}^2\right]}$$

(14)

3.2 Thermal analysis

Digimat 2022.1 offers the option of applying indirect sequentially coupled thermomechanical analysis for stress and heat analysis. Heat transfer is considered in the numerical model to determine the temperature profile and variation during the printing process. The heat transfer’s governing partial differential equation is:

$$\rho {C}_p\frac{\partial T}{\partial t}=k\left(\frac{\partial^2T}{\partial {x}^2}+\frac{\partial^2T}{\partial {y}^2}+\frac{\partial^2T}{\partial {z}^2}\right)$$

(15)

ρ, C_p, and k are the polymer’s density, specific heat capacity, and thermal conductivity, respectively. The energy that the phase solidification requires is about equal to:

$$H=\int \rho {C}_p(T) dT$$

(16)

A newly deposited layer at temperature T_m cools with the chamber temperature T_c. The underlying layers are reheated by conduction during the printing process, and their temperature exceeds T_g. The thickness of the part was printed in the z-direction with a constant chamber temperature of T_c. In this direction, the evolution of the temperature T (z, t) for each position at time t satisfies the following heat equation:

$$\rho {C}_p\frac{\partial T}{\partial t}=k\frac{\partial^2T}{\partial {z}^2}$$

(17)

This equation has the following solution

$$T={T}_{\textrm{c}}+\frac{H}{\rho {C}_{\textrm{p}}}\frac{1}{\sqrt{\pi \varphi t}}\exp \left(-\frac{Z^2}{4\varphi t}\right)$$

(18)

where the polymer’s thermal diffusivity is given by the formula $\varphi =\frac{k}{{\rho C}_p}$.

The thermal energy of the layer can be calculated as follows if the FDM portion has a suitably high dimension and a thickness h that is higher than the layer thickness Δh:

$$H=\rho {C}_{\textrm{p}}\Delta h\left({T}_{\textrm{m}}-{T}_{\textrm{c}}\right)$$

(19)

Additionally, the temperature variation across the part’s thickness can be determined as:

$$T={T}_{\textrm{c}}+\left({T}_{\textrm{m}}-{T}_{\textrm{c}}\right)\frac{\Delta h}{\sqrt{\pi \varphi t}}\exp \left(-\frac{Z^2}{4\varphi t}\right)$$

(20)

The temperature fluctuation at the Z position can be calculated using Eq. (20). For instance, to determine the layer where the temperature T_g (T = T_g) is reached at a certain time t, we have:

$$Z=2\sqrt{\varphi t}\sqrt{\ln \left(\frac{\Delta h}{\sqrt{\pi \varphi}}\frac{T_{\textrm{m}}-{T}_{\textrm{c}}}{T_{\textrm{g}}-{T}_{\textrm{c}}}\right)-\ln \sqrt{t}}$$

(21)

4 Implementation of the numerical study

A numerical model has been developed to simulate the experimental results reported by Parham et al. [24]. As seen in Fig. 4, the method for validating the model is based on alternating between the two numerical simulation programs, Abaqus and Digimat. The combination of Abaqus and Digimat offers various advantages, including the results’ accuracy due to the mesh’s superposition between the two models and a significant set of developments related to the printed specimen [31].

Fig. 4

Kinetics of a coupled Abaqus/Digimat computation

At each integration point, Abaqus’ role is to determine the strain increment under different contact types, boundary conditions, and loads before handing off to Digimat to determine the stress increment on each element, and then it will give a hand back to Abaqus to continue calculation (loads, contacts, etc.). Moreover, for the next step, Abaqus will compute the strain increment so that Digimat will use all the information recorded at the integration points (orientation tensor, residual stresses...) (Fig. 5a). Fig. 5b shows the different steps to carry out a calculation by coupling Abaqus/Digimat.

Fig. 5

Coupling procedure between Abaqus and Digimat

One of the crucial points of this Abaqus/Digimat coupling is the consideration of the implementation process (effect of 3D printing: deflection, residual stress, warping) on the mechanical performance of the structure. Fig. 6 shows the mapped manufacturing data visualised on the structural model.

Fig. 6

Mapped manufacturing data visualised on the structural model, filament orientation (eigenvector)

4.1 Finite element model

• a) First modelling: Abaqus

The initial part of the model validation process was the creation of an ASTM-D638 specimen in the simulation program Abaqus, using a C3D8R mesh with a 0.5 mm cell size (a total of 94,913 nodes and 84,768 linear hexahedral elements of type C3D8R) (Fig. 7). Then the curve corresponding to a printing speed of 10 mm/s was fitted to identify the elastic and plastic properties of ABS, which were estimated from the experimental results, Table 4. After that, the boundary conditions were inserted, and our model was meshed.

Fig. 7

Specimen mesh C3D8R

Table 4 ABS properties for a printing speed of 10 mm/s

The stress-strain curve for a first printing speed of 10 mm/s is shown in Fig. 8. A good correlation between the experimental and the numerical results can be noted.

Fig. 8

Stress-strain curve for a printing speed of 10 mm/s

• b) Second modelling: Abaqus/Digimat coupling

Digimat software is the second approach for simulating the material’s response under tensile loading for the printing speed of 10 mm/s. The coupling between Abaqus and Digimat, mentioned in Fig. 5, was used. The first step is to work on Digimat-AM, where all the printing parameters, including the nozzle and bed temperatures and the manufacturing process, have been entered (Table 3).

The G-code file must also be inserted, which includes details on the filling density, filler type, filament and nozzle diameters, printing speed, and printing density. To get the Gcode file, we used the software Slic3r where we inserted in the windows of Slic3r all the parameters. Finally, the specimen has meshed. Fig. 9 depicts the workflow for Digimat-AM.

Fig. 9

Work sequences in Digimat-AM

Digimat-RP and the superposition of the mesh between Abaqus and Digimat-AM (Fig. 10) and considering the results found in Digimat-AM (residual stresses, deflection, undeformed mesh, temperature), we obtained the curve shown in Fig. 11.

Fig. 10

Superposition of the mesh between Abaqus and Digimat

Fig. 11

Stress-strain curves for a printing speed of 10 mm/s

Furthermore, the curve determined by this approach and the experimental data are compared, and a good correlation was found. This curve will be used as a reference to establish the curves for the printing speeds of 30, 50, and 70 mm/s.

It is essential to validate the working sequence using different printing speeds, including 30, 50, and 70 mm/s, to confirm this approach after evaluating the mechanical behaviour of ABS for a printing speed of 10 mm/s using the Digimat/Abaqus coupling technique. Therefore, a comparison with the experimental data has been built to validate the numerical models developed in this study. Fig. 12 displays the stress-strain curves determined experimentally and numerically for printing rates of 10, 30, 50, and 70 mm/s. Generally, we can state a good correlation between the numerical simulations and the experimental results. We can thus conclude that the models predict the mechanical behaviour of the tested composites for the different printing speeds.

Fig. 12

Stress-strain curve determined numerically for 4 printing speeds

4.2 Effect of printing speed on residual stresses

The mechanical characteristics and dimensional accuracy of additive manufacturing items are significantly affected by residual stresses introduced during the 3D printing process [32]. Therefore, the last layer of the print, where residual stresses accumulate (at the end of the manufacturing process), was selected to adequately investigate the effect of printing speed on the residual stresses and deflection induced by the FDM process and to precisely measure the residual stresses.

Figure 13 shows the evolution of stresses as a function of printing time. The residual stresses were less important as the printing speed increased, and the maximum value of 11.87 MPa was reached with a speed of 10 mm/s. Conversely, the lowest residual stresses, with a value of 8.46 MPa, were observed at 70 mm/s.

Fig. 13

Residual stresses at the end of the manufacturing process

4.3 Effect of printing speed on the deflection

Figure 14 displays the deflection and temperature evolution as a function of printing speed and time, respectively. Fig. 14b showed that the deflection interval for printing at 10 and 30 mm/s was nearly identical (0.91, 0.93 mm) and that the deflection values for printing at 50 and 70 mm/s were extremely comparable (about 0.87 mm). As a result, the deflection reduces as printing speed increases, which can be explained by the fact that at higher printing speeds, defects (such as voids and gaps) can cause a reduction in the part’s strength.

Fig. 14

Deflection at the end of the manufacturing

5 Parametric study of 3D printing

The specimen’s temperature and Von Mises stress variations were recorded at several sample locations. Most previous research has focused on considering temperature as the most important parameter influencing the mechanical behaviour of polymers when designing industrial parts during the additive manufacturing process [33]. In this part, two distinct configurations of the FDM process, the filament deposit FDM process and the layered deposit FDM method, are evaluated in terms of temperature evolution and stress field during the manufacture of the ASTM D638 specimen. As seen in Fig. 15, the characteristics were examined in various parts. Several frames from a simulation of the deposit layer process, which consists of the first layer, the sixth layer, and the twelfth layer, are shown in Fig. 16.

Fig. 15

Technique for scanning many layers of an ASTM-D638 part (type IV)

Fig. 16

A few frames for 3D printing of polymer composites using layer deposit FDM process: variation of the temperature

Additionally, the part temperature is depicted in this picture at various points during the printing process. For instance, the top layer section is always the hottest and eventually cools down since the second layer is hotter than the first. Fig. 16’s depiction of this occurrence makes it easier to understand. When printing the part, the temperature field in the three specified layers follows three phases:

• The printing phase is where a sharp drop in temperature is noted (from 250 to 140 °C).

• The holding phase is where the temperature remains stable with very small decreases.

• The cooling phase reaches the final temperature of 23 °C.

Figure 16 shows the structure of the different printed layers and how the temperature changes for different thicknesses of ABS. The top surface of the first layer is where the hottest zone is located, with maximum temperatures of about 136.6 °C. However, the bottom surface’s temperature drops to that of the bed. In the first layer’s case, the polymer thickness examination reveals a minimal temperature difference between 135 and 136.6 °C. When the top layer is printed, the adjacent layer is reheated, which assumes the adhesion between layers and modifies the temperature gradient and the polymer’s crystallinity process. The surface temperature rises when comparing the 6th layer to the 1st layer, creating a significant gradient of 135 to 140 °C. The printing process proceeds, and at 1830 s, the 12th layer, which corresponds to the overall thickness of the polymer, starts. At this moment, the element gradually cools down.

Figure 17 depicts the temperature and Von Mises stress changes that occurred throughout the printing process in three zones of the ABS thickness: zone 1 (first layer), zone 2 (sixth layer), and zone 3 (12th layer). However, as the portion solidifies, the stress concentration rises and reaches its peak at t = 1830 s (Fig. 17c). The layer’s temperature stabilises at about 137 °C, at t = 830 s, while the stress grows quickly.

Fig. 17

Profile of temperature and Von Mises stress utilising the layer deposit technique at various points of the ABS thickness

5.1 Effect of discretisation method: layer-by-layer vs filament

The evolution of stress and temperature for the two discretisations layer-by-layer and filament are examined in this section for a printing speed of 10 mm/s, as shown in Fig. 18.

Fig. 18

Layer-by-layer vs filament discretisation

To assess the impact of the discretisation method (layer by layer and filament) used to simulate the 3D printing process on the final printed part, the temperature and stress fields as a function of printing time were compared and presented in Figs. 19 and 20. These results show that as the layer (filament) is printed, the top of the bottom layer is reheated, which generates temperature variations that affect the part’s deformation. Using the layer deposition method, the temperature of the specimen remained relatively constant throughout the printed layers and was nearly similar to the platform fabrication temperature (23 °C), whereas, using the filament deposition method (FDM), the temperature varies within the same layer and has a significant effect on the part distortion. Compared to the other layers, the temperature of the first layer drops dramatically and quickly. According to Fig. 20b, the 6th layer experienced the largest stress, roughly 37.08 MPa.

Fig. 19

Comparison of the temperature profile for two printing techniques

Fig. 20

Variation of the stress concentration and the temperature for two processes

The temperature difference between the printed layers and the platform construction process caused this concentration (reheating phenomenon). Moreover, the stress variation is almost identical for both studied processes and increases as the part solidifies. The solidification phase starts at the beginning of the cooling phase when the temperature is below the glass transition temperature, and the residual stress significantly decreases.

5.2 Effect of the printing direction

Studying how the printing direction affects the mechanical behaviour of the considered material (ABS) in the narrow part of the tested specimen is crucial. This part has been the focus of several studies [34, 35]. Experimental research on the tensile properties of PLA specimens produced in 3D using FDM was carried out by Cristina et al. [36]. The main mechanical properties were examined concerning size (various thicknesses) and spatial orientation (0°, 45°, and 90°). They found that spatial orientation has more of an effect on tensile strength than Young’s modulus. This section examines three printing orientations (45/−45, 0/90, and 60/−60) using the coupling between Abaqus and Digimat software (Fig. 21). The printing direction 45/−45 demonstrates the maximum stress of 35.84 MPa and the highest deformation of 6.5% in the narrow region of the specimen when compared to the other two orientations (Fig. 22a). As an illustration, the curve for the 45/−45 printing direction starts with a stress value of 5.11 MPa, reflected by the stresses that accumulate in each layer as they cool on top of one another. This curve demonstrates how the printing process affects the initial state of the specimen (i.e. after the sample is fully printed and before the tensile test). The dynamics of stress accumulation also depend on the preheating of the support plate. Fig. 22b depicts the load versus displacement over the entire specimen. The residual stresses (impression effect) are also observable from the start of our tensile test.

Fig. 21

Printing direction

Fig. 22

Curves determined numerically for printing direction 45/−45, 0/90, 60/−60

5.3 Effects of 3D printing on the geometry of the part

Warping is the most important phenomenon that occurs after the piece is printed [37], and it occurs when thermoplastics such as the ABS expand slightly and then, during cooling, retract. Due to the higher extrusion temperature, a thermal reaction occurs, resulting in the plastic shrinking during cooling.

Figure 23 shows the warpage of the part after printing. It can be observed that the warpage is significant in the sharp corners of the sample. Therefore, it is possible to conclude that the corners are more susceptible to warping than the central part.

Fig. 23

Warping of ABS specimen

6 Cost of printing

The cost of printing an ABS specimen may be assessed following these observations. Depending on machine, material, or labour, various expenses can be accounted for by considering the part number’s impact on the total package. An estimation of the costs for the current print configuration may be done during the costing process. Finally, the cost of the material used for printing (ABS) must be considered. Therefore, several inputs are needed, such as the material’s price, the part’s mass, and the support’s mass.

When calculating the depreciation cost of the printing machine, it is possible to take into consideration the total service time of the printer in the plan as well as the operating time of the printer for each batch, which includes setup time, warm-up time, printing time, cooling time, and removal/cleaning time. It is also possible to account for the cost of electricity used during the printing process, which can be calculated using the cost of electricity and the printer’s power during preheating, printing, and cooling. The prices of printing a single ABS specimen of type ASTM-D638 are summarised in detail in the table and graphic in Fig. 24. When compared to raw materials and printing equipment, it should be highlighted that labour and electric energy costs are the most important. Fig. 24 depicts curves that can be used to estimate the costs and time required to print one or more samples (one by one).

Fig. 24

Printing cost for an ABS specimen

7 Conclusion

A 3D numerical model was created to examine the effects of printing speed (10, 30, 50, and 70 mm/s) and printing parameters on the ABS specimen’s tensile ASTM D638 behaviour. The objective was to replicate temperature and residual stress changes during the FDM process. The following is a summary of the study’s findings:

• Development and validation of the numerical model using Abaqus/Digimat coupling with experimental results.

• Understanding the impact of process factors on 3D printed parts can be facilitated by the availability and accuracy of numerical tools.

• The residual stress and deflection are reduced by accelerating the printing speed.

• The most significant temperature gradient was observed for the printing discretisation while filaments were deposited. While varied values were observed on the surface of the printed part with filament deposit, the temperature was constant across the part surface when layers were deposited.

• Due to the temperature difference between the platform plate and the part layers, high residual stresses were projected between the first and the sixth layer. With each passing minute of printing, the part solidifies, and the temperature drops, increasing the stress’s magnitude. The Von Mises stress reaches its maximum value during the cooling phase; for the layer deposit process and the filament deposit process, this value is 37.08 MPa.

• The temperature was found to vary significantly over the thickness of the polymer. Therefore, if the printed item’s temperatures changed drastically, the concentration of stresses was higher. These residual stresses can lead to the development of cracks in the material and delamination between the layers of the printed part.

• The estimated cost of the ASTM-D638 test piece by the FDM process is 12.59 €.

Experimental tests will be performed for future work to validate the numerical results of residual stress variation, deflection, and warpage. One of the important aspects that will be studied in our next paper will be the experimental quantification of the effect of the printing direction and the filling ratio on the behaviour of the ABS material.