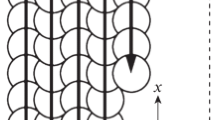
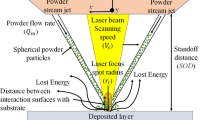
Abstract
Simulations of laser-based directed energy deposition of metals have received increasing interest aimed at reducing the experimental effort to select the proper processing condition for the repair or overhaul of actual components. One of the main issues to be addressed is the evaluation of the residual stress, which may lead to part failure under nominal loading. In this frame and specifically relating to aluminum alloys, few works have been developed and validated. This lack of knowledge is addressed in this paper: namely, the proper approach to simulate the activation of the deposited metal is discussed in case of single deposition and is shifted to a case of multiple depositions over a substrate. The validation of the predicted residual stress is made by comparison with the actual stress resulting from X-ray diffraction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The process of directed energy deposition (DED) of metals, in the family of additive manufacturing technologies, is increasingly used thanks to its flexibility in terms of base material [1]. Many advantages are also offered in terms of precision, thanks to the highly focused laser beam allowing local addition of metal in the form of powder or wire, with reduced thermal affection and distortion of the substrate. Also, recent studies demonstrated that common structural defects such as residual porosity and gradients in the nominal chemical composition of the products could be addressed by stringent control standards on the filler metal [2]. Consequently, the process has been proposed for the purpose of repairing [3], overhauling [4, 5] and even locally improving the wear resistance [6] for many applications.
Nevertheless, the component being processed is exposed to high thermal gradients leading to residual stress [7, 8]. Namely, residual stress is any self-equilibrated stress system developed in a component in the absence of any externally applied load; indeed, as for any laser-based process [9], in DED, the formation of the residual stress is ascribed to rapid heating and cooling, due to focused energy. It has been already shown that untreated residual stress may induce fracture under loading and reduce the fatigue life and the mechanical properties of the repaired or coated part [10, 11]; moreover, although proper heat treating can be performed to release the stresses depending on the metal alloy [12, 13], deformations arising during the process may result in a mismatch with respect to the intended geometry and even compromise the product integrity [7, 10] or the repair quality in general [3].
Given this background, the residual stress must be accurately addressed. To this purpose, a reference classification for the types of residual stress has been proposed [14]: type-I relates to a macro-scale level, whereas type-II and type-III have limited effect on the mechanical properties, being at grain scale and nanoscale, respectively.
As regarding the estimation, three approaches are basically offered: analytical solving, experimental measurement and simulation. Unfortunately, with respect to other laser-based processes, the analytical approach in DED is significantly complicated because the mechanical behaviour is coupled to the thermal history, hence to the deposition sequence [15]. Consequently, past analytical works have been only devoted to predicting the thermal field, and a first attempt involving the full thermomechanical system of equations has been only recently published [16].
Proper testing methods have been validated, some for the stress of type-II and -III [14], although most of the available techniques are focused on type-I stress. Among them, X-ray diffraction is a well-established, non-destructive technique [17] allowing precise, spatially resolved stress measurements over areas of few square millimetres, without any direct contact between the sample and the measurement probe. These features suit the evaluation in DED: Indeed, the region of interest, where the highest residual stress occurs, is located few millimetres from the melt front [11], where an extensimeter rosette could not be effectively laid. Therefore, the hole-drilling method would hardly be applicable in this case. The approach of X-ray diffraction has already been applied to additively manufactured parts [18], including DED [16, 19, 20]. Unfortunately, as a drawback, assessing the residual stress over the surface of the deposited metal is more difficult with this method: Through-thickness stress gradients within the probed volume complicate the analysis and interpretation of results, and the roughness of the as-deposited material also increases the measurement uncertainty. Indeed, as the roughness height on an additively manufactured surface is often comparable to the X-ray penetration depth [21], the stress relation occurring on asperities would affect the measured stress value [17, 22,23,24]. Nevertheless, in the processing of actual components, the accumulated stress in the substrate is the most critical feature; therefore, the present study focuses on the latter.
Many preliminary trials would be required to measure the residual stress experimentally in different processing conditions before suggesting the optimum on convincing grounds. Consequently, a significant effort is devoted at present to implement reliable simulations, allowing to predict of multiple responses including not only the residual stress but also the final geometry, the thermal field and the deformations, based on the levels of the governing factors. With this approach, the need for an expensive and time-consuming experimental campaign would be significantly reduced.
Given this, simulations received increasing interest in recent years, and many papers have been presented. The physics to be included in the numerical model depend on the aimed resolution; namely, increasing levels of details are addressed in macro-, meso- and micro-scale models [25, 26] so that the solutions evaluated over the macro-scale, such as the interaction between the heat source and the feeding material, are projected to the micro-scale to predict the overall response, such as the residual stress.
A 2D finite element method has been proposed with the main purpose of controlling the dilution of the deposited metal with respect to the substrate [27]; the same approach has been shifted to stress control [28], although a more flexible model is required over complex geometries. At first, similarities with the process of laser beam welding have been explored to simulate the fabrication of metal walls: Indeed, the same mechanism of the temperature gradient is effective to explain the formation of the residual stress [14, 15]. In detail, it has been shown that the residual stress changes along with the height when a metal wall is built, due to the thermal history of the part [29]. The prediction of the thermomechanical response of more complex parts has been documented: e.g., rectangular and S-shaped parts [30], single- and multi-trace cylindrical depositions [19] and V-shaped (triangular-slot) defects [3]; nevertheless, due to the specific geometry addressed, the results are not fully generalisable to other case studies. Eventually, as regarding the base material, the literature mainly addressed steel [31], nickel- [20, 32] and titanium-based alloys [30], leading to a lack of knowledge about the simulation of the residual stress arising when processing aluminium alloys of common application in many crucial fields such as aerospace and automotive [33]. The specific challenge when dealing with aluminium alloy is the correct implementation of material-related thermal-dependant properties such as high reflectivity to the laser beam and high conductivity; also, specific constitutive laws must be developed or collected from the literature [34]. For instance, an attempt has been made to develop a numerical thermo-mechanical model in the case of direct metal laser sintering of the AlSi10Mg alloy [35]. It has been found that the magnitude of the residual stress increases with the size of the melting pool, although the transient temperature distribution over the powder bed is not representative of the temperature field over a substrate in the case of DED.
In the frame of modelling the process of DED of aluminum alloys, this paper is specifically focused on presenting a structured approach to predict the residual stress, considering the governing factors and the geometry of the deposited metal (Fig. 1). More specifically, to place this work in the context of similar efforts in the literature, the classification offered by Wei et al. can be referred to [36]. A molten pool model is implemented without directly simulating the powder stream; as an element of novelty, the shape and the size of the deposited metal are fed to the simulation, based on the governing parameters. All the crucial material-related thermal-dependant properties have been obtained from relevant references.
The approach presented in this paper has already been validated by the authors to simulate the thermal and deformation fields in case of single- and multiple-trace deposition of the same alloy [37]; since this validation provided convincing grounds, the model has been further upgraded in this paper to include the residual stress. Aluminum alloy 2024 has been selected as the base material for both the powder and the substrate. A case of single-trace deposition has been simulated with two different approaches, so to assess the time scale for natural stress-relieving at laser shut-off and select the proper method to further implement the simulation for a case study of multi-trace deposition. The predicted residual stress has been validated by comparison with the actual stress resulting from X-ray diffraction.
2 Materials and methods
2.1 Deposition line
The station (Fig. 2) used for the experimental campaign (Table 1), as described in a previous paper [37], is composed of a Yb:YAG thin-disc laser (Trumpf, Ditzingen, Germany) source operating in continuous mode emission and a powder feeder with oscillating conveyor (Medicoat, Mägenwil, Switzerland), receiving argon as carrier gas and delivering the powder to a three-way feeding nozzle (Trumpf, Ditzingen, Germany), moved by an industrial robot (ABB, Zurich, Switzerland). Additional argon has been supplied via the nozzle itself to prevent oxidation of the substrate. As a common practice, a stand-off distance has been set between the nozzle tip and the surface; the laser head has been tilted to 4° to prevent any damage in the optics train due to possible back-reflections. The levels of the governing factors (Table 2) have been set based on a previous study aimed at minimizing the dilution in the substrate and concurrently increasing the catching efficiency [4].
Scheme of the three-way feeding nozzle; components not to scale [37]
Commercial, gas-atomized and spherically shaped powder of AA 2024 (LPW Technologies, Chester, UK) has been used, with the particle size distribution ranging from 20 to 60 μm. Plates of homologous nominal chemical composition, 10 mm thick, have been considered.
As regarding the case study of single deposition, a 55 mm long trace has been performed in the longitudinal direction over a 90 mm × 60 mm plate. Instead, as regarding the case study of multi-trace deposition, five traces, 40 mm long, have been performed over a 50 mm × 50 mm plate with 25% mutual overlapping, resulting from a 3 mm side shift of the laser beam between adjacent traces; a time delay of 2 s has been allowed between laser shut-off and next shut-on. The plates have been clamped so that a condition of simply supported beam applies.
2.2 Experimental evaluation of the residual stress
To validate the computed residual stress, a comparison with the experimental response has been conducted. Based on the considerations presented in the ‘Introduction’, the X-ray diffraction method has been used. An X’Pert PRO diffractometer (Malvern Panalytical, Malvern, UK) with Cu-Kα source operated in line focus mode has been used. The stresses have been measured on the substrate, over an area of approximately 1×1 mm2 size at two distinct locations A and B at the surface, 1.5 mm away from the metal deposited during the first and the last trace, respectively (Fig. 3).
The measurements have been conducted using the sin2ψ method in ω-tilt configuration, with parallel beam optics on both the incident and diffracted beams and a 0-D point detector to minimise possible errors due to sample alignment [38]. More specifically, an X-ray mirror has been mounted on the incident beam path; a parallel plate collimator together with a graphite single-crystal monochromator has been employed before a gas-proportional detector on the diffracted beam path.
The (422) peak of aluminum, located approximately at 137.5°, has been acquired through a 2θ-scan between 134.875 and 140.325° with a step size of 0.05° and a counting time of 15 s per step. The acquisition has been performed at 12 distinct positive and pseudo-negative ψ angles corresponding to sin2ψ = 0, 0.1, …, 0.6. This procedure has been repeated along three distinct orientations, i.e., ϕ = 0°, ϕ = 45°, ϕ = 90°, where ϕ = 0° corresponds to the longitudinal directions (AL and BL), whereas ϕ = 90° to the transverse directions (AT and BT) with respect to laser scanning).
The exact peak position measured at every ϕ, ψ orientation and the corresponding lattice spacing have been obtained by fitting each acquisition with a pseudo-Voigt function through the X’Pert HighScore Plus software. The lattice strain is given as a function of the stress-free peak position:
This has been plotted against sin2ψ at every ϕ orientation for a complete resolution of a plane stress state, assuming that any out-of-plane stress component is likely negligible in the vicinity of the free surface. Normal stress components have been obtained from the slopes of linear fitting to these plots [39], according to the general equation:
The X-ray elastic constants are as follows [40]:
2.3 Implementation of the simulation
The model for the process of DED discussed in this paper has been built in COMSOL Multiphysics, as a further evolution of a previously documented research [37, 41]. Some advantages are offered by the selected solver, including flexibility in setting up the model, thanks to its modular architecture, although it has been reported that larger physical memory is required compared to other solvers [42]. The crucial hypothesis to build the model, the initial and boundary conditions and the items to feed the simulation are discussed in this section.
2.3.1 Governing equations
The transient heat conduction equation is the main governing equation [43, 44] and has been implemented in the hypothesis of homogeneous and isotropic material:
Namely, the heat source on the right-hand side is only ascribed to laser irradiation. Losses for radiation and convection due to fluid flow within the pool should be included, using Newton’s law of cooling and the Stefan–Boltzmann law, respectively. Nevertheless, it has been estimated in the literature [45, 46] that for operating irradiance in the order of 105 W·cm−2, as in laser-based DED, irradiation is about 200 times greater than losses; therefore, for a leaner description, both radiation and convection can be neglected.
The mechanical analysis is thermal history-dependent since temperature and phase proportions affect the material properties. Namely, the problem is governed by the equation of balancing of the momentum [30, 47]:
Moreover, the mechanical constitutive law is given as follows:
The total strain produced during the process is computed as a concurrent contribution of elastic, plastic and thermal strain [25, 48]:
2.3.2 Material properties
Room temperature of 22°C has been set as the initial temperature of the plate and the surrounding environment. Physical properties such as density [49], heat capacity [50, 51], conductivity [51] and reflectivity [41] at the Yb:YAG wavelength for AA 2024 have been implemented as a function of temperature. The trends have been imported from several literature references and have already been employed to model simple laser heating or predicting the thermal field in DED [37, 41]. In addition to these, the temperature dependence of the Young modulus (Fig. 4), the yield stress (Fig. 5) and the isotropic tangent modulus (Fig. 6) have been included [52] to define the mechanical response in both the elastic and plastic range, assuming a bilinear isotropic hardening [53, 54] and neglecting the mechanical contribution of the liquid phase.
Where required, the usual rule of mixtures has been considered to evaluate a balanced value for each physical or mechanical material property G in the solidification range of the alloy [36], i.e., between the liquidus and the solidus temperature, hence depending on the volume fractions:
The approach is based on a phase-field modelling tool: The effectiveness of the formulation has been discussed in the literature [55] for many applications beyond additive manufacturing because it allows to capture a variety of phenomena such as solidification, solid-state phase transformations and mechanical deformations as well. In the frame of this simulation, the phase-field tool is effective in managing the phase transition induced by the laser beam: The resulting volume fractions affect the evolution of the material properties [26].
2.3.3 Laser irradiation and attenuation
Typical theoretical formulations proposed in the literature for the laser heat source are based on the original model suggested by Goldak [56]. Nevertheless, the calibration of the source strongly depends on the application because the layer height is involved in the formulation as a physical input; therefore, this must be measured in advance [20].
A more general approach has been considered here. Indeed, preliminary monitoring of the laser source has been conducted using a beam profiler (Ophir Photonics, Darmstadt, Germany) to assess the effectiveness of implementing a conventional Gaussian beam distribution of the transverse optical intensity. A super-Gaussian profile of order 20 has been found in the operating plane when defocusing is set, irrespective of the layer height. The corresponding equation, with peak intensity computed analytically [57], has been given to the heat source:
Since powder feeding results in scattering the electromagnetic radiation and attenuating the nominal irradiance of the laser beam, a laser-surface coupling coefficient must be adopted to take into account the laser attenuation. Unfortunately, many complex and concurrent effects are involved, such as directional absorption, solute partitioning and Marangoni convection [58]; therefore, to manage the attenuation, many theoretical and empirical approaches have been suggested in the literature. With respect to these, a 10% attenuation has been set in this paper, in agreement with two references: a map for the attenuation factor as a function of the radial distance and the feeding rate [59]; a study involving coaxial feeding to a stand-off distance in the order of 10 mm [60]. Neglection of the ricochet of the particles during feeding has been suggested in the literature [11].
2.3.4 Time and space discretization
A time step of 0.1 s has been set as a valuable compromise, considering that different time scales are involved in transient thermal modelling of DED [61], namely, milliseconds for the laser-material interaction and seconds for each deposition, instead.
The virtual specimens have been given the same size of the actual plates used for the experimental tests. All the simulations have been run with the implementation of mechanical constraints resembling the actual clamping; namely, the condition of the simply supported beam has been reproduced by limiting the possible displacements of the lower surface.
A condition of symmetry about the plane containing the laser path and the scanning direction is beneficial in the case of single deposition; therefore, the computational effort can be reduced. Instead, symmetry is lost when simulating multiple traces, evidently, thus resulting in exponential growth of the solving time.
As regarding the mesh, the need for an adaptive discretization has been widely discussed and approved in the literature [37, 62], with finer elements at the exposed surface and along the laser path, accounting for steeper thermal gradients; coarser elements are allowed at the edges of the plate instead. More specifically, a central slot, 4 mm deep with respect to the exposed surface (Fig. 7, Fig. 8), with ultrafine mesh edges of average 0.15 mm size, has been modelled, whereas elements ranging up to 6 mm size have been considered in the remaining domain. The total number of elements of the mesh depends on the approach to implement the addition of the deposited metal, as discussed in the following section.
2.3.5 The deposited metal
The specific geometry of the deposited material to feed the simulation tool depends on the condition of processing. Usually, the actual printed size is measured and set as the built height [20]. A more flexible approach is proposed here, instead. Indeed, it has been widely discussed [4, 37, 60] that a parabolic shape function can be assumed in the cross-section:
Width and height above the substrate can be given as a function of laser power, speed and feeding rate, according to a regression model specifically validated for AA 2024 processed by a Yb:YAG laser [37]:
As a result, the shape profile of the deposited material can be easily scaled, depending on the processing conditions. Although the effects of the operating power and the scanning speed are directly considered in the heat source equation and the transient heat conduction equation, respectively, it is worth noting how the approach of a regression model for the shape of the deposited material offers a method to consider the effect of the feeding rate, which would require additional, complex solving moduli, otherwise.
Furthermore, in the case of multi-trace overlapping depositions (Fig. 9), only the first trace is deposited over a flat substrate; instead, the shape functions of the following depositions are affected by the previous depositions and can be found under the main assumption of mass conservation (i.e., the subtended area of each shape function) for a given condition of processing. Once the shape functions have been found, the geometry of the deposited material is known and is fed to the simulation tool. Depending on the application, fine-tuning of this approach can be furtherly performed, including additional terms in the regression models to take account of possible other processing factors, thus providing a more representative solution.
Shape functions of the deposited metal in case of multiple depositions: the subtended area of each shape function is constant for a given condition of processing [37]
The method of the deformed geometry is already available in COMSOL to simulate the addition of material: namely, a deforming speed equal to the speed of the laser beam must be set to extend a given slice of deposited metal and known shape, until the overall length of the laser path is completed. This approach has been proven to be effective to predict the temperature evolution and the size of the fusion zone for both single- and multi-trace depositions [37]; nevertheless, severe issues must be addressed in terms of continuity of the stress field when a coupled mechanical problem is set, due to singularities at the nodes of the extruded geometry.
Therefore, two different approaches have been tested and compared in this paper in the case of single-trace deposition to select the most appropriate method which is then employed for the multi-trace case study. The first approach is the incremental activation (IA) of the deposited material in the form of slices, behind the laser beam, at each discrete time step. The second is the global activation (GA) of the overall deposited material at laser shut-off after each deposition: The driving idea, to the purpose of reducing the computational effort, is to demonstrate that each individual deposited trace can be considered as simple heating of the exposed surface because the irradiation is not affected by the deposited metal behind the laser beam; therefore, GA is both effective and time-saving, provided that a proper attenuation of the laser irradiation is implemented to take account of the powder flow. In both cases, a condition of union between the substrate and the activated material must be set so that the deposited metal is capable of matching the deformation field of the substrate.
Based on these grounds, the GA approach has been shifted to simulate multi-trace deposition. In this case, two specific regions of interest have been defined on the virtual specimen to measure the stress and compare it with the actual monitoring, as previously defined. Namely, two areas of 1×1 mm2 size, 1.5 mm away from the deposited metal of the first and the last deposition, have been virtually probed; the average stress over each probed area has been compared to the actual measure at each location.
The overall number of each type of mesh element depends on many factors such as the size of the virtual specimen, the allowed symmetry and the approach to implement the addition of the deposited material. These are different among the three case studies (Table 3).
3 Results and discussion
3.1 Single deposition
At first, the approaches of IA and GA have been compared. Solving the coupled temperature and mechanical problem required 5 h, 40 min and 2 h, 20 min, respectively; therefore, an approximate 60% reduction has been achieved in the case of GA, and the same results have been obtained in terms of temperature and stress field.
As regarding the temperature field, the cross-section of the plate at halfway of the laser path can be considered, at a time of 1.85 s from laser shut-on, corresponding to the time of local irradiation of the selected cross-section. The temperature field over this section (Fig. 10) and the temperature trend as a function of the distance from the exposed surface (Fig. 11) can be compared: The same results have been found and a depth of fusion of 0.66 mm, in agreement with the experimental results, has been detected for both approaches.
The approaches of IA and GA provide the same results even in terms of residual stress. To discuss this point, it is worth noting that natural partial stress relief of the metal is expected over a time scale depending on the processing condition and the heat transfer, before the final residual stress is approached. In this case, the equivalent von Mises stress (Fig. 12) for a point located on the substrate surface at halfway of the laser path, 0.5 mm away from the deposited material, becomes stationary upon a relief time of approximately 5 s after laser shut-off, i.e., approximately 10 s after laser shut-on.
Therefore, referring again to the cross-section at halfway of the laser path, the von Mises stress field over the cross-section (Fig. 13) and its trend as a function of the distance from the exposed surface (Fig. 14) have been compared at a time of 10 s after laser shut-on: An average difference below 4% resulted between the equivalent stresses computed through the IA and GA approaches. Discontinuities affecting the stress trend are possibly ascribed to changing of the mesh type along with the domain. Based on these findings, the GA has been implemented to solve the case of multiple depositions.
3.2 Multiple depositions
The simulation of five overlapping traces covered a total time of 30 s approximately, consisting of 2.7 s for each deposition, 2 s time of delay between consecutive depositions and 10 s after the last shut-off to allow natural partial relief of the substrate and assess the actual residual stress to be compared with the experimental results; the solver required 54 h, 10 min.
The simulated maximum temperature of the trace, intended as the highest temperature calculated considering all the nodes along the laser path, approaches 1300 K at the exposed surface (Fig. 15). In agreement with previous findings relating to the monitoring of the actual thermal field produced by laser heating of the aluminum substrate [41], the induced thermal gradient develops over a time scale in the order of tenths of second; namely, this yields a time delay of 0.2 s with respect to laser shut-on and -off. As expected, the peak temperature at each given point is reached at the time of direct laser irradiation; e.g., the temperature evolution at halfway of the first laser path exhibits its peak at approximately 1.4 s after laser shut-on, although the time step of the solver may not allow to detect the actual local maximum.
As for the case of single deposition, mesh nodes where the temperature field exceeded the solidus temperature of the base metal have been flagged to find the edge of the fusion zone: To validate the solution of the thermal problem, the simulated depth of fusion in the transverse cross-section at halfway of the laser path (Fig. 16) has been compared with the actual depth (Table 4), as measured by optical microscopy (Fig. 17): an average difference of 7.6% resulted. Interestingly, the depth of fusion increases when moving to the next adjacent deposition, although the same processing conditions are taken: This is ascribed to the increasing average temperature of the base metal, leading to a reduction of the reflectivity and an increase of the energy absorption in turn.
Significant residual stress is built up in an area of a few millimetres around each deposition, as suggested by the evolution of the von Mises stress during the overall process (Fig. 18). A cumulated stress is experienced by the substrate at the last laser shut-off. The simulated response has been validated by comparison to X-ray diffraction measurements at the probing location described in ‘Experimental evaluation of the residual stress’ (Table 5).
Each measured stress value is associated with an experimental error obtained from the uncertainty (i.e., the standard deviation) of the fitted slope on the plot of lattice strain vs. sin2ψ; as an example, the plot for the measurement at location B is shown (Fig. 19). The experimental error, which reflects some scattering in the experimentally measured data points, is consistent with the ±20 MPa accuracy typical of X-ray stress measurements [17, 21]. Moreover, the plots of lattice strain vs. sin2ψ do not show significant ψ-splitting, which corroborates the assumption of a plane stress state in analysing the data.
Accounting for the experimental error, the simulated residual stress is reasonably consistent with the measured value, with an absolute difference depending on the direction of probing (Fig. 20, Fig. 21).
Measurements and simulations especially agree in highlighting higher stress in the transverse direction, i.e., the direction orthogonal to the laser path. These findings are in agreement with the usual model adopted for laser heating in additive manufacturing and consequent stress formation [9]. Interestingly, the cumulated residual stress decreases during the process because the thermal history of the part is a factor [29]. Specifically, lower stresses are produced when laser irradiation is delivered over a preheated part; consequently, the overall stress in the neighbourhood of B is lower, although the heat affection is deeper due to a higher depth of fusion.
4 Conclusions
This paper presented a finite element modelling technique to predict the residual stress state induced by directed energy deposition on a workpiece. The approach discussed in this paper has been conceived to achieve reasonable flexibility, being this a crucial requirement to allow the designer to change the deposition path and the levels of the governing parameters to find the optimum condition of processing and exposure strategy, aiming at reducing the residual stress. The main features are highlighted as follows:
-
The calibration of the heat source is based on monitoring via beam profiling, irrespective of the material and the application; this is an advantage over other heat source models suggested in the literature, where specific material-related inputs are required to set other heat sources suggested in the literature;
-
The shape of the deposited metal, both in single- and multi-trace deposition, can be fed to the simulation tool based on the levels of the governing factors, thus allowing to take account of the feeding rate as well, which would require complex simulation moduli otherwise;
-
The global activation of the deposited metal after laser shut-off is effective and time-saving, allowing to save half the computational time in case of single deposition, compared to an incremental activation;
-
Convincing matches with the actual stress, as measured via X-ray diffraction, are provided.
As regarding the main findings achieved via simulation and experimental validation in terms of understanding of the formation of the residual stress, it is worth noting that
-
the time scale of stress development is in the order of tenths of seconds at laser direct exposure, whereas seconds are required before a stationary value is approached after laser shut-off;
-
a tensile residual stress, in the order of 100 MPa, is developed in the transverse direction of deposition, at 1.5 mm distance from the deposited metal at the surface of the substrate;
-
a reduced stress is experienced at the last deposition, thanks to cumulated heating of the plate, although deeper fusion results due to reduced reflectivity.
Further developments may consider the application of this simulation approach to evaluate the residual stress in different conditions of processing, including changing the scanning strategy. Even the simulation of preheating to reduce the stress may be addressed.
Abbreviations
- α :
-
coefficient of absorption
- γ :
-
volume fraction
- ε :
-
strain
- ε e :
-
elastic strain
- ε ij :
-
lattice strain
- ε p :
-
plastic strain
- ε T :
-
thermal strain
- θ :
-
diffraction angle
- σ i :
-
stress component along the i-direction
- φ :
-
Azimuth angle of the stress measurement direction with respect to the specimen reference system
- ψ :
-
pole angle of the specimen normal with respect to the diffraction vector
- ω :
-
incidence angle of X-ray beam with respect to the sample surface plane
- ρ :
-
density
- b :
-
body forces
- C :
-
Cauchy stress tensor
- c p :
-
specific heat at constant pressure
- d 0 :
-
stress-free peak position
- d ij :
-
lattice spacing
- f :
-
shape function of the deposited metal
- G :
-
physical or mechanical property
- h :
-
height of the deposited metal
- k :
-
thermal conductivity
- \( \dot{m} \) :
-
powder feeding rate
- P :
-
laser power
- Q v :
-
specific heat source
- r :
-
radial coordinate
- S i :
-
Elastic constant for X-ray diffraction
- T :
-
temperature
- t :
-
time
- u :
-
laser travelling speed
- w 0 :
-
beam radius
- w :
-
width of the deposited metal
- x :
-
overlapping direction
- y :
-
direction of deposition
- z :
-
direction of laser beam propagation
References
A. Bandyopadhyay and S. Bose, Additive manufacturing, CRC Press, Taylor & Francis Group, 2016.
Kakinuma Y, Mori M, Oda Y, Mori T, Kashihara M, Hansel A, Fujishima M (2016) Influence of metal powder characteristics on product quality with directed energy deposition of Inconel 625. CIRP Annals - Manufacturing Technology 65(1):209–212
Li L, Zhang X, Liou F (2021) experimental and numerical investigation in directed energy deposition for component repair. Materials 14:1409
Caiazzo F, Alfieri V, Argenio P, Sergi V (2017) Additive manufacturing by means of laser-aided directed metal deposition of 2024 aluminium powder: investigation and optimization. Advances in MEchanical Engineering 9:1–12
Caiazzo F (2018) Laser-aided directed metal deposition of Ni-based superalloy powder. Optics and Laser Technology 103:193–198
Baek G, Shin G, Lee K, Shim D (2019) Mechanical properties of tool steels with high wear resistance via directed energy deposition. Metals 9:282
H. Liu and F. Liou, “Residual stress modeling and deformation measurement in laser metal deposition process,” in New Challenges in Residual Stress Measurement and Evaluation, London, IntechOpen, 2019, pp. 1-20.
Mukherjee T, Zhang W, DebRoy T (2017) An improved prediction of residual stresses and distortion in additive manufacturing. Computational Materials Science 126:360–372
Mercelis P, Kruth J (2006) Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyping Journal 12(5):254–265
Moat R, Pinkerton A, Li L, Withers P, Preuss M (2011) Residual stresses in laser direct metal deposited Waspaloy. Materials Science and Engineering A 528:2288–2298
C. Vundru, R. Singh, W. Yan and S. Karagadde, “Non-dimensional process maps for residual stress in laser directed energy deposition,” in 48th SME North American Manufacturing Research Conference, NAMRC 48, 2020, 697, 705.
Rittinghaus S, Hecht U, Werner V, Weisheit A (2018) Heat treatment of laser metal deposited TiAl TNM alloy. Intermetallics 95:94–101
Junker D, Hentschel O, Schmidt M, Merklein M (2018) Investigation of heat treatment strategies for additively-manufactured tools of X37CrMoV5-1. Metals 8(854):1–13
Li C, Liu Z, Fang X, Guo Y (2018) Residual stress in metal additive manufacturing. Procedia CIRP 71:348–353
S. Zekovic, D. Rajeev and K. Radovan, “Thermo-structural finite element analysis of direct laser metal deposited thin-walled structures,” in International Solid Freeform Fabrication Symposium, 2005.
Mirkoohi E, Dobbs J, Liang S (2020) Analytical modeling of residual stress in direct metal deposition considering scan strategy. The International Journal of Advanced MAnufacturing Technology 106:4105–4121
Hauk V (1997) Structural and residual stress analysis by nondestructive methods. Elsevier, Amsterdam
Di Giovanni M, de Menezes J, Bolelli G, Cerri E, Castrodeza E (2019) Fatigue crack growth behavior of a selective laser melted AlSi10Mg. Engineering Fracture Mechanics 217
Zhang Z, Kovacevic R (2019) A thermo-mechanical model for simulating the temperature and stress distribution during laser cladding process. International Journal of Advanced Manufacturing Technology 102:457–472
Song X, Feih S, Zhai W, Sun C, Li F, Maiti R, Wei J, Yang Y, Oancea V, Brandt L, Korsunsky A (2020) Advances in additive manufacturing process simulation: residual stresses and distortion predictions in complex metallic components. Materials and Design 193
Guo J, Fu H, Pan B, Kang R (2021) Jiang Guo, Haiyang Fu, Bo Pan, Renke Kang, Recent progress of residual stress measurement methods: a review. Chinese Journal of Aeronautics 34(2):54–78
Gill SCT (1994) Investigation of residual stress generation during thermal spraying by continuous curvature measurement. Thin Solid Films 250:172–180
Kesler O, Matejicek J, Sampath S, Suresh S, Gnaeupel-Herold T, Brand P, Prask H (1998) Measurement of residual stress in plasma-sprayed metallic, ceramic and composite coatings. Materials Science and Engineering A 257:215–224
Chen Y, Sun H, Li Z, Wu Y, Xiao Y, Chen Z, Zhong S, Wang H (2020) Strategy of residual stress determination on selective laser melted Al alloy using XRD. Materials 13(451):1–11
Megahed M, Mindt H, N'Dri N, Duan H, Desmaison O (2016) Metal additive-manufacturing process and residual stress modeling. Integrating Materials and Manufacturing Innovation 5(4):1–33
Gatsos T, Elsayed K, Zhai Y, Lados D (2020) Review on computational modeling of process-microstructure-property relationships in metal additive manufacturing. Journal of Metals 72(1):403–419
Kim J, Peng Y (2000) Time-dependent fem simulation of dilution control of laser cladding by adaptive mesh method. KSME International Journal 14(2):177–187
P. Aggarangsi, J. Beuth and M. Griffith, “Melt pool size and stress control for laser-based deposition near a free edge,” in Solid Freeform Fabrication Proceedings, Austin, 2003.
Kamara A, Marimuthu S, Li L (2011) A numerical investigation into residual stress characteristics in laser deposited multiple layer waspaloy parts. Transactions of the ASME-B-Journal Manufacturing Science Engineering 133(3):031013.1–031013.9
Lu X, Lin X, Chiumenti M, Cervera M, Hu Y, Ji X, Ma L, Yang H, Huang W (2019) Residual stress and distortion of rectangular and S-shaped Ti-6Al-4V parts by Directed energy deposition: modelling and experimental calibration. Additive Manufacturing 26:166–179
Chew Y, Pang J, Bi G, Song B (2015) Thermo-mechanical model for simulating laser cladding induced residual stresses with single and multiple clad beads. Journal of Materials Processing Technology 224:89–101
Zhang C, Li L, Deceuster A (2011) Thermomechanical analysis of multi-bead pulsed laser powder deposition of a nickel-based superalloy. Journal of Materials Processing Technology 211(9):1478–1487
Dorward R, Pritchett T (1988) Advanced aluminium alloys for aircraft and aerospace applications. Materials & Design 9(2):63–69
Davis JR (1993) Aluminum and aluminum alloys. ASM International, Materials Park
B. Panda and S. Sahoo, “Numerical simulation of residual stress in laser base additive manufacturing process,” Materials Science and Engineering, vol. 338, 2018.
H. Wei, T. Mukherjee, W. Zhang, J. Zuback, G. Knapp, A. De and T. DebRoy, “Mechanistic models for additive manufacturing of metallic components,” Progress in Materials Science, vol. 116, 2021.
Caiazzo F, Alfieri V (2019) Simulation of laser-assisted directed energy deposition of aluminum powder: prediction of geometry and temperature evolution. Materials 12(13):2019
Vermeulen A (2005) The sensitivity of focusing, parallel beam and mixed optics to alignment errors in XRD residual stress measurements. Materials Science Forum 490-491:131–136
Welzel U, Ligot J, Lamparter P, Vermeulen A, Mittemeijer E (2005) Stress analysis of polycrystalline thin films and surface regions by X-ray diffraction. Journal of Applied Crystallography 38:1–29
Eigenmann B, Macherauch E (1996) Röntgenographische Untersuchung von Spannungszuständen in Werkstoffen Teil IV. Fortsetzung von Matwiss. und Werkstofftechn. Heft 3/1995, S. 148–160, Heft 4/1995, S. 199–216 und Heft 9/1996, S. 426–437. Materials Science & Engineering Technology 27(10):491–501
Caiazzo F, Alfieri V (2018) Simulation of laser heating of aluminum and model validation via two-color pyrometer and shape assessment. Materials 11(1506):1–13
Salvi D, Boldor D, Ortego J, Aita G, Sabliov C (2010) Numerical modeling of continuous flow microwave heating: a critical comparison of COMSOL and ANSYS. Journal of Microwave Power and Electromagnetic Energy 44(4):187–197
Toyserkani E, Khajepour A, Corbin S (2005) Laser Cladding. CRC Press, Boca Raton
Huang Y, Khamesee M-B, Toyserkani E (2019) A new physics-based model for laser directed energy deposition (powder-fed additive manufacturing): from single-track to multi-track and multi-layer. Optics and Laser Technology 109:584–599
Fu Y, Loredo A, Martin B, Vannes A (2002) A theoretical model for laser and powder particles interaction during laser cladding. Journal of Materials Processing Technology 128:106–112
Costa L, Vilar R, Reti T, Deus A (2005) Rapid tooling by laser powder deposition: process simulation using finite element analysis. Acta Materialia 53:3987–3999
Heigel J, Michaleris P, Reutzel E (2015) Thermo-mechanical model development and validation of directed energy deposition additive manufacturing of Ti-6Al-4V. Additive Manufacturing 5:9–19
Moumni Z, Roger F, Trinh NT (2011) Theoretical and numerical modeling of the thermomechanical and metallurgical behavior of steel. International Journal of Plasticity 27:414–439
Kurochkin A, Popel P, Yagodin D, Borisenko A, Okhapkin A (2013) Density of copper–aluminum alloys at temperatures up to 1400 °C determined by the gamma ray technique. High Temperature 51(2):197–205
Sarmast A, Serajzadeh S, Kokabi A (2013) A study on thermal responses, microstructural issues, and natural aging in gas tungsten arc welding of AA2024-T4. Journal of Engineering Manufacture 228(3):413–421
Hrbek J (2015) Induction heating of thin nonmagnetic sheets in transverse time-variable magnetic field. Acta Technica 60:15–29
Bachmann M, Carstensen J, Bergmann L, dos Santos J, Wu C, Rethmeier M (2017) Numerical simulation of thermally induced residual stresses in friction stir welding of aluminum alloy 2024-T3 at different welding speeds. International Journal of Advanced Manufacturing Technology 91:1443–1452
Xin-Lin G (1994) An exact elasto-plastic solution for a thick-walled spherical shell of elastic linear- hardening material with finite deformations. International Journal of Pressure Vessels and Piping 57:45–56
Szabó L (2009) A semi-analytical integration method for J2 flow theory of plasticity with linear isotropic hardening. Computational Methods of Applied Mechanical Engineering 198:2151–2166
A. Choudhury, “Phase-field modeling as a method relevant for modeling phase transformation during interdiffusion,” in Handbook of Solid State Diffusion, 2017, pp. 363-389.
Goldak J, Chakravarti A, Bibby M (1984) A new finite element model for welding heat sources. Metallurgical Transactions B 15:299–305
Paschotta R (2008) Encyclopedia of Laser Physics and Technology. Wiley-VCH, Berlin
Thompson S, Bian L, Shamsaei N, Yadollahi A (2015) An overview of direct laser deposition for additive manufacturing; part I: transport phenomena, modeling and diagnostics. Additive Manufacturing 8:36–62
X. He and J. Mazumder, “Transport phenomena during direct metal deposition,” Journal of Applied Physics, vol. 101, 2007.
Ocelik V, Nenadl O, de Hosson A (2014) On the geometry of coating layers formed by overlap. Surface and Coatings Technology 242:54–61
Kundakcioglu E, Lazoglu I, Rawal S (2016) Transient thermal modeling of laser-based additive manufacturing for 3D freeform structures. International Journal of Advanced Manufacturing Technology 85:493–501
Ya W, Pathiraj B, Liu S (2016) 2D modelling of clad geometry and resulting thermal cycles during laser cladding. Journal of Materials Processing Technology 230:217–232
Availability of data and material
Data required to reproduce these findings have been given in the text. Any additional data can be shared upon request.
Code availability
Data required to reproduce the code for the optimization are given in the text. If needed, they can be shared upon request.
Funding
Open access funding provided by Università degli Studi di Salerno within the CRUI-CARE Agreement. This work was supported by the Italian Ministero dell’Istruzione, dell’Università e della Ricerca through project ‘ISAF – Fabbrica di montaggio integrata intelligente’, grant agreement PON ARS01_01188.
Author information
Authors and Affiliations
Contributions
Conceptualization: F.C.; data curation: F.C, V.A., G.B.; formal analysis: F.C, V.A., G.B.; funding acquisition: F.C.; investigation: F.C, V.A., G.B.; methodology: F.C.; project administration: F.C.; resources: F.C.; software: F.C, V.A.; supervision: F.C.; validation: F.C, V.A., G.B.; visualisation: F.C, V.A., G.B.; writing – original draft: V.A.; writing – review and editing: F.C., G.B.
Corresponding author
Ethics declarations
Ethics approval
This material is the authors’ own original work, which has not been previously published elsewhere.
Consent to participate
Not applicable
Consent for publication
Not applicable
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Caiazzo, F., Alfieri, V. & Bolelli, G. Residual stress in laser-based directed energy deposition of aluminum alloy 2024: simulation and validation. Int J Adv Manuf Technol 118, 1197–1211 (2022). https://doi.org/10.1007/s00170-021-07988-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-07988-2