1 Introduction

Laser melting deposition (LMD) is an economically viable and innovative technique to repair and manufacture fully functional, geometrically complex, and fully dense parts [1]. The LMD process promises manufacturing advantages in comparison with conventional approaches, including complex geometries, control of the heat-affected zone, and the removal of several technological steps from the manufacturing process. These factors establish LMD as a potential candidate for many aerospace, automobile, industrial, and biomedical applications [2]. The LMD manufacturing process uses a laser beam to liquefy the substrate’s surface, and the powder particles are delivered into the melt pool from a powder feeding nozzle where they melt and rapidly solidify, forming a layer of bulk material. These steps are repeated layer after layer until the required CAD shape is formed [3].

The contraction of the molten material can build up the residual stress distribution, which can lead to part failure either by plate delamination/deformation, cracking, or re-coater interference [4]. Expensive experimental trials are conducted for the tuning of experimental parameters until the pieces are successfully built, or the errors within the process are eliminated. In the LMD process, the 1st deposited layer controls the quality and properties for all deposited layers. Various studies implying analytical and numerical modeling have been focused on geometrical accuracy for better understanding and managing the LMD process. In a recent study, investigations on the operating parameters and resultant wearing characteristics of the manufactured parts, by the LMD process, were reported. The defect-free coatings were fabricated using the titanium metal matrix composites with an Nd: YAG laser [5]. An appropriate LMD methodology was presented to analyze the effect of operating parameters on geometrical properties of 316L steel powder depositions. It was found that the powder feed rate influences the depth of the melt pool, thereby reducing fusion-levels between the substrate and deposited material at lower energy densities.

It is well known that the repeatedly rapid heating and cooling in the additive manufacturing (AM) process has a significant influence on the quality of the produced part, such as residual stress and part distortion. In this context, recently, various efforts have been carried out in the thermal analytical modeling of AM processes. An analytical model, to investigate the in-process temperature gradient distribution in the metal powder bed AM process, was developed. The model was verified using experimental data for Inconel 625. It was found that the average computation time, defined by the proposed model for 2D temperature prediction in the case of single-tracks, was 19.44 s. Besides, the time needed for 2D temperature prediction, in bidirectional scans, was 88.17 s [6]. A quasi-analytical solution was developed. The heat transfer boundary conditions, laser power absorption, scanning strategy, and latent heat were considered to estimate the time-dependent thermal profiles. Temperature profiles were predicted in multiple layers for Ti6Al4V alloy thin-walled structures. The stabilized molten pool dimensions in multiple layers were obtained from predicted temperatures. In this model, the computation time was recorded as 11.87, 74.6, 246.04, and 563.41 s for 2nd, 4th, and 8th layers, respectively [7]. A physics-based predictive model for transient temperature distribution, during the heating and cooling states, was presented for the powder feed metal AM process. The temperature profiles and melt pool evolution were predicted w.r.t the processing time in the single-track deposition of Inconel 718. The average computational time for temperature prediction, during heating and cooling states, was recorded as 80 s and 144 s, respectively. The prediction error for peak temperature was equivalent to 4.91% [8]. A predictive model based on the solid heat transfer for temperature profiles in the powder bed metal AM process was presented. The heat transfer boundary condition and powder material properties were also taken into account. By considering the powder size statistical distribution and powder packing, powder properties were calculated. The model was tested for AlSi10Mg under various process conditions. It was found that the average computational time was 217.9 s [9].

The influence of the powder feeding rate, laser power, and re-melting along with ultrasonic vibrations on the relative density of Al4047 alloy parts was investigated. With periodical positive-negative pressures, ultrasonic vibration generated two non-linear actions of acoustic streaming and transient cavitation, resulting in a steady flow. The optimal operating parameters presented refined microstructures of columnar Al-dendrites and equiaxed Si-particles at the boundary of each deposited layer, which impacted the tensile properties. The deposited material showed better tensile strength (227 MPa), ductility (12.2%), and yield strength (107 MPa) as compared to the cast materials [10]. Various investigations were directed, and deterministic relations between the 3D-printed layers’ features and operational framework were developed. It was found that the deposited layers’ height and width can be estimated by (P/Qm)0.25(Qm/V), and (P)0.75(V)−0.25, where P is the laser power, Qm is powder flow rate, and V is the laser scanning speed [11]. Various efforts have been carried out to measure, estimate, and control the residual stress distribution in LMD, SLS, and SLM techniques. A finite element analysis model, combining the thermal and mechanical effects, was developed to explain the relation between thermal gradient and maximum residual stresses for thin-walled layers produced by LMD [12]. The finite element analyses of the LMD process were carried out. Simulation results exhibited that the control of melt-pool size can reduce stresses on the edges [13].

Various studies to estimate the deposited clad geometry and residual stress distribution using the finite element (FE) analyses have been reported in the literature. One of the significant limitations of the FE models is that the prediction of the solution is dependent on the mesh accuracy. The meshing quality is directly linked to the computation time. A fine mesh requires a longer computing time. For FE simulations, one needs specialized and dedicated skills to carry out computations. Up to the best of knowledge, no analytical model to estimate the clad dimensions and corresponding residual stresses for all deposited layers with the inclusion of hatch distance and re-melting depth has been presented. This study proposes two analytical models to estimate the clad geometry characteristics and corresponding residual stress distribution in the LMD-ed part/substrate configurations, based on the operating parameters. Initially, the clad dimensions (width, height, and depth) for the 1st deposited layer have been estimated. Then, a hatch distance is used to calculate the re-melting depth and total clad geometry for all the deposited layers. Finally, the output of the 1st model is used as an input to the 2nd model to analyze the residual stress distribution within the 3D printed layers-substrate assembly. By implementing the steps regarding the clad dimension and residual stresses, one will be able to adequately estimate the influence of operating parameters on printed layers features and residual stress distribution.

2 Analytical modeling

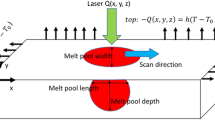
Figure 1 provides a scheme of the laser beam interaction with a stream of powder particles and substrate. With the coaxial addition of powder debits, they consume a fraction of the laser beam. A portion is absorbed by the substrate to generate a melt pool. At the same time, the rest of the laser energy is reflected by the substrate [14]. The powder debits are feed directly into the melt pool, produced by the high-power focused laser beam, resulting in clad formation.

Fig. 1
figure 1

Schematic of the laser-melting deposition process

Full size image

2.1 An analytical model to estimate clad geometry

The following assumptions have been opted to determine the clad geometry:

  1. 1.

    The laser beam moving with a constant scanning speed, Vs, interacts with the powder particles at a distance (h). This interaction point is crucial as it assists in estimating the attenuation ratio between the laser beam and powder stream. For simplicity, h is considered as 25% of the standoff distance (SOD) (Fig. 1), which also justifies studying the gravity and drag effects negligible [15, 16]. The laser beam spot focused on the substrate has been assumed as circular.

  2. 2.

    Impact forces generated by the powder elements on the geometrical characteristics of the clad are neglected. The width of the clad depends on the width of the regime (2q), where the powder elements are melted [14]. This assumption serves to determine the width of the laser clad. The surface tension was neglected throughout the whole deposition process.

  3. 3.

    The powder flow (Qm) is considered as steady-state, while the dissipation of laser beam energy by the powder particles is constant. The powder particles are considered spherical, having mean-radius (rp) [17, 18]. Thermo-physical properties of the powder particles are independent of the temperature change. The laser absorption coefficient for the substrate in liquid and solid form is considered equal. To keep the powder flow rate constant, overlapping between powder particles is neglected. This assumption is used to implement the energy balance and mass balance laws. Moreover, the energy losses by the powder particles are neglected.

  4. 4.

    In the LMD process, the dilution effect is neglected as it is less than 10% [19]. Furthermore, powder elements that undergo the laser beam must participate in clad geometry, while the clad geometry is considered elliptical. This assumption is useful, as all the powder elements passing through the laser beam participate in clad formation. It, in-return, assists in estimating powder efficiency.

2.1.1 Attenuation ratio between laser beam and powder stream

Laser energy is usually consumed, reflected, and dispersed by the powder elements as they enter the laser beam that leads to the attenuation of the laser beam energy received on the substrate’s surface [14]. This attenuated laser energy, known as the shading rate (∀1), causes significant effects upon the deposited material quality. ∀1 can be calculated by using the powder elements area (Ap) and laser beam area (AL), focused on the substrate, as:

$$ {\forall}_1=\frac{A_P}{A_L}. $$
(1)

The area of N spherical powder particles in the powder flow with mean radius rp is expressed as:

$$ {A}_p= N\pi {r}_p^2. $$
(2)

According to assumption 3, the law of mass conservation can be implemented effectively, given as:

Mass of N powder elements fused on the sample surface after passing through the laser beam = powder efficiency × powder feed rate × time required by the powder particles while passing through the laser beam.

$$ N\frac{4}{3}\pi {r_p}^3{\rho}_p={\forall}_2{Q}_mt, $$
(3)

where ρp is the powder granules’ density, Qm is the feed rate of powder elements, ∀2 is the power efficiency, and t is the time needed by powder elements undergoing the laser beam, expressed as:

$$ t=\frac{h}{V_p}=\frac{0.25 SOD}{V_p}, $$
(4)

where h is the interval covered by the powder particles in the laser beam, h = 25 % of SOD, and Vp is the velocity of powder particles. In Eq. (3), ∀2 is defined as the power efficiency, which can be calculated based on the experimental data by the following relation, if the dilution rate is ignored, given as:

$$ {\forall}_2=\frac{w_{(c)\mathit{\exp}}{h}_{(c)\mathit{\exp}}}{\pi {r}_s^2}, $$
(5)

where rs is the powder nozzle radius, and w(c)exp and h(c)exp are the experimental deposited clad width and height, respectively. In the LMD process, the powder flow majorly depends on the radius of the powder nozzle outlet. Therefore, the dimensions of the deposited clad depend on the cross-sectional area of the nozzle outlet, keeping the laser beam parameters and powder flow rate constant. Thereby, taking a ratio between the clad dimensions to the cross-sectional area of the nozzle can allow us to estimate the powder efficiency presented in Eq. (5).

Substituting Eqs. (4) and (5) into Eq. (3) provides the N value as:

$$ N=\frac{3{w}_{(c)\mathit{\exp}}{h}_{(c)\mathit{\exp}}{Q}_m\left(0.25 SOD\right)}{4{\pi}^2{r}_s^2{r}_p^3{\rho}_p{V}_p}. $$
(6)

Substitute Eq. (6) into Eq. (2) yields:

$$ {A}_p=\frac{3{w}_{(c)\mathit{\exp}}{h}_{(c)\mathit{\exp}}{Q}_m\left(0.25 SOD\right)}{4\pi {r}_s^2{r}_p{\rho}_p{V}_p}. $$
(7)

The area of a circular laser beam spot on the substrate (AL) is given as:

$$ {A}_L=\pi {r}_l^2. $$
(8)

Dividing Eq. (7) by (8) gives shading rate as:

$$ {\forall}_1=\frac{3{w}_{(c)\mathit{\exp}}{h}_{(c)\mathit{\exp}}{Q}_m\left(0.25 SOD\right)}{\pi^2{r}_l^2{r}_s^2{r}_p{\rho}_p{V}_p}. $$
(9)

Equation 9 indicates that the shading rate has a direct relation with the powder flow rate (Qm) and standoff distance (SOD) while having an inverse relationship with the powder particles’ mean radius (rp), velocity, and radius of the laser beam (rl).

2.1.2 Estimation of clad geometry for single layer

Based upon the assumption 2, the width of the clad can be determined by the melting situation of powder particles in a laser beam, which can be determined by a Gaussian distribution relation, expressed as [20]:

$$ P(q)=\frac{2P}{\pi {r}_l^2}{\mathit{\exp}}^{\left(\frac{-2{q}^2}{r_l^2}\right)}, $$
(10)

where P is the laser power. The energy (Emp) needed by the powder particles for complete melting from ambient temperature (To) to the melting temperature (Tmp) is calculated as:

$$ {E}_{\mathrm{mp}}=\frac{4}{3}\pi {r}_p^3{\rho}_p{C}_p^{\ast }, $$
(11.1)

where \( {C}_p^{\ast } \) is the modified specific heat based upon the ratio of powder particles’ enthalpy fusion (Lfp) to the temperature difference (Tmp − To) with the addition of powder particles’ specific heat (Cp), expressed as:

$$ {C}_p^{\ast }=\frac{L_{\mathrm{fp}}}{T_{\mathrm{mp}}-{T}_o}+{C}_{p.} $$
(11.2)

Here, Lfp is the powder particles’ enthalpy fusion, defined as the energy absorbed or released by the material while changing its phase without changing the temperature [21]. Cp is explained as the heat demanded by a unit mass to raise the temperature by 1 °C [22]. Under assumption 3, the energy balance can be implemented on one of the powder particles, expressed as:

$$ {E}_{\mathrm{mp}}=\left(1-{\forall}_1\right){\forall}_3\frac{2P}{\pi {r}_l^2}{\mathit{\exp}}^{\left(\frac{-2{q}^2}{r_l^2}\right)}\pi {r}_p^2t, $$
(12)

where ∀3, is a dimensionless factor, defined as the percentage of laser energy consumed by the powder particles and substrate, collectively. According to assumption 2, the width of the deposited clad depends on the location where powder debits can be completely liquified. Therefore, the relation between the width of the clad (W1) and position (q) where the particles can be melted entirely can be calculated by the following relationship:

$$ {W}_1=2q. $$
(13)

By comparing Eqs. (11) and (12), the value of q can be calculated. Substituting the q value into the Eq. (13) results in the width of the clad (W1), expressed as:

$$ {W}_1={\left[\ln \left(\frac{6{\forall}_3\left(1-{\forall}_1\right)P\left(0.25 SOD\right){r}_p^2}{V_p{r}_l^2\left\{4\pi {r}_p{\rho}_p{r}_l^2{C}_p^{\ast}\right\}}\right)\right]}^{\frac{1}{2}}\times 1.414\left({r}_l\right). $$
(14)

After determining the width of clad, the law of mass conservation can be implemented on the clad mass, which is an ellipse in shape, to calculate the height of clad (∆h1) that is equal to the mass of the effectively utilized powder, expressed as:

$$ {\forall}_2{Q}_mt=\pi \frac{W_1}{2}\frac{{\Delta h}_1}{2}{V}_st{\rho}_p, $$
(15)
$$ {h}_{T1L}={\Delta h}_1=\frac{4{\forall}_2{Q}_m}{\pi {W}_1{V}_s{\rho}_p}, $$
(16)

where Vs is the laser scanning speed. The energy reaching on the substrate surface (Qs) can be divided into two parts: (a) energy absorbed by the upper hemisphere of the powder particle (Qp), and (b) energy consumed by the substrate surface to form a melt pool (QRS), expressed as:

$$ {Q}_S={Q}_P+{Q}_{RS}. $$
(17)

Qs can be expressed as:

$$ {Q}_S={\forall}_3\left(1-{\forall}_1\right)\left(\frac{P{L}_1}{V_s}\right). $$
(18)

Here, L1 is the length of the deposited clad. QP absorbed by the powder particles having Qm while depositing a clad of L1 with Vs, can be expressed as:

$$ {Q}_P=\left({\forall}_2{Q}_m\frac{L_1}{V_S}\right){C}_p^{\ast }. $$
(19)

QRS is the energy needed by the substrate to generate a melt pool with depth (∆d1), which can be expressed as:

$$ {Q}_{\mathrm{RS}}=\frac{\pi }{6}{W}_1{\Delta d}_1{L}_1{\rho}_s{C}_s^{\ast }. $$
(20.1)
$$ {C}_s^{\ast }=\frac{L_{\mathrm{fs}}}{T_{\mathrm{ms}}-{T}_o}+{C}_{s.} $$
(20.2)

Here \( {C}_s^{\ast } \) is the modified specific heat based upon the ratio of the substrate's enthalpy fusion (Lfs) to the temperature difference (Tms − To) with the addition of the substrate’s specific heat (Cs).. Combining Eqs. (18) to (20) results in:

$$ \Delta {d}_1=\frac{\left[{\forall}_2\left(1-{\forall}_1\right)\left(P{L}_1-{V}_s\right)\right]-\left[{\forall}_2{Q}_m{L}_1{C}_p^{\ast}\right]}{\left[\frac{\pi }{6}{\rho}_s{V}_s{W}_1{L}_1{C}_s^{\ast}\right]}. $$
(21)

Equations (14), (16), and (21) can be used to estimate the clad dimensions (W1, ∆h1, and ∆d1). The wetting angle (α) presented in Fig. 2, also known as a clad angle, can be estimated from the following relation as [23]:

$$ \alpha ={180}^o-2\times {\mathit{\tan}}^{-1}\left(\frac{2{\Delta h}_1}{W_1}\right). $$
(22)
Fig. 2
figure 2

Schematic representation of the wetting angle

Full size image

2.1.3 Estimation of total clad height along the z-axis for all deposited layers

The following assumptions are made to estimate the total clad height, along the z-axis, for all the deposited layers:

  1. 1.

    The primary operating conditions are kept constant while depositing n number of layers.

  2. 2.

    The re-melting depth (∆d2) of the 1st deposited layer is a function of hatch distance (HD), and 1st deposited layer’s height ∆h1.

  3. 3.

    The length of the deposited clad (L1) is equal to the length of the substrate (Ls).

Figure 3 a illustrates that 1st layer with dimensions (L1 × W1 × ∆h1) has been deposited on the substrate having dimensions (Ls × Ws × Hs). Figure 3 b presents that a melt pool of depth (∆d1), represented by a blue textured area, was generated by a laser beam in the substrate to deposit the 1st layer with height (∆h1)). The laser beam will re-melt the 1st layer up to the depth (∆d2) while depositing the 2nd layer on the 1st layer (Fig. 3). It can be, therefore, named as melt pool depth for the 2nd layer. Due to ∆d2∆d2, the height of the 1st deposited layer will decrease up to ∆h’1, expressed as:

$$ {\Delta h}_1^{\prime }=\Delta {h}_1-{\Delta d}_2. $$
(23)
Fig. 3
figure 3

Schematic diagram of clad geometry. a 1st deposited layer and b n number of deposited layers

Full size image

Here, ∆d2 can be calculated using the hatch distance (HD), defined as the separation between two consecutive laser scans [24] (Fig. 3b). The expression for HD, is given as:

$$ HD=\frac{{\Delta h}_1^{\prime }}{2}+\frac{{\Delta h}_2}{2}, $$
(24)

where ∆h’1 = ∆h1 - ∆d2. As the experimental conditions for building a part are optimized, the layer thickness is preserved from layer to layer as:

$$ {\Delta h}_2=\kern0.5em {\Delta h}_1. $$
(25)

Substituting Eqs. (23) and (25) into Eq. (24), and simplifying will give:

$$ {\Delta d}_2=2\left({\Delta h}_1- HD\right). $$
(26)

Equation (26) gives the value of re-melted depth (∆d2) for the 2nd layer based on the hatch distance and the height of the 1st deposited layer. So, the total clad height for two deposited layers (hT(2)L) along the z-axis, can be calculated by the following expression (Fig. 3b):

$$ {h}_{T(2)L}=\Delta {h}_1+\Delta {h}_2-{\Delta d}_2. $$
(27)

Similarly, the total clad height for three deposited layers (hT(3)L), along the z-axis, is calculated as (Fig. 3b):

$$ {h}_{T(3)L}=\Delta {h}_1+\Delta {h}_2+\Delta {h}_3-\left({\Delta d}_2+{\Delta d}_3\right). $$
(28)

Here, ∆h3 is the height of the 3rd deposited layer, which is equal to ∆h1, while ∆d3 will be similar to ∆d2, as the operating conditions are constant. So, the total height hT(n)L along the z-axis for n number of layers deposited on the substrate can be estimated analytically, by the following relations:

$$ {\Delta d}_i=\left|2\left({\Delta h}_1- HD\right)\right|,\mathrm{where}\ 0< HD<{\Delta h}_1. $$
(29a)
$$ {h}_{T(n)L}=\sum \limits_{i=1}^n\Delta {h}_i-\sum \limits_{i=2}^n\Delta {d}_i,\mathrm{where}\ n=\mathrm{number}\ \mathrm{of}\ \mathrm{layers}. $$
(29b)

In Eq. (29), Δhi is the height of the layer to be deposited, where i = 1, 2, 3, ..., n (number of layers), and Δdi is the re-melting depth, where i = 2, 3, ..., n (number of layers). It is essential to mention that Δd1 is the re-melting depth in the substrate to deposit the 1st layer. The substrate and deposited material’s properties have been considered the same in current modeling. The thermophysical properties of the powder particles are constant that can assist in keeping the surface roughness consistent for the deposited material, resulting in ∆d1 = ∆d2. But, ∆d1 ≠ ∆d2, when substrate and deposited material are heterogeneous in properties, and ∆d2 will be re-calculated, using Eq. (21), based upon the given material’s property.

2.2 An analytical model to estimate residual stress distribution

In the LMD process, there are two main mechanisms which cause residual stresses:

  • The first mechanism is known as the thermal gradient mechanism (TGM), as shown in Fig. 4 a. TGM occurs due to the vast temperature difference around the laser spot. Rapid heating with slow conduction at the top of the deposited layer’, or substrate’ surface, generates a sharp temperature gradient. The material strength instantaneously decreases with the rise in temperature. As the layer controls the extension of the heated layer beneath the heated ones, it results in compressive stress-strain phenomena. Moreover, these phenomena do not demand the solid-material to be melted completely [25].

  • The second mechanism is known as the cool-down mechanism (CDM), presented in Fig. 4 b. It happens when the laser beam moves away from the irradiated regime, which starts to cool down, and results in shrinkage. The underlying material counteracts to these results, causing tensile stress distribution in the newly added deposit and compressive stress below the freshly added deposit [25].

Fig. 4
figure 4

Mechanisms for residual stress development during the LMD process. a Thermal gradient, and b cool-down

Full size image

An analytical model has been developed to calculate the residual stress distribution induced in the deposited layers by the LMD process. The following assumptions have been made for the modeling:

Figure 5 provides the schematic diagram for the layers deposited by the LMD process. All the layers are deposited on the top of the substrate’s surface at ambient temperature.

  1. 1.

    Before the deposition process, the substrate does not contain any residual stress. Besides, no external forces are applied to the deposited layers-substrate assembly. This assumption is necessary to implement the generalized beam theory.

  2. 2.

    All the major operating parameters are kept fixed throughout the layers' printing process. This assumption helps to keep height (∆hn, n = 1,2,3,…), and generated stress (\( \overline{\sigma} \)) constant for each deposited layer.

  3. 3.

    Few studies claimed that the most significant stress components are usually developed along the scanning direction [26]. In current modeling, stress-induced in the x-direction is independent of the y-direction, which means that the stresses along the width of the deposited layers are neglected.

  4. 4.

    An increase in the residual stress distribution within the substrate (σn), generated to the addition of a new layer with height (Δhn) on the substrate’ surface, is considered to be linear [25]. It will help us to use force and moment equations (described later) to find the an and bn values in the following equation:

Fig. 5
figure 5

Stress build-up in the part-substrate assembly while depositing n number of layers

Full size image
$$ {\sigma}_n(z)={a}_nz+{b}_n $$
(30)
  1. 5.

    The total stress in the substrate due to the deposition of 1st to nth layer is given as (Fig. 5):

$$ {\displaystyle \begin{array}{c}{\sigma}_1(z)+{\sigma}_2(z)+{\sigma}_3(z)+\dots +{\sigma}_n(z)=\sum \limits_{i=1}^n\left({a}_iz+{b}_i\right),\\ {}\mathrm{where}\ \mathrm{i}=1,2,3,\dots, \mathrm{n}\ \left(\mathrm{number}\ \mathrm{of}\ \mathrm{layers}\right).\end{array}} $$
(31)
  1. 6.

    The external forces are ignored, resulting in the implementation of force and equilibrium equations [25] as:

Force equation,

$$ {\int}_{z_{\mathrm{min}}}^{z_{\mathrm{max}}}{\sigma}_n(z) dz=0. $$
(32)

Moment equation,

$$ {\int}_{z_{\mathrm{min}}}^{z_{\mathrm{max}}}{\sigma}_n(z) zdz=0. $$
(33)

where the number of layers = 1, 2, 3, …, n. In the LMD process, laser beam usually re-melts the substrate having a height (Hs) to the depth (Δd1), resulting in the net height of the substrate (Hs − ∆d1), as shown in Fig. 5. Equations (33) and (34) can be modified as:

$$ {\int}_0^{\left({H}_s-\Delta {d}_1\right)}\left({a}_1z+{b}_1\right)\ dz+{\int}_{\left({H}_s-\Delta {d}_1\right)}^{h_{T1L}}\overline{\sigma} dz=0. $$
(34)
$$ {\int}_0^{\left({H}_s-\Delta {d}_1\right)}\left({a}_1z+{b}_1\right)\ zdz+{\int}_{\left({H}_s-\Delta {d}_1\right)}^{h_{T1L}}\overline{\sigma} zdz=0. $$
(35)

After solving Eqs. (35) and (36), and re-arranging, the enhancement in the stress distribution within the substrate due to the addition of the 1st layer, σS1L(z), can be written as:

$$ 1\mathrm{st}\ \mathrm{layer},{\sigma}_{S1L}(z)=\overline{\sigma}{h}_{T1L}\left[\frac{2\left({H}_s-\Delta {d}_1\right)+3{h}_{T1L}}{{\left({H}_s-\Delta {d}_1\right)}^2}\right]-6\overline{\sigma}{zh}_{T1L}\ \left[\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T1L}}{{\left({H}_s-\Delta {d}_1\right)}^3}\right] $$
(36a)
$$ 2\mathrm{nd}\ \mathrm{layer},{\sigma}_{S2L}(z)=\overline{\sigma}\left(\frac{h_{T2L}}{2}\right)\left[\begin{array}{c}\frac{2\left({H}_s-\Delta {d}_1\right)+3{h}_{T1L}}{{\left({H}_s-\Delta {d}_1\right)}^2}+\\ {}\frac{2\left({H}_s-\Delta {d}_1\right)+5\left(\frac{h_{T2L}}{2}\right)}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(\frac{h_{T2L}}{2}\right)\right\}}^2}\end{array}\right]-6\overline{\sigma}z\left(\frac{h_{T2L}}{2}\right)\ \left[\begin{array}{c}\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T1L}}{{\left({H}_s-\Delta {d}_1\right)}^3}+\\ {}\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T2L}}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(\frac{h_{T2L}}{2}\right)\right\}}^3}\end{array}\right] $$
(36b)
$$ nth\ \mathrm{layer},{\sigma}_{S(n)L}(z)=\overline{\sigma}\left(\frac{h_{T(n)L}}{n}\right)\left[\frac{2\left({H}_s-\Delta {d}_1\right)+\left(2n+1\right)\left(\frac{h_{TnL}}{n}\right)}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(n-1\right)\left(\frac{h_{TnL}}{n}\right)\right\}}^2}\right]-6\overline{\sigma}z\left(\frac{h_{T(n)L}}{n}\right)\ \left[\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T(n)L}}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(n-1\right)\left(\frac{h_{TnL}}{n}\right)\right\}}^3}\right] $$
(36c)

The total residual stress (σST(n)L(z)) in the substrate while depositing n number of layers by the LMD process is given as:

$$ {\displaystyle \begin{array}{c}{\sigma}_{ST(n)L}(z)=\overline{\sigma}\left(\frac{h_{T(n)L}}{n}\right)\sum \limits_{i=1}^n\left[\frac{2\left({H}_s-\Delta {d}_1\right)+\left(2i+1\right)\left(\frac{h_{T(i)L}}{i}\right)}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(i-1\right)\left(\frac{h_{T(i)L}}{i}\right)\right\}}^2}\right]\\ {}-6\overline{\sigma}z\left(\frac{h_{T(n)L}}{n}\right)\sum \limits_{i=1}^n\left[\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T(i)L}}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(i-1\right)\left(\frac{h_{T(i)L}}{i}\right)\right\}}^3}\right],\\ {}\mathrm{where}\ i=1,2,3,\dots, n\ \left(\mathrm{number}\ \mathrm{of}\ \mathrm{layers}\right).\end{array}} $$
(37)

To calculate the total stress enhancement within the 1st layer (σT1L(nL)(z)) as a result in the addition of 2nd, 3rd, 4th, …, nth depositions by the LMD process (see Fig. 5) as:

$$ {\displaystyle \begin{array}{c}\mathrm{In}\ {1}^{\mathrm{st}}\ \mathrm{layer},{\sigma}_{T1L(nL)}(z)=\sigma \bar{\mkern6mu}-6\overline{\sigma}z\left(\frac{h_{T(n)L}}{n}\right)\ \left[\begin{array}{c}\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T2L}}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(\frac{h_{T2L}}{2}\right)\right\}}^3}+\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T3L}}{{\left\{\left({H}_s-\Delta {d}_1\right)+2\left(\frac{h_{T3L}}{3}\right)\right\}}^3}\\ {}+\dots +\\ {}\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T(n)L}}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(n-1\right)\left(\frac{h_{T(n)L}}{n}\right)\right\}}^3}\end{array}\right]\\ {}+\overline{\sigma}\left(\frac{h_{T(n)L}}{n}\right)\ \left[\begin{array}{c}\frac{2\left({H}_s-\Delta {d}_1\right)+5\left(\frac{h_{T2L}}{2}\right)}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(\frac{h_{T2L}}{2}\right)\right\}}^2}+\frac{2\left({H}_s-\Delta {d}_1\right)+7\left(\frac{h_{T3L}}{3}\right)}{{\left\{\left({H}_s-\Delta {d}_1\right)+2\left(\frac{h_{T3L}}{3}\right)\right\}}^2}\\ {}+\dots +\\ {}\frac{2\left({H}_s-\Delta {d}_1\right)+\left(2n+1\right)\left(\frac{h_{T(n)L}}{n}\right)}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(n-1\right)\left(\frac{h_{T(n)L}}{n}\right)\right\}}^2}\end{array}\right]\end{array}} $$
(38)

Therefore, the stress increment (σT(n − 1)L(nL)(z)) in the (n-1)th layer is given as:

$$ {\displaystyle \begin{array}{c}\mathrm{In}\ {\left(n-1\right)}^{\mathrm{th}}\ \mathrm{layer},{\sigma}_{T\left(n-1\right)L(nL)}(z)=\overline{\sigma}-6\overline{\sigma}z\left(\frac{h_{T(n)L}}{n}\right)\sum \limits_{i=n-1}^n\left[\frac{\left({H}_s-\Delta {d}_1\right)+{h}_{T(i)L}}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(i-1\right)\left(\frac{h_{T(i)L}}{i}\right)\right\}}^3}\right]\\ {}+\overline{\sigma}\left(\frac{h_{T(n)L}}{n}\right)\sum \limits_{i=n-1}^n\left[\frac{2\left({H}_s-\Delta {d}_1\right)+\left(2i+1\right)\left(\frac{h_{T(i)L}}{i}\right)}{{\left\{\left({H}_s-\Delta {d}_1\right)+\left(i-1\right)\left(\frac{h_{T(i)L}}{i}\right)\right\}}^2}\right],\\ {}\mathrm{where}\ i=1,2,3,\dots, \left(n-1\right)\ \mathrm{layer}.\end{array}} $$
(39)

Equations (37) and (39) are used to estimate the residual stress distribution within the part grown by the LMD process. One should calibrate the \( \overline{\sigma} \) experimentally by measuring the residual stress distribution in the nth (top) deposited layer. However, the \( \overline{\sigma} \) can also be used as the yield strength of the deposited material [25].

3 Materials and methods

3.1 Analytical simulations: steps to perform

Figure 6 presents a flow chart to estimate the total deposited clad height (hT(n)L) for n number of layers and overall residual stress distribution within the layers-substrate assembly. One should proceed as follows.

  1. Step 1.

    clad geometry for 1st deposited layer

Fig. 6
figure 6

Flow chart to carry out simulations for the clad geometry and corresponding residual stress distribution for part-substrate assembly

Full size image

Clad geometry, including W1, hT1L = ∆hT1L and ∆d1, are calculated with the input of operating parameters including laser power, laser scanning speed, powder particle radius, powder stream proportion and particle velocity, radius of the laser spot on the substrate, laser attenuation ratio, powder efficiency, deposited clad length, and melting temperature, laser absorptivity, and density, heating capacity and fusion enthalpy for powder particles and substrate, respectively.

  1. Step 2.

    re-melting depth estimation based on hatch distance and 1st deposited layer height

In the LMD process, re-melting depth is taken into account when the number of layers to be deposited larger than 1. This re-melting depth mainly depends on the hatch distance between two consecutive scans. Therefore, in this step, re-melting depth (∆dn) has been calculated for each set of deposited layers. It is worthful to mention that ∆di ≠ ∆d1, where i = 2, 3, 4, …, n (number of layers).

  1. Step 3.

    total clad height (hT(n)L) for the deposited layers

In this step, the height for the 1st deposited layer (step 1) has been selected as the starting clad height, and ∆dn is calculated from step 2. Both parameters are used as input to estimate the total deposited clad height hT(n)L.

  1. Step 4.

    residual stress formation within the 3D printed layers-substrate assembly

The output of step 3 (hT(n)L), in addition to few parameters such as height and width of the substrate, the width of the deposited layers, yield strength of the deposited material, and stiffness ratio are given as inputs to estimate the total residual stress formation within the 3D printed layers-substrate assembly.

In this study, the simulation strategy presented in Fig. 6 has been used. A Core i7, 8th Generation with 16 GB Ram computing system, was used for analytical simulations. The user-defined functions were written in a script file via MATLAB software.

3.2 Experimental data

Experimental data that reported the depositions of AISI316L powder debits on AISI321 bulk substrate [27] have been used to prove the reliability of the proposed model for clad geometry (Sec. 2.1). Table 1 collects the numerical data, with various operating conditions, used to carry out analytical computations.

Table 1 1st deposited layer clad geometry published data for the depositions AISI316L powder debits and AISI321 bulk substrate [27]
Full size table

The study of Sun et al. [28] has been selected to verify the model developed for residual stress distribution. AISI4340 steel powder debits were deposited on the AISI4140 bulk substrate via the LMD process. A total of three layers were deposited. Following on, the X-ray diffractometry (XRD) technique was used to measure the residual stress formation within the deposited layers. Besides experimental comparison, finite element simulation results presented by Liu [29] for the depositions of three layers in the case of AISI304 powder deposition on AISI304 bulk substrate by the LMD process were compared with proposed model’s results.

4 Results and discussion

The models presented to estimate the 1st deposited layer geometry, total deposited height (hT(n)L), and the residual stress distribution in the total deposited height by the LMD have been validated below.

4.1 Validation of 1st deposited layer geometry estimation model with the experimental data

A comparison between the current analytical modeling and experimental [27] results is presented in Fig. 7 a–c. The presented model can estimate clad width (W1), heights (Δh1), and depth (Δd1) within the range of 10–15 % mean absolute error. The deviations between the experimental and simulation results might be caused due to surface tension, which was assumed to be negligible. Besides, the powder efficiency equivalent to 40% was taken into account, which restricts the accuracy of the proposed model. The powder efficiency is defined as the ratio between the actual powder volume utilized by the deposition to the total powder supplied during the LMD process. In Fig. 7, error bars have been added to experimental data. The length of the error bars is influenced by primary operating parameters, including laser power, scanning speed, and powder feeding rate (Table 1). The standard deviation explains that the characteristics of the layer to be deposited strongly depend on the primary operating parameters. Deterministically, a variation in such parameters will then influence the clad characteristics (W1, Δh1, and Δd1).

Fig. 7
figure 7

Depositions of AISI316L powder debits on AISI32 bulk substrate: Experimental [27] and simulations comparisons of 1st deposited clad geometry (a) width, (b) height, and (c) depth

Full size image

4.2 Validation of re-melting depth relation with hatch distance and deposited height

Figure 8 presents an inverse relationship between the hatch distance (HD) and re-melting depth (Δd2) in case of deposition of the 2nd layer on the 1st layer. Consider a scenario in which the 1st layer of height (Δh1) has been deposited on the substrate. An HD value would be required (Eq. (29)) to generate a Δd2 on the 1st layer to form the 2nd layer with height (Δh2). If the HD is zero, the laser beam will re-melt the 1st deposited layer completely plus a portion of the substrate (Δd1) as well; the resultant height after depositing 2nd layer will be analytically equivalent to the altitude of the 1st added layer. It is worthy of mentioning that Δd1 value decreases with the increase in HD (see Fig. 8). That is why an optimum amount of HD, 0 < HD < Δh1, must be chosen to achieve a height increase in our developed analytical model.

Fig. 8
figure 8

Influence of hatch distance on re-melting depth in the LMD process

Full size image

4.3 Validation of residual stress estimation model for deposited layers: experimental and numerical comparisons

Figure 9 compares the results for residual stress distribution within the deposited layers of the current analytical model with the published experimental and numerical simulation results [28, 29]. For experimental comparison, the stress in the top layer equal to 1200 MPa was used for calibration of \( \overline{\sigma} \). A close correlation is found between the experimental and analytical modeling results, with the exception of 8–14 % mean absolute deviation. In present analytical model, a linear stress distribution has been taken into account, resulting in accuracy declination between the experimental and simulation results. In addition, the results have been compared with Liu’s [29] finite element (FE) simulations. A close correlation can be observed between Liu’s and current analytical simulations with an absolute error of 9%. The analytical models do not consider the meshing and iterative calculations, thus, reducing the computational accuracy. On the other hand, the analytical models present high computational efficiency. However, the errors are found to be in an acceptable regime. The error bars plotted for the experimental data, and FE simulations in Fig. 9 show that the values are dispersed in a wide range. The variations within the data are due to the induced residual stress distribution caused by the rapid heating and cooling mechanisms, combined with the slow conduction. These phenomena became incrementally iterative with the number of deposited layers. As a consequence, a direct relationship between the residual stress distribution and the number of layers deposited on the substrate can be established.

Fig. 9
figure 9

Comparison between experiments and simulations in case of residual stress analyses [28, 29].

Full size image

4.4 Computational efficiency: current and reported models

It is well-known that the analytical models have significant advantages in computational efficiency over FE simulations. In this aspect, the computational capability and time of the proposed model have been reported and compared with previously reported models from the literature. Using MATLAB software, the time needed by analytical computations was found to be 39 s. This time is less than those reported for the analytical models in the literature, equivalent to 19.44 s (single-track scan), 88.17 s (bidirectional scans), 80 s (heating time), 144 s (cooling time), and 217.9 s (temperature simulation), respectively [6, 8, 9]. Besides, current model’s computation time (39 s) is found to be far less than the time required by the FE simulations (≈ 6 h) in the case of LMD process [29, 30].

5 Limitations of current analytical models

While the analytical models provide results that are very close to the experimental and numerical simulations results. A few drawbacks prevent it from being 100% accurate. Some apparent limitations are listed below:

  • The LMD process can be classified based on the feedstock: (a) powder-based LMD, and (b) wire-based LMD. The presented model is limited to the powder-based LMD process, only.

  • Besides, the proposed model has been tested for the metallic powder depositions, and cannot be utilized for ceramics-based material. The main hindrance restricting its implementation is the complex rheological properties involved in ceramics materials for 3D printing. However, the authors believe that an extended version of the current model can be utilized in the case of ceramics.

  • The current model does not take into consideration the surface tension effects occurring in the LMD process due to the melting of solid particulates. This assumption restricts the accuracy of analytical simulation results.

  • The laser absorption coefficient, in solid and liquid states, is taken as constant and considered to be independent of process parameters. This assumption reduces the accuracy of the proposed analytical model. In the real-time analysis, the laser absorption strongly depends on the primary process parameters, including laser power, scanning speed, powder flow rate, and temperature gradient [31]. If in analytical simulations, the laser absorption and temperature gradient are defined to be dependent on each other, it will be impossible to calculate a specific solution for laser absorption based upon the temperature gradient, as both quantities will be unknown for a given material. Therefore, it is necessary to fix one quantity.

  • In Eqs. (29) (a and b) and Fig. 8, it has been assumed that “if the HD is zero, the laser beam will re-melt the 1st deposited layer completely, in addition to a portion of the substrate (Δd1).” However, it has been found experimentally by the authors of the current study, that actually if too much amount of powder particles is added, with HD = 0, the resultant height will yield some quantitative value.

  • For the residual stress distribution model, a linear stress-distribution relationship has been taken into account. This assumption restricts the accuracy of the proposed model, as stress formation is a complex phenomenon and involves various factors. However, the consideration of all elements in the modeling will give a complex model resulting in long computation time.

It is suggested that the present model can be a handy tool for laboratory work. It can predict the clad geometry and residual stress distribution satisfactorily, allowing researchers to gain time during parameter optimization steps. Thus, by taking out the parameters indicated by the simulation unsuitable for an application or causing process failure, a drastic reduction of the number of actual experiments can be achieved by using the current model.

6 Conclusions and future outlook

Multi-physics mathematical models have been developed to estimate the clad dimensions and corresponding residual stress distribution based on the primary operating parameters in the LMD process. Initially, fundamental operating parameters are used to calculate the dimensions of the 1st deposited layer. Following on, a hatch distance is used to convert the single deposited layer dimensions into n layers’ aspects. This output was used as an input in the 2nd model to quantify the residual stress distribution within the deposited layers and substrate. The models have been validated with the experimental data. Besides, a comparison has been made between finite element and current analytical simulations for residual stress distribution model. It has been found that the present analytical model can estimate the clad width, height, depth, and corresponding residual stresses, within the range of 8–15% mean absolute error. Based on the computational efficiency and accuracy, the proposed models have been found reliable for further estimations based on the defined operating process parameter.

The following conclusions have been deduced based on current findings:

  • With the coaxial addition of powder, a significant portion of the laser beam energy is consumed by the powder debits to transform their phase from solid to liquid, causing laser energy attenuation. This attenuation ratio strongly depends on the standoff distance and powder flow rate. With the increase in the powder flow rate, the attenuation ratio prevails within the LMD process, as the volume of powder debits crossing the laser beam increases. The same applies to standoff distance.

  • The assumption considering the width of the clad as elliptical is found reliable. Further, it has been determined that the width of the deposited layer is strongly dependent on the radius of the laser spot focused on the substrate, ignoring the heat-affected zone. The height and depth of the clad can be determined based on the clad’s width.

  • A correlation between the growth along the z-axis and layer thickness is essential, as the misalliance between the deposited layer height and z-plane increment will cause extra-energy utilization and disturb dimensional accuracy, resulting in less qualitative part. Hence, an optimum selection of hatch distance is necessary for proper energy density utilization and dimensional control stability.

  • The induced residual stress distribution was caused by the heating and cooling mechanisms, which appeared due to rapid heating and moderate cooling, in combination with slow conduction. These phenomena become incrementally iterative with the number of layers to be deposited, resulting in a direct relationship between the residual stress distribution and the number of deposited layers.

  • A few topics regarding future work have been identified. A large thermal gradient caused by repeated rapid heating and solidification results in various defects within the manufactured part. In this context, the high prediction accuracy and computational efficiency allow that presented model be employed for prediction of part porosity [32] and part distortion [33], life-expectancy of a manufactured part, mechanical properties of the produced piece, and process parameter planning based on the given ones. The optimization of process parameters can be achieved with inverse analysis, such as gradient search method and topology optimization [34].

The scheme developed provides a time- and cost-effective method to quickly estimate the characteristics and corresponding residual stress distribution for n layers in the LMD process, based on the hatch distance.