Simulation model for uncertainty estimation of measurements performed on five-axis measuring systems

Abstract

Five-axis measuring systems (i.e. coordinate measuring machines equipped with articulated probe heads capable of continuous indexation or five-axis machine tools with inspection probe mounted on a tilt and swivel head) are becoming more and more popular, especially in industrial applications, since their usage speeds up the measurement process without significant loss in accuracy. Widespread adoption of these systems necessitates development of viable and easy-to-use measurement uncertainty estimation methods. This paper describes the experiments required for identification of errors of five-axis measuring systems based on usage of LasrTracer system and measurements of ring standard. It also expounds the methodology for implementation of virtual CMM-based simulation model for these systems giving the explanation on all input quantities used in the model along with detailed mathematical explanations on uncertainty propagation procedure. Eventually, it presents the validation methodology and the results of validation measurements performed in order to prove the correct functioning of developed model. Basing on these results, the main conclusion drawn in the paper is that presented virtual model should be regarded as working properly and producing metrologically correct values of measurement uncertainty for common metrological tasks known from GD&T framework.

1 Introduction

Uncertainty estimation for measuring systems is still a challenging task [1,2,3,4]. Among the developed solutions, simulation methods show significant promise, since they are designed to shorten the length of the quality control process and enable automated evaluation of measurement uncertainty. Although individual simulation methods are structured differently, the most common concept among them is the so-called virtual machine, which enables simulation of multiple measurement processes, including possible variability of errors occurring during measurement. To this day, several different virtual machines were developed and described in literature [5, 6], primarily models of classic three-axis coordinate measuring machines (CMMs) and three-axis machine tools equipped with a contact probe. In [7], Ramus et al. presents a virtual CMM model for five-axis CMM, where in addition to three translational movements, two rotations were possible due to the implementation of rotary and tilt stages. There is also a significant number of publications devoted to error models for five-axis machine tools [8,9,10], but these focus mostly on machines with rotary or tilt tables. And there is currently no virtual model for machines that utilize articulated probe heads with continuous indexation capability or five-axis machine tools with inspection probe mounted on a tilt and swivel head, i.e. the so-called five-axis measuring systems.

Five-axis measuring systems have two basic advantages associated with the function of articulated probe head, i.e. shorter measurement time and improved repeatability. Five-axis systems enable the performance of measurements using rotational movements of the probe. In the case of certain measuring tasks (mostly measurements of solids of revolution), this significantly reduces the duration of the measuring process, as it eliminates the need to accelerate and decelerate heavy components of the machine support system. Presently, only a handful of publications examine the issue of five-axis measuring systems using probe heads with continuous articulation, and neither of these focuses on uncertainty estimation. Naturally, measurement uncertainty can be determined using the calibrated workpieces method (CWM) [11,12,13]; however, the reliance on time-consuming methodology seems ill-advised in the case of a system designed to reduce the time needed for quality control processes. For this reason, the authors decided to conduct studies aimed at development of a virtual machine model for a five-axis measuring system.

Previous work of the authors included the development of methodology for describing the field of CMM geometric errors based on residual error distributions [14] and the formulation of a model for probe head errors in touch-trigger probe heads used in five-axis coordinate measuring systems [15]. This paper presents the method for combining the two abovementioned models to create a fully functional virtual model of a five-axis measuring system and discusses its application for simulating measurement uncertainty. The authors also present results of verification measurements that prove the correct functioning of the presented model (in the scope of uncertainty determination for common metrological tasks from the GD&T framework). The same verification method may also be used for testing correct installation of the virtual model each time it is implemented on a new CMM.

The virtual CMM discussed in this paper is the first solution of its kind for five-axis coordinate systems that use articulated probe heads with continuous indexation capability, and in authors’ opinion, may also be easily transferred to five-axis machine tools equipped with an inspection probe (this paper only focuses on the application of the developed model in five-axis CMMs, but with certain modifications, it should also be possible to use the presented methodology with machine tools). The developed model allows for close to real-time analysis of measurement uncertainty (the uncertainty of measurement is given together with the result of a single measurement immediately after its completion). The standard methods for determining measurement uncertainty (calibrated workpieces method or multiple measurement strategy) entail multiple repetitions of the evaluated measurements [11, 16,17,18]. The number of repetitions depends on the exact type of procedure used. Most commonly, the number of repetitions varies between 15 and 30. In the long term, the model presented in this paper may contribute to a significant reduction in the time required for estimating the uncertainty of measurements carried out on five-axis measuring systems, and thus cut down the cost of quality control of manufactured items (which is a large part of total manufacturing costs) by a factor of 30.

2 Implementation of the virtual five-axis measuring system model

All measurements presented in this paper were performed on a Zeiss WMM850S bridge coordinate measuring machine equipped with a PH20 probe head. The measuring volume of the machine has the dimensions of 1000 mm × 1200 mm × 500 mm.

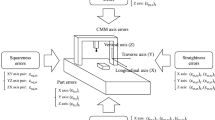
The virtual model of a five-axis measuring machine is based on two main modules [18]. The first module is responsible for simulation of errors related to the kinematic system of the machine, and the second module simulates the values of probe head errors (Fig. 1) (input values for the model are explained in Sect. 3 and graphically presented in Fig. 3). The simulation must be possible to perform for points measured at any position and approach direction in the measuring volume of the machine. Since the functioning of the abovementioned modules is based on experimentally determined errors at chosen reference points, the first necessary steps for the implementation of the virtual model are associated with identification of their values and variability.

Fig. 1

Concept of the virtual CMM model for a five-axis coordinate measuring system

The first stage in implementing the model consists in determination of residual errors of the kinematic system. The process is carried out experimentally using the LaserTracer interferometric system. The measuring volume of the machine is described by a grid of reference points. The model presented herein uses a grid based on 9 points, which form the nodes of the grid (detailed operating principles of this model are described in [14, 19]). Eight points are located in the vertices of the cuboid, whose edges are equal to half the axis length of the measuring machine coordinate system, and the final ninth point is located at the intersection of the cuboid spatial diagonals, that is, in the centre of the measuring volume (let Xmax, Ymax, Zmax denote the length of coordinate system axes, the coordinates of centre point are given as 0.5·Xmax, 0.5·Ymax, 0.5·Zmax). After determining the structure of this grid, the measurements take place. The measuring machine is fitted with a retroreflector in place of the standard probe and performs 14 approaches from different directions to each node of the grid. Since the LaserTracer system is only capable of measuring the distances, while the calculation of residual errors is based on the coordinates of reference points, the entire sequence has to be repeated four times, each time with a different position of the LaserTracer system. This approach enables the use of a multilateration technique described in [14, 20] to obtain the point coordinates from measured lengths. As a result of this experiment and the representation of residual errors, it is possible to determine the mean value of differences between the programmed and obtained values for each point coordinate (x, y, z) and standard deviations of their reproduction denoted as s(X), s(Y), s(Z). It must be noted here that the CAA (computer-aided accuracy) matrix of the machine (if available) has to be switched on during the described measurement. The matrix is formed using data obtained through measurements of machine geometric errors, which are performed at chosen reference points distributed within the measuring volume of the machine. Once the obtained data is uploaded to the machine controller, it is then possible to correct particular errors for any point in the measuring volume.

The second stage of the process involves determination of probe head errors. For this purpose, the model presented in [15] is used (see [15] for a detailed overview of the mathematical model used for simulation of probe head errors). The probe heads used over the course of presented research utilize axial adjustment with two orthogonal axes of rotation. The range of possible rotations for the vertical axis of revolution, hereinafter referred to as the B axis, equals − 180° to 180°, and for the horizontal axis, hereinafter referred to as the A axis, the range is < − 115°; 115° > (A and B are graphically presented in Fig. 3). The probe head is oriented vertically (along the machine quill) when A and B angles are set to 0. The experiment designed to identify probe head errors is based on measurement of a standard ring at specified angular orientation of the probe head. A standard ring with diameter of 20 mm was chosen for this purpose and used throughout the course of measurements. The standard ring was attached to solid block installed in a swivel and tilt vise. As a result, it was possible to rotate the ring around two perpendicular axes of revolution, in such a way that its axis was parallel to stylus in A, B orientation. The material standard was measured in 24 positions defined by A and B angles. The A angle changes at 30° within a range between 0° and 90°, while the B angle changes at 60° within a range between − 120° and 180°. Most of the probe head working range was covered by this selection of positions. In each arrangement, the standard was measured 15 times at 64 evenly distributed measuring points. In order to minimize possible influences of machine kinematics, all measurements of the reference ring were done using only rotational probe head movements. As a result of this experiment, it was possible to determine probe head errors for A, B, α, where α is an angle defined on a plane perpendicular to the probe, when it is oriented in A and B angular positions, and its zero indication lies in the direction in which the probe rotates along A axis in the positive direction. The α angle increases in a counter-clockwise direction.

The next stage consisted in computer implementation of virtual CMM algorithms described in Sect. 3. The MODUS metrological software was installed on the modelled machine. Using DMIS and Python languages, an add-on to this software was developed to allow for online determination of measurement uncertainty for measurements performed on the modelled five-axis measuring system.

Following the completion of preliminary measurements and installation of the required software, the validation stage was performed. This stage plays a crucial role in the implementation of the virtual CMM as it proves that the results and corresponding uncertainties produced by the virtual model are correct, and that the implementation of the model on a CMM (including determination of kinematic system and probe head errors) was carried out properly. The process should be performed each time the virtual model of a five-axis system is installed on a new machine. Validation measurements consist of select measuring tasks and evaluation of the obtained results using two methods, i.e. through the presented virtual model, and the calibrated workpiece method [11], which serves as a reference for comparison. After the results and uncertainties are determined, they are then cross-compared using the chosen statistical test. In the case of presented experiments, the statistical test is based on the concept of consistency control. The model of consistency control, according to [21,22,23], refers to classical statistics, such as a weighted mean of both methods (denoted here as the reference value (RV)) and the chi-squared test. This model can be applied on condition that one of the methods used in the comparison may be regarded as a reference method (hence the use of the calibrated workpiece method as part of the presented experiments). If the consistency of results produced by the reference method and the method under validation is confirmed, the latter may be also considered as properly validated.

A simplified mathematical procedure of the validation model is presented below (for more details, please refer to [21]):

• 1. Calculation of the so-called reference value (RV) (1):

$$ RV=\frac{x/{u}^2(x)+y/{u}^2(y)}{1/{u}^2(x)+1/{u}^2(y)} $$

(1)

where

x, y:

the mean values of results obtained from the calibrated workpieces method (x) and the virtual CMM method (y),

u(x), u(y):

uncertainties calculated according to the respective method

• 2. A chi-squared test calculated as (2):

$$ {\chi}_{obs}^2=\frac{{\left(x- RV\right)}^2+{\left(y- RV\right)}^2}{u^2(x)+{u}^2(y)} $$

(2)

$$ \mathit{\Pr}\left\{{\chi}^2(v)>{\chi}_{obs}^2\right\}<0.05 $$

(3)

where

ν = N − 1:

the degrees of freedom for N, being the number of methods used for determination of RV

If formula (3) is true, the chi-squared test rejects the hypothesis regarding consistency of results obtained through the considered methods.

• 3. If the test described in item 2 results in a failure, the consistency of the examined methods may be assumed. In this case, it is possible to proceed with the following steps. Otherwise, the validation ends with a negative result (in such case, the experiments aiming at determination of kinematic residual errors and probe head residual errors are usually repeated, followed by a validation stage as described).

• 4. Calculation of standard uncertainty associated with the reference value (RV) using (4):

$$ \frac{1}{u^2(RV)}=\frac{1}{u^2(x)}+\frac{1}{u^2} $$

(4)

• 5. Determination of a validation acceptance interval (VAI) in the form of (5):

$$ < RV-u(RV); RV+u(RV)> $$

(5)

VAI is the proposed mathematical range, which should overlap with the intervals that contain the true value of the measured quantity obtained using the examined methods. It is used as a criterion for verifying if the results obtained through the examined methods may be regarded as statistically comparable with the reference method.

• 6. Determination of intervals that contain the true value of the measured quantity obtained using all of the compared methods in the form of (6):

$$ <x-u(x);x+u(x)>\kern0.5em ;\kern0.5em <y-u(y);y+u(y)\kern0.5em > $$

(6)

• 7. If all intervals presented in (6) share a common part with the VAI, then the validation ends with a positive result and the developed model may be considered as properly validated.

  A visual example of the VAI and intervals that contain the true value of the measured quantity determined using the developed virtual model and the calibrated workpieces method for measurement of an internal cylinder diameter (presented in Table 2) is shown in Fig. 2. As discussed, both intervals share a common part with the VAI and the developed model may be considered as properly validated with regard to the results and standard uncertainty of internal cylinder diameter measurement.

Fig. 2

Graphical representation of VAI and intervals containing the true value of the measured quantity determined using the developed virtual model (Virtual CMM) and the calibrated workpieces method for measurement of internal cylinder diameter

The mathematical procedure described above should be performed for all measuring tasks included in the measurement routine. In the case of the discussed research, the procedure was repeated for all six measuring tasks presented in Table 2.

3 Methodology of virtual CMM implementation

This section discusses the manner in which input quantities (measured point coordinates, direction of approach to the point, actual values of A and B angles during point measurement and effective length of stylus used) required for running the simulations performed by the virtual model are processed in order to obtain the output quantity (point coordinates with simulated errors). All simulations performed with the described virtual model utilize the Monte Carlo method (parameters defining the probability density functions assigned to input quantities, and general course of the simulation are given below; for more details regarding each of the modules, please refer to [14, 15]). In order to facilitate understanding of the presented model, an example of the probe head used in five-axis coordinate systems with all input quantities marked is presented in Fig. 3.

Fig. 3

Diagram of probe head used in five-axis coordinate systems with graphical explanation of input quantities

Data flow in the developed virtual model is presented below:

• 1. Gathering the values of x′, y′, z′, i′, j′, k′, A_a, B_a (Fig. 3) during a single measurement, where x′, y′, z′ are the actual measured point coordinates in the part coordinate system, i′, j′, k′ are the actual direction cosines defining the direction of approach to a given measured point in the part coordinate system, and A_a, B_a are the actual values of A and B angles of the probe head. All numeric input values can be obtained from the machine controller either by the user or via an external application.

• 2. Transformation of x′, y′, z′, i′, j′, k′ to the global coordinate system of the machine as detailed below in (7) (for transformation of [i′, j′, k′] into [i, j, k] in formula (7), i′, j′, k′ should be substituted in place of x′, y′, z′):

$$ \left[\begin{array}{c}x\\ {}y\\ {}z\\ {}1\end{array}\right]= Tr\cdot {R}_Z\cdot {R}_y\cdot {R}_x\cdot \left[\begin{array}{c}{x}^{\hbox{'}}\\ {}{y}^{\hbox{'}}\\ {}{z}^{\hbox{'}}\\ {}{1}^{\hbox{'}}\end{array}\right] $$

(7)

where Tr is the coordinate system translation matrix, and R_x, R_y, R_z are the respective rotation matrices along x, y, z axes

• 3. The residual errors of machine kinematic system are determined with through the use of a retroreflector mounted in place of a probe/tool. The error distributions are identified for intermediate points, in which the centre point of retroreflector stops during the measuring sequence. During measurements, when the probe is mounted to the quill of the machine, it records coordinates located in a different position (in relation to the quill reference point) than in the case of measurements performed with a retroreflector. Thus, in order to obtain the values of residual errors for the actual stopping point of the machine, it is necessary to translate x, y, z coordinates of the measured point in the global coordinate system of the machine into x_R, y_R, z_R coordinates of the point in which machine with retroreflector stopped during implementation measurements. This is accomplished using Eqs. (8–10):

$$ {x}_R=x-r\cos \left(A-90{}^{\circ}\right)\cos \left(B-90{}^{\circ}\right) $$

(8)

$$ {y}_R=y-r\cos \left(A-90{}^{\circ}\right)\cos \left(B-90{}^{\circ}\right) $$

(9)

$$ {z}_R=z-r\sin \left(A-90{}^{\circ}\right)+{z}_{off} $$

(10)

where r is the effective length of stylus used during measurement (as determined during probe qualification), and z_off is the offset from reflector centre to the probe head rotation point (the point where A and B axes should theoretically cross). The determined values x_R, y_R, z_R are used as an input for the residual kinematic error module.

• 4. Simulation of residual kinematic errors for a single point is performed using the following procedure:

• For the point defined by x_R, y_R, z_R coordinates, it is necessary to find the nearest reference point (one of the nine reference points mentioned in Sect. 2), whose coordinates are x_ref, y_ref, z_ref.

• N simulations (for simulations discussed in this paper N was set as 10,000) of point reproduction error have to be performed for the chosen reference point using the t-distribution with parameters ($\overline{x}$, σ, υ), where $\overline{x}$ is the mean value of the distribution, σ standard deviation and υ the number of degrees of freedom. The mean value of differences between the programmed and obtained values of each point coordinate (for a considered reference point) determined during experiments performed with the LaserTracer is taken as $\overline{x}$, as the standard deviation, values of s(X), s(Y), s(Z) mentioned in Sect. 2 are taken. The number of degrees of freedom for each of the points is set at 13, because it was assumed that the number of degrees of freedom should be equal to the number of measurements performed for each point (during experiments conducted with the LaserTracer system) minus one, i.e. 14–1 = 13. The t-distribution was chosen according to guidelines of ISO-IEC (Supplement), because of a relatively small number of measurement results (14) used for determining error distributions. The Kolmogorov–Smirnov test was carried out for all probability distributions. The tests suggested no grounds for rejecting the hypothesis about the tested distributions being t-distributions. Examples of error distribution histograms are given below (Fig. 4) for errors related to the probe head and the kinematic system of CMM.

Fig. 4

Histograms showing distribution of a probe head errors for chosen A, B and α angles (A = 90°, B = 120°, α ≅ 331°) and b residual errors of y-coordinate reproduction for chosen reference point (x = 395, y = 580, z = 240)

• Calculation of residual kinematic errors x_res, y_res, z_res as mean values of all simulated x_{ref_sim}, y_{ref_sim}, z_{ref_sim} coordinates (calculated separately for each coordinate, e.g. x_res being calculated as mean value from all simulated x_{ref_sim} values).

As a result of these operations, the simulated values of residual errors for x_R, y_R, z_R are given as x_res, y_res, z_res.

• 5. The simulation of probe errors is divided into several stages. The probe error model used in the described virtual machine requires three input values: the angular positions of the head A_a, B_a and the α angle, which carries information about the direction of approach to a measured point. The A_a and B_a values can be obtained directly from the machine driver, whereas α is calculated on the basis of direction cosines of the considered point recorded during actual measurements. The first step consists in selecting the appropriate reference grid nodes for the probe head based on previously obtained A_a and B_a values (according to [15], four nodes have to be chosen for the simulation of probe errors in a single set of A, B, α; they are denoted here as P1, P2, P3, P4 and are described by the following pairs of A and B angles: P1 (A_a-1,B_a-1), P2 (A_a + 1,B_a-1), P3 (A_a-1,B_a + 1), P4 (A_a + 1,B_a + 1), where A_s-1, B_s-1 are the angle values for the nearest node with angles narrower than A_s, B_s respectively, and the A_s + 1, B_s + 1 are the angle values for the nearest node with corresponding angles broader than A_s, B_s). Subsequently, the approach direction recorded as [i′, j′, k′] is used to determine the α value. The approach direction cosines are dependent on feature orientation in the part coordinate system, which means that the approach vector transformed into the base coordinate system of the machine (i.e. into the [i, j, k] form) in step 2 of this procedure may be used. In the next step, the values are transformed again into a coordinate system used for determining probe errors in the previously selected reference grid nodes. Since the rotation and transformation matrices are recorded for those coordinate systems during implementation measurements, the transformation of cosine vectors into a node coordinate system can be performed easily (using a reverse transformation to this presented in (7)). The final step involves projection of direction cosines on the XY planes of the node coordinate systems, determining the α_P values for a given measuring point in the node coordinate systems using Eq. (11), as well as finding the closest α that could be used as reference (two values for each node are determined this way for a total of eight α values; they are denoted as α_P1 + 1, α_P1–1, α_P2 + 1, α_P2–1α_P3 + 1, α_P3–1, α_P4 + 1, α_P4–1, where α_P1 + 1 means value of α angle for the first angle greater then α included in the measurements of the standard ring (described in Sect. 2) for P1 node, and α_P1–1 means value of α angle for the first angle smaller then α included in these measurements).

$$ {\alpha}_P=\operatorname{arccos}\left(\frac{v_{xy}\cdot \hat{x}}{\left|{v}_{xy}\right|\cdot \hat{\left|x\right|}}\right)=\operatorname{arccos}\left(\frac{x_v}{\sqrt{\left({x_v}^2+{y_v}^2+{z_v}^2\right)}}\right) $$

(11)

where α_P is value of α angle determined for node P, v_xy = [x_v, y_v, z_v] − [i,j,k] vector transformed into the P node coordinate system and projected on xy plane of this coordinate system, $\hat{x}$ the unit vector in the direction of the x-axis of the P node coordinate system (it is used here because α has its zero value in this direction).

As a result of operations presented in this section, the probe head error (PE) is simulated for a chosen set of (A_a, B_a, α_P1, α_P2, α_P3, α_P4) as a scalar, using Eq. (12).

$$ {\displaystyle \begin{array}{c} PE\left({A}_a,{B}_a,{\alpha}_{P1},{\alpha}_{P2},{\alpha}_{P3},{\alpha}_{P4}\right)=\left(\left({A}_{a+1}-{A}_a\right)/\left({A}_{a+1}-{A}_{a-1}\right)\ast \left(\left({B}_{a+1}-{B}_a\right)/\left({B}_{a+1}-{B}_{a-1}\right)\ast P1+\left({B}_a-{B}_{a-1}\right)/\left({B}_{a+1}-{B}_{a-1}\right)\ast P3\right)\right)+\\ {}+\left(\left({A}_a-{A}_{a-1}\right)/\left({A}_{a+1}-{A}_{a-1}\right)\ast \left(\left({B}_{a+1}-{B}_a\right)/\left({B}_{a+1}-{B}_{a-1}\right)\ast P2+\left({B}_a-{B}_{a-1}\right)/\left({B}_{a+1}-{B}_{a-1}\right)/\ast P4\right)\right)\end{array}} $$

(12)

where

P1:

(((α_P1 + 1-α_P1)/(α_P1 + 1-α_P1–1)) * PE(A_a-1,B_a-1,α_P1–1)) + (((α_P1-α_P1–1)/(α_P1 + 1-α_P1–1)) * PE(A_a-1,B_a-1,α_P1 + 1))

P2:

(((α_P2 + 1-α_P2)/(α_P2 + 1-α_P2–1)) * PE(A_a + 1,B_a-1,α_P2–1)) + (((α_P2-α_P2–1)/(α_P2 + 1-α_P2–1)) * PE(A_a + 1,B_a-1,α_P2 + 1))

P3:

(((α_P3 + 1-α_P3)/(α_P3 + 1-α_P3–1)) * PE(A_a-1,B_a + 1,α_P3–1)) + (((α_P3-α_P3–1)/(α_P3 + 1-α_P3–1)) * PE(A_a-1,B_a + 1,α_P3 + 1))

P4:

(((α_P4 + 1-α_P4)/(α_P4 + 1-α_P4–1)) * PE(A_a + 1,B_a + 1,α_P4–1)) + (((α_P4-α_P4–1)/(α_P4 + 1-α_P4–1)) * PE(A_a + 1,B_a + 1,α_P4 + 1))

Similarly as in case of residual kinematic errors, the probe errors (PEs) are simulated via the Monte Carlo method that utilizes the scaled and shifted t-distributions with parameters ($\overline{x}$,s,ν), where $\overline{x}$ denotes the mean radial PE determined for the considered A, B and α, s is the standard deviation associated with $\overline{x}$, and ν is the number of degrees of freedom (14 in the case of the presented module, since PE values were determined using 15 measurements of a standard ring). The exact parameters of these distributions are determined through the experiment discussed in Sect. 2.

• 6. Calculating the effect of PE on simulated point coordinates as (13):

$$ {\displaystyle \begin{array}{c}{PE}_x= PE\ast i\\ {}{PE}_y= PE\ast j\\ {}{PE}_z= PE\ast k\end{array}} $$

(13)

• 7. Calculating coordinates of simulated point in the form of (14):

$$ {\displaystyle \begin{array}{c}{x}_{sim}=x+{x}_{res}+{PE}_x\\ {}{y}_{sim}=y+{y}_{res}+{PE}_y\\ {}{z}_{sim}=z+{z}_{res}+{PE}_z\end{array}} $$

(14)

• 8. Steps 3–7 should be repeated for all points included in the simulated measurement to generate N sets of x_sim, y_sim, z_sim values.

• 9. The coordinates of all simulated points (N sets of coordinates for each point) are then sent to metrological software to construct N features whose characteristics (such as diameter, form deviation, etc.) are further examined. The uncertainty of geometrical relations (e.g. plane–plane distance, parallelism deviation, coaxiality deviation, etc.) is evaluated by constructing all features comprising a given geometrical relation N-times.

• 10. Specific geometrical characteristics or relations are evaluated for all N features (or sets of features), producing N values of those characteristics (relations) denoted as y_i, where i changes in the range from 1 to N.

• 11. Standard uncertainty for the individual characteristics (relations) is determined using Eq. (15):

$$ u(y)=\frac{1}{N-1}{\sum}_{i=1}^N\Big({y}_i-{\overline{y\Big)}}^2 $$

(15)

where $\overline{y}=\frac{1}{N}\sum \limits_{i=1}^N{y}_i$ .

4 Verification measurements and results

Verification measurements were carried out on a Multi-Feature Check (MFC) standard. It is a complex measuring standard (Fig. 5) commonly used for assessing measurement accuracy and uncertainty for nearly all features and dimensions applicable to the coordinate measuring technique. The standard has a nominal length of 200 mm and external diameter of 100 mm. Further information regarding the MFC standard can be found in [https://www.eumetron.de].

Fig. 5

Diagram of Multi-Feature Check standard used for validation measurements [https://www.eumetron.de]

The MFC was measured in two different positions. In the first position, the main axis of the standard was oriented along the x axis of the machine, in order to verify proper functioning of the developed virtual model at different orientations of a measured workpiece. The MFC standard was also measured in a second position (Fig. 6), in which the main axis of the standard is inclined at a certain angle towards the x and y axes of the machine. Table 2 and Fig. 7 present results obtained for measurements of MFC in its second position.

Fig. 6

Measurement of MFC standard and calibrated workpieces (in second position) during verification of virtual model

Fig. 7

Results of cylindricity measurement with corresponding uncertainty estimated using the examined methods

The following features were measured on the MFC standard: distance between front planes, cylindricity and diameter of internal cylinder, plane flatness, parallelism deviation between front planes and angle between two planes (front and side plane). Calibration results for geometrical characteristics and relations of the MFC measured during presented experiments are listed in Table 1. The MFC standard was calibrated on a PMM 12106 Leitz Messtechnik measuring machine with CMC (calibration and measurement capability) for calibration of geometrical standards equal to 0.0006 + 0.0007·L mm (where L is measured length given in m).

Table 1 Results of MFC standard calibration

The detailed procedure for measurement of the MFC consisted of manual measurement of external cylinder using 16 points divided into two sections, each containing eight points regularly distributed over the circumference of the cylinder section; measurement of side and front plane using eight regularly distributed points; construction of manual alignment, where the axis of cylinder forms the main axis of the part coordinate system; the side plane is used to indicate the direction of the second axis and the origin of the coordinate system lies at the intersection point of the front plane and the external cylinder axis. The next step involved repetition of the discussed measurements in an automatic mode, followed by the construction of a part coordinate system using features measured in this way, as well as automatic measurements of the second front plane (also using eight points) and the chosen internal cylinder using similar points distribution as for the external cylinder.

A ring standard and gauge block that satisfies the similarity conditions postulated in [11] were used as reference objects during uncertainty estimation, in accordance with the guidelines of the calibrated workpiece method. A total of 20 measuring cycles were performed, each consisting of measurements carried out on both the MFC standard and calibrated workpieces. The whole measuring procedure lasted approximately 200 min. For the measurements of calibrated workpieces, the same number of points was used for each feature as in the case of the MFC, and their distribution over the surface of the standard was similar for both measurements. The results given for the developed virtual model come from a single measurement (performed separately from the measurements according to the calibrated workpieces method) with its corresponding uncertainty determined as a result of simulations presented in Sect. 3. A single measuring cycle lasted about 7 min, whereas the simulation lasted less than 1 min. This clearly suggests that the use of a virtual CMM reduces the time necessary for determination of measurement uncertainty by about 25 times.

Additionally, the measurement routine was repeated for a CMM working in three-axis mode. The same numbers and distributions of points were used for measurements of all features. However, one major difference between five-axis and three-axis modes is that during five-axis measurements, point coordinates are obtained using a combination of three translational movements of a CMM and two rotational movements of probe head axes, while in the case of three-axis mode, point coordinates are measured using only three translational movements of CMM axes and the angular position of the probe head does not change during point measurements (angular position of the probe head may still change between measurements of consecutive features, like it is done during measurements performed with commonly used motorized indexing probe heads).

The results in Table 2 show that for all the presented measuring tasks (performed both in three- and five-axis mode), the intervals containing the true value of a measured quantity share a common part with the validation acceptance interval, which indicates that the validation process discussed in Sect. 2 concludes with a positive result. On this basis, the developed virtual model may be regarded as working properly and providing accurate uncertainty values for measurements performed on five-axis measuring systems. The primary aim of this paper was to present a fully functional virtual model of a five-axis measuring system that uses an articulated probe head with continuous indexation capability and prove its correct functioning. The results gathered in Table 2 clearly indicate that this aim was fulfilled. What is more, in light of the presented results, it should also be noted that the virtual model of a five-axis measuring system works properly regardless of the mode in which the measuring points are gathered. Due to this, it may be used for uncertainty estimation for measurements performed using both the mentioned modes (three- and five-axis mode) over the course of a single measurement routine. This situation happens quite frequently, seeing as complex shapes of the currently manufactured parts make it so that it is rarely possible to measure all the necessary features solely in five-axis mode.

Table 2 Verification results for the developed virtual model (for MFC standard located as in Fig. 4). Results for angle measurement given in °, other features/relations expressed in mm

Proper functioning of the developed virtual model may also be demonstrated by direct comparison of the intervals containing the true value of a measured quantity produced by the model and the results of MFC calibration (Table 1). In the case of all performed measurements, these two intervals (as the second interval, the interval < calibration result − standard uncertainty of calibration, calibration result + standard uncertainty of calibration > should be taken) share a common portion. Basing on that, when calibration results are regarded as a reference value, it is possible to conclude that this value is correctly determined by the presented model.

It is also worth mentioning that a detailed analysis of the obtained results proves the authors’ observation from previous research with respect to lesser uncertainty values during five-axis measurements than in the case of measurements of the same geometrical features or relations performed in three-axis mode (Fig. 7). The difference is clearly noticeable, especially for measurements of circular or cylindrical features. Over the course of measurements presented in this paper, the standard uncertainty of cylindricity measurement determined using the calibrated workpieces method was over two times greater for measurements in three-axis mode. Moreover, due to improved point probing kinematics, measurements performed in five-axis mode are characterized by significantly higher repeatability than those performed in three-axis mode, which also partially explains the lesser measurement uncertainty in case of the former.

5 Conclusion

The developed virtual model is the first fully functional model of five-axis measuring systems that use probe heads with continuous indexation capability. Five-axis machining systems and CMMs attract increasing attention, mainly due to the promise of significant reduction in manufacturing and quality control time. Furthermore, the increasing appeal of five-axis measuring systems can also be attributed to the rising awareness about the importance of uncertainty estimation for measurements performed during assessment of products compliance with geometrical specifications. This suggests that the developed model may find a vast number of potential users, and due to its simplicity, ease of use without the need for advanced metrological knowledge and short implementation time (the entire implementation of system including verification measurements may be done in less than 8 h), it has a high chance of becoming a popular method of uncertainty estimation, especially in cases where the results of performed measurements remain close to tolerance limits.

As shown in the previous section, the virtual model implemented using the methodology presented in Sect. 2, and operated on the basis of data flow specified in Sect. 3, successfully passed verification measurements and should be regarded as working properly and producing correct values of measurement uncertainty for common metrological tasks from the GD&T framework. Correct function of the model was additionally confirmed in a secondary way, through comparison of results and uncertainties produced by the model with the results of an MFC standard calibration, given with corresponding uncertainty values.

The verification method adopted for the performance of measurements presented in Sect. 4 may be used in an analogous way for verification of other virtual models developed in the future (or already existing virtual models that have not yet been experimentally validated). Understandably, it is essential that in addition to a purely theoretical verification (usually based on a comparison of the results produced by the examined model with the mathematical/simulation model of a given process/phenomenon), all virtual models, created across different scientific disciplines, should also undergo practical verification, which may be based on the procedure presented in this paper.

Experiments presented in this paper were performed using a CMM equipped with an articulated probe head with continuous indexation capability. In the authors’ opinion, it should be possible to transfer the presented model into five-axis machine tools with inspection probes mounted on a tilt and swivel head following minor adjustments to the implementation procedure. This stems from the fact that the kinematic structure of these two systems is identical and that touch-trigger inspection probes used in machine tools are based on the same working principle as the TP20 probe used with the five-axis measuring system presented in this paper. The usage of the presented model with a five-axis machine tool is one of the possible directions of further research within this field.

The presented model of kinematic residual errors may also be used for modelling machine tool kinematics during machining processes, as an alternative for models presented in [24, 25]. However, in such instances, residual errors may be strongly influenced by forces related to the machining operations. Additional research into the impact of such operations is currently underway at the Laboratory of Coordinate Metrology of the Krakow University of Technology.