1 Introduction

Heat transmission is the phenomenon used to explain heat transfer from higher temperatures toward lower concentrations (Gireesha and Sowmya 2020). In recent years, the process of heat transfer has emerged as the most important subject in the field of thermal engineering due to the prediction of heat exchanger in variety of circumstances including solar collector, gas turbines, radiators in cars, and energy production (Alkam and Al-Nimr 1999; Deshamukhya et al. 2018; Sowmya et al. 2019; Khan et al. 2021d). The heat exchangers or extended surfaces are an integral part of any device that generates heat during its working process. They are used to increase the heat transfer rate from surfaces cooled by gases under natural or forced convection. Usually, heat transfer occurs through the mechanisms of conduction, convection, and radiation, or a combination of these methods (Ma et al. 2017; Sun and Li 2020). Many studies on extended surfaces have been conducted, and some examples are provided in the references (Ye 2017; Ben-Nakhi and Chamkha 2006; Khan et al. 2021c; Chamkha et al. 2010). To improve the rate of heat transfer, the fins are designed using a porous medium such as sintered powder or perforated plates and metal sponge so that it can be easily used in critical systems. The porous heat exchangers are commonly used in powerful lasers, spacecraft thermal management systems, phased-array radar systems, industrial furnaces, and catalytic-chemical particle beds.

During the course of the last decade, the analysis of fins with the purpose of enhancing heat transmission has attracted the interest of a great number of researchers. When the cross-sectional area of a fin is not very large, there is not a significant difference in temperature throughout the cross-section. Then the only direction in which it undergoes a significant change in temperature is the one that corresponds to the length of the fin. To put it another way, the temperature field over the length of the fin is a one-dimensional field, despite the fact that it fluctuates in temperature as it travels down the length of the fin. A number of researchers have made various contributions toward the development and the enhancement in heat transmission of a one-dimensional porous structure with thermal conductance. An earlier study was conducted by Hung and Appl (1967) to investigate how heat is transferred within straight fins with internal heat generation. Razelos and Kakatsios (2000) studied the radiation effects of rectangular fins, which is quite significant in the design of reliable equipment, gas turbines, and nuclear plants. Further, the concept of heat transmission through porous fins was presented by Kiwan and Al-Nimr (2001), which was later improved by using Darcy’s model to formulate the mathematical models of heat transfer in porous mediums (Kiwan 2007; Kiwan and Zeitoun 2008). Heat transfer through a porous fin in a nanofluid subjected to convective and radiative environments was examined by Baslem et al. (2020). They examined the effect that heat transport via convection and radiation had on the fin. They concluded that the heat transmission from the fin is greatly improved with the use of the Cu-water nanofluid compared to \({\text{Al}}_2{\text{O}}_3\)-water and \({\text{TiO}}_2\)-water nanofluids. Taklifi et al. (2010) studied the influence of magnetohydrodynamics (MHD) on heat transfer in rectangular fin. Their analysis indicates that the heat transfer rate decreases by employing the effect of MHD near the tip of the fin. Selimefendigil and Öztop (2012) predicted heat transport through a square cavity in the presence of an adiabatic thin fin using a fuzzy-based model.

In airborne and space applications, trapezoidal, triangular, and concave parabolic features, which result in a lighter design, are preferred than rectangular fins of equivalent size. This is because these characteristics result in a more efficient distribution of the heat over the fin. On the other hand, fin structures with a thinner profile are more difficult and costly to manufacture (Buonomo et al. 2021; Kiwan et al. 2020). In last few decades, several researchers have worked in this area by considering different fin profiles to improve the heat distribution performance of the fins. Aziz and Makinde (2010) examined the entropy generation and thermal performance of two-dimensional orthotropic pin fins used in advanced light weight heat sinks. The Darcy model and the LTE assumption were utilised for the research that was conducted by Ndlovu and Moitsheki (2018) on a porous pin fin that was subjected to natural convection heat transfer. The research conducted by Turkyilmazoglu (2018) focused on heat transmission from moving exponential fins that have internal heat production. The exact formulae for the thermal aspects, such as the distribution of temperature, as well as the efficiency, were developed and studied. Fox et al. (1969) was among the first to do an analytical study on the heat transmission of moving fins in a non-Newtonian fluid. The rigorous impact of the Cattaneo-Christov heat flow model on thermal conductivity, internal resistance and magnetic stagnation of non-Newtonian fluids,has been studied by Zhao et al. (2021).

Most of the physical phenomena that emerge in the real world, especially the occurrence of heat and mass transfer under diverse effects, are well recognized and modeled as nonlinear differential equations (Das and Kundu 2020). In this regard, various numerical and analytical techniques are developed to study the temperature distribution. The homotopy perturbation method was adopted by Domairry and Fazeli (2009); Cuce and Cuce (2015); Hoshyar et al. (2015) to detect the fin efficiency of variable thermal conductive longitudinal fin. In order to get the solutions to the heat equation describing a rectangular contoured circumferential fin, Sarwe and Kulkarni (2021) used the idea of the differential transformation approach. The effect of environmental temperatures such as convective sink temperature, radiative sink temperature, as well as the impact of the heat production number on the distribution and temperature profile of a convective-radiative stationary fin was studied by Pranab KantiRoy using Adomain decomposition method (ADM). Tejani et al. (2017, 2019a) proposed an approach called the modified heat transfer search (MHTS). This method combines sub-population-based simultaneous heat transfer modes such conduction, convection, and radiation. This was done in order to investigate the dynamic behaviour of the structures and remove vibrations that had not been meant to be there. Patel and Meher (2015) have revisted the traditional Adomian decomposition method and modified the technique by including the adjustment parameters for controlling the convergence of solutions to highly nonlinear porous structures with different profiles of conductance. Similarly, the M. Matinfar, solved the nonlinear unsteady mathematical model of the convective-radiative equation and a nonlinear convective-radiative-conductive equation by adjusting the small parameters \(\epsilon _1\) and \(\epsilon _2\) with modified variational iteration method and He’s polynomials. The homotopy analysis method was applied by Moitsheki et al. (2015); Dinarvand and Hosseini (2013) for predicting the changes in thermal behaviour of the porous fin with thermal conductance. The impact of thermal conductivity with magnetic field on straight rectangular fin with insulated tip and nanofluid was studied by using the Akbari-Ganji’s method (AGM) (Hosseinzadeh et al. 2022). Sobamowo et al. (2019) implemented the finite difference method (FDM) to examine the impact of compositions of fin materials on heat flow rate, temperature distribution, and effectiveness of fin truncated with cone shape. These numerical and analytical methods have been effectively applied to study the solutions of linear and nonlinear stiff problems. But besides their advantages, these techniques have several limitations. The finite difference (FD) methods are intuitive and easy to implement for simple problems. However, FDM may easily run into a problem while handling curved/ moving boundaries, complicated domains, unstructured grid and multiple disjoint manifolds within a problem. On the other hand, the requirement of a small parameter is the most significant drawback that is associated with the perturbation methods. Sometimes the small parameter may also be artificially introduced into the equations. The solutions, therefore, have a limited range of validity (Şenol et al. 2013). Also, numerical solvers such as the Runge–Kutta methods are a family of iterative methods used by several researchers to approximate the solutions to a variety of differential equations. Such methods use discretization to calculate the solutions in small steps. Runge-Kutta methods have several drawbacks, the most notable of which are that they demand a substantial amount of additional computer time compared to multi-step approaches of equivalent accuracy and that they do not readily produce reliable global estimates of the truncation error.

In addition, since the 1950s, there has been substantial development of gradient-based techniques, and today there are multiple excellent options available for dealing with smooth nonlinear issues. These approaches only converge to a local minimum point for the objective function since the search process that they employ uses only local information (functions and their gradients at a place) (Dalla et al. 2021). The gradient-based methods estimate the motion by analysis of the strong differences in brightness between analyzed regions. The disadvantage of such approaches is the dependence on noise, occlusions, and discontinuity of the function (Starostenko et al. 2005).When traversing a parameter space using gradient-based approaches, there is a significant risk that the algorithm will become mired in a local minimum or maximum (s). This is due to the fact that the gradient is always zero at any local minima or maxima. To overcome these drawbacks, direct search and gradient free techniques are designed that are currently used for solving complex multidisciplinary design optimization problems (Talgorn et al. 2017; Alarie et al. 2021; Audet and Hare 2017). The algorithmic global convergence property of mesh adaptive direct search, supported by mathematical proof, makes it outperform heuristics in blackbox optimization as there is no guarantee/proof that heuristics will not converge to a non-minimizer (Audet 2014; Audet et al. 2022a). Mesh adaptive direct search is recommended to be used in blackbox optimization specially in the case of unreliable approximation of gradients (Audet et al. 2022b). So, in recent times researchers have focused their attention on developing artificial neural networks based evolutionary gradient-free techniques that do not require prior information about the problem. It is becoming more standard practise to use evolutionary computing as a method for resolving challenging real-world problems in fields such as industry, health, and the defence sector (Erdal et al. 2011; Tejani et al. 2018; Saka et al. 2016). The special advantages include the processes’ flexibility and their capacity to self-adapt on the fly in order to search for optimal solutions (Aydoğdu et al. 2016; Tejani et al. 2019b; Aydoğdu and Saka 2012; Yousif and Saka 2021).

In this study, we have developed and implanted an intelligent technique based on metaheuristic approach (Tejani et al. 2021; Kumar et al. 2021b) of global and local search mechanism to study the temperature distribution in conductive-convective-radiative moving rod. Nowadays, metaheuristic optimization algorithms have turned out to be quite attractive because of their distinct advantages over traditional algorithms. They can be easily hybridized and broadly implemented to any complex problem that can be formulated as optimization problem. For the purpose of solving optimization issues, the metaheuristic algorithms have been selected because of their ease of use, simplicity, ability to avoid reaching a local optimal solution, and adaptability to a diverse set of challenges originating from a variety of academic fields. In recent years, nature-inspired, human-inspired and biological-inspired meta-heuristic optimizers have gained the attention of researchers. Some recently developed meta-heuristic techniques include artificial hummingbird algorithm (AHA) (Zhao et al. 2022), sooty tern optimization algorithm (STOA) (Dhiman and Kaur 2019; He et al. 2022), multi-objective plasma generation optimizer (MOPGO) (Kumar et al. 2021a), dynastic optimization algorithm (DOA) (Wagan et al. 2020), Tiki-Taka algorithm (TTA) (Rashid 2020), color harmony algorithm (CHA) (Zaeimi and Ghoddosian 2020), arithmetic optimization algorithm (AOA) (Abualigah et al. 2021). Also, the hybridized stochastic methodologies have been used by researchers to study the variety of problems arising in various domain of optimization (Kumar et al. 2021c), thermal engineering (Khan et al. 2022b; Zhu et al. 2021; Khan et al. 2022a), civil engineering (Huang et al. 2021; Nguyen et al. 2021; Singh et al. 2022; Cui et al. 2021), computational chemistry (Khan et al. 2021e, 2021a), and fluid dynamics (Khan et al. 2021b; Tahani et al. 2016). These applications have motivated authors to extend and incorporated the computational strength of neural networks with hybridization of meta-heuristic techniques. The salient features of the proposed methodology are summarized as:

  • This study analyzes the mathematical model of the moving hot rod subjected to convective and radiative environments with variable thermal conductivity and constant velocity. Further, an integrated soft computing technique based on the function approximating ability of artificial neural networks and the stochastic exploitation and exploration search strategies of arithmetic optimization algorithm and sequential quadratic optimization algorithms are utilized to construct the series solutions for different cases of the moving rod.

  • The proposed FANN-AOA-SQP algorithm is implemented in an unsupervised manner to study the effect of variations in significant parameters such as ambient temperature, radiation-conduction number, Peclet number, nonconstant thermal conductivity, and initial temperature parameter on the temperature gradient of the rod.

  • The results are validated by comparing the statistics with the numerical solutions by Runge-Kutta-Fehlberg method and other machine learning techniques. The accuracy of the solutions in further dictates by the values of absolute errors and performance measures. In addition, the proposed FANN-AOA-SQP algorithm is simple to put into practice because it only requires the basic settings for the parameters and sufficient termination condition before execution.

2 Mathematical formulation

This study explores the heat transfer between the moving, convective and radiative hot rod with the surrounding. The rod of length L has a constant cross sectional area A, as illustrated in Fig. 1 is considered that emerges from a furnace or an intermediary heating station at a constant velocity of V. The initial temperature of the rod is \(T_{\text{i}}\) and is instantly exposed to ambient temperature denoted by \(T_{\mathrm {ambient}}\). It is assumed that \(T_{\text{i}}\) is greater than \(T_{\mathrm {ambient}}\) and that the rod’s movement in the environment results in the formation of airflow at the rod’s surface. In this scenario, both convection and radiation heat transfer is occurring simultaneously. Radiative heat transmission greatly influences the cooling process when there is no forced heat transfer, i.e., only the natural convective heat transfer occurs.

Fig. 1
figure 1

Schematic view of the hot moving rod

Full size image

In addition to that, it is presumed that the rod is grey in colour, and the coefficient of emissivity is thought to remain unchanged. The swaying motion and rising temperature of the hot rod, as previously stated, provide a steady and consistent convective flow around the rod. As a result, the heat transfer coefficient, denoted by h, may be thought of as being constant over the rod’s surface up to the end of the cooling process (Kundu and Yook 2021). The influence of temperature on thermal conductivity varies depending on whether the material is a metal or a nonmetal. Thermal conductivity in metals is mainly owing to the presence of free electrons. When the temperature of a pure metal is raised, the electrical conductivity of the metal drops. As a direct consequence of this, the thermal conductivity is very stable. When it comes to alloys, the amount by which electrical conductivity shifts is typically just a marginal one; hence, the increase in thermal conductivity is typically proportionate to the increase in temperature (Sheikholeslami and Ganji 2018). Mathematically, the relation between the temperature and conduction of heat transfer coefficient is defined as Fallah Najafabadi et al. (2021)

$$\begin{aligned} k=k_{0}\left( 1-\left( T_{\mathrm {ambient}-T}\right) \omega \right) , \end{aligned}$$
(1)

here \(k_0\) is the coefficient of heat transmission by conduction at the surrounding temperature, \(\omega\) is variation coefficient of thermal conductivity, which may be positive or negative, and zero in the case when conduction heat transfer coefficient is constant. The heat transfer process of the rod begins when it is deposited into the environment. The initial unstable and fluctuating condition of heat transport is eliminated immediately, leaving behind a significant majority of the absorbed energy within the rod, with just a minimal amount of energy exiting the rod’s surface via convection and radiation. In this work, the temperature distribution of the rod is investigated under steady-state conditions. Furthermore, the radiation is only being emitted from the surface of the moving rod and into the surrounding environment, and since the rod is not receiving any substantial radiation from the surrounding environment, fluctuating radiation sink temperature may be ignored. The only direction in which heat is transferred is the x-direction, the airflow in the environment around the rod is laminar and consistent, and the rod does not experience any volumetric or longitudinal expansion while this process is taking place. The energy equation of the rod with convective and radiative heat transfer moving with constant speed is given as

$$\begin{aligned}&\frac{{\text{d}}}{{\text{d}} x}\left( \left[ 1+\omega \left( T-T_{\mathrm {ambient}}\right) \right] \frac{{\text{d}} T}{{\text{d}} x}\right) \nonumber \\&\quad -\frac{h p}{k_{0} A}\left( T-T_{\mathrm {ambient}}\right) -\frac{\varepsilon \sigma p}{k_{0} A}\left( T^{4}-T_{\mathrm {ambient}}^{4}\right) -\frac{1}{\alpha } V \frac{{\text{d}} T}{{\text{d}} x}=0, \end{aligned}$$
(2)

here T is the temperature of the rod, \(\sigma\) is density, \(\alpha =k_{0} / \rho c\) is thermal diffusivity, \(\epsilon\) is Stefan-Boltzmann constant and c is the specific heat capacity. Following dimensionless parameters are define to solve 2.

$$\begin{aligned} \lambda =\frac{T_{\text{ ambient } }}{T_{l}}, \Theta =\frac{T}{T_{i}}, \eta =\frac{x L^{*}}{A}, L^{*}=\frac{p L}{A}, \end{aligned}$$
(3)

here L denotes the length of the rod and p represents the circumference. Using dimensionless variables in Eq. (2) will result in following differential equation as Fallah Najafabadi et al. (2021)

$$\begin{aligned}&\frac{{\text{d}}}{{\text{d}} \eta }\left( [1+\gamma (\Theta -\lambda )] \frac{{\text{d}} \Theta }{{\text{d}} \eta }\right) -N_{\text{c}}(\Theta -\lambda )\nonumber \\&\quad -N_{\text{r}}\left( \Theta ^{4}-\lambda ^{4}\right) -P e \frac{{\text{d}} \Theta }{{\text{d}} \eta }=0, \end{aligned}$$
(4)

subjected to the boundary conditions which are defined as

$$\begin{aligned} \begin{aligned} \text {at} \quad \eta =0, \quad \Theta =1, \\ \text {at} \quad \eta =L^{*}, \quad \frac{{\text{d}} \Theta }{{\text{d}} \eta }=0, \end{aligned} \end{aligned}$$
(5)

where Pe is Peclet number that shows the dimensionless velocity profile of the moving rod, \(N_{\text{r}}, N_{\text{c}}\) is radiative-conductive parameter, and \(\gamma\) is thermal conductivity. These parameters are defined as

$$\begin{aligned} N_{\text{c}}=\frac{h A}{p k_{0}}, \gamma =\omega T_{l}, P e=\frac{V A}{\alpha p}, N_{\text{r}}=\frac{\varepsilon \sigma T_{l}^{3}}{p k_{0}}. \end{aligned}$$
(6)

3 Design methodology

In this section, the detailed procedure of the proposed soft computing algorithm i.e. FANN-AOA-SQP is presented that is based on the two phases. Initially, an unsupervised fitness function is constructed with FANN modeling in sense of mean square error. Further, the optimization procedures based on the global search ability of arithmetic optimization algorithm and local search mechanism of sequential quadratic programming are hybridized to optimize the neurons in FANN structure for the series solution of the nonlinear temperature distribution model of moving hot rod.

3.1 FANN modeling

Fig. 2
figure 2

Construction of FANN architecture for mathematical model of convective, radiative and moving rod

Full size image

The mathematical modeling of the feedforward artificial neural networks for solving the governing model in Eqs. (4), (5) is presented in this section. The approximate solution of the problem \({\hat{\Theta }}(\eta )\) in the form of continuous mapping of FANN with log-sigmoid (\(J(\eta )=(1+\exp (-\eta ))^{-1}\)) is given as

$$\begin{aligned} {\hat{\Theta }}(\eta )=\sum _{i=1}^{k} {\tilde{a}}_{i} J\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) =\sum _{i=1}^{k} \frac{{\tilde{a}}_{i}}{\left( 1+e^{-\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) }\right) }, \end{aligned}$$
(7)

first and second order continuous derivatives of Eq. (7) are defined as

$$\begin{aligned} \frac{d {\hat{\Theta }}}{d \eta }= & {} \sum _{i=1}^{k} {\tilde{a}}_{i} \frac{d}{d \eta } J\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) \nonumber \\= & {} \sum _{i=1}^{k} \frac{{\tilde{a}}_{i} {\tilde{w}}_{i} e^{-\left( {\tilde{w}}_{i}\eta +{\tilde{b}}_{i}\right) }}{\left( 1+e^{-\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) }\right) ^{2}}, \end{aligned}$$
(8)
$$\begin{aligned} \frac{{\text{d}}^{2} {\hat{\Theta }}}{{\text{d}} \eta ^{2}}= & {} \sum _{i=1}^{k} {\tilde{a}}_{i} \frac{{\text{d}}^{2}}{{\text{d}} \eta ^{2}} J\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) \nonumber \\= & {} \sum _{i=1}^{k} {\tilde{a}}_{i} {\tilde{w}}_{i}^{2}\left( \frac{2 e^{-2\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) }}{\left( 1+e^{-\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) }\right) ^{3}}-\frac{e^{-\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) }}{\left( 1+e^{-\left( {\tilde{w}}_{i} \eta +{\tilde{b}}_{i}\right) }\right) ^{2}}\right) , \end{aligned}$$
(9)

where \({\tilde{a}}=\left[ {\tilde{a}}_{1}, {\tilde{a}}_2, {\tilde{a}}_3, \ldots , {\tilde{a}}_{k}\right] , {\tilde{b}}=\left[ {\tilde{b}}_{1}, {\tilde{b}}_{2}, {\tilde{b}}_{3}, \ldots , {\tilde{b}}_{k}\right]\) and \({\tilde{c}}=\left[ {\tilde{c}}_{1}, {\tilde{c}}_{2}, {\tilde{c}}_{3}, \ldots , {\tilde{c}}_{k}\right]\) are the unknown neurons in FANN structure that are to be found during the optimization procedure of the unsupervised fitness function which is defined as

$$\begin{aligned} E_{F i t}=E_{F i t-1}+E_{F i t-2}, \end{aligned}$$
(10)

where \(E_{F i t-1}\) and \(E_{F i t-2}\) are associated to the ANN models of differential equation and the boundary conditions which are given as

$$\begin{aligned} E_{F i t-1}= & {} \frac{1}{N} \sum _{m=1}^{N}\left( \frac{{\text{d}}}{{\text{d}} \eta _m}\left( [1+\gamma (\Theta _m-\lambda )] \frac{{\text{d}} \Theta _m}{{\text{d}} \eta _m}\right) \right. \nonumber \\&-\left. N_{\text{c}}(\Theta _m-\lambda )-N_{\text{r}}\left( \Theta _m^{4}-\lambda ^{4}\right) -P e \frac{{\text{d}} \Theta _m}{{\text{d}} \eta _m}\right) , \end{aligned}$$
(11)
$$\begin{aligned} E_{F i t-2}= & {} \frac{1}{2}\left( {\hat{\Theta }}(1)-1\right) ^{2}+\frac{1}{2}\left( \frac{{\text{d}} {\hat{\Theta }}}{{\text{d}} \eta }(L^*)-0\right) ^{2}. \end{aligned}$$
(12)

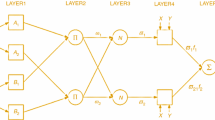
where \(N h=1, \Theta _{m}=\Theta \left( \eta _{m}\right)\), and \(\eta _{m}=m h\). The FANN structure for the governing model of moving rod interms of input, hidden and output layers is shown through Fig. 2.

3.2 Optimization procedure

Fig. 3
figure 3

Model for repositioning math operators in AOA in the direction of the optimum solution (Abualigah et al. 2021)

Full size image

This section, explains the optimization process of the FANN weights in fitness function by operating the integrated strength of meta-heuristic computing process based on AOA supported with local search strategy of SQP.

Arithmetic optimization algorithm (AOA) is meta-heuristic technique which is inspired by the application of basic mathematical operators such as addition (A), subtraction (S), multiplication (M), and division (D) in searching the optimal solution for mathematical optimization problems (Abualigah et al. 2021). Since, AOA is population-based gradient-free algorithm so initially, it generates the set of random solutions as given in Eq. (13)

$$\begin{aligned} X=\left[ \begin{array}{cccccc} x_{1,1} &{} \cdots &{} \cdots &{} x_{1, j} &{} x_{1, n-1} &{} x_{1, n} \\ x_{2,1} &{} \cdots &{} \cdots &{} x_{2, j} &{} \cdots &{} x_{2, n} \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ x_{N-1,1} &{} \cdots &{} \cdots &{} x_{N-1, j} &{} \cdots &{} x_{N-1, n} \\ x_{N, 1} &{} \cdots &{} \cdots &{} x_{N, j} &{} x_{N, n-1} &{} x_{N, n} \end{array}\right] \end{aligned}$$
(13)

Following the initialization process, the search phases of exploration and exploitation are selected based on a function known as the Math Optimizer Accelerated (MOA) which is defined as

$$\begin{aligned}&{\text {MOA}}\left( t_{\text{c}}\right) \nonumber \\&\quad ={\text {Min}}+t_{\text{c}} \times \left( \frac{{\text {Max}}-{\text {Min}}}{t_{M}}\right) , \end{aligned}$$
(14)

here \(t_{\text{c}}\) and \(T_M\) are current and maximum iteration. Max and min represents the MAXIMUM accelerated values of MOA. The exploration phase is conditioned by MOA when \(r1 > MOA\), where r1 is a random number. The mathematical model for the search strategy of multiplication and division in exploration phase in modeled as

$$x_{{i,j}} \left( {t_{{\text{c}}} + 1} \right){\text{ }}\quad = \left\{ {\begin{array}{*{20}c} {{\text{ best }}\left( {x_{j} } \right) \times {\text{MOP}} \times \left( {\left( {{\text{UB}}_{j} - {\text{LB}}_{j} } \right) \times \mu + {\text{LB}}_{j} } \right),{\text{ for }}r_{2} } & {gt;0.5} \\ {{\text{ best }}\left( {x_{j} } \right) \div ({\text{MOP}} + \varepsilon ) \times \left( {\left( {{\text{UB}}_{j} - {\text{LB}}_{j} } \right) \times \mu + {\text{LB}}_{j} } \right),{\text{ for }}r_{2} } & {lt;0.5} \\ \end{array} } \right.{\text{ }}$$
(15)

where \(\varepsilon\) is constant (small integer), \(x_{i, j}\left( t_{\text{c}}+1\right)\), represents the solution and at ith iteration, \(\text{ best } \left( x_{j}\right)\) shows the best so far solution, \(\text{L B}_{j}, \text{U B}_{j}\) are lower and upper bounds of jth position, and \(\mu\) is the controlling parameter to adjust the search process of this phase. To control the range of the candidate solution in AOA, another function known as Math Optimizer Probability (MOP) is defined given in Eq. (16).

$$\begin{aligned} {\text {MOP}}\left( t_{\text{c}}\right) =1-\frac{\left( t_{\text{c}}\right) ^{1 / \alpha }}{\left( t_{M}\right) ^{1 / \alpha }}, \end{aligned}$$
(16)

here \(\alpha\) is sensitive parameter that reflects the search through the iteration. In second phase, the arithmetic operators such as addition and subtraction are incorporated to update the position of the candidate solution and achieve the optimum solution. The searching methodology of different operators towards the optimal solution is shown through Fig. 3. Mathematically, the exploitation phase is modeled as

$$\begin{aligned}&x_{i, j}\left( t_{\text{c}}+1\right) \nonumber \\&\quad = {\left\{ \begin{array}{ll}{\text {best}}\left( x_{j}\right) -\mathrm {MOP} \times \left[ \left( \mathrm {UB}_{j}-\mathrm {LB}_{j}\right) \times \mu +\mathrm {LB}_{j}\right] , &{} r_{3}<0.5 \\ {\text {best}}\left( x_{j}\right) +\mathrm {MOP} \times \left[ \left( \mathrm {UB}_{j}-\mathrm {LB}_{j}\right) \times \mu +\mathrm {LB}_{j}\right] , &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$
(17)

the decision on whether to execute A or S is made based on the value of r3. When r3 is more than 0.5, the addition operator is performed and the subtraction operator is ignored until the A completes the task, however when r3 is less than 0.5 then viceversa occurs. The detailed flow chart of the working mechanism of AOA is shown in Fig. 4.

Fig. 4
figure 4

Working mechanism of the proposed technique

Full size image

3.2.1 The proposed FANN-AOA-SQP algorithm

Metaheuristic algorithms (MA) are a class of high-level strategies or heuristics that are used to find, or generate a sufficiently good solution to optimization problems encountered in a various applications of applied physics and mathematics.The AOA algorithm is a metahierarchical one, and its drawbacks include poor exploration capabilities and a high propensity to settle for local optimal solutions. In order, to encounter this drawback, the designed variable of FANNs initially with AOA are fed into sequential quadratic programming for rapid local convergence. SQP is a prominent local search method which has been effectively used for solving constrained and unconstrained optimization problems with low dimensions. Some recent application of SQP includes the prediction of powertrain torque and vehicle speed (Yang et al. 2021), cost minimization of a hybrid photovoltaic, diesel generator, and battery energy storage system (Tian et al. 2021), dynamic combined economic emission dispatch problem (Gul et al. 2021), robust design of power system stabilizers and static VAR compensator (Welhazi et al. 2022), and transient control of turbofan engines (Wang et al. 2021).

4 Numerical experimentation and discussion

In this section, the proposed methodology (FANN-AOA-SQP) is implemented on the nonlinear governing model of the convective, radiative, and moving rod to study the influence of the variation in different parameters (ambient temperature, radiation-conduction number, Peclet number, nonconstant thermal conductivity, and initial temperature parameter) on the temperature distribution of the rod. An overview of the problem and different cases based on variations of the parameters are shown in Fig. 5.

Fig. 5
figure 5

An overview of the problem and different cases based on changes in physical parameters

Full size image

The fitness function given in Eqs (10)–(12) are optimized using the design strength of the FANN-AOA-SQP algorithm to calculate the approximate solutions. The comparison of the statistics, showing the results for the temperature distribution in moving fin for \(N_{\text{c}} = N_{\text{r}} =4, \lambda = 0.2, Pe =3\) and \(\gamma = 0.2\) obtained by proposed algorithm are compared with radial basis function approximation method (RBFM) (Fallah Najafabadi et al. 2021), Runge-Kutta-Fehlberg method and machine learning algorithm such as FNN and Levenberg–Marquardt algorithm (Hsiang et al. 2020) as dictated in Table 1. Figure 6 illustrates the solutions’ accuracy compared to the state-of-the-art techniques. It is observed that results by the FANN-AOA-SQP algorithm overlap the numerical solution with absolute minimum errors that lie between \(10^{-6}\) to \(10^{-8}\).

Table 1 Comparison of results with radial basis function approximation method (RBFM), Runge–Kutta–Fehlberg method, and machine-learning technique such as FNN and Levenberg–Marquardt algorithm
Full size table
Fig. 6
figure 6

a, b Illustrates the comparison of solutions and absolute errors in temperature distribution of the moving rod with \(N_{\text{c}} = N_{\text{r}} =4, \lambda = 0.2, Pe =3\) and \(\gamma = 0.2\)

Full size image
Fig. 7
figure 7

Illustration of influence due to changes in different physical parameters on the temperature distribution of the moving fin with a \(\lambda =0.4, \gamma =1, N_{\text{c}}=2, P e=2\), b \(\gamma =1, \lambda =0.4, N_{\text{r}} = N_{\text{c}}= 2,\) c \(Pe =2, \gamma =1, N_{\text{r}} = N_{\text{c}}= 2,\) d \(\gamma =1, \lambda =0.4, Pe=2, N_{\text{r}}=2,\) and e \(N_{\text{r}}=N_{\text{c}} =2, \lambda =0.4, Pe =2\)

Full size image
Fig. 8
figure 8

Illustration of the absolute errors in the solutions of FANN-AOA-SQP algorithm for different cases of Eq. (4) with a \(\lambda =0.4, \gamma =1, N_{\text{c}}=2, P e=2\), b \(\gamma =1, \lambda =0.4, N_{\text{r}} = N_{\text{c}}= 2,\) c \(Pe =2, \gamma =1, N_{\text{r}} = N_{\text{c}}= 2,\) d \(\gamma =1, \lambda =0.4, Pe=2, N_{\text{r}}=2,\) and e \(N_{\text{r}}=N_{\text{c}} =2, \lambda =0.4, Pe =2\)

Full size image

The influence of physical parameters \((N_{\text{r}}, Pe, \lambda , N_{\text{c}}, \gamma )\) on temperature distribution \(\Theta\) of the moving hot rod are dictated in Tables 2, 3, 4 and 5 and graphically demonstrated through Fig. 7. It is observed from Fig. 7a and b that the temperature distribution of the rod in the passive device reduces when the conductive-convective parameter increases, implying that the pace at which heat is transferred via the fin is increased, and as a result, the efficiency with which the fin transfers heat is enhanced. This is due to the fact that convective heat transfer occurs when the temperature rises, convective cooling becomes more effective, lowering the fin’s temperatures. By extension, a reduction in the value of the fin efficiency is produced by increasing the value of the convective-conductive parameter. In addition, the influence in Peclet number is shown through Fig. 7c. The values of the temperature distribution in the fin rise in proportion to the increase in the Peclet number. This is expected because, as the Peclet number increases, the material moves faster, and the time during which the material is exposed to the environment shortens. Additionally, the heat loss from the fin surface becomes stronger, increasing the temperature of the fin surface. Figure 7d depicts the effect of ambient temperature on the thermal performance of the heat exchanger. The greater the dimensionless ambient temperature, the higher the temperature in the surrounding area. As a result, heat transfer from the fin surface to the surrounding environment is reduced. So, more the ambient temperature less will be the transfer of heat. Further, Fig. 8 is plotted to demonstrate the accuracy of the approximate solutions obtained by the proposed algorithm for different cases of the moving rod. The approximate solution for different cases can be generated by using the equations given in “Appendix”.

Fig. 9
figure 9

a, b Shows the combine effects of \(N_{\text{c}}, N_{\text{r}}\) and Pe on the temperature performance of the rod

Full size image

The combined effect of different parameters on the temperature performance at the rod’s tip is shown in Fig. 9. The three-dimensional surface plots show that temperature at the rod’s tip is maximum when convective and radiative parameters are minimum, and Peclet number is maximum. It is further noticed that the effect of these critical parameters is nonlinear, reflecting the higher temperature dependency on \(N_{\text{c}}\) and \(N_{\text{r}}\).

Table 2 Statistics of the calculated results for thermal distribution of a wetted porous structure and their corresponding AE obtained by the proposed scheme for variations in radiations parameter with \(N_{\text{c}} = 2, \gamma = 1, \lambda = 0.4\) and \(Pe = 2\)
Full size table
Table 3 The statistical analysis of the approximated solutions and magnitude of the errors in the results by the designed paradigm for variations in conduction parameter with \(N_{\text{r}} = 2, \gamma = 1, \lambda = 0.4\) and \(Pe = 2\)
Full size table
Table 4 Statistics of the calculated results for thermal distribution of a wetted porous structure and their corresponding AE obtained by the proposed scheme for variations in velocity parameter (Pe) with \(N_{\text{r}} = N_{\text{c}} = 2, \gamma = 1\) and \(\lambda = 0.4\)
Full size table
Table 5 The statistical analysis of the approximated solutions and magnitude of the errors in the results by the designed paradigm for variations in \(\lambda\) with \(N_{\text{r}} = N_{\text{c}} = Pe= 2\) and \(\gamma = 1\)
Full size table

5 Performance measures

This section incorporates different performance measures to explore the efficiency, stability, and accuracy of the approximate solutions calculated by the proposed computational (FANN-AOA-SQP) algorithm. The performance indices are defined in terms of mean absolute deviations (MAD), Theil’s inequality coefficient (TIC), root mean square error (RMSE), and error in Nash–Sutcliffe Efficiency (ENSE). Mathematical relations for these indices are defined as Umar et al. (2020)

$$\begin{aligned} {\text{MAD}}= & {} \frac{1}{M} \sum _{i=1}^{M}\left( \left| {\hat{\Theta }}\left( \eta _{i}\right) -\Theta \left( \eta _{i}\right) \right| \right) , \end{aligned}$$
(18)
$$\begin{aligned} {\text{TIC}}= & {} \frac{\sqrt{\frac{1}{M} \sum _{i=1}^{M}\left( {\hat{\Theta }}\left( \eta _{i}\right) -\Theta \left( \eta _{i}\right) \right) ^{2}}}{\sqrt{\frac{1}{M} \sum _{i=1}^{M}\left( {\hat{\Theta }}\left( \eta _{i}\right) ^{2}\right. }+\sqrt{\frac{1}{M} \sum _{i=1}^{M}\left( \Theta \left( \eta _{i}\right) \right) ^{2}}}, \end{aligned}$$
(19)
$$\begin{aligned} {\text{RMSE}}= & {} \sqrt{\frac{1}{M} \sum _{i=1}^{M}\left( {\hat{\Theta }}\left( \eta _{i}\right) -\Theta \left( \eta _{i}\right) \right) ^{2}}, \end{aligned}$$
(20)
$$\begin{aligned} {\text{ENSE}}= & {} |1-{\text{NSE}}|, \end{aligned}$$
(21)

where NSE is Nash-Sutcliffe Efficiency and is defined as Umar et al. (2020); Khan et al. (2021a)

$$\begin{aligned} N S E=1-\left( \frac{\sum _{i=1}^{M}\left( {\hat{\Theta }}\left( \eta _{i}\right) -\Theta \left( \eta _{i}\right) \right) ^{2}}{\sum _{i=1}^{M}\left( \Theta \left( \eta _{i}\right) -\frac{1}{M} \sum _{i=1}^{M}\left( \Theta \left( \eta _{i}\right) \right) \right) ^{2}}\right) . \end{aligned}$$
(22)

here \({\hat{\Theta }}\) and \(\Theta\) are the approximate and exact solutions for the problem. M corresponds to the total number of mesh (grid) points, and i denotes the number of current solution points. Since the FANN-AOA-SQP algorithm is an unsupervised learning strategy, it is important to use these performance indices to justify the accuracy of the solutions. For perfect modeling of approximate solutions, values of MAD, TIC, RMSE, and ENSE approach to zero.

To investigate the stability and durability of the results, the design method is executed for 100 times. The solution curves for the temperature distribution in the moving rod obtained during each run are plotted through Fig. 10. It is concluded that the approximate solutions for different cases overlap the numerical solution with 100\(\%\) accuracy and stability. The behavior of fitness value and MAD of solution in each run is graphically shown through Fig. 11. The mean values of fitness function and MAD lies in the range of \(10^{-5}\) to \(10^{-6}\) and \(10^{-4}\) to \(10^{-5}\), respectively. The detailed statistics of the performance indicators in terms of minimum value, mean and standard deviations are provided in Table 6. Clearly, it can be observed that for each case minimum values of fitness function, MAD, TIC, RMSE and ENSE lies between \(10^{-8}\) to \(10^{-9}\), \(10^{-6}\) to \(10^{-7}\), \(10^{-4}\) to \(10^{-5}\), \(10^{-5}\) to \(10^{-6}\), and \(10^{-9}\) to \(10^{-10}\) respectively. The global (average) values for each case lies around \(10^{-4}\) to \(10^{-6}\). The results of ENSE are shown through the boxplots in Fig. 12. It can be seen that the upper quartile (maximum values) of boxplots for each case lie between \(10^{-6}\) to \(10^{-7}\), which shows that the solutions of the proposed technique are accurate and stable. The normal distribution curves for the root mean square error of the approximate solutions of moving rod with \(\lambda =0.2, Nr = Nr = 1, Pe = 2\) and \(\gamma = 1\) are plotted through Fig. 13.

Fig. 10
figure 10

a, b, c, and d Approximate solution obtained by FANN-AOA-SQP algorithm in each run for different cases of moving rod

Full size image
Fig. 11
figure 11

a, b, c, and d Shows the behaviour of values of fitness function and mean absolute deviation by varying \(N_{\text{r}}, N_{\text{c}}, \lambda\) and Pe during 100 independent execution of the design algorithm

Full size image
Table 6 Values of statistical operators for each case of the mathematical model of moving fin
Full size table
Fig. 12
figure 12

a, b, c, and d Results of ENSE obtained by FANN-AOA-SQP algorithm during multiple runs for variations in critical parameters

Full size image
Fig. 13
figure 13

Normal distribution curves for root mean square error in the solutions of the proposed technique for \(Nr = 1 = Nr\) with \(\lambda =0.2, Pe = 2\) and \(\gamma = 1\) . Black line shows the minimum value

Full size image

6 Conclusion

This paper investigates the thermal performance and heat transfer of the convective, radiative and moving rod with thermal conductivity by developing a met-heuristic driven approach based on the approximating computational ability of neural networks. Furthermore, the feedforward network is optimized by combining global and local search mechanisms such as Arithmetic optimization algorithm and sequential quadratic programming. The proposed FANN-AOA-SQP algorithm is implemented to study the rod’s temperature distribution behavior by varying critical parameters (radiation parameter \(N_{\text{r}}\), conduction parameter \(N_{\text{c}}\), ambient temperature \(\lambda\), Peclet number Pe and thermal conductivity \(\gamma\)). The results demonstrate that increase in \(N_{\text{c}}\), Pe and \(N_{\text{r}}\) causes an increase in the temperature of the rod. In addition, the increase in velocity parameter (Pe) from 1 to 2 causes an increase in the temperature up to 7 to 10\(\%\).

Further, the design algorithm’s accuracy, stability, and effectiveness are established by calculating the errors based on MAD, TIC, RMSE, ENSE, and AE. The values of these errors are approaching to zero, reflecting the perfect modeling of the solution compared to the other techniques available in the latest literature. The results and graphical analysis illustrate that the proposed approach is accurate and reliable in calculating solutions to complex real-world problems.

In the future, the author aims to extend the proposed meta-heuristic technique to solve high-dimensional problems, especially partial differential equations and fractional differential equations about complex problems such as epidemiology and population study, magnetic resonance electrical impedance tomography, image inpainting, google mobility data to predict COVID-19 in Arizona, and prostate tumor growth under intermittent hormone therapy.