Multiobjective reliability-based optimization for crashworthy structures coupled with metal forming process

Abstract

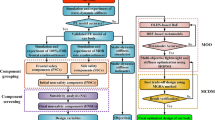
Crashworthiness design for manufacturing of thin-walled structures remains a main challenge in vehicle industry. Conventionally, there have been two main stream procedures (1) conducting the crashworthiness optimization and manufacturing deign separately in a sequential manner; or (2) neglecting the effects of manufacturing process on final outcomes. Note that most of the energy absorbing members in vehicle body are fabricated by stamping process which likely results in non-uniform thickness, substantial residual strains/stresses especially for high strength steel or advanced high strength steels, etc. Furthermore, the uncertainties of the material properties, stamping process and geometry generally propagate from manufacturing phase to operational phase, likely leading to the uncontrollable fluctuations of crashing responses. In other words, a deterministic optimization could result in unreliable or unstable designs. To address these critical issues, a multiobjective reliability-based design optimization was proposed here to optimize the double-hat thin-walled structure by coupling with stamping uncertainties. First, the finite element analysis results of stamping process are transferred to crashworthiness simulation. As such the uncertainties of material properties, process parameters and resultant geometry can be propagated from forming stage to crashing stage in a non-deterministic context. Second, the surrogate modeling techniques were adopted to approximate the forming and crashing responses in terms of mean and standard deviation. Third, the multiobjective particle swarm optimization (MOPSO) algorithm was employed to seek optimal reliable design solutions which were combined with Monte Carlo Simulation (MCS). The optimal results of the double-hat structure show that the proposed method not only significantly improved the formability and crashworthiness, but also was capable of enhancing the reliability of Pareto solutions.

Appendix: brief of the Sobol’s method

In this study, the global sensitivity analysis (GSA), i.e., Sobol’s method (Sobol 2003, 2001), was employed to quantify the influences of input parameters on output responses. Brief description of the Sobol’s method was provided as follows for the completeness of this paper.

The quadratic integral function g(x) can be expressed in a functional Analysis of Variance (ANOVA) form (Sobol 2003, 2001):

$$ g\left(\mathbf{x}\right)={g}_0+{\sum}_i{g}_i\left({x}_i\right)+{\sum}_{i<j}{g}_{ij}\left({x}_i,{x}_j\right)+\cdots +{g}_{1\cdots s}\left({x}_1,\dots, {x}_s\right) $$

(9)

where ${\int}_0^1{g}_{i_1,{i}_2\dots {i}_t}\left({x}_{i_1},\dots, {x}_{i_t}\right){dx}_k=0,\kern0.5em k={i}_{1,2,\dots, {i}_t.}$

The g _i (x _i ) represents the main responses and g _ij (x _i , x _j ) is regarded to be the first-order interaction effects. The total number of summands in (9) is 2ⁿ. Squaring (9) and integrating over the n-dimensional unit hypercube, the following equation can be obtained:

$$ {\displaystyle \begin{array}{l}D=\int {g}^2\left(\mathbf{x}\right)d\mathbf{x}-{g}_0\kern0.5em ={\sum}_{s=1}^n{\sum}_{i_1<\cdots <{i}_s}^n\int {g}_{i_1\dots {i}_s}^2{dx}_{i_1}{dx}_{i_s}\\ {}\kern1.5em ={\sum}_{s=1}^n{\sum}_{i_1<\cdots <{i}_s}^n{D}_{i_1\dots {i}_s}={\sum}_i{D}_i+{\sum}_{1\le i<j\le n}{D}_{ij}+\cdots +{D}_{i_1\dots {i}_s}\end{array}} $$

(10)

where D is the total variance of g(x) and ${D}_{i_1\dots {i}_s}$ is the partial variance in the response due to concurrent change of factors i ₁ to i _s.

According to (9) and (10), the first-order and kth-order sensitivity indices and the total sensitivity index for the ith design variable can be defined as (Sobol 2001):

$$ {S}_i={D}_i/D,\kern1em {S}_{i_1\dots {i}_k}={D}_{i_1\dots {i}_k}/D,\kern1em {S}_i^{total}=1-{S}_{-i} $$

(11)

where S _-i is the sum of all the ${S}_{i_1\dots {i}_s}$ terms which do not include the ith variable. The first-order sensitivity index represents the main effect of a design variable and higher-order sensitivity indices can capture the effects of interactions among the design variables. In general, the relative importance of different design variables can be thus obtained by ranking each variable based on its respective total sensitivity index (Cannavó 2012).