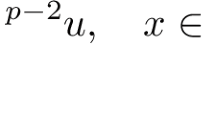Skip to main content
SpringerLink
Log in

Symmetry and monotonicity of nonnegative solutions to pseudo-relativistic Choquard equations

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

In this paper, we consider the following pseudo-relativistic Choquard equations:

$$\begin{aligned} (-\Delta +m^{2})^{s} u+wu=R_{N,t}\left( \frac{1}{|x-y|^{N-2t}}*u^{p}\right) u^{q}, \quad \mathrm{in} \;\;\mathbb {R}^{N}, \end{aligned}$$

where \(s,t\in (0,1)\), mass \(m>0\), \(w>-m^{2s}\), \(2<p<\infty \), and \(0<q\le p-1\). We first establish a narrow region principle for pseudo-relativistic Choquard equations and estimate the decay of the solutions at infinity. Using the generalized direct method of moving planes, we obtain the radial symmetry and monotonicity of nonnegative solutions for the above equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ambrosio, V.: Ground states solutions for a non-linear equation involving a pseudo-relativistic Schrödinger operator. J. Math. Phys. 57(5), 051502 (2016)

    Article  MathSciNet  Google Scholar 

  2. Abatangelo, N., Valdinoci, E.: Getting acquainted with the fractional Laplacian. In: Contemporary Research in Elliptic PDEs and Related Topics, 1C105, Springer INdAM Series, vol. 33. Springer, Cham (2019)

  3. Berestycki, H., Caffarelli, L.A., Nirenberg, L.: Inequalitites for second-order elliptic equations with applications to unbounded domains, I. Duke Math. J. 81, 467–494 (1996)

    Article  MathSciNet  Google Scholar 

  4. Berestycki, H., Caffarelli, L.A., Nirenberg, L.: Monotonicity for elliptic equations in unbounded Lipschitz domains. Commun. Pure Appl. Math. 50, 1089–1111 (1997)

    Article  MathSciNet  Google Scholar 

  5. Brandle, C., Colorado, E., de Pablo, A., Sanchez, U.: A concave–convex elliptic problem involving the fractional Laplacian. Proc. R. Soc. Edinb. A Math. 143, 39–71 (2013)

    Article  MathSciNet  Google Scholar 

  6. Bertoin, J.: Lévy Processes, Cambridge Tracts in Mathematics, vol. 121. Cambridge University Press, Cambridge (1996)

    Google Scholar 

  7. Chang, S.-Y.A., Gonzàlez, M.D.M.: Fractional Laplacian in conformal geometry. Adv. Math. 226, 1410–1432 (2011)

    Article  MathSciNet  Google Scholar 

  8. Chen, Y., Liu, B.: Symmetry and non-existence of positive solutions for fractional p-Laplacian systems. Nonlinear Anal. 183, 303–322 (2019)

    Article  MathSciNet  Google Scholar 

  9. Chen, W., Li, C., Li, Y.: A direct method of moving planes for the fractional Laplacian. Adv. Math. 308, 404–437 (2017)

    Article  MathSciNet  Google Scholar 

  10. Chen, W., Li, Y., Ma, P.: The Fractional Laplacian, p. 350. World Scientific Publishing Co. Pte. Ltd., Singapore (2019). https://doi.org/10.1142/10550

    Book  Google Scholar 

  11. Chen, W., Li, C.: Moving planes, moving spheres, and a priori estimates. J. Differ. Equ. 195(1), 1–13 (2003)

    Article  MathSciNet  Google Scholar 

  12. Chen, W., Li, C., Ou, B.: Classification of solutions for an integral equation. Commun. Pure Appl. Math. 59, 330–343 (2006)

    Article  MathSciNet  Google Scholar 

  13. Chen, W., Li, Y., Zhang, R.: A direct method of moving spheres on fractional order equations. J. Funct. Anal. 272(10), 4131–4157 (2017)

    Article  MathSciNet  Google Scholar 

  14. Constantin, P.: Euler equations, Navier–Stokes equations and turbulence. In: Mathematical Foundation of Turbulent Viscous Flows, Vol. 1871 of Lecture Notes in Mathematics, pp. 1–43. Springer, Berlin (2006)

  15. Chen, W., Qi, S.: Direct methods on fractional equations. Discrete Contin. Dyn. Syst. A 39, 1269–1310 (2019)

    Article  MathSciNet  Google Scholar 

  16. Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Commun. PDEs 32, 1245–1260 (2007)

    Article  MathSciNet  Google Scholar 

  17. Cabré, X., Tan, J.: Positive solutions of nonlinear problems involving the square root of the Laplacian. Adv. Math. 224, 2052–2093 (2010)

    Article  MathSciNet  Google Scholar 

  18. Caffarelli, L., Vasseur, L.: Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. Math. 171(3), 1903–1930 (2010)

    Article  MathSciNet  Google Scholar 

  19. Chen, W., Wu, L.: The sliding methods for the fractional \(p\)-Laplacian. Adv. Math. 361, 106933 (2020)

    Article  MathSciNet  Google Scholar 

  20. Carmona, R., Masters, W.C., Simon, B.: Relativistic Schrödinger operators: asymptotic behavior of the eigenfunctions. J. Funct. Anal. 91, 117–142 (1990)

    Article  MathSciNet  Google Scholar 

  21. Dai, W., Fang, Y., Huang, J., Qin, Y., Wang, B.: Regularity and classification of solutions to static Hartree equations involving fractional Laplacians. Discrete Contin. Dyn. Syst. A 39(3), 1389–1403 (2019)

    Article  MathSciNet  Google Scholar 

  22. Dai, W., Liu, Z.: Classification of nonnegative solutions to static Schrödinger–Hartree and Schrödinger–Maxwell equations with combined nonlinearities. Calc. Var. PDEs 58(4), 24 (2019)

    Article  Google Scholar 

  23. Dai, W., Liu, Z., Qin, G.: Classification of nonnegative solutions to static Schrödinger–Hartree–Maxwell type equations. SIAM J. Math. Anal. 53(2), 1379–1410 (2021)

    Article  MathSciNet  Google Scholar 

  24. Dai, W., Qin, G.: Classification of nonnegative classical solutions to third-order equations. Adv. Math. 328, 822–857 (2018)

    Article  MathSciNet  Google Scholar 

  25. Dai, W., Qin, G., Wu, D.: Direct methods for pseudo-relativistic Schrödinger operators. J. Geom. Anal. (2020). https://doi.org/10.1007/s12220-020-00492-1

    Article  Google Scholar 

  26. Dipierro, S., Soave, N., Valdinoci, E.: On fractional elliptic equations in Lipschitz sets and epigraphs: regularity, monotonicity and rigidity results. Math. Ann. 369, 1283–1326 (2017)

    Article  MathSciNet  Google Scholar 

  27. Erdélyi, A., Magnus, W., Oberhettinger, F., Tricomi, F.G.: Higher Transcendental Functions, vol. II. McGraw-Hill, New York (1953)

    MATH  Google Scholar 

  28. Elgart, A., Schlein, B.: Mean field dynamics of boson stars. Commun. Pure Appl. Math. 60(4), 500–545 (2007)

    Article  MathSciNet  Google Scholar 

  29. Fall, M.M., Felli, V.: Sharp essential self-adjointness of relativistic Schrödinger operators with a singular potential. J. Funct. Anal. 267(6), 1851–1877 (2014)

    Article  MathSciNet  Google Scholar 

  30. Fall, M.M., Felli, V.: Unique continuation properties for relativistic Schrödinger operators with a singular potential. Discrete Contin. Dyn. Syst. A 35(12), 5827–5867 (2015)

    Article  MathSciNet  Google Scholar 

  31. Fröhlich, J., Jonsson, B.L.G., Lenzmann, E.: Boson stars as solitary waves. Commun. Math. Phys. 274, 1–30 (2007)

    Article  MathSciNet  Google Scholar 

  32. Fröhlich, J., Lenzmann, E.: Blowup for nonlinear wave equations describing boson stars. Commun. Pure Appl. Math. 60, 1691–1705 (2007)

    Article  MathSciNet  Google Scholar 

  33. Frank, R.L., Lenzmann, E., Silvestre, L.: Uniqueness of radial solutions for the fractional Laplacian. Commun. Pure Appl. Math. 69(9), 1671–1726 (2013)

    Article  MathSciNet  Google Scholar 

  34. Gross, E.P.: Physics of Many-Particle Systems, vol. 1. Gordon Breach, New York (1966)

    Google Scholar 

  35. Herbst, I.W.: Spectral theory of the operator \((p^{2}+m^{2})^{1/2}-Ze^{2}/r\). Commun. Math. Phys. 53, 285–294 (1977)

    Article  Google Scholar 

  36. Liu, J., Guo, Y., Zhang, Y.: Liouville-type theorems for polyharmonic systems in \(R^{N}\). J. Differ. Equ. 225, 685–709 (2006)

    Article  Google Scholar 

  37. Liu, B., Ma, L.: Radial symmetry results for fractional Laplacian systems. Nonlinear Anal. 146, 120–135 (2016)

    Article  MathSciNet  Google Scholar 

  38. Li, Y.Y., Zhu, M.: Uniqueness theorems through the method of moving spheres. Duke Math. J. 80, 383–417 (1995)

    Article  MathSciNet  Google Scholar 

  39. Ma, L., Zhao, L.: Classification of positive solitary solutions of the nonlinear Choquard equation. Arch. Ration. Mech. Anal. 195(2), 455–467 (2010)

    Article  MathSciNet  Google Scholar 

  40. Peng, S.: Liouville theorems for fractional and higher order Hénon-Hardy systems on \(\mathbb{R}^{n}\). Complex Var. Elliptic Equ. (2020). https://doi.org/10.1080/17476933.2020.1783661

  41. Qu, M., Yang, L.: Solutions to the nonlinear Schrödinger systems involving the fractional Laplacian. J. Inequal. Appl. 297, 16 (2018)

    Google Scholar 

  42. Silvestre, L.: Regularity of the obstacle problem for a fractional power of the Laplace operator. Commun. Pure Appl. Math. 60, 67–112 (2007)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the referees for their careful reading and valuable comments and suggestions, which greatly improved this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Tsinghua University, Beijing, 100084, People’s Republic of China

    Yuxia Guo & Shaolong Peng

Authors
  1. Yuxia Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shaolong Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuxia Guo.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Yuxia Guo was supported by NSFC (Nos. 11771235 and 12031015). Shaolong Peng is supported by the NSFC (No. 11971049)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guo, Y., Peng, S. Symmetry and monotonicity of nonnegative solutions to pseudo-relativistic Choquard equations. Z. Angew. Math. Phys. 72, 120 (2021). https://doi.org/10.1007/s00033-021-01551-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-021-01551-5

Keywords

Mathematics Subject Classification

Search

Navigation