Skip to main content
SpringerLink
Log in

Asymptotic behavior of coupled linear systems modeling suspension bridges

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

We consider the coupled linear system

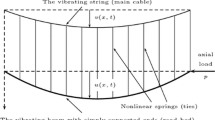
$$\left\{\begin{array}{ll} \partial_{tt} u + \partial_{xxxx}u + \gamma \partial_t u + k(u - v) + h\partial_{t} (u-v) = 0\\\epsilon \partial_{tt} v - \partial_{xx}v - k(u - v) - h\partial_{t} (u - v) = 0\end{array}\right.$$

describing the vibrations of a string-beam system related to the well-known Lazer–McKenna suspension bridge model. For ε > 0 and k > 0, the decay properties of the solution semigroup are discussed in dependence of the nonnegative parameters γ and h, which are responsible for the damping effects.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ahmed N.U., Harbi H.: Mathematical analysis of dynamic models of suspension bridges. SIAM J. Appl. Math. 109, 853–874 (1998)

    MathSciNet  Google Scholar 

  2. An Y.: Nonlinear perturbations of a coupled system of steady state suspension bridge equations. Nonlinear Anal. 51, 1285–1292 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  3. Arendt W., Batty J.K.: Tauberian theorems and stability of one-parameter semigroups. Trans. Am. Math. Soc. 306, 837–852 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  4. Bochicchio, I., Giorgi, C., Vuk, E.: On some nonlinear models for suspension bridges. In: Andreucci, D., Carillo, S., Fabrizio, M., Loreti, P. Sforza, D. (eds.) Proceedings of the Conference “Evolution Equations and Materials with Memory Proceedings” Rome, 12–14 July 2010. “La Sapienza” Università di Roma, pp. 1–18 (2011)

  5. Bochicchio, I., Giorgi, C., Vuk, E.: Long-term dynamics of the coupled suspension bridge system. Math. Models Methods Appl. Sci. 22, 1250021, 22 pp. (2012)

  6. Bochicchio I., Giorgi C., Vuk E.: Asymptotic dynamics of nonlinear coupled suspension bridge equations. J. Math. Anal. Appl. 402, 319–333 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  7. Choi Q.H., Jung T.: A nonlinear suspension bridge equation with nonconstant load. Nonlinear Anal. 35, 649–668 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  8. Coti Zelati M., Dell’Oro F., Pata V.: Energy decay of type III linear thermoelastic plates with memory. J. Math. Anal. Appl. 401, 357–366 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  9. Dell’Oro F., Muñoz Rivera J.E., Pata V.: Stability properties of an abstract system with applications to linear thermoelastic plates. J. Evol. Equ. 13, 777–794 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  10. Giorgi C., Naso M.G., Pata V.: Exponential stability in linear heat conduction with memory: a semigroup approach. Commun. Appl. Anal. 5, 121–134 (2001)

    MATH  MathSciNet  Google Scholar 

  11. Glover J., Lazer A.C., McKenna P.J.: Existence and stability of large scale nonlinear oscillations in suspension bridges. Z. Angew. Math. Phys. 40, 172–200 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  12. Goremikins V., Rocens K., Serdjuks D.: Rational structure of cable truss. World Acad. Sci. Eng. Technol. 52, 4–23 (2011)

    Google Scholar 

  13. Holubová G., Matas A.: Initial-boundary problem for the nonlinear string-beam system. J. Math. Anal. Appl. 288, 784–802 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  14. Kato T.: Perturbation Theory for Linear Operators. Springer, New York (1980)

    MATH  Google Scholar 

  15. Irvine H.M.: Cable Structures. Mit Press, Boston (1981)

    Google Scholar 

  16. Luongo A., Rega G., Vestroni F.: Planar nonlinear free vibrations of an elastic cable. Int. J. Non-linear Mech. 19, 39–52 (1984)

    Article  MATH  Google Scholar 

  17. Luongo A., Zulli D., Piccardo G.: A linear curved-beam model for the analysis of galloping in suspended cables. J. Mech. Mater. Struct. 2, 675–694 (2007)

    Article  Google Scholar 

  18. Luongo A., Zulli D., Piccardo G.: On the effect of twist angle on nonlinear galloping of suspended cables. Comput. Struct. 87, 1003–1014 (2009)

    Article  Google Scholar 

  19. Ma Q., Zhong C.: Existence of strong solutions and global attractors for the coupled suspension bridge equations. J. Differ. Equ. 246, 3755–3775 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  20. McKenna P.J., Walter W.: Nonlinear oscillations in a suspension bridge. Arch. Ration. Mech. Anal. 98, 167–177 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  21. Pazy A.: Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer, New York (1983)

    Book  MATH  Google Scholar 

  22. Prüss J.: On the spectrum of C0-semigroups. Trans. Am. Math. Soc. 284, 847–857 (1984)

    Article  MATH  Google Scholar 

  23. Rega G.: Nonlinear vibrations of suspended cables—Part I: modeling and analysis. Appl. Mech. Rev. 57, 443–478 (2005)

    Article  Google Scholar 

  24. Zhong C., Ma Q., Sun C.: Existence of strong solutions and global attractors for the suspension bridge equations. Nonlinear Anal. 67, 442–454 (2007)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. DICATAM, Università di Brescia, Via Valotti 9, 25133, Brescia, Italy

    Filippo Dell’Oro & Claudio Giorgi

  2. Dipartimento di Matematica “F. Brioschi”, Politecnico di Milano, Via Bonardi 9, 20133, Milan, Italy

    Vittorino Pata

Authors
  1. Filippo Dell’Oro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Claudio Giorgi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vittorino Pata
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Claudio Giorgi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dell’Oro, F., Giorgi, C. & Pata, V. Asymptotic behavior of coupled linear systems modeling suspension bridges. Z. Angew. Math. Phys. 66, 1095–1108 (2015). https://doi.org/10.1007/s00033-014-0414-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00033-014-0414-9

Mathematics Subject Classification (2010)

Keywords

Search

Navigation