A reverse Hölder inequality for the gradient of solutions to Trudinger’s equation

Abstract

We provide a higher integrability result for the gradient of positive solutions to Trudinger’s equation (also known as the doubly non-linear equation) for the range $p\in [2,\infty )$. The estimate is achieved by refining a construction of intrinsic cylinders from the vectorial setting by incorporating estimates that are only available in the scalar case.

1 Introduction

We study doubly non-linear parabolic partial differential equations modeled by Trudinger’s equation

$$\begin{aligned} \dfrac{\partial ( u^{p-1} ) }{\partial t} - {{\,\mathrm{div}\,}}( |\nabla u|^{p-2} \nabla u ) = 0, \quad 1< p < \infty . \end{aligned}$$

(1.1)

It was introduced by Trudinger in [25], where a scale and location invariant parabolic Harnack inequality for positive weak solutions was proved, generalizing the work of Moser [22]. The Eq. (1.1) is motivated for instance by its connection to the non-linear eigenvalue problem and sharp constants in Sobolev inequalities. Given any bounded domain $\Omega \subset {\mathbb {R}}^{n}$, one defines the first non-linear eigenvalue of the p-Laplacian

$$\begin{aligned} \lambda _p = \inf _{u \in W^{1,p}_0(\Omega ) \setminus \{0\}} \frac{\int _{\Omega } |\nabla u|^{p} \, dx}{\int _{\Omega } |u|^{p} \, dx} .\end{aligned}$$

(1.2)

The minimizer v of the Raleygh quotient is unique up to a multiplicative constant [17, 18]. On the other hand, given any weak solution $u \in L_{loc}^{p}( 0, \infty ;W_0^{1,p} (\Omega ))$ to (1.1), then either

$$\begin{aligned} \lim _{t \rightarrow \infty } e^{\frac{\lambda _p}{p-1} t} u = v , \end{aligned}$$

or the limit, understood in $L^{p}$ sense, is identically zero [11]. This is the connection of the evolution equation (1.1) and the geometric quantity (1.2).

Our focus is on local regularity theory of positive weak solutions to (1.1). Despite the simple form of the parabolic Harnack estimate, the regularity theory of (1.1) is not as simple as one might expect. Weak solutions are known to be locally Hölder continuous [26], but to the best of our knowledge already Hölder continuity of the gradient is unknown. In addition, some fundamental questions such as the ones about uniqueness of solutions and validity of comparison principles are still partially open, see [16] for results and a discussion on open problems. We also refer to [12, 14, 15, 24] for more on regularity theory.

In the present paper, we prove a new regularity result for the non-negative solutions of (1.1). Our proof also applies to solutions of more general equations with principal part satisfying the natural growth conditions, see Sect. 2.2. The following theorem includes all exponents $p\in [2,\infty )$, which extends over what can be deduced from the vectorial case in [1] by allowing arbitrarily large values of p.

Theorem 1.1

Let $n \ge 1$, $p \ge 2$ and $\Lambda \ge 1$. Then there exist $c, \epsilon > 0$ only depending on n, p and $\Lambda$ so that for all space time cylinders $Q_{r,r^{p}} = I_{r^{p}} \times B_{ r}$ and for all non-negative solutions $u \in L_{loc}^{p}(I_{(4r)^{p}}; W_{loc}^{1,p}(B_{4r}))$ to (2.1) and (2.2) it holds

We briefly recall the history of the topic. The study of higher integrability of gradients of solutions to partial differential equations goes back to Bojarski [3] and quasiregular mappings in the plane. See also [6] for quasiconformal mappings in space. Meyers [19] studied general linear elliptic equations, and elliptic systems were later treated in [20]. The first results for linear uniformly parabolic equations and systems are due to Giaquinta and Struwe [9]. Extending the results on higher gradient integrability to nonlinear parabolic equations remained an open problem for some time until in their seminal paper [13] Kinnunen and Lewis managed to deal with systems of p-parabolic type. Their proof relies on the method of intrinsic scaling, which was originally introduced by DiBenedetto and Friedman [5] for other purposes. The p-parabolic equation

$$\begin{aligned} \dfrac{\partial u }{\partial t} - {{\,\mathrm{div}\,}}( |\nabla u|^{p-2} \nabla u ) = 0, \quad 1<p< \infty \end{aligned}$$

(1.3)

becomes degenerate or singular when the gradient of the solution vanishes, which accounts for the behaviour qualitatively very different from what is seen in the linear setting. The class of weak solutions is not closed under multiplication by constants and consequently no proper homogeneous reverse Hölder condition can be expected to hold for the gradients of all solutions.

Equations of porous medium type

$$\begin{aligned}\dfrac{\partial u }{\partial t} - m {{\,\mathrm{div}\,}}( u^{m-1} \nabla u ) = 0, \quad m > 0 \end{aligned}$$

exhibit a distinct difficulty as the equations become degenerate or singular depending on the values of the solution itself rather than its gradient. The higher gradient integrability was established only very recently by Gianazza and the second author in [7, 8]. These results require a very careful analysis of the covering properties of the intrinsic cylinders relative to the solution. The ideas there, in part originating from [23], have later also been used to study systems of porous medium type [2] and global variants of the above mentioned problems [21].

Equations of the type (1.1) studied in this paper can be formally understood as equations for $v=u^{p-1}$ given by

$$\begin{aligned}\dfrac{\partial v }{\partial t} - \frac{1}{(p-1)^{p-1}}{{\,\mathrm{div}\,}}( v^{2-p} |\nabla v|^{p-2} \nabla v ) = 0 .\end{aligned}$$

From this formulation it is clear that the equation becomes degenerate or singular depending on both the values of the solution and the values of its gradient. Prior to this work, the higher gradient integrability was only known in the restricted range $p \in (2n/(n+2), 2n/(n-2)_{+} )$ when the dimension $n > 2$ and for all $p>1$ when the dimension $n \in \{1,2\}$. These results can be found in [1], whose methods actually apply in the full generality of systems and sign-changing solutions. The two restrictions on exponents are connected to the construction of intrinsic cylinders and the Sobolev embeddings. While the lower bound $2n/(n+2)$ also appears in the analogous results for the p-Laplacian (1.3) (see [13]), the upper bound does not. Our contribution is to remove it when dealing with non-negative solutions to equations. Whether or not the upper bound can be removed even in the vectorial setting remains an open problem.

2 Preliminaries

2.1 Notation

We work on ${\mathbb {R}} \times {\mathbb {R}}^{n}$ where the first coordinate is called time and the remaining ones space. The dimension $n \ge 1$ is fixed throughout the paper. The symbols c and C refer to constants that only depend on quantities we do not keep track of. Their actual value may change from expression to expression even within a single line. Given two numbers $a,b > 0$, such that $a \le cb$ holds for a constant c as above, we sometimes write $a \lesssim b$. The binary relations $\gtrsim$ and $\sim$ are defined analogously. We write $\chi _{E}$ for the indicator function of a set $E \subset {\mathbb {R}}^{1+n}$.

Given a (positive locally finite Borel) measure $\mu$, usually given by a locally integrable weight function $\eta$, we denote the mean value over a Borel set E of positive measure by

In case $\mu$ is the Lebesgue measure, it is suppressed from the notation. We write |E| for the Lebesgue outer measure of a set E. We use the same notation for both n-dimensional and $(n+1)$-dimensional Lebesgue measures. It will always be clear from the context which one is being used.

Given $x \in {\mathbb {R}}^{n}$ and $r > 0$, we write $B_r(x) = \{y \in {\mathbb {R}}^{n}: |x-y| < r\}$ for a Euclidean ball. If the center x and the radius r are clear from the context or not important for the argument, we suppress them from the notation. Even the letter B alone is reserved for n-dimensional Euclidean balls as above. Similarly, given $t \in {\mathbb {R}}$ and $h > 0$, we write $I_h(t) = (t-h/2,t+h/2)$ and omit h and t whenever we can without disturbing the reading of the argument.

Given two positive numbers r and s, we write $Q_{r,s}$ for the space time cylinder $I_s \times B_r$. We use the shorthand notation $bQ_{r,s} = Q_{br,bs}$ for concentric dilations. Similar notation is used for intervals and balls.

2.2 Solutions

Let $\Lambda \ge 1$ and $p > 1$. Let $A : {\mathbb {R}}^{n+1} \times {\mathbb {R}} \times {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{n}$ be a function measurable in each variable and satisfying the structural conditions

$$\begin{aligned} A ( t,x,u , \xi ) \cdot \xi \ge \Lambda ^{-1} |\xi |^{p}, \quad |A ( t,x,u , \xi ) | \le \Lambda |\xi |^{p-1} . \end{aligned}$$

(2.1)

We study non-negative weak solutions to the equations

$$\begin{aligned}\dfrac{\partial u^{p-1} }{\partial t} - {{\,\mathrm{div}\,}}A ( t,x,u,\nabla u ) = 0 .\end{aligned}$$

Consider a space time cylinder $I_{r^{p}} \times B_{r}$. A function $u \in L^{p}_{loc}(I_{r^{p}}; W^{1,p}_{loc}(B_{r}))$ is a weak solution if

(2.2)

holds for all test functions $\varphi \in C_c^{\infty }(I_{r^{p}} \times B_{r})$. If the left hand side is non-positive for all non-negative test functions, u is said to be a subsolution. If the left hand side is non-negative for all non-negative test functions, u is said to be a supersolution. By a standard apporximation argument, we can use compactly supported Sobolev functions as test functions as opposed to smooth functions. In what follows, u will always denote a positive weak solution to the equation. As our main result is inherently local, we do not refer to the the cylinder $I_{r^{p}} \times B_r$ anymore but work as if it were the full space time.

2.3 Time derivative

As the solutions are not required to exhibit any a priori differentiability in the time variable, there is a technical difficulty when trying to use the solution itself as a test function. To overcome this problem, we can use a mollified version of the equation as an intermediate step in the proof. For a smooth and even function $\chi _{[-4^{-1},4^{-1}]} \le \zeta \le \chi _{[-2^{-1},2^{-1}]}$ and $\epsilon > 0$, we set for any locally integrable $\varphi$

$$\begin{aligned}\varphi _\epsilon (t,x) := \int _{{\mathbb {R}}} \varphi (s,x) \zeta \left( \frac{t-s}{\epsilon } \right) \, \frac{ds}{\epsilon } . \end{aligned}$$

Using $\varphi _{\epsilon }$ with $\varphi \in C_c^{\infty }({\mathbb {R}}^{1+n})$ as a test function, we can convert the Eq. (2.2) to

This together with the correct use of the mollified solution as a test function can then be used to justify certain computations to follow that we decided to keep at formal level for the sake of better readability.

2.4 Auxiliary inequalitites

Given a Borel probability measure $\mu$ and $q\in [1,\infty )$, the mean value $(f)_{E}^{\mu }$ always satisfies

$$\begin{aligned} \bigg (\int _{E} |f -(f)_{E}^{\mu }|^q \, d \mu \bigg )^\frac{1}{q} \le 2 \inf _{c} \bigg (\int _{E} |f -c |^q \, d \mu \bigg )^\frac{1}{q}.\end{aligned}$$

We refer to this fact in its various forms as the best constant property of the mean value and it can be used to justify all occasions where we change a constant inside a mean oscillation integral as the one above.

In order to effectively carry out certain iterative arguments, we use the following lemma, which can be found as Lemma 6.1 on page 191 of [10].

Lemma 2.1

Let $A,B, \alpha > 0$ and $\delta \in (0,1)$. Let $0< r< R < \infty$ and let Z be a bounded and positive function such that for all $r \le \rho _1 < \rho _2\le R$ it holds

$$\begin{aligned}Z(\rho _1) \le A(\rho _2 - \rho _1)^{-\alpha } + B + \delta Z(\rho _2) .\end{aligned}$$

Then

$$\begin{aligned}Z(r) \le c(\alpha ,\delta ) \left( A(R-r)^{-\alpha } + B \right) .\end{aligned}$$

2.5 Positivity

When it comes to Harnack estimates, there is some discrepancy in the positivity assumptions imposed on solutions in the literature, and we clarify that point here. For our estimates, we need not use the full strength of the Harnack inequality, but a much weaker supremum estimate for subsolutions will do. In particular, the use of Hölder continuity and strict positivity can be avoided.

We recall the following observation. Given $\epsilon > 0$ and a positive subsolution u, we let $u_ \epsilon = \max (u,\epsilon )$. Consider a test function $\eta \in C_c^{\infty }({\mathbb {R}}^{1+n})$. Following the proof of Lemma 1.1 of Section II in [4], we see that the choice of test function $\varphi = \eta (u_{\epsilon } - \epsilon ) (u_\epsilon - \delta )^{-1}$ with $\delta \in (0,\epsilon )$ gives (using an approximation argument as in Sect. 2.3)

as $\delta \rightarrow \epsilon$. We could extend the domain of integration on the last line from $\{ u > \epsilon \}$ to ${\mathbb {R}}^{1+n}$ because $|A(t,x,u_\epsilon ,\nabla u_\epsilon )| \le \Lambda |\nabla u_\epsilon |^{p-1}$ by (2.1) and $\nabla u_{\epsilon } = 0$ almost everywhere in $\{ u \le \epsilon \}$. Hence the truncated function $u_\epsilon$ is a subsolution that is bounded from below by $\epsilon > 0$.

The following lemma is stated in [12] for subsolutions u with $u \ge \epsilon > 0$ but approximating by truncations as above, we can use it for all non-negative subsolutions $u \ge 0$.

Lemma 2.2

(Lemma 5.1 [12]). Consider weak subsolutions to (2.1) and (2.2). There exist positive constants $C = C(n,p, \Lambda )$ and $\theta (n,p)$ such that for all $\sigma \in (1,2)$, all $s > 0$ and all weak subsolutions $u \ge 0$ in

$$\begin{aligned} Q_{2R,(2R)^{p}} = I_{(2R)^{p}} \times B_{2R} \end{aligned}$$

it holds

2.6 Energy estimate

Next we derive an energy estimate for the solution. The proof is standard, but we repeat the short argument for completeness.

Lemma 2.3

(Caccioppoli estimate). There is a constant $C = C(n,p,\Lambda )$ such that for all non-negative weak solutions u, for all $1\le a < b \le 2$, and for all space time cylinders $Q_{r,r^{p}} = I_{r^{p}} \times B_{r}$

(2.3)

Proof

As the structure of the Eq. (2.2) is scaling and translation invariant, it suffices to prove the estimate in the case $Q = (-2^{-1},2^{-1}) \times B(0,1)$. Consider a smooth function $\eta$ with

$$\begin{aligned} \chi _{aQ} \le \eta \le \chi _{bQ} ,\qquad |\partial _t \eta | + |\nabla \eta | \le 2 (b-a)^{-1}. \end{aligned}$$

Let $s \in (-a,a)$ and $h \in (0,a-s)$. Let $\tau$ be the piecewise linear function of one variable with

$$\begin{aligned} \chi _{(-\infty , s]} \le \tau \le \chi _{(-\infty , s+h]}, \qquad |\tau '| \le h^{-1}. \end{aligned}$$

We use $\varphi = \eta ^{p} \tau u$ as a test function in (2.2).

We start by estimating the first term on the left hand side of the claimed estimate. Note first that

$$\begin{aligned} u^{p-1} \varphi _t = u^{p-1} u_t \eta ^{p} \tau + u^{p } ( \eta ^{p} \tau )_t = p^{-1}(u^{p})_t \eta ^{p} \tau + u^{p} (\eta ^{p} \tau )_{t}. \end{aligned}$$

Integrating by parts in the time variable and using the definition of $\tau$

By the Eq. (2.2) and the structural condition (2.1)

(2.4)

Applying Young’s inequality to the second term, we bound it by

Putting the estimates together we obtain

Sending $h \rightarrow 0$ and taking the supremum over $s \in I_{ar^{p}}$, we conclude the bound for the first term on the left hand side of (2.3). The second term is clear by sending $s \rightarrow a$. $\square$

Remark 2.4

By essentially the same proof, we see that there is $C= C(n,p,\Lambda )$ such that given a general cylinder $Q_{r,s} = I_s \times B_r$ and $1\le a <b \le 2$, then for all non-negative solutions u

(2.5)

We argue as before, but instead of applying Young’s inequality to the right hand side of (2.4), we accept the second term to the right hand side of (2.5). This form of the energy estimate will also be needed later.

Lemma 2.5

Let u be a non-negative weak solution to (2.2). Let $\eta \in C_{c}^{\infty }({\mathbb {R}}^{n})$. Then it holds

$$\begin{aligned} \left|\int _{{\mathbb {R}}^{n}} u(s,x)^{p-1} \eta (x) \, dx - \int _{{\mathbb {R}}^{n}} u(x,t)^{p-1} \eta (x) \, dx \right|\le \Lambda \int _{s}^{t} \int _{{\mathbb {R}}^{n}} | \nabla u|^{p-1} |\nabla \eta | \, dxdt. \end{aligned}$$

Proof

Take the piecewise linear $\tau _h$ such that $\chi _{(s,t)} \le \tau _h \le \chi _{(s-h,t+h)}$ with $|(\tau _h)'| \le h^{-1}$. Then the left hand side of the claimed inequality equals

$\square$

3 Intrinsic cylinders

Consider a cylinder $Q_{\delta r,r^{p}}$ with $\delta \in (0,1]$. Fix a number $K \ge 1$. Given a fixed value of $\alpha \ge 1$, we call a cylinder K-sub-intrinsic if

(3.1)

and K-super-intrinsic if

(3.2)

A cylinder that is both super-intrinsic and sub-intrinsic is said to be intrinsic. A general cylinder $Q_{\delta r, r^{p}}$ may or may not satisfy these conditions for a pair of values $\alpha$ and K. The argument in [1] is based on constructing a cover of the level set of the gradient of the solution so that every cylinder in the cover satisfies the conditions above with $\alpha = 1$. We carry out the corresponding construction for larger values of $\alpha$.

Proposition 3.1

Fix $\delta$, r and a cylinder $Q_{\delta r, r}$. Let $\alpha \ge 1$ and assume that one of the alternatives in (3.2) holds. Then for a constant $C = C(n,p,\Lambda ,\alpha ,K)$

Proof

We cover $Q_{\delta r, r^{p}}$ by cylinders $Q_i$ of dimensions $(\delta r)^{p} \times \delta r$. We let $1< \gamma< \beta <2$. as we aim for applying the iteration Lemma 2.1, we can let all the constants appearing on the right hand side of the following estimates grow polynomially on $(\gamma -1)^{-1}(\beta - \gamma )^{-1}$.

As $\gamma \in (1,2)$, by Lemma 2.2

By the Caccioppoli inequality for general cylinders (2.5)

We assume that one of the alternatives in (3.2) holds. We start with the case when the first alternative in (3.2) holds.

First, note that as $1< \beta < 2$, we know that $Q_{\beta \delta r, (\beta r)^{p}} \subset Q_{ 2 \delta r, (2 r)^{p}}$ and consequently (3.2) implies

Using this as an upper bound for $\delta ^{-p}$, we estimate

Applying Hölder’s inequality to the third factor, we get an upper bound by

Applying Young’s inequality with $\epsilon$, we bound this by

Bounding $L^{\alpha }$ norm by $L^{\infty }$ norm, simplifying the exponents and applying Young’s inequality again, we bound the quantity inside the square bracket by

Multiplying through by $\delta ^{p}$, we have concluded

so that in particular

where the constant C grows polynomially in $\gamma - \beta$. This estimate is amenable for an application of the iteration lemma 2.1 so the proof is complete if $Q_{\delta r, r^{p}}$ satisfies the first condition in (3.2).

It remains to study the case when the second alternative in (3.2) holds instead of the first one. In that case we simply conclude

so that by Young’s inequality

Hence the proof is complete by Lemma 2.1. $\square$

4 Construction of a differentiation basis

We use the intrinsic scaling given by

as a model for the construction of a basis of almost intrinsic cylinders.

As before, we keep $p > 2$ fixed throughout the section. We also fix $\alpha > (n/2)(1-p/2)$. Let $R > 0$ and consider a cylinder $Q_{R,R^{p}} = I_{R^{p}} \times B_R$. Let $C_{0}$ be a large constant whose exact value we will fix later. Consider a non-negative function $u \in L^{\alpha p}_{loc}({\mathbb {R}}^{1+n})$, and consider numbers $\lambda \ge C_0 \lambda _0$ where

Given $z = (t,x) \in Q_{2R,(2R)^{p}}$ and $\rho \in (0,R]$, define

(4.1)

When z is fixed and no confusion can arise, we drop it from the notation. The minimum is taken in order to make $\rho \mapsto d_z(\rho )$ an increasing function. As it is not strictly increasing, we cannot directly invert it. We define instead for $\eta \in (0,1]$.

$$\begin{aligned} \rho _{max}(z, \eta ) = \max \{ r : d_z( r) = \eta \} . \end{aligned}$$

(4.2)

If no confusion can arise, we drop z from the notation. It either holds

(4.3)

or $\eta = 1$.

For brevity, we denote $S(z,\rho ) := Q_{d_z(\rho ) \rho , \rho ^{p}}(z)$. Again, we drop z from the notation whenever convenient. We will use the sets $S(z,\rho )$ as a basis for the covering argument to follow. If the number $\lambda$ is taken to be the appropriate mean value of the gradient of u, then the cylinders $S(z,\rho )$ will be sub-intrinsic in the sense of (3.1).

Proposition 4.1

Let p, $\alpha$, $C_0$, R, $Q_{R,R^{p}}$ and u as above be given. Then

• (i) For all $z \in Q_{2R,(2R)^{p}}$, it holds $d_z( \rho ) > 0$.

• (ii) For all $z \in Q_{2R,(2R)^{p}}$, $d_z(\rho )$ is a continuous and increasing function in $\rho$.

• (iii) If $0<\rho \le s \le R$, then for all $z \in Q_{2R,(2R)^{p}}$ it holds $d_z(\rho ) \le d_z(s)$ and

  $$\begin{aligned}d_z( s ) \le \left( \frac{s}{\rho } \right) ^{\frac{(n+p \alpha + p)(p-2)}{2 \alpha p - n(p-2)}} d_z( \rho ).\end{aligned}$$

  In particular $S(z,\rho ) \subset S(z,s)$.

• (iv) Let $1 < N \le 4^{-1} (4C_0)^{(\alpha p)/(n+p+\alpha p)}$. If $\rho \in [R/N,2R]$, then for all $z \in Q_{2R,(2R)^{p}}$

  $$\begin{aligned} d_z(\rho ) = 1. \end{aligned}$$

• (v) There are constants $c_i = c_i(n,p,\alpha )$, $i \in \{1,2\}$, so that if $z,w \in Q_{2R,(2R)^{p}}$, $0< r \le R$ and $S(z, r ) \cap S(w,r) \ne \varnothing$, then

  $$\begin{aligned} S(z,r) \subset S(w, c_1 r ) \end{aligned}$$

  and

  $$\begin{aligned} \frac{1}{c_2} d_z(r) \le d_w(r) \le c_2 d_z(r) . \end{aligned}$$

Proof

We start with the first item. Simplifying the expression defining $d_z( \rho )$ in (4.1), we write the relevant left and right hand sides as

(4.4)

Now $L(z,r,\cdot )$ is increasing and $L(z,r,\delta ) \rightarrow 0$ as $\delta \rightarrow 0$. The right hand side $R(\cdot )$ is decreasing and $R(\delta ) \rightarrow \infty$ as $\delta \rightarrow 0$ because

$$\begin{aligned}\beta := \frac{n(p-2) - 2 \alpha p}{\alpha p (p-2)} < 0.\end{aligned}$$

This is the key point which imposes the lower bound on $\alpha$. Hence there is a positive $\delta > 0$ so that $L(z,r,\delta ) < R(\delta )$ and consequently $d_z(r) > 0$.

To verify the second item, we first consider

$$\begin{aligned} {\tilde{d}}_z(\rho ) = \sup \{ \delta \in (0,1] : L(z,\rho ,\delta ) \le R(\delta ) \}. \end{aligned}$$

(4.5)

We first show that ${\tilde{d}}(\rho )$ (we suppress z from now on) is continuous. Take any $r \in (0,R]$. We first show that $\limsup _{\rho \rightarrow r } {\tilde{d}}(\rho ) \le {\tilde{d}}(r)$. This is satisfied by definition in case ${\tilde{d}}(r)=1$. In the other case, when ${\tilde{d}}(r)<1$, then (again by definition), for all $1>\delta > {\tilde{d}}(r)$ the condition (4.4) is violated so that $L(z,r,\delta ) > R(\delta )$. As $L(z,\rho ,\delta )$ is continuous in $\rho$, it holds $L(z,\rho ,\delta ) > R(\delta )$ for $|r-\rho |$ small enough. For such $\rho$ we then have $\delta > {\tilde{d}}(\rho )$ and consequently $\limsup _{\rho \rightarrow r } {\tilde{d}}(\rho ) \le {\tilde{d}}(r)$. To prove $\liminf _{\rho \rightarrow r } {\tilde{d}}(\rho ) \ge {\tilde{d}}(r)$, suppose for contradiction that $\liminf _{\rho \rightarrow r} {\tilde{d}}(\rho ) = \theta {\tilde{d}}(r)$ for some $\theta < 1$. Then there is a sequence $\rho _i \rightarrow r$ so that ${\tilde{d}}(\rho _i) = \theta _i {\tilde{d}}(r)$ for all i and $\theta _i \rightarrow \theta < 1$. Moreover, as L is continuous and increasing and R continuous and decreasing, we see that the supremum in (4.5) is a maximum. Then

which is a contradiction as the exponent of $\theta$ is negative. Finally, taking the minimum preserves continuity so the continuity claim on $d_z(r)$ in the second item follows. The fact that $d_z(r)$ is monotone increasing is immediate as the definition (4.1) is in terms of a minimum.

The first inequality in the third item is an immediate consequence of the second item. To prove the other bound, take $0 < \rho \le s \le R$. Denote $\rho _{max}(d(\rho ) ) := {\tilde{\rho }}$ and $\delta := d(\rho ) = d({\tilde{\rho }})$. If $s \le {\tilde{\rho }}$, it holds $d(\rho ) = d(s)$ and the claimed bound is trivially satisfied. Hence we can assume $s > {\tilde{\rho }}$. We recall that by (4.3) Eq. (4.4) holds now with equality $L(z,{\tilde{\rho }}, \delta ) = R(\delta )$. Then by the definitions

so that using $\beta < 0$, $\rho \le {\tilde{\rho }}$ and the fact that $d_z(\cdot )$ is increasing we see

$$\begin{aligned}d(s) \le \left( \frac{s}{\rho } \right) ^{\frac{(n+p \alpha + p)(p-2)}{2 \alpha p - n(p-2)}} d( \rho ) .\end{aligned}$$

This concludes the proof of the third item.

It remains to prove the last two items in the list. Consider two points z and w and a length r so that $S(z, r ) \cap S(w,r) \ne \varnothing$. We want to show $S(z,r) \subset S(w, c_1 r )$. This is trivially true for $c_1 = 3$ if $d_z(r) \le d_w(r)$. Let $N \ge 1$. If $r \in [R/N,2R]$, it holds

Hence, if we choose $C_0 \ge 4^{-1}(4N)^{\frac{n+p}{\alpha p} + 1}$, then any $\delta$ with

$$\begin{aligned} \delta ^{-\frac{n}{\alpha p} - 1} \le \delta ^{- \frac{p}{p-2}} \end{aligned}$$

satisfies $\delta \le d_w(r)$. In particular because $\alpha > (n/2)(1-2/p)$, this is the case for all $\delta \in (0,1]$. This proves the fourth item of the claim as a side product. When $r \ge R/10$, we can also use this with $N = 10$ to conclude $d_w(r) = 1 \ge d_z(r)$ so that the claim in the fifth item follows with $c_1 = 3$.

It remains to deal with the case when $r < R / 10$ and $d_z(r) > d_w(r)$. For a moment, we denote

$$\begin{aligned} \delta _z = d_z(r), \quad \delta _w = d_w(r), \quad \rho _w = \rho _{max}(w, \delta _w) \end{aligned}$$

Because $\delta _z > \delta _w$ and $\rho _w \ge r$, it follows

$$\begin{aligned} Q_{ 3 \delta _z \rho _w , ( 3 \rho _w )^{p} }(z) \supset Q_{ \delta _w \rho _w, \rho _w^{p} }(w) .\end{aligned}$$

Then by monotonicity of $d_z(\cdot )$ and the definitions

so that

$$\begin{aligned} \delta _z \le 3^{- \frac{1}{\beta } \left( \frac{n+p}{\alpha p}+1 \right) } \delta _w. \end{aligned}$$

Consequently, there exist constants $c_1$ and $c_2$ as claimed. $\square$

The following lemma is a formulation of a Vitali type covering theorem, and we quote it from [8]. The properties established in the previous proposition show that the basis $\{S(z,r): z \in {\mathbb {R}}^{n} , \ r > 0\}$ satisfies the assumptions.

Lemma 4.2

(Lemma 3.2 in [8]). Let

$$\begin{aligned} \{U(x,r) : x \in \Omega ,\, r\in (0,R]\} \end{aligned}$$

be a family of open sets which satisfy the following properties

• (i) Nestedness:

  $$\begin{aligned} \text { If } \quad x\in \Omega \quad \text { and } \quad 0<s<r\le R, \quad \text {then} \quad U(x,s)\subset U(x,r); \end{aligned}$$

• (ii) Almost uniform shape: There exists a constant $c_1 > 1$, such that

  $$\begin{aligned} \text {if} \quad U(x,r)\cap U(y,r)\ne \emptyset , \quad \text {then} \quad U(x,r)\subset U(y,c_1r). \end{aligned}$$

• (iii) Doubling property: There exists a constant $a>1$ such that, for all $r\in (0,R]$,

  $$\begin{aligned} 0< |U(x,2r) |\le a |U(x,r) |<\infty . \end{aligned}$$

Then we can find a countable and disjoint subfamily $\{ U_i \}$, such that

$$\begin{aligned} \bigcup _{x\in \Omega } U(x,r_x) \subset \bigcup _{i} {\tilde{U}}_i, \end{aligned}$$

where ${\tilde{U}}_i=U(x_i,2c_1 r_{x_i})$, $|U_i|\sim |{\tilde{U}}_i|$ and

$$\begin{aligned} |\Omega | \le c\sum _i |U_i |, \end{aligned}$$

where the constant $c>1$ depends only on $c_1$, a, and the dimension M.

5 A Gehring type argument

To conclude the Gehring lemma for the gradient of the solution, we study coverings of its level sets. Although the construction of S(z, r) only gave us sub-intrinsic cylinders, we can extract some additional information from the actual stopping time construction. The stopping cylinders from the sub-intrinsic basis will turn out to be intrinsic in the sense of (3.1) and (3.2).

Fix a center point in the space time, let $R > 0$ and fix

$$\begin{aligned} \alpha > \max \left\{ \frac{n}{2} \left( 1- \frac{2}{p}\right) , 1+ \frac{p}{n} \right\} . \end{aligned}$$

(5.1)

The lower bound $1+p/n$ is related to use of (iv) of Proposition 4.1, and it is likely that it can be lowered by replacing the equation $d_z(\rho ) = 1$ there by a smaller lower bound on $d_z(\rho )$ following the reasoning of [1]. However, as the particular choice of $\alpha$ only plays a qualitative role in our argument, due to Proposition 3.1, we do not attempt to optimize its exact value.

Fix a cylinder $Q_{4R,(4R)^{p}}$ and let

In what follows, we consider sets $S(z,\rho )$ constructed using a value of $\alpha$ as in (5.1). Fix $R\le R_1 < R_2 \le 2R$ and denote

$$\begin{aligned} E (r, \lambda ) = Q_{r,r^{p}} \cap \{ |\nabla u| > \lambda \} \cap \{ \text {Lebesgue points of} \ |\nabla u| \} \end{aligned}$$

(5.2)

for $r \in (0,2R)$.

Lemma 5.1

There exist constants $D = D(n,p,\Lambda )$ and $K = K(n,p,\Lambda ,D)$ such that the following holds. Let u be a non-negative weak solution to (2.2) and (2.1). Let $C_0 = [4 D R / (R_2 - R_1) ]^{1+ n/p}$ and $\lambda \ge C_0 \lambda _0$. Then for almost every $z \in E(R_1,\lambda )$ there is $\rho _z \in (0,(R_2-R_1)/(2D))$ such that

• it holds for all $\rho \in [ \rho _z, 2R)$

  

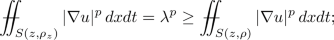
• every modified cylinder ${\tilde{S}}(z,\rho _z) := Q_{D d(\rho _z) \rho _z , (D\rho _z)^{p} }$ is K-intrinsic with $\alpha = 1$ in the sense of (3.1) and (3.2).

Proof

We consider a positive number D, whose exact value will be determined in the course of the proof. We set $C_0 = (4D R /(R_2-R_1))^{(n+p)/p}$. Let $z \in E(R_1, \lambda )$ and $\rho \le R_2- R_1$. By the assumption $\lambda \ge C_0 \lambda _0$ and hence

(5.3)

Because $\alpha > 1+p/n$, it holds

$$\begin{aligned} \frac{\alpha p}{n+p+\alpha p} \ge \frac{p}{n+p} \end{aligned}$$

and because $C_0 \ge 1$ it further holds

$$\begin{aligned} C_0^{\frac{\alpha p}{n+p+\alpha p}} \ge \frac{4DR}{R_2-R_1} \end{aligned}$$

so that if $\rho \ge (R_2-R_1)/(2D)$, then by the fourth item in Proposition 4.1 it holds $d_z(\rho ) = 1$. For these values of $\rho$, the right hand side of (5.3) is bounded by

$$\begin{aligned} 4^{n+p} (R/\rho )^{n+p} C_0^{-p} \lambda ^{p} \le \lambda ^{p}. \end{aligned}$$

As

is continuous, we define $\rho _z$ to be the maximal number in $(0,(R_2-R_1)/(2D)]$ such that

By the Lebesgue differentiation theorem such a number exists for almost every $z \in E(R_1,\lambda )$. By continuity, the inequality above holds as an equality for the maximal $\rho _z$, and the reverse inequality holds for all $\rho > \rho _z$ by maximality of $\rho _z$. This concludes the argument for the first item in the lemma.

To prove the second item, fix $z \in Q_{R_1,R_1^{p}}$ and take the cylinder $S(z,\rho _z) = Q_{d_z(\rho _z) \rho _z, \rho _z^{p}}$ as constructed above. We show first that $Q_{D\rho _z d(\rho _z) , (D \rho _z)^{p}}$ satisfies (3.1) and (3.2) with $\alpha$ as specified in (5.1). We start with (3.1). Note that for all $s \in [\rho _z, R]$

(5.4)

as follows from item (iii) of Proposition 4.1. By (5.4) with $s = 2D \rho _z$

(5.5)

Further, by (ii) and (iii) of Proposition 4.1$d_z( \rho _z) \sim d_z( 2D \rho _z)$. This together with the definition of $d_z(\rho _z)$ and Eq. (5.5) implies

which is (3.1) for some value of K only depending on n, p, $\alpha$ and D.

Next we verify the other condition (3.2). We abbreviate $d_z(\rho _z) = \delta$. If $\delta = 1$, the second alternative in (3.2) is satisfied and there is nothing to prove. Assume $\delta < 1$ and consider first the case

$$\begin{aligned}\rho _z \le \rho _{max}(z,d_z(\rho _z) ) \le D \rho _z .\end{aligned}$$

The function $\rho _{max}$ is the one defined in (4.2). Then by (4.3) and (5.5)

which is the first alternative in (3.2).

We are left with the case $\rho _{max}(z, \delta ) > D \rho _z$, and we shall show that the second alternative in (3.2) holds.

Set

$$\begin{aligned}\rho _{*} = \frac{ \rho _{max}(z, \delta )}{D}\end{aligned}$$

so that $\rho _* \in (\rho _z, \rho _{max}(z, \delta ))$. Now by (4.3) and Proposition 3.1 we find

None of our definitions applies to values of u in the large cylinder above, but we do know about the values of $\nabla u$. On the right hand side of the display above, we estimate by the Poincaré inequality

By (5.5), the first term is bounded by $C \lambda$, which is good. The second term has a spatial support smaller than previously but still rather long support in time. This can be dealt with using the equation.

As $p\ge 2$, we can use Jensen’s inequality to bound the second term by

According to Lemma 2.5, Hölder’s inequality and the definition of $\rho _{*}$ and $\delta$, the first term is bounded by

Writing $q = p-1$ and $q' = (p-1)/(p-2)$, we use Young’s inequality with $\epsilon$ to bound

$$\begin{aligned} C \delta ^{-\frac{p}{p-1}}\lambda = ( \lambda ^{\frac{1}{q'}} \delta ^{-\frac{p}{p-1}}) \cdot (C\lambda ^{\frac{1}{q}}) \le \epsilon \lambda \delta ^{- \frac{p}{p-2}} + C_\epsilon \lambda . \end{aligned}$$

As the first term can be sent back to the left hand side, we are done with this expression. Finally, by Hölder’s inequality

Altogether we have shown

$$\begin{aligned} \lambda \delta ^{-\frac{p}{p-2}} \le C_1 \lambda + \epsilon \lambda \delta ^{-\frac{p}{p-2}} + \frac{C_2}{D} \delta ^{-\frac{p}{p-2}} \lambda . \end{aligned}$$

As $C_2$ is independent of D, we can choose D large enough so that $\delta ^{-\frac{p}{p-2}} \le C$ for a constant only depending on n, p, $\alpha$ and $\Lambda$. This is the second case of (3.2).

As we have shown that (3.1) and (3.2) hold for $Q_{D \delta \rho _z , (D \delta \rho _z)^{p} }$ with $\alpha$ as specified in (5.1), it follows from Proposition 3.1 and the fact

due to the maximality of $\rho _z$ that they also hold for $Q_{2D \delta \rho _z , (2D \delta \rho _z)^{p} }$ and $\alpha = 1$.

$\square$

We can now use the following reverse Hölder inequality from [1] and the rest of the argument is standard.

Proposition 5.2

(Proposition 6.1 in [1]). Let $Q_{\delta r,r^{p}}$ be such that (3.1) and (3.2) hold with $\alpha = 1$. Then

where $q = \max ( np/(n+2), p-1 )$ and $C = C(n,p,\Lambda ,K)$.

Proposition 5.3

It holds

where $E(R_2, \lambda )$ is the set from (5.2) and $\lambda$ as in Lemma 5.1.

Proof

The sets ${\tilde{S}}(z,r) = Q_{D r d_z(r) , (D r)^{p}}(z)$ are defined as the anisotropic $(D^{p},D)$-dilations of S(z, r) (as in Lemma 5.1). The basis ${\tilde{S}}(z, r)$ satisfies the hypotheses of Lemma 4.2 as can be seen from Proposition 4.1. Consider the cover $\{ {\tilde{S}}(z, \rho _z ) : z \in E(R_1, \lambda ) \}$ of the set $E(R_1, \lambda )$ where the cylinders ${\tilde{S}}(z, \rho _z)$ are the ones from Lemma 5.1 and the constant $c_1$ is as in Lemma 4.2. By Lemma 4.2, we can extract a countable collection of points $\{z_i\}$ so that

$$\begin{aligned}E(R_1, \lambda ) \subset \bigcup _{i} {\tilde{S}}(z_i, 2c_1 \rho _i) \subset E(R_2, \lambda ), \quad {\tilde{S}}(z_i, \rho _i ) \quad \text {are disjoint}. \end{aligned}$$

Because for any $\epsilon > 0$

it holds for $\epsilon = (2c)^{-1}$ that

By the inequality in Lemma 5.1, it holds

so that

Because of the (trivial) estimate

and the fact that $\epsilon$ only depends on the data, we conclude

as was claimed. $\square$

Proof of Theorem 1.1

Given the Proposition 5.3, the theorem follows by a standard argument for Gehring’s lemma. This has been done, for instance, in section 7.6 of [1] starting from the inequality as given in Proposition 5.3. The result in [1] comes with an additional constant term 1 on the right hand side, but that can be removed as the structure of the PDE is invariant under scaling. Indeed, by applying the result to $u(\delta ^{-p}t, \delta ^{-1}x)$ on $Q_{\delta \rho , (\delta \rho )^{p}}$ and sending $\delta \rightarrow 0$ one recovers the scaling invariant version of the estimate. $\square$