3-D DC Resistivity Forward Modeling Using the Multi-resolution Grid

Abstract

We implemented a novel multi-resolution grid approach to direct current resistivity (DCR) modeling in 3-D. The multi-resolution grid was initially developed to solve the electromagnetic forward problem and helped to improve the modeling efficiency. In the DCR forward problem, the distribution of the electric potentials in the subsurface is estimated. We consider finite-difference staggered grid discretization, which requires fine grid resolution to accurately model electric potentials around the current electrodes and complex model geometries near the surface. Since the potential variations attenuate with depth, the grid resolution can be decreased correspondingly. The conventional staggered grid fixes the horizontal grid resolution that extends to all layers. This leads to over-discretization and therefore unnecessary high computational costs (time and memory). The non-conformal multi-resolution grid allows the refinement or roughening for the grid’s horizontal resolution with depth, resulting in a substantial reduction of the degrees of freedom, and subsequently, computational requirements. In our implementation, the coefficient matrix maintains its symmetry, which is beneficial for using the iterative solvers and solving the adjoint problem in inversion. Through comparison with the staggered grid, we have found that the multi-resolution grid can significantly improve the modeling efficiency without compromising the accuracy. Therefore, the multi-resolution grid allows modeling with finer horizontal resolutions at lower computational costs, which is essential for accurate representation of the complex structures. Consequently, the inversion based on our modeling approach will be more efficient and accurate.

1 Introduction

The direct current resistivity (DCR) method is one of the classical geophysical techniques, which is nowadays widely used in the mineral exploration (Oldenburg et al. 1997; Schoor 2005; Zhang et al. 2015), groundwater (Andrade 2011; Thompson et al. 2012), engineering (Chambers et al. 2014; Lysdahl et al. 2017), and environmental problems (LaBrecque et al. 1996; Rosales et al. 2012). The method is often used both for ground measurements and in the boreholes (Loke et al. 2013). Subsequently, the measured electric potential data are inverted to obtain a resistivity image of the subsurface to a depth depending on the separation distance between electrodes.

The forward modeling is an essential step of any inversion algorithm. Over the past few decades, the 1-D (O’Neil and Merrick 1984; Das and Verma 1980) and 2.5-D (Mundry 1984; Pidlisecky and Knight 2008) modeling of the DCR has been developed and used routinely. The 3-D DCR surveying became feasible with the development of the multi-electrode and multi-channel systems (Dahlin 2016; Loke et al. 2013). Therefore, the data in 3-D case can only be fully exploited using 3-D modeling and inversion algorithms. There is a number of algorithms developed so far for 3-D DCR modeling based on the integral equation method (Schulz 1985; Mendez-Delgado et al. 1999), finite-element method (Li and Spitzer 2002a; Rucker et al. 2006; Ren et al. 2018) and finite-difference method (Dey and Morrison 1979; Scriba 1981; Spitzer 1995; Zhang et al. 1995; Loke and Barker 1996; Zhao 1996; Wang et al. 2000; Wu et al. 2003a; Śebastien Penz et al. 2013). The integral equation approach is efficient to handle the models with a few anomaly bodies. On the contrary, the commonly used finite-element method (FEM) and finite-difference method (FDM) are more suitable to cope with models having an arbitrary number of structures (Li and Spitzer 2002b; Wu et al. 2003b). Despite the efforts to improve the efficiency, available 3-D modeling algorithms are still heavy in terms of computational requirements. Since the inversion requires numerous forward calculations, optimized modeling algorithm naturally leads to an efficient inversion.

The electrical field potentials induced by the current electrodes create a singularity effect around the source positions. In order to cope with it, the secondary potentials’ formulation is often used (Lowry 1989). However, for both of the total and secondary field approaches, the simulated electric field potentials generally attenuate with depth, meaning that no significant variations can be expected at larger depth. Therefore, responses can be modeled on a grid using coarser resolution (discretization) in the deeper regions, without loss of accuracy.

The conventional staggered (SG) grid employs rectangular cells to discretize the model, which simplifies the gridding process. However, the conformal SG grid fixes the horizontal resolution, which extends to all depths. This may cause over-discretization of the deeper regions, hence leading to redundant computational requirements. The unstructured grid, generally adopted by FEM, commonly employs the tetrahedral cells to discretize the model, which allows local refinement and roughening to avoid the over-discretization condition.

We present a new 3-D DCR forward modeling based on a finite-difference multi-resolution (MR) grid approach. The MR grid was initially developed for the electromagnetic forward problem and proved to be an efficient alternative to the conventional structured finite-difference approach (Cherevatova et al. 2018). The MR grid is a simplified implementation of the non-conformal grid, it resembles the approach suggested in the octree scheme of Haber and Heldmann (2007), but limited to only the horizontal resolution’s refinement. The MR grid can be derived from a fundamental SG grid by horizontally combining adjacent cells. Thus, MR grid represents a vertical stack of several SG grids (sub-grids) with different horizontal resolutions. In this way, the forward modeling operators developed for SG grid are readily applied for each sub-grid.

The main difficulty in MR modeling is the definition of the forward operators at common interfaces between the adjacent sub-grids. Several approaches to defining differential operators at the interfaces were considered and tested in Cherevatova et al. (2018). Generally, all grid nodes and edges are separated into two groups: ‘active’ and ‘inactive’. Inactive elements are not evaluated in the solution, but represented by their neighboring active elements through interpolation. This allows defining differential operators in the physically correct way at the common interfaces. The only difference between the approaches to handle operators on the interfaces lies in the definition of active and inactive grid elements and the interpolation scheme. As a result, different accuracy might be achieved, depending on the selected approach. Following the conclusion of Cherevatova et al. (2018), we selected the Coarse Active (CA) approach, which is shown to be the most efficient and accurate. Moreover, within the CA approach the discrete divergence operator is the adjoint of the discrete gradient operator, which leads to the symmetry of the coefficients matrix. In this case the linear equations set can be solved efficiently using the Preconditioned Conjugate Gradient method. As a result, the time required for solving the system of equations is nearly linear with respect to the degrees of freedom (DoF). The MR grid allows us to substantially reduce the amount of DoF leading to a significant speed-up of the forward modeling.

The paper is organized as follows. In the methods part, we briefly describe the standard staggered grid formulation of the DCR modeling problem, and its modification to define the problem on the multi-resolution grid. In order to verify our newly developed algorithm, in the following sections we present several synthetic examples to examine the speed and accuracy of the MR solution.

2 Methods

The DCR forward modeling problem can be viewed in terms of solving the Poisson-type equations for the electrical potentials $\varphi$ in a modeling domain $\varOmega$. The corresponding partial differential equations (PDEs) is:

$$\begin{aligned} \nabla \cdot [\sigma (x,y,z) \nabla \varphi (x,y,z) ]= -I \delta (x-x_0) \delta (y-y_0) \delta (z-z_0), \end{aligned}$$

(1)

where $\sigma (x,y,z)$ is the electrical conductivity arbitrarily distributed in $\varOmega$; $\nabla \cdot$ and $\nabla$ are the divergence and gradient operators, respectively. The right-hand side in Eq. (1) defines the source term, where I is the current intensity, $(x_0,y_0,z_0)$ denotes the current electrode’s coordinate, and $\delta (\cdot )$ is the delta function.

In order to solve the PDEs, boundary conditions are required on the boundaries confining $\varOmega$ into a finite space. In our approach, we implemented Neumann boundary condition on the top boundary $\varGamma _0$ to prevent the electrical current from flowing out. For the distant side boundaries $\varGamma _{\infty }$, we simply employed the Dirichlet boundary condition (Mufti 1976; Tripp et al. 1984) in our tests.

Since the multi-resolution (MR) grid is based on the conventional staggered (SG) grid, first we briefly describe the DCR modeling on SG grid. Then we explain the implementation of MR grid approach and emphasize its differences.

2.1 Staggered Grid Approach

The modeling domain $\varOmega$ on the SG is discretized into $N_{x}$, $N_{y}$ and $N_{z}$ rectangular cells in the x, y and z directions, respectively. The entire modeling domain is divided into $N_{c}$ cells ($=N_{x}\times N_{y}\times N_{z}$) in total, and each cell holds a constant conductivity value $\sigma$.

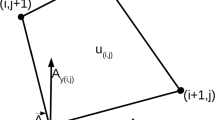
Nodes and edges are construction elements of the primary-grid. $N_{n}$ and $N_{e}$ denote the number of nodes and edges, respectively. Edge-lengths $L_{E}$ and cell-volumes $V_{C}$ are metric elements of the primary-grid. The dual-edges are defined as the lines between the adjacent cell-center points and constitute the dual-grid. Metric elements of the dual-grid include dual-cell-volumes $\tilde{V}_{C}$ and dual-face areas $\tilde{A}_{F}$, as shown in Fig. 1.

Fig. 1

Staggered grid discretization. Black points and solid lines are nodes and edges of the primary-grid, respectively. Dashed lines are dual-edges of the dual-grid. The abbreviations denote: $L_{E}$, the edge-length; $V_{C}$, the cell volume (e.g. the blue region); $\tilde{A}_{F}$, the dual-face area (e.g. the yellow face); $\tilde{V}_{C}$, the dual-cell-volume (e.g. the red region)

Using conventional SG grid finite-difference formulation, Eq. (1) can be represented in a discrete form as:

$$\begin{aligned} {[}{} \mathbf{G} ^ {\dagger } {\text {diag}} (\overline{\sigma }) \mathbf{G} {]} \mathbf{\varphi } = \mathbf{J}, \end{aligned}$$

(2)

where $\mathbf{J}$ is the source elements vector ($N_n\times 1$) defined on the nodes. The injected current is assumed to be distributed over $\tilde{V}_{C}$ of the dual-cell around the ‘lucky’ node where the current electrode is placed (Scriba 1981; Pidlisecky et al. 2007). The elements of $\mathbf{J}$ are:

$$\begin{aligned} \mathbf{J} = \left\{ \begin{array}{ll} 0&{}\quad \text {node} \ne \text { current electrode } \\ -\frac{I}{\tilde{V}_{C}}&{}\quad \text {node } = \text { current electrode}. \end{array}\right. \end{aligned}$$

(3)

On the left-hand side of Eq. (2), $\mathbf{\varphi }$ denotes a vector ($N_{n} \times 1$) of the unknown potential values defined on the grid nodes. $\mathbf{G}$ is the discrete gradient operator matrix ($N_e\times N_n$), which maps from nodes to edges and is derived as:

$$\begin{aligned} \mathbf{G} = {\text {diag}} (\mathbf{L}_{E}^{-1}) \overline{\mathbf{G}}, \end{aligned}$$

(4)

where $\overline{\mathbf{G}}$ is a sparse topology matrix ($N_e\times N_n$) of the first derivatives with $\pm 1$ non-zero entries mapping from nodes to edges; $\mathbf{L}_{E}^{-1}$ is a vector ($N_e\times 1$) with elements of reciprocal of the edge-lengths. The discrete divergence operator matrix $\mathbf{G}^{\dagger }$ ($N_{n} \times N_{e}$) is an adjoint of $\mathbf G$, which maps back from edges to nodes. $\mathbf{G} ^ { \dagger }$ can be derived using a topology matrix ($N_{n} \times N_{ e }$) combined with the metric weighting as well. It is readily verified that the transpose of $-\overline{\mathbf{G}}$ works as a reasonable approximation to the topology matrix of $\mathbf{G} ^ { \dagger }$ (Cherevatova et al. 2018), see the spatial illustrations and matrix forms of $\overline{\mathbf{G}}$ and $-\overline{\mathbf{G}}^{T}$ in Appendix. Thus, $\mathbf{G} ^ { \dagger }$ is defined as:

$$\begin{aligned} \mathbf{G} ^ { \dagger }=-{\text {diag}}\left( \tilde{\mathbf{V}}_{C}^{-1}\right) \overline{\mathbf{G}}^{T}{\text {diag}}(\tilde{\mathbf{A}}_{F}), \end{aligned}$$

(5)

where $\tilde{\mathbf{V}}_{C}$ and $\tilde{\mathbf{A}}_{F}$ are the dual-cell-volumes vector ($N_{n} \times 1$) and dual-face-areas vector ($N_{e}\times 1$), respectively.

The conductivity parameters, initially defined at cell centers, need to be mapped to the cell edges to evaluate current densities from the Ohm’s law. Hence, we need to estimate $\overline{{\sigma }}$ which represents the averaged conductivity vector ($N_e\times 1$) on the edges. This can be done using the volume-weighted averaging approach which maps from cells’ conductivity to $\overline{{\sigma }}$ as:

$$\begin{aligned} \overline{\sigma } = {\text {diag}} \left[ \left( \hat{\mathbf{W}}{} \mathbf{V}_{C}\right) ^{-1}\right] \hat{\mathbf{W}} {\text {diag}} \left( \mathbf{V}_{C}\right) \mathbf{\sigma } =\mathbf{W} \mathbf{\sigma }, \end{aligned}$$

(6)

where $\hat{\mathbf{W}}$ is a sparse averaging topology matrix ($N_e\times N_c$) mapping cells to edges, see Appendix for further details. $\mathbf{V}_{C}$ and $\mathbf{\sigma }$ are the cell volumes and cell conductivity vectors ($N_c\times 1$), respectively. Thus, the derived $\mathbf{W}$ is regarded as a volume-weighted averaging operator.

In short, Eq. (2) can be expressed as a system of linear equations:

$$\begin{aligned} \mathbf{A}\mathbf{\varphi }=\mathbf{b}, \end{aligned}$$

(7)

where $\mathbf{b}$ ($N_{n} \times 1$) represents the source term with boundary conditions; $\mathbf{A}$, i.e. the product of $\mathbf{G}^{ \dagger }{\text {diag}}(\overline{\sigma })\mathbf{G}$, denotes the derived non-symmetric coefficients matrix ($N_{n} \times N_{n}$). However, by multiplying both sides of Eq. (7) with $-{\text {diag}}(\tilde{\mathbf{V}}_{C})$, i.e. the corresponding dual-cell-volumes, we obtain a new coefficient matrix $\widetilde{\mathbf{A}}$, which is a symmetric and positive definite matrix, the source term is also changed to $\widetilde{\mathbf{b}}=-{\text {diag}}(\tilde{\mathbf{V}}_{C})\mathbf{b}$. Therefore the system of equations can be rewritten in the following form:

$$\begin{aligned} \left[ \overline{\mathbf{G}}^{T}{\text {diag}}(\tilde{\mathbf{A}}_{F}){\text {diag}}\left( \mathbf{W} \mathbf{\sigma } \right) {\text {diag}}\left( \mathbf{L}_{E}^{-1}\right) \overline{\mathbf{G}}\right] \mathbf{\varphi }=-{\text {diag}}(\tilde{\mathbf{V}}_{C})\mathbf{b}. \end{aligned}$$

(8)

A natural choice for solving a large symmetric system of linear equations would be one of the Krylov subspace iterative methods. We choose to solve Eq. (8) using the Preconditioned Conjugate Gradient (PCG) method, which takes advantage of the symmetry of $\widetilde{\mathbf{A}}$ and is superior to the generalized solvers (Spitzer 1995). As a preconditioner, the Symmetric Successive Over-Relaxation (SSOR) method is employed. The combination (SSOR-PCG) shows a fast and stable convergence in our tests. Later we refer to the left and right-hand sides of Eq. (8) as $\mathbf{A}\mathbf{\varphi }$ and $\mathbf{b}$ correspondingly omitting the tilde.

2.2 Secondary Field Formulation

The most significant potential variations appear around the current electrodes, causing the singular solutions at those points. Local refinement of the grid around the source region is one of the options to alleviate the numerical errors, but it requires very fine discretization around the current electrodes positions, and therefore, inevitably increases the computational costs. Alternatively, secondary field approach is commonly applied (Lowry 1989) to tackle this problem.

The total potential $\varphi$ can be decomposed into primary potential $\varphi _p$ and secondary potential $\varphi _s$. Primary potential $\varphi _p$ is the response of the background model, including the source. We use the homogeneous half-space as the background model, therefore $\varphi _p$ can be calculated using the analytical solution (Lowry 1989) as:

$$\begin{aligned} \varphi _p(r)=\frac{I}{4\pi \sigma _b}\left( \frac{1}{\left| r-r_0\right| }+\frac{1}{\left| r-r_0^*\right| }\right) , \end{aligned}$$

(9)

where $r_0$ and $r _ { 0 } ^ { * }$ are the positions of the actual and mirrored (against the surface) current electrodes, respectively; $\sigma _{ b}$ represents the conductivity of the background model.

Since $\varphi _p$ is generated from the same source as $\varphi$, meaning that the equations for the total potential and primary potential have the same right-hand side, we have:

$$\begin{aligned} \mathbf{A}\mathbf{\varphi }=\mathbf{A}\left( \mathbf{\varphi }_p+\mathbf{\varphi }_s\right) =\mathbf{A}_p\mathbf{\varphi }_p, \end{aligned}$$

(10)

where $\mathbf{A}_p$ is the coefficient matrix of $\mathbf{\varphi }_p$ that is derived in a similar manner as $\mathbf{A}$, but with $\sigma _{b}$. By reorganizing Eq. (10), we obtain an expression for the secondary potential:

$$\begin{aligned} \mathbf{A}\mathbf{\varphi }_s=\mathbf{b}_s, \end{aligned}$$

(11)

where $\mathbf{b}_s=\left( \mathbf{A}_p-\mathbf{A}\right) \mathbf{\varphi }_p$ is the source term of the secondary potentials. Since, $\mathbf{\varphi }_p$ is exactly evaluated using the analytical solution of Eq. (9), the new right-hand side could provide a correction effect to the $\mathbf{\varphi }_s$ solution.

2.3 Multi-resolution Grid Approach

In the following, we demonstrate the implementation of the MR grid for the DCR modeling. MR grid can be represented as a vertical stack of several sub-grids. Each sub-grid can be regarded as a standard SG grid. An example of MR grid is shown in Fig. 2a. We implemented the DCR modeling on both SG and MR grids within the ModEMM framework (Cherevatova et al. 2018), based on an object-oriented scheme (in Matlab). Thus, it allows the operations of the SG grid to be extended to the sub-grids in the MR grid.

Fig. 2

Multi-resolution grid with two sub-grids based on the CA approach (see 2.4). a Red interface denotes the common interface between upper and lower sub-grids. Only the active nodes and edges are shown. b Classification of the nodes and edges on the common interface. Green elements from the lower (coarser) sub-grid are active; red elements from the upper (finer) sub-grid are inactive

The horizontal resolution of each sub-grid ($N_{x}^{(i)}\times N_{y}^{(i)}$) is determined by the following rule:

$$\begin{aligned} N_{x}^{(i)}=\frac{N_{x}^{f}}{2^{Cs^{(i)}}}\,,\,\, N_{y}^{(i)}=\frac{N_{y}^{f}}{2^{Cs^{(i)}}}, \end{aligned}$$

(12)

where i denotes the index of the sub-grid, $N_{x}^{f} \times N_{y}^{f}$ is the finest horizontal resolution used in the whole MR grid, $Cs^{(i)}$ is the Coarseness parameter (a non-negative integer) of the $i\hbox {th}$ sub-grid. $N_{x}^{(i)}$ and $N_{y}^{(i)}$ between adjacent sub-grids can only change by a factor of two. It is noteworthy that $Cs^{(i)}$ is not only limited to increase with depth but also allowed to decrease. Thus, $N_{x}^{f}\times N_{y}^{f}$ is not fixed in the top sub-grid (although, we commonly implement it in this way), which could also be assigned to the lower sub-grids to describe complex geometries.

Based on the above rule, the MR grid can be derived from a fundamental SG grid with a discretization: $N_{x}^{f} \times N_{y}^{f} \times N_{z}^{f}$. First, one split the SG grid into $N_{sg}$ sub-grids, such as $\sum _{i=1}^{N_{sg}}N_{z}^{(i)}=N_{z}^{f}$, where $N_{z}^{(i)}$ is the vertical discretization of each sub-grid. Second, for a sub-grid with $Cs^{(i)} > 0$, horizontally combine each set of $2 ^ { Cs^{(i)} } \times 2 ^ { Cs^{(i)}}$ cells to form a coarser cell. Following the above rule, the discretization of the MR grid is only controlled by the fundamental SG grid and the parameters: $\left. \left[ Cs^{(i)} , N_{z}^{(i)} ; \right] \right| _ { i = 1 , N_{ sg } }$, which leads to a very simple gridding process. For instance, the MR grid in Fig. 2a with parameters: $\left. \left[ Cs^{(i)} , N_{z}^{(i)} ; \right] \right| _ {i = 1,2 } = ( 0,2 ; 1,2 )$ is derived from a $4 \times 4 \times 4$ SG grid. Alternatively, the discretization can start from the coarsest SG grid by refining the sub-grids, however, we always describe sub-grids relative to the finest sub-grid.

2.4 Multi-resolution Grid Elements Classification

Since each sub-grid could be regarded as a standard SG grid, at the interior of each sub-grid, the spatial relations between the grid elements are the same as the SG grid, therefore the forward operators ($\mathbf{G} ^ { \dagger }$, $\mathbf{G}$ and $\mathbf{W}$) have the same structure as Eqs. (4), (5) and (6). However, the main challenge in the MR grid implementation is the definition of the forward operators on the overlapped interface between the adjacent sub-grids, e.g. the red interface in Fig. 2a.

On a common interface, part of the grid elements (nodes and edges) from the finer sub-grid overlap with the grid elements from the coarser sub-grid, which will lead to redundant elements. In addition, due to the changing of horizontal resolution, the remained grid elements from the finer sub-grid without the corresponding partner from the coarser sub-grid will be ‘hanging’ on the interface. See an illustration of the interface in Fig. 2b.

The nodes and edges in the MR grid are classified into two groups: active and inactive elements. The active elements are involved in the calculation explicitly, whilst the inactive elements are eliminated from the solution. All the nodes and edges at the interior of the sub-grids are classified as active, whilst the choice at the common interface will affect the overall solution accuracy. Three approaches were considered and tested in Cherevatova et al. (2018). (1) Face Active (FA) case classifies the nodes and edges from the finer sub-grid as active and the elements from the coarser sub-grid as inactive similar to Haber and Heldmann (2007) results and provides operators symmetry; (2) Ghost Faces (GF) case is similar to FA, but it extends one ‘ghost’ interpolated finer layer into the coarser sub-grid, resulting in a second-order accuracy but lacks symmetry (Horesh and Haber 2011); (3) Coarse Active case (CA) is a reverse to FA that takes the nodes and edges from the coarser sub-grid as active. It has accuracy similar to GF but also maintains symmetry. Therefore, CA case is a preferable approach, which we used to implement the MR DCR modeling. Figure 2b shows the classification of CA case. Later we use $N_{n}^{active}$ and $N_{e}^{active}$ to denote the number of the active nodes and edges on MR grid, respectively.

2.5 Multi-resolution Grid Forward Modeling Operators

In order to construct the coefficient matrix $\mathbf{A}$, the discrete gradient operator $\mathbf{G}$ on MR grid should be defined. In a similar manner to SG grid, $\mathbf{G}$ is represented by its topology matrix $\overline{\mathbf{G}}$ mapping from active nodes to active edges and corresponding metric elements. As it was described before, inside the sub-grids, $\mathbf{G}$ is the same as the gradient operator on SG grid. However, we need to deal with the inactive elements on the common interfaces as well, this can be achieved by decomposing the topology operator $\overline{\mathbf{G}}$ into three matrices as:

$$\begin{aligned} \overline{\mathbf{G}}=\mathbf{R}_{coarse} \overline{\mathbf{G}}_{full} \mathbf{A}_{coarse}. \end{aligned}$$

(13)

Sparse matrix $\mathbf{A}_{coarse}$ ($N_{n} \times N_{n}^{active}$) interpolates a set of active nodes to a full set of nodes (both the active and inactive nodes). At the common interfaces, $\mathbf{A}_{coarse}$ has the different interpolation entries depending on the following conditions:

• 1. For an active node, $\mathbf{A}_{coarse}$ acts as a self-mapping operator, therefore the corresponding interpolation coefficient in $\mathbf{A}_{coarse}$ is 1.

• 2. For an inactive node from the finer sub-grid overlapping with an active node from the coarser sub-grid, e.g. the inactive and active nodes with label i1 and a1 respectively in Fig. 2b, the corresponding interpolation coefficient from a1 to i1 is 1 as well.

• 3. For an inactive node located on an active edge, the entries are defined by the linear interpolation. In Fig. 2b, the mapped inactive node i2 is interpolated from the adjacent active nodes a2 and a3.

• 4. For a ‘hanging’ inactive node located on a face of a coarser cell, it is linearly interpolated from four surrounding active nodes. For example, the inactive node with label i3 is interpolated by the active nodes with label a4 to a7 in Fig. 2b.

In general horizontally non-uniform case, the interpolation coefficients are derived by the corresponding metric elements.

Full gradient topology matrix $\overline{\mathbf{G}}_{full}$ is represented as a block diagonal matrix ($N_{ e } \times N_{n}$) with gradient topology operators $\overline{\mathbf{G}}^{(i)}$ of each sub-grid on the diagonal:

$$\begin{aligned} \overline{\mathbf{G}}_{full}= \left[ \begin{array}{lllll} \overline{\mathbf{G}}^{(1)}&{}&{}&{}&{}\\ &{}\ddots &{}&{}&{}\\ &{}&{}\overline{\mathbf{G}}^{(i)}&{}&{}\\ &{}&{}&{}\ddots &{}\\ &{}&{}&{}&{}\overline{\mathbf{G}}^{(N_{sg})}\end{array}\right] . \end{aligned}$$

(14)

Thus, $\overline{\mathbf{G}}_{full}$ is the gradient topology matrix of the full MR grid that maps from the full node set to the full edge set, and the sparse selection matrix $\mathbf{R}_{coarse}$ ($N_{e}^{active} \times N_{ e }$) picks out the rows corresponding to the active edges only.

It is also readily verified that the transpose of $-\overline{\mathbf{G}}$ is a good approximation to the topology matrix of the discrete divergence operator $\mathbf{G} ^ { \dagger }$ on MR grid, even around the common interface (Cherevatova et al. 2018), see the spatial illustrations and matrix forms of $\overline{\mathbf{G}}$ and $-\overline{\mathbf{G}}^{T}$ in Appendix. Thus, $\mathbf{G}$ and $\mathbf{G} ^ { \dagger }$ on MR grid can be derived in a similar manner as Eqs. (4) and (5) for SG grid. However, $\tilde{\mathbf{V}}_{C}$ ($N_{n}^{active} \times 1$) includes only dual-cell-volumes around the active nodes, $\mathbf{L}_{E}$ and $\tilde{\mathbf{A}}_{F}$ vectors ($N_{e}^{active} \times 1$) include only edge-lengths and dual-face-areas elements of the active edges, respectively.

$\overline{\sigma }$ ($N_{e}^{active} \times 1$) is only evaluated on the active edges and can be derived from Eq. (6) as well. The topology matrix $\hat{\mathbf{W}}$ maps from the cells set to the active edges set. However, the rows of $\hat{\mathbf{W}}$, which correspond to the active edges at the common interfaces, include more nonzero coefficients related to the extra cells from the adjacent finer sub-grid, see Appendix for further details.

We take the advantage of CA symmetry, i.e. $\mathbf{G}^{ \dagger }$ is well approximated by the adjoint of $\mathbf{G}$ similarly to SG case, therefore, the derived coefficients matrix $\mathbf{A}$ is also symmetric. In the MR case, the system of equations can also be solved efficiently using SSOR-PCG iterative solver, but the degree of freedom (DoF) of the system can be significantly decreased compared to the original SG grid.

3 Results

In this section, several examples were presented to verify the accuracy and efficiency of our algorithm. All the modeling of the SG and MR grid approaches were computed on a PC with 2.60 GHz CPU and 16GB memory.

3.1 Example 1

The first example, we considered a 1-D model with three layers. The layers’ resistivity and thickness were $(\rho ,\varDelta h;)=(100\; \varOmega {\text {m}},30\;{\text {m}};300\, \varOmega {\text {m}}, 30\;{\text {m}};10\; \varOmega {\text {m}},\sim )$ from top to bottom, as shown in Fig. 3. We calculated vertical electrical sounding data for Wenner-Schlumberger configuration. The electrodes spacing adopted $a = 20\,{\text {m}}$ and $n = 1$ to 8 levels (separation between the current and potential electrodes is $n \times a$).

Fig. 3

2D slice (central region, $\hbox {y}=0\,{\text {m}}$) of the model from example 1. Solid grid denotes the common discretization for both of SG and MR grids; dashed lines represent the removed edges in MR grid, which exist in SG grid; white lines highlight the common interfaces between the adjacent sub-grids in MR grid

The model was discretized by an SG grid with resolution $120 \times 120 \times 40$ at first, the central region was divided by 5 m uniform-cells, see Fig. 3. An MR grid was derived from the SG grid and decomposed it into three sub-grids with parameters: $\left. \left[ Cs^{(i) } , N_{z}^{(i)}; \right] \right| _ {i = 1,3 } = ( 0,9; 1,21; 2,10)$, i.e. the horizontal resolution was gradually roughened downwards as $120 \times 120$, $60 \times 60$ and $30 \times 30$. The common interfaces between adjacent sub-grids were located inside layers, as shown in Fig. 3.

The apparent resistivity responses ($\rho _ {a}$) of SG and MR grid solutions as well as the linear filter method solution (Ingeman-Nielsen and Baumgartner 2006) are shown in Fig. 4a, they all represent the characters of the layered model. Since the differences between them are nearly indistinguishable, we calculated the relative differences of the SG and MR grid solutions against the linear filter method solution, as shown in Fig. 4b. The maximum relative differences of the SG and MR solutions are $0.165\%$ and $0.176\%$, which are nearly the same, meaning that the solutions are both accurate. The relative difference of the MR grid solution is slightly higher than the SG grid solution, which could due to the coarser discretization of the deeper regions, but it’s negligible.

Fig. 4

a Apparent resistivity responses $\rho _ {a}$ and b relative differences from example 1. The abbreviations denote: SG the staggered grid solution, MR the multi-resolution grid solution, 1-D the linear filter method solution

3.2 Example 2

Next, we considered a 3-D case to demonstrate the accuracy and speed of the MR grid approach against the SG grid approach. The model with $100\; \varOmega \,{\text {m}}$ background included two anomalous blocks with the same resistivity of $1 \varOmega m$ and size of $60\,{\text {m}} \times 60\,{\text {m}} \times 40\,{\text {m}}$, where they were placed at different depths of $20\,{\text {m}}$ and $80\,{\text {m}}$, as shown in Fig. 5a. The data were calculated for one $600\,{\text {m}}$ pole-dipole profile with 30 m electrode distance (a) and $n = 1$ to 8 levels, which includes 21 electrodes in total.

A larger SG grid $176 \times 176 \times 50$ was created to fit the longer electrode offsets, and its central part was uniformly discretized with 5 m cells. Since the electric field implies the intensity of the potential variation ($\mathbf{E}=\mathbf{G}\mathbf{\varphi }$), the secondary electric fields ($\mathbf{E}_s$) on SG grid generated by the current electrode at $(x,y,z)= 0\,{\text {m}}$ was calculated. The distribution of $\mathbf{E}_s$ is shown in Fig. 5b to demonstrate the behavior of $\mathbf{\varphi }_s$. Based on the intensity of $\mathbf{E}_s$, the most significant $\mathbf{\varphi }_s$ variations are observed around the shallow block, which is closer to the current electrode. On the contrast, the perturbations around the deeper block (with the same resistivity and shape) are much weaker. Therefore, it demonstrates a general tendency that $\mathbf{\varphi }_s$ is gradually losing the sensitivity with increasing the distance from the source. Since the potential variations attenuate with depth, the grid resolution can be decreased correspondingly.

Fig. 5

2D slices (central region, $\hbox {y}=0\hbox {m}$) of the model and $\mathbf{E}_{s}$ vector diagram from example 2. Insignificant regions are omitted to show. a MR grid discretization. White lines highlight the common interfaces between the adjacent sub-grids. b$\mathbf{E}_{s}$ vector calculated on SG grid generated by the positive current electrode at $( x , y , z ) = 0\,{\text {m}}$ (red cone). Dashed lines show the outlines of the anomaly blocks

An MR grid was designed subsequently based on the SG grid, it consists of three sub-grids with the parameters: $\left. \left[ Cs^{(i) } , N_{z}^{(i)};\right] \right| _ {i = 1,3 } = ( 0,14; 1,26; 2,10 )$. The deeper block was placed in the middle sub-grid, which is one step coarser, see Fig. 5a.

The $\rho _ {a}$ pseudo-section of the MR grid solution is shown in Fig. 6a. Due to the closer distance to the source, the shallow block induced much stronger anomaly than the deeper block. The MR and SG grid responses were compared, and the relative difference between them is shown in Fig. 6b. Larger differences are mainly focused at the anomaly areas caused by the coarser discretization of the deeper block (− 100 to − 50 m of the profile coordinate). However, the maximum relative difference is merely $0.35\%$.

Fig. 6

Pseudo-sections from example 2. a$\rho _ {a}$ response of the MR grid solution. b Relative difference between the MR and SG grid responses

The $\mathbf{\varphi }_s$ on MR grid generated by the same current electrode at $(x,y,z) = 0\,{\text {m}}$ was calculated, and its distribution is shown in Fig. 7a. It is noteworthy that the contour map of each sub-grid was plotted separately without any interpolated connection between them. The contour lines of $\mathbf{\varphi }_s$ demonstrate that the sub-grids are well-connected and there are no artifices or interruptions due to the horizontal resolution changing between sub-grids. It means that we have sufficient accuracy at the common interfaces.

The relative difference of $\mathbf \varphi$ between the MR and SG solutions is shown in Fig. 7b. The higher relative differences were induced by the deeper block with coarser discretization, but does not exceed $1.52\%$. Moreover, there are no obvious differences at the surface where data were measured.

Fig. 7

2D slices (central region, $\hbox {y}=0\,{\text {m}}$) of the contour plots from example 2, the potential is generated by the positive current electrode at $( x , y , z ) = 0\,{\text {m}}$ (red cone). Dashed lines show the outlines of the anomaly blocks. Thicker solid lines highlight the common interfaces between the adjacent sub-grids. a$\mathbf{\varphi }_s$ distribution, the contour map of each sub-grid was plotted by independent sections without interpolated connection between them. b The relative differences of $\mathbf \varphi$ between the MR and SG solutions

We compared the run-times and memory usage of the forward modeling in the SG and MR approaches. In order to avoid uncertainties, the modeling was tested for 5 times, and the averaged values are presented in Table 1.

Table 1 Comparison of the modeling efficiency between SG and MR grid approaches from example 2

The MR grid approach requires less time for solving the system of equations (43.33% of the SG grid), which is nearly linear with respect to the reduction in the amount of DoF. As solving the equations set is the most time-consuming part of the forward modeling, the MR approach allows us to greatly improve the efficiency of the forward modeling. The memory usage is also reduced accordingly.

3.3 Example 3

The topography has a profound effect in the DCR modeling. Hence, we present a 3-D model that incorporates a 40 m deep valley with $11^{\circ }$ surface slope. The background of the model was $100\, \varOmega \,{\text {m}}$, and the air cells were assigned with $10 ^ {10 }\, \varOmega \,{\text {m}}$. Block 1 and 2 with the same size ($40\,{\text {m}} \times 40\,{\text {m}} \times 30\,{\text {m}}$) and resistivity ($500\, \varOmega \,{\text {m}}$) were placed at depths of $55\,{\text {m}}$ and $65\,{\text {m}}$, respectively. In addition, block 3 with a bigger size ($60\,{\text {m}} \times 60\,{\text {m}} \times 50\,{\text {m}}$) and higher resistivity ($1000\, \varOmega \,{\text {m}}$) located at a deeper depth of $85\,{\text {m}}$. The data of two $400\,{\text {m}}$ dipole-dipole profiles along $x=0\,{\text {m}}$ and $y=0\,{\text {m}}$ directions were calculated. Each profile adopted the geometry factors of $a = 40m$, $n = 1$ to 8 levels and included 11 electrodes. The electrode arrays followed the topography and located above the block anomalies. See the model and measurement configurations in Fig. 8.

Fig. 8

Central part of the model from example 3. Two perpendicular dipole–dipole profiles locate on the ground surface following the topography. Black cones show the locations of the electrodes array

Fine grid discretization is required near the surface to describe the topography. For the SG grid, the $2.5\,{\text {m}}\times 2.5\,{\text {m}}\times 2\,{\text {m}}$ cells were employed in the central region of the topography layers. In the deeper layers ($46\,{\text {m}}\le z \le 225\,{\text {m}}$), the cells’ thickness was gradually extended to 5 m. It makes the total discretization of the SG equal to $248 \times 248 \times 70$. The MR grid divided the SG grid into four sub-grids with parameters: $\left. \left[ Cs^{(i) } , N_{z}^{(i)}; \right] \right| _ {i = 1,4 } = ( 0,23 ; 1,9 ; 2,23 ; 3,15 )$. The finest horizontal resolution ($248 \times 248$) was only used in the topmost sub-grid ($0\,{\text {m}}\le z \le 46\,{\text {m}}$) to discretize the topography portion, afterwards the horizontal resolution was gradually reduced in the lower sub-grids. Block 1 and 3 located in the second (horizontal resolution: $124 \times 124$) and third sub-grids ($62 \times 62$) respectively, and the common interface ($z=85\,{\text {m}}$) between them crossed block 2. The bottom padding layers were discretized with the coarsest horizontal resolution of $31 \times 31$. See the MR grid discretization in Fig. 9.

Fig. 9

2D slice ($y=0$ m, central region) of the MR grid discretization from example 3. White lines highlight the common interfaces between the adjacent sub-grids in MR grid; black cones denote one electrodes array along $y=0$ m direction

In order to avoid the influences from using an improper background model in the secondary field approach (e.g. using the flat half-space model for this topography case), the total field approach was employed. The $\rho _ {a}$ pseudo-sections of the MR grid response are shown in Fig. 10a, b. As it can be seen from the figures, the high $\rho _ {a}$ values caused by the blocks can be observed, where the anomaly responses of two shallow blocks are more obvious. The topography caused perturbations in $\rho _ {a}$, which could heavily disturb the anomaly responses, especially for the response of block 3, which is hard to find out. Therefore, the topography effect should be taken into account when interpreting the data to avoid inadequate interpretations.

The MR and SG grid solutions were compared with the finite-element method (FEM) solution, which used unstructured grid (Ren et al. 2017). The relative differences between the SG and MR grid solutions against the FEM solution were calculated and presented in Fig. 10c–f. As one can see, the relative differences of the SG and MR grid solutions against the FEM solution are generally less than $1\%$. The deviations could mainly come from the discretization approaches with respect to the topography. The topography was discretized by SG and MR grids using a mass of fine rectangular cells to fit the surface in a staircase approximation manner. Contrarily, the tetrahedral cells used by FEM can preferably fit the topography surface, which is more suitable for coping with the topography case. Even so, the overall solutions are comparable.

The maximum relative differences of SG and MR grids are $0.99\%$ and $1.13\%$, respectively. The slightly larger differences occurred at $n>5$ part of MR grid solution, which can be explained by using the coarser discretization for the deeper regions of the MR grid comparing with SG grid. However, the relative differences of SG and MR grids generally resemble each other, thus, the MR grid achieved a proximate accuracy with the SG grid.

Fig. 10

Pseudo-sections from example 3. a, c, e, b, d, f Represent the pseudo-sections of the profiles along $y=0\,{\text {m}}$ and $x=0\,{\text {m}}$ directions, respectively; a, b are the $\rho _{a}$ response of the MR grid solution; c, d are the relative differences of the SG grid solution against the FEM solution; e, f are the relative differences of the MR grid solution against the FEM solution

Table 2 Comparison of the modeling efficiency between SG and MR grid approaches from example 3. The abbreviations denote: DoF, the degrees of freedom; $\overline{t}_{F w d}$, averaged time of forward modeling; $\overline{t} _ { e q }$, averaged time for solving the system of equations (one source); RAM, maximum memory usage. The last row compares the ratio of the above parameters in percent

We present results of the speed-up test for example 3 in a similar manner as example 2, see Table 2. The fine horizontal resolution required to handle the topography leads to a higher number of DoF in the SG case and naturally caused higher computational demands (Table 2). The MR grid roughen horizontal resolution downwards to avoid the over-discretization in the deep. Consequently, it reduced the DoF significantly to only $38.37\%$ of the SG grid, and resulted in a smaller forward problem. Comparing run-times and memory usage, the MR grid reduced the computational costs to nearly one third of SG grid case, but without loss of the modeling accuracy. It means that the MR grid is more suitable than the SG grid for solving large modeling problem.

4 Conclusions

We implemented the multi-resolution (MR) grid approach to 3-D Direct Current Resistivity (DCR) modeling. The MR grid allows to adjust the horizontal resolution with depth, which is more flexible than the conventional staggered (SG) grid with respect to description of the shallow geometries, topography, and measurements configuration.

We applied a Coarse Active (CA) approach, which was carefully studied in Cherevatova et al. (2018), to handle the common interfaces between the sub-grids. Beneficial from the definition of the differential operators on the interface layers, the derived coefficient matrix remains in symmetric form as in the SG grid approach. Preconditioned conjugate gradient method was used as the solver, which provides fast and stable convergence due to the symmetry of the system of linear equations. We presented three synthetic studies to verify the accuracy and efficiency of the MR DCR modeling. The SG grid solution with fine discretization guarantees the accurate response, but leads to higher computational demands. The MR grid allows us to reduce the computational costs (CPU time and RAM usage) substantially without loss of accuracy. This is specifically important for inversion algorithms, which require numerous modeling calculations. Taking into account, that MR code can be parallelized to further accelerate calculations, the MR solver opens perspectives for large inversions, which are in high demand for geophysical problems.

Appendix: Topology Matrices of Forward Operators on SG and MR Grids

Fig. 11

Spatial illustrations of the topology matrices: $\overline{\mathbf{G}}$ (z component) mapping from nodes (blue points) to an edge (blue line), $-\overline{\mathbf{G}}^{T}$ mapping from edges (blue lines) to a node (blue point) and $\hat{\mathbf{W}}$ mapping from cells (blue volumes) to an edge (blue line). a, c, e$\overline{\mathbf{G}}$, $-\overline{\mathbf{G}}^{T}$ and $\hat{\mathbf{W}}$ on SG grid, respectively. b, d, f$\overline{\mathbf{G}}$, $-\overline{\mathbf{G}}^{T}$ and $\hat{\mathbf{W}}$ on MR grid, respectively, the red interface denotes the common interface between two adjacent sub-grids in MR grid

Three parts of an uniform SG grid are used to present the spacial illustrations of $\overline{\mathbf{G}}$, $-\overline{\mathbf{G}}^{T}$ and $\hat{\mathbf{W}}$, which are the topology matrices of the gradient, divergence and volume-weighted averaging operators, respectively. Figure 11a shows a portion of $\overline{\mathbf{G}}$ (z component) mapping from two nodes to an edge, Fig. 11c shows a portion of $-\overline{\mathbf{G}}^{T}$ mapping from six edges to a node, and Fig. 11e shows a portion of $\hat{\mathbf{W}}$ mapping from four cells to an edge. The corresponding coefficients in $\overline{\mathbf{G}}$, $-\overline{\mathbf{G}}^{T}$ and $\hat{\mathbf{W}}$ matrices are:

$$\begin{aligned} \overline{\mathbf{G}}= & {} \left[ \begin{array}{llll} \ddots &{}&{}&{} \\ &{} -1 &{} 1 &{} \\ &{}&{}&{} \ddots \end{array}\right] , \end{aligned}$$

(15)

$$\begin{aligned} -\overline{\mathbf{G}}^{T}= & {} \left[ \begin{array}{llll} \ddots &{}&{}&{}\\ &{} \begin{array}{cccccccc} -1 &{} 1 &{} \cdots &{} -1 &{}1 &{} \cdots &{} -1 &{} 1 \end{array} &{}\\ &{}&{}&{} \ddots \end{array} \right] , \end{aligned}$$

(16)

$$\begin{aligned} \hat{\mathbf{W}}= & {} \left[ \begin{array}{llll} \ddots &{}&{}&{}\\ &{} \begin{array}{cccc} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} \end{array} &{}\\ &{}&{}&{} \ddots \end{array}\right] . \end{aligned}$$

(17)

An MR grid was formed based on the above SG grid. Three positions, where include common interfaces between adjacent sub-grids, are used to present the spacial illustrations of $\overline{\mathbf{G}}$, $-\overline{\mathbf{G}}^{T}$ and $\hat{\mathbf{W}}$ on MR grid, which involve more complicated forms. Figure 11b shows a portion of $\overline{\mathbf{G}}$ (z component) mapping from five nodes to an edge, Fig. 11d shows a portion of $-\overline{\mathbf{G}}^{T}$ mapping from fourteen edges to a node, and Fig. 11f shows a portion of $\hat{\mathbf{W}}$ mapping from ten cells to an edge. The corresponding coefficients in $\overline{\mathbf{G}}$, $-\overline{\mathbf{G}}^{T}$ and $\hat{\mathbf{W}}$ matrices are:

$$\begin{aligned} \overline{\mathbf{G}}= & {} \left[ \begin{array}{lllllll} \ddots &{}&{}&{}&{}&{}&{} \\ &{} -1 &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \\ &{}&{}&{}&{}&{}&{} \ddots \end{array}\right] , \end{aligned}$$

(18)

$$\begin{aligned} -\overline{\mathbf{G}}^{T}= & {} \left[ \begin{array}{llll} \ddots &{}&{}&{}\\ &{} \begin{array}{cccccccccccccccccccccc} -1 &{} 1 &{} \cdots &{} -1 &{} 1 &{} \cdots &{} -\frac{1}{4} &{} -\frac{1}{2} &{} -\frac{1}{4} &{} -\frac{1}{2} &{} -1 &{} -\frac{1}{2} &{} -\frac{1}{4} &{} -\frac{1}{2} &{} -\frac{1}{4} &{} 1 \end{array} &{}\\ &{}&{}&{} \ddots \end{array}\right] , \end{aligned}$$

(19)

$$\begin{aligned} \hat{\mathbf{W}}= & {} \left[ \begin{array}{llll} \ddots &{}&{}&{}\\ &{} \begin{array}{ccccccccccc} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \cdots &{} \frac{1}{4} &{} \frac{1}{4} \end{array} &{}\\ &{}&{}&{} \ddots \end{array}\right] . \end{aligned}$$

(20)