On the Influence of Known Diurnal and Subdiurnal Signals in Polar Motion and UT1 on Ring Laser Gyroscope Observations

Abstract

The ring laser gyroscope (RLG) technique has been investigated for about 20 years as a potential complement to space geodetic techniques in measuring variations of Earth rotation. The technique is of great interest, especially in the context of monitoring rapid changes of rotation with sub-daily resolution. In this paper, we review how the known high frequency signals in Earth rotation parameters, including the so-called diurnal polar motion, diurnal and semidiurnal ocean tide effects in polar motion and UT1 and librations, prograde diurnal in polar motion and semidiurnal in UT1, contribute to the RLG observable, the Sagnac frequency. Our results suggest that at the current accuracy level of the technique, the signals coming from diurnal polar motion and ocean tides should be taken into account in analysis while the influence of libration can be neglected. We also point out that the contributing signals are superimposed upon each other and can hardly be separated from the data from a single instrument. Our computations are done taking parameters of the RLG at the Wettzell Observatory in Germany. However, we also consider how the strength of a particular signal depends on the geographic location of a horizontally mounted instrument. Finally, we discuss the relationship between the geographical location and terrestrial orientation of RLG and its consequence for the observed Sagnac signal.

1 Introduction

The Earth rotation vector continuously undergoes variations due to, e.g. the gravitational attraction of the Moon and the Sun or processes in the liquid envelopes of the solid Earth, including the atmosphere, the oceans and the outer core. These fluctuations differ in time-scales and magnitudes. Nevertheless, it is of great importance to study all of them in detail, as knowledge about variations in Earth rotation gives information about the phenomena causing them and helps in studying Earth’s interior. Moreover, parameters of Earth rotation define the instantaneous orientation of the Earth in space, which is necessary for practical purposes, like transformation between terrestrial and celestial reference frames, space navigation, or point positioning.

Variations in Earth rotation can be observed by space geodetic techniques, like very long baseline interferometry (VLBI), global navigation satellite systems (GNSS) or satellite laser ranging (SLR), but recently also by a strictly ground-based technique which is the ring laser gyroscope (RLG). The RLG has been investigated for about 20 years as a potential complement to the space geodetic techniques in the determination of Earth rotation parameters (ERP). Its potential has been noticed by Chao (1991) and studied by, for instance, Schreiber et al. (2004), Stedman et al. (2007). Additionally, Mendes Cerveira et al. (2009) and Nilsson et al. (2012) reported the advantages of combining RLG data with VLBI observations. Although RLG data are considered mainly for investigation of high-frequency variations in ERP, Schreiber et al. (2011) demonstrated the feasibility of detecting the Chandler and annual wobbles from these observations. Nevertheless, the technique constantly undergoes improvement so that today the RLG observations are more accurate than a few years ago. Consequently, its potential in the monitoring of Earth rotation increases and requires further investigation.

For a correct interpretation of the RLG data, it is necessary to properly model the expected signals. The main factors that affect the observable of an RLG, i.e. the Sagnac frequency, refer to changes in the geometry of an instrument due to thermal and pressure variations, to laser performance (e.g. backscatter coupling, dispersion), to variations of the normal vector of an instrument with respect to the terrestrial reference frame, and to variations of the Earth rotation vector. In this paper, we deal with the last effect, i.e. changes in ERP. We review the known, predictable diurnal and subdiurnal signals in polar motion (PM) and the universal time (UT1), which influence the observed Sagnac frequency. We consider the following three phenomena: the so-called diurnal polar motion of the instantaneous rotation axis, diurnal and semidiurnal signals in PM and UT1 caused by ocean tides, and the so-called libration in PM and UT1. As we consider here the impact of three-dimensional effects on the one-dimensional signal, we study whether components of those effects amplify or cancel out each other. We also verify how the impact of perturbations in ERP on the RLG observations varies with the change of location or orientation of an instrument.

In Sect. 2 we present the mathematical background and a brief description of the RLG apparatus at the Wettzell Observatory, on which we conducted our investigation. In Sect. 3 we provide a description of the investigated phenomena and their contribution to observations of the G-ring at the Wettzell Observatory. In Sect. 4 we discuss the issue of orientation of the normal vector of an instrument with respect to the axes of the terrestrial system. We present the influence of ERP signals on observations from an instrument like the Wettzell one, but depending on its geographical location and other than horizontal orientation of the instrument. Conclusions are outlined in Sect. 5. This work represents a preliminary study of the use of RLG data for monitoring diurnal and subdiurnal signals (especially non-harmonic of geophysical origin) in Earth rotation parameters.

2 The G-Ring Laser and the Sagnac Effect

In general, gyroscopes are rotation sensors mostly used in navigation (aircraft, marine), but also in consumer electronics (mobile phones, tablets) or in robotic guidance. Sensors used for these purposes are relatively small and not very sensitive. For instance, gyroscopes used for navigation are usually not bigger than 0.02 m$^{2}$ and have a sensitivity of about $5\times 10^{-7}$ ${\rm rad / s} \sqrt{ Hz }$ (Schreiber and Wells 2013), which is an insufficient level for geodetic aims. Nevertheless, the sensitivity is directly proportional to the scale factor (a constant depending on the size of the instrument and the laser wavelength), which, in turn, increases with the area of a gyroscope. Consequently, large ring laser gyroscopes having areas between 1 and about 834 m$^{2}$ have been constructed to improve the sensitivity by increasing the scale factor. However, large instruments bring about other issues, like increasing difficulty in constructing monolithic instrument and, consequently, problems with mechanical stability. Taking into account all of those technical aspects, the 4 m$\,\times\,$4 m large quasi-monolithic G-ring at the Wettzell Observatory is nowadays the most stable and sensitive gyroscope, with the highest potential to be used in geodesy (Schreiber and Wells 2013).

The Wettzel gyroscope has been operating since 2001. It is located in a purpose-built underground laboratory, effectively isolated from external atmospheric conditions. A detailed description of the G-ring is given in Schreiber and Wells (2013). The whole monumentation minimizes external influences and protects the instrument from extensive tilting. Nevertheless, six high precision tiltmeters, allowing detection of 1 nrad tilts, are placed on the top of the RLG to monitor orientation variations with respect to the plumb line, e.g. due to the solid Earth tides or local ground movements. However, taking into account the horizontal orientation of the RLG, only tilts in the North-South direction must be monitored, as they cause variations in observations which are 3 orders of magnitude higher than the sensor resolution. The East-West directed tilts have a negligible influence on the observed RLG signal.

The observable of the RLG is the so-called Sagnac effect. In physical terms, the observed effect is a phase shift of two light beams propagating in opposite directions around a circuit of a rotating gyroscope. Although the two beams travel the same path in the same conditions, due to the sensor rotation they traverse different distances. As a result the phase shift is observed which is directly proportional to the dot product of the area vector, normal to the gyroscope plane, and the vector of its rotation (Chao 1991). However, as the transition from phase to frequency measurement greatly improves the gyroscope sensitivity (Schreiber and Wells 2013), instead of the phase shift the beat frequency, called the Sagnac frequency, is used to describe the effect (e.g. Nilsson et al. 2012):

$$\begin{aligned} f_{\mathrm{sagn}} = K\varvec{\Omega }\cdot \mathbf {n}+f_{\mathrm{instr}}, \quad \text{ with the scale factor } \; K=\frac{4\cdot A}{\lambda L}, \end{aligned}$$

(1)

where L, A and $\lambda$ are the laser beam path length, the area enclosed by the path and the wavelength of the laser, respectively. They are assumed to be constant for a particular instrument. In practice, these geometric quantities are subject to fluctuations due to temperature- and pressure-induced deformations, which is out of the scope of the paper. Vector $\varvec{\Omega }=\Omega _0[m_x\; m_y\; 1+m_z]^T$ is the instantaneous rotation vector of the Earth-fixed system in space, with the dimensionless parameters $m_{x}, m_{y}, m_{z}$ defining perturbations, and $\Omega _0$ denoting the mean angular speed of rotation. Vector $\mathbf {n}$ is the normal vector of the instrument. For the horizontally mounted RLG it is defined by $\mathbf {n}=[\cos \varphi \cos \lambda \; \cos \varphi \sin \lambda \; \sin \varphi ]^T$, where $\varphi$ and $\lambda$ are the geodetic latitude and longitude of an instrument’s location. Finally, $f_{\mathrm{instr}}$ is an instrumental offset. Consequently, (neglecting the instrumental errors, as we do not deal with them within this paper) the basic Sagnac frequency equation can be expressed by:

$$\begin{aligned} f_{\mathrm{sagn}} = K\Omega _{0}(\sin \varphi + m_{x} \cos \lambda \cos \varphi +m_{y} \sin \lambda \cos \varphi + m_{z}\sin \varphi ). \end{aligned}$$

(2)

Its unit is [Hz], and the variations in Earth rotation we study here cause variations in the observed Sagnac frequency at the level of $10^{-5}$ [Hz], i.e tens of $[\upmu$Hz], which strictly depends on the scale factor K. Moreover, to use the relation (2) for modeling the impact of the known high frequency signals in ERP on the RLG observations, we must take into account the fact that the available models of Earth rotation refer to the conventional celestial intermediate pole (CIP), and not to the instantaneous rotation pole (IRP). Consequently, the relationship between CIP and IRP must be considered. For polar motion the first-order relationship is given by Brzeziński and Capitaine (1993):

$$\begin{aligned} m = p-\frac{i}{\Omega _{0}}\left( \dot{p}-\dot{P}e^{-i\theta }\right) , \end{aligned}$$

(3)

where the complex parameter $m=m_x+im_y$, with the imaginary unit i, denotes the polar motion of the IRP, $p=x_p-iy_p$ describes the polar motion of the CIP, $\theta$ denotes the Earth rotation angle, $P = dX+idY$ defines position of the CIP in the geocentric celestial reference system (GCRS). Parameters dX and dY are the celestial pole offsets (nutation) of the CIP (observed by VLBI) with respect to the position predicted by the conventional precession-nutation model. The dot denotes the time derivative. By taking the real and imaginary parts of Eq. (3) we get the equivalent representation by 2 real-valued equations:

$$\begin{aligned} m_{x} = \frac{1}{\Omega _{0}} (\Omega _{0} x_{p} - \dot{y}_{p} + d\dot{X} \sin \theta -d\dot{Y} \cos \theta ), \nonumber \\ m_{y} = \frac{1}{\Omega _{0}} (-\Omega _{0} y_{p} - \dot{x}_{p} + d\dot{X} \cos \theta + d\dot{Y}\sin \theta ). \end{aligned}$$

(4)

See Mendes Cerveira et al. (2009) for extensive discussion of the equations. Note, that the polar motion components $m_x$, $m_y$ in Eq. (4) do not contain this part of the lunisolar effect which is expressed by the conventional precession–nutation model, the retrograde diurnal signals, but the effect might be taken into account using a model reffered directly to the IRP (e.g. Brzeziński 1986). Moreover, as we showed in Tercjak et al. (2015) and as it was discussed by Brzeziński (2009), the part involving the time derivatives of the nutation parameters ($d\dot{X}$, $d\dot{Y}$) as yet can be neglected, and a simpler form of Eq. (3) can be used:

$$\begin{aligned} m = p-\frac{i}{\Omega _{0}}\dot{p}, \end{aligned}$$

(5)

and consequently:

$$\begin{aligned} m_{x} = \frac{1}{\Omega _{0}} (\Omega _{0} x_{p} - \dot{y}_{p}), \qquad m_{y} = \frac{1}{\Omega _{0}} (-\Omega _{0} y_{p} - \dot{x}_{p}). \end{aligned}$$

(6)

Variations of the axial component of rotation are expressed as the time derivative of $\mathrm{dUT1} = UT1-UTC$, where UTC denotes so-called coordinated universal time (see Petit and Luzum 2010 for a definition):

$$\begin{aligned} m_{z} = \frac{\partial \mathrm{dUT1}}{\partial t}. \end{aligned}$$

(7)

Although Eqs. 6 and 7 are adequate for reflecting the influence of signals in PM and dUT1 in the RLG observations, we can also take advantage of the relationship (5) expressed in the frequency domain:

$$\begin{aligned} m(\sigma ) = \left( 1+\frac{\sigma }{\Omega _{0}}\right) p(\sigma ), \end{aligned}$$

(8)

where $\sigma = \frac{2\pi }{T}$ is the angular frequency of a particular harmonic component with period T, positive for prograde (counterclockwise) motion and negative for retrograde (clockwise) motion. This form of the relationship between CIP and IRP is usable when considering splitting up PM signals into prograde and retrograde terms. Following e.g. Tian (2013) we can derive the relationship for the polar motion of the IRP as a function of prograde and retrograde amplitudes $a_{p}$ and $a_{r}$, respectively, and the argument $\mathrm{arg}(t)$ which is a linear combination of the five fundamental arguments (Petit and Luzum 2010, section 5.7):

$$\begin{aligned} m = a_{p}(\cos [\mathrm{arg}(t)]+i\sin [\mathrm{arg}(t)])+a_{r}(\cos [\mathrm{arg}(t)]-i\sin [\mathrm{arg}(t)]). \end{aligned}$$

(9)

Consequently, the components $m_x$ and $m_y$ of m are obtained as real and imaginary parts of the above relation. The corresponding expressions for $a_{p}$ and $a_{r}$ are presented below.

3 Signals in Polar Motion and dUT1

The long-term aim of our research is to find out whether it is possible to use the RLG data for monitoring high-frequency variations in ERP, especially the non-harmonic signals of geophysical origin. However, before we do that, we first want to review all known and modeled diurnal and subdiurnal signals affecting such observations. We start our studies with signals in PM and dUT1.

As we have already mentioned, we consider here three phenomena: diurnal polar motion according to the model developed by Brzeziński (1986), the influence of diurnal and semidiurnal ocean tides on PM and dUT1 and librations in PM and dUT1, both according to the models recommended in the IERS Conventions 2010 (Petit and Luzum 2010). Based on the above-mentioned models we compute components of the instantaneous rotation vector, then substitute it into Eq. (2) and derive the corresponding variations of the Sagnac frequency, using parameters of the G-ring and the location of Wettzell. We take 1 $\upmu$Hz as the resolution limit of the Sagnac frequency signal (Prof. Ulrich Schreiber, personal communication). The absolute value of 1 $\upmu$Hz refers to a relative precision of about $3\times 10^{-9}$. The time span of our computation is 118 days, from 19.09.2014 to 15.01.2015. Below, we present a short description of the models and the corresponding influence on the observed Sagnac frequency.

3.1 Diurnal polar motion

The diurnal polar motion (DPM) refers to the variations of the IRP in a body-fixed frame, due to a torque exerted by the tesseral components of the lunisolar tidal force. The perturbation is a near-circular retrograde motion with a period of approximately one sidereal day and an amplitude varying in time (Brzeziński 1986). The terrestrial perturbation of the IRP is associated with a celestial perturbation which is not seen by the RLG. In case of the CIP the whole perturbation appears as a celestial motion, i.e. precession–nutation. See Brzeziński and Capitaine (1993) for an extensive discussion about the relationship between the motions of the instantaneous and conventional rotation poles.

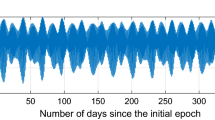
The issue of the DPM has been thoroughly investigated for different Earth models, for instance Woolard (1953) presented results for a rigid Earth; McClure (1973) corrected those results for a purely elastic Earth. Brzeziński (1986) corrected the results of McClure (1973) for liquid-core effects using the dynamical theory of Wahr (1981a, b) and tabulated numerical values of about 160 amplitudes for the three axes: the instantaneous rotation axis, the angular momentum axis, and the axis of figure. The DPM model refers to the IRP, not the CIP, so the corresponding variations might be directly substituted into Eq. (2). A time series of the theoretical Sagnac frequency based on the Brzeziński (1986) DPM model is presented in Fig. 1a.

3.2 Ocean tides

Gravitationally forced ocean tides (OT) contribute to variations in Earth rotation via the angular momentum exchange and, when considering polar motion and dUT1, it is a dominant effect in the diurnal and semidiurnal frequency bands. The phenomenon is quite regular and predictable, the frequencies are well known, while the amplitudes and phases can be derived from ocean tide models and/or from observations of Earth rotation (Brzeziński 2009). There have been several investigations of the subject. Some of them (e.g. Ray et al. 1994) resulted in analytical, geophysical models derived with the use of the TOPEX/Poseidon altimetry data, others (e.g. Watkins and Eanes 1994) derived empirical models with parameters estimated from space geodetic techniques.

The currently recommended model of the diurnal and semidiurnal variations in polar motion and UT1 provided by the IERS Conventions 2010 is based on the work of Ray et al. (1994). It enables the estimation of semidiurnal and prograde diurnal PM variations, as well as semidiurnal and diurnal dUT1 perturbations. The retrograde diurnal equatorial component of the OT contribution is included in the IAU 2000/2006 precession–nutation model (Mathews et al. 2002), but regarding IRP it should be included in a retrograde DPM model. The DPM model, which we use here, does not take into account the OT effects. However, the inclusion of the OT effect in the DPM model causes differences in amplitudes not bigger than 10 $\upmu as$ (compare e.g. Brzeziński 1986 and Tian 2013). This corresponds to a Sagnac frequency signal at the level of 0.20 $\upmu Hz$, which is negligible at the current level of observation accuracy.

As the conventional model of OT effect in polar motion refers to the CIP, we performed and compared two ways of computation. In the first method we evaluated variations of all components of the CIP and then computed perturbations of the IRP by applying relationships (6) and (7). In the second approach we further converted Eqs. (7) and (9) by taking into account the parameterization applied in the IERS Conventions model. In the case of polar motion, we took coefficients $x_{s}$, $x_{c}$, $y_{s}$, $y_{c}$ from Tables 8.2a and 8.2b of the IERS Conventions 2010 ($x_{s}$, $x_{c}$ are the sin and the cos coefficients of $x_{p}$ and $y_{s}$, $y_{c}$ are the corresponding amplitudes of $y_{p}$) and computed the prograde and retrograde amplitudes $a_{p}$ and $a_{r}$ as follows (Tian 2013):

$$\begin{aligned} a_{p} = \left( 1+\frac{\sigma }{\Omega _{0}}\right) \left( \frac{x_{c}-y_{s}}{2}-i\frac{x_{s}+y_{c}}{2}\right) , \quad a_{r} = \left( 1-\frac{\sigma }{\Omega _{0}}\right) \left( \frac{x_{c}+y_{s}}{2}+i\frac{x_{s}-y_{c}}{2}\right) , \end{aligned}$$

(10)

where $\left( 1\pm \frac{\sigma }{\Omega _{0}}\right)$ are transfer coefficients taken from Eq. (8). For the $m_{z}$ component we started with the expression:

$$\begin{aligned} \mathrm{dUT1} = u_{s}\sin (\mathrm{arg}(t))+u_{c}\cos (\mathrm{arg}(t)), \end{aligned}$$

(11)

where $u_{s}$ and $u_{c}$ are the sine and cosine amplitudes from Tables 8.3a and 8.3b of the IERS Conventions 2010. Then we used Eq. (11) in Eq. (7) assuming additionally that arg(t) is a linear function of time. That led us to the following expression for $m_z$:

$$\begin{aligned} m_{z} =\sigma u_{s} \cos (\mathrm{arg}(t))-\sigma u_{c} \sin (\mathrm{arg}(t)) = u_{s}^{*} \cos (\mathrm{arg}(t))+ u_{c}^{*}\sin (\mathrm{arg}(t)). \end{aligned}$$

(12)

As expected, both approaches gave same results, and therefore, they might be used interchangeably. The Sagnac frequency based on the OT model is presented separately for PM (Fig. 1b) and dUT1 (Fig. 1c).

3.3 Libration

Assuming a triaxial Earth with the principal moments of inertia A, B, C (and ${A<B<C}$) the libration is the direct effect of external (lunisolar) torque exerted on B-A, in the same way as precession and nutation arise from the torque exerted on C-A (Chao et al. 1991). Because of the axial asymmetry and the fact that the equator and ecliptic are not coplanar, the lunisolar torque gives rise to variations in both polar motion (diurnal signal in the prograde direction) and UT1 (semidiurnal perturbation). The phenomenon was named “libration”, because of its generic similarity to the libration of the Moon, by Chao et al. (1991), who also estimated and then corrected its amplitudes (Chao et al. 1996). Further contribution to the topic came from, e.g. Brzeziński and Capitaine (2003, 2009) whose work constitutes a basis for models provided by the IERS Conventions 2010.

Although the libration has relatively small amplitudes and we expect that the signal might be not visible in the RLG observations, we decided to investigate the signal, as the ring laser technique is still under development. For this purpose we used coefficients given in Tables 5.1a and 5.1b of the IERS Conventions 2010 and applied the same methods of computations as in the case of ocean tides. The Sagnac frequency variations based on the libration model are presented together for PM and dUT1 in Fig. 1d.

Fig. 1

Influence of the modeled diurnal and semidiurnal signals in Earth rotation parameters on the Sagnac frequency as could be observed by the G-ring at the Wettzell Observatory; a diurnal polar motion, b diurnal (greater amplitude) and semidiurnal ocean tides effect in polar motion, c diurnal (upper) and semidiurnal (lower) ocean tides effect in dUT1, d libration effect in polar motion (upper) and in dUT1 (lower). For better visibility of the libration and OT effect in dUT1 the curves have been shifted vertically. For OT effect in PM the curves are superimposed upon each other to show the difference in the amplitudes

3.4 Results

From Fig. 1a–d, one can see that the main effect is the DPM with a maximum amplitude of about 26 $\upmu$Hz. The signal is clearly visible in the RLG observations, which has been reported even in early works dealing with RLG data (e.g. Schreiber and Wells 2013). This is not surprising, as amplitudes of the DPM are much larger than those from other effects. The next largest signals are the semidiurnal OT effect in dUT1 and the diurnal OT effect in dUT1 and PM. The maximum amplitudes are 1.5, 1.1 and 1.0 $\upmu$Hz, respectively. They are up to 30 times smaller than the DPM influence. However, they are above the current detection limit of the G-ring and should, therefore, be taken into account in the analysis of the signal. The smallest signals are the libration, both in PM and dUT1, and the semidiurnal OT effect in PM with the maximum amplitudes of 0.09, 0.17 and 0.13 $\upmu$Hz, respectively. All of them are by one order of magnitude below the detection threshold, thus at the current level of accuracy of the technique they might be omitted in the analysis.

Fig. 2

Variation of the Sagnac frequency due to the aggregated contribution of different signals in Earth rotation (from top to bottom): libration in dUT1 and PM (offset 9 $\upmu$Hz), diurnal and semidiurnal ocean tides effect in PM (offset 8 $\upmu$Hz), diurnal and semidiurnal ocean tides effect in dUT1 (offset 5 $\upmu$Hz), the sum of all “small” effects in PM and dUT1

Apart from the separate influence of each signal we also compared the aggregated contribution of the ocean tides and librations to check whether they amplify or cancel each other out. It can be seen from Fig. 2 that although the libration signals amplify each other, they are still much lower than the contribution of OT and are still below the sensitivity threshold of the observations. Similarly, diurnal and semidiurnal ocean tides effect in PM and dUT1 also amplify each other. This suggests that their combined contribution will be visible, but there might be a problem to separate them. Although libration is negligibly small for now, we added the signal to the influence of OT and it turned out that the sum is slightly smaller than the sum of OT only. This might be helpful in future analysis, when the RLG technique will be more accurate.

Fig. 3

Variation of the Sagnac frequency due to the retrograde and prograde semidiurnal signals in polar motion excited by the ocean tides

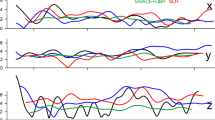
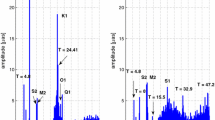
Although most of the results were quite expected, the semidiurnal ocean tides effect in PM yielded a surprisingly small signal, especially in comparison with the original amplitudes reported in the IERS Conventions 2010. This suggests that the influence of the prograde signals might be counterbalanced by the retrograde ones. To study this case in detail, we used Eq. (8) and split up the semidiurnal tidal signals into prograde and retrograde components. The Sagnac frequency variations based on those signals are shown in Figs. 3 and 4. Each of the curves shown in Fig. 3 consists of the influence of all components of prograde (top) and retrograde (bottom) semidiurnal ocean tides over the entire period of analysis. It can be seen that the Sagnac frequency variations, due to both prograde and retrograde signals, are visible as modulated sinusoids. Both sine waves are of similar amplitude, however, they are almost out of phase, so the sum of both is strongly reduced. To see that more clearly, we separated the two largest semidiurnal tidal components, M$_{2}$ and S$_{2}$, and plotted the first two days in Fig. 4. (for better visibility only the first two days are depicted there). The comparison shows that the prograde amplitudes are only slightly smaller than the retrograde, and the two signals are roughly shifted by 180$^{\circ }$ in phase. Moreover, it is visible that the $M_2$ and $S_2$ signals are also shifted relative to each other, and consequently the retrograde signal of the $M_2$ cancel out the retrograde signal of the $S_2$, and the same with the prograde counterparts. However, when studying a longer time period it turns out that their amplitudes do not vary much, but the shift between the $M_2$ and $S_2$ varies, and there are places where the signals coincide and amplify each other, and then the whole semidiurnal OT signal in PM reaches its maximum.

Fig. 4

Same as in Fig. 3 but only the largest tidal components M$_{2}$ (left plot) and S$_{2}$ (right plot) are plotted over 2 days

4 Simulation of Changing the Location or Orientation of an RLG

It can be seen from Eq. (1) that the RLG observations depend on the orientation of the normal vector of the instrument with respect to the instantaneous Earth rotation vector. The normal vector of the horizontally mounted instrument can be expressed by geodetic latitude $\varphi$ and longitude $\lambda$, as in Eq. (2). We can easily conclude that the influence of a particular phenomena influencing Earth rotation on the observed Sagnac frequency will be different in horizontally mounted instruments at different locations. Therefore, we also performed computations for the whole time span, with one hour resolution, using parameters (size and wavelength) of the G-Ring, but introducing other locations. We prepared a grid having a resolution of 3 by 6$^{\circ }$ (latitude and longitude, respectively) and at each point of the grid we computed the Sagnac frequency based on all analyzed models. In Figs. 5 and 6 we present results for the DPM and diurnal ocean tides for every 6 h of the 94th day of our time span (22.12.2014), and for every 3 h of the first half of the same day for the semidiurnal effects. A chosen day is a day with the highest amplitudes in all signals.

Fig. 5

Variation of the Sagnac frequency based on the model of the DPM depending on the location of a horizontally mounted instrument, given by latitude $\varphi$ and longitude $\lambda$. Figures depict results for the day with the strongest influence of the effects, i.e. 22.12.2014. Units are [$\upmu$Hz]

Fig. 6

Variation of the Sagnac frequency due to the diurnal and semidiurnal signals in polar motion and dUT1 excited by the ocean tides, depending on the geographical location of a horizontally mounted instrument. The location is given by latitude $\varphi$ and longitude $\lambda$. Figures depict results for the day with the strongest influence of the effects, i.e. 22.12.2014. Please note that for diurnal effects the time step is 6 h and for semidiurnal 3 h. Units are [$\upmu$Hz]

Fig. 7

Polar motion of IRP caused by semidiurnal ocean tides effect. Minus sign of the longitude refers to the Western hemisphere and units are [mas]

The influence of the libration is not considered here since the total libration signal does not exceed the level of 0.40 $\upmu$Hz, independently of location. However, it also turned out that the impact of the semidiurnal ocean tides effect in polar motion, during the whole investigated period, may reach 1.8 $\upmu$Hz, and it is comparable to the other OT components, and therefore, the signal cannot be ignored in further analysis. Nevertheless, at the location of the Wettzell Observatory this signal is always as small, as visible in Fig. 1b. In fact, there are two areas where the influence of the semidiurnal ocean tides effect on polar motion have a negligibly small contribution to the observed RLG signal between about $5^{\circ }$ and $25^{\circ }$ and between $-155^{\circ }$ and $-17^{\circ }$ in longitude (where the sign ‘−’ indicates the Western hemisphere). In contrast, the strongest signal is expected $\pm 10^{\circ }$ around the meridians $-75^{\circ }$ and $102^{\circ }$ at the equator. The reason is a strong polarization of the semidiurnal polar motion excited by the ocean tides, shown in Fig. 7. One can see that the signal is strongly polarized in the direction being perpendicular to the Wettzell meridian plane. Therefore, the polar motion excited by the semidiurnal ocean tide is not visible in the G-ring signal. In general its magnitude on the observed Sagnac frequency strongly depends on the longitude of an RLG.

Fig. 8

Variation of the Sagnac frequency due to the aggregated influence of all ocean tide signals in Earth rotation depending on the geographical location of an instrument, given by latitude $\varphi$ and longitude $\lambda$. Figures depict results for the day with the strongest influence of the effects, i.e. 22.12.2014. Units are [$\upmu$Hz]

However, there is no such dependence for the DPM and the diurnal OT effect in PM. Their maxima and minima (of the absolute value 39.9 $\upmu$Hz for the DPM and 1.6 $\upmu$Hz for the OT) move due to the spinning Earth, and they are always in two points at the equator, distant from each other by about 180$^{\circ }$ (which is not surprising as we consider here diurnal effects). As also expected, the diurnal and semidiurnal ocean tides on dUT1 varies with latitude with the strongest impact at the poles and the weakest at the equator. The maximum amplitudes at the poles are 1.5 $\upmu$Hz for the diurnal and 2.0 $\upmu$Hz for the semidiurnal OT effect in dUT1. However, from the investigation of the aggregated influence of all ocean tide signals over the whole time period, we can point out that at some epochs the signals may have either the same or opposite signs, and thus their superposition may be constructive or destructive. This is visible in Fig. 8, where the sum of all OT components is depicted for the day of the strongest influence of the signals.

Hence, our analysis shows that the geographical location of a horizontally mounted RLG instrument is an important factor in the context of observations of Earth rotation variations. Looking at Figs. 5, 6, 7, 8 we can point out several locations which are of crucial importance from the point of view of the visibility of the investigated signals. They are tabulated in Table 1.

Table 1 The most desirable locations of an RLG, where the maximum amplitude of the investigated signals is expected

Although we do not consider here the real construction of a new instrument from Table 1 it is obvious that some of the locations, e.g. the polar regions, are not accessible. Moreover, locations desirable for monitoring signals in PM and dUT1 exclude each other. However, regarding Earth rotation monitoring any change of the geographical location of the ring laser is equivalent to a change of its orientation with respect to the crust, while keeping the location unchanged. Therefore, we decided to discuss this problem in a more detailed way.

4.1 Location vs. orientation of an RLG

As has already been expressed by Eq. (1), RLG observations depend on the orientation of a plane representing the optical cavity of an RLG with respect to the terrestrial reference system. If the planes of two instruments are parallel, the Sagnac signal, due to change of Earth rotation axis with respect to the solid Earth, should be the same in both RLG, independently of their locations. Hence, instead of considering other locations we can consider the same place but a different orientation of the RLG. In other words, we can orient an instrument at location 1 (given by $\varphi _{1}$, $\lambda _{1}$) to make the same register observations as a horizontally mounted RLG from location 2 (given by $\varphi _{2}$, $\lambda _{2}$). All we have to do is to introduce the normal vector of an instrument mounted horizontally at location 2 ($\mathbf {n}_{2}$) into location 1 and derive the azimuth (A) and the zenith angle (z) of the vector $\mathbf {n}_{2}$ at location 1 ($\mathbf {v}_{1}$). From a mathematical point of view, we can simply use the transformation from the global terrestrial system to the local astronomical system (e.g. Seeber 2003):

$$\begin{aligned} \mathbf {v}_{1}= & {} \mathbf D ^{-1}\mathbf {n}_{2} \Rightarrow \left[ \begin{array}{c} \sin z \cos A \\ \sin z \sin A \\ \cos z \end{array} \right] = \left[ \begin{array}{ccc} -\sin \varphi _{1}\cos \lambda _{1} &{} -\sin \varphi _{1}\sin \lambda _{1} &{} \cos \varphi _{1} \\ -\sin \lambda _{1} &{} \cos \lambda _{1}&{} 0\\ \cos \varphi _{1}\cos \lambda _{1} &{} \cos \varphi _{1}\sin \lambda _{1} &{} \sin \varphi _{1} \end{array}\right] \nonumber \\& \,\left[ \begin{array}{c} \cos \varphi _{2}\cos \lambda _{2}\\ \cos \varphi _{2}\sin \lambda _{2}\\ \sin \varphi _{2} \end{array} \right] . \end{aligned}$$

(13)

If we want to find out what location would be “observed” by an instrument oriented in a particular way, we can use the formula $\mathbf {n}_{2} = \mathbf D \mathbf {v}_{1}$. Using relation (13) we can derive the orientation of an instrument at location 1 being equivalent to any location 2. However, for the sake of completeness, we discuss below the locations which are pointed out in Table 1.

Location 1 from Table 1 refers to the poles. The latitude equals $90^{\circ }$ (the North Pole) or $-90^{\circ }$ (the South Pole) and consequently in the terrestrial reference frame $\mathbf {n}_{2} = [0 \;\; 0 \;\; \pm 1]^{ {T} }$. That leads to:

$$\begin{aligned} \mathbf {v}_{2} = \left[ \begin{array}{ccc} \pm \cos \varphi _{1}&0&\pm \sin \varphi _{1} \end{array} \right] ^{ {T} }, \end{aligned}$$

(14)

therefore, the normal vector of an instrument at location 1 should have the zenith angle $z = 90^{\circ } - |\varphi _{1}|$ and the azimuth $A = 0^{\circ }$ or $180^{\circ }$.

Locations 2–5 from the table refer to different points at the equator. The normal vector of a horizontally mounted instrument located at the equator ($\varphi =0^{\circ }$) takes the form of $\mathbf {n}_{2} = [\cos \lambda _{2} \;\; \sin \lambda _{2} \;\; 0]^{ {T} }$. After substituting the vector into Eq. (13) and making further derivations we get:

$$\begin{aligned} \cos z = \cos \varphi _{1}\cos \Delta \lambda \quad \text { and } \quad \tan A = -\frac{\tan \Delta \lambda }{\sin \varphi _{1}}. \end{aligned}$$

(15)

Additionally, if we want the instrument to be placed in the plane $\lambda _{2}$ equals $0^{\circ }$ or $90^{\circ }$ then $z = \cos \varphi _{1}\cos \lambda _{1}$ and $A = \tan \lambda _{1}/\sin \varphi _{1}$ or $z = \cos \varphi _{1}\sin \lambda _{1}$ and $A = -\tan \lambda _{1}\sin \varphi _{1}$, respectively.

We should emphasize here that we are conducting only a theoretical discussion, not taking into account any technical aspects of the construction of ring lasers. However, as regards the orientation of existing instruments, most of them are mounted horizontally and some of them vertically. Therefore, finally we also take a quick look at signals observed by a vertically mounted instrument. In such an instrument the zenith angle of the normal vector is always $90^{\circ }$ and the observed signal will differ with the change of the azimuth. To determine what location would be “observed” we can use the formula $\mathbf {n}_{2} = \mathbf D [\cos A \;\; \sin A \;\; 0]^{ {T} }$, which leads to the relation:

$$\begin{aligned} \left[ \begin{array}{c} \cos \varphi _{2}\cos \lambda _{2} \\ \cos \varphi _{2}\sin \lambda _{2} \\ \sin \varphi _{2} \end{array}\right] = \left[ \begin{array}{c} -\sin \varphi _{1}\cos \lambda _{1}\cos A - \sin \lambda _{1}\sin A \\ -\sin \varphi _{1}\sin \lambda _{1}\cos A + \cos \lambda _{1}\sin A\\ \cos \varphi _{1}\cos A \end{array}\right] . \end{aligned}$$

(16)

Additionally, if the azimuth were $0^{\circ }$ or $90^{\circ }$ (North or East direction), the observed location would be $|\varphi _{2}| = 90^{\circ } -|\varphi _{1}|$, $\lambda _{2} = \lambda _{1}$ or $|\varphi _{2}| = 0^{\circ }$, $\lambda _{2} = 90^{\circ }+\lambda _{1}$, respectively.

5 Concluding Remarks

Our investigation concerns the contribution of the known modeled high frequency components of Earth rotation to the signal observed by ring laser gyroscopes. For this purpose we computed, based on available models, the theoretical Sagnac frequency observed by the G ring at the Wettzell Observatory. Then we introduced new locations for a ring laser like the Wettzell one to study how the signals vary with longitude and latitude. Lastly, we discussed equivalence between the change of location and change of orientation of an instrument in the context of registered signals. Based on the derived results we can point out a few conclusions and remarks.

First of all, we can point out that the lunisolar diurnal polar motion is definitely the dominant signal, from all of the Earth rotation variations at diurnal and subdiurnal frequencies, affecting the RLG observations. However, the influence of diurnal and semidiurnal ocean tides on both polar motion and dUT1 should also be taken into account in analysis, but they are rather visible as a sum of harmonics with the same frequencies, and there might be a problem to separate them. The influence of the libration can hardly be detected at the current accuracy of the RLG. However, as the total influence of libration (in PM and dUT1) reaches about 0.4 $\upmu$Hz corresponding to a relative accuracy level of $1 \times 10^{-9}$, with the increasing accuracy of the RLG measurements the signal should be considered.

Moreover, it is important that the high frequency signal observed by a horizontally mounted RLG depends considerably on the geographical location of the instrument. For instance, there are areas where the semidiurnal OT effect in PM are hardly noticeable, the signals in dUT1 are negligibly small at the equator, and the influence of signals in PM decreases when moving towards the poles. Also, the desired location for monitoring signals in PM and dUT1 exclude each other. Consequently, the component of interest is crucial for the choice of the location, and if all the components of Earth rotation should be monitored using the RLG technique, several instruments located at appropriate places worldwide would be required. However, any change of geographical location of a horizontally mounted instrument is equivalent to an appropriate change of its orientation with respect to the crust. This theoretically means that instead of considering several locations, only one location with several instruments can be considered. For example, imagining that at the Wettzell location there were three instruments with the normal vectors oriented in up, north and east directions, it would be possible to observe signals at points $\varphi \approx 40.9^\circ$S, $\lambda \approx 12.9^\circ$E and $\varphi = 0^\circ$, $\lambda \approx 102.9^\circ$E. Hence, the mid-latitude point becomes an appropriate location for observing signals in polar motion. Also, subdiurnal OT signals, although strongly polarized in the direction perpendicular to the Wettzell meridian plane, could be then observed. Moreover, though it is beyond the scope of this work, we also should remember that the normal vector of an instrument undergoes some perturbations, and having several instruments at the same place makes it easier to identify and model local effects affecting observations. In fact, such variations of the normal vector might be assumed the same for all instruments at the location, which limits the number of degrees of freedom in a set of observations. The number of degrees of freedom has been discussed by, e.g. Chao (1991), and we are going to deal with the issue in further analysis.

Summarizing, we reviewed the main diurnal and subdiurnal signals in PM and dUT1, which influence gyroscopic observations. This study can easily be extended for other high frequency effects in Earth rotation, like the contributions of the atmospheric S1 tide. The next step of our investigation will be a study of the contribution of local phenomena (like Earth tides or non-tidal loading effects) to the observed Sagnac frequency.