1 Introduction

Ring laser gyroscopes (RLGs) are instruments for measuring absolute rotation. They observe the Sagnac effect, which arises due to a difference in the respective optical path lengths of the counter-propagating laser beams within a cavity (Schreiber and Wells 2013). Although the two beams travel the same path, under the same conditions, they traverse different distances in space due to the sensor rotation. It results in the beat frequency (Sagnac frequency), which is directly proportional to the dot product of the vector normal to the gyroscope plane, and the vector of its rotation (Stedman 1997). For large RLGs firmly tied to the ground, the rotation vector is actually the rotation vector of the Earth. Therefore, any changes in the normal vector of the instrument or in the Earth’s rotation will reflect themselves as variations in the observed Sagnac frequency.

The impact of signals in the Earth rotation vector on RLG observations has been investigated and summarized in our previous paper (Tercjak and Brzeziński 2017). It has also been shown that RLGs are used for an estimation of Earth rotation parameters as a supportive technique for Very Long Baseline Interferometry (by e.g. Mendes Cerveira et al. 2009; Nilsson et al. 2012). This paper is on the subject of phenomena that affect the terrestrial orientation of the normal vector of the instrument.

As it has been shown by e.g. Schreiber et al. (2003) or Schreiber and Wells (2013) RLG instruments are sensitive to solid Earth tides and to ocean tidal loading. Their impact can be separated from the data if there are tiltmeters installed on site. However, prior to using tiltmeter corrections, the attraction part of the observed tilt should be removed as ring lasers are sensitive only to the geometrical part (Schreiber and Wells 2013). Additionally, any instrument, also a tiltmeter, has its own instrumental noises or offsets (more details on the influence of diurnal and subdiurnal signals in the normal vector about tiltmeter observations and their sensitivity to the phenomena discussed in this paper can be found in the PAGEOPH Topical volume Braitenberg et al. (2018) as for instance Ruotsalainen (2018), Grillo et al. (2018) and Rossi et al. (2018)). Therefore, we decided to verify how the local phenomena, solid Earth tides, ocean tidal loading and non-tidal atmospheric pressure and continental water storage loading, reflect themselves in the observed Sagnac frequency and compare the modeled signal with the one observed by a tiltmeter. For this purpose, first we compared available models of the aforementioned phenomena and assessed the importance of the Love numbers used in the modeling of solid Earth tides. Finally we modeled Sagnac frequency variations caused by those effects and compared the obtained signal with tiltmeter observations reduced by the attraction part of the tilt.

Our study was carried out for the horizontally-mounted G-ring laser and one of its tiltmeter, located at the Geodetic Observatory Wettzell (for more details see e.g. Schreiber and Wells 2013). We used data from the entire year 2016 (with the initial epoch set to midnight January 1), however we focused on the signals having frequencies higher than 0.5 cycle per day (cpd). This is connected to the fact that we are interested in deriving high frequency variations of the Earth rotation based on the RLG data, therefore we firstly need to identify and reduce all undesired signals within this band. The sensitivity threshold of the G-ring is 1 \(\upmu \)Hz corresponding to about 3 nrad of the normal vector tilt with respect to the rotation axis, while for the tiltmeter the threshold is at the level of 0.5 nrad. The main aim of this study was to summarize which deformation effects are detectable by the G-ring laser and to assess whether tiltmeter data reduce these signals efficiently enough.

2 Theoretical Background

The Sagnac frequency is given by the formula (e.g. Schreiber and Wells 2013):

$$ f_{{sagn}} = K\Omega \cdot {\mathbf{n}} + \Delta f_{{instr}} ,{\text{with the scale factor}}\;K = \frac{{4 \cdot P}}{{\lambda _{l} \cdot L}} $$
(1)

where L, P and \(\lambda _l\) are the laser beam path length, the area enclosed by the path and the wavelength of the laser beam, respectively. Vector \({\varvec{\varOmega }}\) is the instantaneous Earth rotation vector in the Earth-fixed system, and vector n is the normal vector of the instrument in this system. The term \(\varDelta f_{instr}\) refers to the instrumental offset, understood as perturbations in the laser’s behavior. However, this aspect is out of the scope of the paper, and we treat them as a signal noise. For signal modeling we assume the geometry and laser length to be constant and for the G-ring equal as follows: \(L = 16\) m, \(P = 16\) m\(^2\) and \(\lambda _l = 632.8\) nm (Schreiber and Wells 2013). Within this study we focus on the normal vector, which is expressed in the global frame by the transformation:

$$\begin{aligned} {\varvec{n}} = D\cdot {\varvec{n}}_{loc} = \left[ \begin{array}{ccc} -\sin {{\upvarphi }}\cos {{\uplambda }}&{} -\sin {{\uplambda }}&{} \cos {{\upvarphi }}\cos {{\uplambda }}\\ -\sin {{\upvarphi }}\sin {{\uplambda }}&{} \cos {{\uplambda }}&{} \cos {{\upvarphi }}\sin {{\uplambda }}\\ \cos {{\upvarphi }}&{} 0&{} \sin {{\upvarphi }}\end{array}\right] \left[ \begin{array}{ccc} \sin {z}\cos {A} \\ \sin {z}\sin {A} \\ \cos {z} \end{array}\right] , \end{aligned}$$
(2)

where \({{\upvarphi }}= 49.145^\circ \) and \({{\uplambda }}=12.875^\circ \) are the geodetic latitude and longitude of the instrument’s location, z and A are the zenith angle and the azimuth of the normal vector in the local North–East–Up (NEU) reference system. The zenith angle is counted positive from the Up-direction and the azimuth clockwise from North. For the horizontally-mounted ring laser the nominal value of z is zero, therefore n\(_{loc}\) = [0 0 1]\(^\text {T}\), and consequently n = \([\cos {{\upvarphi }}\cos {{\uplambda }}\; \cos {{\upvarphi }}\sin {{\uplambda }}\; \sin {{\upvarphi }}]^\text {T}\). Variations in the normal vector terrestrial direction \(\delta \mathbf{n }\) lead to changes in the observed Sagnac frequency \(\delta f_n\) given by:

$$\begin{aligned} \delta f_n = K{\varvec{\varOmega }}\cdot {\varvec{\delta }}\mathbf{n } = K{\varvec{\varOmega }}\cdot [\delta n_1\; \delta n_2\; \delta n_3]^\text {T}. \end{aligned}$$
(3)

The \({\varvec{\varOmega }}\) vector is expressed in the terrestrial reference system by \(\varOmega _0[m_x\; m_y\; 1+m_z]^\text {T}\) with \(\varOmega _0\) denoting the mean angular speed of Earth’s rotation and the dimensionless parameters \(m_{x}, m_{y}, m_{z}\) defining its perturbations. Taking into account that variations of both, Earth rotation and normal vector orientation are small, the components \(m_x\delta n_1\), \(m_y\delta n_2\) and \(m_z\delta n_3\) are negligible. Therefore, only the third component of the \({\varvec{\delta }}\)n vector should be considered in the first order approximation. Additionally, if we express orientation changes as variations of the azimuth and zenith angle, we can further develop:

$$\begin{aligned} \delta f_n = K\varOmega _0\cdot \delta n_3 = K\varOmega _0\cdot (\cos {{\upvarphi }}\cos {z}\cos {A}\delta z-\sin {{\upvarphi }}\sin {z}\delta z-\cos {{\upvarphi }}\sin {z}\sin {A}\delta A). \end{aligned}$$
(4)

As we stated previously, \(z = 0\) and consequently only the first component on the right hand-side of the above equation remains. Also, although for horizontally mounted rings the azimuth is indefinite, it goes here with the cosine function. It means that variations of the zenith angle in East–West direction have practically no impact on the observations and \(\delta z\) might be considered as latitude variations or simply as the North–South tilt \(\varDelta T^{ns}\). Consequently, we can develop the relation:

$$\begin{aligned} \delta f_n = K\varOmega _{0}\cos {{\upvarphi }}\delta z = K\varOmega _{0}\cos {{\upvarphi }}\varDelta T^{ns}, \end{aligned}$$
(5)

which is used to evaluate how particular signals reflect themselves as Sagnac frequency variations.

3 Solid Earth Tides

The first part of our investigation considers the impact of solid Earth tides. We start with a comparison of two methods of defining the NS tidal tilt. Method 1 (further referred to as M1) is based on the tidal potential (V) partial derivative with respect to the colatitude (\(\theta = 90^\circ - \varphi \)):

$$\begin{aligned} \varDelta T^{ns}_{M1} = \frac{(l_n-h_n)}{gR}\frac{\partial V}{\partial \theta }, \end{aligned}$$
(6)

where g is Earth’s gravitational acceleration at the equator, R is the geocentric radius at the point of observation, \(l_n\) and \(h_n\) are tidal Love numbers of a degree n. It should be noted that in Eq. (6) the coefficient \(l_n-h_n\) is used instead of \(1+k_n-h_n\), because the ring laser is sensitive only to the geometrical part of tilt (for more details see e.g. Tian 2014; Rautenberg et al. 1997). Method 2 (M2) is a combination of the relation defining meridional site displacement \(d^{ns}= \frac{l_n}{g}\frac{\partial V}{\partial \theta }\) and Eq. (6):

$$\begin{aligned} \varDelta T^{ns}_{M2} = \left( 1-\frac{h_n}{l_n}\right) \frac{d_{ns}}{R}. \end{aligned}$$
(7)

To verify the numerical equivalence between M1 and M2 we prepared two time series of theoretical tilt-induced variations of Sagnac frequency sensed by the G-ring. We used for this purpose Eq. (5) and we refer to these solutions as \(dS_{M1}\) and \(dS_{M2}\). In the first time series we used solid-Earth-tide-induced tilt \(\varDelta T^{ns}_{M1}\) computed using the ETERNA software (Wenzel 1996), and in the second one we used \(\varDelta T^{ns}_{M2}\) computed using a time series of solid-Earth-tide-induced displacement \(d^{ns}\), also prepared with ETERNA. Both \(\varDelta T^{ns}_{M1}\) and \(\varDelta T^{ns}_{M2}\) were prepared for the entire year 2016. The Love numbers used in this comparison were derived from Eq. (7.2) of the International Earth Rotation and Reference Systems Service (IERS) Conventions 2010 (Petit et al. 2010), and \(h_n\) equals 0.60759 and \(l_n \) to 0.08477. The maximum difference between the \(dS_{M1}\) and \(dS_{M2}\) solutions was about 0.001 \(\upmu \)Hz and most likely results from the different accuracy of computed tilt (0.001 mas) and displacements (0.001 mm). Nevertheless, it is far below the accuracy and visibility level of the G-ring and we can confirm that the two approaches are equivalent.

To make an additional verification, we prepared another time series of the Sagnac frequency variations, \(dS_{solid}\). For this purpose we prepared the solid-Earth-tide-induced site displacement, \(d^{ns}_{solid}\), using the solid software (Milbert 2018). Then we filtered the series to remove signals having periods greater than 2 days, and converted it into tilt \(\varDelta T^{ns}_{solid}\) using Eq. (7). The solid software utilizes the algorithm proposed by Mathews et al. (1997) and recommended by the IERS Conventions 2010 (chapter 7, Petit et al. (2010)). It differs from the one realized by ETERNA, as it is based on the positions of Sun and Moon with respect to the Earth instead of the tidal potential harmonic expansion. The difference between time series \(dS_{M2}\) and \(dS_{solid}\) (we compare these two, as both are prepared using the second approach) is shown in Fig. 1.

Fig. 1
figure 1

Differences between Sagnac frequency time series \(dS_{M2}\) and \(dS_{solid}\) modeled using ETERNA (Wenzel 1996) and solid (Milbert 2018) software, respectively

Full size image

The maximum difference does not exceed 1 \(\upmu \)Hz. It might result not only from the different method, but also from the different set of Love numbers used in computations. Here we used only one value of h and one of l, not taking into account any corrections due to the frequencies of diurnal tides, while the solid software includes such corrections. Also, we used only one set of Love numbers to compute the coefficient \(1-\frac{h_n}{l_n}\) in Eq. (7). However, ETERNA also enables introducing different Love numbers, therefore the next step of our investigation was an evaluation of discrepancies arising from the use of different Love numbers.

To verify how important values of Love numbers adopted in computations are, we prepared six additional solutions: \(dS_1\), \(dS_2\), \(dS_3\), \(dS_4\), \(dS_{solid}^{D}\) and \(dS_{solid}^{IC}\). The first four solutions were prepared based on the NS tilt predicted using ETERNA software, following the first approach. Solutions \(dS_1\), \(dS_2\) and \(dS_3\) were prepared using Love numbers derived by Dehant et al. (1999), adopting variations due to tidal frequencies. We distinguished 17 tidal groups (19 for the solution \(dS_3\)), starting with the tidal group \(\hbox {Q}_1\) and ending with \(\hbox {M}_3\) (\(\hbox {M}_5\hbox {M}_6\) for \(dS_3\)), like it is proposed by Wenzel (1996). However, in the solution \(dS_1\) we did not modify Love numbers according to the station latitude. The fourth solution was prepared using Love numbers derived from Eq. (7.3a) and (7.3b) and values from Table 7.2 of the IERS Conventions (2010). The other two solutions, \(dS_{solid}^{D}\) and \(dS_{solid}^{IC}\), are based on the time series \(d^{ns}_{solid}\) and the second approach. The series \(d^{ns}_{solid}\) was filtered to remove long-term signals. During this step it was multiplied by the coefficient \(1-h_n/l_n\), with Love numbers taken from Dehant et al. (1999) for solution \(dS_{solid}^{D}\), and from the IERS Conventions for solution \(dS_{solid}^{IC}\). Therefore, the coefficient \(1-h_n/l_n\) is different for each tidal group in the solution \(dS_{solid}^{D}\), and is different for each tidal group and each epoch in the solution \(dS_{solid}^{IC}\). Details about Love numbers used in particular solutions are tabulated in Table 1.

In Table 2 the maximum differences between considered solutions are tabulated. We do not show solutions \(dS_1\) and \(dS_3\) because the maximum differences between solutions \(dS_1\) and \(dS_2\) and \(dS_2\) and \(dS_3\) do not exceed 0.015 and 0.002 \(\upmu \)Hz, respectively. This indicates that neglecting the variation of Love numbers due to the latitude and the inclusion of tides degree higher than 3 have almost no impact on the theoretical signal. The maximum differences between other solutions are at least one order of magnitude higher, although still at or below the sensitivity level of the G-ring. However, differences arising from the use of different sets of Love numbers (\(dS_2-dS_4\) or \(dS_{solid}^D-dS_{solid}^{IC}\)) are smaller than those arising from the use of only one set of \(h_n\) and \(l_n\) for all tidal groups (e.g. \(dS_2-dS_{M1}\) or \(dS_{solid}^{IC}-dS_{solid}\)) or from the use of different software (Fig. 1). It means, that the Love numbers adopted for computations do not play such an important role as the modeling approach applied to predict theoretical tilt. Finally, for further comparison and analysis we chose the solution \(dS_4\), shown in Fig. 2a, as it was prepared directly as tilts, without any additional filtering or modification. From the depicted results, it is clearly visible that solid Earth tides have a considerable impact and are definitely visible by the G-ring. Also, as it can be concluded from Fig. 2b (and further from Fig. 5c, e) it is the main signal in the semi-diurnal band, visible by the ring laser.

Fig. 2
figure 2

Theoretical Sagnac frequency caused by solid Earth tides (solution \(dS_4\)) and its amplitude spectrum

Full size image
Table 1 Details of Love numbers used in compared solutions
Full size table
Table 2 Maximum discrepancies between solutions \(dS_2\), \(dS_4\), \(dS_{solid}\), \(dS_{solid}^{D}\) and \(dS_{solid}^{IC}\) in [\(\upmu \)Hz]
Full size table

4 Ocean Tidal Loading and Non-tidal Loading Effects

The next part of our study considered the impact of ocean tidal loading (OTL) and non-tidal loading effects. It should be noted here, that the above relationships between tilts and displacements, and between tilts sensed by a tiltmeter and the one sensed by a RLG (Eqs. 6, 7) are valid only for tidal effects. For loading effects such operations are not so straightforward. Therefore, to obtain separately the deformation and attraction part of the tilt due to OTL effects we adopted the software Some Programs for Ocean-Tide Loading (SPOTL, Agnew 1997). In case of atmospheric pressure and continental hydrosphere loading we made use of data provided by services EOST (Boy et al. 2009) and ATMACS (Klügel and Wziontek 2009), but not being available on the website.

A verification of the impact of ocean tidal loading on the Sagnac frequency observed by the G-ring was done by Tian (2013), nevertheless we also did such a study for the sake of completeness of our investigation. We prepared and compared a few time series of tilt caused by the OTL effect. For this purpose we used the adopted version of SPOTL software (Gebauer et al. 2007). For tilt computations there is no difference if we use a reference frame coincident with the center of mass of the solid Earth or of the solid Earth and the load (Agnew 1997). Also, as we checked, the maximum absolute difference between the use of available Earth models does not exceed 0.1 nrad (0.03 \(\upmu \)Hz), what is a far negligible value. Bigger differences might arise from the use of different global ocean tide models. Therefore, following Tian (2013), we prepared time series of deformation tilt using the Green’s function gr.gbcont.wef.p01.ce (Farrell 1972) and the same eight global ocean tide models (FES04, DTU10, EOT11A, GOT4p7, HAMTIDE11a, TPXO72, TPXO72ATLAS, NAO99b). Next, we computed theoretical Sagnac frequencies by inserting each tilt time series into Eq. (5). In Table 3 we show maximum differences between time series of the Sagnac frequency obtained when using different OTL models.

Table 3 Maximum differences between theoretical Sagnac frequency caused by tilts due to OTL effect, modeled using investigated global ocean tide models, in [\(\upmu \)Hz]
Full size table

The maximum value does not exceed 0.21 \(\upmu \)Hz (0.7 nrad), and it refers to models FES04 and TPXO72. The differences arise due to the fact that different models use different group of tides (apart of the biggest ones). In the next step we applied also local and regional models (again following Tian 2013): osu.europeshelf.2008 and osu.mediterranean.2011 (Agnew 1997). Nevertheless, the obtained differences did not exceed 0.04 \(\upmu \)Hz, even if both models were applied. It means that, for now, local models can be neglected. In his work Tian (2013) also applied the osu.redsea.2010 model, however due to the distance between Wettzell and the Red Sea it is obvious that the model will have no visible impact, therefore we omitted it in our analysis.

Eventually, for further analysis we chose the HAMTIDE11a model, as the mean discrepancy between this one and other models is the lowest. The theoretical Sagnac frequency variations caused by the OTL effect when using the HAMTIDE11a model are shown in Fig. 3a. From the depicted results it is visible that the impact of the OTL effect barely exceeds 1 \(\upmu \)Hz, which is close to the G-ring’s current threshold. It reaches 1.1 \(\upmu \)Hz (3.8 nrad) and constitutes about 9% of solid Earth tides impact. Also, similarly to the solid Earth tides, the main OTL effect is visible in the semi-diurnal band (Fig. 3b).

Fig. 3
figure 3

Theoretical Sagnac frequency due to ocean tidal loading (HAMTIDE11a model) and its amplitude spectrum

Full size image

Regarding non-tidal loading effects, it was also already mentioned that the transition from displacements to tilts is not as straightforward as in the case of solid Earth tides. At the same time, available models describing the influence of non-tidal loading effects are usually expressed by displacements, not by tilts. Even if there are available tilt time series, the signal is given as sensed by a tiltmeter not by a ring laser. Fortunately, there was a possibility to obtain separately deformation and attraction tilts due to atmospheric pressure and continental hydrosphere loading from EOST service (http://loading.u-strasbg.fr) and due to atmospheric pressure loading from ATMACS service (http://atmacs.bkg.bund.de). In order to obtain the theoretical Sagnac frequency caused by both phenomena we inserted respective tilt time series into Eq. (5). However, as we expected the impact of non-tidal effects to be small, we compared not only the high-frequency signal but also the entire band of the effects.

At first we compared the EOST and ATMACS models of the atmospheric effect. The maximum difference reaches about 1.2 \(\upmu \)Hz, i.e. 3.8 nrad in tilt domain, while the entire effect has a maximum amplitude of about 2.8 \(\upmu \)Hz, i.e. 9.4 nrad (EOST model). It means that the absolute difference is not large, but it contributes by 40% to the entire effect. When comparing the high-frequency band only, the maximum difference is about 0.45 \(\upmu \)Hz (1.5 nrad) contributing by 57% to the maximum amplitude, which reaches about 0.78 \(\upmu \)Hz (2.6 nrad). The differences between both models are not surprising since some boundary conditions and initial assumptions (e.g. oceanic response) are rather different. Eventually, for further analysis we used the EOST model for the sake of consistency with the continental hydrosphere loading model.

Calculated Sagnac frequency variations due to non-tidal atmospheric pressure and continental hydrosphere loading are shown in Fig. 4a, c, respectively. While the red line shows the entire signal the blue line represents only the high-frequency band. It is noticeable, when considering the entire frequency spectrum, that both non-tidal effects should be visible by the G-ring. However, the high frequency band is below the visibility level in both cases.

As it was indicated above, the maximum amplitudes of the atmospheric effect reach 2.8 \(\upmu \)Hz for the entire signal and 0.78 \(\upmu \)Hz for the high-frequency band amounting to about 23% and 6% of the solid Earth tide effect, respectively. Moreover, the high frequency band has a visible peak at \(\hbox {S}_2\) frequency (Fig. 4b), but it slightly exceeds 0.03 \(\upmu \)Hz and it is rather a remaining \(\hbox {S}_2\) radiation tide in atmospheric pressure fields used to compute atmospheric loading effect.

The impact of the continental hydrosphere even exceeds 4 \(\upmu \)Hz, amounting to about 37% of the solid Earth tide effect, at long periods. High-frequency variations barely exceed 0.15 \(\upmu \)Hz (0.5 nrad), representing 1% of the solid Earth tides variations. The high frequency part of the effect has two visible peaks, in the diurnal and semi-diurnal band, the amplitudes however are so small that the signal is hardly visible in ring laser data.

Fig. 4
figure 4

Theoretical Sagnac frequency due to non-tidal atmospheric pressure loading (plot A) and non-tidal continental hydrosphere loading (plot C) and their amplitude spectra (plots B and D respectively). The blue lines represent the high frequency band, while the red lines depict the entire signal (note different scales)

Full size image

Nevertheless, we should note here that even if the described effects are not visible by the G-ring, they might be visible by its tiltmeters. As it was mentioned in the introduction, the visibility threshold for the G-ring tiltmeters is 0.5 nrad (0.15 \(\upmu \)Hz), which means that the only effect mentioned here which is not detectable by them is the continental hydrology loading. It is important in the context of using tiltmeter observations for removing deformation effects from ring laser data.

5 Models and Real Data

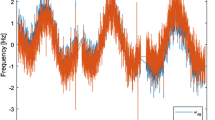
To verify how consistent the modeled high-frequency variations are with observations, we compared the modeled signal with those observed by the G-ring and one of its tiltmeters. In Fig. 5 we show raw RLG data filtered with a high-pass filter (plot A) and its spectrum (plot C), data reduced using model time series as well as data reduced using the tiltmeter observations (Fig. 5b). Also, spectra of two latter series are shown in Fig. 5d, e. It is visible that the raw G-ring observations have very strong diurnal and semi-diurnal components. The former band is caused mainly by the diurnal polar motion (we discussed this subject in our previous work Tercjak and Brzeziński 2017) and can be modeled using the model of Brzeziński (1986). Phenomena discussed in this paper are responsible mainly for the latter band as it is seen in Figs. 2b, 3b and 4b, d. Therefore in Fig. 5 (plots D and E) we show diurnal and semi-diurnal bands separately.

To reduce ring laser data using tiltmeter observations, firstly it is needed to subtract the tidal attraction part of the tilt (Schreiber and Wells 2013). Therefore, for each phenomena we additionally prepared time series of the tilt due to the tidal potential. For solid Earth tides, we used solution \(dS_4\) as describe in Sect. 4, just instead of (\(l_n-h_n\)) coefficient in Eq. (6) we used (\(1+k_n-l_n\)). For the OTL effect we used again the adopted version of SPOTL software and HAMTIDE11a model. For non-tidal effects we used attraction part of tilt obtained from EOST service.

The reduced tilt was then subtracted from the raw G-ring observations and shown in Fig. 5b as yellow line (\(\varDelta _1\)). The difference between the raw ring laser observations and the modeled data (\(\varDelta _2\)) is shown in blue. Also, the diurnal polar motion model (Brzeziński 1986) was subtracted from both time series. From the depicted results it is visible that the residuals of data reduced with tiltmeter observations are comparable to those reduced with models, especially regarding the diurnal band (Fig. 5d). In the semi-diurnal band (Fig. 5d), however, there is a visible discrepancy between time series at a range of frequencies between 1.6 and 2.2 cpd. The difference suggests that models removed tilt better than tiltmeter observations, but the real cause of it is not really clear. Local atmospheric pressure variations can be rather excluded, as in this case a peak at \(\hbox {S}_2\) would be expected. It might arise from the fact that tiltmeter data are additionally disturbed by instrumental effects, but we can not exclude any artificial effects (e.g. spectral leakage).

Fig. 5
figure 5

Sagnac frequency sensed by the G-ring: raw data (a) and after removal of tiltmeter observations (b, yellow line) and modeled effects (b, blue line); Also, the diurnal polar motion model (Brzeziński 1986) was subtracted from both time series; amplitude spectrum of the raw G-ring observations (c); amplitude spectra of the reduced data in diurnal and semi-diurnal band, respectively (d, e). In plots d, e yellow and blue lines refer to the respective signals in plot b

Full size image

Additionally we computed the differences between the ring laser data and the solid Earth tide model only (\(\varDelta _3\)), between the ring laser data and the solid Earth tides plus OTL effect (\(\varDelta _4\)), between the ring laser data and the solid Earth tides plus atmospheric effect (\(\varDelta _5\)) and between the ring laser data and the solid Earth tides plus hydrospheric effect (\(\varDelta _6\)). Then we computed their amplitude spectra to verify if the application of models of small effects has any impact. Results are shown in Fig. 6, where the difference \(\varDelta _3\) (yellow line) is compared to \(\varDelta _4\) (plots A and B, blue line), to \(\varDelta _5\) (plots C and D, blue line) and to \(\varDelta _6\) (plots E and F, blue line).

Fig. 6
figure 6

Comparison of amplitude spectra of the differences \(\varDelta _3\), \(\varDelta _4\), \(\varDelta _5\) and \(\varDelta _6\) in diurnal and semi-diurnal bands, see explanation within text

Full size image

The depicted results mostly confirm what we expected. The OTL effect is visible in the observed signal and the application of the models slightly decreases the amplitudes. At frequencies of the diurnal tides \(\hbox {O}_1\) and \(\hbox {K}_1\) the amplitudes are decreased by 0.01 and 0.08 \(\upmu \)Hz respectively. At frequencies of the semi-diurnal tides \(\hbox {N}_2\), \(\hbox {M}_2\) and \(\hbox {S}_2\) the improvement reaches 0.07, 0.49 and 0.17 \(\upmu \)Hz, respectively. Although all these values are below the visibility level, there is a noticeable improvement in the semi-diurnal band after application of the OTL model (Fig. 6b). For the non-tidal effects the improvement is currently of minor significance. The application of the model of the atmospheric effect slightly improves (by 0.05–0.06 \(\upmu \)Hz) the amplitudes in the diurnal band at frequencies between 0.60 and 0.75 cycle per day (cpd). However, at the frequency of the \(\hbox {S}_2\) tide the amplitude slightly increases, by about 0.02 \(\upmu \)Hz. Although the variation is not big and might be not noticeable from the plot, it might suggest that the tidal part remaining in the atmospheric model introduces undesired signal into our data. Regarding the effect of the continental hydrosphere, it has practically no visible impact on the high-frequency band. Differences between solutions \(\varDelta _3\) and \(\varDelta _6\) do not exceed 0.01 \(\upmu \)Hz so the comparison is shown here only for the sake of completeness.

It should be underlined here that the obtained results are valid for the Wettzell G-ring only. Phenomena discussed here depend on the geographical location, so their impact on RLG observations do not depend solely on the orientation of the instrument, but also on its location. For instance, at seaside we can expect much higher impact of the ocean tidal loading effect. Nevertheless, the orientation of the instrument is also an important issue. As it is explained in Sect. 2, horizontally-oriented ring lasers have zenith angle equal to zero, this makes them sensitive only to the tilt in North–South direction (Eq. 5). However, if the condition \(z=0\) is not met (an instrument is not mounted horizontally), then Eq. (4) does not simplify to Eq. (5), and two other terms remain. It means that a non-horizontal ring laser would be sensitive not only to the North–South but also to Up–Down variations in its terrestrial orientation. Therefore, it is not possible to consider a horizontally-mounted instrument at the location corresponding to the local orientation of a non-horizontal ring, like it is possible in the case of Earth rotation variations (Tercjak and Brzeziński 2017), or at least is not so straightforward.

6 Conclusion

We investigated how signals causing variations in the orientation of the normal vector of a ring laser contribute to the observed Sagnac frequency. For this purpose first we compared different approaches of modeling the impact of solid Earth tides and we assessed the importance of the selected Love numbers. Also, we compared models of ocean tidal loading and non-tidal loading effects. Finally we modeled the impact of aforementioned phenomena on the observations of the horizontally-mounted G ring laser and compared them with the recorded data. Based on the derived results we can point out the following conclusions and remarks:

  • the solid Earth tides are the dominant effect causing variations of the normal vector in the G-ring observations; however, when modeling its impact, the main important factor is the algorithm used for tilt computations, although the maximum difference between ETERNA and solid software does not exceed 1 \(\upmu \)Hz, the G-ring visibility threshold. With the growing sensitivity and accuracy of the technique an additional evaluation might be required;

  • at this level of accuracy the Love numbers are not of great importance in solid Earth tides signal modeling; using different sets of Love numbers we got discrepancies in the modeled signal not exceeding 0.3 \(\upmu \)Hz, what constitutes about 2.5% of the solid Earth tides maximum amplitudes;

  • ocean tidal loading, although accounting for only 9% of the solid Earth tide impact, contributes visibly to the semi-diurnal band; however, there is no difference which global model of ocean tides is used for modeling tilts, and local models can totally be neglected;

  • non-tidal atmospheric pressure loading constitutes only about 6% of the solid Earth tides signal (in the high-frequency band) and there are quite big differences between available models;

  • non-tidal continental water storage loading has no visible impact in the high-frequency band, but it might be visible if long-term signals were considered;

  • the reduction of RLG signals using models seems to be more effective than using tiltmeter observations; it might be connected to additional instrumental effects in tiltmeter data; however, we can not forget that models discussed here do not account for all local site effects (e.g. for strain-tilt coupling due to geological inhomogeneities), so their effectiveness is also limited.

  • non-horizontally oriented rings sense not only the North–South variations of the normal vector, but also the Up–Down one, therefore they require slightly more attention than horizontal ones in terms of modeling the impact of local effects.

We have to remember that in case of the phenomena discussed in the paper, both orientation and the geographical location of an instrument are important. Since ring lasers are not sensitive to variations of the plumb line, a discrimination between the deformation and attraction part for tilt is required when applying tidal or loading models for the correction of ring laser observations, an issue which is barely discussed in the literature.