Response times in gated M/G/1 queues: The processor-sharing case

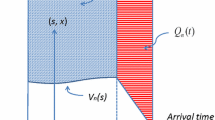
Abstract

A class of single server queues with Poisson arrivals and a gated server is considered. Whenever the server becomes idle the gate separating it from the waiting line opens, admitting all the waiting customers into service, and then closes again. The batch admitted into service may be served according to some arbitrary scheme. The equilibrium waiting time distribution is provided for the subclass of conservative schemes with arbitrary service times and the processor-sharing case is treated in some detail to produce the equilibrium time-in-service and response time distributions, conditional on the length of required service. The LIFO and random order of service schemes and the case of compound Poisson arrivals are treated briefly as examples of the effectiveness of the proposed method of analysis. All distributions are provided in terms of their Laplace transforms except for the case of exponential service times where the L.T. of the waiting time distribution is inverted. The first two moments of the equilibrium waiting and response times are provided for most treated cases and in the exponential service times case the batch size distribution is also presented.