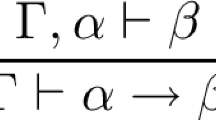Skip to main content
SpringerLink
Log in

Proof theory for minimal quantum logic I

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

Abstract

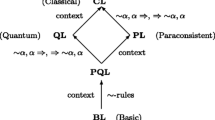
In this paper we give a sequential system of minimal quantum logic which enjoys cut-freeness naturally. The duality theorem, the cut-elimination theorem, and the completeness theorem with respect to the relational semantics of R. I. Goldblatt are presented. Due to severe limitations of space, technically heavy proofs of the first two theorems are relegated to a subsequent paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Bruns, G. (1976). Free ortholattices,Canadian Journal of Mathematics,28, 977–985.

    Google Scholar 

  • Cutland, N. J., and Gibbins, P. F. (1982). A regular sequent calculus for quantum logic in which ⋀ and ⋁ are dual,Logique et Analyse,99, 221–248.

    Google Scholar 

  • Dalla Chiara, M. L. (1986). Quantum logic, inHandbook of Philosophical Logic, D. Gabbay and F. Guenthner, eds., Reidel, Dordrecht, Volume III, pp. 427–469.

    Google Scholar 

  • Dishkant, H. (1972). Semantics for the minimal logic of quantum mechanics,Studia Logica,30, 23–36.

    Google Scholar 

  • Dishkant, H. (1977). Imbedding of the quantum logic in the modal system of Brower,Journal of Symbolic Logic,42, 321–328.

    Google Scholar 

  • Gentzen, G. (1935). Untersuchungen über das logische Schliessen, I and II,Mathematische Zeitschrift,39, 176–210, 405-431.

    Google Scholar 

  • Goldblatt, R. I. (1974). Semantical analysis of orthologic,Journal of Philosophical Logic,3, 19–36.

    Google Scholar 

  • Goldblatt, R. I. (1975). The Stone space of an ortholattice,Bulletin of the London Mathematical Society,7, 45–48.

    Google Scholar 

  • Goldblatt, R. I. (1984). Orthomodularity is not elementary,Journal of Symbolic Logic,49, 401–404.

    Google Scholar 

  • Jammer, M. (1974).The Philosophy of Quantum Mechanics, Wiley, New York.

    Google Scholar 

  • Maeda, S. (1980).Lattice Theory and Quantum Logic, Maki, Tokyo [in Japanese].

    Google Scholar 

  • Nishimura, H. (1980). Sequential method in quantum logic,Journal of Symbolic Logic,45, 339–352. Nishimura, H. (1983). A cut-free sequential system for the propositional modal logic of finite chains,Publications of RIMS, Kyoto University,19, 305–316.

    Google Scholar 

  • Takeuti, G. (1975).Proof Theory, North-Holland, Amsterdam.

    Google Scholar 

  • Tamura, S. (1988). A Gentzen formulation without the cut rule for ortholattices,Kobe Journal of Mathematics,5, 133–150.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, University of Tsukuba, 305, Ibaraki, Japan

    Hirokazu Nishimura

Authors
  1. Hirokazu Nishimura
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Nishimura, H. Proof theory for minimal quantum logic I. Int J Theor Phys 33, 103–113 (1994). https://doi.org/10.1007/BF00671616

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00671616

Keywords

Search

Navigation