Abstract
This paper provides a framework to treat the problem of building signature schemes from identification schemes in a unified and systematic way. The outcomes are (1) Alternatives to the Fiat-Shamir transform that, applied to trapdoor identification schemes, yield signature schemes with tight security reductions to standard assumptions (2) An understanding and characterization of existing transforms in the literature. One of our transforms has the added advantage of producing signatures shorter than produced by the Fiat-Shamir transform. Reduction tightness is important because it allows the implemented scheme to use small parameters (thereby being as efficient as possible) while retaining provable security.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
This paper provides a framework to treat the problem of building signature schemes from identification schemes in a unified and systematic way. We are able to explain and characterize existing transforms as well as give new ones whose security proofs give tight reductions to standard assumptions. This is important so that the implemented scheme can use small parameters, thereby being efficient while retaining provable security. Let us begin by identifying the different elements involved.
id-to-sig transforms. Recall that in a three-move identification scheme \(\mathsf {ID}\) the prover sends a commitment \(Y\) computed using private randomness y, the verifier sends a random challenge \(c\), the prover returns a response \(z\) computed using y and its secret key  , and the verifier computes a boolean decision from the conversation transcript \(Y\Vert c\Vert z\) and public key
, and the verifier computes a boolean decision from the conversation transcript \(Y\Vert c\Vert z\) and public key  (see Fig. 3). We are interested in transforms
(see Fig. 3). We are interested in transforms  that take \(\mathsf {ID}\) and return a signature scheme \(\mathsf {DS}\). The transform must be generic, meaning \(\mathsf {DS}\) is proven to meet some signature security goal
that take \(\mathsf {ID}\) and return a signature scheme \(\mathsf {DS}\). The transform must be generic, meaning \(\mathsf {DS}\) is proven to meet some signature security goal  assuming only that \(\mathsf {ID}\) meets some identification security goal
assuming only that \(\mathsf {ID}\) meets some identification security goal  . This proof is supported by a reduction
. This proof is supported by a reduction  that may be tight or loose. Boxing an item here highlights elements of interest and choice in the id-to-sig process.
that may be tight or loose. Boxing an item here highlights elements of interest and choice in the id-to-sig process.
Canonical example. In the most canonical example we have, \(\mathbf {Id2Sig}= \mathbf {FS}\) is the Fiat-Shamir transform [16] ; \(\mathrm {P}_{\mathrm {id}}=\) IMP-PA is security against impersonation under passive attack [1, 14] ; \(\mathrm {P}_{\mathrm {sig}}=\) UF is unforgeability under chosen-message attack [20] ; and the reduction \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) is that of AABN [1], which is loose.
We are going to revisit this to give other choices of the different elements, but first let us recall some more details of the above. In the Fiat-Shamir transform \(\mathbf {FS}\) [16], a signature of a message \(m\) is a pair \((Y,z)\) such that the transcript \(Y\Vert c\Vert z\) is accepting for \(c= \textsc {H}(Y\Vert m)\), where \(\textsc {H}\) is a random oracle. IMP-PA requires that an adversary given transcripts of honest protocol executions still fails to make the honest verifier accept in an interaction where it plays the role of the prover, itself picking \(Y\) any way it likes, receiving a random \(c\), and then producing \(z\). The loss in the \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) reduction of AABN [1] is a factor of the number q of adversary queries to the random oracle \(\textsc {H}\): If \(\epsilon _{\mathrm {id}},\epsilon _{\mathrm {sig}}\) denote, respectively, the advantages in breaking the IMP-PA security of \(\mathsf {ID}\) and the UF security of \(\mathsf {DS}\), then \(\epsilon _{\mathrm {sig}}\approx q\, \epsilon _{\mathrm {id}}\).
Algebraic assumption to id. Suppose a cryptographer wants to build a signature scheme meeting the definition \(\mathrm {P}_{\mathrm {sig}}\). The cryptographer would like to base security on some algebraic (or other computational) assumption  . This could be factoring, RSA inversion, bilinear Diffie-Hellman, some lattice assumption, or many others. Given an id-to-sig transform as above, the task amounts to designing an identification scheme \(\mathsf {ID}\) achieving \(\mathrm {P}_{\mathrm {id}}\) under \(\mathrm {P}_{\mathrm {alg}}\). (Then one can just apply the transform to \(\mathsf {ID}\).) This proof is supported by another reduction
. This could be factoring, RSA inversion, bilinear Diffie-Hellman, some lattice assumption, or many others. Given an id-to-sig transform as above, the task amounts to designing an identification scheme \(\mathsf {ID}\) achieving \(\mathrm {P}_{\mathrm {id}}\) under \(\mathrm {P}_{\mathrm {alg}}\). (Then one can just apply the transform to \(\mathsf {ID}\).) This proof is supported by another reduction  that again may be tight or loose. The tightness of the overall reduction \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) thus depends on the tightness of both \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) and \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\).
that again may be tight or loose. The tightness of the overall reduction \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) thus depends on the tightness of both \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) and \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\).
Canonical example. Continuing with the FS+AABN-based example from above, we would need to build an identification scheme meeting \(\mathrm {P}_{\mathrm {id}}=\) IMP-PA under \(\mathrm {P}_{\mathrm {alg}}\). The good news is that a wide swathe of such identification schemes are available, for many choices of \(\mathrm {P}_{\mathrm {alg}}\) (GQ [23] under RSA, FS [16] under Factoring, Schnorr [36] under Discrete Log, ...). However the reduction \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) is (very) loose.
Again, we are going to revisit this to give other choices of the different elements, but first let us recall some more details of the above. The practical identification schemes here are typically Sigma protocols (this means they satisfy honest-verifier zero-knowledge and special soundness, the latter meaning that from two accepting conversation transcripts with the same commitment but different challenges, one can extract the secret key) and \(\mathrm {P}_{\mathrm {alg}}=\) KR (“key recovery”) is the problem of computing the secret key given only the public key. To solve this problem, we have to run a given IMP-PA adversary twice and hope for two successes. The analysis exploits the Reset Lemma of [6]. If \(\epsilon _{\mathrm {alg}},\epsilon _{\mathrm {id}}\) denote, respectively, the advantages in breaking the algebraic problem and the IMP-PA security of \(\mathsf {ID}\), then it results in \(\epsilon _{\mathrm {id}}\approx \sqrt{\epsilon _{\mathrm {alg}}}\). If \(\epsilon _{\mathrm {sig}}\) is the advantage in breaking UF security of \(\mathsf {DS}\), combined with the above, we have \(\epsilon _{\mathrm {sig}}\approx q\, \sqrt{\epsilon _{\mathrm {alg}}}\).
Approach. We see from the above that a tight overall reduction \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) requires that the \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) and \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) reductions both be tight. What we observe is that we have a degree of freedom in achieving this, namely the choice of the security goal \(\mathrm {P}_{\mathrm {id}}\) for the identification scheme. Our hope is to pick \(\mathrm {P}_{\mathrm {id}}\) such that (1) We can give (new) transforms \(\mathbf {Id2Sig}\) for which \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) is tight, and simultaneously (2) We can give identification schemes such that \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) is tight. We view these as two pillars of an edifice and are able to provide both via our definitions of security of identification under constrained impersonation coupled with some new id-to-sig transforms. We first pause to discuss some prior work, but a peek at Fig. 1 gives an outline of the results we will expand on later. Following FS, we work in the random oracle model.
Prior work. The first proofs of security for \(\mathbf {FS}\)-based signatures [35] reduced UF security of the \(\mathbf {FS}\)-derived signature scheme directly to the hardness of the algebraic problem \(\mathrm {P}_{\mathrm {alg}}\), assuming \(\textsc {H}\) is a random oracle [8]. These proofs exploit forking lemmas [4, 5, 35]. Modular proofs of the form discussed above, that use identification as an intermediate step, begin with [1, 33]. The modular approach has many advantages. One is that since the id-to-sig transforms are generic, we have only to design and analyze identification schemes. Another is the better understanding and isolation of the role of random oracles: they are used by \(\mathbf {Id2Sig}\) but not in the identification scheme. We have accordingly adopted this approach. Note that both the direct (forking lemma based) and the AABN-based indirect (modular) approach result in reductions of the same looseness we discussed above. Our (alternative but still modular) approaches will remove this loss.
Consideration of reduction tightness for signatures begins with BR [9], whose PSS scheme has a tight reduction to the RSA problem. KW [24] give another signature scheme with a tight reduction to RSA, and they and GJ [18] give signature schemes with tight reductions to the Diffie-Hellman problem. GPV [17] give a signature scheme with a tight reduction to the problem of finding short vectors in random lattices.
The lack of tightness of the overall reduction for \(\mathbf {FS}\)-based signatures is well recognized as an important problem and drawback. Micali and Reyzin [30] give a signature scheme, with a tight reduction to factoring, that is obtained from a particular identification scheme via a method they call “swap”. ABP [2] say that the method generalizes to other factoring-based schemes. However, “swap” has never been stated as a general transform of an identification scheme into a signature scheme. This lack of abstraction is perhaps due in part to a lack of definitions, and the ones we provide allow us to fill the gap. In Sect. 6.5 we elevate the swap method to a general \(\mathbf {Swap}\) transform, characterize the identification schemes to which it applies, and prove that, when it applies, it gives a tight \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) reduction.
ABP [2] show a tight reduction of \(\mathbf {FS}\)-derived GQ-based signatures to the \(\varPhi \)-hiding assumption of [12]. In contrast, our methods will yield GQ-based signatures with a tight reduction to the standard one-wayness of RSA. AFLT [3] use a slight variant of the Fiat-Shamir transform to turn lossy identification schemes into signature schemes with security based tightly on key indistinguishability, resulting in signature schemes with tight reductions to the decisional short discrete logarithm problem, the shortest vector problem in ideal lattices, and subset sum.
Constrained impersonation. Recall our goal is to define a notion of identification security \(\mathrm {P}_{\mathrm {id}}\) such that (1) We can give transforms \(\mathbf {Id2Sig}\) for which \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) is tight, and (2) We can give identification schemes such that \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) is tight. In fact our definitional goal is broader, namely to give a framework that allows us to understand and encompass both old and new transforms, the former including \(\mathbf {FS}\) and \(\mathbf {Swap}\). We do all this with a definitional framework that we refer to as constrained impersonation. It yields four particular definitions denoted \(\mathrm {CIMP}\text {-}\mathrm {XY}\) for \(\mathrm {XY}\in \{ \mathrm {CU}, \mathrm {UC}, \mathrm {UU}, \mathrm {CC}\}\). Each, in the role of \(\mathrm {P}_{\mathrm {id}}\), will be the basis for an id-to-sig transform such that \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) is tight, and two will allow \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) to be tight.
In constrained impersonation we continue, as with IMP-PA, to allow a passive attack in which the adversary \(\mathcal{A}\) against the identification scheme \(\mathsf {ID}\) can obtain transcripts \(Y_1\Vert c_1\Vert z_1, Y_2\Vert c_2\Vert z_2,\ldots \) of interactions between the honest prover and verifier. Then \(\mathcal{A}\) tries to impersonate, meaning get the honest verifier to accept. If X = C then the commitment in this impersonation interaction is adversary-chosen, while if X = U (unchosen) it must be pegged to a commitment from one of the (honest) transcripts. If Y = C, the challenge is adversary-chosen, while if Y = U it is as usual picked at random by the verifier. In all cases, multiple impersonation attempts are allowed. The formal definitions are in Sect. 3. CIMP-CU is a multi-impersonation version of IMP-PA, but the rest are novel.
Top: Relations between notions \(\mathrm {P}_{\mathrm {id}}\) of security for an identification scheme \(\mathsf {ID}\) under constrained impersonation. Solid arrows denote implications, barred arrows denote separations. A solid box around a notion means a tight \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) reduction for Sigma protocols; dotted means a loose one; no box means no known reduction. Bottom: Transforms of identification schemes into UUF (row 2, 3) or UF (rows 1, 4, 5) signature schemes. The first column is the assumption \(\mathrm {P}_{\mathrm {id}}\) on the identification scheme. The third column indicates whether or not the identification scheme is assumed to be trapdoor. \({\mathsf {ID}.\mathsf {cl}}\) is the challenge length and \(\mathsf {sl}\) is a seed length. In rows 1, 4 the commitment \(Y\) is chosen at random. The third transform has the shortest signatures, consisting of a response plus a single bit.
What do any of these notions have to do with identification if one understands the latter as the practical goal of proving one’s identity to a verifier? Beyond \(\mathrm {CIMP}\text {-}\mathrm {CU}\), very little. In practice it is unclear how one can constrain a prover to only use, in impersonation, a commitment from a prior transcript. It is even more bizarre to allow a prover to pick the challenge. Our definitions however are not trying to capture any practical usage of identification. They view the latter as an analytic tool, an intermediate land allowing a smooth transition from an algebraic problem to signatures. The constrained impersonation notions work well in this regard, as we will see, both to explain and understand existing work and to obtain new signature schemes with tight reductions.
Relations between the four notions of constrained impersonation are depicted in Fig. 1. An arrow \(\mathrm {A}\rightarrow \mathrm {B}\) is an implication: Every identification scheme that is \(\mathrm {A}\)-secure is also \(\mathrm {B}\)-secure. A barred arrow \(\mathrm {A}\not \rightarrow \mathrm {B}\) is a separation: There exists an identification scheme that is \(\mathrm {A}\)-secure but not \(\mathrm {B}\)-secure. (For now ignore the boxes around notions.) In particular we see that \(\mathrm {CIMP}\text {-}\mathrm {UU}\) is weaker than, and \(\mathrm {CIMP}\text {-}\mathrm {UC}\) incomparable to, the more standard \(\mathrm {CIMP}\text {-}\mathrm {CU}\). See Proposition 1 for more precise renditions of the implications.
Auxiliary definitions and tools. Before we see how to leverage the constrained impersonation framework, we need a few auxiliary definitions and results that, although simple, are, we believe, of independent interest and utility.
We define a signature scheme to be UUF (Unique Unforgeable) if it is UF with the restriction that a message can be signed at most once. (The adversary is not allowed to twice ask the signing oracle to sign a particular \(m\).) It turns out that some of our id-to-sig transforms naturally achieve UUF, not UF. However there are simple, generic transforms of UUF signature schemes into UF ones —succinctly, \(\mathrm {UF}\mathbf {\rightarrow }\mathrm {UUF}\)— that do not introduce much overhead and have tight reductions. One is to remove randomness, and the other is to add it. In more detail, a well-known method to derandomize a signature scheme is to specify the coins by hashing the secret key along with the message. This has been proved to work in some instances [26, 32] but not in general. We observe that this method has the additional benefit of turning a \(\mathrm {UUF}\) scheme into a \(\mathrm {UF}\) one. We call the transform \(\mathbf {DR}\). Theorem 3 shows that it works. (In particular it shows \(\mathrm {UF}\)-security of the derandomized scheme in a more general setting than was known before.) The second transform, \(\mathbf {AR}\), appends a random salt to the message before signing and includes the salt in the signature. Theorem 4 shows that it works. The first transform is attractive because it does not increase signature size. The second does, but is standard-model. We stress that the reductions are tight in both cases, so this step does not impact overall tightness. Now we can take (the somewhat easier to achieve) UUF as our goal.
Recall that in an identification scheme, the prover uses private randomness y to generate its commitment \(Y\). We call the scheme trapdoor if the prover can pick the commitment \(Y\) directly at random from the space of commitments and then compute the associated private randomness y using its secret key via a prescribed algorithm. The concept is implicit in [30] but does not seem to have been formalized before, so we give a formal definition in Sect. 3. Many existing identification schemes will meet our definition of being trapdoor modulo possibly some changes to the key structure. Thus the GQ scheme of [23] is trapdoor if we add the decryption exponent d to the secret key. With similar changes to the keys, the Fiat-Shamir [16] and Ong-Schnorr [34] identification schemes are trapdoor. The factoring-based identification scheme of [30] is also trapdoor. But not all identification schemes are trapdoor. One that is not is Schnorr’s (discrete-log based) scheme [36].
Summary of results. For each notion \(\mathrm {P}_{\mathrm {id}}\in \{ \mathrm {CIMP}\text {-}\mathrm {CU},\mathrm {CIMP}\text {-}\mathrm {UC}, \mathrm {CIMP}\text {-}\mathrm {UU}, \mathrm {CIMP}\text {-}\mathrm {CC}\}\) we give an id-to-sig transform that turns any given \(\mathrm {P}_{\mathrm {id}}\)-secure identification scheme \(\mathsf {ID}\) into a \(\mathrm {P}_{\mathrm {sig}}=\) UUF signature scheme \(\mathsf {DS}\); the transform from \(\mathrm {CIMP}\text {-}\mathrm {CC}\) security achieves even a UF signature scheme. The reduction \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) is tight in all four cases. (To further make the signature schemes UF secure, we can apply the above-mentioned \(\mathrm {UF}\mathbf {\rightarrow }\mathrm {UUF}\) transforms while preserving tightness.) The table in Fig. 1 summarizes the results and the transforms. They are discussed in more detail below and then fully in Sect. 6.
This is one pillar of the edifice, and not useful by itself. The other pillar is the \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) reduction. In the picture at the top of Fig. 1, a solid-line box around \(\mathrm {P}_{\mathrm {id}}\) means that the reduction \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) is tight, a dotted-line box indicates a reduction is possible but is not tight, and no box means no known reduction. These results assume the identification scheme is a Sigma protocol, as most are, and are discussed in Sect. 4. We see that two points of our framework can be tightly obtained from the algebraic problem, so that in these cases the overall \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) reduction is tight, which was the ultimate goal.
More details on results. The id-to-sig transform from \(\mathrm {CIMP}\text {-}\mathrm {CU}\) is the classical \(\mathbf {FS}\) one. The reduction is now tight, even though it was not from IMP-PA [1], simply because \(\mathrm {CIMP}\text {-}\mathrm {CU}\) is IMP-PA extended to allow multiple impersonation attempts. The result, which we state as Theorem 8, is implicit in [1], but we give a proof to illustrate how simple the proof now is. In this case our framework serves to better understand, articulate and simplify something implicit in the literature, rather than deliver anything particularly new.
For \(\mathrm {CIMP}\text {-}\mathrm {UC}\), we give a transform called \(\mathbf {MdCmt}\), for “Message-Derived Commitment”, where, to sign \(m\), the signer computes the commitment \(Y\) as a hash of the message, picks a challenge at random, uses the identification trapdoor to compute the coins y corresponding to \(Y\), uses y and the secret key to compute a response \(z\), and returns the challenge and response as the signature. See Sect. 6.1.
For \(\mathrm {CIMP}\text {-}\mathrm {UU}\), the weakest of the four notions, our transform \(\mathbf {MdCmtCh}\), for “Message-Derived Commitment and Challenge”, has the signer compute the commitment \(Y\) as a hash of the message. It then picks a single random bit \(s\) and computes the challenge as a hash of the message and seed \(s\), returning as signature the seed and response, the latter computed as before. Beyond a tight reduction, this transform has the added feature of short signatures, the signature being a response plus a single bit. (In all other transforms, whether prior or ours, the signature is at least a response plus a challenge, often more.) See Sect. 6.2.
Since \(\mathrm {CIMP}\text {-}\mathrm {CC}\) implies \(\mathrm {CIMP}\text {-}\mathrm {UC}\) and \(\mathrm {CIMP}\text {-}\mathrm {UU}\) (Fig. 1, top), for the former the \(\mathbf {MdCmt}\) and \(\mathbf {MdCmtCh}\) transforms would both work. However, these require the identification scheme to be trapdoor and achieve \(\mathrm {UUF}\) rather than \(\mathrm {UF}\). (The above-mentioned \(\mathrm {UF}\mathbf {\rightarrow }\mathrm {UUF}\) transforms would have to be applied on top to get \(\mathrm {UF}\).) We give an alternative transform called \(\mathbf {MdCh}\) (“Message-Derived Challenge”) from \(\mathrm {CIMP}\text {-}\mathrm {CC}\) that directly achieves \(\mathrm {UF}\) and works (gives a tight reduction) even if the identification scheme is not trapdoor. It has the signer pick a random commitment, produce the challenge as in \(\mathbf {MdCmtCh}\), namely as a randomized hash of the message, compute the response, and return the conversation transcript as signature. See Sect. 6.3.
The salient fact is that the reductions underlying all four transforms are tight. To leverage the results we now have to consider achieving \(\mathrm {CIMP}\text {-}\mathrm {XY}\). We do this in Sect. 4. We give reductions \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) of the \(\mathrm {P}_{\mathrm {id}}= \mathrm {CIMP}\text {-}\mathrm {XY}\) security of identification schemes that are Sigma protocols to their key-recovery (KR) security, the latter being the problem of recovering the secret key given only the public key, which is typically the algebraic problem \(\mathrm {P}_{\mathrm {alg}}\) whose hardness is assumed. For \(\mathrm {CIMP}\text {-}\mathrm {UC}\) and \(\mathrm {CIMP}\text {-}\mathrm {UU}\) the \(\mathrm {P}_{\mathrm {id}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) reduction is tight, as per Theorem 1, making these the most attractive starting points. For \(\mathrm {CIMP}\text {-}\mathrm {CU}\) we must use the Reset Lemma [6] so the reduction (cf. Theorem 2) is loose. \(\mathrm {CIMP}\text {-}\mathrm {CC}\) is a very strong notion and, as we discuss at the end of Sect. 4, not achieved by Sigma protocols but achievable by other means.
Swap. As indicated above, our framework allows us to generalize the swap method of [30] into an id-to-sig transform \(\mathbf {Swap}\) and understand and characterize what it does. In Sect. 6.5 we present \(\mathbf {Swap}\) as a generic transform of a trapdoor identification scheme \(\mathsf {ID}\) to a signature scheme that is just like \(\mathbf {MdCmt}\) (cf. row 2 of the table of Fig. 1) except that the challenge \(c\) is included in the input to the hash function (cf. row 5 of the table of Fig. 1). Recall that \(\mathbf {MdCmt}\) turns a \(\mathrm {CIMP}\text {-}\mathrm {UC}\) identification scheme into a UUF signature scheme. We can thence get a UF signature scheme by applying the \(\mathbf {AR}\) transform of Sect. 5.2. \(\mathbf {Swap}\) is a shortcut, or optimization, of this two step process: it directly turns a \(\mathrm {CIMP}\text {-}\mathrm {UC}\) identification scheme into a UF signature scheme by effectively re-using the randomness of \(\mathbf {MdCmt}\) in \(\mathbf {AR}\). We note that the composition of our \(\mathbf {DR}\) with our \(\mathbf {MdCmtCh}\) yields a \(\mathrm {UF}\) signature scheme with shorter signatures than \(\mathbf {Swap}\) while also having a tight reduction to the weaker \(\mathrm {CIMP}\text {-}\mathrm {UU}\) assumption, and would thus be superior. However we think \(\mathbf {Swap}\) is of historical interest and accordingly present it. See Sect. 6.5 for details.
Instantiation. As a simple and canonical example, in [7] we apply our framework and transforms to the \(\mathsf {GQ}\) identification scheme to get signature schemes with tight reductions to RSA. It is also possible to give instantiations based on claw-free permutations [20] and factoring. An intriguing application area to explore for our transforms is in lattice-based cryptography. Here signatures have been obtained via the \(\mathbf {FS}\) transform [28, 29]. The underlying lattice-based identification schemes do not appear to be trapdoor, so our transforms would not apply. However, via the techniques of MP [31], one can build lattice-based trapdoor identification schemes to which our transforms apply. Whether there is a performance benefit will depend on the trade-off between the added cost from having the trapdoor and the smaller parameters permitted by the improved security reduction.
Discussion. We measure reduction tightness stringently, in a model where running time, queries and success probability are separate parameters. The picture changes if one considers the expected success ratio, namely the ratio of running time to success probability. Reduction tightness under this metric is considered in PS [35] and the concurrent and independent work of KMP [25].
We establish the classical notion of standard unforgeability (UF) [20]. Our transforms also establish strong unforgeability if the identification scheme has the extra property of unique responses. (For any public key, commitment, and challenge, there exists at most one response that the verifier accepts.)
A reviewer commented that “The signature scheme with the tightest security in this paper is derived from the Swap transform, which makes the result less surprising since the Swap method, first used in [30], has already been found to be generic to some extent by ABP [2].” In response, first, the tightness of the reductions is about the same for \(\mathbf {Swap}\), \(\mathbf {DR}\circ \mathbf {MdCmt}\) and \(\mathbf {DR}\circ \mathbf {MdCmtCh}\) (cf. Fig. 14), but the third has shorter signatures, an advantage over \(\mathbf {Swap}\). Second, while, as indicated above, prior work including ABP [2] did discuss Swap in a broader context than the original MR [30], the discussion was informal and left open to exactly what identification schemes Swap might apply. We have formalized prior intuition using the concept of trapdoor identification, and thus been able to provide a general transform and result for Swap. We view this as a contribution towards understanding the area, making intuition rigorous and providing a result that future work can apply in a blackbox way. Also, as noted above, our framework helps understand Swap, seeing it as an optimized de-randomization of the simpler \(\mathbf {MdCmt}\). We understand, as per what the reviewer says, that our results for \(\mathbf {Swap}\) may not be surprising, but we don’t think surprise is the only measure of contribution. Clarifying and formalizing existing intuition, as we have done in this way with \(\mathbf {Swap}\), puts the area on firmer ground and helps future work.
GK [22] give an example of a 3-move ID protocol where \(\mathbf {FS}\) yields a secure signature scheme in the ROM, but the RO is not instantiable. Their protocol however is not a Sigma protocol, as is assumed for the ones we start with and is true for practical identification schemes. Currently, secure instantiation of the RO, both for \(\mathbf {FS}\) and our transforms, is not ruled out for such identification schemes.
2 Notation and Basic Definitions
Notation. We let \(\varepsilon \) denote the empty string. If X is a finite set, we let  denote picking an element of X uniformly at random and assigning it to x. We use \(a_1\Vert a_2\Vert \cdots \Vert a_n\) as shorthand for \((a_1,a_2,\ldots ,a_n)\). By \(a_1\Vert a_2\Vert \cdots \Vert a_n \leftarrow x\) we mean that x is parsed into its constituents. We use bracket notation for associative arrays, e.g., \(T[x]=y\) means that key x is mapped to value y. Algorithms may be randomized unless otherwise indicated. Running time is worst case. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with random coins r on inputs \(x_1,\ldots \) and assigning the output to y. We let
denote picking an element of X uniformly at random and assigning it to x. We use \(a_1\Vert a_2\Vert \cdots \Vert a_n\) as shorthand for \((a_1,a_2,\ldots ,a_n)\). By \(a_1\Vert a_2\Vert \cdots \Vert a_n \leftarrow x\) we mean that x is parsed into its constituents. We use bracket notation for associative arrays, e.g., \(T[x]=y\) means that key x is mapped to value y. Algorithms may be randomized unless otherwise indicated. Running time is worst case. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with random coins r on inputs \(x_1,\ldots \) and assigning the output to y. We let  be the result of picking r at random and letting \(y \leftarrow A(x_1,\ldots ;r)\). We let \([A(x_1,\ldots )]\) denote the set of all possible outputs of (randomized) A when invoked with inputs \(x_1,\ldots \). We use the code based game playing framework of [10]. (See Fig. 2 for an example.) By \(\Pr [\mathrm {G}]\) we denote the event that the execution of game \(\mathrm {G}\) results in the game returning \(\mathsf {true}\). Boolean flags (like \(\mathsf {bad}\)) in games are assumed initialized to \(\mathsf {false}\), and associative arrays empty. We adopt the convention that the running time of an adversary refers to the worst case execution time of the game with the adversary. This means that the time taken for oracles to compute replies to queries is included.
be the result of picking r at random and letting \(y \leftarrow A(x_1,\ldots ;r)\). We let \([A(x_1,\ldots )]\) denote the set of all possible outputs of (randomized) A when invoked with inputs \(x_1,\ldots \). We use the code based game playing framework of [10]. (See Fig. 2 for an example.) By \(\Pr [\mathrm {G}]\) we denote the event that the execution of game \(\mathrm {G}\) results in the game returning \(\mathsf {true}\). Boolean flags (like \(\mathsf {bad}\)) in games are assumed initialized to \(\mathsf {false}\), and associative arrays empty. We adopt the convention that the running time of an adversary refers to the worst case execution time of the game with the adversary. This means that the time taken for oracles to compute replies to queries is included.
Our treatment of random oracles is more general than usual. In our constructions, we will need random oracles with different ranges. For example we may want one random oracle returning points in a group \({{\mathbb Z}}_N^*\) and another returning strings of some length l. To provide a single unified definition, we have the procedure \(\textsc {H}\) in the games take not just the input x but a description \(\mathrm {Rng}\) of the set from which outputs are to be drawn at random. Thus  will return a random element of \({{\mathbb Z}}_N^*\), while
will return a random element of \({{\mathbb Z}}_N^*\), while  will return a random l-bit string, and so on. Sometimes if the range set is understood, it is dropped as an argument.
will return a random l-bit string, and so on. Sometimes if the range set is understood, it is dropped as an argument.
Signatures. In a signature scheme \(\mathsf {DS}\), the signer generates signing key  and verifying key
and verifying key  via
via  where \(\textsc {H}\) is the random oracle, the latter with syntax as discussed above. Now it can compute a signature
where \(\textsc {H}\) is the random oracle, the latter with syntax as discussed above. Now it can compute a signature  on any message \(m\in \{0,1\}^*\). A verifier can deterministically compute a boolean
on any message \(m\in \{0,1\}^*\). A verifier can deterministically compute a boolean  indicating whether or not \(\sigma \) is a valid signature of \(m\) relative to
indicating whether or not \(\sigma \) is a valid signature of \(m\) relative to  . Correctness as usual requires that
. Correctness as usual requires that  with probability one. Game \(\mathbf {G}^{\mathrm {uf}}_{\mathsf {DS}}(\mathcal{A})\) associated to \(\mathsf {DS}\) and adversary \(\mathcal{A}\) as per Fig. 2 captures the classical unforgeability notion of [20] lifted to the ROM as per [8], and we let \(\mathbf {Adv}^{\mathrm {uf}}_{\mathsf {DS}}(\mathcal{A})= \Pr [\mathbf {G}^{\mathrm {uf}}_{\mathsf {DS}}(\mathcal{A})]\) be the UF-advantage of \(\mathcal{A}\). The same figure also defines game \(\mathbf {G}^{\mathrm {uuf}}_{\mathsf {DS}}(\mathcal{A})\) to capture unique unforgeability. The difference is the inclusion of the boxed code, which disallows \(\mathcal{A}\) from getting more than one signature on the same message. We let \(\mathbf {Adv}^{\mathrm {uuf}}_{\mathsf {DS}}(\mathcal{A})= \Pr [\mathbf {G}^{\mathrm {uuf}}_{\mathsf {DS}}(\mathcal{A})]\) be the UUF-advantage of \(\mathcal{A}\).
with probability one. Game \(\mathbf {G}^{\mathrm {uf}}_{\mathsf {DS}}(\mathcal{A})\) associated to \(\mathsf {DS}\) and adversary \(\mathcal{A}\) as per Fig. 2 captures the classical unforgeability notion of [20] lifted to the ROM as per [8], and we let \(\mathbf {Adv}^{\mathrm {uf}}_{\mathsf {DS}}(\mathcal{A})= \Pr [\mathbf {G}^{\mathrm {uf}}_{\mathsf {DS}}(\mathcal{A})]\) be the UF-advantage of \(\mathcal{A}\). The same figure also defines game \(\mathbf {G}^{\mathrm {uuf}}_{\mathsf {DS}}(\mathcal{A})\) to capture unique unforgeability. The difference is the inclusion of the boxed code, which disallows \(\mathcal{A}\) from getting more than one signature on the same message. We let \(\mathbf {Adv}^{\mathrm {uuf}}_{\mathsf {DS}}(\mathcal{A})= \Pr [\mathbf {G}^{\mathrm {uuf}}_{\mathsf {DS}}(\mathcal{A})]\) be the UUF-advantage of \(\mathcal{A}\).
Of course, UF implies UUF, meaning any signature scheme that is UF secure is also UUF secure. The converse is not true, meaning there exist UUF signature schemes that are not UF secure (we will see natural examples in this paper). In Sect. 5 we give simple, generic and tight ways to turn any given UUF signature scheme into a UF one.
We note that unique unforgeability (UUF) should not be confused with unique signatures as defined in [21, 27]. In a unique signature scheme, there is, for any message, at most one signature the verifier will accept. If a unique signature scheme is UUF then it is also UF. But there are UUF (and UF) schemes that are not unique.
3 Constrained Impersonation Framework
We introduce a framework of definitions of identification schemes secure against constrained impersonation.
Identification. An identification (ID) scheme \(\mathsf {ID}\) operates as depicted in Fig. 3. First, via  , the prover generates a public verification key
, the prover generates a public verification key  , private identification key
, private identification key  , and trapdoor
, and trapdoor  . Via
. Via  it generates commitment
it generates commitment  and corresponding private state \(y\). We refer to
and corresponding private state \(y\). We refer to  as the commitment space associated to
as the commitment space associated to  . The verifier sends a random challenge of length \({\mathsf {ID}.\mathsf {cl}}\). The prover’s response \(z\) and the verifier’s boolean decision \(v\) are deterministically computed per
. The verifier sends a random challenge of length \({\mathsf {ID}.\mathsf {cl}}\). The prover’s response \(z\) and the verifier’s boolean decision \(v\) are deterministically computed per  and
and  , respectively. We assume throughout that identification schemes have perfect correctness. We also assume uniformly-distributed commitments. More precisely, the outputs of the following two processes must be identically distributed: the first processes generates
, respectively. We assume throughout that identification schemes have perfect correctness. We also assume uniformly-distributed commitments. More precisely, the outputs of the following two processes must be identically distributed: the first processes generates  , then lets
, then lets  and returns
and returns  ; the second processes generates
; the second processes generates  , then lets
, then lets  and returns
and returns  . An example ID scheme is \(\mathsf {GQ}\) [23]; see [7] for a description in our notation. For basic ID schemes, the trapdoor plays no role; its use arises in trapdoor identification, as discussed next.
. An example ID scheme is \(\mathsf {GQ}\) [23]; see [7] for a description in our notation. For basic ID schemes, the trapdoor plays no role; its use arises in trapdoor identification, as discussed next.
Trapdoor identification. We now define what it means for an ID scheme to be trapdoor. Namely there is an algorithm  that produces \(y\) from \(Y\) with the aid of the trapdoor
that produces \(y\) from \(Y\) with the aid of the trapdoor  . Formally, the outputs of the following two processes must be identically distributed. Both processes generate
. Formally, the outputs of the following two processes must be identically distributed. Both processes generate  . The first process then lets
. The first process then lets  . The second process picks
. The second process picks  and lets
and lets  . (Here
. (Here  is the space of commitments associated to \(\mathsf {ID}\) and
is the space of commitments associated to \(\mathsf {ID}\) and  .) Both processes return
.) Both processes return  .
.
Security against impersonation. Classically, the security goal for an identification scheme \(\mathsf {ID}\) has been impersonation [1, 15]. The framework has two stages. First, the adversary, given  but not
but not  , attacks the honest,
, attacks the honest,  -using prover. Second, using the information it gathers in the first stage, it engages in an interaction with the verifier, attempting to impersonate the real prover by successfully identifying itself. In the second stage, the adversary, in the role of malicious prover, submits a commitment \(Y\) of its choice, receives an honest verifier challenge \(c\), submits a response \(z\) of its choice, and wins if
-using prover. Second, using the information it gathers in the first stage, it engages in an interaction with the verifier, attempting to impersonate the real prover by successfully identifying itself. In the second stage, the adversary, in the role of malicious prover, submits a commitment \(Y\) of its choice, receives an honest verifier challenge \(c\), submits a response \(z\) of its choice, and wins if  . A hierarchy of possible first-phase attacks is defined in [6]. In the context of conversion to signatures, the relevant one is the weakest, namely passive attacks, where the adversary is just an eavesdropper and gets honestly-generated protocol transcripts. This is the IMP-PA notion. (Active and even concurrent attacks are relevant in other contexts [6].) We note that in the second stage, the adversary is allowed only one interaction with the honest verifier.
. A hierarchy of possible first-phase attacks is defined in [6]. In the context of conversion to signatures, the relevant one is the weakest, namely passive attacks, where the adversary is just an eavesdropper and gets honestly-generated protocol transcripts. This is the IMP-PA notion. (Active and even concurrent attacks are relevant in other contexts [6].) We note that in the second stage, the adversary is allowed only one interaction with the honest verifier.
Security against constrained impersonation. We introduce a new framework of goals for identification that we call constrained impersonation. There are two dimensions, the commitment dimension X and the challenge dimension Y, for each of which there are two choices, \(\mathrm {X}\in \{\mathrm {C},\mathrm {U}\}\) and \(\mathrm {Y}\in \{\mathrm {C},\mathrm {U}\}\), where \(\mathrm {C}\) stands for chosen and \(\mathrm {U}\) for unchosen. This results in four notions, \(\mathrm {CIMP}\text {-}\mathrm {UU}\), \(\mathrm {CIMP}\text {-}\mathrm {UC}\), \(\mathrm {CIMP}\text {-}\mathrm {CU}\), \(\mathrm {CIMP}\text {-}\mathrm {CC}\). It works as follows. The adversary is allowed a passive attack, namely the ability to obtain transcripts of interactions between the honest prover and the verifier. The choices pertain to the impersonation, when the adversary interacts with the honest verifier in an attempt to make it accept. When \(\mathrm {X}=\mathrm {C}\), the adversary can send the verifier a commitment of its choice, as in classical impersonation. But when \(\mathrm {X}=\mathrm {U}\), it cannot. Rather, it is required (constrained) to use a commitment that is from one of the transcripts it obtained in the first phase and thus in particular honestly generated. Next comes the challenge. If \(\mathrm {Y}=\mathrm {U}\), this is chosen freshly at random, as in the classical setting, but if \(\mathrm {Y}=\mathrm {C}\), the adversary actually gets to pick its own challenge. Regardless of choices made in these four configurations, to win the adversary must finally supply a correct response. And, also regardless of these choices, the adversary can mount multiple attempts to convince the verifier, contrasting with the strict two-phase adversary in classical definitions of impersonation security.
For choices \(\mathrm {xy} \in \{\mathrm {uu},\mathrm {uc},\mathrm {cu},\mathrm {cc}\}\) of parameters, the formalization considers game \(\mathbf {G}^\mathrm{cimp\text{- }xy}_{\mathsf {ID}}(\mathcal{P})\) of Fig. 4 associated to identification scheme \(\mathsf {ID}\) and adversary \(\mathcal{P}\). We let

The transcript oracle \(\textsc {Tr}\) returns upon each invocation a transcript of an interaction between the honest prover and verifier, allowing \(\mathcal{P}\) to mount its passive attack, and is the same for all four games. The impersonation attempts are mounted through calls to the challenge oracle \(\textsc {Ch}\), which creates a partial transcript \(\mathrm {CT}[j]\) consisting of a commitment and a challenge, where j is a session id, and it returns the challenge. Multiple impersonation attempts are captured by the adversary being allowed to call \(\textsc {Ch}\) as often as it wants. Eventually the adversary outputs a session id k and a response \(z\) for session k, and wins if the corresponding transcript is accepting. In the \(\mathrm {UU}\) case, \(\mathcal{P}\) would give \(\textsc {Ch}\) only an index l of an existing transcript already returned by \(\textsc {Tr}\), and \(\mathrm {CT}[j]\) consists of the commitment from the l-th transcript together with a fresh random challenge. In the \(\mathrm {UC}\) case, \(\textsc {Ch}\) takes in addition a challenge \(c\) chosen by the adversary. The game requires that it be different from \(c_l\) (the challenge in the l-th transcript), and \(\mathrm {CT}[j]\) then consists of the commitment from the l-th transcript together with this challenge. In \(\mathrm {CU}\), the adversary can specify the commitment but the challenge is honestly chosen. In \(\mathrm {CC}\), it can specify both, as long as the pair did not occur in a transcript. The adversary can call the oracles as often as it wants and in whatever order it wants.
\(\mathrm {CIMP}\text {-}\mathrm {CU}\) is a multi-impersonation extension of the classical IMP-PA notion. The other notions are new, and all will be the basis of transforms of identification to signatures admitting tight security reductions. \(\mathrm {CIMP}\text {-}\mathrm {CU}\) captures a practical identification security goal. As discussed in Sect. 1, the other notions have no such practical interpretation. However we are not aiming to capture some practical form of identification. We wish to use identification only as an analytic tool in the design of signature schemes. For this purpose, as we will see, our framework and notions are indeed useful, allowing us to characterize past transforms and build new ones.
Implications. Figure 1 shows the relations between the four \(\mathrm {CIMP}\text {-}\mathrm {XY}\) notions. The implications are captured by Proposition 1. (The separations will be discussed below.) The bounds in these claims imply some conditions or assumptions for the implications which we did not emphasize before because they hold for typical identification schemes. Namely, \(\mathrm {CIMP}\text {-}\mathrm {UC}\rightarrow \mathrm {CIMP}\text {-}\mathrm {UU}\) assumes the identification scheme has large challenge length. \(\mathrm {CIMP}\text {-}\mathrm {CC}\rightarrow \mathrm {CIMP}\text {-}\mathrm {UC}\) assumes it has a large commitment space. \(\mathrm {CIMP}\text {-}\mathrm {CC}\rightarrow \mathrm {CIMP}\text {-}\mathrm {CU}\) again assumes it has a large challenge length. We remark that in all but one case, the adversary constructed in the proof makes only one \(\textsc {Ch}\) query, regardless of how many the starting adversary made. The proof of the following is in [7].
Proposition 1
Let \(\mathsf {ID}\) be an identification scheme. Let

Then:
- 1.:
-
[\(\mathrm {CIMP}\text {-}\mathrm {UC}\rightarrow \mathrm {CIMP}\text {-}\mathrm {UU}\)] Given \(\mathcal{P}_{\mathrm {uu}}\) making \(q_c\) queries to \(\textsc {Ch}\), we construct \(\mathcal{P}_{\mathrm {uc}}\), making one \(\textsc {Ch}\) query, such that \(\mathbf {Adv}^\mathrm{cimp\text{- }uu}_{\mathsf {ID}}(\mathcal{P}_{\mathrm {uu}}) \le \mathbf {Adv}^\mathrm{cimp\text{- }uc}_{\mathsf {ID}}(\mathcal{P}_{\mathrm {uc}}) + q_c\cdot 2^{-{\mathsf {ID}.\mathsf {cl}}}\).
- 2.:
-
[\(\mathrm {CIMP}\text {-}\mathrm {CU}\rightarrow \mathrm {CIMP}\text {-}\mathrm {UU}\)] Given \(\mathcal{P}_{\mathrm {uu}}\), we construct \(\mathcal{P}_{\mathrm {cu}}\) making as many \(\textsc {Ch}\) queries as \(\mathcal{P}_{\mathrm {uu}}\), such that \(\mathbf {Adv}^\mathrm{cimp\text{- }uu}_{\mathsf {ID}}(\mathcal{P}_{\mathrm {uu}}) \le \mathbf {Adv}^\mathrm{cimp\text{- }cu}_{\mathsf {ID}}(\mathcal{P}_{\mathrm {cu}})\).
- 3.:
-
[\(\mathrm {CIMP}\text {-}\mathrm {CC}\rightarrow \mathrm {CIMP}\text {-}\mathrm {UC}\)] Given \(\mathcal{P}_{\mathrm {uc}}\) making \(q_t\) queries to \(\textsc {Tr}\), we construct \(\mathcal{P}_{\mathrm {cc}}\), making one \(\textsc {Ch}\) query, such that \(\mathbf {Adv}^\mathrm{cimp\text{- }uc}_{\mathsf {ID}}(\mathcal{P}_{\mathrm {uc}}) \le \mathbf {Adv}^\mathrm{cimp\text{- }cc}_{\mathsf {ID}}(\mathcal{P}_{\mathrm {cc}}) + q_t(q_t-1) / 2\mathsf {ID}.\mathsf {CSS}\).
- 4.:
-
[\(\mathrm {CIMP}\text {-}\mathrm {CC}\rightarrow \mathrm {CIMP}\text {-}\mathrm {CU}\)] Given \(\mathcal{P}_{\mathrm {cu}}\) making \(q_t\) queries to \(\textsc {Tr}\) and \(q_c\) queries to \(\textsc {Ch}\), we construct \(\mathcal{P}_{\mathrm {cc}}\), making one \(\textsc {Ch}\) query, such that \(\mathbf {Adv}^\mathrm{cimp\text{- }cu}_{\mathsf {ID}}(\mathcal{P}_{\mathrm {cu}}) \le \mathbf {Adv}^\mathrm{cimp\text{- }cc}_{\mathsf {ID}}(\mathcal{P}_{\mathrm {cc}}) + q_tq_c\cdot 2^{-{\mathsf {ID}.\mathsf {cl}}}\).
In all cases, the constructed adversary makes the same number of \(\textsc {Tr}\) queries as the starting adversary and has about the same running time.
Separations. We now discuss the separations, beginning with  . Start with any \(\mathrm {CIMP}\text {-}\mathrm {CU}\) scheme. We will modify it so that it remains \(\mathrm {CIMP}\text {-}\mathrm {CU}\)-secure but is not \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure. Distinguish a single challenge \(c^*\in \{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\), e.g., \(c^*=0^{{\mathsf {ID}.\mathsf {cl}}}\). Revise the verifier’s algorithm so that it will accept any transcript with challenge \(c^*\). This is still \(\mathrm {CIMP}\text {-}\mathrm {CU}\)-secure (as long as \({{\mathsf {ID}.\mathsf {cl}}}\) is large) since, in the \(\mathrm {CIMP}\text {-}\mathrm {CU}\) game, challenges are picked uniformly at random for the adversary, so existence of the magic challenge is unlikely to be useful. This is manifestly not \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure since there the adversary can use any challenge of its choice.
. Start with any \(\mathrm {CIMP}\text {-}\mathrm {CU}\) scheme. We will modify it so that it remains \(\mathrm {CIMP}\text {-}\mathrm {CU}\)-secure but is not \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure. Distinguish a single challenge \(c^*\in \{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\), e.g., \(c^*=0^{{\mathsf {ID}.\mathsf {cl}}}\). Revise the verifier’s algorithm so that it will accept any transcript with challenge \(c^*\). This is still \(\mathrm {CIMP}\text {-}\mathrm {CU}\)-secure (as long as \({{\mathsf {ID}.\mathsf {cl}}}\) is large) since, in the \(\mathrm {CIMP}\text {-}\mathrm {CU}\) game, challenges are picked uniformly at random for the adversary, so existence of the magic challenge is unlikely to be useful. This is manifestly not \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure since there the adversary can use any challenge of its choice.  for the same reason.
for the same reason.
We turn to  . Start with any \(\mathrm {CIMP}\text {-}\mathrm {UC}\) scheme. Again we will modify it so that it remains \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure but is not \(\mathrm {CIMP}\text {-}\mathrm {CU}\)-secure. This time, distinguish a single commitment \(Y^*\): one way of doing this is for \(\mathsf {ID}.\mathsf {Kg}\) to sample
. Start with any \(\mathrm {CIMP}\text {-}\mathrm {UC}\) scheme. Again we will modify it so that it remains \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure but is not \(\mathrm {CIMP}\text {-}\mathrm {CU}\)-secure. This time, distinguish a single commitment \(Y^*\): one way of doing this is for \(\mathsf {ID}.\mathsf {Kg}\) to sample  and include \(Y^*\) in the public key
and include \(Y^*\) in the public key  ; another is to agree for example that
; another is to agree for example that  where l is the number of random bits required by \(\mathsf {ID}.\mathsf {Ct}\). Revise the verifier’s algorithm so that it will accept any transcript with commitment \(Y^*\). This is still \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure (assuming
where l is the number of random bits required by \(\mathsf {ID}.\mathsf {Ct}\). Revise the verifier’s algorithm so that it will accept any transcript with commitment \(Y^*\). This is still \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure (assuming  is large) since, in the \(\mathrm {CIMP}\text {-}\mathrm {UC}\) game, commitments are generated randomly for the adversary, so existence of a magic commitment is unlikely to be useful. This is manifestly not \(\mathrm {CIMP}\text {-}\mathrm {CU}\)-secure since there the adversary can use any commitment of its choice.
is large) since, in the \(\mathrm {CIMP}\text {-}\mathrm {UC}\) game, commitments are generated randomly for the adversary, so existence of a magic commitment is unlikely to be useful. This is manifestly not \(\mathrm {CIMP}\text {-}\mathrm {CU}\)-secure since there the adversary can use any commitment of its choice.  for the same reason.
for the same reason.
Finally,  and
and  since otherwise, by transitivity in Fig. 1, we would contradict the separation between \(\mathrm {CIMP}\text {-}\mathrm {UC}\) and \(\mathrm {CIMP}\text {-}\mathrm {CU}\).
since otherwise, by transitivity in Fig. 1, we would contradict the separation between \(\mathrm {CIMP}\text {-}\mathrm {UC}\) and \(\mathrm {CIMP}\text {-}\mathrm {CU}\).
4 Achieving CIMP-XY Security
Here we show how to obtain identification schemes satisfying our \(\mathrm {CIMP}\text {-}\mathrm {XY}\) notions of security. We base \(\mathrm {CIMP}\text {-}\mathrm {XY}\) security on the problem of recovering the secret key of the identification scheme given nothing but the public key, which plays the role of the algebraic problem \(\mathrm {P}_{\mathrm {alg}}\) in typical identification schemes and corresponds to a standard assumption. (For example for \(\mathsf {GQ}\) it is one-wayness of RSA.) For \(\mathrm {CIMP}\text {-}\mathrm {UC}\) and \(\mathrm {CIMP}\text {-}\mathrm {UU}\), the reductions are tight. For \(\mathrm {CIMP}\text {-}\mathrm {CU}\), the reduction is not tight. \(\mathrm {CIMP}\text {-}\mathrm {CC}\) cannot be obtained via these paths, and instead we establish it from signatures. First we need to recall a few standard definitions.
HVZK and extractability. We say that an identification scheme \(\mathsf {ID}\) is honest verifier zero-knowledge (HVZK) if there exists an algorithm \(\mathsf {ID}.\mathsf {Sim}\) (called the simulator) that given the verification key, generates transcripts which have the same distribution as honest ones, even given the verification key. Formally, if \(\mathcal{A}\) is an adversary, let \(\mathbf {Adv}^{\mathrm {zk}}_{\mathsf {ID}}(\mathcal{A}) = 2\Pr [\mathbf {G}^\mathrm{zk}_{\mathsf {ID}}(\mathcal{A})]-1\) where the game is shown in Fig. 5. Then \(\mathsf {ID}\) is HVZK if \(\mathbf {Adv}^{\mathrm {zk}}_{\mathsf {ID}}(\mathcal{A}) = 0\) for all adversaries \(\mathcal{A}\) (regardless of the running time of \(\mathcal{A}\)). We say that an identification scheme \(\mathsf {ID}\) is extractable if there exists an algorithm \(\mathsf {ID}.\mathsf {Ex}\) (called the extractor) which from any two verifying transcripts that have the same commitment but different challenges can recover the secret key. Formally, if \(\mathcal{A}\) is an adversary, let \(\mathbf {Adv}^{\mathrm {ex}}_{\mathsf {ID}}(\mathcal{A}) = \Pr [\mathbf {G}^\mathrm{ex}_{\mathsf {ID}}(\mathcal{A})]\) where the game is shown in Fig. 5. Then \(\mathsf {ID}\) is extractable if \(\mathbf {Adv}^{\mathrm {ex}}_{\mathsf {ID}}(\mathcal{A}) = 0\) for all adversaries \(\mathcal{A}\) (regardless of the running time of \(\mathcal{A}\)). We say that an identification scheme is a Sigma protocol [13] if it is both HVZK and extractable.
Security against key recovery. An identification scheme \(\mathsf {ID}\) is resilient to key recovery if it is hard to recover the secret identification key given nothing but the verification key. This was defined by OO [33]. Formally, if \(\mathcal{I}\) is an adversary, let \(\mathbf {Adv}^{\mathrm {kr}}_{\mathsf {ID}}(\mathcal{I}) = \Pr [\mathbf {G}^\mathrm{kr}_{\mathsf {ID}}(\mathcal{I})]\) where the game is shown in Fig. 5. Security against key recovery is precisely the (standard) assumption \(\mathrm {P}_{\mathrm {alg}}\) underlying most identification schemes (e.g., the one-wayness of RSA for the \(\mathsf {GQ}\) identification scheme, and the factoring assumption for factoring-based schemes).
Obtaining \(\mathrm {CIMP}\text {-}\mathrm {UU}\) and \(\mathrm {CIMP}\text {-}\mathrm {UC}\). Here we show that for Sigma protocols, \(\mathrm {CIMP}\text {-}\mathrm {UU}\) and \(\mathrm {CIMP}\text {-}\mathrm {UC}\) security reduce tightly to security under key recovery. The proof of the following is in [7].
Theorem 1
Let \(\mathsf {ID}\) be an identification scheme that is honest verifier zero-knowledge and extractable. Then for any adversary \(\mathcal{P}\) against \(\mathrm {CIMP}\text {-}\mathrm {UC}\) we construct a key recovery adversary \(\mathcal{I}\) such that
Also for any adversary \(\mathcal{P}\) against \(\mathrm {CIMP}\text {-}\mathrm {UU}\) that makes \(q_c\) queries to its \(\textsc {Ch}\) oracle we construct a key recovery adversary \(\mathcal{I}\) such that
In both cases, the running time of \(\mathcal{I}\) is about that of \(\mathcal{P}\) plus the time for one execution of \(\mathsf {ID}.\mathsf {Ex}\) and the time for a number of executions of \(\mathsf {ID}.\mathsf {Sim}\) equal to the number of \(\textsc {Tr}\) queries of \(\mathcal{P}\).
Obtaining \(\mathrm {CIMP}\text {-}\mathrm {CU}\). \(\mathrm {CIMP}\text {-}\mathrm {CU}\) security of Sigma protocols can also be established under their key recovery security, but the reduction is not tight.
Theorem 2
Let \(\mathsf {ID}\) be an identification scheme that is honest verifier zero-knowledge and extractable. For any adversary \(\mathcal{P}\) against \(\mathrm {CIMP}\text {-}\mathrm {CU}\) making q queries to its \(\textsc {Ch}\) oracle, we construct a key recovery adversary \(\mathcal{I}\) such that
The running time of \(\mathcal{I}\) is about twice that of \(\mathcal{P}\).
To establish Theorem 2, our route will be via standard techniques and known results, and the proof can be found for completeness in [7].
Obtaining \(\mathrm {CIMP}\text {-}\mathrm {CC}\). This is our strongest notion, and is quite different from the rest. Sigma protocols will fail to achieve \(\mathrm {CIMP}\text {-}\mathrm {CC}\) because an HVZK identification scheme cannot be \(\mathrm {CIMP}\text {-}\mathrm {CC}\)-secure. The attack (adversary) \(\mathcal{P}\) showing this is as follows. Assuming \(\mathsf {ID}\) is HVZK, our adversary \(\mathcal{P}\), given the verification key  , runs the simulator to get a transcript
, runs the simulator to get a transcript  . It makes no \(\textsc {Tr}\) queries, so the set \(\mathrm {S}\) in the game is empty. It then makes query \(\textsc {Ch}(Y,c)\) and returns \((1,z)\) to achieve \(\mathbf {Adv}^\mathrm{cimp\text{- }cc}_{\mathsf {ID}}(\mathcal{P})=1\).
. It makes no \(\textsc {Tr}\) queries, so the set \(\mathrm {S}\) in the game is empty. It then makes query \(\textsc {Ch}(Y,c)\) and returns \((1,z)\) to achieve \(\mathbf {Adv}^\mathrm{cimp\text{- }cc}_{\mathsf {ID}}(\mathcal{P})=1\).
This doesn’t mean \(\mathrm {CIMP}\text {-}\mathrm {CC}\) is unachievable. We show in [7] how to achieve it from any \(\mathrm {UF}\) digital signature scheme.
While this shows \(\mathrm {CIMP}\text {-}\mathrm {CC}\) is achievable, and even under standard assumptions, it is not of help for us, since we want to obtain signature schemes from identification schemes and if the latter are themselves built from a signature scheme then nothing has been gained. We consider \(\mathrm {CIMP}\text {-}\mathrm {CC}\) nonetheless because our framework naturally gives rise to it and we wish to see the full picture, and also because there may be other ways to achieve \(\mathrm {CIMP}\text {-}\mathrm {CC}\).
5 From \(\mathrm {UUF}\) to \(\mathrm {UF}\)
Some of our transforms of identification schemes into signature schemes naturally achieve \(\mathrm {UUF}\) security rather than \(\mathrm {UF}\) security. To achieve the latter, one can take our \(\mathrm {UUF}\) schemes and apply the transforms in this section. The reductions are tight and the costs are low. First we observe that standard derandomization (removing randomness) has the additional benefit (apparently not noted before) of turning \(\mathrm {UUF}\) into \(\mathrm {UF}\). Second, we show that message randomization (adding randomness) is also a natural solution.
Left: Our construction of deterministic signature scheme \(\mathsf {DS}^*=\mathbf {DR}[\mathsf {DS}]\) from a signature scheme \(\mathsf {DS}\). By \(\textsc {H}(\cdot )\) we denote \(\textsc {H}(\cdot ,\{0,1\}^{\mathsf {DS}.\mathsf {rl}})\), which has range \(\{0,1\}^{\mathsf {DS}.\mathsf {rl}}\). Right: Our construction of added-randomness signature scheme \(\mathsf {DS}^*=\mathbf {AR}[\mathsf {DS},\mathsf {sl}]\) from a signature scheme \(\mathsf {DS}\) and a seed length \(\mathsf {sl}\in {{\mathbb N}} \).
5.1 From \(\mathrm {UUF}\) to \(\mathrm {UF}\) by Removing Randomness
It is standard to derandomize a signing algorithm by obtaining the coins from a secretly keyed hash function applied to the message. This has been shown to preserve \(\mathrm {UF}\) security —meaning, if the starting scheme is \(\mathrm {UF}\)-secure, so is the derandomized scheme— in some cases. One secure instantiation is to use a PRF as the hash function with the PRF key added to the signing secret key [19], however this changes the signing key and can be undesirable in practice. Instead one can hash the signing key with the message using a hash function that one models as a random oracle. This has been proven to work for certain particular choices of the starting signature scheme, namely when this scheme is ECDSA [26]. Such de-randomization is also used in the Ed25519 signature scheme [11]. However, it has not been proven in the general case. This will follow from our results.
The purpose of the method, above, was exactly to derandomize, namely to ensure that the signing process is deterministic, and the starting signature scheme was assumed \(\mathrm {UF}\) secure. We observe here that the method has an additional benefit which does not seem to have been noted before, namely that it works even if the starting scheme is only \(\mathrm {UUF}\) secure, meaning it upgrades \(\mathrm {UUF}\) security to \(\mathrm {UF}\) security. It is an attractive way to do this because it preserves signature size and verification time, while adding to the signing time only the cost of one hash. We specify a derandomization transform and prove that it turns \(\mathrm {UUF}\) schemes into \(\mathrm {UF}\) ones in general, meaning assuming nothing more than \(\mathrm {UUF}\) security of the starting scheme. In particular, we justify derandomization in a broader context than previous work.
The construction. For a signature scheme \(\mathsf {DS}\), let \(\mathsf {DS}.\mathsf {rl}\) denote the length of the randomness (number of coins) used by the signing algorithm \(\mathsf {DS}.\mathsf {Sig}\). We write  for the execution of \(\mathsf {DS}.\mathsf {Sig}\) on inputs
for the execution of \(\mathsf {DS}.\mathsf {Sig}\) on inputs  and coins \(r\in \{0,1\}^{\mathsf {DS}.\mathsf {rl}}\). Let signature scheme \(\mathsf {DS}^*= \mathbf {DR}[\mathsf {DS}]\) be obtained from \(\mathsf {DS}\) as in Fig. 6. Here, the function \(\textsc {H}(\cdot )\) used to compute \(r\) in algorithm \(\mathsf {DS}^*.\mathsf {Sig}\) is \(\textsc {H}(\cdot ,\{0,1\}^{\mathsf {DS}.\mathsf {rl}})\), meaning the range is set to \(\{0,1\}^{\mathsf {DS}.\mathsf {rl}}\).
and coins \(r\in \{0,1\}^{\mathsf {DS}.\mathsf {rl}}\). Let signature scheme \(\mathsf {DS}^*= \mathbf {DR}[\mathsf {DS}]\) be obtained from \(\mathsf {DS}\) as in Fig. 6. Here, the function \(\textsc {H}(\cdot )\) used to compute \(r\) in algorithm \(\mathsf {DS}^*.\mathsf {Sig}\) is \(\textsc {H}(\cdot ,\{0,1\}^{\mathsf {DS}.\mathsf {rl}})\), meaning the range is set to \(\{0,1\}^{\mathsf {DS}.\mathsf {rl}}\).
While algorithms of the starting scheme \(\mathsf {DS}\) may invoke the random oracle (and, in the schemes we construct in Sect. 6, they do), it is assumed they do not invoke \(\textsc {H}(\cdot ,\{0,1\}^{\mathsf {DS}.\mathsf {rl}})\). This can be ensured in a particular case by domain separation. Given this, other calls of the algorithms of the starting scheme to the random oracle can be simulated directly in the proof via the random oracle available to the constructed adversaries. Accordingly in the scheme description of Fig. 6, and proof below, for simplicity, we do not give the algorithms of the starting signature scheme access to the random oracle. That is, think of the starting scheme as being a standard-model one.
Unforgeability. The following says that the constructed scheme \(\mathsf {DS}^*\) is \(\mathrm {UF}\) secure assuming the starting scheme \(\mathsf {DS}\) was \(\mathrm {UUF}\) secure, with a tight reduction. The reason a deterministic scheme that is \(\mathrm {UUF}\) is also \(\mathrm {UF}\) is clear, namely there is nothing to gain by calling the signing oracle more than once on a particular message, because one just gets back the same thing each time. What the proof needs to ensure is that the method of making the scheme deterministic does not create any weaknesses. The danger is that including the secret key as an input to the hash increases the exposure of the key. The proof says that it might a little, but the advantage does not go up by more than a factor of two. The proof is in [7].
Theorem 3
Let signature scheme \(\mathsf {DS}^*= \mathbf {DR}[\mathsf {DS}]\) be obtained from signature scheme \(\mathsf {DS}\) as in Fig. 6. Let \(\overline{\mathcal{A}}\) be a \(\mathrm {UF}\)-adversary against \(\mathsf {DS}^*\) that makes \(q_h\) queries to \(\textsc {H}\) and \(q_s\) queries to \(\textsc {Sign}\). Then from \(\overline{\mathcal{A}}\) we can construct \(\mathrm {UUF}\)-adversary \(\mathcal{A}\) such that
Adversary \(\mathcal{A}\) makes \(q_s\) queries to \(\textsc {Sign}\). It has running time about that of \(\overline{\mathcal{A}}\) plus the time for \(q_h\) invocations of \(\mathsf {DS}.\mathsf {Sig}\) and \(\mathsf {DS}.\mathsf {Vf}\).
We remark that adversary \(\mathcal{A}_0\) actually violates key recovery security of \(\mathsf {DS}\), not just its \(\mathrm {UUF}\) security.
5.2 From \(\mathrm {UUF}\) to \(\mathrm {UF}\) by Adding Randomness
A complementary and natural method for constructing \(\mathrm {UF}\) signatures from \(\mathrm {UUF}\) ones is by adding randomness: before being signed, the message is concatenated with a random seed \(s\) of some length \(\mathsf {sl}\), so even for the same message, the inputs to the \(\mathrm {UUF}\) signing algorithm are (with high probability) distinct. Compared to derandomization, the drawback of this method is that the signature size increases because the seed must be included in the signature. The potential advantage is that the transform is standard model, not using a random oracle, while preserving the secret key. (Derandomization can be done in the standard model via a PRF, but this requires augmenting the signing key with the PRF key.)
The construction. Let signature scheme \(\mathsf {DS}^*= \mathbf {AR}[\mathsf {DS},\mathsf {sl}]\) be obtained from \(\mathsf {DS}\) as in Fig. 6. As above, \(\mathsf {DS}\) is for simplicity assumed to be a standard-model scheme, so that its algorithms do not have access to \(\textsc {H}\). The transform itself does not use \(\textsc {H}\).
Unforgeability. The following says that the constructed scheme \(\mathsf {DS}^*\) is \(\mathrm {UF}\) secure assuming the starting scheme \(\mathsf {DS}\) was \(\mathrm {UUF}\) secure, with a tight reduction. The reason is quite simple, namely that unless seeds collide, the messages being signed are distinct. The proof of the following is in [7].
Theorem 4
Let signature scheme \(\mathsf {DS}^*= \mathbf {AR}[\mathsf {DS},\mathsf {sl}]\) be obtained from signature scheme \(\mathsf {DS}\) and seed length \(\mathsf {sl}\in {{\mathbb N}} \) as in Fig. 6. Let \(\overline{\mathcal{A}}\) be a \(\mathrm {UF}\)-adversary against \(\mathsf {DS}^*\) making \(q_s\) queries to its \(\textsc {Sign}\) oracle. Then from \(\overline{\mathcal{A}}\) we construct a \(\mathrm {UUF}\) adversary \(\mathcal{A}\) such that
Adversary \(\mathcal{A}\) makes \(q_s\) queries to its \(\textsc {Sign}\) oracle and has about the same running time as \(\overline{\mathcal{A}}\).
6 Signatures from Identification
We specify our three new transforms of identification schemes to signature schemes, namely the ones of rows 2, 3, 4 of the table of Fig. 1. In each case, we give a security proof based on the assumption \(\mathrm {P}_{\mathrm {id}}\) listed in the 1st column of the corresponding row of the table, so that we give transforms from \(\mathrm {CIMP}\text {-}\mathrm {UC},\mathrm {CIMP}\text {-}\mathrm {UU}\) and \(\mathrm {CIMP}\text {-}\mathrm {CC}\). It turns out that these transforms naturally achieve UUF rather than UF, and this is what we prove, with tight reductions of course. The transformation \(\mathrm {UF}\mathbf {\rightarrow }\mathrm {UUF}\) can be done at the level of signatures, not referring to identification, in generic and simple ways, and also with tight reductions, as detailed in Sect. 5. We thus get UF-secure signatures with tight reductions to each of \(\mathrm {CIMP}\text {-}\mathrm {UC},\mathrm {CIMP}\text {-}\mathrm {UU}\) and \(\mathrm {CIMP}\text {-}\mathrm {CC}\). In this section we further study the \(\mathbf {FS}\) transform from [16] and our transform \(\mathbf {Swap}\) which is inspired by the work of MR [30].
6.1 From \(\mathrm {CIMP}\text {-}\mathrm {UC}\) Identification to \(\mathrm {UUF}\) Signatures: \(\mathbf {MdCmt}\)
\(\mathbf {MdCmt}\) transforms a \(\mathrm {CIMP}\text {-}\mathrm {UC}\) trapdoor identification scheme to a UUF signature scheme using message-dependent commitments.
The construction. Let \(\mathsf {ID}\) be a trapdoor identification scheme and \({\mathsf {ID}.\mathsf {cl}}\) its challenge length. Our \(\mathbf {MdCmt}\) (message-dependent commitment) transform associates to \(\mathsf {ID}\) the signature scheme \(\mathsf {DS}= \mathbf {MdCmt}[\mathsf {ID}]\). The algorithms of \(\mathsf {DS}\) are defined in Fig. 7. By \(\textsc {H}(\cdot )\) we denote  , meaning the range is set to commitment space
, meaning the range is set to commitment space  . Signatures are effectively identification transcripts, but the commitments are chosen in a particular way. Recall that with trapdoor ID schemes it is the same whether one executes
. Signatures are effectively identification transcripts, but the commitments are chosen in a particular way. Recall that with trapdoor ID schemes it is the same whether one executes  directly, or samples
directly, or samples  followed by computing
followed by computing  . Our construction exploits this: To each message \(m\) it assigns an individual commitment \(Y\leftarrow \textsc {H}(m)\). The signing algorithm, using the trapdoor, completes this commitment to a transcript \((Y,c,z)\) and outputs the pair \(c,z\) as the signature. Verification then consists of recomputing \(Y\) from \(m\) and invoking the verification algorithm of the ID scheme.
. Our construction exploits this: To each message \(m\) it assigns an individual commitment \(Y\leftarrow \textsc {H}(m)\). The signing algorithm, using the trapdoor, completes this commitment to a transcript \((Y,c,z)\) and outputs the pair \(c,z\) as the signature. Verification then consists of recomputing \(Y\) from \(m\) and invoking the verification algorithm of the ID scheme.
Unforgeability. The following theorem establishes that the (unique) unforgeability of a signature scheme constructed with \(\mathbf {MdCmt}\) tightly reduces to the \(\mathrm {CIMP}\text {-}\mathrm {UC}\) security of the underlying ID scheme, in the random oracle model. The proof of the following is in [7].
Theorem 5
Let signature scheme \(\mathsf {DS}= \mathbf {MdCmt}[\mathsf {ID}]\) be obtained from trapdoor identification scheme \(\mathsf {ID}\) as in Fig. 7. Let \(\mathcal{A}\) be a \(\mathrm {UUF}\)-adversary against \(\mathsf {DS}\). Suppose the number of queries that \(\mathcal{A}\) makes to its \(\textsc {H}\) and \(\textsc {Sign}\) oracles are \(q_h\) and \(q_s\), respectively. Then from \(\mathcal{A}\) we construct a \(\mathrm {CIMP}\text {-}\mathrm {UC}\) adversary \(\mathcal{P}\) such that
Adversary \(\mathcal{P}\) makes \(q_h+q_s+1\) queries to \(\textsc {Tr}\) and one query to \(\textsc {Ch}\). Its running time is about that of \(\mathcal{A}\).
The bound of Eq. (5) may be a bit hard to estimate. The following simpler bound is also true and may be easier to use:
The justification for Eq. (6) is in [7].
6.2 From \(\mathrm {CIMP}\text {-}\mathrm {UU}\) Identification to \(\mathrm {UUF}\) Signatures: \(\mathbf {MdCmtCh}\)
\(\mathbf {MdCmtCh}\) transforms a \(\mathrm {CIMP}\text {-}\mathrm {UU}\) trapdoor identification scheme to a UUF signature scheme using message-dependent commitments and challenges.
The construction. Our \(\mathbf {MdCmtCh}\) (message-dependent commitment and challenge) transform associates to trapdoor identification scheme \(\mathsf {ID}\) the signature scheme \(\mathsf {DS}= \mathbf {MdCmtCh}[\mathsf {ID}]\) whose algorithms are defined in Fig. 8. We specify the commitment \(Y\) as a hash of the message and use the trapdoor property to allow the signer to obtain  . We then specify the challenge as a randomized hash of the message. (Unlike in the \(\mathbf {FS}\) transform, the commitment is not hashed along with the message.) The randomization is captured by a one-bit seed \(s\). The construction, and proof below, both use the technique of KW [24].
. We then specify the challenge as a randomized hash of the message. (Unlike in the \(\mathbf {FS}\) transform, the commitment is not hashed along with the message.) The randomization is captured by a one-bit seed \(s\). The construction, and proof below, both use the technique of KW [24].
By \(\textsc {H}_1(\cdot )\) we denote random oracle  with range
with range  and by \(\textsc {H}_2(\cdot )\) we denote random oracle \(\textsc {H}(\cdot ,\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}})\) with range \(\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\). We assume
and by \(\textsc {H}_2(\cdot )\) we denote random oracle \(\textsc {H}(\cdot ,\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}})\) with range \(\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\). We assume  so that these random oracles are independent. In case
so that these random oracles are independent. In case  , the scheme should be modified to use domain separation, for example prefix a 1 to any query to \(\textsc {H}_1\) and a 0 to any query to \(\textsc {H}_2\).
, the scheme should be modified to use domain separation, for example prefix a 1 to any query to \(\textsc {H}_1\) and a 0 to any query to \(\textsc {H}_2\).
Notice that the signature consists of a response plus a bit. It is thus shorter than for \(\mathbf {MdCmt}\) (where it is a response plus a challenge) or for \(\mathbf {FS}\) (where it is a response plus a commitment or, in the more compact form, a response plus a challenge). These shorter signatures are a nice feature of \(\mathbf {MdCmtCh}\).
Our construction of signature scheme \(\mathsf {DS}=\mathbf {MdCmtCh}[\mathsf {ID}]\) from a trapdoor identification scheme \(\mathsf {ID}\). By \(\textsc {H}_1(\cdot )\) we denote random oracle  with range
with range  and by \(\textsc {H}_2(\cdot )\) we denote random oracle \(\textsc {H}(\cdot ,\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}})\) with range \(\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\).
and by \(\textsc {H}_2(\cdot )\) we denote random oracle \(\textsc {H}(\cdot ,\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}})\) with range \(\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\).
Unforgeability of our construction. The following shows that unique unforgeability of our signature tightly reduces to the \(\mathrm {CIMP}\text {-}\mathrm {UU}\) security of the underlying ID scheme. Standard unforgeability follows immediately (and tightly) by applying one of the UUF-to-UF transforms in Sect. 5.
Theorem 6
Let signature scheme \(\mathsf {DS}= \mathbf {MdCmtCh}[\mathsf {ID}]\) be obtained from trapdoor identification scheme \(\mathsf {ID}\) as in Fig. 8. Let \(\mathcal{A}\) be a \(\mathrm {UUF}\) adversary against \(\mathsf {DS}\). Suppose the number of queries that \(\mathcal{A}\) makes to its \(\textsc {H}_1\) and \(\textsc {H}_2\) oracles is \(q_h\), and the number to its \(\textsc {Sign}\) oracle is \(q_s\). Then from \(\mathcal{A}\) we construct \(\mathrm {CIMP}\text {-}\mathrm {UU}\) adversary \(\mathcal{P}\) such that
Adversary \(\mathcal{P}\) makes \(q_h+q_s+1\) queries to \(\textsc {Tr}\) and \(q_h+q_s\) queries to \(\textsc {Ch}\). It has running time about that of \(\mathcal{A}\).
Adversary for proof of Theorem 6.
Proof
(Theorem 6 ). Adversary \(\mathcal{P}\) is shown in Fig. 9. It executes \(\mathcal{A}\), responding to \(\textsc {H}_1\), \(\textsc {H}_2\) and \(\textsc {Sign}\) queries of the latter via the shown procedures, which are subroutines in the code of \(\mathcal{P}\). We assume the message \(m\) in the forgery \((m,\sigma )\) returned by \(\mathcal{A}\) was not queried to \(\textsc {Sign}\) and is not in the set M, since otherwise \(\mathcal{A}\) would automatically lose. The “\(Y\leftarrow \textsc {H}_1(m)\)” instructions in the code of \(\textsc {Sign}\), the code of \(\textsc {H}_2\) and following the execution of \(\mathcal{A}\) ensure that \(\textsc {H}_1(m)\) is queried at this point. Each time a new \(\textsc {H}_1(m)\) query is made, a transcript is generated by \(\mathcal{P}\) using its \(\textsc {Tr}\) oracle. The commitment in this transcript is the reply to the \(\textsc {H}_1(m)\) query. Additionally, however, steps are taken to ensure that, if, later, a \(\textsc {Sign}(m)\) query is made, then a signature to return is available. This is done by picking a random one-bit seed \(s_i\) and assigning \(\textsc {H}_2(m\Vert s_i)\) the value \(c_i\). At the time of a signing query, one can use \(s_i\) as the seed and use the response of the corresponding transcript to create the signature. To be able to win via the forgery, \(\textsc {H}_2(m\Vert \overline{s}_i)\) is assigned a challenge via \(\textsc {Ch}\), where \(\overline{s}_i\) denotes the complement of the bit \(s_i\). Now, when the forgery \((m,(z,s))\) is obtained from \(\mathcal{A}\), the associated index j is computed, and then \(z\) is returned as a response for that session. Adversary \(\mathcal{P}\) will be successful as long as \(\mathcal{A}\) is successful and \(s= \overline{s}_j\). The events being independent we have
Transposing terms yields Eq. (7). \(\square \)
6.3 From \(\mathrm {CIMP}\text {-}\mathrm {CC}\) Identification to \(\mathrm {UF}\) Signatures: \(\mathbf {MdCh}\)
The \(\mathbf {MdCmt}\) and \(\mathbf {MdCmtCh}\) transforms described above rely on the trapdoor property of the underlying identification scheme and achieve UUF rather than UF. The \(\mathbf {MdCh}\) transform we describe here does not have these limitations. (It does not require the identification scheme to be trapdoor, and it directly achieves UF.) However, among the security notions for ID schemes that we defined, \(\mathbf {MdCh}\) assumes the strongest one: \(\mathrm {CIMP}\text {-}\mathrm {CC}\).
The construction. Our \(\mathbf {MdCh}\) (message-dependent challenge) transform associates to identification scheme \(\mathsf {ID}\) and a seed length \(\mathsf {sl}\in \mathbb {N}\) the signature scheme \(\mathsf {DS}= \mathbf {MdCh}[\mathsf {ID},\mathsf {sl}]\) whose algorithms are defined in Fig. 10. Signing picks the commitment directly rather than (as in our prior transforms) specifying it as the hash of the message. The challenge is derived as a randomized hash of the message, the randomization being captured by a seed \(s\) of length \(\mathsf {sl}\). By \(\textsc {H}(\cdot )\) we denote random oracle \(\textsc {H}(\cdot ,\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}})\) with range \(\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\).
Unforgeability. As we prove below (with tight reduction), the \(\mathbf {MdCh}\) construction yields a \(\mathrm {UF}\) secure signature scheme if the underlying identification scheme offers \(\mathrm {CIMP}\text {-}\mathrm {CC}\) security.
The construction of signature scheme \(\mathsf {DS}=\mathbf {MdCh}[\mathsf {ID},\mathsf {sl}]\) from identification scheme \(\mathsf {ID}\) and seed length \(\mathsf {sl}\). By \(\textsc {H}(\cdot )\) we denote random oracle \(\textsc {H}(\cdot ,\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}})\) with range \(\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\).
Theorem 7
Let signature scheme \(\mathsf {DS}= \mathbf {MdCh}[\mathsf {ID},\mathsf {sl}]\) be obtained from identification scheme \(\mathsf {ID}\) and seed length \(\mathsf {sl}\in {{\mathbb N}} \) as in Fig. 10. Let \(\mathcal{A}\) be a \(\mathrm {UF}\) adversary against \(\mathsf {DS}\) making \(q_h\) queries to its \(\textsc {H}\) oracle and \(q_s\) queries to its \(\textsc {Sign}\) oracle. Then from \(\mathcal{A}\) we construct a \(\mathrm {CIMP}\text {-}\mathrm {CC}\) adversary \(\mathcal{P}\) such that
Adversary \(\mathcal{P}\) makes \(q_s\) queries to \(\textsc {Tr}\) and one query to \(\textsc {Ch}\) and has running time about that of \(\mathcal{A}\).
Games and adversary for proof of Theorem 7.
Proof
(Theorem 7 ). Game \(\mathrm {G}_0\) of Fig. 11 includes the boxed code, while game \(\mathrm {G}_1\) does not. Game \(\mathrm {G}_0\) is precisely the \(\mathrm {UF}\) game of Fig. 2 with the algorithms of \(\mathsf {DS}\) plugged in. We assume the message \(m\) in the forgery \((m,\sigma )\) returned by \(\mathcal{A}\) was not queried to \(\textsc {Sign}\). Games \(\mathrm {G}_0,\mathrm {G}_1\) are identical until \(\mathsf {bad}\). By the Fundamental Lemma of Game Playing [10] we have
Adversary \(\mathcal{P}\) of Fig. 11 executes \(\mathcal{A}\), responding to \(\textsc {Sign}\) and \(\textsc {H}\) queries of the latter via the shown procedures, which are subroutines in the code of \(\mathcal{P}\).
Adversary \(\mathcal{P}\) simulates for \(\mathcal{A}\) the environment of game \(\mathrm {G}_1\). In the execution of game \(\mathbf {G}^\mathrm{cimp\text{- }cc}_{\mathsf {ID}}(\mathcal{P})\) of Fig. 4, let \(\textsc {B}\) denote the event that \((Y,c)\in \mathrm {S}\), where \(Y,c\) is the argument to the single \(\textsc {Ch}\) query made by our \(\mathcal{P}\). Then
To complete the proof, it suffices to show that
We bound \(\Pr [\textsc {B}]\) by the probability that \(c\) is a challenge in one of the transcripts. The message \(m\) in the forgery is assumed not one of those signed, so \(\mathrm {HT}[m,s]\) was not set by \(\textsc {Sign}\) and is thus independent of the transcript challenges. There are at most \(q_s\) transcript challenges and at most \(q_h\) queries to \(\textsc {H}\), so \(\Pr [\textsc {B}] \le q_hq_s/2^{{\mathsf {ID}.\mathsf {cl}}}\). \(\square \)
6.4 From \(\mathrm {CIMP}\text {-}\mathrm {CU}\) Identification to \(\mathrm {UF}\) Signatures: \(\mathbf {FS}\)
The first proofs of \(\mathrm {UF}\) security of \(\mathbf {FS}\)-based signatures used a Forking Lemma and were quite complex [35]. More modular approaches were given in OO [33] and AABN [1]. AABN reduce \(\mathrm {UF}\) security of the signature scheme to IMP-PA security of the identification scheme. (The latter is established separately via the Reset Lemma of [6].) The reduction of AABN is not tight.
Our framework allows a tight reduction of the \(\mathrm {UF}\) security of \(\mathbf {FS}\)-based signatures to the \(\mathrm {CIMP}\text {-}\mathrm {CU}\) security of the underlying identification scheme. The reason for this is simple, namely that \(\mathrm {CIMP}\text {-}\mathrm {CU}\) is the multi-impersonation version of IMP-PA. The proof is implicit in AABN [1]. We give a proof however for completeness and to illustrate how much simpler this proof is to prior ones.
We note that this tighter reduction does not change overall tightness. That is, in AABN, \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) was not tight, while for us, it is, but the tightness of the overall \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) reduction remains the same in both cases.
The construction. The \(\mathbf {FS}\) transform [16] associates to identification scheme \(\mathsf {ID}\) the signature scheme \(\mathsf {DS}= \mathbf {FS}[\mathsf {ID}]\) whose algorithms are defined in Fig. 12. Signing picks the commitment directly. The challenge is derived as a hash of the commitment and message. By \(\textsc {H}(\cdot )\) we denote random oracle \(\textsc {H}(\cdot ,\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}})\) with range \(\{0,1\}^{{\mathsf {ID}.\mathsf {cl}}}\).
Unforgeability. The following theorem says that the \(\mathbf {FS}\) construction yields a \(\mathrm {UF}\) secure signature scheme if the underlying ID scheme offers \(\mathrm {CIMP}\text {-}\mathrm {CU}\) security and the commitment (as generated by the prover) is uniformly distributed over a large space. The latter condition is true for typical identification schemes. The intuition of the proof is that signing queries are answered via transcripts and hash queries are mapped to challenge queries, this failing only if commitments collide. The proof of the following is in [7].
Theorem 8
Let signature scheme \(\mathsf {DS}= \mathbf {FS}[\mathsf {ID}]\) be obtained from identification scheme \(\mathsf {ID}\) as in Fig. 12. Let  . Let \(\mathcal{A}\) be a \(\mathrm {UF}\) adversary against \(\mathsf {DS}\) making \(q_h\) queries to its \(\textsc {H}\) oracle and \(q_s\) queries to its \(\textsc {Sign}\) oracle. Then from \(\mathcal{A}\) we construct a \(\mathrm {CIMP}\text {-}\mathrm {CU}\) adversary \(\mathcal{P}\) such that
. Let \(\mathcal{A}\) be a \(\mathrm {UF}\) adversary against \(\mathsf {DS}\) making \(q_h\) queries to its \(\textsc {H}\) oracle and \(q_s\) queries to its \(\textsc {Sign}\) oracle. Then from \(\mathcal{A}\) we construct a \(\mathrm {CIMP}\text {-}\mathrm {CU}\) adversary \(\mathcal{P}\) such that
Adversary \(\mathcal{P}\) makes \(q_s\) queries to \(\textsc {Tr}\) and \(q_h+1\) queries to \(\textsc {Ch}\) and has running time about that of \(\mathcal{A}\).
6.5 From \(\mathrm {CIMP}\text {-}\mathrm {UC}\) Identification to \(\mathrm {UF}\) Signatures: \(\mathbf {Swap}\)
Micali and Reyzin [30] use the term “swap” for a specific construction of a signature scheme that they give with a tight reduction to the hardness of factoring. Folklore, and hints in the literature [2], indicate that researchers understand the method is more general. But exactly how general was not understood or determined before, perhaps for lack of definitions. Our definition of trapdoor identification and the \(\mathrm {CIMP}\text {-}\mathrm {XY}\) framework allows us to fill this gap and give a characterization of the swap method and also better understand it.
In this section we define a transform of trapdoor identification schemes to signature schemes that we call \(\mathbf {Swap}\). We show that it yields UF secure signatures if the identification scheme is \(\mathrm {CIMP}\text {-}\mathrm {UC}\) secure.
The construction. The \(\mathbf {Swap}\) transform associates to trapdoor identification scheme \(\mathsf {ID}\) the signature scheme \(\mathsf {DS}= \mathbf {Swap}[\mathsf {ID}]\) whose algorithms are defined in Fig. 13.
Recall that in Sect. 6.1 we gave the \(\mathbf {MdCmt}\) transform that constructs UUF-secure signatures from \(\mathrm {CIMP}\text {-}\mathrm {UC}\)-secure identification. Further, in Sect. 5 we proposed two generic techniques that convert UUF signatures to signatures with full UF security. One of the latter, \(\mathbf {AR}\), achieves its goal by adding randomness to signed messages as follows: for signing \(m\), it picks a fresh random seed \(s\) and signs \(m{\Vert }s\) instead. The seed is included in the signature. Overall, the combination of \(\mathbf {MdCmt}\) with \(\mathbf {AR}\) yields tightly secure signatures of the form \((c,\mathsf {ID}.\mathsf {Rp}(c,\mathsf {ID}.\mathsf {Ct}^{-1}(\textsc {H}(m\Vert s))),s)\). \(\mathbf {Swap}\) effectively says that it is safe to choose \(c\) and \(s\) to be identical. Thus it can be viewed as an optimization of \(\mathbf {MdCmt}+\mathbf {AR}\), giving up on modularity to achieve more compact UF secure signatures.
We note however that our \(\mathbf {MdCmtCh}\) transform coupled with our UUF-to-UF transform \(\mathbf {DR}\) yields UF signatures that seem superior in every way: they are shorter (response plus a bit as opposed to response plus a challenge), the (tight) reduction is to the weaker \(\mathrm {CIMP}\text {-}\mathrm {UU}\) notion, and the efficiency is the same. Thus we would view \(\mathbf {Swap}\) at this point as of mostly historical interest.
Unforgeability. The following theorem says that the \(\mathbf {Swap}\) construction yields a \(\mathrm {UF}\) secure signature scheme if the underlying ID scheme offers \(\mathrm {CIMP}\text {-}\mathrm {UC}\) security and has sufficiently large challenge length. The proof of the following is in [7].
Theorem 9
Let signature scheme \(\mathsf {DS}= \mathbf {Swap}[\mathsf {ID}]\) be obtained from trapdoor identification scheme \(\mathsf {ID}\) as in Fig. 13. Let \(\mathcal{A}\) be a \(\mathrm {UF}\) adversary against \(\mathsf {DS}\). Suppose the number of queries that \(\mathcal{A}\) makes to its \(\textsc {H}\) oracle is \(q_h\) and the number of queries it makes to \(\textsc {Sign}\) is \(q_s\). Then from \(\mathcal{A}\) we construct a \(\mathrm {CIMP}\text {-}\mathrm {UC}\) adversary \(\mathcal{P}\) such that
Adversary \(\mathcal{P}\) makes \(q_h+q_s+1\) queries to \(\textsc {Tr}\) and one query to \(\textsc {Ch}\). Its running time is about that of \(\mathcal{A}\).
\(\mathrm {UF}\) signature schemes obtained from identification scheme \({\varvec{\mathsf {ID}}}\) . We show bounds on the uf advantage of an adversary \(\mathcal{A}\) making \(q_h\) queries to \(\textsc {H}\) and \(q_s\) queries to \(\textsc {Sign}\). Here \(\epsilon =\mathbf {Adv}^{\mathrm {kr}}_{\mathsf {ID}}(\mathcal{I})\) is the kr advantage of an adversary \(\mathcal{I}\) of roughly the same running time as \(\mathcal{A}\). By l, k, c we denote the lengths of the challenge, response and commitment, respectively. By C we denote the size of the commitment space. By \(\mathrm {P}_{\mathrm {id}}\) we denote the notion of identification security used in the \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) reduction.
6.6 From Identification to \(\mathrm {UF}\) Signatures: Summary
Figure 14 puts things together. We consider obtaining a \(\mathrm {UF}\) (not just \(\mathrm {UUF}\)) signature scheme \(\mathsf {DS}\) from a given identification scheme \(\mathsf {ID}\) via the various transforms in this paper. In the first three rows, the identification scheme is assumed to be trapdoor. Whenever a transform achieves (only) \(\mathrm {UUF}\), we apply \(\mathbf {DR}\) on top to get \(\mathrm {UF}\). We give bounds on the uf advantage \(\mathbf {Adv}^{\mathrm {uf}}_{\mathsf {DS}}(\mathcal{A})\) of an adversary \(\mathcal{A}\) making \(q_h\) queries to \(\textsc {H}\) and \(q_s\) queries to \(\textsc {Sign}\). By \(l = {\mathsf {ID}.\mathsf {cl}}\) we denote the challenge length of \(\mathsf {ID}\), and by \(C = \mathsf {ID}.\mathsf {CSS}\) the size of the commitment space. We show the full \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) reduction, so that the bounds are in terms of the kr advantage \(\epsilon =\mathbf {Adv}^{\mathrm {kr}}_{\mathsf {ID}}(\mathcal{I})\) of a kr-adversary \(\mathcal{I}\) having about the same running time as \(\mathcal{A}\). The bounds are obtained by combining the various relevant theorems, referring to the indicated equations. We show the notion \(\mathrm {P}_{\mathrm {id}}\) of identification security used as an intermediate point, namely \(\mathrm {P}_{\mathrm {sig}}\rightarrow \mathrm {P}_{\mathrm {id}}\rightarrow \mathrm {P}_{\mathrm {alg}}\). Signature size is shown as a function of challenge, response and commitment lengths. In summary, the bounds in the first three rows are tight, but the transform of the third row has the added advantage of shorter signatures and a linear (as opposed to quadratic) additive term in the bound. We do not show the \(\mathbf {MdCh}\) transform from \(\mathrm {CIMP}\text {-}\mathrm {CC}\) because the latter is not achieved by Sigma protocols. We note that the bound for \(\mathbf {FS}\) is the same as in [1]. (Our \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {id}}\) reduction, unlike theirs, is tight, but there is no change in the tightness of the full \(\mathrm {P}_{\mathrm {sig}}\mathbf {\rightarrow }\mathrm {P}_{\mathrm {alg}}\) reduction.)
References
Abdalla, M., An, J.H., Bellare, M., Namprempre, C.: From identification to signatures via the Fiat-Shamir transform: minimizing assumptions for security and forward-security. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 418–433. Springer, Heidelberg (2002). doi:10.1007/3-540-46035-7_28
Abdalla, M., Ben Hamouda, F., Pointcheval, D.: Tighter reductions for forward-secure signature schemes. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 292–311. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36362-7_19
Abdalla, M., Fouque, P.-A., Lyubashevsky, V., Tibouchi, M.: Tightly-secure signatures from lossy identification schemes. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 572–590. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_34
Bagherzandi, A., Cheon, J.H., Jarecki, S.: Multisignatures secure under the discrete logarithm assumption and a generalized forking lemma. In: Ning, P., Syverson, P.F., Jha, S. (eds.) ACM CCS 2008, pp. 449–458. ACM Press, October 2008
Bellare, M., Neven, G.: Multi-signatures in the plain public-key model and a general forking lemma. In: Juels, R., Wright, N., Vimercati, S. (eds.) ACM CCS 2006, pp. 390–399. ACM Press, October/November 2006
Bellare, M., Palacio, A.: GQ and Schnorr identification schemes: proofs of security against impersonation under active and concurrent attacks. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 162–177. Springer, Heidelberg (2002). doi:10.1007/3-540-45708-9_11
Bellare, M., Poettering, B., Stebila, D.: From identification to signatures, tightly: a framework and generic transforms. Cryptology ePrint Archive, Report 2015/1157 (2015). http://eprint.iacr.org/2015/1157
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 1993, pp. 62–73. ACM Press, November 1993
Bellare, M., Rogaway, P.: The exact security of digital signatures-how to sign with RSA and Rabin. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 399–416. Springer, Heidelberg (1996). doi:10.1007/3-540-68339-9_34
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). doi:10.1007/11761679_25
Bernstein, D.J., Duif, N., Lange, T., Schwabe, P., Yang, B.-Y.: High-speed high-security signatures. In: Preneel, B., Takagi, T. (eds.) CHES 2011. LNCS, vol. 6917, pp. 124–142. Springer, Heidelberg (2011). doi:10.1007/978-3-642-23951-9_9
Cachin, C., Micali, S., Stadler, M.: Computationally private information retrieval with polylogarithmic communication. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 402–414. Springer, Heidelberg (1999). doi:10.1007/3-540-48910-X_28
Cramer, R.: Modular design of secure, yet practical protocls. Ph.D. thesis, University of Amsterdam (1996)
Feige, U., Fiat, A., Shamir, A.: Zero knowledge proofs of identity. In: Aho, A. (ed.) 19th ACM STOC, pp. 210–217. ACM Press, May 1987
Feige, U., Fiat, A., Shamir, A.: Zero-knowledge proofs of identity. J. Cryptology 1(2), 77–94 (1988)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). doi:10.1007/3-540-47721-7_12
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Ladner, R.E., Dwork, C. (eds.) 40th ACM STOC, pp. 197–206. ACM Press, May 2008
Goh, E.-J., Jarecki, S.: A signature scheme as secure as the Diffie-Hellman problem. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 401–415. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_25
Goldreich, O.: Two remarks concerning the Goldwasser-Micali-Rivest signature scheme. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 104–110. Springer, Heidelberg (1987). doi:10.1007/3-540-47721-7_8
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
Goldwasser, S., Ostrovsky, R.: Invariant signatures and non-interactive zero-knowledge proofs are equivalent. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 228–245. Springer, Heidelberg (1993). doi:10.1007/3-540-48071-4_16
Goldwasser, S., Tauman Kalai, Y.: On the (in)security of the Fiat-Shamir paradigm. In: 44th FOCS, pp. 102–115. IEEE Computer Society Press, October 2003
Guillou, L.C., Quisquater, J.-J.: A “Paradoxical” indentity-based signature scheme resulting from zero-knowledge. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 216–231. Springer, Heidelberg (1990). doi:10.1007/0-387-34799-2_16
Katz, J., Wang, N.: Efficiency improvements for signature schemes with tight security reductions. In: Jajodia, S., Atluri, V., Jaeger, T. (eds.) ACM CCS 2003, pp. 155–164. ACM Press, October 2003
Kiltz, E., Masny, D., Pan, J.: Optimal security proofs for signatures from identification schemes. Cryptology ePrint Archive, Report 2016/191 (2016). http://eprint.iacr.org/2016/191
Koblitz, N., Menezes, A.: The random oracle model: a twenty-year retrospective. Cryptology ePrint Archive, Report 2015/140 (2015). http://eprint.iacr.org/2015/140
Lysyanskaya, A.: Unique signatures and verifiable random functions from the DH-DDH separation. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 597–612. Springer, Heidelberg (2002). doi:10.1007/3-540-45708-9_38
Lyubashevsky, V.: Fiat-Shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009). doi:10.1007/978-3-642-10366-7_35
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_43
Micali, S., Reyzin, L.: Improving the exact security of digital signature schemes. J. Cryptology 15(1), 1–18 (2002)
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_41
M’Raïhi, D., Naccache, D., Pointcheval, D., Vaudenay, S.: Computational alternatives to random number generators. In: Tavares, S., Meijer, H. (eds.) SAC 1998. LNCS, vol. 1556, pp. 72–80. Springer, Heidelberg (1999). doi:10.1007/3-540-48892-8_6
Ohta, K., Okamoto, T.: On concrete security treatment of signatures derived from identification. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 354–369. Springer, Heidelberg (1998). doi:10.1007/BFb0055741
Ong, H., Schnorr, C.P.: Fast signature generation with a Fiat Shamir — like scheme. In: Damgård, I.B. (ed.) EUROCRYPT 1990. LNCS, vol. 473, pp. 432–440. Springer, Heidelberg (1991). doi:10.1007/3-540-46877-3_38
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptology 13(3), 361–396 (2000)
Schnorr, C.-P.: Efficient signature generation by smart cards. J. Cryptology 4(3), 161–174 (1991)
Acknowledgments
Bellare was supported in part by NSF grant CNS-1526801, a gift from Microsoft corporation and ERC Project ERCC (FP7/615074). Poettering was supported by ERC Project ERCC (FP7/615074). Stebila was supported in part by Australian Research Council (ARC) Discovery Project grant DP130104304 and Natural Sciences and Engineering Research Council (NSERC) of Canada Discovery grant RGPIN-2016-05146.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Bellare, M., Poettering, B., Stebila, D. (2016). From Identification to Signatures, Tightly: A Framework and Generic Transforms. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10032. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53890-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-662-53890-6_15
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53889-0
Online ISBN: 978-3-662-53890-6
eBook Packages: Computer ScienceComputer Science (R0)




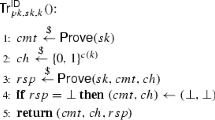







 .
.





 .
.
