Abstract
We study Authenticated Encryption with Associated Data (AEAD) from the viewpoint of composition in arbitrary (single-stage) environments. We use the indifferentiability framework to formalize the intuition that a “good” AEAD scheme should have random ciphertexts subject to decryptability. Within this framework, we can then apply the indifferentiability composition theorem to show that such schemes offer extra safeguards wherever the relevant security properties are not known, or cannot be predicted in advance, as in general-purpose crypto libraries and standards.
We show, on the negative side, that generic composition (in many of its configurations) and well-known classical and recent schemes fail to achieve indifferentiability. On the positive side, we give a provably indifferentiable Feistel-based construction, which reduces the round complexity from at least 6, needed for blockciphers, to only 3 for encryption. This result is not too far off the theoretical optimum as we give a lower bound that rules out the indifferentiability of any construction with less than 2 rounds.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Authenticated Encryption with Associated Data (AEAD) [10, 54] is a fundamental building block in cryptographic protocols, notably those enabling secure communication over untrusted networks. The syntax, security, and constructions of AEAD have been studied in numerous works. Recent, ongoing standardization processes, such as the CAESAR competition [14] and TLS 1.3, have revived interest in this direction. Security notions such as misuse-resilience [38, 43, 52, 56], robustness [2, 6, 41], multi-user security [19], reforgeability [36], and unverified plaintext release [5], as well as syntactic variants such as online operation [43] and variable stretch [41, 57] have been studied in recent works.
Building on these developments, and using the indifferentiability framework of Maurer, Renner, and Holenstein [48], we propose new definitions that bring a new perspective to the design of AEAD schemes. In place of focusing on specific property-based definitions, we formalize when an AEAD behaves like a random one. A central property of indifferentiable schemes is that they offer security with respect to a wide class of games. This class includes all the games above plus many others, including new unforeseen ones. Indifferentiability has been used to study the security of hash functions [15, 21] and blockciphers [4, 24, 33, 44], where constructions have been shown to behave like random oracles or ideal ciphers respectively. We investigate this question for authenticated encryption and ask if, and how efficiently, can indifferentiable AEAD schemes be built.
Our main contributions are as follows.
-
Definitions: We define ideal authenticated-encryption as one that is indifferentiable from a random keyed injection. This definition gives rise to a new model that is intermediate between the random-oracle and the ideal-cipher models. Accordingly, the random-injection model offers new efficiency and security trade-offs when compared to the ideal-cipher model.
-
Constructions: We obtain both positive and negative results for indifferentiable AEAD schemes. For most well-known constructions our results are negative. However, our main positive result is a Feistel construction that reduces the number of rounds from eight for ideal ciphers to only three for ideal keyed injections. This result improves the concrete parameters involved as well. We also give a transformation from offline to online ideal AEADs.
-
Lower bounds: Three rounds of Feistel are necessary to build injections. However, we prove a stronger result that lower bounds the number of primitive queries as a function of message blocks in any construction. This, in turn, shows that the rate of our construction is not too far off the optimal solution. For this we combine two lower bound techniques, one for collision resistance and the other for pseudorandomness, which may be of independent interest.
1.1 Background on Indifferentiability
A common paradigm in the design of symmetric schemes is to start from some simple primitive, such as a public permutation or a compression function, and through some “mode of operation” build a more complex scheme, such as a blockcipher or a variable-length hash function. The provable-security of such constructions has been analyzed mainly through two approaches. One is to formulate specific game-based properties, and then show that the construction satisfies them if its underlying primitives are secure. This methodology has been successfully applied to AEAD schemes. (See works cited in the opening paragraph of the paper.) Following this approach, higher-level protocols need to choose from a catalog of explicit properties offered by various AEAD schemes. For example, one would use an MRAE scheme whenever nonce-reuse cannot be excluded [38, 43, 52, 56] or a key-dependent message (KDM) secure one when the scheme is required to securely encrypt its own keys [7, 18].
The seminal work of Maurer, Renner, and Holenstein (MRH) on the indifferentiability of random systems [48] provides an alternative path to study the security of symmetric schemes. In this framework, a public primitive f is available. The goal is to build another primitive F from f via a construction \(C^f\). Indifferentiability formalizes a set of necessary and sufficient conditions for the construction \(C^f\) to securely replace its ideal counterpart F in a wide range of environments: there exists a simulator S such that the systems \((C^f,f)\) and \((F,S^F)\) are indistinguishable, even when the distinguisher has access to f. Indeed, the composition theorem proved by MRH states that, if \(C^f\) is indifferentiable from F, then \(C^f\) can securely replace F in arbitrary (single-stage) contexts. Thus, proving that a construction C is indifferentiable from an ideal object F amounts to proving that \(C^f\) retains essentially all security properties implicit in F. This approach has been successfully applied to the analysis of many symmetric cryptographic constructions in various ideal-primitive models; see, e.g., [21, 26, 33, 44]. Our work is motivated by this composition property.
1.2 Motivation
Maurer, Renner, and Holenstein proposed indifferentiability as an alternative to the Universal Composability (UC) framework [20] for compositional reasoning in idealized models of computation such as the random-oracle (RO) and the ideal-cipher (IC) models. Indifferentiability permits finding constructions that can safely replace ideal primitives (e.g., the random oracle) in various schemes.
The UC framework provides another general composition theorem, which has motivated the study of many UC-secure cryptographic protocols. Küsters and Tuengerthal [47] considered UC-secure symmetric encryption and defined an ideal functionality on par with standard notions of symmetric encryption security. This, however, resulted in an intricate functionality definition that adds complexity to the analysis of higher-level protocols. By adopting indifferentiability for the study of AEADs, we follow an approach that has been successfully applied to the study of other symmetric primitives. As random oracles formalize the intuition that well-designed hash functions have random-looking outputs, ideal encryption formalizes random-looking ciphertexts subject to decryptability. This results in a simple and easy-to-use definition. We discuss the benefits of this approach next and give limitations and open problems at the end of the section.
Once a primitive is standardized for general use, it is hard to predict in which environments it will be deployed, and which security properties may be intuitively expected from it. For example, consider a setting where a protocol designer follows the intuition that an AEAD scheme “essentially behaves randomly” and, while not knowing that AE security does not cover key-dependent message attacks [7, 18, 40] (KDM), uses a standardized general-purpose scheme for disk encryption. In other settings, a designer might create correlations among keys (as in 3GPP) expecting the underlying scheme to offer security against related-key attacks [8] (RKAs). Certain protocols rely on AE schemes that need to be committing against malicious adversaries, which can choose all inputs and thus also the keys. This has lead to the formalizations of committing [39] and key-robust [34] authenticated encryption. When there is leakage, parts of the key and/or randomness might be revealed [9]. All of these lie beyond standard notions of AE security, so the question is how should one deal with such a multitude of security properties.
One approach would be to formulate a new “super” notion that encompasses all features of the models above. This is clearly not practical. The model (and analyses using it) will be error-prone and, moreover, properties that have not yet been formalized will not be accounted for. Instead, and as mentioned above, we consider the following approach: a good AEAD scheme should behave like a random oracle, except that its ciphertexts are invertible. We formulate this in the language of indifferentiability, which results in a simple, unified, and easy to use definition. In indifferentiability, all inputs are under the control of the adversary. This means that the security guarantees offered extend to notions that allow for tampering with keys or creation of dependencies among the inputs. Once indifferentiability is proved, security with respect to all these games, combinations thereof and new unforeseen ones, jointly follows from the composition theorem.
Therefore one use-case for indifferentiable schemes would be to provision additional safeguards against primitive misuse in various deployment scenarios, such as general-purpose crypto libraries or standards, where the relevant security properties for target applications are complex or not known. We discussed some of these in the paragraph above. Protocol designers can rely on the intuition given by an ideal view of AEADs when integrating schemes into higher-level protocols, keeping game-based formulations implicit. Other applications include symbolic protocol analysis, where such idealizations are intrinsic [49] and security models where proof techniques such as programmability may be required [59].
A concrete example. In Facebook’s message-franking protocol, an adversary attempts to compute a ciphertext that it can later open in two ways by revealing different keys, messages and header information. (Facebook sees one (harmless) message, whereas the receiver gets another (possibly abusive) message.) Grubbs, Lu, and Ristenpart [39] formalize the security of such protocols and show that a standard AEAD can be used here, provided that it satisfies an additional security property called r-BIND [39, Fig. 17 (left)].
One important feature of this definition is that it relies on a single-stage game in the sense of [53]. The single-stage property immediately implies that any indifferentiable scheme is r-BIND if the ideal encryption scheme itself satisfies the r-BIND property. In contrast, not every AE-secure scheme is r-BIND secure [39]. Interestingly, it is easy to see that the ideal encryption scheme (a keyed random injection) indeed satisfies r-BIND and this is what, intuitively, the protocol designers seem to have assumed: that ciphertexts look random and thus collisions are hard to find, even if keys are adversarially chosen.
Indifferentiable AEADs therefore allow designers to rely on the above (arguably pragmatic) random-behavior intuition much in the same way as they do when using hash functions as random oracles. As the practicality of random oracles stems from their random output behavior (beyond PRF security or collision resistance) indifferentiable AEAD offers similar benefits: instead of focusing on a specific game-based property, it considers a fairly wide class of games for which the random behavior provably holds.
Thus an indifferentiable AE can be used as a safety net to ensure any existing or future single-stage assumptions one may later need is satisfied (with the caveat of possibly weaker bounds). However, we note that for RO indifferentiability there is the additional motivation that a fair number of security proofs involving hash functions rely on modeling the hash as RO. Our work also unlocks the possibility to use the full power of random injections in a similar way (see [46] and Footnote 2).
To summarize, in the context of Facebook’s protocol, if an indifferentiable scheme was used from the start, it would have automatically met the required binding property. The same holds for RKA security (in 3GPP), KDM security (in disk encryption), and other single-stage AEAD applications.
1.3 Overview of Technical Contributions
Definitions. The MRH framework has been formulated with respect to a general class of random systems. We make this definition explicit for AEAD schemes by formulating an adequate ideal reference object. This object has been gradually emerging through the notion of a pseudorandom injection (PRI) in a number of works [41, 43, 56], and has been used to study the security of offline and online AEADs [41, 43]. We lift these notions to the indifferentiability setting by introducing offline and online random injections, which may be also keyed or tweaked. As a result, we obtain a new idealized model of computation: the ideal-encryption (or ideal-injection) model, which is intermediate between the RO and IC models. Along the way, we give an extension of the composition theorem to include game-based properties with multiple adversaries.
Analysis of known schemes. We examine generic and specific constructions of AEADs that appear in the literature. Since indifferentiability implies security in the presence of nonce-misuse (MRAE) as well as its recent strengthening to variable ciphertext stretch, RAE security,Footnote 1 we rule out the indifferentiability of a number of (classical) schemes that do not achieve these levels of security. This includes OCB [55], CCM, GCM, and EAX [13], and all but two of the third-round CAESAR candidates [14]. The remaining two candidates, AEZ [42] and DEOXYS-II [45], are also ruled out, but only using specific indifferentiability attacks. We discuss our conclusions for CAESAR submissions in [1, Sect. 4.2].
We then turn our attention to generic composition [10, 51]. We study the well-known Encrypt-then-MAC and MAC-then-Encrypt constructions via the composition patterns of Namprempre, Rogaway and Shrimpton [51]. These include Synthetic Initialization Vector (SIV) [56] and EAX [13]. To simplify and generalize the analysis, we start by presenting a template for generic composition, consisting of a preprocessing and a post-processing phase, that encompasses a number of schemes that we have found in the literature. We show that if there is an insufficient flow of information in a scheme—a notion that we formalize—differentiating attacks exist. Our attacks render all of these constructions except A8 and key reusing variants of A2 and A6 as indifferentiability candidates.
In short, contrarily to our expectations based on known results for hash functions and permutations, we could not find a well-known AEAD construction that meets the stronger notion of indifferentiability. We stress that these findings do not contradict existing security claims. However, an indifferentiability attack can point to environments in which the scheme will not offer the expected levels of security. For example, some of our differentiators stem from the fact that ciphertexts do not depend on all keying material, giving way to related-key attacks. In others, the attacks target intermediate computation values and are reminiscent of padding oracles. For these reasons, and even though our results do not single out any of the CAESAR candidates as being better or worse than the others, we pose that our results are aligned with the fundamental goal of CAESAR and prior competitions such as AES and SHA-3, to “boost to the cryptographic research community’s understanding” of the primitive [14].
Building injections. We revisit the classical Encode-then-Encipher (EtE) transform [11]. Given expansion \(\tau \), which indicates the required level of authenticity, EtE pads the input message with \(0^\tau \) and enciphers it with a variable-input-length (VIL) blockcipher. Decryption checks the consistency of the padding after recovering the message. We show that EtE is indifferentiable from a random injection in the VIL ideal-cipher model for any (possibly small) value of \(\tau \).
The ideal cipher underlying EtE can be instantiated via the Feistel construction [23] in the random-oracle model or via the confusion-diffusion construction [33] in the random-permutation model. In a series of works, the number of rounds needed for indifferentiability of Feistel has been gradually reduced from 14 [23, 44] to 10 [25, 27] and recently to 8 [28]. Due to the existence of differentiators [23, 24], the number of rounds must be at least 6. For confusion-diffusion, 7 rounds are needed for good security bounds [33]. This renders the above approach to construct random injections somewhat suboptimal in terms of queries per message block to their underlying ideal primitives (i.e., their rate).
Our main positive result is the indifferentiability of three-round Feistel for large (but variable) expansion values \(\tau \). Three rounds are also necessary, as we give a differentiator against the 2-round Feistel network for any \(\tau \). In light of the above results, and state-of-the-art 2.5-round constructions such as AEZ, this is a surprisingly small price to pay to achieve indifferentiability. Our results, therefore, support inclusion of redundancy for achieving authenticity (as opposed to generic composition). Furthermore, when using a blockcipher for encryption with redundancy, a significantly reduced number of rounds may suffice.
The simulator. Our main construction is an unbalanced 3-round Feistel network \(\mathrm {\Phi }_3\) with independent round functions where an input \(X_1\) is encoded with redundancy as \((0^\tau ,X_1)\) (see Fig. 1). The main task of our indifferentiability simulator is to consistently respond to round-function oracle queries that correspond to those that the construction makes for some (possibly unknown) input \(X_1\). We show that with overwhelming probability the simulator can detect when consistency with the construction must be enforced; the remaining isolated queries can be simulated using random and independent values.
Take, for example, a differentiator that computes \((X'_3,X'_4):={\Phi }_3(X_1)\) for some random \(X_1\), then computes the corresponding round-function outputs \(X_2:=F_1(X_1)\), \(Y_2:=F_2(X_2)\), \(Y_3:=F_3(X_1 \oplus Y_2)\), and finally checks if \((X'_3,X'_4) = (X_1 \oplus Y_2, X_2 \oplus Y_3)\). Note that these queries need not arrive in this particular order. Indeed, querying \(F_1(X_1)\) first gives the simulator an advantage as it can preemptively complete this chain of queries and use its ideal injection to give consistent responses. A better (and essentially the only) alternative for the differentiator would be to check the consistency of outputs by going through the construction in the backward direction. We show, however, that whatever query strategy is adopted by the differentiator, the simulator can take output values fixed by the ideal injection and work out answers for the round function oracles that are consistent with the construction in the real world.
A crucial part of this analysis hinges on the fact that the output of the first round function is directly fed as input to the second round function as a consequence of fixing parts of the input to \(0^\tau \).Footnote 2 As corollaries of our results we obtain efficient and (simultaneously) RKA and KDM-secure offline (and, as we shall see, online) AEAD schemes in the random-permutation model under natural, yet practically relevant restrictions on these security models. For example, if the ideal AEAD  is secure under encryptions of
is secure under encryptions of  for some oracle machine
for some oracle machine  , then so is an indifferentiable construction \(C^\pi \) in presence of encryptions of \(\phi ^{C^\pi }(K)\), the restriction being that \(\phi \) does not directly access \(\pi \).
, then so is an indifferentiable construction \(C^\pi \) in presence of encryptions of \(\phi ^{C^\pi }(K)\), the restriction being that \(\phi \) does not directly access \(\pi \).
Bounds. Security bounds, including simulator query complexity, are important considerations for practice. Our bound for the Encode-then-Encipher construction is essentially tight. Our simulator for the 3-round Feistel construction has a quadratic query complexity and overall bounds are birthday-type. Improving these bounds, or proving lower bounds for them [32], remain open for subsequent work.
Our construction of an ideal encryption scheme from a non-keyed ideal injection introduces an additional multiplicative factor related to the number of different ideal injection keys queried by the differentiator, resulting from a hybrid argument over keys. Furthermore, the number of ideal injection keys used in the construction is bound to the number of encryption and decryption operations that are carried out. This means that the overall bound for our authenticated encryption construction includes a multiplicative factor of \(q^3\) (see Sect. 5.3).
We note that the concrete constructions that we analyze may satisfy (R)AE, RKA or KDM security with improved bounds (via game-specific security analyses), while remaining compatible with the single proof and bound that we present for all single-stage games.
Online AEADs. We give simple solutions to the problem of constructing an indifferentiable segment-oriented online AEAD scheme from an offline AEAD. Following [43], we define ideal online AEAD scheme via initialization, next-segment encryption/decryption, and last-segment encryption/decryption procedures. The difference between next-segment and last-segment operations is that the former propagates state values, whereas the latter does not. Since a differentiator typically has access to all interfaces of a system, the state values become under its control/view. For this we restrict the state size of the ideal object to be finite and hence definitionally deviate from [43] in this aspect. Therefore our constructions have the extra security property that the state value hides all information about past segments.
The most natural way to construct an ideal online AEAD would be to chain encryptions of the segments by tweaking the underlying encryption primitive with the input history so far, as in the \(\mathbf {CHAIN}\) transform of HRRV [43, Fig. 8]. We show, however, that standard XOR-based tweaking techniques are not sound in the indifferentiability setting and, in particular, we present a differentiating attack on \(\mathbf {CHAIN}\). However, by decomposing the ideal object for online AEAD into simpler ones [29, 48], we recover an indifferentiable variant of the construction called \(\mathbf {HashCHAIN}\), where a random oracle is used to prepare the state for the next segment. Via optimizations specific to 3-round Feistel, we reduce overheads to a constant number of hashes per segment.
Lower bounds. The indifferentiability of Sponge [15] allows us to instantiate the round functions in 3-round Feistel with this construction and derive a random injection in the random-permutation model.Footnote 3 This construction requires roughly 3w calls to its underlying (one-block) permutation, where w is the total number of input blocks. This is slightly higher than 2.5w for AEZ (which shares some of its design principles with us, but does not offer indifferentiability). This leads us to ask whether or not an indifferentiable construction with rate less than 3 is achievable. Our second main result is a lower bound showing the impossibility of any such construction with rate (strictly) less than 2. To prove this lower bound, we combine negative results for constructions of collision-resistant hash functions [17, 58] and pseudorandom number generators by Gennaro and Trevisan [37], and put critical use to the existence of an indifferentiability simulator. To the best of our knowledge, this is the first impossibility result that exploits indifferentiability, so the proof technique may be of independent interest.
Limitations and future work. As clarified by Ristenpart, Shacham, and Shrimpton [53], the indifferentiability composition theorem may not apply to multi-stage games where multiple adversaries cannot be collapsed into a single central adversary. Indifferentiable AEAD schemes come with similar limitations.
Indifferentiability typically operates in an ideal model of computation. This leaves open the question of standard-model security. However, it does not exclude a “best of the two worlds” construction, which is both indifferentiable and is RAE secure in the standard-model. For example, chop-Merkle–Damgård [21] can be proven both indifferentiable from a random oracle and collision resistant in the standard model. We leave exploring this for future work.
2 Basic Definitions
We let \(\{0,1\}^*\) denote the set of all finite-length bit strings, including the empty string \(\varepsilon \). For bit strings X and Y, X|Y denotes concatenation and (X, Y) denotes a decodable encoding of X and Y. The length of a string X is denoted by |X|.
Games. An n-adversary game \(\mathbf {G}\) is a Turing machine  where \(\mathrm {\Sigma }\) is a system (or functionality) and
where \(\mathrm {\Sigma }\) is a system (or functionality) and  are adversarial procedures that can keep full local state but may only communicate with each other through \(\mathbf {G}\). We say an n-adversary game \(\mathbf {G}_n\) is reducible to an m-adversary game if there is a \(\mathbf {G}_m\) such that for any
are adversarial procedures that can keep full local state but may only communicate with each other through \(\mathbf {G}\). We say an n-adversary game \(\mathbf {G}_n\) is reducible to an m-adversary game if there is a \(\mathbf {G}_m\) such that for any  there are
there are  such that for all \(\mathrm {\Sigma }\) we have that
such that for all \(\mathrm {\Sigma }\) we have that  . Two games are equivalent if they are reducible in both directions. An n-adversary game is called n-stage [53] if it is not equivalent to any m-adversary game with \(m < n\). Any single-stage game
. Two games are equivalent if they are reducible in both directions. An n-adversary game is called n-stage [53] if it is not equivalent to any m-adversary game with \(m < n\). Any single-stage game  can be also written as
can be also written as  for some oracle machine \(\overline{\mathbf {G}}\) and a class of adversarial procedures
for some oracle machine \(\overline{\mathbf {G}}\) and a class of adversarial procedures  compatible with a modified syntax in which the game is called as an oracle.
compatible with a modified syntax in which the game is called as an oracle.
Reference objects. Underlying the security definition for a cryptographic primitive there often lies an ideal primitive that is used as a reference object to formalize security. For instance, the security of PRFs is defined with respect to a random oracle, PRPs with respect to an ideal cipher, and as mentioned above, AEADs with respect to a random injection. Given the syntax and the correctness condition of a cryptographic primitive, we will define its ideal counterpart as the uniform distribution over the set of all functions that meet these syntactic and correctness requirements (but without any efficiency requirements). We start by formalizing a general class of ideal functions—that may be keyed, admit auxiliary data (such as nonces or authenticated data), or allow for variable-length outputs—and derive distributions of interest to us by imposing structural restrictions over the class of considered functions. This approach has also been used in [16].
Ideal functions. A variable-output-length (VOL) function  with auxiliary input has signature
with auxiliary input has signature  , where
, where  is the auxiliary-input space,
is the auxiliary-input space,  is the message space,
is the message space,  is the expansion space, and
is the expansion space, and  is the range. We let
is the range. We let  be the set of all such functions satisfying
be the set of all such functions satisfying  , We endow the above set with the uniform distribution and denote the action of sampling a uniform function
, We endow the above set with the uniform distribution and denote the action of sampling a uniform function  via
via  (and analogously for expanding functions). To ease notation, given a function
(and analogously for expanding functions). To ease notation, given a function  , we define
, we define  to be the set of all functions with signature identical to that of
to be the set of all functions with signature identical to that of  . Granting oracle access to
. Granting oracle access to  to all parties (honest or otherwise) results in an ideal model of computation.
to all parties (honest or otherwise) results in an ideal model of computation.
Injections. We define  to be the set of all expanding functions that are injective on
to be the set of all expanding functions that are injective on  :
:  , and satisfy the length restriction
, and satisfy the length restriction  . Each injective function defines a unique inverse function
. Each injective function defines a unique inverse function  that maps \((A,C,\tau )\) to either a unique M if and only if C is within the range of
that maps \((A,C,\tau )\) to either a unique M if and only if C is within the range of  , or to \(\perp \) otherwise. (Such functions are therefore tidy in the sense of [51].) This gives rise to a strong induced model for injections where oracle access is extended to include
, or to \(\perp \) otherwise. (Such functions are therefore tidy in the sense of [51].) This gives rise to a strong induced model for injections where oracle access is extended to include  , which we always assume to be the case when working with injections.
, which we always assume to be the case when working with injections.
When \(k=0\) the key space contains the single \(\varepsilon \) key and we recover unkeyed functions. We use the following abbreviations: \(\mathrm {Fun}[n,m]\) is the set of functions mapping n bits to m bits and \(\mathrm {Perm}[n]\) is the set of permutations over n bits.
Lazy samplers. Various ideal objects (such as random oracles) often appear as algorithmic procedures that lazily sample function values at each point. These procedures can be extended to admit auxiliary data and respect either of our length-expansion requirements above. Furthermore, given a list L of input-output pairs, these samplers can be modified to sample a function that is also consistent with the points defined in L (i.e., the conditional distribution given L is also samplable). We denote the lazy sampler for random oracles with  and that for ideal ciphers with
and that for ideal ciphers with  . The case of random injection is less well known, but such a procedure appears in [56, Fig. 6]. We denote this sampler with
. The case of random injection is less well known, but such a procedure appears in [56, Fig. 6]. We denote this sampler with  .
.
2.1 Authenticated-Encryption with Associated-Data
We follow [43] in formalizing the syntax of (offline) AEAD schemes.Footnote 4 We allow for arbitrary plaintexts and associated data, and also include an explicit expansion parameter \(\tau \) specifying the level of authenticity. Associated data may contain information that may be needed in the clear by a higher-level protocol that nevertheless should be authentic. We also only allow for public nonces as the benefits of the AE5 syntax with a private nonce are unclear [50].
Syntax and correctness. An AEAD scheme is a triple of algorithms  where: (1)
where: (1)  is the randomized key-generation algorithm which returns a key K. This algorithm defines a non-empty set, the support of
is the randomized key-generation algorithm which returns a key K. This algorithm defines a non-empty set, the support of  , and an associated distribution on it. Slightly abusing notation, we denote all these by
, and an associated distribution on it. Slightly abusing notation, we denote all these by  . (2)
. (2)  is the deterministic encryption algorithm with signature
is the deterministic encryption algorithm with signature  . Here
. Here  is the nonce space,
is the nonce space,  is the associated data space, and
is the associated data space, and  is the set of allowed expansion values. We typically have that
is the set of allowed expansion values. We typically have that  ,
,  for \(k, n \in \mathbb {N}\),
for \(k, n \in \mathbb {N}\),  , and the expansion space contains a single value. (3)
, and the expansion space contains a single value. (3)  is the deterministic decryption algorithm with signature
is the deterministic decryption algorithm with signature  . As usual we demand that
. As usual we demand that  for all inputs from the appropriate spaces. We also impose the ciphertext expansion restriction that for all inputs from the appropriate spaces
for all inputs from the appropriate spaces. We also impose the ciphertext expansion restriction that for all inputs from the appropriate spaces  .
.
Ideal AEAD. An ideal AEAD is an injection with signature  and satisfying the ciphertext-expansion restriction. Therefore an ideal AEAD is a random injection in
and satisfying the ciphertext-expansion restriction. Therefore an ideal AEAD is a random injection in  . Given a concrete AEAD scheme \({\Pi }\) with signature
. Given a concrete AEAD scheme \({\Pi }\) with signature  we associate the space
we associate the space  to it.
to it.
Naming conventions. When referring to AEAD schemes we use  instead of
instead of  . When the associated-data space is empty, we use
. When the associated-data space is empty, we use  for (encryption without associated data), when the nonce space is also empty we use
for (encryption without associated data), when the nonce space is also empty we use  (for keyed injection), when \(\tau =0\) as well we use \((\mathsf {E},\mathsf {E}^{-})\) (for blockcipher), and if these are also unkeyed we use \((\rho ,\rho ^{-})\) and \((\pi ,\pi ^{-})\) respectively. For a random function (without inverse) we use
(for keyed injection), when \(\tau =0\) as well we use \((\mathsf {E},\mathsf {E}^{-})\) (for blockcipher), and if these are also unkeyed we use \((\rho ,\rho ^{-})\) and \((\pi ,\pi ^{-})\) respectively. For a random function (without inverse) we use  .
.
RAE security. Robust AE (RAE) security [41, 43] requires that an AEAD scheme behaves indistinguishably from an ideal AEAD under a random key. Formally, for scheme  and adversary
and adversary  we define
we define

where games  and
and  are defined in Fig. 2. Informally, we say \({\Pi }\) is RAE secure if
are defined in Fig. 2. Informally, we say \({\Pi }\) is RAE secure if  is “small” for any “reasonable”
is “small” for any “reasonable”  . Misuse-resilient AE (MRAE) security [56] weakens RAE security by constraining the adversary to a fixed and sufficiently large value of expansion \(\tau \). AE security [54] weakens MRAE security and requires that the adversary does not repeat nonces in its queries to either oracle. These definitions lift to idealized models of computation where, for example, access to an ideal injection in both the forward and backward directions is provided.
. Misuse-resilient AE (MRAE) security [56] weakens RAE security by constraining the adversary to a fixed and sufficiently large value of expansion \(\tau \). AE security [54] weakens MRAE security and requires that the adversary does not repeat nonces in its queries to either oracle. These definitions lift to idealized models of computation where, for example, access to an ideal injection in both the forward and backward directions is provided.
The proposition below formalizes the intuition that the ideal AEAD, i.e., the trivial AEAD scheme in the ideal AEAD model, is RAE secure. This fact will be used when studying the relation between indifferentiability and RAE security. The proof follows from the fact that unless the attacker can discover the secret key, the construction oracle behaves independently from the ideal AEAD oracle.
Proposition 1
(Ideal AEAD is RAE secure). For any q-query adversary  attacking the trivial ideal AEAD \({\Pi }\) in the ideal AEAD model we have that
attacking the trivial ideal AEAD \({\Pi }\) in the ideal AEAD model we have that  .
.
3 AEAD Indifferentiability
The indifferentiability framework of Maurer, Renner, and Holenstein (MRH) [48] formalizes a set of necessary and sufficient conditions for one system to securely replace another in a wide class of environments. This framework has been successfully used to justify the structural soundness of a number of cryptographic constructions, including hash functions [21, 31], blockciphers [4, 23, 33], and domain extenders for them [22]. The indifferentiability framework is formulated with respect to general systems. When the ideal AEAD object defined in Sect. 2.1 is used, a notion of indifferentiability for AEAD schemes emerges. In this section, we recall indifferentiability of systems and make it explicit for AEAD schemes. We will then discuss some of its implications that motivate our work.
3.1 Definition
A random system or functionality \(\mathrm {\Sigma }:=(\mathrm {\Sigma }{.}\mathrm {hon},\mathrm {\Sigma }{.}\mathrm {adv})\) is accessible via two interfaces \(\mathrm {\Sigma }{.}\mathrm {hon}\) and \(\mathrm {\Sigma }{.}\mathrm {adv}\). Here, \(\mathrm {\Sigma }{.}\mathrm {hon}\) provides a public interface through which the system can be accessed. \(\mathrm {\Sigma }{.}\mathrm {adv}\) corresponds to a (possibly extended) interface that models adversarial access to the inner workings of the system, which may be exploited during an attack on constructions. A system typically implements some ideal object  , or it is itself a construction
, or it is itself a construction  relying on some underlying (lower-level) ideal object
relying on some underlying (lower-level) ideal object  .
.
Indifferentiability [48]. Let \(\mathrm {\Sigma }_1\) and \(\mathrm {\Sigma }_2\) be two systems and  be an algorithm called the simulator. The (strong) indifferentiability advantage of a (possibly unbounded) differentiator
be an algorithm called the simulator. The (strong) indifferentiability advantage of a (possibly unbounded) differentiator  against \((\mathrm {\Sigma }_1,\mathrm {\Sigma }_2)\) with respect to
against \((\mathrm {\Sigma }_1,\mathrm {\Sigma }_2)\) with respect to  is
is

where games  and
and  are defined in Fig. 3. Informally, we call \(\mathrm {\Sigma }_1\) indifferentiable from \(\mathrm {\Sigma }_2\) if, for an “efficient”
are defined in Fig. 3. Informally, we call \(\mathrm {\Sigma }_1\) indifferentiable from \(\mathrm {\Sigma }_2\) if, for an “efficient”  , the advantage above is “small” for all “reasonable”
, the advantage above is “small” for all “reasonable”  .
.
In the rest of the paper we consider a specific application of this definition to two systems with interfaces  and
and  , where
, where  and
and  are two ideal cryptographic objects sampled from their associated distributions and
are two ideal cryptographic objects sampled from their associated distributions and  is a construction of
is a construction of  from
from  . To ease notation, we denote the advantage function by
. To ease notation, we denote the advantage function by  when
when  and
and  are clear from context. Typically
are clear from context. Typically  will be an ideal AEAD and
will be an ideal AEAD and  a random oracle or an ideal cipher.
a random oracle or an ideal cipher.
3.2 Consequences
MRH [48] prove the following composition theorem for indifferentiable systems. Here we state a game-based formulation from [53].
Theorem 1
(Indifferentiability composition). Let  and
and  be two indifferentiable systems with simulator
be two indifferentiable systems with simulator  . Let \(\mathbf {G}\) be a single-stage game. Then for any adversary
. Let \(\mathbf {G}\) be a single-stage game. Then for any adversary  there exist an adversary
there exist an adversary  and a differentiator
and a differentiator  such that
such that

As discussed in [53], the above composition does not necessarily extend to multi-stage games since the simulator often needs to keep local state in order to guarantee consistency. However, some (seemingly) multi-stage games can be written as equivalent single-stage games (see Sect. 2 for a definition of game equivalence). Indeed, any n-adversary game where only one adversary can call the primitive directly and the rest call it indirectly via the construction can be written as a single-stage game as the game itself has access to the construction. We summarize this observation in the following theorem, which generalizes a result for related-key security in [35].
Theorem 2
Let  and
and  be two indifferentiable systems with simulator
be two indifferentiable systems with simulator  . Let \(\mathbf {G}\) be an n-adversary game and
. Let \(\mathbf {G}\) be an n-adversary game and  be an n-tuple of adversaries where
be an n-tuple of adversaries where  can access
can access  but
but  for \(i>1\) can only access
for \(i>1\) can only access  . Then there is an n-adversary
. Then there is an n-adversary  and a differentiator
and a differentiator  such that
such that

Remark 1
There is a strong practical motivation for the restriction imposed on the class of games above. Consider, for example, security against related-key attacks (RKAs) where the related-key deriving (RKD) function  may depend on the ideal primitive [3]. The RKA game is not known to be equivalent to a single-stage game. The authors in [35] consider a restricted form of this game where dependence of \(\phi \) on the ideal primitive
may depend on the ideal primitive [3]. The RKA game is not known to be equivalent to a single-stage game. The authors in [35] consider a restricted form of this game where dependence of \(\phi \) on the ideal primitive  is constrained to be through the construction
is constrained to be through the construction  only. In other words, an RKD function takes the form
only. In other words, an RKD function takes the form  rather than
rather than  . When comparing the RKA security of a construction
. When comparing the RKA security of a construction  to the RKA security of its ideal counterpart, one would expect the set of RKD functions from which \(\phi \) is drawn in two games to be syntactically fixed and hence comparable. Since no underlying ideal primitive for
to the RKA security of its ideal counterpart, one would expect the set of RKD functions from which \(\phi \) is drawn in two games to be syntactically fixed and hence comparable. Since no underlying ideal primitive for  exists, RKD functions take the form
exists, RKD functions take the form  and hence it is natural to consider RKD functions of the form
and hence it is natural to consider RKD functions of the form  with respect to
with respect to  . The same line of reasoning shows that an indifferentiable construction would resist key-dependent message (KDM) attacks for key-dependent deriving functions that depend on the underlying ideal primitive via the construction only. Other (multi-stage) security notions that have a practically relevant single-stage formulation include security against bad-randomness attacks, where malicious random coins are computed using the construction, and leakage-resilient encryption where leakage functions may rely on the construction. Therefore from a practical point of view, composition extends well beyond 1-adversary games.
. The same line of reasoning shows that an indifferentiable construction would resist key-dependent message (KDM) attacks for key-dependent deriving functions that depend on the underlying ideal primitive via the construction only. Other (multi-stage) security notions that have a practically relevant single-stage formulation include security against bad-randomness attacks, where malicious random coins are computed using the construction, and leakage-resilient encryption where leakage functions may rely on the construction. Therefore from a practical point of view, composition extends well beyond 1-adversary games.
Remark 2
Theorem 1 reduces the security of one system to that of another. For instance, one can deduce the RKA (resp., KDM or leakage-resilient) security of an indifferentiable construction  of
of  if
if  itself can be proven to be RKA (resp., KDM or leakage-resilient) secure. We have seen an example of the latter in Proposition 1, where the ideal AEAD scheme is shown to be RAE secure. Hence Theorem 1 and Proposition 1 immediately allow us to deduce that an indifferentiable AEAD construction
itself can be proven to be RKA (resp., KDM or leakage-resilient) secure. We have seen an example of the latter in Proposition 1, where the ideal AEAD scheme is shown to be RAE secure. Hence Theorem 1 and Proposition 1 immediately allow us to deduce that an indifferentiable AEAD construction  will be RAE secure in the idealized model of computation induced by its underlying ideal primitive
will be RAE secure in the idealized model of computation induced by its underlying ideal primitive  . Analogous propositions for RKA, KDM, leakage resilience of the ideal AEAD scheme (for quantified classes of related-key deriving functions, key-dependent deriving, and leakage functions) can be formulated. This in turn implies that an indifferentiable AEAD scheme will resist strong forms of related-key, KDM, and leakage attacks.
. Analogous propositions for RKA, KDM, leakage resilience of the ideal AEAD scheme (for quantified classes of related-key deriving functions, key-dependent deriving, and leakage functions) can be formulated. This in turn implies that an indifferentiable AEAD scheme will resist strong forms of related-key, KDM, and leakage attacks.
4 Differentiators
Having defined AEAD indifferentiability, we ask whether or not (plausibly) indifferentiable constructions of AEAD schemes in the literature exist. In this section we present a number of generic and specific attacks that essentially rule out the indifferentiability of many constructions that we have found in the literature. We emphasize that existing schemes were not designed with the goal of meeting indifferentiability, and our attacks do not contradict any security claims made under the standard RAE, MRAE, or AE models. Indeed, many AEAD schemes are designed with the goal of maximizing efficiency, forsaking stronger security goals such as misuse resilience or robustness.
4.1 Generic Composition
Any construction that is not (M)RAE secure (in the sense of [41, 56]) can be immediately excluded as one that is indifferentiable: the ideal AEAD is RAE secure (Proposition 1), furthermore RAE is a single-stage game and hence implied by indifferentiability (Theorem 1). This simple observation rules out the indifferentiability of a number notable AEAD schemes such as OCB [55], CCM, GCM, EAX [13], and many others. The MRAE insecurity of these schemes are discussed in the respective works.
RAE insecurity can be used to also rule out the indifferentiability of some generic AEAD constructions. In this section, we present a more general result by giving differentiators against a wide class of generically composed schemes, some of which have been proven to achieve RAE security. This class consists of schemes built from a hash function  , which we treat as a random oracle, and an encryption scheme
, which we treat as a random oracle, and an encryption scheme  , which we consider to be an ideal AEAD without associated data. We assume that the encryption algorithm of the composed scheme operates as follows. An initialization procedure
, which we consider to be an ideal AEAD without associated data. We assume that the encryption algorithm of the composed scheme operates as follows. An initialization procedure  is used to prepare the inputs to a preprocessing algorithm
is used to prepare the inputs to a preprocessing algorithm  and a post-processing algorithm
and a post-processing algorithm  . The preprocessing algorithm prepares the inputs to the underlying
. The preprocessing algorithm prepares the inputs to the underlying  algorithm. The post-processing algorithm gets the output ciphertext and completes encryption (e.g., by appending a tag value). The decryption algorithm operates analogously by reversing this process via an initialization procedure
algorithm. The post-processing algorithm gets the output ciphertext and completes encryption (e.g., by appending a tag value). The decryption algorithm operates analogously by reversing this process via an initialization procedure  , a preprocessing algorithm
, a preprocessing algorithm  and a post-processing algorithm
and a post-processing algorithm  . See Fig. 4 for the details.
. See Fig. 4 for the details.
The next theorem shows that this class of schemes are differentiable if certain conditions on information passed between the above sub-procedures are met.
Theorem 3
(Differentiability of generic composition). Let \({\Pi }\) be a generically composed AEAD scheme from an encryption scheme (without associated data)  and a hash function
and a hash function  following the structure shown in Fig. 4 for some algorithms
following the structure shown in Fig. 4 for some algorithms  . Let \(\varDelta _C:=|C|-|C'|\) denote the ciphertext overhead. Suppose that the following condition holds.
. Let \(\varDelta _C:=|C|-|C'|\) denote the ciphertext overhead. Suppose that the following condition holds.
-
Type-I: Let \(est_1\) be the state passed to
 . We require that for all inputs (K, N, A, M) and for a sufficiently large \(\varDelta _1\) we have that \(|(K,N,A,M)| - |est_1| \ge \varDelta _1\).Footnote 5 Furthermore, there is a recovery algorithm
. We require that for all inputs (K, N, A, M) and for a sufficiently large \(\varDelta _1\) we have that \(|(K,N,A,M)| - |est_1| \ge \varDelta _1\).Footnote 5 Furthermore, there is a recovery algorithm 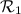 (with no oracle access) that on input C recovers \(C'\), the internal ciphertext output by
(with no oracle access) that on input C recovers \(C'\), the internal ciphertext output by  .
.
Then \({\Pi }\) is differentiable. More precisely, for any type-I scheme \({\Pi }\) there exists a differentiator  such that for any simulator
such that for any simulator  making at most q queries in total to its ideal AEAD oracles
making at most q queries in total to its ideal AEAD oracles

The complete version of this theorem in [1, Sect. 4.1] covers also type-II schemes, where decryption omits \(\varDelta _2\) bits of information about (K, N, A, C) from the partial information used to recover plaintexts.
Proof
We give the proof for type-I schemes. The differentiator computes a ciphertext for a random set of inputs using the construction in the forward direction and then checks if the result matches that computed via the generic composition using the provided primitive oracles. To rule out the existence of successful simulators the differentiator must ensure that it does not reveal information that allows the simulator to use its ideal construction oracles to compute a correct ciphertext. The restriction on the size of \(est_1\) (and the ability to recompute the internal ciphertext \(C'\) via  ) will be used to show this. The pseudocode for the differentiator, which we call
) will be used to show this. The pseudocode for the differentiator, which we call  , is shown in Fig. 4 (left). The attack works for any given value of \(\tau \) and to simplify the presentation, we have assumed all spaces consist of bit strings of length n.
, is shown in Fig. 4 (left). The attack works for any given value of \(\tau \) and to simplify the presentation, we have assumed all spaces consist of bit strings of length n.
Analysis of  . It is easy to see that when
. It is easy to see that when  is run in the real world its output will be always 1. This follows from the fact that
is run in the real world its output will be always 1. This follows from the fact that  will correctly recover the internal ciphertext \(C'\) and hence
will correctly recover the internal ciphertext \(C'\) and hence  , being run with respect to correct inputs and hash oracle, will also output C.
, being run with respect to correct inputs and hash oracle, will also output C.
We now consider the ideal world. We first modify the ideal game so that the ideal object presented to the simulator is independent of that used to answer construction queries placed by the differentiator. This game is identical to the ideal world unless  queries the forward construction oracle on \((K,N,A,M,\tau )\) (call this event \(E_1\)) or the backward construction oracle on \((K,N,A,C,\tau )\) (call this event \(E_2\)). We will bound the probability of each of these events momentarily. In the modified game, we claim that no algorithm
queries the forward construction oracle on \((K,N,A,M,\tau )\) (call this event \(E_1\)) or the backward construction oracle on \((K,N,A,C,\tau )\) (call this event \(E_2\)). We will bound the probability of each of these events momentarily. In the modified game, we claim that no algorithm  can compute C from \((C',est_1)\). This is the only information about C that is revealed to a simulator and this claim in particular means that running
can compute C from \((C',est_1)\). This is the only information about C that is revealed to a simulator and this claim in particular means that running  within
within  won’t output the correct C either. The answers to oracle queries placed by
won’t output the correct C either. The answers to oracle queries placed by  can be computed independently of the ideal construction oracles. Furthermore, \((C',est_1)\) misses at least \(\varDelta _C\) bits of information about C as \(est_1\) is computed independently of C. The simulator therefore has at most a probability of \(1/2^{\varDelta _C}\) of outputting C in this game. The bound in the theorem statement follows from a simple analysis of the probabilities of events \(E_1\) and \(E_2\) in the modified game.
can be computed independently of the ideal construction oracles. Furthermore, \((C',est_1)\) misses at least \(\varDelta _C\) bits of information about C as \(est_1\) is computed independently of C. The simulator therefore has at most a probability of \(1/2^{\varDelta _C}\) of outputting C in this game. The bound in the theorem statement follows from a simple analysis of the probabilities of events \(E_1\) and \(E_2\) in the modified game.
The proof for type-II schemes follows along the same lines and yields similar bounds. The full details for schemes of both types are given in [1, Sect. 4.1]. \(\square \)
Consequences for generic composition. Namprempre, Rogaway, and Shrimpton [51] explore various methods to generically compose an AEAD scheme from a nonce-based AE scheme (without associated data) and a MAC. In their analysis the authors single out eight favored schemes A1–A8. Roughly speaking, schemes A1, A2, and A3 correspond to Encrypt-and-MAC where, respectively, N, (N, A), and (N, A, M) are used in the preparation of the input IV to the base AE scheme. Scheme A4 is the Synthetic Initialization Vector (SIV) mode of operation [56, Fig. 5], which is misuse resilient. Schemes A5 and A6 correspond to Encrypt-then-MAC, where IV is computed using N and (N, A), respectively. Schemes A7 and A8 correspond to MAC-then-Encrypt, where IV is computed using N and (N, A) respectively. The MAC component in all these schemes is computed over (N, A, M). Key L is used for IV and MAC generation, and an independent key K is used in encryption. We refer the reader to the original paper [51, Fig. 2] for further details. For convenience, we have also included the diagrams for the A (as well as B and N) schemes in [1, Appendix A] with the authors’ permission.
In [1, Sect. 4.1] we give an analysis of how each of these schemes, as well as all the others discussed in [56], are affected by the generic attacks given in Theorem 3. We find that all A schemes except A8 (which generalizes the structure of the constructions we give in the next section) are differentiable. When looking at the same schemes but assuming that the encryption and authentication keys are identical (i.e., under key reuse), schemes A2, A6, and A8 no longer fall prey to our generic attacks. We leave analyzing their indifferentiability as an open problem. Finally, all B-schemes and N-schemes are found to be differentiable as well. In the literature, we also found a recent scheme called Robust Initialization Vector (RIV) [2] that is MRAE secure and bears similarities to our constructions. We show in [1, Appendix C] that RIV is type-I and hence differentiable.
5 Ideal Offline AEAD
We now give two constructions of ideal AEAD from simpler ideal primitives. The first is based on a VIL blockcipher, it enjoys a simpler analysis and supports any expansion \(\tau \). The second is based on the unbalanced 3-round Feistel network, where round functions are alternatively compressing and expanding random oracles. It achieves higher efficiency, but here \(\tau \) must be sufficiently large.
We present our proofs in a modular way. We first build ideal AEADs that achieve indifferentiability in a restricted setting where all parameters except the input message are fixed. More precisely, we first show that there is a simulator  that for any arbitrary but fixed value of \(K':=(K,N,A,\tau )\) is successful against all differentiators that are \(K'\)-bound in the sense that they only query the construction and primitive oracles on values specified by \(K'\). To this end, we also begin with the simplifying assumption that the underlying ideal objects can be keyed with keys of arbitrary length. We then show how these restrictions and simplifying assumptions can be removed to obtain fully indifferentiable AEADs.
that for any arbitrary but fixed value of \(K':=(K,N,A,\tau )\) is successful against all differentiators that are \(K'\)-bound in the sense that they only query the construction and primitive oracles on values specified by \(K'\). To this end, we also begin with the simplifying assumption that the underlying ideal objects can be keyed with keys of arbitrary length. We then show how these restrictions and simplifying assumptions can be removed to obtain fully indifferentiable AEADs.
5.1 Indifferentiability of Encode-then-Encipher
Our first construction transforms a VIL ideal cipher with arbitrary key space into an ideal AEAD. It follows the Encode-then-Encipher (EtE) transform of Bellare and Rogaway [11]. In its most simple form, EtE fixes \(\tau \) bits of the input to \(0^\tau \) and checks the correctness of the included redundancy upon inversion (see Fig. 5).Footnote 6 The domain of the underlying blockcipher should therefore be at least \(\tau \) bits longer than that needed for the injection. This, in particular, is the case when both objects have variable input lengths. The results of this section (in contrast to the attacks against other generic schemes) support the soundness of EtE-based schemes from an indifferentiability perspective.
Theorem 4
(EtE is indifferentiable). The EtE construction in Fig. 5 is indifferentiable from an ideal AEAD for any fixed \(K':=(K,N,A,\tau )\) when instantiated with a VIL ideal cipher \((\mathsf {E},\mathsf {E}^{-})\). More precisely, there is an expected 4q-query simulator  that presents a perfect simulation of the underlying permutation for any \(K'\)-bound q / 2-query differentiator
that presents a perfect simulation of the underlying permutation for any \(K'\)-bound q / 2-query differentiator  for \(q/2 \le 2^{n+\tau }/8\).
for \(q/2 \le 2^{n+\tau }/8\).
Proof
(Sketch). Since the key values are fixed, we denote \((\mathsf {E},\mathsf {E}^{-})\) with \((\rho ,\rho ^-)\), an unkeyed VIL random injection. The simulator will simulate the permutation on inputs of the form \(0^\tau |M\) via the ideal AEAD oracle \(\rho \) and will use a lazily sampled injection disjoint from \(\rho \) (i.e., one whose domain and range are disjoint from those of \(\rho \)) for inputs of the form T|M with \(T\ne 0^\tau \). The simulator can always detect when a query must be consistent with the ideal AEAD oracle: such queries will always correspond to inputs of the form \(0^\tau |M\) in forward queries and outputs that are invertible under \(\rho ^{-}\) in backward queries. All other queries are answered by lazily sampling the disjoint injection. However, in order to offer a perfect simulation, the simulator must condition this lazy sampling by rejecting any sampled inverses of the form \(0^\tau |M\) and sampled outputs that are invertible under \(\rho ^{-}\). This rejection sampling yields a simulator that runs in expected polynomial time as stated in the theorem. This simulator can be converted into one that runs in strict polynomial time in the standard way by capping the number of samples to t tries. With \(q \le 2^{n+\tau }/4\), this simulator fails with probability at most \((2/3)^t\) for each differentiator query, and hence introduces a statistical distance of \(q(2/3)^t\). The full proof and the simulator are given in [1, Sect. 5.1]. \(\square \)
5.2 Indifferentiability of 3-round Feistel
A variable-input-length (VIL) permutation can be constructed via the Feistel construction [23] from a VIL/VOL random oracle, or via the confusion-diffusion construction [33] from a fixed-input-length (FIL) random permutation.Footnote 7 The number of rounds needed for indifferentiability of Feistel from an ideal cipher has been gradually reduced to 8 [28]; whereas for confusion-diffusion 7 rounds are needed for good security bounds [33]. This state of affairs leaves the above approach to the design of random injections somewhat suboptimal in terms of the number of queries per message block to a random permutation.
We ask whether this rate can be improved for random injections. We start from the observation that indifferentiability attacks against 5-round Feistel do not necessarily translate to those that fix parts of the input to \(0^\tau \). Despite this, we show that differentiating attacks against 2-round Feistel still exist.
Proposition 2
(Differentiability of 2-round Feistel). The 2-round unbalanced Feistel construction \(\mathrm {\Phi }_2\) (cf. Fig. 1) with the left part of the input fixed to \(0^\tau \) is differentiable from an ideal injection.
Proof
(Sketch). Consider the differentiator  in Fig. 6 that checks the consistency of simulated output against the construction on a random input X. In the real world,
in Fig. 6 that checks the consistency of simulated output against the construction on a random input X. In the real world,  will output 1 with probability 1. In the ideal world the simulator has to guess value \(Y_2\), which it won’t be able to do except with probability negligible in n as the query placed by
will output 1 with probability 1. In the ideal world the simulator has to guess value \(Y_2\), which it won’t be able to do except with probability negligible in n as the query placed by  is hidden from its view. \(\square \)
is hidden from its view. \(\square \)
The simplicity of the above attack and the necessity for large number of rounds in building indifferentiable permutations raise the undesirable possibility that many rounds would also be needed for building random injections. We show, perhaps surprisingly, that this is not the case and adding only one extra round results in indifferentiability as long as \(\tau \) and the input size are sufficiently large. This means, somewhat counter-intuitively, that the efficiency of constructions of ideal injections can be increased when a higher level of security is required. The 3-round Feistel construction and variable names are shown in Fig. 1.
We present the more intricate part of the proof of the following theorem in the code-based game-playing framework [12] to help its readability and verifiability.
Theorem 5
(Indifferentiability of 3-round Feistel). Take the 3-round Feistel construction \(\mathrm {\Phi }_3\) shown in Fig. 1 when it is instantiated with three independent keyed random oracles (the round functions are all keyed with the same key). This construction is indifferentiable from an ideal AEAD scheme for any fixed key of the form \(K':=(K,N,A,\tau )\). More precisely, there is a simulator  such that for all \((q_{e},q_{d},q_1,q_2,q_3)\)-query \(K'\)-bound differentiators
such that for all \((q_{e},q_{d},q_1,q_2,q_3)\)-query \(K'\)-bound differentiators  with \(q_{e} + q_{d} + 2 q_1 + q_2 + q_3\le q\) we have
with \(q_{e} + q_{d} + 2 q_1 + q_2 + q_3\le q\) we have

as long as \(q_2 (q_1 + q_2 + q_3) \le 2^{n+\tau }/2\) and \(q_{e} + q_1 \le 2^{n}/2\). The simulator places at most \(q^2\) queries to its oracles.
Proof
To make the notation lighter we omit the key input to the various ideal objects (as we are dealing with \(K'\)-bound differentiators) and indicate forward/backward queries to the construction or ideal AEAD by \(C/C^{-}\), and queries to the real or simulated round functions by \(F_1\), \(F_2\), and \(F_3\). To simplify the analysis, we consider a restricted class of differentiators that (1) query \(C(X_1)\) before any query \(F_1(X_1)\), and (2) never query \(C^{-}\). We also call a simulator C-respecting if it calls C only when simulating \(F_1(X_1)\), in which case it places a single query \(C(X_1)\). The following lemma deals with this simplification.
Lemma 1
(Restricting  ). For any \((q_{e},q_{d},q_1,q_2,q_3)\)-query differentiator
). For any \((q_{e},q_{d},q_1,q_2,q_3)\)-query differentiator  there is a restricted \((q_{e}+q_1,0,q_1,q_2,q_3)\)-query differentiator
there is a restricted \((q_{e}+q_1,0,q_1,q_2,q_3)\)-query differentiator  such that for any C-respecting simulator
such that for any C-respecting simulator  , and as long as \(q_{e}+q_1 \le 2^{n}/2\), we have
, and as long as \(q_{e}+q_1 \le 2^{n}/2\), we have

We give the proof of this auxilliary lemma in [1, Sect. 5.2]. Intuitively, we can convert any distinguisher  into a restricted
into a restricted  that always calls the construction before it answers a query to \(F_1\) and intercepts all queries to the inverse construction oracle and returns \(\perp \) if the queried value was never computed by the construction in the forward direction. The lemma follows from bounding the probability that
that always calls the construction before it answers a query to \(F_1\) and intercepts all queries to the inverse construction oracle and returns \(\perp \) if the queried value was never computed by the construction in the forward direction. The lemma follows from bounding the probability that  provides a wrong answer in either world. The C-respecting restriction is used to upper-bound the total number of forward construction queries in the ideal world (including simulator calls).
provides a wrong answer in either world. The C-respecting restriction is used to upper-bound the total number of forward construction queries in the ideal world (including simulator calls).
We prove indifferentiability with respect to restricted differentiators via a sequence of games as follows. We start with the real game, which includes oracles for the construction and the round functions, and gradually modify the implementations of these oracles until: (1) the construction no longer places any queries to the round functions and is implemented as an ideal injection; and (2) the round functions use this (ideal) construction oracle. We now describe these games. We give the pseudocode in Figs. 7 and 8.
- \(\mathbf {G}_0\)::
-
This game is identical to the (restricted) real game. Here the construction oracle C calls \(F_1\), \(F_2\) and \(F_3\) and adds entries to lists \(L_1\), \(L_2\), and \(L_3\).
- \(\mathbf {G}_1\)::
-
This game introduces \(\mathsf {flag}_1\). The game sets \(\mathsf {flag}_1\) if \(F_1\) chooses an output value that was already queried to \(F_2\). As we will see, we can easily bound the probability of this flag getting set via the birthday bound.Footnote 8
- \(\mathbf {G}_2\)::
-
This game explicitly samples fresh values that are added to \(L_1\) and \(L_2\) as a result of a non-repeat query \(X_1\) to C within the code of C rather than under the corresponding round functions. This is a conceptual modification and the game is identical to \(\mathbf {G}_1\). Indeed, the sampled \(L_1\) entry is always guaranteed to be fresh assuming a non-repeat value \(X_1\), and the \(L_2\) entry will be also non-repeat or \(\mathsf {flag}_1\) is set. List \(L_C\) is used to deal with repeat queries and avoid spurious samplings.
- \(\mathbf {G}_3\)::
-
This game introduces a (conceptual) change of random variables. Instead of choosing \(Y_1\) and \(Y_2\) (i.e., the outputs of \(F_1\) and \(F_2\)) randomly and computing the outputs \((X_3,X_4)\) of the construction, it first chooses \((X_3,X_4)\) and sets \(Y_1\) and \(Y_2\) based on these, the input, and \(Y_3\). This is done via a linear change of variables that will not affect the distributions of \(Y_1\) and \(Y_2\), as we show below. This game constitutes our first step in constructing the simulator by defining the outputs of \(F_1\) and \(F_2\) in terms of those for C. The proof, however, is not yet complete: although C is implemented independently of the round functions, \(F_2\) and \(F_3\) need access to the list of queries made to C.
- \(\mathbf {G}_4\)::
-
This game removes \(\mathsf {flag}_1\) (which allowed the previous transitions to be carried out in a conservative way) as we wish to gradually construct the code of the simulator, and this code is not needed in the final simulation.Footnote 9
- \(\mathbf {G}_5\)::
-
This game shifts most of the code from the C oracle to the \(F_1\) oracle. In particular, the manipulations of \(L_1\) and \(L_2\) are now done within \(F_1\). The outputs of C are still sampled within the construction procedure and C makes a call to \(F_1\). Procedure \(F_1\) retrieves the necessary \((X_3,X_4)\) values by calling back the construction (note these are now added to \(L_C\) prior to calling \(F_1\)). This modification is conceptual since (1) restricted differentiators always call the construction oracle before calling \(F_1\) and hence the entry for \(X_1\) will already be in the list \(L_C\), and (2) although some queries to \(F_2\) and \(F_3\) may no longer be done, these oracles behave as random oracles and hence performing such queries earlier or later does not affect the view of the adversary.
- \(\mathbf {G}_6\)::
-
This game removes the query to \(F_1\) from C and adds a bad event based on \(\mathsf {flag}_2\) to \(F_2\) that guarantees that this game is identical to \(\mathbf {G}_5\) until \(\mathsf {flag}_2\). Removing the call to \(F_1\) from C has implications for \(F_2\), since the operation of this oracle depends on entries that were added to \(L_2\) whenever a call to C (and therefore a call to \(F_1\)) occurred. For each \(F_2\) query, we therefore need to ensure that processing left undone in this modified construction oracle (which may influence the view of the adversary) is carried out as before. To this end, we go through the entries in \(L_C\) and check if an entry \((X_1,(X_3,X_4))\) occurred that might have set the value of \(Y_2\). If more than one such entry exists, then this is detected as a collision at the output of \(F_1\) and \(\mathsf {flag}_2\) is set. If only one candidate is found, this corresponds exactly to the query that would have been made by the removed \(F_1\) call. If no candidate is found, then the oracle simply samples a fresh value as before. The games are therefore identical until \(\mathsf {flag}_2\) is set, the probability of which we bound below.
- \(\mathbf {G}_7\)::
-
This game introduces a conceptual change in the way the loops in \(F_2\) are executed. First, all \(X_3\) values corresponding to entries in \(L_C\) are queried to \(F_3\) if they were not previously done so. This means that the subsequent search for a good \(Y_3\) can be equivalently made by going through those entries in \(L_C\) whose \(X_3\) value is already present in \(L_3\). This change sets the ground for the next game where we drop the first loop completely.
- \(\mathbf {G}_8\)::
-
We now remove the code that corresponds to the first loop in \(F_2\) completely and argue that there is a rare event that allows us to prove the games identical until bad and bound the statistical distance between the two. This rare event is explicitly shown, for convenience, as a dummy \(\mathsf {flag}_3\): it is activated whenever the first loop was adding to list \(L_3\) a freshly sampled entry \((X_3,Y_3)\), which is used by the second loop. Again we can bound the probability of this event easily, as \(F_3\) implements a random oracle.
- \(\mathbf {G}_9\)::
-
This game rewrites the loops in \(F_2\) and only looks in \(L_C\) for values that will be used by \(F_2\), i.e., only those entries with \(X_4 = X_2 \oplus Y_3\) will be searched over. This is a conceptual change.
- \(\mathbf {G}_{10}\)::
-
This game introduces \(\mathsf {flag}_C\), which is set if collisions in the outputs of C are found. This prepares us to modify the implementation of C from a random function to a random injection. We bound this via a standard RF/RI switching lemma. This game also introduces a (partial and so far unused) inverse \(C^-\) to C that returns the preimage to \((X_3,X_4)\) if this value was queried to C. This will allow us to remove the dependency on the \(L_C\) next. (Recall that the differentiator is restricted and it cannot call \(C^-\) at all.)
- \(\mathbf {G}_{11}\)::
-
In this game \(F_2\) no longer uses \(L_C\); instead it uses \(C^-\) to check if a value was queried to C. Since this partial inverse oracle always returns \(\perp \) for inputs that are not on \(L_C\), this game is identical to the previous game. (Note also that we may also omit the re-computation of \((X_3,X_4)\).)
- \(\mathbf {G}_{12}\)::
-
This game modifies C to the forward direction of a random injection oracle and \(C^-\) to its backward direction (which could return a non-\(\perp \) value even if an inverse is not found in \(L_C\)). This modification can be bounded by looking at the probability that the simulator places an inverse query that was not previously obtained from the forward construction oracle.
Now observe that \(\mathbf {G}_{12}\) is the ideal game where procedures \(F_1\), \(F_2\) and \(F_3\) make use of random injection oracles \((C,C^{-})\) but not its internal list \(L_C\). By viewing the implementations of these procedures as three (sub-)simulators  ,
,  and
and  we arrive at our simulator. We note that
we arrive at our simulator. We note that  can omit \(\mathsf {flag}_2\) in \(F_2\) with no loss in advantage (cf. footnote in the conservative jump to \(\mathbf {G}_4\) above). We also note that this simulator is C-respecting as needed in Lemma 1 above, and that it places at most \(q^2\) oracle queries (it is quadratic due to the loop in
can omit \(\mathsf {flag}_2\) in \(F_2\) with no loss in advantage (cf. footnote in the conservative jump to \(\mathbf {G}_4\) above). We also note that this simulator is C-respecting as needed in Lemma 1 above, and that it places at most \(q^2\) oracle queries (it is quadratic due to the loop in  ). The remainder of the proof consists of bounding the probabilities of setting the four flags in the game sequence above. The details of this analysis and the extracted code for the simulator can be found in [1, Sect. 5.2]. \(\square \)
). The remainder of the proof consists of bounding the probabilities of setting the four flags in the game sequence above. The details of this analysis and the extracted code for the simulator can be found in [1, Sect. 5.2]. \(\square \)
5.3 Removing Restrictions and Simplifications
Our AEAD schemes were analyzed with respect to differentiators that were bound to a fixed \((K,N,A,\tau )\). We deal with arbitrary \((K,N,A,\tau )\) by applying a hybrid argument. For this argument to hold, it is important to ensure that the simulators do not “interfere” with each other: not only should they be run on independent coins, but also their ideal AEAD oracles should be independent. We formalize this argument in a more general form.
From key-wise to full indifferentiability. We call a keyed ideal object  uniformly keyed if
uniformly keyed if  and
and  are identically and independently distributed for any X and distinct keys K and \(K'\). Let
are identically and independently distributed for any X and distinct keys K and \(K'\). Let  be a construction of a uniformly keyed object
be a construction of a uniformly keyed object  from a uniformly keyed object
from a uniformly keyed object  . We call the construction key-respecting if for all inputs (K, X) it queries
. We call the construction key-respecting if for all inputs (K, X) it queries  on K only. We call a simulator (for
on K only. We call a simulator (for  ) key-respecting if for all inputs (K, X) it queries
) key-respecting if for all inputs (K, X) it queries  on K only. We call a differentiator key-respecting if it always queries both the construction and the primitive oracles on K only. We call the construction key-wise indifferentiable if it is indifferentiable with a key-respecting simulator against all key-respecting differentiators. The following lemma follows from a standard hybrid argument (see [1, Appendix D]).
on K only. We call a differentiator key-respecting if it always queries both the construction and the primitive oracles on K only. We call the construction key-wise indifferentiable if it is indifferentiable with a key-respecting simulator against all key-respecting differentiators. The following lemma follows from a standard hybrid argument (see [1, Appendix D]).
Lemma 2
(Hybrid over keys). Let  and
and  be two uniformly keyed objects and
be two uniformly keyed objects and  be a key-respecting construction of
be a key-respecting construction of  from
from  . Then if
. Then if  is key-wise indifferentiable, it is also (fully) indifferentiable. More precisely, for any key-respecting simulator
is key-wise indifferentiable, it is also (fully) indifferentiable. More precisely, for any key-respecting simulator  and any q-query (unrestricted) differentiator
and any q-query (unrestricted) differentiator  there is a key-respecting differentiator
there is a key-respecting differentiator  such that
such that

In order to apply this result to the EtE and 3-round Feistel it suffices to syntactically express all underlying ideal objects as a single keyed primitive and then show that they are key respecting. We note that the key-respecting restriction forces the use of the same key on all underlying ideal objects, which agrees with our observations on the benefits of key reuse in Sect. 4.1.
Dealing with keys of arbitrary size. Objects with an arbitrarily large key space can be indifferentiably built from those with a smaller key space in the standard way by hashing the key using a random oracle. This means we can remove the assumption of variable key lengths on the VIL ideal cipher in our construction. We prove the following result in [1, Sect. 5.3].
Proposition 3
(Key extension via hashing). Let  and
and  be two uniformly keyed ideal objects with key spaces
be two uniformly keyed ideal objects with key spaces  and
and  respectively. Let
respectively. Let  be a random oracle. Suppose further that for some (and hence any)
be a random oracle. Suppose further that for some (and hence any)  and
and  we have that
we have that  is identically distributed to
is identically distributed to  . Then
. Then  is indifferentiable from
is indifferentiable from  . More precisely, there is a simulator
. More precisely, there is a simulator  such that for any q / 3-query differentiator
such that for any q / 3-query differentiator  ,
,

The full construction. Our final AEAD construction can be written as  , where
, where  and \(\mathrm {\Phi }_3\) is the ideal injection instantiated with 3-round Feistel. The latter uses independent keyed random oracles
and \(\mathrm {\Phi }_3\) is the ideal injection instantiated with 3-round Feistel. The latter uses independent keyed random oracles  all with key space
all with key space  matching the co-domain of
matching the co-domain of  . Combining Theorem 5 with Lemmas 2 and 3 we obtain an overall bound
. Combining Theorem 5 with Lemmas 2 and 3 we obtain an overall bound  , where q is an upper bound on the number of oracles queries.
, where q is an upper bound on the number of oracles queries.
5.4 Ideal Online AEAD
Offline AEAD schemes can fall short of providing adequate levels of functionality or efficiency in settings where data arrives one segment at a time and should be processed immediately without the knowledge of future segments. In an online AEAD scheme, the encryption and decryption algorithms are replaced by stateful segment-oriented ones that process the inputs one segment at a time. We formalize ideal online AEAD next and briefly present our results in indifferentiably constructing online AEAD schemes.
Online functions and ideal online AEAD. An online function(ality) is a triple of functions with signatures

We define  as the set of online functions for which
as the set of online functions for which  and
and  are injective over
are injective over  and respect the length-expansion requirement. An ideal online AEAD is a uniform function in
and respect the length-expansion requirement. An ideal online AEAD is a uniform function in  where
where  ,
,  , and
, and  .
.
Indifferentiable online AEAD. The \(\mathbf {CHAIN}\) construction of [43] is trivially differentiable from an ideal online AEAD as its initialization procedure  and state-update procedures are not random. Indeed, we need to modify this and other aspects of its design (cf. [1, Sect. 7.2]) to achieve indifferentiability. Intuitively, the computation of a ciphertext/state pair must be done in a way that forces the differentiator to reveal all necessary information that is needed to recompute them via the ideal objects accessible to the simulator. Following this, we propose a new construction in Fig. 9, which we call \(\mathbf {HashCHAIN}\). Here,
and state-update procedures are not random. Indeed, we need to modify this and other aspects of its design (cf. [1, Sect. 7.2]) to achieve indifferentiability. Intuitively, the computation of a ciphertext/state pair must be done in a way that forces the differentiator to reveal all necessary information that is needed to recompute them via the ideal objects accessible to the simulator. Following this, we propose a new construction in Fig. 9, which we call \(\mathbf {HashCHAIN}\). Here,  is an offline ideal AEAD with key length k, and
is an offline ideal AEAD with key length k, and  are VIL/VOL keyed random oracles with key size k that admit outputs of lengths k and 2k. These are implemented from a single random oracle via domain separation. The nonce and associated-data spaces of the online scheme are arbitrary. Its message, expansion and ciphertext spaces match those of the offline scheme. The state space is
are VIL/VOL keyed random oracles with key size k that admit outputs of lengths k and 2k. These are implemented from a single random oracle via domain separation. The nonce and associated-data spaces of the online scheme are arbitrary. Its message, expansion and ciphertext spaces match those of the offline scheme. The state space is  . A formal statement and proof of the following theorem are given in [1, Sect. 7.2]. In the proof we apply parallel composition of indifferentiability, which permits modifying the ideal AEAD reference object until we arrive at \(\mathbf {HashCHAIN}\).
. A formal statement and proof of the following theorem are given in [1, Sect. 7.2]. In the proof we apply parallel composition of indifferentiability, which permits modifying the ideal AEAD reference object until we arrive at \(\mathbf {HashCHAIN}\).
Theorem 6
(\(\mathbf {HashCHAIN}\) is indifferentiable). The \(\mathbf {HashCHAIN}\) construction in Fig. 9 is indifferentiable from an ideal online AEAD.
6 Efficiency Lower Bounds
Suppose we instantiate the random oracles underlying our Feistel-based construction with the Sponge construction. Suppose also that the underlying Sponges absorb inputs and expand outputs in blocks of n bits (i.e., the Sponge has bit-rate n). Finally, assume that our input message is w blocks long. This means that in both of our constructions roughly w primitive calls are used in each round of Feistel. This adds up to 3w overall primitive calls for the second construction and 8w calls for the first one. Our second construction is therefore almost 3 times faster than the first. We next show that our more efficient construction is not too far from the theoretically optimal solution by proving that at least 2w calls are necessary for any indifferentiable construction. We do this by first giving a lower bound for indifferentiable constructions of random oracles (which is tight as it is essentially matched by Sponge) and then show how to derive the lower bound for random injections from it.
Theorem 7
(Efficiency lower bound). Any indifferentiable construction of a random function \(\mathrm {C}^\pi : \{0,1\}^{wn} \longrightarrow \{0,1\}^{wn}\) from a random permutation \(\pi : \{0,1\}^n \longrightarrow \{0,1\}^n\) must place at least \(q \ge 2w-2\) queries to \(\pi \). More precisely, for any such q-query construction \(\mathrm {C}^\pi \) and any \(q_S\)-query indifferentiability simulator  there is a w-query differentiator
there is a w-query differentiator  such that
such that

Proof
We prove this result by constructing a differentiator against any construction \(\mathrm {C}^\pi \) that places \(q < 2w-2\) queries to \(\pi \). Any such \(\mathrm {C}^\pi \) can be written using (\(\pi \)-independent) functions \(f_1,\ldots f_{q+1}\) where
This reflects the fact that each \(f_i\) can recompute everything that depends only on the initial inputs, but also needs to take as additional inputs the values returned by \(\pi \) at each of the previous calls. See [1, Sect. 6] for a schematic diagram.
Consider the first \(w-1\) calls to \(\pi \). There are \(2^{(w-1)n}\) possible tuples \(\mathrm {P}=(P_1,\ldots ,P_{w-1})\) that can define the inputs to such queries. Since in total there are \(2^{wn}\) possible inputs, by a counting argument, a subset \(\mathrm {D}[\mathrm {C},\pi ]\) of the input values of size at least \(2^n=2^{wn}/2^{(w-1)n}\) will be mapped by a construction C to the same \(\mathrm {P}[\mathrm {C},\pi ]\), for any given \(\pi \). Set \(\mathrm {D}[\mathrm {C},\pi ]\) and points \(\mathrm {P}[\mathrm {C},\pi ]\) can be found by a (possibly unbounded) attacker  using only \(w-2\) queries to \(\pi \). Algorithm
using only \(w-2\) queries to \(\pi \). Algorithm  proceeds in rounds as follows. There is at least one point \(P_1 \in \{0,1\}^n\) such that \(f_1\) always chooses \(P_1\) for at least \(2^{wn}/2^{n} = 2^{(w-1)n}\) of its inputs. No queries to \(\pi \) are needed to find \(P_1\) and we set \(\mathrm {D}[\mathrm {C},\pi ]\) to a corresponding set of colliding inputs. We then get \(Z_1:=\pi (P_1)\) and we use it to analyze the operation of \(f_2\). Given \(Z_1\) and \(\mathrm {D}[\mathrm {C},\pi ]\), at least \(2^{(w-1)n}/2^n\) of the inputs in \(\mathrm {D}[\mathrm {C},\pi ]\) are such that \(f_2\) always chooses the same query point \(P_2\) to \(\pi \). We update \(\mathrm {D}[\mathrm {C},\pi ]\) to this subset. Continuing in this manner, we obtain a set \(\mathrm {D}[\mathrm {C},\pi ]\) of at least \(2^n\) points such that \(f_{w-1}\) chooses a point \(P_{w-1}\) for all inputs in \(\mathrm {D}[\mathrm {C},\pi ]\).
proceeds in rounds as follows. There is at least one point \(P_1 \in \{0,1\}^n\) such that \(f_1\) always chooses \(P_1\) for at least \(2^{wn}/2^{n} = 2^{(w-1)n}\) of its inputs. No queries to \(\pi \) are needed to find \(P_1\) and we set \(\mathrm {D}[\mathrm {C},\pi ]\) to a corresponding set of colliding inputs. We then get \(Z_1:=\pi (P_1)\) and we use it to analyze the operation of \(f_2\). Given \(Z_1\) and \(\mathrm {D}[\mathrm {C},\pi ]\), at least \(2^{(w-1)n}/2^n\) of the inputs in \(\mathrm {D}[\mathrm {C},\pi ]\) are such that \(f_2\) always chooses the same query point \(P_2\) to \(\pi \). We update \(\mathrm {D}[\mathrm {C},\pi ]\) to this subset. Continuing in this manner, we obtain a set \(\mathrm {D}[\mathrm {C},\pi ]\) of at least \(2^n\) points such that \(f_{w-1}\) chooses a point \(P_{w-1}\) for all inputs in \(\mathrm {D}[\mathrm {C},\pi ]\).
Put together, the restriction of \(\mathrm {C}^\pi \) to inputs in \(\mathrm {D}[\mathrm {C},\pi ]\) guarantees that the construction always queries \(\pi \) at \(P_i\) for queries \(i=1,\ldots ,{w-1}\) and then places an arbitrary sequence of \(q-(w-1)\) queries to \(\pi \). Furthermore, from the previous discussion we can assume that differentiator  knows the description of set \(\mathrm {D}[\mathrm {C},\pi ]\) and values \(\mathrm {Z}[\mathrm {C},\pi ]:=(Z_1,\ldots ,Z_{w-1})=(\pi (P_1),\ldots ,\pi (P_{w-1}))\).
knows the description of set \(\mathrm {D}[\mathrm {C},\pi ]\) and values \(\mathrm {Z}[\mathrm {C},\pi ]:=(Z_1,\ldots ,Z_{w-1})=(\pi (P_1),\ldots ,\pi (P_{w-1}))\).
Now consider a pseudorandom generator \(\mathrm {PRG}: \mathrm {D}[\mathrm {C},\pi ] \times \{0,1\}^{(q-(w-1))n} \longrightarrow \{0,1\}^{wn}\) that has \(\mathrm {Z}[\mathrm {C},\pi ]\) hardwired in and operates as
where \(\mathrm {C}^{Z_1,\ldots ,Z_q}(X)\) denotes running \(\mathrm {C}^\pi (X)\), answering the i-th query with \(Z_i\). It is at this step that we follow the techniques of Gennaro and Trevisan [37]. If  can distinguish the output of \(\mathrm {PRG}\) from a random string, this will allow differentiating \(C^\pi \) from a random function. We now show that such an attack is guaranteed to exist if C does not make a sufficient number of queries to \(\pi \).
can distinguish the output of \(\mathrm {PRG}\) from a random string, this will allow differentiating \(C^\pi \) from a random function. We now show that such an attack is guaranteed to exist if C does not make a sufficient number of queries to \(\pi \).
Our first claim is that if \(\mathrm {C}^\pi \) is indifferentiable then \(\mathrm {PRG}[{\mathrm {Z}[\mathrm {C},\pi ]}]\) is a secure pseudorandom generator over a random choice of \(\pi \). More precisely, our goal is to show that under the indifferentiability of \(\mathrm {C}^\pi \), the distribution  is statistically close to
is statistically close to

The points in \(\mathrm {Z}[\mathrm {C},\pi ]\) are computed using oracle access to \(\pi \) at the onset and, being part of the description of the PRG, are in the view of a PRG distinguisher. Take distribution  . We first argue this is statistically close to
. We first argue this is statistically close to

To see this, note that the simulation of \(\pi \) using \(Z_i\) is fully consistent for queries \(i=1,\ldots ,{w-1}\). This is also the case for \(i \ge w\) unless \(Z_1,\ldots ,Z_{q}\) are not all distinct, which by the birthday bound occurs with probability at most \(q^2/2^{n}\).
We are left with proving the following distributions statistically close.

Here we cannot directly apply indistinguishability of \(\mathrm {C}^\pi (X)\) from a truly random wn-bit function  (which follows from indifferentiability) as the hardwired values \(\mathrm {Z}[\mathrm {C},\pi ]\) are in the distinguisher’s view. Instead we proceed via a sequence of games as follows. First, we use the indifferentiability simulator
(which follows from indifferentiability) as the hardwired values \(\mathrm {Z}[\mathrm {C},\pi ]\) are in the distinguisher’s view. Instead we proceed via a sequence of games as follows. First, we use the indifferentiability simulator  to deduce that the following distributions are statistically close.
to deduce that the following distributions are statistically close.

This follows directly from the definition of indifferentiability. Consider a differentiator that constructs \(\mathrm {Z}[\mathrm {C},\textsc {Prim}]\) and \(\mathrm {D}[\mathrm {C},\textsc {Prim}]\) using the real or simulated \(\pi \)-oracle \(\textsc {Prim}\), then queries its real or ideal construction oracle on  to obtain the first component above. Any successful distinguisher for the above distributions could be used by this differentiator to contradict the indifferentiability assumption with the same advantage. This differentiator places exactly w queries (\(w-1\) queries to the real or simulated \(\pi \)-oracle \(\textsc {Prim}\) to construct \(\mathrm {Z}[\mathrm {C},\textsc {Prim}]\) and one extra query to the real or ideal construction oracle). Note that this argument also shows that
to obtain the first component above. Any successful distinguisher for the above distributions could be used by this differentiator to contradict the indifferentiability assumption with the same advantage. This differentiator places exactly w queries (\(w-1\) queries to the real or simulated \(\pi \)-oracle \(\textsc {Prim}\) to construct \(\mathrm {Z}[\mathrm {C},\textsc {Prim}]\) and one extra query to the real or ideal construction oracle). Note that this argument also shows that  must also have at least \(2^n\) points.
must also have at least \(2^n\) points.
The next step is to show that we can replace  with Y for an independently sampled random string Y that is not computed via the random oracle. More precisely, we argue that the following distributions are statistically close.
with Y for an independently sampled random string Y that is not computed via the random oracle. More precisely, we argue that the following distributions are statistically close.

Suppose  places at most \(q_S\) queries to
places at most \(q_S\) queries to  . The set \(\mathrm {D}[\mathrm {C},\pi ]\) has size at least \(2^n\) and hence so does the set
. The set \(\mathrm {D}[\mathrm {C},\pi ]\) has size at least \(2^n\) and hence so does the set  . Now since X is chosen uniformly at random from
. Now since X is chosen uniformly at random from  , the simulator
, the simulator  will query
will query  on X with probability at most \(q_S/2^n\). Hence
on X with probability at most \(q_S/2^n\). Hence  is independent of the simulators view and we may replace it with independent random value Y.
is independent of the simulators view and we may replace it with independent random value Y.
Finally, we use indifferentiability once more to show that we can replace  back by \(\mathrm {Z}[\mathrm {C},\pi ]\) in the presence of the independently sampled random string Y. The differentiator we construct uses the real or simulated \(\pi \)-oracle \(\textsc {Prim}\) to construct set \(\mathrm {Z}[\mathrm {C},\pi ]\) or
back by \(\mathrm {Z}[\mathrm {C},\pi ]\) in the presence of the independently sampled random string Y. The differentiator we construct uses the real or simulated \(\pi \)-oracle \(\textsc {Prim}\) to construct set \(\mathrm {Z}[\mathrm {C},\pi ]\) or  , respectively, and then samples value Y. Again, any successful distinguisher for the above distributions will be translated into a differentiating attack with the same advantage, resulting in a successful differentiator that places exactly \(w-1\) queries.
, respectively, and then samples value Y. Again, any successful distinguisher for the above distributions will be translated into a differentiating attack with the same advantage, resulting in a successful differentiator that places exactly \(w-1\) queries.
This concludes the proof of our claim that \(\mathrm {PRG}\) is secure over seed space \(\mathrm {D}'[\mathrm {C},\pi ]:=\mathrm {D}[\mathrm {C},\pi ] \times \{0,1\}^{(q-(w-1))n}\) (of overall size at least \(2^{(q-{w+2})n}\)) and range \(\mathrm {R}:=\{0,1\}^{wn}\) with advantage at most \((q^2+q_S)/2^n+2\delta \), where \(\delta \) is the maximum advantage  over all
over all  placing at most w queries.
placing at most w queries.
We now show that, unless \(\mathrm {C}^\pi \) makes a large number of queries to \(\pi \) the above PRG cannot be secure. The queries of \(\mathrm {C}^\pi \) translate to the size of the seed space of \(\mathrm {PRG}\) as this does not make any queries to \(\pi \) beyond the initial \(w-1\) queries used to hardwire the fixed \({\mathrm {Z}[\mathrm {C},\pi ]}\) values. However, the outputs of any PRG with domain \(\mathrm {D}'[\mathrm {C},\pi ]\) and range \(\mathrm {R}\) can be information-theoretically distinguished from random with advantage \(1-|\mathrm {D}'[\mathrm {C},\pi ]|/|\mathrm {R}|\). We therefore must have that
If \(\mathrm {C}^\pi \) is indifferentiable, we get \(q \ge 2w-2\), when \(q^2+q_S \le 2^n/2\) and \(\delta =1\). \(\square \)
The above lower bound is essentially tight for random functions as the Sponge construction meets it up to constant terms. The proof, however, does not directly apply to random injections \(\rho \), as the inverse oracle \(\rho ^{-}\) would allow an adversary to invert the outputs of the PRG. The next proposition shows that by chopping sufficiently many bits of the outputs of \(\rho \), a random function can be indifferentiably obtained from a random injection in a single query. Together with the above result this extends the lower bound to random injections as well.
Proposition 4
Let \(\rho :\{0,1\}^{wn} \longrightarrow \{0,1\}^{wn+n}\) be a random injection with inverse \(\rho ^{-}\). Let \(\mathrm {C}^\rho (X):=\rho (X)[1..wn]\) be the construction that chops n bits of \(\rho (X)\). Then \(\mathrm {C}^\rho \) is indifferentiable from a length-preserving random function.
The proof is given in [1, Sect. 6] where we construct a simulator that uses the random oracle output and samples the extension bits independently, keeping a list for consistency. Our construction of random injections via the 3-round Feistel construction places \(3w+O(1)\) queries to \(\pi \). This is somewhat higher than the \(2w-2\) required by the lower bound. We leave bridging this gap for random injections (and indeed also permutations) as the main open problem in this area.
Notes
- 1.
The notion of RAE security that we use deviates from the original notion proposed in [41] by not considering benevolous leakage of information during decryption. This is because all indifferentiable constructions must guarantee that, like the ideal object, decryption gives the stronger guarantee that \(\perp \) is returned for all invalid ciphertexts.
- 2.
Padding with \(0^\tau \) has also been used by Kiltz, Pietrzak, and Szegedy [46] who study the public indifferentiability of injections while building digital signature schemes with message recovery. The motivation there is to design schemes with optimal overhead that also come with tight security reductions. However, this level of indifferentiability is not sufficient in the AEAD setting as it does not even imply CPA security.
- 3.
The intermediate (expanding) round function can alternatively be fully parallelized.
- 4.
When referring to an AEAD without specifying its type, we mean an offline AEAD.
- 5.
We do not count the length of \(\tau \) as our attack also works for fixed values of \(\tau \).
- 6.
In both the EtE construction and the Feistel construction in the next section, the \(0^\tau \) constant can be replaced by any fixed constant \(\varDelta \) of the same length. For EtE the indifferentiability proof is the same. For the Feistel construction the proof can be easily adapted. To see this, note that any round function \(F_1(X)\) can be replaced with an indifferentiable one \(F_1'(X)=\varDelta \oplus F_1(X)\). The resulting construction becomes identical to the one using \(0^\tau \) by cancellation.
- 7.
Using a hybrid argument the indifferentiability of the Feistel and confusion-diffusion constructions carry over to variable input lengths. The VIL/VOL hash function in Feistel can itself be instantiated with the Sponge construction [15] in the random-permutation model. Note that, when dealing with domain and range extension for Sponge one needs to take care of encoding the lengths of inputs and outputs as part of the inputs fed to the random oracle [29].
- 8.
As usual, once a flag is set, nothing matters. E.g., we can assume the game returns 0.
- 9.
We need not introduce additional terms here. Suppose games \(\mathbf {G}\) and \(\mathbf {G}''\) never set \(\mathsf {flag}\), but game \(\mathbf {G}'\) does. If these games are identical until \(\mathsf {flag}\) is set, then the distance between \(\mathbf {G}\) and \(\mathbf {G}''\) is bounded by the probability of \(\mathsf {flag}\) being set in any game.
References
Barbosa, M., Farshim, P.: Indifferentiable Authenticated Encryption. Cryptology ePrint Archive (2018)
Abed, F., Forler, C., List, E., Lucks, S., Wenzel, J.: RIV for robust authenticated encryption. In: Peyrin, T. (ed.) FSE 2016. LNCS, vol. 9783, pp. 23–42. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52993-5_2
Albrecht, M.R., Farshim, P., Paterson, K.G., Watson, G.J.: On cipher-dependent related-key attacks in the ideal-cipher model. In: Joux, A. (ed.) FSE 2011. LNCS, vol. 6733, pp. 128–145. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21702-9_8
Andreeva, E., Bogdanov, A., Dodis, Y., Mennink, B., Steinberger, J.P.: On the indifferentiability of key-alternating ciphers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 531–550. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_29
Andreeva, E., Bogdanov, A., Luykx, A., Mennink, B., Mouha, N., Yasuda, K.: How to securely release unverified plaintext in authenticated encryption. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 105–125. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_6
Ashur, T., Dunkelman, O., Luykx, A.: Boosting authenticated encryption robustness with minimal modifications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 3–33. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_1
Bellare, M., Keelveedhi, S.: Authenticated and misuse-resistant encryption of key-dependent data. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 610–629. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_35
Bellare, M., Kohno, T.: A theoretical treatment of related-key attacks: RKA-PRPs, RKA-PRFs, and applications. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 491–506. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_31
Barwell, G., Martin, D.P., Oswald, E., Stam, M.: Authenticated encryption in the face of protocol and side channel leakage. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 693–723. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_24
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 531–545. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44448-3_41
Bellare, M., Rogaway, P.: Encode-then-encipher encryption: how to exploit nonces or redundancy in plaintexts for efficient cryptography. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 317–330. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44448-3_24
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_25
Bellare, M., Rogaway, P., Wagner, D.: The EAX mode of operation. In: Roy, B., Meier, W. (eds.) FSE 2004. LNCS, vol. 3017, pp. 389–407. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-25937-4_25
Bernstein, D.J.: Cryptographic competitions (2014). https://competitions.cr.yp.to/index.html
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: On the indifferentiability of the sponge construction. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 181–197. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_11
Bellare, M., Bernstein, D.J., Tessaro, S.: Hash-function based PRFs: AMAC and its multi-user security. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 566–595. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_22
Black, J., Cochran, M., Shrimpton, T.: On the impossibility of highly-efficient blockcipher-based hash functions. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 526–541. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_31
Black, J., Rogaway, P., Shrimpton, T.: Encryption-scheme security in the presence of key-dependent messages. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 62–75. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36492-7_6
Bellare, M., Tackmann, B.: The multi-user security of authenticated encryption: AES-GCM in TLS 1.3. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 247–276. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_10
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: FOCS 2001. IEEE Computer Society Press (2001)
Coron, J.-S., Dodis, Y., Malinaud, C., Puniya, P.: Merkle-Damgård revisited: how to construct a hash function. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 430–448. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_26
Coron, J.-S., Dodis, Y., Mandal, A., Seurin, Y.: A domain extender for the ideal cipher. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 273–289. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_17
Coron, J.-S., Holenstein, T., Künzler, R., Patarin, J., Seurin, Y., Tessaro, S.: How to build an ideal cipher: the indifferentiability of the Feistel construction. J. Cryptol. 29(1), 61–114 (2016)
Coron, J.-S., Patarin, J., Seurin, Y.: The random Oracle model and the ideal cipher model are equivalent. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 1–20. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_1
Dachman-Soled, D., Katz, J., Thiruvengadam, A.: 10-round Feistel is indifferentiable from an ideal cipher. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 649–678. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_23
Dai, Y., Seurin, Y., Steinberger, J., Thiruvengadam, A.: Indifferentiability of iterated Even-Mansour ciphers with non-idealized key-schedules: five rounds are necessary and sufficient. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 524–555. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_18
Dai, Y., Steinberger, J.: Indifferentiability of 10-round Feistel networks. Cryptology ePrint Archive, Report 2015/874
Dai, Y., Steinberger, J.: Indifferentiability of 8-round Feistel networks. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 95–120. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_4
Demay, G., Gaži, P., Hirt, M., Maurer, U.: Resource-restricted indifferentiability. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 664–683. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_39
Dodis, Y., Reyzin, L., Rivest, R.L., Shen, E.: Indifferentiability of permutation-based compression functions and tree-based modes of operation, with applications to MD6. In: Dunkelman, O. (ed.) FSE 2009. LNCS, vol. 5665, pp. 104–121. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03317-9_7
Dodis, Y., Ristenpart, T., Shrimpton, T.: Salvaging Merkle-Damgård for practical applications. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 371–388. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_22
Dodis, Y., Ristenpart, T., Steinberger, J., Tessaro, S.: To hash or not to hash again? (In)differentiability results for H2 and HMAC. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 348–366. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_21
Dodis, Y., Stam, M., Steinberger, J., Liu, T.: Indifferentiability of confusion-diffusion networks. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 679–704. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_24
Farshim, P., Orlandi, C., Roşie, R.: Security of symmetric primitives under incorrect usage of keys. IACR Trans. Symm. Cryptol. 2017(1), 449–473 (2017)
Farshim, P., Procter, G.: The related-key security of iterated Even–Mansour ciphers. In: Leander, G. (ed.) FSE 2015. LNCS, vol. 9054, pp. 342–363. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48116-5_17
Forler, C., List, E., Lucks, S., Wenzel, J.: Reforgeability of authenticated encryption schemes. In: Pieprzyk, J., Suriadi, S. (eds.) ACISP 2017. LNCS, vol. 10343, pp. 19–37. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-59870-3_2
Gennaro, R., Trevisan, L.: Lower bounds on the efficiency of generic cryptographic constructions. In: 41st FOCS. IEEE (2000)
Gueron, S., Lindell, Y.: GCM-SIV: full nonce misuse-resistant authenticated encryption at under one cycle per byte. In: ACM CCS 2015. ACM (2015)
Grubbs, P., Lu, J., Ristenpart, T.: Message franking via committing authenticated encryption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 66–97. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_3
Halevi, S., Krawczyk, H.: Security under key-dependent inputs. In: ACM CCS 2007. ACM Press (2007)
Hoang, V.T., Krovetz, T., Rogaway, P.: Robust authenticated-encryption AEZ and the problem that it solves. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 15–44. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_2
Hoang, V.T., Krovetz, T., Rogaway, P.: AEZ v5: authenticated encryption by enciphering (2017). https://competitions.cr.yp.to/round3/aezv5.pdf
Hoang, V.T., Reyhanitabar, R., Rogaway, P., Vizár, D.: Online authenticated-encryption and its nonce-reuse misuse-resistance. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 493–517. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_24
Holenstein, T., Künzler, R., Tessaro, S.: The equivalence of the random oracle model and the ideal cipher model, revisited. In: 43rd ACM STOC. ACM (2011)
Jean, J., Nikolić, I., Peyrin, T., Seurin, Y.: Deoxys v1.41 (2016). https://competitions.cr.yp.to/round3/deoxysv141.pdf
Kiltz, E., Pietrzak, K., Szegedy, M.: Digital signatures with minimal overhead from indifferentiable random invertible functions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 571–588. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_31
Küsters, R., Tuengerthal, M.: Universally composable symmetric encryption. In: CSF 2009. IEEE Computer Society (2009)
Maurer, U., Renner, R., Holenstein, C.: Indifferentiability, impossibility results on reductions, and applications to the random oracle methodology. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 21–39. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_2
Micciancio, D., Warinschi, B.: Soundness of formal encryption in the presence of active adversaries. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 133–151. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_8
Namprempre, C., Rogaway, P., Shrimpton, T.: AE5 security notions: definitions implicit in the CAESAR call. Cryptology ePrint Archive, Report 2013/242
Namprempre, C., Rogaway, P., Shrimpton, T.: Reconsidering generic composition. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 257–274. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_15
Peyrin, T., Seurin, Y.: Counter-in-tweak: authenticated encryption modes for tweakable block ciphers. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 33–63. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_2
Ristenpart, T., Shacham, H., Shrimpton, T.: Careful with composition: limitations of the indifferentiability framework. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 487–506. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_27
Rogaway, P.: Authenticated-encryption with associated-data. In: ACM CCS 2002. ACM (2002)
Rogaway, P., Bellare, M., Black, J., Krovetz, T.: OCB: a block-cipher mode of operation for efficient authenticated encryption. In: ACM CCS 2001. ACM (2001)
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_23
Reyhanitabar, R., Vaudenay, S., Vizár, D.: Authenticated encryption with variable stretch. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 396–425. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_15
Stam, M.: Beyond uniformity: better security/efficiency tradeoffs for compression functions. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 397–412. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_22
Unruh, D.: Programmable encryption and key-dependent messages. Cryptology ePrint Archive, Report 2012/423
Acknowledgments
The authors would like to thank Phillip Rogaway, Martijn Stam, and Stefano Tessaro for their comments. Barbosa was supported in part by Project NORTE-01-0145-FEDER-000020, financed by the North Portugal Regional Operational Programme (NORTE 2020) under the PORTUGAL 2020 Partnership Agreement, and through the European Regional Development Fund (ERDF). Farshim was supported in part by the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement no. 339563 - CryptoCloud). This work was initiated during a short-term scientific mission sponsored by the COST CryptoAction (IC1306).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Barbosa, M., Farshim, P. (2018). Indifferentiable Authenticated Encryption. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10991. Springer, Cham. https://doi.org/10.1007/978-3-319-96884-1_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-96884-1_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96883-4
Online ISBN: 978-3-319-96884-1
eBook Packages: Computer ScienceComputer Science (R0)









 (left) and a differentiator for type-I schemes (right).
(left) and a differentiator for type-I schemes (right). . We require that for all inputs (K, N, A, M) and for a sufficiently large
. We require that for all inputs (K, N, A, M) and for a sufficiently large 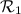 (with no oracle access) that on input C recovers
(with no oracle access) that on input C recovers  .
.
 for a random oracle
for a random oracle  .
.



