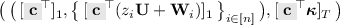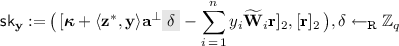Abstract
We present new techniques for achieving strong attribute-hiding in prime-order bilinear groups under the standard k-Linear assumption. Our main result is a “partially hiding” predicate encryption scheme for functions that compute an arithmetic branching program on public attributes, followed by an inner product predicate on private attributes. This constitutes the first “best of both worlds” result in bilinear groups that simultaneously generalizes existing attribute-based encryption schemes and inner product predicate encryption. Our scheme achieves a variant of simulation-based security in the semi-adaptive setting. Along the way, we introduce a conceptually simpler and more modular approach towards achieving the strong attribute-hiding guarantee.
H. Wee—INRIA and Columbia University. Supported in part by ERC Project aSCEND (H2020 639554) and NSF Award CNS-1445424.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Predicate encryption is a novel paradigm for public-key encryption that enables both fine-grained access control and selective computation on encrypted data [12, 23, 26, 34]. In a predicate encryption scheme, ciphertexts are associated with descriptive attributes x and a plaintext M, secret keys are associated with boolean functions f, and a secret key decrypts the ciphertext to recover M if f(x) is true, corresponding to a so-called authorized key. The most basic security guarantee for predicate encryption stipulates that M should remain private if f(x) is false. A stronger security guarantee is attribute-hiding, which stipulates that the attribute x remains hidden apart from leaking whether f(x) is true or false and it comes in two flavors: (i) weak attribute-hiding which guarantees privacy of x provided the adversary only gets unauthorized keys for which f(x) is false; and (ii) strong attribute-hiding where the adversary can get both authorized and unauthorized keys. Henceforth, we use attribute-based encryption (ABE) to refer to schemes which only satisfy the basic guarantee, and reserve predicate encryption for schemes which are attribute-hiding.Footnote 1 Throughout, we also require that the keys are resilient to collusion attacks, namely any group of users holding different secret keys learns nothing beyond what each of them could individually learn.
Over the past decade, tremendous progress has been made towards realizing expressive ABE and weak attribute-hiding predicate encryption [14, 21,22,23, 25, 29]; along the way, we developed extremely powerful techniques for building these primitives under standard assumptions in bilinear groups and lattices. However, much less is known for strong attribute-hiding predicate encryption schemes: the only examples we have are for very simple functionalities related to the inner product predicate [12, 26, 31, 32], and we only have instantiations from bilinear groups. And for the more important setting of prime-order bilinear groups, the only instantiations are the works of Okamoto and Takashima [31, 32].
There is good reason why strong attribute-hiding predicate encryption schemes, even in the simpler selective setting, are so elusive. The security definition requires that we reason about an adversary that gets hold of authorized keys, something that is forbidden for both ABE (even adaptively secure ones) and for weak attribute-hiding, and which we do not have a good grasp of. Moreover, we now know that strong attribute-hiding for sufficiently expressive predicates, namely NC\(^1\), imply indistinguishability obfuscation for circuits, the new holy grail of cryptography [6, 10, 20]. For this, selective security already suffices; in any case, there is a generic transformation from selective to adaptive security for this class [7].
1.1 Our Contributions
We present new techniques for achieving strong attribute-hiding in prime-order bilinear groups under the standard k-Linear assumption. We achieve a variant of simulation-based security in a semi-adaptive setting [17], the latter a strengthening of selective security where the adversary can choose its encryption challenge after seeing \({\textsf {mpk}}\). We proceed to describe the new schemes that we obtain using these techniques, and then our new approach and techniques for strong attribute-hiding.
New Schemes. Our main result is a “partially hiding” predicate encryption (PHPE) scheme that compute an arithmetic branching program (ABP) on public attributes x, followed by an inner product predicate on private attributes z. This simultaneously generalizes ABE for boolean formula and ABPs and attribute-hiding predicate encryption for inner product. This means that we can support richer variants of prior applications captured by inner product predicate encryption, as we can support more complex pre-processing on public attributes before a simple computation on private attributes; see Sect. 4.1 for some concrete examples. Our result constitutes one of the most expressive classes we have to date for predicate encryption based on static assumptions in bilinear groups. See Fig. 1 for a comparison of our results with prior works in the context of expressiveness.
Our scheme achieves simulation-based security, but with respect to an unbounded simulator [4] (which is nonetheless still a strengthening of indistinguishability-based security). Prior results for inner product predicate encryption in [26, 31, 32] only achieve indistinguishability-based security. Our scheme also enjoys short ciphertexts whose size grows linearly with the total length of the attributes (as with prior selectively secure ABE for boolean formula and branching programs [23, 25]) but independent of the size of \(f\).
Along the way, we also obtain the following additional results:
-
A scheme for inner product functional encryption –where ciphertexts and keys are associated with vectors \({\mathbf {z}},{\mathbf {y}}\) and decryption recovers \(\langle {\mathbf {z}},{\mathbf {y}} \rangle \), provided the value falls in a polynomially bounded domain [1]– that achieves simulation-based security (cf. Appendix B). Prior works like [1, 5] only achieve indistinguishability-based security, and in fact, our scheme is essentially the same as the adaptively secure scheme in [5] (our techniques can also be extended to yield a slightly different proof of adaptive security). This scheme has already been used as a building block for a multi-input functional encryption scheme (MIFE) for the inner product functionality based on the k-Linear assumption in prime-order bilinear groups [2].
-
A simple and direct construction of a strongly attribute-hiding inner product predicate encryption scheme with constant-size keys (cf. Sect. 5.1). The previous prime-order schemes with constant-size keys in [31, 32] are fairly complex: they start with a scheme with linear-size keys, and then use carefully crafted subgroups of sparse matrices [30] to compress the keys.
Our Approach. We introduce a conceptually simpler and more modular approach towards achieving the strong attribute-hiding guarantee. In particular, we deviate from the “two parallel sub-systems” paradigm introduced in [26] (cf. Sect. 4.3) and used in all subsequent works on inner product predicate encryption [31, 32].
The main challenge in designing and proving security of strongly attribute-hiding predicate encryption schemes is that the following two invariants must be satisfied throughout the proof of security: (1) all secret keys (including simulated ones) must satisfy decryption correctness with respect to freshly and honestly generated ciphertexts; and (2) authorized secret keys must correctly decrypt the challenge ciphertext. Note that (1) already arises in ABE, whereas (2) does not.
To overcome this challenge, we follow a “private-key to public-key” paradigm [11, 18, 27, 36], which in turn builds on Waters’ dual system encryption methodology [28, 35], introduced in the context of adaptively secure ABE. That is, we will start by building a private-key scheme where encryption requires the private key \(\mathsf{{msk}}\), and for security, the adversary gets a single ciphertext and no \({\textsf {mpk}}\), but an unbounded number of secret keys, and then provide a “compiler” from the private-key scheme to a public-key one. The advantage of working with a private-key scheme is that we need not worry about satisfying the first invariant, since an adversary cannot generate ciphertexts by itself in the private-key setting. Roughly speaking, the first invariant would be handled by the compiler, which ensures that if decryption correctness holds for honestly generated keys in the private-key scheme, then decryption correctness holds for both honestly generated and simulated keys in the public-key scheme.
In the case of building ABE schemes or weak attribute-hiding schemes as in prior works, then we are basically done at this point, since the security game does not allow the adversary access to authorized keys, and the second invariant is moot. Indeed, the main conceptual and technical novelty of this work lies in combining prior compilers with a new analysis to handle the second invariant.
The Compiler and Our Analysis. We proceed to describe the compiler and our analysis in a bit more detail. The compiler relies on the k-Linear (and more generally MDDH assumption) in prime-order groups, which says that \(\bigl (\,[{\mathbf {A}}], [{\mathbf {A}}{\mathbf {s}}]\,\bigr ) \approx _c \bigl (\,[{\mathbf {A}}], [{\mathbf {c}}]\,\bigr )\), where \({\mathbf {A}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k \times (k\,+\,1)}, {\mathbf {s}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k, {\mathbf {c}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\), and \([\,\cdot \,]\) corresponds to exponentiation.
Suppose we have a private-key scheme where the private key is given by \(w_1,\ldots ,w_n \in {\mathbb {Z}}_q\). We require that encryption and key generation be linear with respect to the private key. As with prior compilers, the private key in the “compiled” public-key scheme is given by vectors \({\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n \in {\mathbb {Z}}_q^{k\,+\,1}\) and the public key is given by:
The new ciphertexts and secret keys are defined as follows:
-
Encryption now samples \({\mathbf {s}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\) and the new ciphertext is essentially the original ciphertext with \([{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}{\mathbf {w}}_1],\ldots ,[{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}{\mathbf {w}}_n]\) as the private key, along with \([{\mathbf {A}}{\mathbf {s}}]\). For instance, if the original ciphertext was \(2w_1 + w_2 \in {\mathbb {Z}}_q\), then the new ciphertext is \([{\mathbf {A}}{\mathbf {s}}], [{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}(2 {\mathbf {w}}_1 + {\mathbf {w}}_2)]\).
-
Key generation outputs the original secret key with \({\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\) as the private key. For instance, if the original secret key was \(w_1 + 2w_2 \in {\mathbb {Z}}_q\), then the new secret key is \({\mathbf {w}}_1 + 2{\mathbf {w}}_2 \in {\mathbb {Z}}_q^k\).
The first step in the security proof is to use the MDDH assumption to replace \([{\mathbf {A}}{\mathbf {s}}]\) in the challenge ciphertext with \([{\mathbf {c}}]\) where \({\mathbf {c}}\leftarrow {\mathbb {Z}}_q^{k\,+\,1}\). Now, the challenge ciphertext is a ciphertext in the private-key scheme with
as the private key. A key observation is that given \({\textsf {mpk}}\), the private key \(\mathsf{{msk}}^*\) is completely random, since \({\mathbf {A}},{\mathbf {c}}\) are linearly independent and forms a full basis (with overwhelming probability). We can then leverage the security of the underlying private-key scheme with \(\mathsf{{msk}}^*\) as the private key.
What we have done so far is similar to prior works (e.g. [11, 18, 27]) and this is where the difference begins. Given a secret key \(\mathsf{{sk}}\) in the new scheme (think of it as a column vector over \({\mathbb {Z}}_q\)), we define:
Since \({\mathbf {A}},{\mathbf {c}}\) form a full basis, we have that \((\mathsf{{sk}}^1,\mathsf{{sk}}^2)\) completely determine \(\mathsf{{sk}}\) (a weaker statement, for instance, already suffices for the ABE schemes in [18]Footnote 2) and it is essentially sufficient to reason about \(\mathsf{{sk}}^1,\mathsf{{sk}}^2\). We observe that by linearity:
-
\(\mathsf{{sk}}^1\) is a secret key in the private-key scheme with \({\mathbf {A}}^{\!{\top }}{\mathbf {w}}_1,\ldots ,{\mathbf {A}}^{\!{\top }}{\mathbf {w}}_n\) as the private key, and is therefore completely determined given \({\textsf {mpk}}\). This means that the adversary learns nothing given \(\mathsf{{sk}}^1\) beyond what it already learns from \({\textsf {mpk}}\).
-
\(\mathsf{{sk}}^2\) is a secret key in the private-key scheme with \({\mathbf {c}}^{\!{\top }}{\mathbf {w}}_1,\ldots ,{\mathbf {c}}^{\!{\top }}{\mathbf {w}}_n\) (i.e., \(\mathsf{{msk}}^*\)) as the private key.
That is, the view of the adversary given challenge ciphertext together with \(\mathsf{{sk}}^2\) is essentially the same as the view of the adversary in the private-key scheme with \(\mathsf{{msk}}^*\) as the private key! Therefore, we may then deduce the security of the compiled public-key scheme from the security of the original private-key scheme. In particular,
-
if the original private-key scheme achieves selective security for a single challenge ciphertext and many secret keys, then the ensuing public-key scheme achieves semi-adaptive security with many secret keys. (The strengthening from selective to semi-adaptive comes from the fact that \(\mathsf{{msk}}^*\) is completely hidden given \({\textsf {mpk}}\).)
-
if the original private-key scheme achieves simulation-based security, then the ensuing public-key scheme also achieves simulation-based security.
Building Private-Key Schemes. To complete the construction, we provide a brief overview of the corresponding private-key schemes achieving selective security for a single challenge ciphertext and many secret keys; we refer the reader to Sect. 2 for a more detailed technical overview.
As it turns out, the private-key scheme for inner product functional encryption is fairly straight-forward and can be realized unconditionally. Here, the ciphertext is associated with a vector \({\mathbf {z}}\in {\mathbb {Z}}_q^n\), and the secret key with a vector \({\mathbf {y}}\in {\mathbb {Z}}_q^n\), and decryption recovers \(\langle {\mathbf {z}},{\mathbf {y}} \rangle \):
The private-key scheme for inner product predicate encryption requires DDH in cyclic groups (without pairings) in order to (computationally) hide the value of \(\langle {\mathbf {z}},{\mathbf {y}} \rangle \) beyond whether it is zero or non-zero. Together, these partially explain why in the public-key setting, the former does not require pairings whereas the latter does and why constructions for the former are much simpler (cf. [1] vs [26]).
The private-key scheme for the class \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) of functions considered in our main result, namely an arithmetic branching program on public attributes, followed by an inner product predicate on private attribute, is more involved. We briefly mention that our private-key scheme builds upon the information-theoretic “partial” garbling schemes for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) in [25]. Our construction exploits the fact that for, these schemes enjoy so-called linear reconstruction (analogous to linear reconstruction for secret-sharing schemes). Using these partial garbling schemes, it is easy to build a private-key scheme for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) that is unconditionally secure for a single ciphertext and a single secret key, but where the ciphertext size grows with the size of the function (or alternatively, if we impose a read-once condition where each attribute variable appears once in the function). We then rely on the DDH assumption to (i) compress the ciphertext [3, 17] so that it is linear in the length of the attribute rather than the size of the function, and (ii) to achieve security against many secret keys. To abstract some of these technical issues, we present a somewhat modular approach by appealing to a notion similar to “pair encodings” [3, 8] developed in the context of adaptively secure ABE; see Sect. 4.
1.2 Discussion
On Simulation-Based Security. There are now several results ruling out simulation-based predicate encryption [4, 13, 33], but none of which applies to the selective or semi-adaptive setting with a single ciphertext and unbounded secret key queries, as considered in this work. De Caro et al. [15] gave a feasibility result for all circuits in this setting, but under non-standard assumptions. Our work is the first to achieve simulation-based security in this setting for a non-trivial class of functions under standard cryptographic assumptions.
Perspective. Our (admittedly subjective) perspective is that developing strong attribute-hiding techniques from lattices is a promising route towards basing indistinguishability obfuscation on well-understood cryptographic assumptions. As a first small step towards this goal, we believe (again, admittedly subjective) that it would be useful to gain a better grasp of strongly attribute-hiding techniques in prime-order bilinear groups that work with vectors and matrices of group elements, with a minimal requirement on orthogonality relations amongst these vectors; indeed, this is the case for the schemes in this work (which rely on the “associative relation” framework introduced in [16, 18]), but not for the prior works based on dual vector pairing spaces.
Open Problems. We conclude with a number of open problems:
-
Our work clarifies functional encryption for linear functions as studied in [1, 5] – the reason why this is much easier than inner product predicate is that it is very easy to construct a private-key scheme that is information-theoretically secure against unbounded number of secret key queries. This raises a number of questions pertaining to quadratic functions: (1) Is there a private-key functional encryption scheme for quadratic functions that is information-theoretically secure with a single ciphertext and an unbounded number of secret keys? (2) Can we construct public-key schemes for quadratic functions in to achieve either semi-adaptive or simulation-based security in the standard model? Note that the construction in [9] follows a “two parallel sub-systems” strategy where two copies of the selective challenge are embedded into the public key.
-
Can we construct partial garbling schemes with linear reconstruction for functions outside of \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\)? It is easy to see that for linear reconstruction, we can only support degree one computation in the private input, so we cannot hope to extend substantially beyond \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\).
-
Can we construct PHPE schemes for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) that are adaptively secure under standard assumptions (extending [31])? A first step would be to make the private-key scheme adaptively secure.
2 Detailed Technical Overview
We provide a more detailed technical overview in this section for the inner product functional and predicate encryption schemes.
Notation
Throughout, we fix a pairing group \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\) with \(e: \mathbb {G}_1\times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) of prime order q, and rely on implicit representation notation for group elements: for fixed generators \(g_1\) and \(g_2\) of \(\mathbb {G}_1\) and \(\mathbb {G}_2\), respectively, and for a matrix \({\mathbf {M}}\) over \({\mathbb {Z}}_q\), we define \([{\mathbf {M}}]_1:=g_1^{{\mathbf {M}}}\) and \([{\mathbf {M}}]_2:=g_2^{{\mathbf {M}}}\), where exponentiation is carried out component-wise. In addition, we will rely on the k-Linear (and more generally MDDH assumption) which says that \(\bigl (\,[{\mathbf {A}}]_1, [{\mathbf {A}}{\mathbf {s}}]_1\,\bigr ) \approx _c \bigl (\,[{\mathbf {A}}]_1, [{\mathbf {c}}]_1\,\bigr )\), where \({\mathbf {A}}\leftarrow \mathcal {D}_k, {\mathbf {s}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k, {\mathbf {c}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\).
2.1 Inner Product Functional Encryption
For the inner product functional encryption, the ciphertext is associated with a vector \({\mathbf {z}}\in {\mathbb {Z}}_q^n\), and the secret key with a vector \({\mathbf {y}}\in {\mathbb {Z}}_q^n\), and decryption recovers \(\langle {\mathbf {z}},{\mathbf {y}} \rangle \), provided the value falls in a polynomially bounded domain.
Private-Key Variant. We present a private-key scheme where the ciphertexts and secret keys are over \({\mathbb {Z}}_q\) and which achieves information-theoretic security (for a single challenge ciphertext and many secret keys):
Decryption simply returns \(\langle \mathsf{{ct}}, {\mathbf {y}} \rangle - \mathsf{{sk}}_{\mathbf {y}}\).
For security, fix the selective challenge \({\mathbf {z}}^*\). The simulator picks \(\tilde{{\mathbf {w}}} \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^n\) uniformly at random, and program
Then, we can rewrite \(\mathsf{{ct}},\mathsf{{sk}}_{\mathbf {y}}\) in terms of \(\tilde{{\mathbf {w}}}\) as
It is clear that we can simulate an unbounded number of \(\mathsf{{sk}}_{\mathbf {y}}\) given just \(\tilde{{\mathbf {w}}},{\mathbf {y}}\) and the output of the ideal functionality \(\langle {\mathbf {z}}^*,{\mathbf {y}} \rangle \).
The Actual Scheme. To transform the warm-up scheme into one that remains secure even if the adversary sees \({\textsf {mpk}}\), we apply the “compiler” described in Sect. 1.1 where we replace \({\mathbf {w}}\in {\mathbb {Z}}_q^n\) with a matrix \({\mathbf {W}}\in {\mathbb {Z}}_q^{(k\,+\,1) \,\times \, n}\), upon which we arrive at the following public-key scheme:
Decryption computes \([\langle {\mathbf {z}},{\mathbf {y}} \rangle ]_1 = [({\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}{\mathbf {W}}+ {\mathbf {z}}^{\!{\top }}){\mathbf {y}}]_1 \cdot ([{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}{\mathbf {W}}{\mathbf {y}}])^{-1}\) and uses brute-force discrete log to recover \(\langle {\mathbf {z}},{\mathbf {y}} \rangle \) as in [1]. We refer to Appendix B for the security proof.
On Adaptive Security. As alluded to in the introduction, the same proof plus one small observation essentially yields indistinguishability-based adaptive security as shown in [5] with a somewhat different argument (the approach here was used in the follow-up work [2]). Observe that the private-key scheme achieves perfect indistinguishability-based security in the selective setting (as implied by perfect simulation-based security); by complexity leveraging, this implies indistinguishability-based security in the adaptive setting. Moreover, it is straight-forward to verify that the adaptive security is preserved by the “compiler” since the use of the MDDH Assumption in the first step to switch \([{\mathbf {A}}{\mathbf {s}}]_1\) to \([{\mathbf {c}}]_1\) is oblivious to selective vs adaptive security.
2.2 Inner Product Predicate Encryption
We define predicate encryption in the framework of key encapsulation. For the inner product predicate, the ciphertext is associated with a vector \({\mathbf {z}}\), and the secret key with a vector \({\mathbf {y}}\), and decryption is possible iff \(\langle {\mathbf {z}},{\mathbf {y}} \rangle = 0\). In particular, decryption only leaks the predicate \(\langle {\mathbf {z}},{\mathbf {y}} \rangle {\mathop {=}\limits ^{?}} 0\) and not the exact value of \(\langle {\mathbf {z}},{\mathbf {y}} \rangle \).
Private-Key Variant. We present a private-key scheme where the ciphertexts are over \({\mathbb {Z}}_q\) and secret keys are over \(\mathbb {G}_2\) and which achieves simulation-based security under the DDH assumption in \(\mathbb {G}_2\). Roughly speaking, we start with the inner product functional encryption scheme, with an additional u in the ciphertext (i.e. \(u {\mathbf {z}}+ {\mathbf {w}}\) instead of \({\mathbf {z}}+ {\mathbf {w}}\)) to hide any leakage beyond \(\langle {\mathbf {z}},{\mathbf {y}} \rangle {\mathop {=}\limits ^{?}} 0\); this would already be secure if there was only one secret key (since we cannot reuse the masking factor u). To achieve security against unbounded number of secret keys, we randomize the secret keys and rely on the DDH assumption.
Decryption recovers
which equals \([\kappa ]_2\) when \(\langle {\mathbf {z}},{\mathbf {y}} \rangle = 0\) and uniformly random otherwise.
For security, fix the selective challenge \({\mathbf {z}}^*\). The simulator picks \(\tilde{{\mathbf {w}}} \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^n\) uniformly at random, and program
Then, we can rewrite \(\mathsf{{ct}},\mathsf{{sk}}_{\mathbf {y}}\) in terms of \(\tilde{{\mathbf {w}}}\) as

where we applied the DDH assumption to replace \(([ur]_2,[r]_2)\) with \(([\delta ]_2,[r]_2)\). Now, we can easily simulate \(\mathsf{{sk}}_{\mathbf {y}}\) given \(\kappa + \delta \langle {\mathbf {z}}^*,{\mathbf {y}} \rangle \) (which we can easily simulate given the output from the ideal functionality) along with \({\mathbf {y}},\tilde{{\mathbf {w}}}\).
To achieve security under the k-Lin assumption, we replace u, r with \({\mathbf {u}},{\mathbf {r}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\), as well as \({\mathbf {w}}\) with \({\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\). For the public-key variant, we then end up replacing u with \({\mathbf {U}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{(k\,+\,1) \,\times \, k}\), \({\mathbf {w}}\) with \({\mathbf {W}}_1,\ldots ,{\mathbf {W}}_n \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{(k\,+\,1) \,\times \, k}\), and \(\kappa \) with \(\varvec{\kappa }\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\).
3 Preliminaries
Notation. We denote by \(s \leftarrow _{\mathrm {R}}S\) the fact that s is picked uniformly at random from a finite set S. By PPT, we denote a probabilistic polynomial-time algorithm. Throughout, we use \(1^\lambda \) as the security parameter. We use lower case boldface to denote (column) vectors and upper case boldcase to denote matrices. We use \(\equiv \) to denote two distributions being identically distributed.
Arithmetic Branching Programs. A branching program is defined by a directed acyclic graph (V, E), two special vertices \(v_0,v_1\in V\) and a labeling function \(\phi \). A arithmetic branching program (ABP), where \(q \ge 2\) is a prime power, computes a function \(f : \mathbb {F}_q^{n'}\rightarrow \mathbb {F}_q\). Here, \(\phi \) assigns to each edge in E an affine function in some input variable or a constant, and f(x) is the sum over all \(v_0\)-\(v_1\) paths of the product of all the values along the path. We refer to \(|V| + |E|\) as the size of \(\Gamma \).
We note that there is a linear-time algorithm that converts any boolean formula, boolean branching program or arithmetic formula to an arithmetic branching program with a constant blow-up in the representation size. Thus, ABPs can be viewed as a stronger computational model than all of the above. Recall also that branching programs and boolean formulas correspond to the complexity classes LOGSPACE and NC\(_1\) respectively.
3.1 Cryptographic Assumptions
We follow the notation and algebraic framework for Diffie-Hellman-like assumptions in [19]. We fix a pairing group \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\) with \(e: \mathbb {G}_1\times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) of prime order q, where q is a prime of \(\Theta (\lambda )\) bits.
k -Linear and MDDH Assumptions. The k-Linear Assumption in \(\mathbb {G}_1\) –more generally, the Matrix Decisional Diffie-Hellman (MDDH) Assumption– specifies an efficiently samplable distribution \(\mathcal {D}_k\) over full-rank matrices in \({\mathbb {Z}}_q^{(k\,+\,1) \,\times \, k}\), and asserts that
where \({\mathbf {A}}\leftarrow \mathcal {D}_k, {\mathbf {s}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k, {\mathbf {c}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\). We use \({\textsf {Adv}^{\textsc {mddh}}_{\mathbb {G}_1,\mathcal {A}}(\lambda )}\) to denote the distinguishing advantage of an adversary \(\mathcal {A}\) for the above distributions, and we define \({\textsf {Adv}^{\textsc {mddh}}_{\mathbb {G}_2,\mathcal {A}}(\lambda )}\) analogously for \(\mathbb {G}_2\). For the k-Linear assumption, the distribution \(\mathcal {D}_k\) is given by
where \(a_1,\ldots ,a_k \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^*\). Another example of \(\mathcal {D}_k\) is the uniform distribution over full-rank matrices in \({\mathbb {Z}}_q^{(k\,+\,1) \,\times \, k}\).
3.2 Partially Hiding Predicate Encryption
We define PHPE for arithmetic functionalities with non-boolean output, in the framework of key encapsulation. Following [14, 22, 26], we associate \(=0\) with being true, and \(\ne 0\) with being false.
Syntax. A partially-hiding predicate encryption (PHPE) scheme for a family \({\mathcal {F}}= \{ f : {\mathbb {Z}}_q^{n'}\times {\mathbb {Z}}_q^{{n}} \rightarrow {\mathbb {Z}}_q \}\) consists of four algorithms \((\mathbf{setup }, \mathbf{enc }, {\mathbf {keygen}}, \mathbf{dec })\):
- \(\mathbf{setup }(1^\lambda ,1^{{n'}+\,{n}})\rightarrow (\mathsf{{mpk}}, \mathsf{{msk}})\).:
-
The setup algorithm gets as input the security parameter \(\lambda \) and the attribute length \({n'}+{n}\) and outputs the public parameter \({\textsf {mpk}}\), and the master key \(\mathsf{{msk}}\). All the other algorithms get \({\textsf {mpk}}\) as part of its input.
- \(\mathbf{enc }(\mathsf{{mpk}},(x,z))\rightarrow (\mathsf{{ct}},\mathsf{{kem}})\).:
-
The encryption algorithm gets as input \({\textsf {mpk}}\), an attribute \((x,z) \in {\mathbb {Z}}_q^{n'}\times {\mathbb {Z}}_q^{{n}}\). It outputs a ciphertext \(\mathsf{{ct}}\) and a symmetric-key \(\mathsf{{kem}}\in {\mathcal {M}}\).
- \({\mathbf {keygen}}(\mathsf{{msk}},f)\rightarrow \mathsf{{sk}}_{f}\).:
-
The key generation algorithm gets as input \(\mathsf{{msk}}\) and a function \(f \in {\mathcal {F}}\). It outputs a secret key \(\mathsf{{sk}}_{f}\).
- \(\mathbf{dec }((\mathsf{{sk}}_{f},f),(\mathsf{{ct}},x)) \rightarrow \mathsf{{kem}}\).:
-
The decryption algorithm gets as input \(\mathsf{{sk}}_f\) and \(\mathsf{{ct}}\), along with f and x. It outputs a symmetric key \(\mathsf{{kem}}\).
For notational simplicity, we often write \(\mathbf{dec }(\mathsf{{sk}}_f,\mathsf{{ct}})\) and omit the inputs f, x to \(\mathbf{dec }\). Alternatively, we can think of x and f as part of the descriptions of \(\mathsf{{ct}}\) and \(\mathsf{{sk}}_f\) respectively.
Correctness. We require that for all \((x,z) \in {\mathbb {Z}}_q^{n'}\times {\mathbb {Z}}_q^{{n}}, f \in {\mathcal {F}}\) and for all \(({\textsf {mpk}},\mathsf{{msk}}) \leftarrow \mathbf{setup }(1^\lambda ,1^{n'})\) and \(\mathsf{{sk}}_f \leftarrow {\mathbf {keygen}}(\mathsf{{msk}},f)\),
-
(authorized) if \(f(x,z) = 0\), then \(\Pr [(\mathsf{{ct}},\mathsf{{kem}}) \leftarrow \mathbf{enc }({\textsf {mpk}},(x,z)); \mathbf{dec }((\mathsf{{sk}}_f,f),\mathsf{{ct}}) = \mathsf{{kem}}] = 1\);
-
(unauthorized) if \(f(x,z) \ne 0\), then \(\mathbf{dec }((\mathsf{{sk}}_f,f),\mathsf{{ct}})\) is uniformly distributed over \({\mathcal {M}}\), where \((\mathsf{{ct}},\mathsf{{kem}}) \leftarrow \mathbf{enc }({\textsf {mpk}},(x,z))\).
where both probability distributions are taken over the coins of \(\mathbf{enc }\).
Security Definition. The security definition for semi-adaptively partially (strong) attribute-hiding stipulates that there exists a randomized simulator \((\mathbf{setup }^*,\mathbf{enc }^*,{\mathbf {keygen}}^*)\) such that for every efficient stateful adversary \(\mathcal {A}\),
such that whenever \(\mathcal {A}\) makes a query f to \({\mathbf {keygen}}\), the simulator \({\mathbf {keygen}}^*\) gets f along with
-
\(\mathsf{{kem}}\) if f is authorized (i.e., \(f(x^*,z^*) = 0\)), and
-
\(\perp \) if f is unauthorized (i.e., \(f(x^*,z^*) \ne 0\)), and
Remark 1
(security definition). Note that the security definition is the straight-forward adaptation of strongly attribute-hiding from [12, 26, 32] to PHPE, in the semi-adaptive setting. This simulation-based definition implies the indistinguishability-based formulation of strongly attribute-hiding. Also, working with key encapsulation simplifies the security definition, since the adversary may as well receive the challenge ciphertext before making any secret key queries (indeed, this phenomenon was first noted in the context of CCA security).
4 \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) and Encodings
In this section, we formally describe the class \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) which our PHPE supports, as well as the encoding algorithm \({\mathbf {rE}_f}\) used in the PHPE scheme. Throughout, we work over \({\mathbb {Z}}_q\) where q is prime.
4.1 The Class \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\)
We consider the class
where \(f\) on input \({\mathbf {x}}= (x_1,\ldots ,x_{n'}) \in {\mathbb {Z}}_q^{n'}\) and \({\mathbf {z}}= (z_1,\ldots ,z_{n}) \in {\mathbb {Z}}_q^{n}\) outputs
where \(f_1,\ldots ,f_n : {\mathbb {Z}}_q^{n'}\rightarrow {\mathbb {Z}}_q\) are ABPs which are part of the description of f. We should think of \({\mathbf {x}}\) as the “public attribute”, and \({\mathbf {z}}\) as the “private attribute”. We will also use m to denote the ABP size of f, which is the total number of edges and vertices in the underlying DAG.
Examples. It is clear that \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) contains both standard branching programs with public attributes by setting \({n}=1,z_1=1\), as well as inner product with private attributes by setting \({n'}=0\) and \(f_1,\ldots ,f_{n}\) to output constants \(y_1,\ldots ,y_{n}\). We refer to Fig. 2 for additional examples.
Next, we outline two concrete examples of new functionalities captured by our PHPE for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\):
-
conjunctive comparison predicates [12, Sect. 3.1]: secret keys are associated with boolean functions \(P_{a_1,\ldots ,a_{n}}\) that compute
$$\begin{aligned} P_{a_1,\ldots ,a_{n}}(z_1,\ldots ,z_{n}) = \bigwedge _{i\,=\,1}^{n}(z_i \ge a_i) \end{aligned}$$Here, the \(a_i\)’s and \(z_i\)’s lie in polynomial-size domains. With inner product predicate encryption, \(a_1,\ldots ,a_{n}\) are fixed constants that are specified in the secret key. With PHPE for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\), we can carry out more complex computation where \(a_1,\ldots ,a_{n}\) are derived as the output of an ABP computation on public ciphertext attribute x. (Fixed \(a_1,\ldots ,a_{n}\) are a special case since we can have ABPs that ignore x and output the fixed constant.)
-
polynomial evaluation [26, Sect. 5.3]: secret keys are associated with polynomials in z of degree less than \({n}\). With inner product predicate encryption, the coefficients of the polynomial are fixed constants that are specified in the secret key. With PHPE for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\), we may derive the coefficients as the output of an ABP computation on public ciphertext attribute x.
4.2 Encodings \({\mathbf {rE}_f}\) for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\)
Suppose we want to build a private-key PHPE for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) secure against a single ciphertext and a single secret key. Our ciphertext corresponding to public attribute \({\mathbf {x}}\in {\mathbb {Z}}_q^{n'}\) and private attribute \({\mathbf {z}}\in {\mathbb {Z}}_q^{n}\) will be of the form:
where \(u'_j, v'_{ij}, w'_i\) are part of the private key. In particular, the ciphertext size grows linearly with \({n'}+{n}\) and is independent of the function \(f \in \mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\). Then, we can think of the output of \({\mathbf {rE}_f}\) as a secret key for f that combined with the ciphertext, allows us to learn \(\kappa + f({\mathbf {x}},{\mathbf {z}})\), where \(\kappa \) is the “master secret key” which is used to mask the plaintext.
The Encoding \({\mathbf {rE}_f}\). We require a randomized algorithm \({\mathbf {rE}_f}\) parameterized by a function \(f \in \mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) that takes as input
along randomness \({\mathbf {t}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{m\,+\,{n}}\), which satisfies the following properties:
-
linearity: \({\mathbf {rE}_f}\) computes a linear function of its inputs and randomness over \({\mathbb {Z}}_q\);
-
reconstruction: there exists an efficient algorithm \(\mathbf{rec }\) that on input
$$\begin{aligned} \begin{array}{l} f,\;{\mathbf {x}},\;{\mathbf {rE}_f}\bigl (\,\kappa , \bigl \{\,w'_i\,\bigr \}_{i \in [{n}]}, \bigl \{\,u'_j\,\bigr \}_{j \in [m]}, \bigl \{\,v'_{ij}\,\bigr \}_{i \in [{n'}], j \in [m]}; {\mathbf {t}}\,\bigr ),\\ \bigl \{\,u'_j x_i + v'_{ij}\,\bigr \}_{i \in [{n'}], j \in [m]},\; \bigl \{\,z_i + w'_i\,\bigr \}_{i \in [{n}]} \end{array} \end{aligned}$$outputs \(\kappa + f({\mathbf {x}},{\mathbf {z}})\). This holds for all \(f, {\mathbf {x}}, {\mathbf {z}}, \kappa , {\mathbf {t}}\). Moreover, \(\mathbf{rec }(f,{\mathbf {x}},\cdot )\) computes a linear function of the remaining inputs.
-
privacy: there exists an efficient simulator \(\mathbf{sim }\) such that for all \(f, {\mathbf {x}}, {\mathbf {z}}, \kappa \), the output of \(\mathbf{sim }(f, {\mathbf {x}}, \kappa + f({\mathbf {x}},{\mathbf {z}}))\) is identically distributed to that of
$$\begin{aligned} {\mathbf {rE}_f}\bigl (\,\kappa , \bigl \{\,-z_i\,\bigr \}_{i \in [{n}]}, \bigl \{\,\delta _j\,\bigr \}_{j \in [m]}, \bigl \{\,-\delta _j x_i\,\bigr \}_{i \in [{n'}], j \in [m]}; {\mathbf {t}}\,\bigr ), \end{aligned}$$where \(\bigl \{\,\delta _j \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q\,\bigr \}_{j \in [m]},{\mathbf {t}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{m\,+\,{n}}\) are random.
We defer the description of the algorithm to Appendix A, which builds upon the “partial garbling scheme” for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) from [24, 25] in a somewhat straight-forward manner.
Extension to Vectors. In the scheme, we will run \({\mathbf {rE}_f}\) with vectors instead of scalars as inputs, by applying \({\mathbf {rE}_f}\) to each coordinate. That is, \({\mathbf {rE}_f}\) takes as input
along randomness \({\mathbf {T}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k \times (m\,+\,{n})}\), and outputs
The first row of the output is obtained by applying \({\mathbf {rE}_f}\) to the first coordinate/row of each input, etc. Linearity (as captured by left-multiplication by a matrix) is clearly preserved, whereas we will only invoke reconstruction and privacy for scalar inputs.
5 Our PHPE Construction
In this section, we present our partially-hiding predicate encryption scheme for the class
defined in Sect. 4. We also fix a pairing group \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\) with \(e: \mathbb {G}_1\times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) of prime order q.
5.1 Warm-Up I: Inner Product Predicate, i.e. \({n'}=0\)
As a warm-up, we sketch the scheme and the proof for inner product predicate encryption, corresponding to the special case:
That is, the ciphertext is associated with a vector \({\mathbf {z}}\), and the secret key with a vector \({\mathbf {y}}\), and decryption is possible iff \(\langle {\mathbf {z}},{\mathbf {y}} \rangle = 0\). We refer the reader to the private-key variant in Sect. 2.2.
The scheme. The scheme is as follows:
Decryption relies on the fact that whenever \(\langle {\mathbf {z}},{\mathbf {y}} \rangle = 0\), we have
Proof sketch. The proof of security follows a series of games:
- Game 1. :
-
Switch \((\mathsf{{ct}},\mathsf{{kem}})\) to
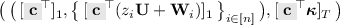
where \({\mathbf {c}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\). That is, we used the MDDH assumption in \(\mathbb {G}_1\) to replace \([{\mathbf {A}}{\mathbf {s}}]_1\) with \([{\mathbf {c}}]_1\).
- Game 2. :
-
Given the semi-adaptive challenge \({\mathbf {z}}^*\), the simulator picks \(\tilde{{\mathbf {W}}}_i \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{(k\,+\,1) \,\times \, k}, \hat{{\mathbf {s}}} \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\), and programs
$${\mathbf {c}}^{\!{\top }}{\mathbf {U}}= \hat{{\mathbf {s}}}^{\!{\top }}, \; \widetilde{{\mathbf {W}}}_i = {\mathbf {W}}_i + z^*_i {\mathbf {a}^{\perp }}\hat{{\mathbf {s}}}^{\!{\top }}$$where \({\mathbf {a}^{\perp }}\in {\mathbb {Z}}_q^{k\,+\,1}\) satisfies \({\mathbf {A}}^{\!{\top }}{\mathbf {a}^{\perp }}= \mathbf 0, {\mathbf {c}}^{\!{\top }}{\mathbf {a}^{\perp }}= 1\). Note that \({\mathbf {A}}^{\!{\top }}{\mathbf {W}}_i = {\mathbf {A}}^{\!{\top }}\widetilde{{\mathbf {W}}}_i\), which allows us to program \(z_i^*\) into \(\widetilde{{\mathbf {W}}}_i\) even though \(z_i^*\) is chosen after the adversary sees \({\textsf {mpk}}\). This parallels the step in the private-key variant where we program \(\tilde{{\mathbf {w}}} = u{\mathbf {w}}+{\mathbf {z}}^*\). Now, we can rewrite \((\mathsf{{ct}},\mathsf{{kem}})\) and \(\mathsf{{sk}}_{\mathbf {y}}\) as
$$\begin{aligned} (\mathsf{{ct}},\mathsf{{kem}}) :=&\,\bigl (\,\bigl (\,[{\mathbf {c}}^{\!{\top }}]_1, \bigl \{\,[{\mathbf {c}}^{\!{\top }}\widetilde{{\mathbf {W}}}_i]_1\,\bigr \}_{i \in [{n}]}\,\bigr ), [{\mathbf {c}}^{\!{\top }}\varvec{\kappa }]_T\,\bigr )\\ \mathsf{{sk}}_{\mathbf {y}}:=&\,\bigl (\,[\varvec{\kappa }+\langle {\mathbf {z}}^*,{\mathbf {y}} \rangle {\mathbf {a}^{\perp }}\hat{{\mathbf {s}}}^{\!{\top }}{\mathbf {r}}-\sum _{i\,=\,1}^{n}y_i \widetilde{{\mathbf {W}}}_i {\mathbf {r}}]_2, [{\mathbf {r}}]_2\,\bigr ) \end{aligned}$$ - Game 3. :
-
We use the MDDH assumption in \(\mathbb {G}_2\) to replace \(([\hat{{\mathbf {s}}}^{\!{\top }}{\mathbf {r}}]_2,[{\mathbf {r}}]_2)\) in \(\mathsf{{sk}}_{\mathbf {y}}\) with \(([\delta ]_2,[{\mathbf {r}}]_2)\): that is, we switch \(\mathsf{{sk}}_{\mathbf {y}}\) to
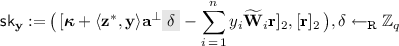
This parallels the step in the private-key variant where we applied the DDH assumption to switch ur to \(\delta \).
- Game 4. :
-
To complete the proof, it suffices to show that we can simulate \(\varvec{\kappa }+\langle {\mathbf {z}}^*,{\mathbf {y}} \rangle {\mathbf {a}^{\perp }}\delta \) (and thus \(\mathsf{{sk}}_{\mathbf {y}}\)) given \(a = {\mathbf {c}}^{\!{\top }}\varvec{\kappa }+ \delta \langle {\mathbf {z}}^*,{\mathbf {y}} \rangle \) (which we can simulate given the output from the ideal functionality). This follows from the fact that we can compute
$$[{\mathbf {A}}\mid {\mathbf {c}}]^{\!{\top }}(\varvec{\kappa }+\langle {\mathbf {z}}^*,{\mathbf {y}} \rangle {\mathbf {a}^{\perp }}\delta ) = \begin{bmatrix}{\mathbf {A}}^{\!{\top }}\varvec{\kappa }\\a\end{bmatrix}$$and then invert \([{\mathbf {A}}\mid {\mathbf {c}}]\).
5.2 Warm-Up II: A Private-Key Scheme
We sketch a private-key PHPE scheme for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) where the ciphertexts are over \({\mathbb {Z}}_q\) and secret keys are over \(\mathbb {G}_2\) and which achieves simulation-based security for a single challenge ciphertext and many secret keys under the DDH assumption in \(\mathbb {G}_2\).
The scheme. The scheme uses the algorithm \({\mathbf {rE}_f}\) described in the previous section.
Decryption computes \(\mathbf{rec }\) “in the exponent” over \(\mathbb {G}_2\) to recover \([\kappa ]_2\). The proof is similar to that for the private-key inner product predicate encryption; we omit the details here since we will directly prove security of the public-key scheme.
5.3 Our PHPE Scheme
Our PHPE scheme for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) also uses the algorithm \({\mathbf {rE}_f}\) described in the previous section:
- \(\mathbf{setup }(1^\lambda ,1^{{n'}+{n}})\) :
-
: pick \({\mathbf {A}}\leftarrow \mathcal {D}_k\), \({\mathbf {U}},{\mathbf {W}}_1,\ldots ,{\mathbf {W}}_{n},{\mathbf {V}}_1,\ldots ,{\mathbf {V}}_{n'}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{(k\,+\,1) \times k}, \varvec{\kappa }\leftarrow {\mathbb {Z}}_q^{k\,+\,1}\) and output
$$\begin{aligned} {\textsf {mpk}}&:= \Bigl (\;[{\mathbf {A}}]_1, [{\mathbf {A}}^{\!{\top }}{\mathbf {U}}]_1, \bigl \{\,[{\mathbf {A}}^{\!{\top }}{\mathbf {W}}_i]_1\,\bigr \}_{i \in [{n}]}, \bigl \{\,[{\mathbf {A}}^{\!{\top }}{\mathbf {V}}_i]_1\,\bigr \}_{i \in [{n'}]},\; [{\mathbf {A}}^{\!{\top }}\varvec{\kappa }]_T \;\Bigr ),\\ \mathsf{{msk}}&:= \Bigl (\;\varvec{\kappa },{\mathbf {U}},\bigl \{\,{\mathbf {W}}_i\,\bigr \}_{i \in [{n}]},\bigl \{\,{\mathbf {V}}_i\,\bigr \}_{i \in [{n'}]}\;\Bigr ) \end{aligned}$$ - \(\mathbf{enc }(\mathsf{{mpk}},({\mathbf {x}},{\mathbf {z}}))\) :
-
: pick \({\mathbf {s}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\) and output
$$\begin{aligned} \mathsf{{ct}}&:= \Bigl (\;\overbrace{[{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}]_1}^{C_0}, \bigl \{\,\overbrace{[{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}({\mathbf {U}}z_i + {\mathbf {W}}_i)]_1}^{C_{1,i}}\,\bigr \}_{i \in [{n}]}, \bigl \{\,\overbrace{[{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}({\mathbf {U}}x_i + {\mathbf {V}}_i)]_1}^{C_{2,i}}\,\bigr \}_{i \in [{n'}]}\;\Bigr )\\ \mathsf{{kem}}&:= [{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}\varvec{\kappa }]_T \end{aligned}$$ - \({\mathbf {keygen}}(\mathsf{{msk}},f\)):
-
: pick \({\mathbf {r}}_0,{\mathbf {r}}_1,\ldots ,{\mathbf {r}}_m \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\), sample \({\mathbf {T}}\), and output
$$\mathsf{{sk}}_{f} := \Bigl (\;\bigl [{\mathbf {rE}_f}\bigl (\,\varvec{\kappa },\bigl \{\,{\mathbf {W}}_i {\mathbf {r}}_0\,\bigr \}_{i \in [{n}]}, \bigl \{\,{\mathbf {U}}{\mathbf {r}}_j\,\bigr \}_{j \in [m]}, \bigl \{\,{\mathbf {V}}_i {\mathbf {r}}_j\,\bigr \}_{i \in [{n'}], j \in [m]};{\mathbf {T}}\,\bigr )\bigr ]_2, [{\mathbf {r}}_0]_2, \bigl \{\,[{\mathbf {r}}_j]_2\,\bigr \}_{j \in [m]}\;\Bigr )$$ - \(\mathbf{dec }((\mathsf{{sk}}_f,f),(\mathsf{{ct}},{\mathbf {x}}))\) :
-
: parse \(\mathsf{{ct}}= \bigl (\,C_0,\bigl \{\,C_{1,i}\,\bigr \}_{i \in [{n}]},\bigl \{\,C_{2,i}\,\bigr \}_{i \in [{n'}]}\,\bigr ), \mathsf{{sk}}_{f} = \bigl (\,D_0,[{\mathbf {r}}_0]_2,\bigl \{\,[{\mathbf {r}}_j]_2\,\bigr \}_{j \in [m]}\,\bigr )\), and output
$$\begin{aligned} \mathbf{rec }\bigl (\,f,{\mathbf {x}},e(C_0,D_0),\, \bigl \{\,e(C_{2,i},[{\mathbf {r}}_j]_2)\,\bigr \}_{i \in [{n'}], j \in [m]},\, \bigl \{\,e(C_{1,i},[{\mathbf {r}}_0]_2)\,\bigr \}_{i \in [{n}]}\,\bigr ) \end{aligned}$$where \(\mathbf{rec }\) is computed “in the exponent” over \(\mathbb {G}_T\).
5.4 Analysis
Theorem 1
Our PHPE scheme for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) described in Sect. 5.3 achieves simulation-based semi-adaptively partially (strongly) attribute-hiding under the MDDH assumption in \(\mathbb {G}_1\) and in \(\mathbb {G}_2\), with an unbounded simulator.
Note that unbounded simulation as considered in [4] implies (and is therefore stronger than) indistinguishability-based security.
Correctness. By the linearity and reconstruction properties for \({\mathbf {rE}_f}\), we have

Therefore, \(\mathbf{dec }\) outputs \([{\mathbf {s}}^{\!{\top }}{\mathbf {A}}\varvec{\kappa }]_T\) if \(f({\mathbf {x}},{\mathbf {z}})=0\) and a uniformly random value in \(\mathbb {G}_T\) otherwise.
5.5 Simulator
We start by describing the simulator for our scheme. Fix the semi-adaptive challenge \({\mathbf {x}}^*,{\mathbf {z}}^*\). Recall that for a query f to \({\mathbf {keygen}}\), the simulated \({\mathbf {keygen}}^*\) gets \(\mathsf{{kem}}\) from the ideal functionality if \(f({\mathbf {x}}^*,{\mathbf {z}}^*) = 0\), and \(\perp \) otherwise. In the first case, we assume that \({\mathbf {keygen}}^*\) gets \(\mathsf{{kem}}\) as a value in \({\mathbb {Z}}_q\) instead of \(G_T\), in which case it can be implemented efficiently. Otherwise, we would have an unbounded simulator (that computes discrete log via brute force) as considered in [4], which still implies indistinguishability-based security. In fact, to avoid the case analysis, we assume that the simulator gets \(\mathsf{{kem}}+ \delta _0 f({\mathbf {z}}^*,{\mathbf {z}}^*)\) where a fresh \(\delta _0 \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q\) is chosen for each f; it is easy to simulate this quantity given the output of the ideal functionality.
- \(\mathbf{setup }^*(1^\lambda ,1^{{n'}+{n}})\) :
-
: pick \({\mathbf {A}}\leftarrow \mathcal {D}_k\), \(\widetilde{{\mathbf {W}}}_1,\ldots ,\widetilde{{\mathbf {W}}}_{n},\widetilde{{\mathbf {V}}}_1,\ldots ,\widetilde{{\mathbf {V}}}_{n'}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{(k\,+\,1) \,\times \, k}, \widetilde{{\mathbf {U}}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k \times k}, \varvec{\kappa }\leftarrow {\mathbb {Z}}_q^{k\,+\,1}\), \({\mathbf {c}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\) and output
$$\begin{aligned} {\textsf {mpk}}&:= \Bigl (\;[{\mathbf {A}}]_1, [{\mathbf {A}}^{\!{\top }}\widetilde{{\mathbf {U}}}]_1, \bigl \{\,[{\mathbf {A}}^{\!{\top }}\widetilde{{\mathbf {W}}}_i]_1\,\bigr \}_{i \in [{n}]}, \bigl \{\,[{\mathbf {A}}^{\!{\top }}\widetilde{{\mathbf {V}}}_i]_1\,\bigr \}_{i \in [{n'}]},\; [{\mathbf {A}}^{\!{\top }}\varvec{\kappa }]_T \;\Bigr ),\\ \mathsf{{msk}}^*&:= \Bigl (\;\varvec{\kappa },\widetilde{{\mathbf {U}}},\bigl \{\,\widetilde{{\mathbf {W}}}_i\,\bigr \}_{i \in [{n}]},\bigl \{\,\widetilde{{\mathbf {V}}}_i\,\bigr \}_{i \in [{n'}]},{\mathbf {c}},\mathbf {C}^\perp ,{\mathbf {a}^{\perp }}\;\Bigr ) \end{aligned}$$where \(({\mathbf {A}}{\mid }{\mathbf {c}})^{\!{\top }}(\mathbf {C}^\perp {\mid } {\mathbf {a}^{\perp }}) = {\mathbf {I}}_{k\,+\,1}\). In particular, \({\mathbf {A}}^{\!{\top }}{\mathbf {a}^{\perp }}= \mathbf 0, {\mathbf {c}}^{\!{\top }}\mathbf {C}^\perp = \mathbf 0, {\mathbf {c}}^{\!{\top }}{\mathbf {a}^{\perp }}= 1\).
- \(\mathbf{enc }^*(\mathsf{{msk}}^*,{\mathbf {x}}^*)\) :
-
: output
$$\begin{aligned} \mathsf{{ct}}&:= \bigl (\,[{\mathbf {c}}^{\!{\top }}]_1, \bigl \{\,[{\mathbf {c}}^{\!{\top }}\widetilde{{\mathbf {W}}}_i]_1\,\bigr \}_{i \in [{n}]}, \bigl \{\,[{\mathbf {c}}^{\!{\top }}\widetilde{{\mathbf {V}}}_i]_1\,\bigr \}_{i \in [{n'}]}\,\bigr )\\ \mathsf{{kem}}&:= [{\mathbf {c}}^{\!{\top }}\varvec{\kappa }]_T \end{aligned}$$ - \({\mathbf {keygen}}^*(\mathsf{{msk}}^*,{\mathbf {x}}^*,f,a = {\mathbf {c}}^{\!{\top }}\varvec{\kappa }+ \delta _0 f({\mathbf {x}}^*,{\mathbf {z}}^*))\) :
-
: pick \({\mathbf {r}}_0,{\mathbf {r}}_1,\ldots ,{\mathbf {r}}_m \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\), sample \({\mathbf {T}}\), and output
$$\begin{aligned} \mathsf{{sk}}_{f}:= & {} \Bigl (\;\bigl [{\mathbf {rE}_f}\bigl (\,\mathbf 0,\bigl \{\,\widetilde{{\mathbf {W}}}_i {\mathbf {r}}_0\,\bigr \}_{i \in [{n}]}, \bigl \{\,\mathbf {C}^\perp \widetilde{{\mathbf {U}}}{\mathbf {r}}_j\,\bigr \}_{j \in [m]}, \bigl \{\,\widetilde{{\mathbf {V}}}_i {\mathbf {r}}_j\,\bigr \}_{i \in [{n'}], j \in [m]};{\mathbf {T}}\,\bigr )\bigr ]_2\\&+ \bigl [ \mathbf {C}^\perp \cdot {\mathbf {rE}_f}\bigl (\,{\mathbf {A}}^{\!{\top }}\varvec{\kappa }, \mathbf 0, \mathbf 0, \mathbf 0; \tilde{{\mathbf {T}}}\,\bigr ) + {\mathbf {a}^{\perp }}\cdot \mathbf{sim }(f,{\mathbf {x}}^*,a) \bigr ]_2 , [{\mathbf {r}}_0]_2, \bigl \{\,[{\mathbf {r}}_j]_2\,\bigr \}_{j \in [m]}\;\Bigr ) \end{aligned}$$
5.6 Security Proof
We show that for any adversary \(\mathcal {A}\) against the scheme, there exist adversaries \(\mathcal {A}_1,\mathcal {A}_2\) whose running times are essentially the same as that of \(\mathcal {A}\), such that
We proceed via a series of games and we use \(\textsf {Adv}_i\) to denote the advantage of \(\mathcal {A}\) in Game i.
Game 0. Real game.
Game 1. We replace \([{\mathbf {A}}{\mathbf {s}}]_1\) in \(\mathbf{enc }({\textsf {mpk}},({\mathbf {x}}^*,{\mathbf {z}}^*))\) with \([{\mathbf {c}}]_1\) where \({\mathbf {c}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\). That is, the challenge ciphertext is now given by
This follows readily from the MDDH Assumption (cf. Sect. 3.1), so we have
Game 2. We sample \(\hat{{\mathbf {s}}} \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\) and replace \(\mathbf{setup },\mathbf{enc }\) with \(\mathbf{setup }^*,\mathbf{enc }^*\) and \({\mathbf {keygen}}\) with \({\mathbf {keygen}}^*_2\) where
\({\mathbf {keygen}}^*_2(\mathsf{{msk}},f,{\mathbf {x}}^*)\): pick \({\mathbf {r}}_0,{\mathbf {r}}_1,\ldots ,{\mathbf {r}}_m \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\), sample \({\mathbf {T}}\), and output
$$\begin{aligned} \mathsf{{sk}}_{f}:= & {} \Bigl (\;\bigl [{\mathbf {rE}_f}\bigl (\,\varvec{\kappa }, \bigl \{\,\widetilde{{\mathbf {W}}}_i {\mathbf {r}}_0 - z_i^* {\mathbf {a}^{\perp }}\hat{{\mathbf {s}}}^{\!{\top }}{\mathbf {r}}_0\,\bigr \}_{i \in [{n}]}, \bigl \{\,\mathbf {C}^\perp \widetilde{{\mathbf {U}}}{\mathbf {r}}_j - {\mathbf {a}^{\perp }}\hat{{\mathbf {s}}}^{\!{\top }}{\mathbf {r}}_j\,\bigr \}_{j \in [m]},\\&\bigl \{\,\widetilde{{\mathbf {V}}}_i {\mathbf {r}}_j - x_i^* {\mathbf {a}^{\perp }}\hat{{\mathbf {s}}}^{\!{\top }}{\mathbf {r}}_j\,\bigr \}_{i \in [{n'}], j \in [m]} ;{\mathbf {T}}\,\bigr )\bigr ]_2, [{\mathbf {r}}_0]_2, \bigl \{\,[{\mathbf {r}}_j]_2\,\bigr \}_{j \in [m]}\;\Bigr ) \end{aligned}$$
The differences between \({\mathbf {keygen}}\) and \({\mathbf {keygen}}^*_2\) is that we have replaced occurrences of \(({\mathbf {U}},{\mathbf {W}}_i,{\mathbf {V}}_i)\) with those of \((\widetilde{{\mathbf {U}}},\widetilde{{\mathbf {W}}}_i,\widetilde{{\mathbf {V}}}_i)\) and introduced additional terms involving \({\mathbf {a}^{\perp }}\) and the semi-adaptive challenge \({\mathbf {x}}^*,{\mathbf {z}}^*\).
The change from Game 1 to Game 2 follows from the following change of variables which embeds the semi-adaptive challenge into the \({\mathbf {U}},{\mathbf {W}}_i,{\mathbf {V}}_i\):
which in particular implies that
where the LHS corresponds to \(\mathbf{enc }\) and the RHS to \(\mathbf{enc }^*\) and we use the fact that \(({\mathbf {A}}\mid {\mathbf {c}})^{\!{\top }}(\mathbf {C}^\perp \mid {\mathbf {a}^{\perp }}) = {\mathbf {I}}_{k\,+\,1}\).
For semi-adaptive security, we crucially rely on the fact that the terms \(\bigl (\,\widetilde{{\mathbf {U}}}, {\mathbf {A}}^{\!{\top }}\widetilde{{\mathbf {W}}}_i,{\mathbf {A}}^{\!{\top }}\widetilde{{\mathbf {V}}}_i\,\bigr )\) in \({\textsf {mpk}}\) in Game 2 only depends on \(\widetilde{{\mathbf {U}}},\widetilde{{\mathbf {W}}}_i,\widetilde{{\mathbf {V}}}_i\) (since \({\mathbf {A}}^{\!{\top }}{\mathbf {a}^{\perp }}= \mathbf 0\)), which allows us to embed the semi-adaptive challenge even though it may depend on \({\textsf {mpk}}\). Formally, to justify the change of variables, observe that for all \({\mathbf {A}},\mathbf {C}^\perp ,{\mathbf {a}^{\perp }},\hat{{\mathbf {s}}},{\mathbf {x}}^*,{\mathbf {z}}^*\), we have
where the distributions are taken over the random choices of \({\mathbf {U}},{\mathbf {W}}_i,{\mathbf {V}}_i,\widetilde{{\mathbf {U}}},\widetilde{{\mathbf {W}}}_i,\widetilde{{\mathbf {V}}}_i\). Then, by a complexity leveraging argument, we have that the distributions are identically distributed even if \(({\mathbf {x}}^*,{\mathbf {z}}^*)\) is adaptively chosen after seeing the first three terms in these distributions, as is the case for semi-adaptive security. Therefore, we have
Game 3. We replace \({\mathbf {keygen}}^*_2\) with \({\mathbf {keygen}}^*_3\) where
\({\mathbf {keygen}}^*_3(\mathsf{{msk}},f,{\mathbf {x}}^*)\): pick \({\mathbf {r}}_0,{\mathbf {r}}_1,\ldots ,{\mathbf {r}}_m \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k, \delta _0,\delta _1,\ldots ,\delta _m \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q\), sample \({\mathbf {T}}\), and output
where the grayed terms indicate the changes from \({\mathbf {keygen}}^*_2\). This follows from the MDDH Assumption (cf. Sect. 3.1), which tells us that

In fact, this tightly reduces to the MDDH Assumption [19] (think of the concatenation of \({\mathbf {r}}_0,{\mathbf {r}}_1,\ldots ,{\mathbf {r}}_m\) as a uniformly random matrix in \({\mathbb {Z}}_q^{k \,\times \, (m\,+\,1)}\), corresponding to the matrix \({\mathbf {A}}^{\!{\top }}\) in the original MDDH formulation).
Therefore, we have
Game 4. We replace \({\mathbf {keygen}}_3^*\) with \({\mathbf {keygen}}\). By linearity of \({\mathbf {rE}_f}\), we can write the output of \({\mathbf {keygen}}_3^*\) as
Write \({\mathbf {T}}= {\mathbf {C}}\tilde{{\mathbf {T}}} + {\mathbf {a}^{\perp }}{\mathbf {t}}\) where \(\tilde{{\mathbf {T}}},{\mathbf {t}}\) are uniformly random and independent. Then, again by linearity, we have

And therefore,
where the latter is exactly as computed in \({\mathbf {keygen}}^*\). This means
Notes
- 1.
Some early works around 2010–2011 use functional encryption (FE) to refer to ABE. Some more recent works also use predicate encryption to refer to ABE. For instance, we clarify here that the OT10 “KP-FE Scheme” in [29] for boolean formula with inner product gates is in fact an ABE and does not provide any attribute-hiding guarantee.
- 2.
Consider ABE in composite-order groups of order \(p_1p_2\). It is sufficient to show that the \(p_2\)-component of the encapsulated key accompanying the challenge ciphertext is completely hidden in the final hybrid, since we can always hash the encapsulated key, even if the \(p_1\)-component is completely leaked. In the case of strong attribute-hiding predicate encryption, it is not okay to leak the private attribute modulo \(p_1\), even if the \(p_2\)-component is completely hidden. For this reason, we need to ensure that there is no leakage in \(\mathsf{{sk}}\) beyond \(\mathsf{{sk}}^1,\mathsf{{sk}}^2\), which means that \(\mathsf{{sk}}^1,\mathsf{{sk}}^2\) need to completely determine \(\mathsf{{sk}}\).
- 3.
To achieve this, we need to also pre-process \(f'\) by first replacing every edge e for the public variable \({\mathbf {x}}\) with a pair of edges labeled 1 and \(\phi (e)\).
References
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 733–751. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_33
Abdalla, M., Gay, R., Raykova, M., Wee, H.: Multi-input inner-product functional encryption from pairings. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 601–626. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_21
Agrawal, S., Chase, M.: A study of pair encodings: predicate encryption in prime order groups. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 259–288. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_10
Agrawal, S., Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption: new perspectives and lower bounds. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 500–518. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_28. Also, Cryptology ePrint Archive, Report 2012/468
Agrawal, S., Libert, B., Stehlé, D.: Fully secure functional encryption for inner products, from standard assumptions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 333–362. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_12
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_15
Ananth, P., Brakerski, Z., Segev, G., Vaikuntanathan, V.: From selective to adaptive security in functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 657–677. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_32
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Baltico, C.E.Z., Catalano, D., Fiore, D., Gay, R.: Practical functional encryption for quadratic functions with applications to predicate encryption. Cryptology ePrint Archive, Report 2017/151 (2017)
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: FOCS (2015)
Blazy, O., Kiltz, E., Pan, J.: (Hierarchical) identity-based encryption from affine message authentication. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 408–425. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_23
Boneh, D., Waters, B.: Conjunctive, subset, and range queries on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 535–554. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_29
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_16
Boneh, D., Gentry, C., Gorbunov, S., Halevi, S., Nikolaenko, V., Segev, G., Vaikuntanathan, V., Vinayagamurthy, D.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
De Caro, A., Iovino, V., Jain, A., O’Neill, A., Paneth, O., Persiano, G.: On the achievability of simulation-based security for functional encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 519–535. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_29
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_25
Chen, J., Wee, H.: Semi-adaptive attribute-based encryption and improved delegation for boolean formula. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 277–297. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10879-7_16
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for diffie-hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS, pp. 40–49. Also, Cryptology ePrint Archive, Report 2013/451 (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: STOC, pp. 545–554. Also, Cryptology ePrint Archive, Report 2013/337 (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: ACM Conference on Computer and Communications Security, pp. 89–98 (2006)
Ishai, Y., Kushilevitz, E.: Perfect constant-round secure computation via perfect randomizing polynomials. In: Widmayer, P., Eidenbenz, S., Triguero, F., Morales, R., Conejo, R., Hennessy, M. (eds.) ICALP 2002. LNCS, vol. 2380, pp. 244–256. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45465-9_22
Ishai, Y., Wee, H.: Partial garbling schemes and their applications. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014. LNCS, vol. 8572, pp. 650–662. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43948-7_54. Also, Cryptology ePrint Archive, Report 2014/995
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Kiltz, E., Wee, H.: Quasi-adaptive NIZK for linear subspaces revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 101–128. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_4
Lewko, A.B., Waters, B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_27
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_11
Okamoto, T., Takashima, K.: Achieving short ciphertexts or short secret-keys for adaptively secure general inner-product encryption. In: Lin, D., Tsudik, G., Wang, X. (eds.) CANS 2011. LNCS, vol. 7092, pp. 138–159. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25513-7_11
Okamoto, T., Takashima, K.: Adaptively attribute-hiding (hierarchical) inner product encryption. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 591–608. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_35
Okamoto, T., Takashima, K.: Efficient (hierarchical) inner-product encryption tightly reduced from the decisional linear assumption. IEICE Trans. 96–A(1), 42–52 (2013)
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Acknowledgments
I would like to thank the anonymous reviewers for helpful feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Instantiating \({\mathbf {rE}_f}\) for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\)
In this section, we present our encoding algorithm \({\mathbf {rE}_f}\).
1.1 A.1 Partial Garbling for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\)
Our encoding algorithm \({\mathbf {rE}_f}\) uses as a building block the “partial garbling scheme” for \(\mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) from [24, 25]. Informally, a partial garbling scheme for each \(f \in \mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) takes as input as a secret \(\kappa \) along with \(({\mathbf {x}},{\mathbf {z}})\) and randomness \({\mathbf {t}}\) and outputs a collection of \(m+{n}+1\) shares
Here, \(m,\rho \) depends only on f, and \(\tau ,\sigma _i,\beta _j,\gamma _j\) depend on both f and \({\mathbf {t}}\). Given the shares along with \(f,{\mathbf {x}}\), we should be able to recover \(\kappa + f({\mathbf {x}},{\mathbf {z}})\) but learn nothing else about \(\kappa ,{\mathbf {z}}\).
Syntax and Properties of \(\mathbf{pgb }\). We will rely on a randomized algorithm \(\mathbf{pgb }\) that takes as input \(f \in \mathcal {F}_{{\textsf {ABP}} \circ {\textsf {IP}}}\) and randomness \({\mathbf {t}}\in {\mathbb {Z}}_q^{m\,+\,{n}}\) and outputs
Together with \({\mathbf {x}},{\mathbf {z}},\kappa \), this specifies a collection of \(m\,+\,{n}\,+\,1\) “shares”
Here, m is the ABP size of f and \(\rho \) is deterministically derived from f. The algorithm satisfies the following properties:
-
linearity: for a fixed f, \(\mathbf{pgb }(f;\cdot )\) computes a linear function of its randomness over \({\mathbb {Z}}_q\).
-
reconstruction: there exists an efficient algorithm \(\mathbf{rec }\) that on input f, x and the shares in (1), outputs \(\kappa + f({\mathbf {x}},{\mathbf {z}})\). This holds for all \(f, {\mathbf {x}}, {\mathbf {z}}, \kappa \). Moreover, \(\mathbf{rec }(f,{\mathbf {x}},\cdot )\) computes a linear function of the shares.
-
privacy: there exists an efficient simulator \(\mathbf{sim }\) such that for all \(f, {\mathbf {x}}, {\mathbf {z}}, \kappa \), the output of \(\mathbf{sim }(f, {\mathbf {x}}, \kappa + f({\mathbf {x}},{\mathbf {z}}))\) is identically distributed to the shares in (1) (for a random \({\mathbf {t}}\)).
The Algorithm. For completeness, we sketch the algorithm \(\mathbf{pgb }\) from [25]; we omit the analysis for reconstruction and privacy which follows from [25, Theorem 3, Corollary 1] with \(t=1\).
-
1.
Let \(f'\) denote the ABP computing \(({\mathbf {x}},{\mathbf {z}},\kappa ) \mapsto \kappa + f({\mathbf {x}},{\mathbf {z}})\) as shown in Fig. 3, such that \(\kappa ,{\mathbf {z}}\) only appear on edges leading into the sink node.
-
2.
Compute the matrix representation \({\mathbf {L}}_{{\mathbf {x}},{\mathbf {z}},\kappa }\in {\mathbb {Z}}_q^{(m\,+\,{n}\,+\,1) \,\times \, (m\,+\,{n}\,+\,1)}\) of \(f'\) using the algorithm in [25, Lemma 1], where \({\mathbf {L}}_{{\mathbf {x}},{\mathbf {z}},\kappa }\) satisfies the following properties as shown in Fig. 3:
-
\(\det ({\mathbf {L}}_{{\mathbf {x}},{\mathbf {z}},\kappa }) = \kappa + f({\mathbf {x}},{\mathbf {z}})\).
-
for \(j=1,\ldots ,m\), each entry in its j’th row is an affine function in \(x_{\rho (j)}\), where \(\rho : [{n'}] \rightarrow [m]\).Footnote 3
-
\({\mathbf {L}}_{{\mathbf {x}},{\mathbf {z}},\kappa }\) contains only 1’s in the second diagonal (the diagonal below the main diagonal) and 0’s below the second diagonal.
-
the last column of \({\mathbf {L}}_{{\mathbf {x}},{\mathbf {z}},\kappa }\) is \((0,\ldots ,0,z_1,\ldots ,z_{n},\kappa )^{\!{\top }}\).
Specifically, \({\mathbf {L}}_{{\mathbf {x}},{\mathbf {z}},\kappa }\) is obtained by removing the first column and the last row in the matrix \({\mathbf {A}}_{f'}-{\mathbf {I}}\), where \({\mathbf {A}}_{f'}\) is the adjacency matrix for the ABP computing f’.
-
-
3.
Write \({\mathbf {L}}_{{\mathbf {x}},{\mathbf {z}},\kappa } {{\mathbf {t}}\atopwithdelims ()1}\) as
$$\bigl (\,\beta _1 x_{\rho (1)}+\gamma _1, \ldots , \beta _m x_{\rho (1)}\,+\,\gamma _m, z_1+\sigma _1,\ldots ,z_{n}+\sigma _{n},\kappa +\tau \,\bigr )^{\!{\top }}$$ -
4.
Output \(\bigl (\,\tau ,\bigl \{\,\sigma _i\,\bigr \}_{i \in [{n}]}, \bigl \{\,\beta _j\,\bigr \}_{j \in [m]},\gamma _j\,\bigr )\).
It is straight-forward to verify that each of \(\tau ,\bigl \{\,\sigma _i\,\bigr \}_{i \in [{n}]}, \bigl \{\,\beta _j\,\bigr \}_{j \in [m]},\gamma _j\) are indeed linear functions in \({\mathbf {t}}\).
The Algorithm. The algorithm \({\mathbf {rE}_f}\) proceeds as follows:
-
1.
run \(\mathbf{pgb }(f;{\mathbf {t}})\) to sample \(\bigl (\,\tau , \bigl \{\,\sigma _i\,\bigr \}_{i \in [{n}]}, \bigl \{\,\beta _j, \gamma _j\,\bigr \}_{j \in [m]}\,\bigr )\)
-
2.
output
$$\begin{aligned} \Bigl (\;\kappa +\tau , \, \bigl \{\,\sigma _i - w'_i\,\bigr \}_{i \in [{n}]}, \, \bigl \{\,\beta _j + u'_j, \, \gamma _j + v'_{\rho (j)j}\,\bigr \}_{j \in [m]}\;\Bigr ) \in {\mathbb {Z}}_q^{1\,+\,n\,+\,m} \end{aligned}$$
We proceed to verify that \({\mathbf {rE}_f}\) satisfies the above properties:
-
linearity: Linearity follows from that for \(\mathbf{pgb }\).
-
reconstruction: We are given
$$\begin{array}{l} f,\;{\mathbf {x}},\;\kappa +\tau ,\\ \bigl \{\,\sigma _i-w'_i,\;z_i + w'_i\,\bigr \}_{i \in [{n}]},\\ \bigl \{\,\beta _j+u'_j,\;\gamma _j+v'_{\rho (j)j},\;u'_j x_i + v'_{ij}\,\bigr \}_{i \in [{n'}], j \in [m]} \end{array}$$We can compute
$$ \begin{array}{rlll} z_i + \sigma _i&{}=&{} (\sigma _i-w'_i) + (z_i + w'_i),&{}i \in [{n}]\\ \beta _j x_{\rho (j)} + \gamma _j &{}=&{} (\beta _j+u'_j) x_{\rho (j)} + (\gamma _j+v'_{\rho (j)j}) - (u'_j x_{\rho (j)} + v'_{\rho (j)j})&{}j \in [m] \end{array} $$We can then apply linear reconstruction for \(\mathbf{pgb }\) to
$$\begin{aligned} \kappa +\tau , \bigl \{\,z_i + \sigma _i\,\bigr \}_{i \in [{n}]}, \bigl \{\,\beta _j x_{\rho (j)} + \gamma _j\,\bigr \}_{j \in [m]} \end{aligned}$$to recover \(\kappa + f({\mathbf {x}},{\mathbf {z}})\).
-
privacy: The distribution we need to simulate is given by
$$\begin{aligned} \kappa + \tau , \bigl \{\,z_i + \sigma _i\,\bigr \}_{i \in [{n}]}, \bigl \{\,\beta _j + \delta _j\,\bigr \}_{j \in [m]}, \bigl \{\,\gamma _j - \delta _j x_{\rho (j)}\,\bigr \}_{j \in [m]}. \end{aligned}$$Given \(f,{\mathbf {x}},\kappa + f({\mathbf {x}},{\mathbf {z}})\), we can run the simulator for \(\mathbf{pgb }\) to obtain
$$\begin{aligned} \kappa + \tau , \bigl \{\,z_i + \sigma _i\,\bigr \}_{i \in [{n}]}, \bigl \{\,\beta _j x_{\rho (j)} + \gamma _j\,\bigr \}_{j \in [m]}. \end{aligned}$$For each \(j \in [m]\), we can simulate \(\bigl (\,\beta _j + \delta _j, \gamma _j - \delta _j x_{\rho (j)}\,\bigr )\) given \(x_{\rho (j)},\beta _j x_{\rho (j)} + \gamma _j\) as follows:
-
pick \(\tilde{\delta }_j \leftarrow _{\mathrm {R}}{\mathbb {Z}}_q\);
-
output \(\bigl (\,\tilde{\delta }_j,\, (\beta _j x_{\rho (j)} + \gamma _j)-\tilde{\delta }_j x_{\rho (j)}\,\bigr )\).
-
B Our Inner Product Functional Encryption Scheme
In this section, we present our inner product functional encryption scheme. The ciphertext is associated with a vector \({\mathbf {z}}\in {\mathbb {Z}}_q^n\), and the secret key with a vector \({\mathbf {y}}\in {\mathbb {Z}}_q^n\), and decryption recovers \(\langle {\mathbf {z}},{\mathbf {y}} \rangle \), provided the value falls in a polynomially bounded domain. Our scheme achieves simulation-based security as defined in Sect. 3.2, where the simulator \({\mathbf {keygen}}^*\) gets \({\mathbf {y}}, \langle {\mathbf {z}}^*,{\mathbf {y}} \rangle \) whenever the adversary makes a query \({\mathbf {y}}\) to \({\mathbf {keygen}}\).
1.1 B.1 Our Scheme
- \(\mathbf{setup }(1^\lambda ,1^n)\)::
-
pick \({\mathbf {A}}\leftarrow \mathcal {D}_k\), \({\mathbf {W}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{(k\,+\,1) \,\times \, n}\) and output
$$\begin{aligned} {\textsf {mpk}}&:= \Bigl (\;[{\mathbf {A}}]_1, [{\mathbf {A}}^{\!{\top }}{\mathbf {W}}]_1\;\Bigr ),\\ \mathsf{{msk}}&:= {\mathbf {W}}\end{aligned}$$ - \(\mathbf{enc }(\mathsf{{mpk}},{\mathbf {z}})\)::
-
pick \({\mathbf {s}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^k\) and output
$$\begin{aligned} \mathsf{{ct}}&:= \Bigl (\;\overbrace{[{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}]_1}^{{\mathbf {C}}_0}, \overbrace{[{\mathbf {s}}^{\!{\top }}{\mathbf {A}}^{\!{\top }}{\mathbf {W}}+ {\mathbf {z}}^{\!{\top }}]_1}^{{\mathbf {C}}_1}\;\Bigr ) \end{aligned}$$ - \({\mathbf {keygen}}(\mathsf{{msk}},{\mathbf {y}})\)::
-
$$\begin{aligned} \mathsf{{sk}}_{\mathbf {y}}:= {\mathbf {W}}{\mathbf {y}}\end{aligned}$$
- \(\mathbf{dec }((\mathsf{{sk}}_{\mathbf {y}},{\mathbf {y}}),({[C_0]_1,[C_1]_1)})\)::
-
output the discrete log of
$$\begin{aligned}{}[C_1 \cdot {\mathbf {y}}]_1 \cdot [C_0 \cdot \mathsf{{sk}}_{\mathbf {y}}]_1^{-1} \end{aligned}$$
1.2 B.2 Analysis
Theorem 2
Our Inner Product FE scheme described in Appendix B.1 achieves simulation-based semi-adaptively (strongly) attribute-hiding under the MDDH assumption in \(\mathbb {G}_1\) with an efficient simulator.
Correctness. Follows readily from
1.3 B.3 Simulator
- \(\mathbf{setup }^*(1^\lambda ,1^{{n'}\,+\,{n}})\) :
-
: pick \({\mathbf {A}}\leftarrow \mathcal {D}_k, \widetilde{{\mathbf {W}}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{(k\,+\,1) \,\times \, n},{\mathbf {c}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\) and output
$$\begin{aligned} {\textsf {mpk}}&:= \Bigl (\;[{\mathbf {A}}]_1, [{\mathbf {A}}^{\!{\top }}\widetilde{{\mathbf {W}}}]_1\;\Bigr ),\\ \mathsf{{msk}}^*&:= ({\mathbf {A}}, \widetilde{{\mathbf {W}}}, {\mathbf {c}},{\mathbf {a}^{\perp }}) \end{aligned}$$where \({\mathbf {a}^{\perp }}\in {\mathbb {Z}}_q^{k\,+\,1}\) satisfies \({\mathbf {A}}^{\!{\top }}{\mathbf {a}^{\perp }}= \mathbf 0, {\mathbf {c}}^{\!{\top }}{\mathbf {a}^{\perp }}= 1\).
- \(\mathbf{enc }^*(\mathsf{{msk}}^*)\) :
-
: output
$$\begin{aligned} \mathsf{{ct}}&:= \bigl (\,[{\mathbf {c}}^{\!{\top }}]_1,[{\mathbf {c}}^{\!{\top }}\widetilde{{\mathbf {W}}}]_1\,\bigr )\\ \end{aligned}$$ - \({\mathbf {keygen}}^*(\mathsf{{msk}}^*,{\mathbf {y}},a = \langle {\mathbf {z}}^*,{\mathbf {y}} \rangle )\) :
-
: output
$$\begin{aligned} \mathsf{{sk}}_{\mathbf {y}}:=&\widetilde{{\mathbf {W}}}{\mathbf {y}}- a \cdot {\mathbf {a}^{\perp }}\end{aligned}$$
1.4 B.4 Security Proof
We proceed via a series of games.
Game 0. Real game.
Game 1. We replace \([{\mathbf {A}}{\mathbf {s}}]_1\) in \(\mathbf{enc }({\textsf {mpk}},{\mathbf {z}}^*)\) with \([{\mathbf {c}}]_1\) where \({\mathbf {c}}\leftarrow _{\mathrm {R}}{\mathbb {Z}}_q^{k\,+\,1}\). That is, the challenge ciphertext is now given by
This follows readily from the MDDH Assumption (cf. Sect. 3.1), so we have
Game 2. We switch to the simulated game. The change from Game 1 to Game 2 follows from the following change of variables which embeds the semi-adaptive challenge \({\mathbf {z}}^*\) into the \({\mathbf {W}}\):
which in particular implies that
Formally, to justify the change of variables, observe that for all \({\mathbf {A}},{\mathbf {z}}^*\), we have
where the distributions are taken over the random choices of \({\mathbf {W}},\widetilde{{\mathbf {W}}}\). Then, by a complexity leveraging argument, we have that the distributions are identically distributed even if \({\mathbf {z}}^*\) is adaptively chosen after seeing the first term in these distributions, as is the case for semi-adaptive security. Therefore, we have
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Wee, H. (2017). Attribute-Hiding Predicate Encryption in Bilinear Groups, Revisited. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10677. Springer, Cham. https://doi.org/10.1007/978-3-319-70500-2_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-70500-2_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70499-9
Online ISBN: 978-3-319-70500-2
eBook Packages: Computer ScienceComputer Science (R0)