A Split-Merge DP-means Algorithm to Avoid Local Minima

Abstract

We present an extension of the DP-means algorithm, a hard-clustering approximation of nonparametric Bayesian models. Although a recent work [6] reports that the DP-means can converge to a local minimum, the condition for the DP-means to converge to a local minimum is still unknown. This paper demonstrates one reason the DP-means converges to a local minimum: the DP-means cannot assign the optimal number of clusters when many data points exist within small distances. As a first attempt to avoid the local minimum, we propose an extension of the DP-means by the split-merge technique. The proposed algorithm splits clusters when a cluster has many data points to assign the number of clusters near to optimal. The experimental results with multiple datasets show the robustness of the proposed algorithm.

1 Introduction

As we enter the age of “big data”, there is no doubt that there is an increasing need for clustering algorithms that summarize data autonomously and efficiently. Nonparametric models are prospective models to address this need because of their flexibility. Unlike traditional models with fixed model complexity as a parameter, nonparametric Bayesian models [17] dynamically determine the model complexity, i.e., the number of model components, in accordance with the data. The traditional nonparametric Bayesian model often needs a high computation time because the methods need sampling algorithms or variational inference for model optimization; however, the recently introduced DP-means algorithm [20] can determine model complexity with less computational cost. The DP-means uses a technique named small-variance asymptotic (SVA) for nonparametric Bayesian models and derives a hard-clustering algorithm similar to Lloyd’s k-means algorithm. The DP-means automatically determines the number of clusters and cluster centroids efficiently without sampling methods or variational inference techniques.

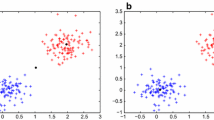
Convergence to a local minimum is a well-known problem in hard-clustering algorithms, especially in k-means clustering. Convergence to a local minimum of the k-means occurs when the initial clusters are assigned to close data points. For example in Fig. 1(a), if the initial two clusters are assigned to the left data points, the final solution can converge to the two clusters of the upper data points (green) and lower data points (red), although the preferred clustering solution is left data points and right data points. This convergence occurs because the k-means assigns the data points to the nearest clusters, so if the cluster initialization is inappropriate, the clustering solution converges to a local minimum. Therefore, initialization to avoid converging to a local minimum is an important step for the k-means algorithms, such as the k-means++ algorithm [4].

The DP-means also assigns the data points to the nearest clusters but generates new clusters when the distances between specific data points and existing clusters are large (Fig. 1(b)). Therefore, the DP-means is believed to be robust for convergence to local minima. However, a recent paper [6] reports that the DP-means can converge to a local minimum with fewer than the optimal number of clusters. The paper has a huge impact, but the condition for the DP-means to converge to a local minimum is still unknown.

Fig. 1.

Local minima of clustering algorithms. (a) The problem of the local minimum of the k-means is well-known; the k-means converges to a local minimum when initialization of clusters is not appropriate. (b) The DP-means is believed to be robust for this type of local minimum because it assigns new clusters when the new data points are distant from existing clusters. (c) However, as shown in this paper, the DP-means has a different type of local minimum; the DP-means cannot assign the optimal number of clusters when data points exist within small distances (Color figure online)

In this paper, we present an analysis of local minima of the DP-means. As shown later, the original DP-means can converge to local minima because the DP-means cannot assign the optimal number of clusters when the many data points exist within small distances. For example, in Fig. 1(b), the solution with the lowest cost (i.e. the preferred solution for the DP-means) is not that with two clusters when the number of data points is large; a solution with lower cost can be acquired when the number of clusters is six (Fig. 1(c)).

To avoid these local minima, we propose an extension of the DP-means by the split-merge technique. The proposed algorithm splits clusters when the original DP-means converges to a local minimum to obtain a good solution¹ with a near-optimal number of clusters.

1.1 Related Work

DP-means and extensions. Like nonparametric Bayesian models, the DP-means has many extensions. For example, the DP-means (i.e. the small-variance asymptotic technique for nonparametric Bayesian models) has been extended to the hard-clustering version of HDP topic models [19], dependent Dirichlet process [8], Bayesian hierarchical clustering [22], nonparametric Bayesian subspace clustering [31], infinite hidden Markov models [26], and infinite support vector machines [30]. Also, the DP-means itself has been extended to efficient algorithms, such as the distributed DP-means algorithm [25], one-pass online clustering for tweet data [28], and approximate clustering with a small subset named a coreset [6]. Although the concept of the DP-means has been extended to many algorithms, the condition of the local minimum of the DP-means is still unknown. To the best of our knowledge, this paper provides the first insight into conditions when the DP-means converges to a local minimum.

Hard-clustering algorithms. The Lloyd’s k-means algorithm [24] was proposed half a century ago, but it is still popular for data mining [32]. Although the original k-means algorithm is a batch clustering algorithm, the k-means algorithm has been extended to online settings [12, 23] and streaming settings [1, 2, 27]. These algorithms are mainly based on the k-means++ algorithm [4] with analysis of the local minimum of k-means clustering. Therefore, analysis of the local minimum of the DP-means provides useful information for future efficient DP-means algorithms.

Split-merge clustering algorithms. Split-merge techniques have been used in clustering including hard-clustering [3, 10, 14, 33]. Recently, split-merge algorithms have been extended to nonparametric Bayesian models optimized by MCMC [9, 11, 18, 29] and by variational inference [7]. This paper is the first to apply split-merge techniques to hard-clustering methods of nonparametric Bayesian models with small-variance asymptotics.

The contributions of this paper are: (1) analysis of a condition of converging to a local minimum for the DP-means, (2) proposal of a novel DP-means algorithm with split-merge techniques to avoid converging to a local minimum, and (3) evaluation of the efficiency of the proposed algorithms with several datasets including real-world data.

2 Analysis of Existing DP-means Approaches

2.1 DP-means Clustering Problem

First, we provide a brief overview of existing DP-means algorithms. The clustering problem is selecting cluster centroids so as to minimize the distance between each data point and its closest cluster. Solving this problem exactly is NP-hard even with two clusters [15], so a local search method known as Lloyd’s k-means algorithm [24] is widely used to acquire clustering solutions for a fixed number of clusters. The DP-means [20] (Algorithm 1) is a local search method to acquire clustering solutions for a variable number of clusters. Like Lloyd’s k-means, the DP-means optimizes clusters by iteratively (a) assigning each data point ${\varvec{x}_i}$ to clusters and (b) updating the centroids of each cluster by using assigned data points. However, unlike the k-means, the number of clusters optimized by the DP-means is not fixed. With hyperparameter $\lambda$ to control clustering granularity, the number of clusters is automatically determined in accordance with data complexity.

In one view, clustering problems can be regarded as optimization problems that minimize objective functions between data points and extracted clusters. Similar to the k-means, the DP-means monotonically decreases the following objective function, which is called the DP-means cost function:

$$\begin{aligned} \text {cost}_{DP}({\mathcal X}, {\mathcal C}) = \sum _{{\varvec{x}} \in {\mathcal X}} \min _{{\varvec{\mu }} \in {\mathcal C}} ||{\varvec{x}} - {\varvec{\mu }}||^2 + \lambda ^2 k \end{aligned}$$

(1)

Here, ${\mathcal X} \in {\mathbb R}^{d \times n}$ is a set of n data points with d feature dimensions, ${\mathcal C \in {\mathbb R}^{d \times k}}$ is a set of cluster centroids, and k is the number of clusters. The first term of Eq. (1) represents the quantization error when approximating data by clusters as the k-means objective function. The second term represents penalization of the number of clusters to avoid over-fitting data with too many clusters.

The DP-means can easily be extended to online algorithms like an online extension of Lloyd’s k-means [12]. Algorithm 2 shows a naive online extension of the DP-means algorithm. Instead of clustering all data at once, the online DP-means algorithm successively updates clusters as new data is loaded.

Because the batch DP-means and the online DP-means needs to perform a nearest-neighbor search for all existing clusters with each data point, the majority of computation time is consumed by this search step. Therefore, the time complexity of the batch DP-means is $\mathcal {O}(knl)$ (l is the number of iterations to convergence), and that of the online DP-means is $\mathcal {O}(kn)$. Note that because the computation time depends on the number of clusters, the computation time of the online DP-means can be larger than that of the batch DP-means.

The batch and online DP-means algorithms may assign new clusters when a new data point is loaded, so intuitively these algorithms seem to be strongly affected by the order of the data points. However, the problem is not data order: convergence to a local minimum can occur in both the existing DP-means approaches regardless of the data order, as shown in the following section.

2.2 Analysis of DP-means Algorithms

First, we provide a simplified condition to analyze DP-means clustering.

Definition 1

(easy case for DP-means clustering). We say the data is in the “easy case” for DP-means clustering when the maximum of the squared Euclidean distance of data is lower than $\lambda ^2$.

In the easy case, the data points exist within the hypersphere whose diameter is $\lambda$ (Fig. 2(a)). Note that even if the data points have multiple clusters, when the distance between clusters is sufficiently large, each individual cluster can be considered as belonging to the easy case. In this case, the solutions of the batch and online DP-means are the same, as shown in the following lemma.

Lemma 1

In the easy case, the solutions of the batch DP-means and the online DP-means are always one cluster whose centroid is the mean of the data points regardless of data order.

Proof

For the batch DP-means, the initial centroid is the mean of the data points regardless of data order by initialization. In this case, all data points are assigned to this centroid because the squared Euclidean distance between data points is less than $\lambda ^2$. For the online DP-means, the initial centroid is the top of data, and all data points are assigned to this cluster because the squared Euclidean distance between data points is less than $\lambda ^2$. In this case, the coordinates of the centroid converge to the mean of the data points regardless of the data order.    $\square$

Lemma 1 suggests the DP-means always converges to the solution with one cluster in easy cases. However, as shown in the following lemma, the solution with one cluster is not always that with the lowest DP-means cost.

Lemma 2

In easy cases, there exists the case when the DP-means cost with two clusters is less than that with one cluster.

Proof

Assume that $\lambda ^2 = 100$ and the data consists of 1000 points on $(-1, 0)$ and 1000 points on (1, 0), as shown in Fig. 2(b). This is an easy case. When the solution has one cluster, the centroid of the cluster is (0, 0). In this case, the DP-means cost is $\text {cost}_{DP}({\mathcal X}, {\mathcal C}_1) = 2000 \times 1^2 + 100 \times 1 = 2100$. However, if the solution has two clusters on $(-1, 0)$ and (1, 0), the DP-means cost is $\text {cost}_{DP}({\mathcal X}, {\mathcal C}_2) = 1000 \times 0^2 + 1000 \times 0^2 + 100 \times 2 = 200$. Therefore, in this case, the lower DP-means cost is acquired when the number of clusters is two.    $\square$

Then, we can find that the DP-means can converge to a local minimum.

Theorem 1

In easy cases, the batch DP-means and the online DP-means can converge to a local minimum with fewer than the optimal number of clusters.

Proof

By Lemma 2, there exists a case when the number of optimal clusters is more than one. However, by Lemma 1, the batch DP-means and the online DP-means always converge to the solution with one cluster. Therefore, in this case, the DP-means can converge to a local minimum with fewer clusters than the optimal number.

Fig. 2.

Analysis of DP-means. (a) Easy case. Although DP-means always converges solution with one cluster in easy case, (b) there exists case of solution with two clusters with less DP-means cost. (c) This characteristic is natural because nonparametric Bayesian models change model complexity according to data complexity.

This result matches a previous experimental result [6]. One reason for converging to the local minimum is that the DP-means ignores the number of data points assigned to clusters. For example, if the data consists of 10 points with $(-1, 0)$ and 10 points with (1, 0), the cost with one cluster is 120, and the cost with two clusters is 210, so the optimal solution is one cluster. Therefore, as suggested above, the optimal solution changes as the number of data points grows. Figure 2(c) shows an intuitive interpretation of this result. On the left and the right of this figure, the data points are generated by a mixture of two Gaussian distributions centered at $(-1, 0)$ and (1, 0), but the numbers of data points are different. When the number of data points is small (Fig. 2(c) left), the boundary between two clusters is vague. However, as the number of data points grows (Fig. 2(c) right), the boundary between two clusters becomes clear. This is the same characterization as for nonparametric Bayesian models, which is original distribution of the DP-means: the number of clusters is determined based on the complexity of data. Therefore, the DP-means should assign more clusters when the complexity of data grows with many data points.

3 Split-Merge DP-means

In this section, we discuss an extension of the DP-means named split-merge DP-means to avoid a local minimum with the split-merge technique. Based on the analysis in the previous section, the proposed algorithm splits clusters when the clusters contain many data points. Also, the proposed algorithm merges insufficiently split clusters.

In particular, as the first step to avoid a local minimum, we derive a split-merge DP-means with the following approximations²: (a) the distributions of clusters are approximated as uniform distributions, (b) the algorithm is executed with a one-pass update rule, and (c) the cluster is split in one dimension³. In the following section, we discuss the details of the proposed algorithm.

3.1 Condition for Splitting One Cluster into Two

Here, we provide the condition for splitting clusters to acquire the optimal DP-means cost. We assume that the data ${\mathcal X} \in {\mathbb R}^{d \times w}$ consists of w points generated by an origin-centered uniform distribution of range ${\varvec{\sigma }} = (\sigma _1, ..., \sigma _d) \in {\mathbb R}^d$. In the following, we consider two cases. The first is when the data is not split, i.e., the solution is one cluster. The second is when the data is split in dimension j, i.e., the solution is two clusters. When the data is not split, the DP-means solution is one cluster on ${\mathcal C}_1 = \{{\varvec{\mu }}_1\}= \{(0, ..., 0)\}$ with w data points. When the data is split on dimension j, the DP-means solution is two clusters on ${\mathcal C}_2 = \{{\varvec{\mu }}_{21}, {\varvec{\mu }}_{22}\} = \{(0, ..., -\sigma _j/2, ..., 0), (0, ..., \sigma _j/2, ..., 0)\}$ with w / 2 points on each cluster because of assumption of a uniform distribution.

Below, we provide the condition when the DP-means cost with two clusters is less than the DP-means cost with one cluster. Now, we consider the expectation values of DP-means cost with one cluster ${\text {Exp}}(\text {cost}_{DP}({\mathcal X}, {\mathcal C}_1))$ and two clusters ${\text {Exp}}(\text {cost}_{DP}({\mathcal X}, {\mathcal C}_2))$. Because of assumption of a uniform distribution, we can compute the expectation value of the squared Euclidean distance between a data point and the cluster center in dimension l when the cluster is not split, as $\text {Exp}((x_l- \mu _l)^2) = \int _{-\sigma _l/2}^{\sigma _l/2} \frac{1}{\sigma _l /2 - (-\sigma _l/2)} x^2 dx = \sigma _l^2/12$. Therefore, we have

$$\begin{aligned} \text {Exp}(\text {cost}_{DP}({\mathcal X}, {\mathcal C}_1))= & {} w \cdot \text {Exp}(\sum _{{\varvec{x}} \in {\mathcal X}} ||{\varvec{x}} - {\varvec{\mu }}_1||^2) + \lambda ^2 \cdot 1 \nonumber \\= & {} w(\frac{\sigma _1^2}{12} + ... + \frac{\sigma _d^2}{12}) + \lambda ^2 \end{aligned}$$

(2)

When the cluster is split in dimension j, the range of distance between the data point and the cluster center is reduced to $\sigma _j/2$. Therefore, the expectation value of the squared Euclidean distance between a data point and the cluster center in dimension j is reduced to $\int _{-\sigma _j/4}^{\sigma _j/4} \frac{1}{\sigma _j/4 - (-\sigma _j/4)} x^2 dx = \sigma _j^2/48$. Therefore,

$$\begin{aligned} \text {Exp}(\text {cost}_{DP}({\mathcal X}, {\mathcal C}_2))= & {} \frac{w}{2} \cdot \text {Exp}(\sum _{{\varvec{x}} \in {\mathcal X}} ||{\varvec{x}} - {\varvec{\mu }}_{21}||^2) + \frac{w}{2} \cdot \text {Exp}(\sum _{{\varvec{x}} \in {\mathcal X}} ||{\varvec{x}} - {\varvec{\mu }}_{22}||^2) + 2\lambda ^2 \nonumber \\= & {} w(\frac{\sigma _1^2}{12} + ... + \frac{\sigma _j^2}{48} + ... + \frac{\sigma _d^2}{12}) + 2\lambda ^2 \end{aligned}$$

(3)

Note that because the cluster range changes only dimension j, the expectation value of distance in each dimension except dimension j is the same value as that of one cluster. Then, the condition in which the solution with two clusters is better than that with one cluster is when $\text {Exp}(\text {cost}_{DP}({\mathcal X}, {\mathcal C}_1)) > \text {Exp}(\text {cost}_{DP}({\mathcal X}, {\mathcal C}_2))$. Therefore, by using Eqs. (2) and (3), we have the condition to split the cluster in dimension j:

$$\begin{aligned} w > 16\left( \frac{\lambda }{\sigma _j}\right) ^2 \end{aligned}$$

(4)

Equation (4) means (a) clusters with many data points should be split and (b) clusters with a wide range should be split. Also, when w is fixed, this condition is first satisfied by the dimension with maximum range. Therefore, we can determine the dimension to split clusters by finding out the dimension with the maximum range of clusters. Note that the derived splitting condition is based only on the expectation values of the distance (i.e. the second moment) between clusters and data points. Therefore, this analysis can easily be extended when the cluster is approximated to other distributions, such as Gaussian distributions.

3.2 Split DP-means

In the following section, we provide an novel online DP-means algorithm by splitting clusters on the basis of the analysis. The basic idea of the proposed online DP-means algorithm is storing the range of each cluster instead of each data point. The range of clusters can easily be updated and split with online update rules. Like the online DP-means algorithm, the proposed algorithm incrementally updates clusters with new data points. However, unlike existing DP-means algorithms, the proposed algorithm splits massive clusters that satisfy Eq. (4) to avoid converging to a local minimum.

Here, we provide online update rules when adding a data point and when splitting clusters. Consider the cluster $C = ({\varvec{\mu }}, w, {\varvec{\sigma }}, {\varvec{p}}, {\varvec{q}})$, where ${\varvec{\mu }} \in {\mathbb R}^d$ is the cluster centroid, $w \in {\mathbb R}$ is the number of data points assigned to the cluster, ${\varvec{\sigma }} \in {\mathbb R}^d$ is the range of the cluster, and ${\varvec{p}} \in {\mathbb R}^d$ and ${\varvec{q}} \in {\mathbb R}^d$ are the minimum values and the maximum values of the data points assigned to the cluster, respectively. When a new piece of data ${\varvec{x}}$ is added to the cluster, the cluster can be updated in the following manner,

(5)

When the splitting condition of Eq. (4) is satisfied in dimension j, the proposed algorithm splits cluster C into two clusters, $C_{L} = ({\varvec{\mu }}_L, w_L, {\varvec{\sigma }}_L, {\varvec{p}}_L, {\varvec{q}}_L)$ and $C_{R} = ({\varvec{\mu }}_R, w_R, {\varvec{\sigma }}_R, {\varvec{p}}_R, {\varvec{q}}_R)$, centered on the centroid $\mu _j$ of C in dimension j. The values of each cluster are computed in the following manner:

(6)

Here, $\mu _{L,m}, \mu _{R,m}, p_{L,m}, p_{R,m}, q_{L,m},$ and $q_{R,m}$ are the values of ${\varvec{\mu }}_L, {\varvec{\mu }}_R, {\varvec{p}}_L, {\varvec{p}}_R, {\varvec{q}}_L,$ and ${\varvec{q}}_R$ in dimension m, respectively. Note that because the real data does not follow uniform distributions, splitting clusters causes approximation errors due to the assumption of uniform distribution. Therefore, reducing the number of cluster splits is desirable. Therefore, in our implementation, if a new point is outside the cluster and the splitting condition of Eq. (4) is satisfied, the point is regarded as a new cluster instead of splitting the cluster. Also, note that as discussed in Sect. 3.1, when selecting the dimension to split the cluster, we select the dimension with the maximum range.

Algorithm 3 shows the derived algorithm. Like the online DP-means, the majority of computation time of split DP-means is consumed by the nearest-neighbor step. Therefore, the time complexity of split DP-means is $\mathcal {O}(kn)$.

3.3 Merge DP-means

The split DP-means (Algorithm 3) uses only the local information of the data, so the solution might have much more clusters than the optimal number. Here, we discuss the condition to merge overestimated clusters.

Merging two clusters. First, we provide the condition for merging two clusters. Consider two clusters: $C_L = ({\varvec{\mu }}_L, w_L, {\varvec{\sigma }}_L, {\varvec{p}}_L, {\varvec{q}}_L)$ and $C_R = ({\varvec{\mu }}_R, w_R, {\varvec{\sigma }}_R, {\varvec{p}}_R, {\varvec{q}}_R)$. Like the discussion in Sect. 3.1, the expected value of the DP-means cost with two clusters $\text {Exp}(\text {cost}_{DP}({\mathcal C}_2))$ can be computed as follows:

$$\begin{aligned} \text {Exp}(\text {cost}_{DP}({\mathcal C}_2)) = w_L(\frac{\sigma _{L,1}^2}{12} + ... + \frac{\sigma _{L,d}^2}{12}) + w_R(\frac{\sigma _{R,1}^2}{12} + ... + \frac{\sigma _{R,d}^2}{12}) + 2\lambda ^2 \end{aligned}$$

(7)

When the two clusters are merged to one cluster, the merged centroid becomes ${\varvec{\mu }}_M = \frac{w_L {\varvec{\mu }}_L + w_R {\varvec{\mu }}_R}{w_L + w_R}$. In this case, the difference vectors of centroids between cluster $C_L, C_R$ and the merged cluster $C_M$ are ${\varvec{\delta }}_L = (\delta _{L,1}, ..., \delta _{L,d}) = (\mu _{M,1} - \mu _{L,1}, ..., \mu _{M,d} - \mu _{L,d})$ and ${\varvec{\delta }}_M = (\delta _{M,1}, ..., \delta _{M,d}) = (\mu _{R,1} - \mu _{M,1}, ..., \mu _{R,d} - \mu _{M,d})$. Under the assumption of a uniform distribution, the expectation value of the squared Euclidean distance between a data point in cluster C and the center of the merged cluster $C_M$ in dimension l is computed as $\text {Exp}((x_l - \mu _m)^2) = \int _{\delta _l - \sigma _l/2}^{\delta _l + \sigma _l/2} \frac{1}{\delta _l+\sigma _l/2-(\delta _l-\sigma _l/2)} x^2 dx = \delta _l^2 + \sigma _l^2/12$. Therefore, the expectation value of the DP-means with one merged cluster $\text {Exp}(\text {cost}_{DP}({\mathcal C}_1))$ is

$$\begin{aligned} \text {Exp}(\text {cost}_{DP}({\mathcal C}_1))= & {} w_L\{(\delta _{L,1}^2 + ... + \delta _{L,d}^2) + (\frac{\sigma _{L,1}^2}{12} + ... + \frac{\sigma _{L,d}^2}{12}) \}\ \nonumber \\&+ w_R\{(\delta _{R,1}^2 + ... + \delta _{R,d}^2) + (\frac{\sigma _{R,1}^2}{12} + ... + \frac{\sigma _{R,d}^2}{12}) \}\ + \lambda ^2 \end{aligned}$$

(8)

The condition in which the solution with one merged cluster has lower cost than that with two clusters is when $\text {Exp}(\text {cost}_{DP}({\mathcal C}_1)) < \text {Exp}(\text {cost}_{DP}({\mathcal C}_2))$. Therefore, by using Eqs. (7) and (8), we have the condition to merge the clusters:

$$\begin{aligned} w_L(\delta _{L,1}^2 + ... + \delta _{L,d}^2) + w_R(\delta _{R,1}^2 + ... + \delta _{R,d}^2) - \lambda ^2 = w_L d_L^2 + w_R d_R^2 - \lambda ^2 < 0 \end{aligned}$$

(9)

Here, $d_L^2$ and $d_R^2$ are the squared Euclidean distance between the cluster centers of $C_L$ and $C_M$, $C_R$ and $C_M$, respectively.

Merging multiple clusters. Because the original cluster information is lost if we naively replace the clusters $C_L$ and $C_R$ with the merged clusters $C_M$, it is preferable to compute merged clusters with original clusters extracted by the split DP-means. Below, we discuss the merging condition when using multiple clusters extracted by the split DP-means.

Consider a cluster $C_k$ that is originally contained in the cluster $C_{old}$ with the centroid ${\varvec{\mu }}_{old}$ and then contained in the cluster $C_{new}$ with the centroid ${\varvec{\mu }}_{new}$ by a merge operation. Like the discussion of merging two clusters, the expectation value of the squared Euclidean distance of the dimension l when $C_k$ is contained by $C_{old}$ is $\text {Exp}((x_l - \mu _{old,l})^2) = d_{old}^2 + \sigma _l^2/12$ and that when $C_k$ is contained by $C_{new}$ is $\text {Exp}((x_l - \mu _{new,l})^2) = d_{new}^2 + \sigma _l^2/12$, where $d_{old}^2$ and $d_{new}^2$ are the squared Euclidean distance between the centroids of C and $C_{old}$, and that between the centroids of C and $C_{new}$, respectively. Therefore, the cost improvement of merging two clusters $\varDelta \text {cost}_{m}(C_L, C_R)$ is computed as follows:

$$\begin{aligned} \varDelta \text {cost}_m(C_L, C_R) = \sum _{C_i \in C_L} w_i (d_{new,i}^2 - d_{old,i}^2) + \sum _{C_i \in C_R} w_i (d_{new,i}^2 - d_{old,i}^2) - \lambda ^2 \end{aligned}$$

(10)

If $\varDelta \text {cost}_m(C_L, C_R) < 0$, the DP-means cost function improves by applying the merge operation. Algorithm 4 shows the derived algorithm. Our algorithm greedily merges the clusters with the lowest $\varDelta \text {cost}_m(C_L, C_R)$ value to improve the total DP-means cost.

Figure 3 shows an example result of the split-merge DP-means. In this example, the data points are generated by five Gaussians (two Gaussians in the left side, three Gaussians in the right side). When the number of data points is small, the split DP-means extracts clusters in the same way as the original DP-means (Fig. 3(a)). However, when the number of data points grows, the split DP-means splits clusters even when the data points are within a circle with diameter $\lambda$ as shown by the gray dotted circles in Fig. 3(b). Finally, the merge DP-means merges insufficiently split clusters (Fig. 3(c)).

Fig. 3.

Example result of split-merge DP-means for synthetic 2D data.

4 Experiments

In this section, we validate the performance of the proposed algorithms. Although we should determine $\lambda ^2$ for evaluation, to determine the “correct” value of $\lambda ^2$ is impossible because the suitable granularity of clusters differs in each application. Therefore, we conducted experiments with multiple $\lambda ^2$ for feasible results, i.e., so as not to generate too many clusters or too few clusters.

Datasets. We compare our algorithms with the following real data.

• (1) USGS [16] contains the locations of earthquakes around the world between 1972 to 2010 mapped to 3D space with WGS 84. The value of each coordinate is normalized by the radius of the earth. USGS has 59, 209 samples with three dimensions. We use $\lambda ^2 = [0.1, 0.32, 1.0, 3.2]$.

• (2) MNIST [21] contains 70,000 images of handwritten digits of size $28 \times 28$ pixels. We transform these images to 10 dimensions by using randomized PCA with whitening. MNIST has 70, 000 samples with 10 dimensions. We use $\lambda ^2 = [8.0 \times 10^0, 4.0 \times 10^1, 2.0 \times 10^2, 1.0 \times 10^3]$.

• (3) KDD2004BIO [13] contains features extracted from native protein sequences. KDD2004BIO has 145,751 samples with 74 dimensions. We use $\lambda ^2 = [3.2 \times 10^7, 1.0 \times 10^8, 3.2 \times 10^8, 1.0 \times 10^9]$.

• (4) SUN SCENES 397 [34] is a widely used image database for large-scale image recognition. We use GIST features extracted from each image for evaluation. SUN SCENES 397 has 198, 500 samples with 512 dimensions. We use $\lambda ^2 = [0.250, 0.354, 0.500, 0.707]$.

Note that our experimental settings include “reasonable” $\lambda ^2$ parameters used in a related work [6] ($\mathtt{USGS}$ with $\lambda ^2=1.0$, $\mathtt{MNIST}$ with $\lambda ^2=1.0\times 10^3$, $\mathtt{KDD2004BIO}$ with $\lambda ^2=1.0\times 10^9$), which are determined by dataset statistics. Additionally, to evaluate non-easy cases, we also conducted evaluations with smaller $\lambda ^2$.

Algorithms. We compared the DP-means costs with the following algorithms:

• (1) BD: Batch DP-means [20] (Algorithm 1).

• (2) OD: Online DP-means (Algorithm 2).

• (3) SD (proposed): Split DP-means (Algorithm 3).

• (4) SMD (proposed): Split-merge DP-means (Algorithms 3 and 4)⁴.

All algorithms were implemented by Python and ran in a single thread on an Intel Xeon machine with eight 2.5 GHz processors and 32 GB RAM. We measured the DP-means convergence when the change in cost was less than 0.01 or the number of iterations was over 300. We ran experiments for each data set with five different orders of data (the original order and four random permutations).

Results. Tables 1, 2, 3 and 4 show comparison results for the USGS data, MNIST data, KDD2004BIO data, and SUN SCENES 397 data, respectively. These tables show the average lowest DP-means cost with a $95\,\%$ confidence interval and the average computation time with five different data orders ($\pm 0$ means the clustering results are the same in the five data orders).

Table 1. DP-means cost and runtime comparison for USGS data.

Table 2. DP-means cost and runtime comparison for MNIST data.

As shown by the results, the proposed split-merge DP-means algorithm provided the solutions with lower cost than the existing DP-means algorithms for all datasets (including “reasonable” $\lambda ^2$ parameters [6]). Also, the result shows that the solutions of the batch DP-means result are the same in five different data orders in several cases (e.g. $\lambda ^2 = 1.0\times 10^3$ with $\mathtt{MNIST}$ data). These cases can be interpreted as when the batch DP-means converges to a local minimum. But even in these cases, the split-merge DP-means solutions have lower DP-means cost. Therefore, the proposed algorithm avoided converging to the local minima where the original DP-means converged. Also, as expected, the solutions provided by the split-merge DP-means have lower cost than those provided by the solutions of the split DP-means algorithm. Note that the split DP-means increases the computation time by more than the batch DP-means does in many cases because the solution of split DP-means has more clusters than that of the batch DP-means. For example, in the case of $\mathtt{MNIST}$ with $\lambda ^2 = 40$, though the split DP-means solution had only one cluster, the split DP-means solution had average 1700 clusters.

Note that though the DP-means solutions of the proposed algorithms are worse than Bachem’s recently reported result using a grid search of cluster numbers on the coresets [6] ($2.50 \times 10^{11}$ DP-means cost for KDD2004BIO dataset with $\lambda = 1.0 \times 10^9$), Bachem’s algorithm requires an exhaustive search to determine the optimal number of clusters. In contrast, the proposed algorithms do not require an exhaustive search for the number of clusters.

Table 3. DP-means cost and runtime comparison for KDD2004BIO data.

Table 4. DP-means cost and runtime comparison for SUN SCENES 397 data.

Table 5. Numbers of clusters for each dataset in original data order. Note that this table uses the same settings as Bachem et al. [6].

Table 5 shows the number of clusters extracted by each algorithm. In this table, “optimal” is the optimal number of clusters reported by the grid-search k-means algorithm of the number of clusters [6]. As reported in this study, the batch and online DP-means tend to converge to the local minimum due to there being too few clusters (less than 1/13 of the optimal number). The proposed algorithms extract the number of clusters nearer the optimal number (the result by the split-merge DP-means is within 2.5 times the optimal number). Although the online split DP-means result tends to extract more clusters than the optimal result, refinement with the split-merge DP-means reduces overestimated clusters.

5 Conclusion

In this paper, we discussed the condition where the DP-means can converge to a local minimum and then showed an extension of the DP-means. We provided an analysis for the condition where the DP-means converges to a local minimum: though more clusters are needed when the number of data points grows, the original DP-means cannot assign the optimal number of clusters. To avoid converging to these local minima, we derived an extension of the DP-means with the split-merge technique. We empirically showed that the proposed algorithm provides solutions with lower cost values.

The limitations of the current form of our algorithm are (a) data points are approximated as a specific distribution (uniform distribution), (b) the information of detailed data points is lost due to online update rules, and (c) the split operation is performed only in one dimension. In the future, we hope to extend the proposed algorithm to an more exact one without these approximations.