Abstract
Numerous confluence criteria for plain term rewrite systems are known. For logically constrained rewrite system, an attractive extension of term rewriting in which rules are equipped with logical constraints, much less is known. In this paper we extend the strongly-closed and (almost) parallel-closed critical pair criteria of Huet and Toyama to the logically constrained setting. We discuss the challenges for automation and present crest, a new tool for logically constrained rewriting in which the confluence criteria are implemented, together with experimental data.
This research is supported by FWF (Austrian Science Fund) Project I 5943-N.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Logically constrained rewrite systems constitute a general rewrite formalism with native support for constraints that are handled by SMT solvers. They are useful for program analysis, as illustrated in numerous papers [2, 3, 5, 13]. Several results from term rewriting have been lifted to constrained rewriting. We mention termination analysis [6, 7, 12], rewriting induction [3], completion [12] as well as runtime complexity analysis [13].
In this paper we are concerned with confluence analysis of logically constrained rewrite systems (LCTRSs for short). Only two sufficient conditions for confluence of LCTRSs are known. Kop and Nishida considered (weak) orthogonality in [8]. Orthogonality is the combination of left-linearity and the absence of critical pairs, in a weakly orthogonal system trivial critical pairs are allowed. Completion of LCTRSs is the topic of [12] and the underlying confluence condition of completion is the combination of termination and joinability of critical pairs. In this paper we add two further confluence criteria. Both of these extend known conditions for standard term rewriting to the constrained setting. The first is the combination of linearity and strong closedness of critical pairs, introduced by Huet [4]. The second, also due to [4], is the combination of left-linearity and parallel closedness of critical pairs. We also consider an extension of the latter, due to Toyama [11].
Overview. The remainder of this paper is organized as follows. In the next section we summarize the relevant background. Section 3 recalls the existing confluence criteria for LCTRSs and some of the underlying results. The new confluence criteria for LCTRSs are reported in Sect. 4. In Sect. 5 the automation challenges we faced are described and we present our prototype implementation crest. Experimental results are reported in Sect. 6, before we conclude in Sect. 7.
2 Preliminaries
We assume familiarity with the basic notions of term rewrite systems (TRSs) [1], but shortly recapitulate terminology and notation that we use in the remainder. In particular, we recall the notion of logically constrained rewriting as defined in [3, 8].
We assume a many-sorted signature \(\mathcal {F}\) and a set \(\mathcal {V}\) of (many-sorted) variables disjoint from \(\mathcal {F}\). The signature \(\mathcal {F}\) is split into term symbols from \(\mathcal {F}_{\textsf{te}}\) and theory symbols from \(\mathcal {F}_{\textsf{th}}\). The set \(\mathcal {T}(\mathcal {F},\mathcal {V})\) contains the well-sorted terms over this signature and \(\mathcal {T}(\mathcal {F}_{\textsf{th}})\) denotes the set of well-sorted ground terms that consist entirely of theory symbols. We assume a mapping \(\mathcal {I}\) which assigns to every sort \(\iota \) occurring in \(\mathcal {F}_{\textsf{th}}\) a carrier set \(\mathcal {I}(\iota )\), and an interpretation \(\mathcal {J}\) that assigns to every symbol \(f \in \mathcal {F}_{\textsf{th}}\) with sort declaration \(\iota _1 \times \cdots \times \iota _n \rightarrow \kappa \) a function \(f_\mathcal {J}:\mathcal {I}(\iota _1) \times \cdots \times \mathcal {I}(\iota _n) \rightarrow \mathcal {I}(\kappa )\). Moreover, for every sort \(\iota \) occurring in \(\mathcal {F}_{\textsf{th}}\) we assume a set \(\mathcal {V}\textsf{al}_\iota \subseteq \mathcal {F}_{\textsf{th}}\) of value symbols, such that all \(c \in \mathcal {V}\textsf{al}_\iota \) are constants of sort \(\iota \) and \(\mathcal {J}\) constitutes a bijective mapping between \(\mathcal {V}\textsf{al}_\iota \) and \(\mathcal {I}(\iota )\). Thus there exists a constant symbol in \(\mathcal {F}_{\textsf{th}}\) for every value in the carrier set. The interpretation \(\mathcal {J}\) naturally extends to a mapping \([\![{\cdot }]\!]\) from ground terms in \(\mathcal {T}(\mathcal {F}_{\textsf{th}})\) to values in \(\mathcal {V}\textsf{al}= \bigcup _{\iota \in \mathcal {D}\textsf{om}(\mathcal {I})} \mathcal {V}\textsf{al}_{\iota }\): \([\![{f({t_1},\dots ,{t_{n}})}]\!] = f_\mathcal {J}([\![{t_1}]\!],\dots ,[\![{t_n}]\!])\) for all \(f({t_1},\dots ,{t_{n}}) \in \mathcal {T}(\mathcal {F}_{\textsf{th}})\). So every ground term in \(\mathcal {T}(\mathcal {F}_{\textsf{th}})\) has a unique value. We demand that theory symbols and term symbols overlap only on values, i.e., \(\mathcal {F}_{\textsf{te}}\cap \mathcal {F}_{\textsf{th}}\subseteq \mathcal {V}\textsf{al}\). A term in \(\mathcal {T}(\mathcal {F}_{\textsf{th}},\mathcal {V})\) is called a logical term.
Positions are strings of positive natural numbers used to address subterms. The empty string is denoted by \(\epsilon \). We write \(q \leqslant p\) and say that p is below q if \(qq' = p\) for some position \(q'\), in which case \(p \backslash q\) is defined to be \(q'\). Furthermore, \(q < p\) if \(q \leqslant p\) and \(q \ne p\). Finally, positions q and p are parallel, written as \(q \parallel p\), if neither \(q \leqslant p\) nor \(p < q\). The set of positions of a term t is defined as \(\mathcal {P}\textsf{os}(t) = \{\epsilon \}\) if t is a variable or a constant, and as \(\mathcal {P}\textsf{os}(t) = \{\epsilon \} \cup \{iq \mid 1 \leqslant i \leqslant n\text { and }q \in \mathcal {P}\textsf{os}(t_i)\}\) if \(t = f({t_1},\dots ,{t_{n}})\) with \(n \geqslant 1\). The subterm of t at position \(p \in \mathcal {P}\textsf{os}(t)\) is defined as \(t|_p = t\) if \(p = \epsilon \) and as \(t|_p = t_i|_q\) if \(p = iq\) and \(t = f({t_1},\dots ,{t_{n}})\). We write \(s[t]_p\) for the result of replacing the subterm at position p of s with t. We write \(\mathcal {P}\textsf{os}_\mathcal {V}(t)\) for \(\{p \in \mathcal {P}\textsf{os}(t) \mid t|_p \in \mathcal {V}\}\) and \(\mathcal {P}\textsf{os}_\mathcal {F}(t)\) for \(\mathcal {P}\textsf{os}(t) \setminus \mathcal {P}\textsf{os}_\mathcal {V}(t)\). The set of variables occurring in the term t is denoted by \(\mathcal {V}\textsf{ar}(t)\). A term t is linear if every variable occurs at most once in it. A substitution is a mapping \(\sigma \) from \(\mathcal {V}\) to \(\mathcal {T}(\mathcal {F},\mathcal {V})\) such that its domain \(\{x \in \mathcal {V}\mid \sigma (x) \ne x\}\) is finite. We write \(t\sigma \) for the result of applying \(\sigma \) to the term t.
We assume the existence of a sort \(\textsf{bool}\) such that \(\mathcal {I}(\textsf{bool}) = \mathbb {B}= \{\top ,\bot \}\), \(\mathcal {V}\textsf{al}_{\textsf{bool}} = \{\textsf{true},\textsf{false}\}\), \([\![{\textsf{true}}]\!] = \top \), and \([\![{\textsf{false}}]\!] = \bot \) hold. Logical terms of sort \(\textsf{bool}\) are called constraints. A constraint \(\varphi \) is valid if \([\![{\varphi \gamma }]\!] = \top \) for all substitutions \(\gamma \) such that \(\gamma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {V}\textsf{ar}(\varphi )\).
A constrained rewrite rule is a triple \(\ell \rightarrow r~[\varphi ]\) where \(\ell , r \in \mathcal {T}(\mathcal {F},\mathcal {V})\) are terms of the same sort such that \(\textsf{root}(\ell ) \in \mathcal {F}_{\textsf{te}}\setminus \mathcal {F}_{\textsf{th}}\) and \(\varphi \) is a logical term of sort \(\textsf{bool}\). If \(\varphi = \textsf{true}\) then the constraint is often omitted, and the rule is denoted as \(\ell \rightarrow r\). We denote the set \(\mathcal {V}\textsf{ar}(\varphi ) \cup (\mathcal {V}\textsf{ar}(r) \setminus \mathcal {V}\textsf{ar}(\ell ))\) of logical variables in \(\rho :\ell \rightarrow r~[\varphi ]\) by \(\mathcal {L}\mathcal {V}\textsf{ar}(\rho )\). We write \(\mathcal {E}\mathcal {V}\textsf{ar}(\rho )\) for the set \(\mathcal {V}\textsf{ar}(r) \setminus (\mathcal {V}\textsf{ar}(\ell ) \cup \mathcal {V}\textsf{ar}(\varphi ))\) of variables that appear only in the right-hand side of \(\rho \). Note that extra variables in right-hand sides are allowed, but they may only be instantiated by values. This is useful to model user input or random choice [3]. A set of constrained rewrite rules is called a logically constrained rewrite system (LCTRS for short).
The LCTRS \(\mathcal {R}\) introduced in the example below computes the maximum of two integers.
Example 1
Before giving the rules, we need to define the term and theory symbols, the carrier sets and interpretation functions:
The interpretations for theory symbols follow the usual semantics given in the SMT-LIB theory IntsFootnote 1 used by the SMT-LIB logic QF_LIA. The LCTRS \(\mathcal {R}\) consists of the following constrained rewrite rules
In later examples we refrain from spelling out the signature and interpretations of the theory Ints. We now define rewriting using constrained rewrite rules. LCTRSs admit two kinds of rewrite steps. Rewrite rules give rise to rule steps, provided the constraint of the rule is satisfied. In addition, theory calls of the form \(f({v_1},\dots ,{v_{n}})\) with \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {V}\textsf{al}\) and values \({v_1},\dots ,{v_{n}}\) can be evaluated in a calculation step. In the definition below, a substitution \(\sigma \) is said to respect a rule \(\rho :\ell \rightarrow r~[\varphi ]\), denoted by \(\sigma \vDash \rho \), if \(\mathcal {D}\textsf{om}(\sigma ) = \mathcal {V}\textsf{ar}(\ell ) \cup \mathcal {V}\textsf{ar}(r) \cup \mathcal {V}\textsf{ar}(\varphi )\), \(\sigma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), and \(\varphi \sigma \) is valid. Moreover, a constraint \(\varphi \) is respected by \(\sigma \), denoted by \(\sigma \vDash \varphi \), if \(\sigma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {V}\textsf{ar}(\varphi )\) and \(\varphi \sigma \) is valid.
Definition 1
Let \(\mathcal {R}\) be an LCTRS. A rule step \(s \rightarrow _{\textsf{ru}}t\) satisfies \(s|_p = \ell \sigma \) and \(t = s[r\sigma ]_p\) for some position p and constrained rewrite rule \(\ell \rightarrow r~[\varphi ]\) that is respected by the substitution \(\sigma \). A calculation step \(s \rightarrow _{\textsf{ca}}t\) satisfies \(s|_p = f({v_1},\dots ,{v_{n}})\) and \(t = s[v]_p\) for some \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {V}\textsf{al}\), \({v_1},\dots ,{v_{n}} \in \mathcal {V}\textsf{al}\) with \(v = [\![{f({v_1},\dots ,{v_{n}})}]\!]\). In this case \(f({x_1},\dots ,{x_{n}}) \rightarrow y~[y = f({x_1},\dots ,{x_{n}})]\) with a fresh variable y is a calculation rule. The set of all calculation rules is denoted by \(\mathcal {R}_\textsf{ca}\). The relation \(\rightarrow _{\mathcal {R}}\) associated with \(\mathcal {R}\) is the union of \(\rightarrow _{\textsf{ru}}\cup \rightarrow _{\textsf{ca}}\).
We sometimes write \(\rightarrow _{p|\rho |\sigma }\) to indicate that the rewrite step takes place at position p, using the constrained rewrite rule \(\rho \) with substitution \(\sigma \).
Example 2
We have \(\textsf{max}(\textsf{1} + \textsf{2}, \textsf{4}) \rightarrow _{\mathcal {R}}\textsf{max}(\textsf{3}, \textsf{4}) \rightarrow _{\mathcal {R}}\textsf{max}(\textsf{4},\textsf{3}) \rightarrow _{\mathcal {R}}\textsf{4}\) in the LCTRS of Example 1. The first step is a calculation step. In the third step we apply the rule \(\textsf{max}(x,y) \rightarrow x~[x \ge y]\) with substitution \(\sigma = \{x \mapsto \textsf{4}, y \mapsto \textsf{3}\}\).
3 Confluence
In this paper we are concerned with the confluence of LCTRSs. An LCTRS \(\mathcal {R}\) is confluent if \(t \rightarrow _{\mathcal {R}}^{*} \cdot \mathrel {_{\mathcal {R}}^{*}{\leftarrow }} u\) for all terms s, t and u such that \(t \mathrel {_{\mathcal {R}}^{*}{\leftarrow }} s \rightarrow _{\mathcal {R}}^{*} u\). Confluence criteria for TRSs are based on critical pairs. Critical pairs for LCTRS were introduced in [8]. The difference with the definition below is that we add dummy constraints for extra variables in right-hand sides of rewrite rules.
Definition 2
An overlap of an LCTRS \(\mathcal {R}\) is a triple \(\langle \rho _1, p, \rho _2 \rangle \) with rules \(\rho _1:\ell _1 \rightarrow r_1~[\varphi _1]\) and \(\rho _2:\ell _2 \rightarrow r_2~[\varphi _2]\), satisfying the following conditions:
-
1.
\(\rho _1\) and \(\rho _2\) are variable-disjoint variants of rewrite rules in \(\mathcal {R}\cup \mathcal {R}_\textsf{ca}\),
-
2.
\(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _2)\),
-
3.
\(\ell _1\) and \(\ell _2|_p\) are unifiable with a mgu \(\sigma \) such that \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\),
-
4.
\(\varphi _1\sigma \wedge \varphi _2\sigma \) is satisfiable, and
-
5.
if \(p = \epsilon \) then \(\rho _1\) and \(\rho _2\) are not variants, or \(\mathcal {V}\textsf{ar}(r_1) \nsubseteq \mathcal {V}\textsf{ar}(\ell _1)\).
In this case we call \( \ell _2\sigma [r_1\sigma ]_p \approx r_2\sigma ~ [\varphi _1\sigma \wedge \varphi _2\sigma \wedge \psi \sigma ] \) a constrained critical pair obtained from the overlap \(\langle \rho _1, p, \rho _2 \rangle \). Here
The set of all constrained critical pairs of \(\mathcal {R}\) is denoted by \(\textsf{CCP}(\mathcal {R})\).
In the following we drop “constrained” and speak of critical pairs. The condition \(\mathcal {V}\textsf{ar}(r_1) \nsubseteq \mathcal {V}\textsf{ar}(\ell _1)\) in the fifth condition is essential to correctly deal with extra variables in rewrite rules. The equations (\(\psi \)) added to the constraint of a critical pair save the information which variables in a critical pair were introduced by variables only occurring in the right-hand side of a rewrite rule and therefore should only be instantiated by values. Critical pairs as defined in [8, 12] lack this information. The proof of Theorem 2 in the next section makes clear why those trivial equations are essential for our confluence criteria, see also Example 9.
Example 3
Consider the LCTRS consisting of the rule

The variable z does not occur in the left-hand side and the condition \(\mathcal {V}\textsf{ar}(r_1) \nsubseteq \mathcal {V}\textsf{ar}(\ell _1)\) ensures that \(\rho \) overlaps with (a variant of) itself at the root position. Note that \(\mathcal {R}\) is not confluent due to the non-joinable local peak \(\mathsf {-4} \leftarrow \textsf{f}(\textsf{16}) \rightarrow \textsf{4}\).
Example 4
The LCTRS \(\mathcal {R}\) of Example 1 admits the following critical pairs:
The originating overlap is given on the right, where we number the rewrite rules from left to right in Example 1.
Actually, there are three more overlaps since the position of overlap (\(\epsilon \)) is the root position. Such overlaps are called overlays and always come in pairs. For instance, \(\textsf{max}(y,x) \approx x~[x \ge y]\) is the critial pair originating from \(\langle 3, \epsilon , 1 \rangle \). For confluence criteria based on symmetric joinability conditions of critical pairs (like weak orthogonality and joinability of critical pairs for terminating systems) we need to consider just one critical pair, but this is not true for the criteria presented in the next section.
Logically constrained rewriting aims to rewrite (unconstrained) terms with constrained rules. However, for the sake of analysis, rewriting constrained terms is useful. In particular, since critical pairs in LCTRSs come with a constraint, confluence criteria need to consider constrained terms. The relevant notions defined below originate from [3, 8].
Definition 3
A constrained term is a pair \(s~[\varphi ]\) of a term s and a constraint \(\varphi \). Two constrained terms \(s~[\varphi ]\) and \(t~[\psi ]\) are equivalent, denoted by \(s~[\varphi ] \sim t~[\psi ]\), if for every substitution \(\gamma \) respecting \(\varphi \) there is some substitution \(\delta \) that respects \(\psi \) such that \(s\gamma = t\delta \), and vice versa. Let \(\mathcal {R}\) be an LCTRS and \(s~[\varphi ]\) a constrained term. If \(s|_p = \ell \sigma \) for some constrained rewrite rule \(\rho :\ell \rightarrow r~[\psi ]\), position p, and substitution \(\sigma \) such that \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\varphi \) is satisfiable and \(\varphi \Rightarrow \psi \sigma \) is valid then
is a rule step. If \(s|_p = f({s_1},\dots ,{s_{n}})\) with \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {F}_{\textsf{te}}\) and \({s_1},\dots ,{s_{n}} \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) then
is a calculation step. Here x is a fresh variable. We write \(\rightarrow _{\mathcal {R}}\) for \({\rightarrow _{\textsf{ru}}} \cup {\rightarrow _{\textsf{ca}}}\) and the rewrite relation
 on constrained terms is defined as \(\sim \cdot \rightarrow _{\mathcal {R}}\cdot \sim \).
on constrained terms is defined as \(\sim \cdot \rightarrow _{\mathcal {R}}\cdot \sim \).
Positions in connection with
 steps always refer to the underlying steps in \(\rightarrow _{\mathcal {R}}\). We give an example of constrained rewriting.
steps always refer to the underlying steps in \(\rightarrow _{\mathcal {R}}\). We give an example of constrained rewriting.
Example 5
Consider again the LCTRS \(\mathcal {R}\) of Example 1. We have
The first step is a calculation step. The second step is a rule step using the rule \(\textsf{max}(x,y) \rightarrow x ~ [x \ge y]\) with the substitution \(\sigma = \{x \mapsto z, y \mapsto \textsf{6}\}\). Note that the constraint \((x \ge \textsf{2} \wedge y \ge \textsf{4} \wedge z = x + y) \Rightarrow z \ge \textsf{6}\) is valid.
Definition 4
A critical pair \(s \approx t~[\varphi ]\) is trivial if \(s\sigma = t\sigma \) for every substitution \(\sigma \) with \(\sigma \vDash \varphi \).Footnote 2 A left-linear LCTRS having only trivial critical pairs is called weakly orthogonal. A left-linear TRS without critical pairs is called orthogonal.
The following result is from [8].
Theorem 1
Weakly orthogonal LCTRS are confluent. \(\square \)
Example 6
The following left-linear LCTRS computes the Ackermann function using term symbols from \(\mathcal {F}_{\textsf{te}}= \{\textsf{ack} : \textsf{int} \times \textsf{int} \Rightarrow \textsf{int}\} \cup \{\textsf{0}, \textsf{1}, \dots : \textsf{int}\}\) and the same theory symbols, carrier sets and interpretations as in Example 1:
Since the conjunction of any two constraints is unsatisfiable, \(\mathcal {R}\) lacks critical pairs. Hence \(\mathcal {R}\) is confluent by Theorem 1.
The following result is proved in [12] and forms the basis of completion of LCTRSs.
Lemma 1
Let \(\mathcal {R}\) be an LCTRS. If \(t \mathrel {_{\mathcal {R}}{\leftarrow }}s \rightarrow _{\mathcal {R}}u\) then \(t \downarrow _{\mathcal {R}}u\) or
 .
.
\(\square \)
In combination with Newman’s Lemma, the following confluence criterion is obtained.
Corollary 1
A terminating LCTRS is confluent if all critical pairs are joinable.
This is less obvious than it seems. Joinability of a critical pair \(s \approx t~[\varphi ]\) cannot simply be defined as
 , as the following example shows.
, as the following example shows.
Example 7
Consider the terminating LCTRS \(\mathcal {R}\) consisting of the rewrite rules
The single critical pair \(\textsf{h}(\textsf{g}(x,\textsf{1} + \textsf{1})) \approx \textsf{h}(\textsf{g}(y,\textsf{1} + \textsf{1}))\) should not be joinable because \(\mathcal {R}\) is not confluent, but we do have
due to the equivalence relation \(\sim \) on constrained terms; since x and y do not appear in the constraints, there is no demand that they must be instantiated with values.
The solution is not to treat the two sides of a critical pair in isolation but define joinability based on rewriting constrained term pairs. So we view the symbol \(\approx \) in a constrained equation \(s \approx t~[\varphi ]\) as a binary constructor symbol such that the constrained equation can be viewed as a constrained term. Steps in s take place at positions \(\geqslant 1\) whereas steps in t use positions \(\geqslant 2\). The same is done in completion of LCTRSs [12].
Definition 5
We call a constrained equation \(s \approx t~[\varphi ]\) trivial if \(s\sigma = t\sigma \) for any substitution \(\sigma \) with \(\sigma \vDash \varphi \). A critical pair \(s \approx t~[\varphi ]\) is joinable if
 and \(u \approx v~[\psi ]\) is trivial.
and \(u \approx v~[\psi ]\) is trivial.
We revisit Example 7.
Example 8
For the critical pair in Example 7 we obtain
The substitution \(\sigma = \{v \mapsto \textsf{2}, z \mapsto \textsf{2}\}\) respects the constraint \(v = \textsf{1} + \textsf{1} \wedge z = \textsf{1} + \textsf{1}\) but does not equate \(\textsf{h}(\textsf{g}(x,v))\) and \(\textsf{h}(\textsf{g}(y,z))\).
The converse of Corollary 1 also holds, but note that in contrast to TRSs, joinability of critical pairs is not a decidable criterion for terminating LCTRSs, due to the undecidable triviality condition. Moreover, for the converse to hold, it is essential that critical pairs contain the trivial equations \(\psi \) in Definition 2.
Example 9
Consider the LCTRS \(\mathcal {R}\) consisting of the rules
which admits the critical pair \(\textsf{g}(y) \approx \textsf{g}(y')~[y = y \wedge y' = y']\) originating from the overlap \(\langle \textsf{f}(x) \rightarrow \textsf{g}(y), \epsilon , \textsf{f}(x') \rightarrow \textsf{g}(y') \rangle \). This critical pair is joinable as y and \(y'\) are restricted to values and thus both sides rewrite to \(\textsf{a}\) using the second rule. As \(\mathcal {R}\) is also terminating, it is confluent by Corollary 1. If we were to drop \(\psi \) in Definition 2, we would obtain the non-joinable critical pair \(\textsf{g}(y) \approx \textsf{g}(y')\) instead and wrongly conclude non-confluence.
4 Main Results
We start with extending a confluence result of Huet [4] for linear TRSs. Below we write \(\rightarrow _{\geqslant p}\) to indicate that the position of the contracted redex in the step is below position p.
Definition 6
A critical pair \(s \approx t~[\varphi ]\) is strongly closed if
-
1.
 for some trivial \(u \approx v~[\psi ]\), and
for some trivial \(u \approx v~[\psi ]\), and -
2.
 for some trivial \(u \approx v~[\psi ]\).
for some trivial \(u \approx v~[\psi ]\).
A binary relation \(\rightarrow \) on terms is strongly confluent if \(t \rightarrow ^{*} \cdot \mathrel {^{=}{\leftarrow }} u\) for all terms s, t and u with \(t \leftarrow s \rightarrow u\). (By symmetry, also \(t \rightarrow ^{=} \cdot \mathrel {^{*}{\leftarrow }} u\) is required.) Strong confluence is a well-known sufficient condition for confluence. Huet [4] proved that linear TRSs are strongly confluent if all critical pairs are strongly closed. Below we extend this result to LCTRSs, using the above definition of strongly closed constrained critical pairs.
Theorem 2
A linear LCTRS is strongly confluent if all its critical pairs are strongly closed.
We give full proof details in order to illustrate the complications caused by constrained rewrite rules. The following result from [12] plays an important role.
Lemma 2
Suppose
 and \(\gamma \vDash \varphi \). If \(p \geqslant 1\) then \(s\gamma \rightarrow u\delta \) and \(t\gamma = v\delta \) for some substitution \(\delta \) with \(\delta \vDash \psi \). If \(p \geqslant 2\) then \(s\gamma = u\delta \) and \(t\gamma \rightarrow v\delta \) for some substitution \(\delta \) with \(\delta \vDash \psi \). \(\square \)
and \(\gamma \vDash \varphi \). If \(p \geqslant 1\) then \(s\gamma \rightarrow u\delta \) and \(t\gamma = v\delta \) for some substitution \(\delta \) with \(\delta \vDash \psi \). If \(p \geqslant 2\) then \(s\gamma = u\delta \) and \(t\gamma \rightarrow v\delta \) for some substitution \(\delta \) with \(\delta \vDash \psi \). \(\square \)
Proof
(of Theorem 2). Consider an arbitrary local peak
with rewrite rules \(\rho _1:\ell _1 \rightarrow r_1~[\varphi _1]\) and \(\rho _2:\ell _2 \rightarrow r_2~[\varphi _2]\) from \(\mathcal {R}\cup \mathcal {R}_\textsf{ca}\). We may assume that \(\rho _1\) and \(\rho _2\) have no variables in common, and consequently \(\mathcal {D}\textsf{om}(\sigma _1) \cap \mathcal {D}\textsf{om}(\sigma _2) = \varnothing \). We have \(s|_{p_1} = \ell _1\sigma _1\), \(t = s[r_1\sigma _1]_{p_1}\) and \(\sigma _1 \vDash \varphi _1\). Likewise, \(s|_{p_2} = \ell _2\sigma _2\), \(u = s[r_2\sigma _2]_{p_2}\) and \(\sigma _2 \vDash \varphi _2\). If \(p_1 \parallel p_2\) then
Hence both \(t \rightarrow ^{*} \cdot \mathrel {^{=}{\leftarrow }} u\) and \(t \rightarrow ^{=} \cdot \mathrel {^{*}{\leftarrow }} u\). If \(p_1\) and \(p_2\) are not parallel then \(p_1 \leqslant p_2\) or \(p_2 < p_1\). Without loss of generality, we consider \(p_1 \leqslant p_2\). Let \(q = p_2 \backslash p_1\). We do a case analysis on whether or not \(q \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _1)\).
-
First suppose \(q \notin \mathcal {P}\textsf{os}_\mathcal {F}(\ell _1)\). Let \(q = q_1q_2\) such that \(q_1 \in \mathcal {P}\textsf{os}_\mathcal {V}(\ell _1)\) and let x be the variable in \(\ell _1\) at position \(q_1\). We have \(\ell _2\sigma _2 = x\sigma _1|_{q_2}\) and thus \(\sigma _1(x) \notin \mathcal {V}\textsf{al}\). Define the substitution \(\sigma _1'\) as follows:
$$ \sigma _1'(y) = {\left\{ \begin{array}{ll} x\sigma _1[r_2\sigma _2]_{q_2} &{}\text {if }y = x \\ \sigma _1(y) &{}\text {otherwise} \end{array}\right. } $$We show \(t \rightarrow ^{=} s[r_1\sigma _1']_{p_1} \leftarrow u\), which yields \(t \rightarrow ^{*} \cdot \mathrel {^{=}{\leftarrow }} u\) and \(t \rightarrow ^{=} \cdot \mathrel {^{*}{\leftarrow }} u\). Since \(\mathcal {R}\) is left-linear, \(\ell _1\sigma _1' = \ell _1\sigma _1[x\sigma _1']_{q_1} = \ell _1\sigma _1[x\sigma _1[r_2\sigma _2]_{q_2}]_{q_1} = \ell _1\sigma _1[r_2\sigma _2]_q\) and thus \(u = s[r_2\sigma _2]_{p_2} = s[\ell _1\sigma _1[r_2\sigma _2]_q]_{p_1} = s[\ell _1\sigma _1']_{p_1}\). If we can show \(\sigma _1' \vDash \rho _1\) then \(u \rightarrow s[r_1\sigma _1']_{p_1}\). Consider an arbitrary variable \(y \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1)\). If \(y \ne x\) then \(\sigma _1'(y) = \sigma _1(y) \in \mathcal {V}\textsf{al}\) since \(\sigma _1 \vDash \rho _1\). If \(y = x\) then \(x \in \mathcal {V}\textsf{ar}(\varphi )\) since \(x \in \mathcal {V}\textsf{ar}(\ell _1)\). However, this contradicts \(\sigma _1 \vDash \rho _1\) as \(\sigma _1(x) \notin \mathcal {V}\textsf{al}\). So \(\sigma _1'(y) = \sigma _1(y)\) for all \(y \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1)\) and thus \(\sigma _1' \vDash \rho _1\) is an immediate consequence of \(\sigma _1 \vDash \rho _1\). It remains to show \(t \rightarrow ^{=} s[r_1\sigma _1']_{p_1}\). If \(x \notin \mathcal {V}\textsf{ar}(r_1)\) then \(r_1\sigma _1' = r_1\sigma _1\) and thus \(t = s[r_1\sigma _1']_{p_1}\). If \(x \in \mathcal {V}\textsf{ar}(r_1)\) then there exists a unique position \(q' \in \mathcal {P}\textsf{os}_\mathcal {V}(r_1)\) such that \(r_1|_{q'} = x\), due to the right-linearity of \(\mathcal {R}\). Hence \(r_1\sigma _1' = r_1\sigma _1[x\sigma _1[r_2\sigma _2]_{q_2}]_{q'} = r_1\sigma _1[r_2\sigma _2]_{q'q_2}\). Since \(r_1\sigma _1|_{q'q_2} = \ell _2\sigma _2\) we obtain \( t = s[r_1\sigma _1]_{p_1} \rightarrow _{p_1q'q_2|\rho _2|\sigma _2} s[r_1\sigma _1']_{p_1} \) as desired.
-
Next suppose \(q \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _1)\). The substitution \(\sigma ' = \sigma _1 \cup \sigma _2\) satisfies \(\ell _1|_q\sigma ' = \ell _1|_q\sigma _1 = \ell _2\sigma _2 = \ell _2\sigma '\) and thus is a unifier of \(\ell _1|_q\) and \(\ell _2\). Since \(\sigma _1 \vDash \rho _1\) and \(\sigma _2 \vDash \rho _2\), \(\sigma '(x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\). Let \(\sigma \) be an mgu of \(\ell _1|_q\) and \(\ell _2\). Since \(\sigma \) is at least as general as \(\sigma '\), \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\). Since \(\varphi _1\sigma ' = \varphi _1\sigma _1\) and \(\varphi _2\sigma ' = \varphi _2\sigma _2\) are valid, \(\varphi _1\sigma \wedge \varphi _2\sigma \) is satisfiable. Hence conditions 1, 2, 3 and 4 in Definition 2 hold for the triple \(\langle \rho _2, q, \rho _1 \rangle \). If condition 5 is not fulfilled then \(q = \epsilon \) (and thus \(p_1 = p_2\)), \(\rho _2\) and \(\rho _1\) are variants, and \(\mathcal {V}\textsf{ar}(r_2) \subseteq \mathcal {V}\textsf{ar}(\ell _2)\) (and thus also \(\mathcal {V}\textsf{ar}(r_1) \subseteq \mathcal {V}\textsf{ar}(\ell _1)\)). Hence \(\ell _1\sigma _1 = \ell _2\sigma _2\) and \(r_1\sigma _1 = r_2\sigma _2\), and thus \(t = u\). In the remaining case condition 5 holds and hence \(\langle \rho _2, q, \rho _1 \rangle \) is an overlap. By definition, \(\ell _1\sigma [r_2\sigma ]_q \approx r_1\sigma ~ [\varphi _2\sigma \wedge \varphi _1\sigma \wedge \psi \sigma ]\) with
$$ \psi = \bigwedge ~\{x = x \mid x \in \mathcal {E}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {E}\mathcal {V}\textsf{ar}(\rho _2)\} $$is a critical pair. To simplify the notation, we abbreviate \(\ell _1\sigma [r_2\sigma ]_q\) to \(s'\), \(r_1\sigma \) to \(t'\), and \(\varphi _2\sigma \wedge \varphi _1\sigma \wedge \psi \sigma \) to \(\varphi '\). Critical pairs are strongly closed by assumption, and thus both
-
1.
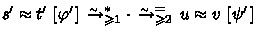 for some trivial \(u \approx v~[\psi ']\), and
for some trivial \(u \approx v~[\psi ']\), and -
2.
 for some trivial \(u \approx v~[\psi ']\).
for some trivial \(u \approx v~[\psi ']\).
Let \(\gamma \) be the substitution such that \(\sigma \gamma = \sigma '\). We claim that \(\gamma \) respects \(\varphi '\). So let \(x \in \mathcal {V}\textsf{ar}(\varphi ') = \mathcal {V}\textsf{ar}(\varphi _2\sigma \wedge \varphi _1\sigma \wedge \psi \sigma )\). We have
$$\begin{aligned} \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1)&= \mathcal {V}\textsf{ar}(\varphi _1) \cup \mathcal {E}\mathcal {V}\textsf{ar}(\rho _1)&\mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)&= \mathcal {V}\textsf{ar}(\varphi _2) \cup \mathcal {E}\mathcal {V}\textsf{ar}(\rho _2) \end{aligned}$$Together with \(\mathcal {V}\textsf{ar}(\psi ) = \mathcal {E}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {E}\mathcal {V}\textsf{ar}(\rho _2)\) we obtain
$$ \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2) = \mathcal {V}\textsf{ar}(\varphi _1) \cup \mathcal {V}\textsf{ar}(\varphi _2) \cup \mathcal {V}\textsf{ar}(\psi ) $$Since \(\sigma '(x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\), we obtain \(\gamma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {V}\textsf{ar}(\varphi ')\) and thus \(\gamma \vDash \varphi '\). At this point repeated applications of Lemma 2 to the constrained rewrite sequence in item 1 yields a substitution \(\delta \) respecting \(\psi '\) such that \(s'\gamma \rightarrow ^{*} u\delta \) and \(t'\gamma = v\delta \). Since \(u \approx v~[\psi ']\) is trivial, \(u\delta = v\delta \) and hence \(s'\gamma \rightarrow ^{*} \cdot \mathrel {^{=}{\leftarrow }} t'\gamma \). Likewise, \(s'\gamma \rightarrow ^{=} \cdot \mathrel {^{*}{\leftarrow }} t'\gamma \) is obtained from item 2. We have
$$\begin{aligned} s'\gamma&= (\ell _1\sigma [r_2\sigma ]_q)\gamma = \ell _1\sigma '[r_2\sigma ']_q = \ell _1\sigma _1[r_2\sigma _2]_q&t'\gamma&= r_1\sigma ' = r_1\sigma _1 \end{aligned}$$Moreover, \(t = s[r_1\sigma _1]_{p_1} = s[t'\gamma ]_{p_1}\) and \(u = s[\ell _1\sigma _1[r_2\sigma _2]_q]_{p_1} = s[s'\gamma ]_{p_1}\). Since rewriting is closed under contexts, we obtain \(u \rightarrow ^{*} \cdot \mathrel {^{=}{\leftarrow }} t\) and \(u \rightarrow ^{=} \cdot \mathrel {^{*}{\leftarrow }} t\). This completes the proof. \(\square \)
-
1.
Example 10
Consider the LCTRS \(\mathcal {R}\) of Example 1 and its critical pairs in Example 4. The critical pair
is not trivial, so Theorem 1 is not applicable and the rule \(\textsf{max}(x,y) \rightarrow \textsf{max}(y,x)\) precludes the use of Corollary 1 to infer confluence. We do have
by applying the rule \(\textsf{max}(x,y) \rightarrow y ~ [y \ge x]\) and the resulting constrained equation \(x \approx x~[x \ge y]\) is obviously trivial. The same reasoning applies to the critical pair \(y \approx \textsf{max}(y,x)~[y \ge x]\). The first critical pair \(x \approx y~[x \ge y \wedge y \ge x]\) in Example 4 is trivial since any (value) substitution satisfying its constraint \(x \ge y \wedge y \ge x\) equates x and y. By symmetry, all critical pairs of \(\mathcal {R}\) are strongly closed. Since \(\mathcal {R}\) is linear, confluence follows from Theorem 2.
The second main result is the extension of Huet’s parallel closedness condition on critical pairs in left-linear TRSs [4] to LCTRSs. To this end, we first define parallel rewriting for LCTRSs.
Definition 7
Let \(\mathcal {R}\) be an LCTRS. The relation
 is defined on terms inductively as follows:
is defined on terms inductively as follows:
-
1.
 for all variables x,
for all variables x, -
2.
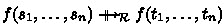 if
if
 for all \(1 \leqslant i \leqslant n\),
for all \(1 \leqslant i \leqslant n\), -
3.
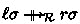 with \(\ell \rightarrow r~[\varphi ] \in \mathcal {R}\) and \(\sigma \vDash \ell \rightarrow r~[\varphi ]\),
with \(\ell \rightarrow r~[\varphi ] \in \mathcal {R}\) and \(\sigma \vDash \ell \rightarrow r~[\varphi ]\), -
4.
 with \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {V}\textsf{al}\), \({v_1},\dots ,{v_{n}} \in \mathcal {V}\textsf{al}\) and \(v = [\![{f({v_1},\dots ,{v_{n}})}]\!]\).
with \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {V}\textsf{al}\), \({v_1},\dots ,{v_{n}} \in \mathcal {V}\textsf{al}\) and \(v = [\![{f({v_1},\dots ,{v_{n}})}]\!]\).
We write
 to indicate that all positions of contracted redexes in the parallel step are below p. In the next definition we add constraints to parallel rewriting.
to indicate that all positions of contracted redexes in the parallel step are below p. In the next definition we add constraints to parallel rewriting.
Definition 8
Let \(\mathcal {R}\) be an LCTRS. The relation
 is defined on constrained terms inductively as follows:
is defined on constrained terms inductively as follows:
-
1.
 for all variables x,
for all variables x, -
2.
 if
if
 for all \(1 \leqslant i \leqslant n\) and \(\psi = \psi _1 \wedge \cdots \wedge \psi _n\),
for all \(1 \leqslant i \leqslant n\) and \(\psi = \psi _1 \wedge \cdots \wedge \psi _n\), -
3.
 with \(\rho :\ell \rightarrow r~[\omega ] \in \mathcal {R}\), \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\varphi \) is satisfiable and \(\varphi \Rightarrow \omega \sigma \) is valid,
with \(\rho :\ell \rightarrow r~[\omega ] \in \mathcal {R}\), \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\varphi \) is satisfiable and \(\varphi \Rightarrow \omega \sigma \) is valid, -
4.
 with \({v_1},\dots ,{v_{n}} \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\), \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {V}\textsf{al}\) and v is a fresh variable.
with \({v_1},\dots ,{v_{n}} \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\), \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {V}\textsf{al}\) and v is a fresh variable.
Here we assume that different applications to case 4 result in different fresh variables. The constraint \(\psi \) in case 2 collects the assignments introduced in earlier applications of case 4. (If there are none, \(\psi = \textsf{true}\) is omitted.) The same holds for \({\psi _1},\dots ,{\psi _{n}}\). We write
 for the relation
for the relation
 .
.
In light of the earlier developments, the following definition is the obvious adaptation of parallel closedness for LCTRSs.
Definition 9
A critical pair \(s \approx t~[\varphi ]\) is parallel closed if

for some trivial \(u \approx v~[\psi ]\).
Note that the right-hand side t of the constrained equation \(s \approx t~[\varphi ]\) may change due to the equivalence relation \(\sim \), cf. the statement of Lemma 2.
Theorem 3
A left-linear LCTRS is confluent if its critical pairs are parallel closed.
To prove this result, we adapted the formalized proof presented in [10] to the constrained setting. The required changes are very similar to the ones in the proof of Theorem 2.
Example 11
Consider the LCTRS \(\mathcal {R}\) with rules
The single critical pair \(\textsf{h}(\textsf{g}(\textsf{a},y + y)) \approx \textsf{h}(\textsf{g}(\textsf{b},\textsf{2}))~ [y \ge x \wedge y = \textsf{1} \wedge x \ge y]\) is parallel closed:

and the obtained equation is trivial. Hence \(\mathcal {R}\) is confluent by Theorem 3. Note that the earlier confluence criteria do not apply.
We also consider the extension of Huet’s result by Toyama [11], which has a less restricted joinability condition on critical pairs stemming from overlapping rules at the root position. Such critical pairs are called overlays whereas critical pairs originating from overlaps \(\langle \rho _1, p, \rho _2 \rangle \) with \(p > \epsilon \) are called inner critical pairs.
Definition 10
An LCTRS \(\mathcal {R}\) is almost parallel-closed if every inner critical pair is parallel closed and every overlay \(s \approx t~[\varphi ]\) satisfies

for some trivial \(u \approx v~[\psi ]\).
Theorem 4
Left-linear almost parallel-closed LCTRSs are confluent.
Again, the formalized proof of the corresponding result for plain TRSs in [10] can be adapted to the constrained setting.
Example 12
Consider the following variation of the LCTRS \(\mathcal {R}\) in Example 11:
The overlay \(\textsf{g}(\textsf{b},\textsf{2}) \approx \textsf{g}(\textsf{a},y + y)~ [x \ge y \wedge y \ge x \wedge y = \textsf{1}]\) is not parallel closed but one readily confirms that the condition in Definition 10 applies.
5 Automation
As it is very inconvenient and tedious to test by hand if an LCTRS satisfies one of the confluence criteria presented in the preceding sections, we provide an implementation. The natural choice would be to extend the existing tool Ctrl [9] because it is currently the only tool capable of analyzing confluence of LCTRSs. However, Ctrl is not actively maintained and not very well documented, so we decided to develop a new tool for the analysis of LCTRSs. Our tool is called crest (constrained rewriting software). It is written in Haskell, based on the Haskell term-rewritingFootnote 3 library and allows the logics QF_LIA, QF_NIA, QF_LRA.
The input format of crest is described on its website.Footnote 4 After parsing the input, crest checks that the resulting LCTRS is well-typed. Missing sort information is inferred. Next it is checked concurrently whether one of the implemented confluence criteria applies. crest supports (weak) orthogonality, strong closedness and (almost) parallel closedness. The tool outputs the computed critical pairs and a “proof” describing how these are closed, based on the first criterion that reports a YES result. Below we describe some of the challenges that one faces when automating the confluence criteria presented in the preceding sections.
First of all, how can we determine whether a constrained critical pair or more generally a constrained equation \(s \approx t~[\varphi ]\) is trivial? The following result explains how this can be solved by an SMT solver.
Definition 11
Given a constrained equation \(s \approx t~[\varphi ]\), the formula \(T(s,t,\varphi )\) is inductively defined as follows:
Lemma 3
A constrained equation \(s \approx t~[\varphi ]\) is trivial if and only if the formula \(\varphi \implies T(s,t,\varphi )\) is valid.
Proof
First suppose \(\varphi \implies T(s,t,\varphi )\) is valid. Let \(\sigma \) be a substitution with \(\sigma \vDash \varphi \). Since \(\sigma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {V}\textsf{ar}(\varphi )\), we can apply \(\sigma \) to the formula \(\varphi \implies T(s,t,\varphi )\). We obtain \([\![{\varphi \sigma }]\!] = \top \) from \(\sigma \vDash \varphi \). Hence also \([\![{T(s,t,\varphi )\sigma }]\!] = \top \). Since \(T(s,t,\varphi )\) is a conjunction, the final case in the definition of \(T(s,t,\varphi )\) is not used. Hence \(\mathcal {P}\textsf{os}(s) = \mathcal {P}\textsf{os}(t)\), \(s(p) = t(p)\) for all internal positions p in s and t, and \(s|_p\sigma = t|_p\sigma \) for all leaf positions p in s and t. Consequently, \(s\sigma = t\sigma \). This concludes the triviality proof of \(s \approx t~[\varphi ]\).
For the only if direction, suppose \(s \approx t~[\varphi ]\) is trivial. Note that the variables appearing in the formula \(\varphi \implies T(s,t,\varphi )\) are those of \(\varphi \). Let \(\sigma \) be an arbitrary assignment such that \([\![{\varphi \sigma }]\!] = \top \). We need to show \([\![{T(s,t,\varphi )\sigma }]\!] = \top \). We can view \(\sigma \) as a substitution with \(\sigma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {V}\textsf{ar}(\varphi )\). We have \(\sigma \vDash \varphi \) and thus \(s\sigma = t\sigma \) by the triviality of \(s \approx t~[\varphi ]\). Hence \(T(s,t,\varphi )\) is a conjunction of equations between values and variables in \(\varphi \), which are turned into identities by \(\sigma \). Hence \([\![{T(s,t,\varphi )\sigma }]\!] = \top \) as desired. \(\square \)
The second challenge is how to implement rewriting on constrained equations in particular, how to deal with the equivalence relation \(\sim \) defined in Definition 3.
Example 13
The LCTRS \(\mathcal {R}\)
over the integers admits two critical pairs:
The first one is trivial, but to join the second one, an initial equivalence step is required:
The transformation introduced below avoids having to look for an initial equivalence step before a rule becomes applicable.
Definition 12
Let \(\mathcal {R}\) be an LCTRS. Given a term \(t \in \mathcal {T}(\mathcal {F},\mathcal {V})\), we replace values in t by fresh variables and return the modified term together with the constraint that collects the bindings:
Applying the transformation \(\textsf{tf}\) to the left-hand sides of the rules in \(\mathcal {R}\) produces
Example 14
Applying the transformation \(\textsf{tf}\) to the LCTRS \(\mathcal {R}\) of Example 13 produces the rules
The critical pair \(\textsf{g}(z) \approx \textsf{a}~[z = \textsf{3}]\) can now be joined by an application of the modified third rule. Note that the modified rule does not overlap with the second rule because z may not be instantiated with \(\textsf{f}(x)\). Hence the modified LCTRS \(\textsf{tf}(\mathcal {R})\) is strongly closed and, because it is linear, also confluent.
In the following we show the correctness of the transformation. In particular we prove that the initial rewrite relation is preserved.
Lemma 4
The relations \(\rightarrow _{\mathcal {R}}\) and \(\rightarrow _{\textsf{tf}(\mathcal {R})}\) coincide on unconstrained terms.
Proof
Consider \(s, t \in \mathcal {T}(\mathcal {F},\mathcal {V})\). Since the transformation \(\textsf{tf}\) does not affect calculation steps, it suffices to consider rule steps. First assume \(s = C[\ell \sigma ] \rightarrow _{\textsf{ru}}C[r\sigma ] = t\) by applying the rule \(\ell \rightarrow r~[\varphi ] \in \mathcal {R}\) and let \(\ell ' \rightarrow r~[\varphi '] \in \textsf{tf}(\mathcal {R})\) be its transformation. So \(\textsf{tf}(\ell ) = (\ell ',\psi )\) and \(\varphi ' = \varphi \wedge \psi \). Define the substitution
and let \(\tau = \sigma \cup \sigma '\). Since \(\mathcal {D}\textsf{om}(\sigma ) \cap \mathcal {D}\textsf{om}(\sigma ') = \varnothing \) by construction, \(\tau \) is well-defined. From \(\sigma \vDash \ell \rightarrow r~[\varphi ]\) and \(\sigma ' \vDash \psi \) we immediately obtain \(\tau \vDash \ell ' \rightarrow r~[\varphi ']\), which yields \(s = C[\ell '\tau ] \rightarrow _{\textsf{ru}}C[r\tau ] = t\) in \(\textsf{tf}(\mathcal {R})\).
For the other direction consider \(s = C[\ell '\sigma ] \rightarrow _{\textsf{ru}}C[r'\sigma ] = t\) by applying the rule \(\ell ' \rightarrow r'~[\varphi '] \in \textsf{tf}(\mathcal {R})\). The difference between \(\ell '\) and its originating left-hand side \(\ell \) in \(\mathcal {R}\) is that value positions in \(\ell \) are occupied by fresh variables in \(\ell '\). Because \(\sigma '\) respects \(\varphi ' = \varphi \wedge \psi \), \(\sigma '\) substitutes the required values at these positions in \(\ell \). As \(\sigma \vDash \ell ' \rightarrow r'~[\varphi ']\), there exists a rule \(\ell \rightarrow r~[\varphi ]\) which is respected by \(\sigma \) and thus \(s = C[\ell \sigma ] \rightarrow _{\textsf{ru}}C[r\sigma ] = t\) in \(\mathcal {R}\). \(\square \)
As the transformation is used in the implementation and rewriting on constrained terms plays a key role, the following result is needed. The proof is similar to the first half of the proof of Lemma 4 and omitted.
Lemma 5
The inclusion \({\rightarrow _{\mathcal {R}}} \subseteq {\rightarrow _{\textsf{tf}(\mathcal {R})}}\) holds on constrained terms.
6 Experimental Results
In order to evaluate our tool we performed some experiments. As there is no official database of interesting confluence problems for LCTRSs, we collected several LCTRSs from the literature and the repository of Ctrl. The problem files in the latter that contain an equivalence problem of two functions for rewriting induction were split into two separate files. The experiments were performed on an AMD Ryzen 7 PRO 4750U CPU with a base clock speed of 1.7 GHz, 8 cores and 32 GB of RAM. The full set of benchmarks consists of 127 problems of which crest can prove 90 confluent, 11 result in MAYBE and 26 in a timeout. With a timeout of 5 s crest needs 141.09 s to analyze the set of benchmarks. We have tested the implementation with 3 well-known SMT solvers: Z3, Yices and CVC5. Among those Z3 gives the best performance regarding time and the handling of non-linear arithmetic. Hence we use Z3 as the default SMT solver in our implementation. In Table 1 we list some interesting systems from this paper and the relevant literature. Full details are available from the website of crest. We choose 5 as the maximum number of steps in the \(\rightarrow ^{*}\) parts of the strongly closed and almost parallel closed criteria.
From Table 2 the relative power of each implemented confluence criterion on our benchmark can be inferred, i.e., it depicts how many of the 127 problems both methods can prove confluent. This illustrates that the relative applicability in theory (e.g., weakly orthogonal LCTRSs are parallel closed), is preserved in our implementation. We conclude this section with an interesting observation discovered by crest when testing [12, Example 23].
We also tested the applicability of Corollary 1, using the tool Ctrl as a black box for proving termination. Of the 127 problems, Ctrl claims 102 to be terminating and 67 of those can be shown locally confluent by crest, where we limit the number of steps in the joining sequence to 100. It is interesting to note that all of these problems are orthogonal, and so proving termination and finding a joining sequence is not necessary to conclude confluence, on the current set of problems. Of the remaining 35 problems, crest can show confluence of 5 of these by almost parallel closedness.
Example 15
The LCTRS \(\mathcal {R}\) is obtained by completing a system consisting of four constrained equations:

Calling crest on \(\mathcal {R}\) results in a timeout. As a matter of fact, the LCTRS is not confluent because the critical pair
between rules 5 and 6 is not joinable. Inspecting the steps in [12, Example 23] reveals some incorrect applications of the inference rules of constrained completion, which causes rule 6 to be wrong. Replacing it with the correct rule
causes crest to report confluence by strong closedness.
7 Concluding Remarks
In this paper we presented new confluence criteria for LCTRSs as well as a new tool in which these criteria have been implemented. We clarified the subtleties that arise when analyzing joinability of critical pairs in LCTRSs and reported experimental results.
For plain rewrite systems many more confluence criteria are known and implemented in powerful tools that compete in the yearly Confluence Competition (CoCo).Footnote 5 In the near future we will investigate which of these can be lifted to LCTRSs. We will also advance the creation of a competition category on confluence of LCTRSs in CoCo.
Our tool crest has currently no support for termination. Implementing termination techniques in crest is of clear interest. The starting point here are the methods reported in [6, 7, 12]. Many LCTRSs coming from applications are actually non-confluent.Footnote 6 So developing more powerful techniques for LCTRSs is on our agenda as well.
Notes
- 1.
- 2.
The triviality condition in [8] is wrong. Here we use the corrected version in an update of [8] announced on Cynthia Kop’s website (accessible at https://www.cs.ru.nl/~cynthiakop/frocos13.pdf).
- 3.
- 4.
- 5.
- 6.
Naoki Nishida, personal communication (February 2023).
References
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998). https://doi.org/10.1017/CBO9781139172752
Ciobâcă, Ş, Lucanu, D.: A coinductive approach to proving reachability properties in logically constrained term rewriting systems. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 295–311. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_20
Fuhs, C., Kop, C., Nishida, N.: Verifying procedural programs via constrained rewriting induction. ACM Trans. Comput. Log. 18(2), 14:1–14:50 (2017). https://doi.org/10.1145/3060143
Huet, G.: Confluent reductions: abstract properties and applications to term rewriting systems. J. ACM 27(4), 797–821 (1980). https://doi.org/10.1145/322217.322230
Kojima, M., Nishida, N.: From starvation freedom to all-path reachability problems in constrained rewriting. In: Hanus, M., Inclezan, D. (eds.) PADL 2023. LNCS, vol. 13880, pp. 161–179. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-24841-2_11
Kop, C.: Termination of LCTRSs. In: Proceedings of the 13th International Workshop on Termination, pp. 59–63 (2013)
Kop, C.: Termination of LCTRSs. CoRR abs/1601.03206 (2016). https://doi.org/10.48550/ARXIV.1601.03206
Kop, C., Nishida, N.: Term rewriting with logical constraints. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 343–358. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_24
Kop, C., Nishida, N.: Constrained term rewriting tool. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR 2015. LNCS, vol. 9450, pp. 549–557. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48899-7_38
Nagele, J., Middeldorp, A.: Certification of classical confluence results for left-linear term rewrite systems. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 290–306. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-43144-4_18
Toyama, Y.: Commutativity of term rewriting systems. In: Fuchi, K., Kott, L. (eds.) Programming of Future Generation Computers II, pp. 393–407. North-Holland (1988)
Winkler, S., Middeldorp, A.: Completion for logically constrained rewriting. In: Kirchner, H. (ed.) Proceedings of the 3rd International Conference on Formal Structures for Computation and Deduction. Leibniz International Proceedings in Informatics, vol. 108, pp. 30:1–30:18 (2018). https://doi.org/10.4230/LIPIcs.FSCD.2018.30
Winkler, S., Moser, G.: Runtime complexity analysis of logically constrained rewriting. In: LOPSTR 2020. LNCS, vol. 12561, pp. 37–55. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-68446-4_2
Acknowledgments
We thank Fabian Mitterwallner for valuable discussions on the presented topics and our Haskell implementation. The detailed comments by the reviewers improved the presentation. Cynthia Kop and Deivid Vale kindly provided us with instructions and a working implementation of Ctrl.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Schöpf, J., Middeldorp, A. (2023). Confluence Criteria for Logically Constrained Rewrite Systems. In: Pientka, B., Tinelli, C. (eds) Automated Deduction – CADE 29. CADE 2023. Lecture Notes in Computer Science(), vol 14132. Springer, Cham. https://doi.org/10.1007/978-3-031-38499-8_27
Download citation
DOI: https://doi.org/10.1007/978-3-031-38499-8_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-38498-1
Online ISBN: 978-3-031-38499-8
eBook Packages: Computer ScienceComputer Science (R0)





 for some trivial
for some trivial  for some trivial
for some trivial 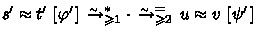 for some trivial
for some trivial  for some trivial
for some trivial  for all variables x,
for all variables x,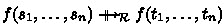 if
if
 for all
for all 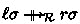 with
with  with
with  for all variables x,
for all variables x, if
if
 for all
for all  with
with  with
with