Abstract
Tweakable block ciphers (TBCs) have been established as a valuable replacement for many applications of classical block ciphers. While several dedicated TBCs have been proposed in the previous years, generic constructions that build a TBC from a classical block cipher are still highly useful, for example, to reuse an existing implementation. However, most generic constructions need an additional call to either the block cipher or a universal hash function to process the tweak, which limited their efficiency.
To address this deficit, Bao et al. proposed Tweak-aNd-Tweak (TNT) at EUROCRYPT’20. Their construction chains three calls to independent keyed permutations and adds the unmodified tweak to the state in between the calls. They further suggested an efficient instantiation TNT-AES that was based on round-reduced AES for each of the permutations. Their work could prove 2n/3-bit security for their construction, where n is the block size in bits. Though, in the absence of an upper bound, their analysis had to consider all possible attack vectors with up to \(2^n\) time, data, and memory. Still, closing the gap between both bounds remained a highly interesting research question.
In this work, we show that a variant of Mennink’s distinguisher on CLRW2 with \(O(\sqrt{n} 2^{3n/4})\) data and \(O(2^{3n/2})\) time from TCC’18 also applies to TNT. We reduce its time complexity to \(O(\sqrt{n} 2^{3n/4})\), show the existence of a second similar distinguisher, and demonstrate how to transform the distinguisher to a key-recovery attack on  from an impossible differential. From a constructive point of view, we adapt the rigorous STPRP analysis of CLRW2 by Jha and Nandi to show \(O(2^{3n/4})\) TPRP security for TNT. Thus, we move towards closing the gap between the previous proof and attacks for TNT as well as its proposed instance.
from an impossible differential. From a constructive point of view, we adapt the rigorous STPRP analysis of CLRW2 by Jha and Nandi to show \(O(2^{3n/4})\) TPRP security for TNT. Thus, we move towards closing the gap between the previous proof and attacks for TNT as well as its proposed instance.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Tweakable Block Ciphers (TBCs) differ from classical block ciphers in the sense that they take a public input called tweak that can increase the security or the performance of higher-level schemes effectively, e.g., in encryption modes [KR11, PS16], MACs [IMPS17, Nai15], or in authenticated-encryption schemes [IMPS17, JNP16]. Initially, TBCs have been built from classical block ciphers and universal hash functions, starting with Liskov et al.’s constructions [LRW02] LRW1 and LRW2. Various works enlarged the portfolio of generic TBC constructions, e.g. the cascade CLRW2 [LST12], Mennink’s constructions \(\widetilde{F}[1]\) and \(\widetilde{F}[2]\) [Men15], XHX [JLM+17], XHX2 [LL18], or the constructions by Wang et al. [WGZ+16]. These proposals processed the tweak either with a universal hash function or an additional call to the classical block cipher.
As An Alternative Approach, several works proposed dedicated TBCs in the previous decade. In particular, the TWEAKEY framework [JNP14b] found wide adoption, e.g. in Deoxys-BC, Joltik-BC [JNP14b], or Skinny [BJK+16]. Though, since TWEAKEY treats key and tweak equally, any update needs a call to (significant parts of) the TWEAKEY schedule. However, tweak updates occur usually considerably more frequently than key updates. For example, modes like CTRT or \(\varTheta \textsf {CB}3\) employ a different tweak in each primitive call. Thus, performant tweak-update functions can boost efficiency. KIASU-BC [JNP14a] or CRAFT [BLMR19] avoid tweak schedules, but need further analysis. Moreover, some applications cannot easily be equipped with novel dedicated TBCs but would profit rather from efficient transformations that turn an existing block-cipher implementation into a TBC. For this purpose, generic constructions such as CLRW2 are still relevant. Yet, it would be desirable if its internal hash function could be eliminated to avoid its implementation and the storage of its keys.
 is a recent proposal by Bao et al. [BGGS20] for generating a TBC from three block ciphers \(E_{K_1}, E_{K_2}, E_{K_3}: \mathcal {K} \times \mathbb {F} _2^n \rightarrow \mathbb {F} _2^n\), where \(\mathbb {F} _2\) is the Galois Field of characteristic 2 and \(\mathcal {K} \) a non-empty set of keys. The encryption of TNT is defined as
is a recent proposal by Bao et al. [BGGS20] for generating a TBC from three block ciphers \(E_{K_1}, E_{K_2}, E_{K_3}: \mathcal {K} \times \mathbb {F} _2^n \rightarrow \mathbb {F} _2^n\), where \(\mathbb {F} _2\) is the Galois Field of characteristic 2 and \(\mathcal {K} \) a non-empty set of keys. The encryption of TNT is defined as

where the tweak space is \(\mathcal {T} = 2^n\). The intermediate values are illustrated in Fig. 1. We will use \(\varDelta M\), \(\varDelta T\), etc. to refer to the differences between two values M and \(M'\), T and \(T'\), and so on. This extends naturally to the other variables. Given ideal secret permutations \(\pi _1, \pi _2, \pi _3 \in \mathsf {Perm} (\mathbb {F} _2^n)\), where \(\mathsf {Perm} (\mathcal {X})\) is the set of all permutations over a set \(\mathcal {X} \), Bao et al. [BGGS20] showed that TNT is a secure tweakable permutation for at least \(O(2^{2n/3})\) queries.
 instantiates the individual keyed permutations in TNT with round-reduced variants of AES. More precisely,
instantiates the individual keyed permutations in TNT with round-reduced variants of AES. More precisely,  denotes the version where \(\pi _i\) uses \(r_i\) rounds of the AES, for \(1 \le i \le 3\), and the tweak matches the state size of the AES, i.e. \(\mathcal {T} = \mathcal {B} = (\mathbb {F} _2^{8})^{4 \times 4}\), and \(n = 128\). The concrete proposal was
denotes the version where \(\pi _i\) uses \(r_i\) rounds of the AES, for \(1 \le i \le 3\), and the tweak matches the state size of the AES, i.e. \(\mathcal {T} = \mathcal {B} = (\mathbb {F} _2^{8})^{4 \times 4}\), and \(n = 128\). The concrete proposal was  [BGGS20]. While the earlier proposal contained no explicit claim, it suggested that TNT should be treated as a secure tweakable block cipher for up to \(O(2^{2n/3})\) queries and TNT-AES should provide n-bit security, even in the related-key chosen-tweak setting: “Following the proven security bound of TNT, TNT-AES offers 2n/3-bit security, i.e., there exists no key-recovery attack, given that the data (the combination of tweak and plaintext with no restriction on individual input) and time complexities are bounded by \(2^{2 \cdot 128/3} \simeq 2^{85}\). Due to the fact that there is no attack against TNT matching the \(2^{2n/3}\) bound, all our security analysis against TNT-AES are following the \(2^n = 2^{128}\) bound for both data and time” [BGGS20, Sect. 5.2]. The best attack in [BGGS20] was a related-tweak boomerang distinguisher on
[BGGS20]. While the earlier proposal contained no explicit claim, it suggested that TNT should be treated as a secure tweakable block cipher for up to \(O(2^{2n/3})\) queries and TNT-AES should provide n-bit security, even in the related-key chosen-tweak setting: “Following the proven security bound of TNT, TNT-AES offers 2n/3-bit security, i.e., there exists no key-recovery attack, given that the data (the combination of tweak and plaintext with no restriction on individual input) and time complexities are bounded by \(2^{2 \cdot 128/3} \simeq 2^{85}\). Due to the fact that there is no attack against TNT matching the \(2^{2n/3}\) bound, all our security analysis against TNT-AES are following the \(2^n = 2^{128}\) bound for both data and time” [BGGS20, Sect. 5.2]. The best attack in [BGGS20] was a related-tweak boomerang distinguisher on  with 21 active S-boxes. The asterisks indicate that the analysis holds for arbitrary values for \(r_1\) and \(r_3\).
with 21 active S-boxes. The asterisks indicate that the analysis holds for arbitrary values for \(r_1\) and \(r_3\).
Contribution. This work aims at narrowing the security gap from both sides. We show in Sect. 2 that a variant of Mennink’s distinguisher on CLRW2 [Men18] also applies to TNT, which yields a theoretical TPRP (i.e., chosen-tweak, chosen-plaintext) distinguisher in \(O(\sqrt{n} 2^{3n/4})\) time, data, and memory complexity. As improvements, we reduce the complexity of Mennink’s information-theoretic distinguisher from \(O(2^{3n/2})\) to \(O(2^{3n/4})\) computations. More precisely, we show two similar TPRP distinguishers that we call parallel-road and cross-road distinguishers. We use one of them to mount a partial key-recovery attack on the instance  with an impossible differential in Sect. 3. Since it needs more message pairs, its complexity exceeds \(O(2^{3n/4})\) but is still considerably below \(2^n\) computations and data. We emphasize that we do not break the proposed version
with an impossible differential in Sect. 3. Since it needs more message pairs, its complexity exceeds \(O(2^{3n/4})\) but is still considerably below \(2^n\) computations and data. We emphasize that we do not break the proposed version  of [BGGS20].
of [BGGS20].
From a constructive point of view, we show that the rigorous STPRP (i.e., chosen plain- and ciphertext queries) analysis by Jha and Nandi on CLRW2, that showed security for up to \(O(2^{3n/4})\) queries, can be adapted to a TPRP proof of TNT with similar complexity. Thus, we move a considerable step towards closing the gap between proofs and attacks for TNT and its proposed instance.
Notation. We use uppercase characters for variables and functions, lowercase characters for indices, calligraphic characters for sets and distributions, and sans-serif characters for random variables. For \(n \in \mathbb {N}\), let \([n] =^{\text {def}} \{1, 2, \ldots , n\}\) and \([0..n] =^{\text {def}} \{0, 1, \ldots , n\}\). For a bit string \(X \in \mathbb {F} _2^n\), let \(X = (X_{n-1} X_{n-2} \ldots X_{0})\) be its individual bits. We assume that the most significant bit is the leftmost, and the least significant bit is the rightmost bit, s.t. the integer representation x of X is \(x = \sum _i 2^i \cdot X_i\). For \(x < 2^n\), we will use \(X = \langle x \rangle _{n} \) as conversion of an integer x into a n-bit string X that represents x. For non-negative integers \(\le n\) and \(X \in \mathbb {F} _2^n\), we will use \(\textsf {lsb} _x(X)\) as function that returns the least significant x bits of X and \(\textsf {msb} _x(X)\) to return the most significant x bits of X. \(\left( n\right) _{k} \) denotes the falling factorial \(n! / (n - k)!\). For non-negative integers \(x + y = n\) and \(Z \in \mathbb {F} _2^n\), we will use \((X, Y) \xleftarrow {x, y} Z\) to denote that \(X \,\Vert \, Y = Z\) where \(|X| = x\) and \(|Y| = y\). Similar to \(\mathsf {Perm}\), we define \(\mathsf {\widetilde{Perm}} (\mathcal {T}, \mathcal {X})\) as the set of all tweakable permutations \(\widetilde{\pi }: \mathcal {T} \times \mathcal {X} \rightarrow \mathcal {X} \) over \(\mathcal {X} \) with tweak space \(\mathcal {T} \).
Practical Implications. While an STPRP proof is desirable, the implications of higher TPRP security already provide a valuable gain for TBC-based schemes that do not need the primitive’s inverse. Considering authenticated encryption schemes, examples of such schemes include SCT [PS16], ZAE [IMPS17], ZOTR [BGIM19], or the TBC-based variants of OTR (\(\mathbb {OTR}\)) [Min14] and COFB (iCOFB) [CIMN17, CIMN20]. Considering MACs, there exist various such constructions, e.g. ZMAC [IMPS17] and its derivates [LN17, Nai18]. The security of those schemes is limited by the minimum of \(O(2^{\min (n,(n + t)/2)})\) queries and the TPRP security of the underlying primitive. Since the latter is the bottleneck, its improvement yields directly higher security guarantees for the schemes.
 We assume that the reader is familiar with the AES. We use \(\mathsf {R}\) to refer to the round function, \(X^i\) for the state after i rounds, starting with \(X^0\) as the plaintext, and \(K^0\) for the initial round key. We use \(X^i_{\textsf {SB}}\), \(X^i_{\textsf {SR}}\), and \(X^i_{\textsf {MC}}\) to refer to the state directly after the SubBytes, ShiftRows, and MixColumns operation in the i-th round, respectively. Moreover, \(X^i[j]\) refers to the j-th byte of \(X^i\). For \(\mathcal {I} \subseteq \{0, 1, 2, 3\}\), we adopt the subspaces for diagonals \(\mathcal {D} _{\mathcal {I}}\), columns \(\mathcal {C} _{\mathcal {I}}\), inverse (or anti-)diagonals \(\mathcal {ID} _{\mathcal {I}}\), and mixed spaces \(\mathcal {M} _{\mathcal {I}}\) from Grassi et al. [GRR16].
We assume that the reader is familiar with the AES. We use \(\mathsf {R}\) to refer to the round function, \(X^i\) for the state after i rounds, starting with \(X^0\) as the plaintext, and \(K^0\) for the initial round key. We use \(X^i_{\textsf {SB}}\), \(X^i_{\textsf {SR}}\), and \(X^i_{\textsf {MC}}\) to refer to the state directly after the SubBytes, ShiftRows, and MixColumns operation in the i-th round, respectively. Moreover, \(X^i[j]\) refers to the j-th byte of \(X^i\). For \(\mathcal {I} \subseteq \{0, 1, 2, 3\}\), we adopt the subspaces for diagonals \(\mathcal {D} _{\mathcal {I}}\), columns \(\mathcal {C} _{\mathcal {I}}\), inverse (or anti-)diagonals \(\mathcal {ID} _{\mathcal {I}}\), and mixed spaces \(\mathcal {M} _{\mathcal {I}}\) from Grassi et al. [GRR16].
2 Distinguishers on TNT
Here, we briefly describe two distinguishers on TNT with \(O(\sqrt{n} \cdot 2^{3n/4})\) queries, which implies an upper bound on the (query) security of TNT of at most \(O(q^4 / (\sqrt{n} \cdot 2^{3n}))\). Our distinguishers are illustrated in Fig. 2. We do not claim that our observations are novel. Instead, both are applications of [LNS18] and [Men18]. The latter, however, is an information-theoretic distinguisher that uses \(O(\sqrt{n} \cdot 2^{3n/4})\) queries, but the description by Mennink demands \(O(2^{3n/2})\) offline operations to identify the required pairs.
We note that Sibleyras’ work [Sib20] proposes generic key-recovery attacks for LRW2 and cascades that also hold for CLRW2. Those attacks slightly reduce the time complexity of Mennink’s attack, but require more queries, roughly \(2^{2(n + k)/3}\), and are hence in \(O(2^n)\) for plausible values of the key size \(k \ge n/2\).
2.1 General Setup
Let \(M^0, M^1 \in \mathbb {F} _2^n\) be two distinct messages and \(\mathcal {T} ^0\) and \(\mathcal {T} ^1\) be two sets of \(q = 2^{3n/4 + x}\) pairwise distinct random tweaks \(T_j\) for \(0 \le j < q\) in each set, where \(\mathcal {T} ^i\) associates all tweaks with a fixed message \(M^i\) for \(\mathcal {T} ^i\) for \(i=0,1\). We describe two ways to combine two pairs to quartets each that differ in the way where the messages are used. Figure 2 may illustrate why we call them parallel- and cross-road distinguishers. For both distinguishers, we want two pairs, \((M_i, T_i)\) and \((M_j, T_j)\) as well as \((M_k, T_k)\) and \((M_{\ell }, T_{\ell })\), with the same tweak difference \(\varDelta T_{i,j} = T_i \oplus T_j = \varDelta T_{k,\ell } = T_k \oplus T_{\ell }\), and for which \(C_i = C_j\) and \(C_k = C_{\ell }\).
2.2 Cross-Road Distinguisher
Here, we denote the queries and intermediate variables
-
related to \((M^0, T^0_i) \in \mathcal {T} ^0\) also as \((S^0_i, U^0_i, V^0_i, W^0_i, C^0_i)\),
-
those related to \((M^1, T^1_j) \in \mathcal {T} ^1\) also as \((S^1_j, U^1_j, V^1_j, W^1_j, C^1_j)\),
-
those related to \((M^0, T^0_k) \in \mathcal {T} ^0\) also as \((S^0_k, U^0_k, V^0_k, W^0_k, C^0_k)\), and
-
those related to \((M^1, T^1_{\ell }) \in \mathcal {T} ^1\) also as \((S^1_{\ell }, U^1_{\ell }, V^1_{\ell }, W^1_{\ell }, C^1_{\ell })\).
Clearly, we want \(i \ne k\) and \(j \ne \ell \) as well as \((i, j) \ne (k, \ell )\).

Procedure. We define two construction functions:

The resulting tweak structures are illustrated in Fig. 3. The distinguisher procedure is given on the left-hand side of Algorithm 1. Let \(\theta \ge 0\) be a threshold. The threshold depends on the desired error (and success) probability and will be discussed in Sect. 3.3. The distinguisher can be described as:
-
1.
Initialize two lists \(\mathcal {L} \) and \(\mathcal {D} \) and initialize a counter \(\textsf {coll} = 0\).
-
2.
For \(i \in [0..q-1]\):
-
Use \(\tau _0(i)\) as tweak-construction function to generate queries \((M^0, T^0_i)\). Encrypt them to obtain \(C^0_i \leftarrow \mathcal {E} _K(T^0_i, M^0)\). Insert \(T^0_i\) to \(\mathcal {L} [C^0_i]\).
-
-
3.
For \(j \in [0..q-1]\):
-
Use \(\tau _1(j)\) as tweak-construction function to generate queries \((M^1, T^1_j)\). Encrypt them to obtain \(C^1_j \leftarrow \mathcal {E} _K(T^1_j, M^1)\).
-
3.1. For each \(T^0_i \in \mathcal {L} [C^1_j]\):
-
Derive \(\varDelta T_{i,j} = T^0_i \oplus T^1_j\). Derive the number of pairs \((T^0_k, T^1_{\ell })\) with the same tweak difference from \(\mathcal {D} [\varDelta T_{i,j}]\), add this number c to the total number of colliding quartets, \(\textsf {coll} \), and increment \(\mathcal {D} [\varDelta T_{i,j}]\).
-
-
-
4.
If \(\textsf {coll} > \theta \), return “real” and “random” otherwise.
Since the i-th and k-th query share the same message \(M^0\), it follows that \(S^0_i = S^0_k\); a similar argument holds from \(M^1_j = M^1_{\ell }\) to \(S^1_j = S^1_{\ell }\). With probability \(2^{-n}\), it holds that \(S^0_i \oplus S^1_{\ell } = T^0_i \oplus T^1_{\ell }\). In this case, it follows that \(U^0_i = U^1_{\ell }\). By combination, there exist approximately \((2^{3n/4 + x})^2 \cdot 1/(2^n - 1) \simeq 2^{n/2 + 2x}\) ordered collision pairs \(U^0_i = U^1_{\ell }\) between \((M^0, T^0_i)\) and \((M^1, T^1_{\ell })\). There exist \((2^{3n/4 + x} - 1)^2 \cdot 1/(2^{n} - 1) \simeq 2^{n/2 + 2x}\) ordered collision pairs \(U^0_k = U^1_j\) between \((M^0, T^0_k)\) and \((M^1, T^1_j)\). Note that this is a conditional probability; since \(S^0_k = S^0_i\) and \(S^1_j = S^1_{\ell }\), it follows from \(T^0_k \oplus T^1_j = S^0_k \oplus S^1_j\) that \(T^0_k \oplus T^1_j = T^0_i \oplus T^1_{\ell }\). Those will be mapped to \(V^0_i = V^1_{\ell }\) and \(V^0_k = V^1_j\). Thus, by combination, there are \(\left( {\begin{array}{c}2^{n/2 + 2x}\\ 2\end{array}}\right) \simeq 2^{n + 4x - 1}\) pairs of pairs (quartets) with \(T^0_i \oplus T^1_{\ell }\) and \(T^0_k \oplus T^1_j\). With probability \(2^{-n}\), a quartet has \(V^0_i \oplus V^1_{\ell } = T^0_k \oplus T^1_j\), which implies \(W^0_i = W^0_j\). Since \(V^0_i = V^1_{\ell }\) and \(V^0_k = V^1_j\), this implies that \(W^0_k = W^1_{\ell }\) also holds. We obtain
Similarly, we expect \((2^{3n/4 + x})^2 \cdot 2^{-n} \simeq 2^{n/2 + 2x}\) pairs \(C^0_i = C^1_j\) formed by accident, which can be combined to
For a random tweakable permutation, only the latter events occur, whereas we have two sources in the real world. Thus, we can expect twice as many quartets in the real construction compared to the ideal world.
Experimental Verification. To improve the understanding, we followed Mennink’s approach and also implemented the distinguisher for small permutations. We used TNT with three independent instances of Small-PRESENT-n [Lea10], the small-scale variants of PRESENT [BKL+07], with the original key schedule of PRESENT as proposed there, where the original round keys \(K^i\) are truncated to their rightmost (least significant) n bits for \(n \in \{16, 20, 24\}\). We employed the full 31 rounds as for the original PRESENT cipher. For the real construction, we sampled uniformly and independently \(1\,000\) random keys, one per experiment, and two random messages. The tweaks were constructed as in Fig. 3. For the ideal world, we sampled the ciphertexts uniformly and independently at random and verified that no message-pair for the same tweak amid any experiment collides. The results of our implementation are summarized in Table 1a. The source code of all experiments can be found freely available to the public.Footnote 1
2.3 Parallel-Road Distinguisher
Our second distinguisher is described in the right-hand side of Algorithm 1 and is illustrated on the right-hand side of Fig. 2. The core difference is the choice of sets for collisions. While the first distinguisher used collisions from different messages, the second one uses collisions from ciphertexts from the same set. Here, we denote the queries and intermediate variables
-
related to \((M^0, T^0_i) \in \mathcal {T} ^0\) also as \((S^0_i, U^0_i, \ldots )\),
-
those related to \((M^0, T^0_j) \in \mathcal {T} ^0\) also as \((S^0_j, U^0_j, \ldots )\),
-
those related to \((M^1, T^1_k) \in \mathcal {T} ^1\) also as \((S^1_k, U^1_k, \ldots )\), and
-
those related to \((M^1, T^1_{\ell }) \in \mathcal {T} ^1\) also as \((S^1_{\ell }, U^1_{\ell }, \ldots )\).
By combination, we obtain about \((2^{3n/4 + x})^2 \cdot 2^{-n} \simeq 2^{n/2 + 2x}\) collisions \(U^0_i = U^1_k\) between \((M^0, T^0_i)\) and \((M^1, T^1_k)\), and the approximately same number of collisions \(U^1_j = U^1_{\ell }\) between \((M^1, T^1_j)\) and \((M^1, T^1_{\ell })\). Those will be mapped to \(V^0_i = V^1_k\) and \(V^0_j = V^1_{\ell }\). We can form \(\left( {\begin{array}{c}2^{n/2 + 2x}\\ 2\end{array}}\right) \simeq 2^{n + 4x - 1}\) pairs of pairs (quartets). With probability \(2^{-n}\), a quartet has \(V^0_i \oplus V^0_j = T^0_i \oplus T^0_j\), which implies \(W^0_i = W^0_j\). Since \(V^0_i = V^1_k\) and \(V^1_j = V^1_{\ell }\), it follows that \(W^1_k = W^1_{\ell }\) holds. Thus, we obtain \(2^{4x - 1}\) quartets. Moreover, we expect \(\left( {\begin{array}{c}2^{3n/4 + x}\\ 2\end{array}}\right) \cdot 2^{-n} \simeq 2^{n/2 + 2x - 1}\) pairs \(C^0_i = C^0_j\) that are formed randomly and can be combined with \(2^{n/2 + 2x - 1}\) pairs \(C^1_k = C^1_{\ell }\). We obtain
formed at random. In sum, this yields
in the real construction, which implies that we can expect roughly three times as many quartets in the real construction compared to a random tweakable permutation wherin only the latter events occur.
Experimental Verification. We implemented the distinguisher with Small-PRESENT and state and tweak sizes of \(n \in \{16, 20, 24\}\) bits. The results are summarized in Table 1b.

2.4 Efficiency
Mennink’s [Men18] distinguisher evaluated the number of quartets for each tweak difference \(\varDelta \in \mathbb {F} _2^n\). From the choice of pairs given \(\tau _0\) and \(\tau _1\), there existed \(2^{n/2 + 2x}\) possible pairs \((C^0_i, C^1_j)\) for each tweak difference. Thus, the naive way needed \(2^n \cdot 2^{n/2 + 2x} \simeq O(2^{3n/2 + 2x})\) operations to exhaust all \(2^{n}\) possible tweak differences. To reduce the computational complexity below \(O(2^n)\), we give an improved description of the parallel-road distinguisher.
The lists \(\mathcal {L} \) and \(\mathcal {D} \) needed to reserve \(2^{n}\) cells each, which was the bottleneck. To reduce the complexity, we shrink \(\mathcal {L} \) to a list of \(2^{3n/4}\) sub-lists, where \(\mathcal {L} [x]\) holds a sub-list of tweaks \(T^0_i\) s.t. \(\textsf {lsb} _{3n/4}(C^0_i) = \langle x \rangle _{3n/4} \). This means that we truncate the n/4 most significant bits (MSB) of \(C^0_i\). Additionally, we store also the n/4 truncated bits as part of the entry: \((T^0_i, \textsf {msb} _{n/4}(C^0_i))\). Similarly, we no longer store a list of \(2^n\) counters in \(\mathcal {D} \). Instead, each entry will be a sub-list of full tweak differences. Thus, \(\mathcal {D} [x]\) contains \(2^{3n/4}\) slots, where \(\varDelta T_{i,j}\) is stored in the sub-list at location \(\textsf {lsb} _{3n/4}(\varDelta T_{i,j}) = \langle x \rangle _{3n/4} \). Clearly, the length of the sub-list at \(\mathcal {D} [x]\) equals the previous counter value that was stored in \(\mathcal {D} [x]\) before.
On average, Line 22 of Algorithm 2 is called
times. The second test in the if-statement on n/4 bits is fulfilled in about \(2^{n/2 + 2x - 1}\) calls. Thus, the first loop from Line 18 in Algorithm 2 has roughly \(2^{3n/4 + 2x}\) operations on average. A similar argument holds for the second test in Line 33 of Algorithm 2. Thus, the second outer loop over q tweaks from Line 29 of Algorithm 2 also contains roughly \(2^{3n/4 + 2x}\) operations on average. More detailed, the first 3n/4-bit filter reduces again the number of pairs
times. The second test in the if-statement on n/4 bits is fulfilled in \(2^{n/2 + 2x - 1}\) times on average. The 3n/4-bit tweak-difference filter lets the check in Line 34 in Algorithm 2 be successful \(2^{n/4 + 4x - 2}\) times for \((2^{3n/4 + 2x - 1})^2\) pairs. Thus, it will be called at most \(2^{3n/4 + x} + 2^{n/2 + 2x} + 2^{n/4 + 4x - 2}\) and the overall computational complexity is in \(O(2^{3n/4 + 2x})\).
3 An Impossible-Differential Attack on 
We combine the well-known impossible differential on four-round AES for key-recovery attacks on versions of TNT-AES. We describe the key-recovery phase in the first round and both key recovery and impossible differential in \(\pi _1\).
3.1 Core Idea
The core idea is based on the following assumption. The \(O(\sqrt{n} \cdot 2^{3n/4})\)-distinguisher works iff we can find pairs that collide in U. Let us consider the parallel-road distinguisher. It needs pairs \((M^0, M^1)\) whose difference \(\pi _1(M^0) \oplus \pi _1(M^1) = S^0 \oplus S^1\) equals the difference of their corresponding tweaks: \(S^0 \oplus S^1 = T^0_i \oplus T^1\), which implies that \(U^0 = U^1\). The adversary can choose differences \(\varDelta T\) of its choice as well as plaintexts with certain input differences. If it can manage to exclude that \(\varDelta T\) occurs for the message inputs of its choice, then, the distinguisher cannot happen. This implies that \(U^0 \ne U^1\) for all choices of \(M^0\) and \(M^1\). As a result, the values \(V^0_i, V^0_j, V^1_k, V^1_{\ell }\) are pairwise unique for each quartet and the number of colliding pairs will then match that of a random tweakable permutation.
For this purpose, the adversary considers tweaks such that their differences \(\varDelta T\) are output differences of an impossible differential. Then, each correct quartet from the distinguisher is possible only if the message was not encrypted through the first (few) round(s) to an input difference of the impossible differential, which allows discarding all keys that would have encrypted it in this way. We need a sufficient number of pairs such that for all key candidates, we will expect a correct quartet (for TNT-AES), except for the correct key.
We use the impossible differential from Fig. 4, where \(\varDelta X^5_{\textsf {MC}}\) (the difference after five rounds) is identical to \(\varDelta T\). Let \(\mathcal {I} = \{0,1,2\}\) and let \(\mathcal {M} _{\mathcal {I}}\) denote the mixed space after applying MixColumns to a vector space that is active in the first three inverse diagonals (cf. [GRR16]). Our choice leaves a space of \(2^{96} - 1\) differences for \(\varDelta T \in \mathcal {M} _{\mathcal {I}}\) and call \(\mathcal {T} \) the space of desired tweak differences.
3.2 Messages
We need message pairs with the impossible difference after \(\pi _1\). Since the difference has 32 zero bits, a zero difference in the rightmost inverse diagonal has a probability of \(2^{-32}\). We try to recover \(K^0[0,5,10,15]\). For a message pair \((M^i, M^j)\) that produces the impossible difference after \(\pi _1\), we can discard all key candidates that would lead to a difference of \(\varDelta X^1 =^{\text {def}} \mathsf {R}(M^i) \oplus \mathsf {R}(M^j)\) that is active in only a single byte after the first round. On average, there exist \(4 \cdot 2^8 = 2^{10}\) possible output differences \(\varDelta X^1\). Since \(M^i \oplus M^j\) is fixed, approximately one input-output mapping exists for the AES S-box on average. Hence, \(2^{10}\) keys produce an impossible \(\varDelta X^1\) on average and can be discarded. Assuming that the discarded keys are uniformly randomly and independently distributed, the probability that a key candidate can be discarded from a given pair \((M^i, M^j)\) is \(2^{-22}\). Under standard assumptions, we need \(N_{\textsf {pairs}} \) pairs to reduce the number of key candidates to \(2^{32 - a}\), where a is the advantage in bits:

Equation (2) yields approximately \(2^{23.47}\), \(2^{24.47}\), \(2^{25.47}\), and \(2^{26.47}\) necessary message pairs that fulfill the impossible difference after \(\pi _1\) to obtain an advantage of \(a = 4\), 8, 16, and 32 bits, respectively. If we fix the position of the inactive diagonal, we need \(2^{26.47} \cdot 2^{32} \simeq 2^{58.47}\) message pairs, or \(2 \cdot 2^{29.24} \simeq 2^{30.24}\) pairwise distinct messages. The number of message pairs with less than four active input bytes is negligible. We define \(2^s \simeq \lceil 2^{29.24} \rceil \). We employ a space of a single plaintext diagonal, where we can focus on the first diagonal \(\mathcal {D} _{\{0\}}\). The remaining diagonals are fixed to constants. We want a certain tweak difference that is zero in the final inverse diagonal. We add computational effort by choosing many messages that we partially compensate for by fixing those 32 bits to constants in all tweaks and define \(\nu =^{\text {def}} n - 32 = 96\) for the AES.
Expected Number of Pairs. To each message \(M^i\), we associate a tweak set \(\mathcal {T} ^i\), where we use the same tweaks for each message. Among the pairs in a single set \((M, T^i)\) and \((M, T^j)\), the probability for \(C^i = C^j\) is approximately \(2^{-n}\).
Using \(2^t\) tweaks in a set, we obtain \(\left( {\begin{array}{c}2^t\\ 2\end{array}}\right) \cdot 2^{-n} \simeq 2^{2t-n-1}\) pairs. Given two messages that do not have the desired tweak difference after \(\pi _1\), we can combine the pairs, where each pair collides in its ciphertexts, to \((2^{2t-n-1})^2\) quartets, which have the correct tweak difference after \(\pi _1\) with probability \(2^{3n/4} = 2^{-96}\). Thus, the number of quartets become
For messages that produce the desired difference after \(\pi _1\), i.e., have 32 zero bits in the rightmost inverse diagonal, we can form \(2^t \cdot 2^t \cdot 2^{-3n/4} \simeq 2^{2t - 3n/4}\) pairs after \(\pi _1\) since only the 96-bit tweak difference must match that of the message difference at that point. From those pairs, we can build quartets that collide with probability \(2^{-n}\) after \(\pi _2\). Thus, the number of quartets becomes
Note that the number of quartets in Eq. (3) differs significantly from the \(2^{4x - 2}\) of Eq. (1) since we restrict the valid tweak differences. Here, we need more message pairs so that enough of them possess the desired 32-bit condition of the zero-difference anti-diagonal after \(\pi _1\). Thus, the here-proposed attack is less efficient but allows us to recover a part of the secret key.
3.3 Success Probability, Advantage, and Data Complexity
Samajder and Sarkar [SS17] gave rigorous upper bounds on the data complexities for differential and linear cryptanalysis that improved previous results. For the parallel-road distinguisher, \(2 \cdot 2^{t}\) message-tweak tuples in total produce \(2^{4t - 5n/2 - 1} + 2^{4t - 11n/4 - 2}\) quartets for the real world, and \(2^{4t - 11n/4 - 2}\) quartets in the ideal world on average. Thus, we can define for the probability of quartets
Let \(\theta \) be a threshold and \(H_0\) be the hypothesis that a given message pair \(M^i, M^j\) has the 32-bit zero difference after \(\pi _1\) in the rightmost anti-diagonal. We say that \(H_0\) holds if \(N_{\textsf {quartets}} ^{i,j} > \theta \). Otherwise, we reject \(H_0\).
Let \(\alpha =^{\text {def}} \Pr [ N_{\textsf {quartets}} ^{i,j} < \theta | M^i \oplus M^j \in \mathcal {T} ]\) be the Type-I error, i.e., a pair with correct difference has too few quartets. This event is not essential, but yields more surviving wrong key candidates. Let \(\beta =^{\text {def}} \Pr [ N_{\textsf {quartets}} ^{i,j} \ge \theta | M^i \oplus M^j \not \in \mathcal {T} ]\) be the Type-II error, i.e., a pair with wrong difference after \(\pi _1\) has more quartets than the threshold and is incorrectly classified as correct. The latter event is crucial since the pair might suggest the correct key as wrong and the attack will fail. Therefore, the success probability is given by
Thus, \(\beta \) should be far below \(2^{-36.5}\). From [SS17, Proposition 5.1], it follows that the number of quartets (for each message pair) should fulfill
Since the distinguisher produces \(N_{\textsf {quartets}} = 2^{4t - 2}\) quartets, we can derive \(t = (\log _2(N_{\textsf {quartets}}) + 2) / 4\). Results of t for plausible values of \(\alpha \) and \(\beta \) are listed in Table 2. For Hypothesis 3, Samajder and Sarkar [SS17] suggest a threshold of
which is given in Table 2 for the sake of simplicity. Equation (5) targets single-differential key-recovery attacks.
Remark 1
We point out that Samajder and Sarkar also studied an upper bound for the data complexity of distinguishers in [SS17, Proposition 8.1]:
Though, [SS17, Sect. 10] showed that Eq. (5) yields a better upper bound for single-differential cryptanalysis. Details can be found in their work.
Data Complexity. Choosing a sufficiently high threshold for the number of quartets allows identifying message pairs with the desired difference after \(\pi _1\). Only those pairs are needed for subkey filtering. \(t = 83.39\) gives approximately \(2^{12.56}\) quartets on average, which implies \(2 \cdot 2^{29.24} \cdot 2^{83.39} \simeq 2^{113.63}\) messages.
We employ Mennink’s way of constructing tweaks. In each set, the tweaks iterate over \(2^{83.39}\) values in the leftmost three anti-diagonals in the state \(X^5_{\textsf {SR}}\) before the MixColumns operation of Round 5 is applied to each tweak. We define that \(\mu _0(i): \mathbb {Z}_{2^{84}} \rightarrow (\mathbb {F} _{2^8})^{4 \times 4}\) encodes the integer i into the 12 bytes 0, 1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 15, from most to least significant bits and define \(\mu _1(j): \mathbb {Z}_{2^{84}} \rightarrow (\mathbb {F} _{2^8})^{4 \times 4}\) encodes \((j \ll 12)\) (left shift by 12 bits) into the 12 bytes 0, 1, 2, 4, 5, 7, 8, 10, 11, 13, 14 , 15, from most to least significant bits. This is illustrated in Figs. 4 and 5. In total, we need \(2 \cdot 2^s \cdot 2^t \simeq 2^{113.63}\) message-tweak pairs.
3.4 Procedure
The attack proceeds as follows:
-
1.
Zeroize \(2^{2s}\) counters \(N_{\textsf {quartets}} ^{i,j}\), and prepare lists \(\mathcal {L} ^{0}\), \(\mathcal {D} ^{0}\), \(\mathcal {L} ^{1}\), and \(\mathcal {D} ^{1}\). Initialize a list \(\mathcal {K} \) of \(2^{32}\) true flags that represent the values of \(K^0[0,5,10,15]\).
-
2.
Construct the messages \(M^i\) and tweak sets \(\mathcal {T} ^i\) as described above and ask for the encryption of all tweak-message tuples. Each message-tweak set can be considered separately.
-
3.
For \(2^{s}\) messages \(M^i\), \(0 \le i < 2^{s}\):
-
3.1
Call the first loop of the parallel-road distinguisher. For tweak set \(\mathcal {T} ^{i}\), store the results into \(\mathcal {L} ^{0,i}[c^{0,i}_k]\), for all \(0 \le k < 2^t\). The \(2^{2t-n-1}\) pairs are stored in \(\mathcal {D} ^{0,i}\).
-
3.1
-
4.
For \(2^{s}\) messages \(M^j\), \(2^{s} \le j < 2^{s + 1}\):
-
4.1
Call the second loop of the parallel-road distinguisher and store their results into \(\mathcal {L} ^{1,j}[c^{1,j}_k]\) for each tweak set \(\mathcal {T} ^{j}\) and \(0 \le k < 2^t\). On average, \(2^{2t-n-1}\) ciphertext pairs per tweak set need lookups in \(\mathcal {D} ^{1,j}\).
-
4.2
For each message \(M^i\):
-
i.
Look up \(\mathcal {D} ^{0,i}\) for matches of the tweak difference. Increase the counter \(N_{\textsf {quartets}} ^{i,j}\) if there are matches.
-
i.
-
4.1
-
5.
For all counters \(N_{\textsf {quartets}} ^{i,j}\) that are above the threshold \(\theta \), derive the \(4 \cdot 2^8 \simeq 2^{10}\) round-key candidates \(K^0[0,5,10,15]\) that would encrypt \(M^i \oplus M^j\) to a single-byte difference after the first round.
-
6.
For all round-key candidates set the corresponding entry in \(\mathcal {K} \) to false.
-
7.
Output the entries of \(\mathcal {K} \) that are still marked as true.
3.5 Computational and Memory Complexity
The total computational complexity is given by
-
1.
\(2 \cdot 2^{29.24} \cdot 2^{83.39} \simeq 2^{113.63}\) encryptions.
-
2.
About \(2^{29.24} \cdot 2^{83.39} \simeq 2^{112.63}\) memory insertions and lookups to obtain all pairs of equal ciphertexts in the sets \(\mathcal {T} ^{0,i}\) that are used to fill \(\mathcal {D} ^{0,i}\).
-
3.
About \(2^{29.24} \cdot 2^{83.39} \simeq 2^{112.63}\) memory insertions and lookups to obtain all pairs of equal ciphertexts in the sets \(\mathcal {T} ^{1,j}\).
-
4.
About \(2^s \cdot 2^{2t - 1 - n} \simeq 2^{29.24} \cdot 2^{2 \cdot 83.39 - 1 - 128} \simeq 2^{67}\) lookups into the sets \(\mathcal {D} ^{0,i}\).
-
5.
We expect to have an advantage of at least \(a \simeq 32\) bits. Thus, there will be at most \(2^{96}\) remaining key candidates on average.
Thus, we have \(2^{113.63} + 2^{96} \simeq 2^{113.63}\) encryptions and \(2^{112.63} + 2^{112.63} + 2^{80.1} \simeq 2^{113.63}\) memory accesses. The memory complexity is upper bounded by storing \(2^{112.63}\) ciphertext-tweak tuples in the lists \(\mathcal {L} ^{0,i}\) and \(\mathcal {L} ^{1,j}\) each and the same amount of tweak differences in \(\mathcal {D} ^{0,i}\) and \(\mathcal {D} ^{1,j}\), which is upper bounded by the memory for \(2^{113.63}\) states and \(2^{32}\) key candidates.
3.6 Experiments
For verification purposes, we considered a reduced version of the AES. A natural starting point is the 64-bit version, Small-AES [CMR05], where each cell is an element in \(\mathbb {F} _{2^4}\). Since the complexity of \(O(2^{3n/4}) = O(2^{48})\) operations and memory, multiplied by 100 keys is still hardly feasible, we reduced the cipher further to a \(3 \times 3\)-matrix structure of cells with 36-bit state, which we will denote as  . We borrow almost all components from Small-AES, except for the MixColumns operation. In
. We borrow almost all components from Small-AES, except for the MixColumns operation. In  , MixColumns employs the circulant MDS matrix \(\textsf {circ} (\texttt {1}, \texttt {1}, \texttt {2})\), with elements in the field \(\mathbb {F} _{2^4}/p(\texttt {x})\) with \(p(\texttt {x}) = (\texttt {x}^4 + \texttt {x} + \texttt {1})\). We verified that the matrix is MDS in the given field with a python script.
, MixColumns employs the circulant MDS matrix \(\textsf {circ} (\texttt {1}, \texttt {1}, \texttt {2})\), with elements in the field \(\mathbb {F} _{2^4}/p(\texttt {x})\) with \(p(\texttt {x}) = (\texttt {x}^4 + \texttt {x} + \texttt {1})\). We verified that the matrix is MDS in the given field with a python script.
The key-recovery phase targets the first diagonal of the first round key \(K^0\). We iterate over all \(2^{12}\) messages of the first diagonal and consider all message pairs \((M^i, M^j)\) for distinct i, j that yield more than \(\theta \) collisions for filtering. Each set \(\mathcal {T} ^{i,0}\) employs \(2^t\) tweaks. Again, we use a variant of Mennink’s tweak encoding: The t-bit tweaks \(\langle i \rangle _{24} = (i_0, i_1, i_2, i_3, i_4, i_5)\) are encoded as \(\textsf {MC} (i_0, i_1, 0, i_2, 0, i_3, 0, i_4, i_5)\) in the cells 0-8, as shown in Fig. 6.
Expected Number of Messages. We experimented with varying numbers of message pairs that fulfilled the desired tweak differences \(\varDelta T\). The results are illustrated in Fig. 7. We experimented with \(1\,000\) random keys and \(2^{12}\) messages that iterated over all values of the first diagonal and used a random value of the other cells. On average, we observed approximately \(2^{11.1}\) message pairs with the desired difference after \(\pi _1\), which yielded a probability of \(2^{-11.9} \simeq 2^{12}\) that matches our expectation since we have 12 bit conditions in \(\varDelta X^5_{\textsf {SR}}\).
Expected Number of Quartets. The distribution of quartets among message pairs with and without the desired difference is shown in Table 3.
Recall Eqs. (3) and (4). In our reduced AES version, we have a 24-bit tweak space, which must replace the 3n/4 terms in those equations. In the following, we use \(2^t = 2^{24 + x}\). First, assume that \(t \le 24\) for a message pair that does not fulfill the correct difference after \(\pi _1\). Then, we can combine \(\left( {\begin{array}{c}2^{t}\\ 2\end{array}}\right) \) tweaks pairs for one message and obtain \(2^{-n}\) pairs that collide in their ciphertexts. We can combine those pairs for both messages to quartets, and have a probability of \(2^{-24}\) that the tweak differences match for both pairs. If \(t > 24\), we have \(\left( {\begin{array}{c}2^{24 + x}\\ 2\end{array}}\right) \cdot 2^{-n}\) pairs per message whose ciphertexts collide. Building quartets, their tweak differences will match with probability \(2^{-x} \cdot 2^{-24}\). Hence, we obtain
For a message pair that produces the desired difference after \(\pi _1\), we have \(2^{t-x} \cdot 2^{t-x}\) tweaks in their tweak sets that lead to a collision with probability \(2^{-24}\) after \(\pi _1\), and thus to \(2^{2t - 2x - 24}\) pairs. Note that we can combine only the tweak sets that share the same 12-bit value in the anti-diagonal \(\textsf {MC} ^{-1}(\varDelta T) [2,4,6]\). If \(t = 24 + x\) for non-negative x, there are \(2^x\) times such pairs on average: \(2^{2t - 2x - 24}\) for every value in the anti-diagonal, assuming \(2^x\) is integer. Thus, we have
quartets. For the messages with the desired difference after \(\pi _1\), we observe approximately \(2^3\), \(2^7\), \(2^{11}\), \(2^{13}\), \(2^{15}\), and \(2^{17}\) quartets with the standard deviation matching about the square root, for \(2^t\) message-tweak tuples per message, and \(t \in \{22, \ldots , 27\}\). This matches our expectations in Eq. (8) including the break at \(t = 24\). For \(t \le 24\), one can observe an increasing factor of \(2^4\) quartets for each increment of t, which becomes \(2^2\) for \(t > 24\).
For message pairs without the desired difference after \(\pi _1\), the numbers of quartets are far below those of pairs with the desired difference, with means of \(2^{-10}\), \(2^{-6}\), \(2^{-2}\), \(2^{1}\), and \(2^4\), and \(2^{7}\). Again, the factor from t to \(t + 1\) changes from \(2^4\) if \(t \le 24\), to a factor of \(2^3\) times more quartets from t to \(t + 1\) when \(t > 24\), as expected.
The standard deviations are about the square root of the expectations, which matches Bernoulli distributions. The major insight is that the gap in the number of quartets is huge enough – in the order of \(2^{13}\), \(2^{12}\), and \(2^{11}\) for \(t = 24, 25, 26\) – to reasonably choose a threshold and not have a single non-desired message pair that could mistakenly filter out the correct partial key.
4 Provable Security Preliminaries
4.1 Provable Security Notations
Given a sequence \(\mathcal {X} = (X_1, \ldots , X_q)\), we use \(\mathcal {X} ^q\) to indicate that it consists of q elements; \(\widehat{\mathcal {X}}^q = \{X_1, \ldots , X_q\}\) denotes their set and \(\mu (\mathcal {X} ^q, X)\) the multiplicity of an element X in \(\mathcal {X} ^q\). For an index set \(\mathcal {I} \subseteq [q]\) and \(\mathcal {X} ^q\), \(\mathcal {X} ^{\mathcal {I}} =^{\text {def}} (X_i)_{i \in \mathcal {I}}\). For a pair of sequences \(\mathcal {X} ^q\) and \(\mathcal {Y} ^q\), \((\mathcal {X} ^q, \mathcal {Y} ^q)\) denotes the two-ary q-tuple \(((X_1, Y_1), \ldots , (X_q, Y_q))\). An n-ary q-tuple is defined naturally. A two-ary tuple \((\mathcal {X} ^q, \mathcal {Y} ^q)\) is said to be permutation-compatible, denoted as  , iff \(X_i = X_j \Leftrightarrow Y_i = Y_j\). A three-ary tuple \((\mathcal {T} ^q, \mathcal {X} ^q, \mathcal {Y} ^q)\) is said to be tweakable-permutation-compatible, denoted as
, iff \(X_i = X_j \Leftrightarrow Y_i = Y_j\). A three-ary tuple \((\mathcal {T} ^q, \mathcal {X} ^q, \mathcal {Y} ^q)\) is said to be tweakable-permutation-compatible, denoted as  , iff \((T_i, X_i) = (T_j, X_j) \Leftrightarrow (T_i, Y_i) = (T_j, Y_j)\). For any function \(F: \mathcal {X} \rightarrow \mathcal {Y} \) and \(\mathcal {X} ^q\), \(F(\mathcal {X} ^q)\) denotes \((F(X_i), \ldots , F(X_q))\). For a set \(\mathcal {X} \), \(X \twoheadleftarrow \mathcal {X} \) means that X is sampled uniformly at random and independently from other variables from \(\mathcal {X} \). Moreover, let \(\exists ^*\) mean “there exist distinct”.
, iff \((T_i, X_i) = (T_j, X_j) \Leftrightarrow (T_i, Y_i) = (T_j, Y_j)\). For any function \(F: \mathcal {X} \rightarrow \mathcal {Y} \) and \(\mathcal {X} ^q\), \(F(\mathcal {X} ^q)\) denotes \((F(X_i), \ldots , F(X_q))\). For a set \(\mathcal {X} \), \(X \twoheadleftarrow \mathcal {X} \) means that X is sampled uniformly at random and independently from other variables from \(\mathcal {X} \). Moreover, let \(\exists ^*\) mean “there exist distinct”.
A distinguisher \(\mathbf {A}\) is an algorithm that tries to distinguish between two worlds \(\mathcal {O}_{\text {real}}\) and \(\mathcal {O}_{\text {ideal}}\) via black-box interaction with one of them chosen randomly and invisible from \(\mathbf {A}\). At the end of its interaction, \(\mathbf {A}\) has to output a decision bit. \(\mathbf {{Adv}}^{}_{\mathcal {O}_{\text {ideal}};\mathcal {O}_{\text {real}}}(\mathbf {A})\) denotes the advantage of \(\mathbf {A}\) to distinguish between both. We consider information-theoretic distinguishers that are bounded only in terms of the number of queries and message material that they can ask to the available oracles. \(\mathbf {{Adv}}^{}_{\mathcal {O}_{\text {ideal}};\mathcal {O}_{\text {real}}}(q) =^{\text {def}} \max _{\mathbf {A}} \left\{ \mathbf {{Adv}}^{}_{\mathcal {O}_{\text {ideal}};\mathcal {O}_{\text {real}}}(\mathbf {A}) \right\} \) denotes the maximum of advantages over all possible adversaries \(\mathbf {A}\) that are allowed to ask at most q queries to its oracles. Later, we exclude trivial distinguishers, i.e., distinguishers who ask duplicate queries or queries to which the answer is already known.
4.2 Expectation Method
Let \(\mathbf {A}\) be a computationally unbounded deterministic distinguisher that tries to distinguish between a real world \(\mathcal {O}_{\text {real}}\) and an ideal world \(\mathcal {O}_{\text {ideal}}\). The queries and responses of the interaction of \(\mathbf {A}\) with its oracles are collected in a transcript \(\tau \). It may also contain additional information which would make the adversary only stronger. By \(\varTheta _{\text {real}} \) and \(\varTheta _{\text {ideal}} \), we denote random variables for the transcript when \(\mathbf {A}\) interacts with the real world or the ideal world, respectively. Since \(\mathbf {A}\) is deterministic, the probability of \(\mathbf {A}\) ’s decision depends only on the oracle and the transcript. A transcript \(\tau \) is called attainable if its probability in the ideal world is non-zero.
The expectation method is a generalization of the popular H-coefficient method by Patarin [Pat08], which is a simple corollary of the following result.
Lemma 1
(Expectation Method [HT16]). Let \(\varOmega \) be a set of all transcripts that can be partitioned into two disjoint non-empty sets of good transcripts, \(\textsc {GoodT} \) and bad transcripts, \(\textsc {BadT} \). For some \(\epsilon _{\textsf {bad}} > 0\) and a non-negative function \(\epsilon _{\textsf {ratio}}: \varOmega \rightarrow [0, \infty )\), suppose \(\Pr [ \varTheta _{\text {ideal}} \in \textsc {BadT} ] \le \epsilon _{\textsf {bad}} \) and for any \(\tau \in \textsc {GoodT} \), it holds that \(\Pr [\varTheta _{\text {real}} = \tau ]/\Pr [\varTheta _{\text {ideal}} = \tau ] \ge 1 - \epsilon _{\textsf {ratio}} \). Then, for any distinguisher \(\mathbf {A}\) that tries to distinguish between \(\mathcal {O}_{\text {real}} \) and \(\mathcal {O}_{\text {ideal}} \), it holds:
4.3 Mirror Theory
Patarin [Pat10] defined the Mirror Theory as an approach to estimate the number of solutions of a linear system of equalities and linear inequalities in cyclic groups. He followed a recursive sophisticated proof [Pat08, Pat10] that was brought to the attention of a wider audience by Mennink and Neves [MN17]. Jha and Nandi [JN20] revisited it for a tight proof of CLRW2 [LRW02]. We follow their description that itself referred to Mennink and Neves’ interpretation of the Mirror theory. For \(q \ge 1\), let \(\mathcal {L} \) be a system of linear equations of the form
where \(U_i\) and \(V_i\) are the unknowns, \(\lambda _i\) the knowns, and \(U_i, V_i, \lambda _i \in \mathbb {F} _2^n\). We denote their sets as \(\mathcal {U} ^q\) and \(\mathcal {V} ^q\), respectively. Moreover, \(\mathcal {L} \) contains a set of inequalities that uniquely determine \(\widehat{\mathcal {U}}^q\) and \(\widehat{\mathcal {V}}^q\), respectively. We assume that \(\widehat{\mathcal {U}}^q\) and \(\widehat{\mathcal {V}}^q\) are indexed in arbitrary order by index sets \([q_u]\) and \([q_v]\), where \(q_u = |\widehat{\mathcal {U}}^q|\) and \(q_v = |\widehat{\mathcal {V}}^q|\). Then, we can define two surjective index maps
Thus, \(\mathcal {L} \) is uniquely determined by \((\varphi _u, \varphi _v, \lambda ^q)\) and vice versa. Let \(\mathcal {G} (\mathcal {L}) =^{\text {def}} ([q_u], [q_v], \mathcal {E})\) be a labeled bipartite graph corresponding to \(\mathcal {L} \), where

is the set of edges and \(\lambda _i\) the edge labels. Thus, each equation in \(\mathcal {L} \) corresponds to a unique labeled edge if there exist no duplicate equations in \(\mathcal {L} \). We need three definitions to use the fundamental theorem of the Mirror Theory.
Definition 1
(Cycle-freeness). We call \(\mathcal {L} \) cycle-free iff \(\mathcal {G} (\mathcal {L})\) is acyclic.
Definition 2
(Maximal Block Size). Two equations \(e_i\) and \(e_j\) for distinct i, j are in the same component iff the corresponding edges (vertices) in \(\mathcal {G} (\mathcal {L})\) are in the same graph component. The size of any component \(\mathcal {C} \in \mathcal {L} \), denoted \(\xi (\mathcal {C})\), is given by the number of vertices in the corresponding component of \(\mathcal {G} (\mathcal {L})\). The maximal component size of \(\mathcal {G} (\mathcal {L})\) is denoted by \(\xi _{\text {max}} (\mathcal {L})\) or short by \(\xi _{\text {max}} \).
Definition 3
(Non-degeneracy).\(\mathcal {L} \) is called non-degenerate iff there exists no path of length \(\ge 2\) in \(\mathcal {G} (\mathcal {L})\) such that the labels along its edges sum to zero.
Theorem 1
(Fundamental Theorem of the Mirror Theory [Pat10]). Let \(\mathcal {L} \) be a system of equations over the unknowns \((\mathcal {U} ^q, \mathcal {V} ^q)\) that is (i) cycle-free, (ii) non-degenerate, and (iii) possesses a maximal component size of \(\xi _{\text {max}} \) with \(\xi _{\text {max}} ^2 \cdot \max \{q_u, q_v\} \le 2^n\). Then, the number of solutions \((U_1, \ldots , U_{q_u}, V_1, \ldots , V_{q_v})\) of \(\mathcal {L} \), denoted as \(h_q\), such that \(U_i \ne U_j\) and \(V_i \ne V_j\) for all \(i \ne j\), satisfies
\(h_q\) is multiplied by a factor of \((1 - \epsilon )\) for some \(\epsilon > 0\) at the end. For \(\xi \ge 2\) and \(\epsilon > 0\), we denote as the \((\xi , \epsilon )\)-restricted Mirror-Theory theorem the variant with \(\xi _{\text {max}} = \xi \) and \(h_q \ge (1 - \epsilon ) \cdot h_q^*\), where \(h_q^*\) is the right-hand side of Eq. (9).
4.4 Transcript Graph
For TNT, a transcript \(\tau \) will consist of the queries and responses \((T_i, M_i, C_i)\) as well as intermediate values. We will later use a transcript of TNT as the tuple of tuples \((\mathcal {T} ^q\), \(\mathcal {M} ^q\), \(\mathcal {C} ^q\), \(\mathcal {X} ^q\), \(\mathcal {Y} ^q\), \(\mathcal {V} ^q)\) that will collect the values \(T_i\), \(M_i\), etc., for \(1 \le i \le q\), respectively. The roles of the individual variables are shown in Fig. 9.
Given a transcript \(\tau \), a transcript graph is a graph-isomorphic unique bipartite representation of the mappings in \(\tau \). For our purpose, the relevant transcript graph will reflect the mappings of \(\mathcal {X} ^q\) and \(\mathcal {U} ^q\). The transcript \(\tau \) is therefore isomorphic to a graph on \((\mathcal {X} ^q, \mathcal {U} ^q)\).
Definition 4
A transcript graph \(\mathcal {G} = (\mathcal {X} ^q, \mathcal {U} ^q, \mathcal {E} ^q)\) that is associated with \((\mathcal {X} ^q, \mathcal {U} ^q)\) is denoted as \(\mathcal {G} (\mathcal {X} ^q, \mathcal {U} ^q)\) and defined as \(\mathcal {X} =^{\text {def}} \left\{ (X_i, 0) : i \in [q] \right\} \), \(\mathcal {U} =^{\text {def}} \left\{ (U_i, 1) : i \in [q] \right\} \), and \(\mathcal {E} =^{\text {def}} \left\{ \left( (X_i, 0), (U_i, 1) \right) : i \in [q] \right\} \). A label \(\lambda _i\) is associated with the edge \(((X_i, 0)\), \((U_i, 1)) \in \mathcal {E} \).
The resulting graph may contain parallel edges. The 0 and 1 in \((X_i, 0)\) and \((U_i, 1)\) will be dropped for simplicity. If for distinct \(i, j \in [q]\), it holds that \(X_i = X_j\) (or \(U_i = U_j\)), we denote that as shared vertex \(X_{i,j}\) (or \(U_{i,j}\)). Since there is a bijection of each edge \((X_i, U_i) \in \mathcal {E} \) to i, we can also represent the edge by i.
4.5 Extended Mirror Theory
Jha and Nandi [JN20] applied the mirror theory to the tweakable-permutation setting. We briefly recall their main result and the necessary notations.
In an edge-labeled bipartite graph \(\mathcal {G} = (\mathcal {Y}, \mathcal {V}, \mathcal {E})\), an edge \((Y, V, \lambda )\) is isolated iff both Y and V have degree one. A component \(\mathcal {S} \subseteq \mathcal {G} \) is called a star iff \(\xi (\mathcal {S}) \ge 3\) (recall that \(\xi (\mathcal {S})\) is the number of vertices in \(\mathcal {S} \)) and there is a unique vertex \(V \in \mathcal {S} \) with degree \(\xi (\mathcal {S}) - 1\). V is called the center of \(\mathcal {S} \). \(\mathcal {S} \) is called a \(\mathcal {Y} \)-star (or \(\mathcal {V} \)-star) if its center \(Y \in \mathcal {Y} \) (or \(V \in \mathcal {V} \)). Consider an equation system \(\mathcal {L} \)
such that each component in \(\mathcal {G} (\mathcal {L})\) is either an isolated edge or a star. Let \(c_1\), \(c_2\), and \(c_3\) denote the number of isolated, \(\mathcal {Y} \)-star, and \(\mathcal {V} \)-star components, respectively. Moreover, \(q_1 = c_1\), \(q_2\), and \(q_3\) denote the number of their equations. The equations in \(\mathcal {L} \) can be arranged in arbitrary order. The isolated edges are indexed first, followed by the star components. Jha and Nandi show the following:
Theorem 2
(Theorem 5.1 in [JN20]). Let \(\mathcal {L} \) be as above with \(q < 2^{n-2}\) and \(\xi _{\text {max}} q \le 2^{n-1}\). Then, the number of tuples \((\mathcal {Y} ^{q_Y}, \mathcal {V} ^{q_V})\) that satisfy \(\mathcal {L} \) with \(Y_i \ne Y_j\) and \(V_i \ne V_j\) for all \(i \ne j\) satisfies
where \(\eta _j = \xi _j - 1\) and \(\xi _j\) denotes the number of vertices of the j-th component for \(j \in [c_1 + c_2 + c_3]\).
4.6 Universal Hashing
Let \(\mathcal {X} \) and \(\mathcal {Y} \) be non-empty sets or spaces in the following, and let \(\mathcal {H} = \{ H | H: \mathcal {X} \rightarrow \mathcal {Y} \}\) be a family of hash functions.
Definition 5
(Almost-Universal Hash Function [CW79]). We say that \(\mathcal {H} \) is \(\epsilon \)-almost-universal (\(\epsilon \)-\(\textsf {AU}\)) if, for all distinct \(X, X' \in \mathcal {X} \), it holds that \(\Pr [ H(X) = H(X') ] \le \epsilon \), where the probability is taken over \(H \twoheadleftarrow \mathcal {H} \).
Definition 6
(Almost-XOR-Universal Hash Function [Kra94, Rog95]). Let \(\mathcal {Y} \subseteq \mathbb {F} _2^*\). We say that \(\mathcal {H} \) is \(\epsilon \)-almost-XOR-universal (\(\epsilon \)-\(\textsf {AXU}\)) if, for all distinct \(X, X' \in \mathcal {X} \) and arbitrary \(\varDelta \in \mathcal {Y} \), it holds that \(\Pr [ H(X) \oplus H(X') = \varDelta ] \le \epsilon \), where the probability is taken over \(H \twoheadleftarrow \mathcal {H} \).
Let \(\mathcal {H}: \{H | H: \mathcal {T} \rightarrow \mathbb {F} _2^n\}\) be a family \(\epsilon \)-almost-universal hash functions and \(H \twoheadleftarrow \mathcal {H} \) be an instance. Let \(\mathcal {X} ^q =^{\text {def}} H(\mathcal {T} ^q)\) be the sequence of outputs \(X_i\) from \(H(T_i)\), for \(i \in [q]\) queries. In the following, [JN20] defined, in an abstract way, variables \(\nu _i\) for the number of occurrences of the hash value i, and defined \(\textsf {coll} \) for the number of colliding pairs in \(\mathcal {X} ^q\).
Lemma 2
(Lemma 4.3 in [JN20]). Since \(\mathbb {E}\left[ \textsf {coll} \right] \le \left( {\begin{array}{c}q\\ 2\end{array}}\right) \epsilon \), it holds that
Thus, Lemma 2 says that the number of collisions is limited by \(2q^2 \epsilon \) on expectation. Furthermore, the corollary below upper bounds the number of occurrences of any single hash value. The proof in [JN20] stems from Markov’s inequality.
Corollary 1
(Corollary 4.1 in [JN20]). Let \(\nu _{\max } = \max \{\nu _i : i \in [r]\}\). Then, for some \(a \ge 1\), it holds that \(\Pr [\nu _{\max } \ge a] \le \frac{2q^2 \epsilon }{a^2}\).
The following lemma from [JN20] bounds the probability that four distinct inputs to two \(\epsilon \)-\(\textsf {AU}\) hash functions yield three alternating collisions.
Lemma 3
(Alternating-collisions Lemma in [JN20]). Let \(H_1, H_2 \twoheadleftarrow \mathcal {H} \) be independently sampled \(\epsilon \)-\(\textsf {AU}\) hash functions with domain \(\mathcal {X} \). Let \(X_1\), \(\ldots \), \(X_q \in \mathcal {X} ^q\) be pairwise distinct inputs. Then, it holds, over \(H_1, H_2 \twoheadleftarrow \mathcal {H} \), that
is at most \(q^2 \epsilon ^{1.5}\).
5 TPRP Proof of TNT
We followed the footsteps of the STPRP proof of CLRW2 by [JN20] closely to show Theorem 3. We provide an extract that highlights where both constructions and proofs differ. Thus, we do not claim novelty of the proof approach but show that it applies also to TNT in encryption direction only with minor adaptions.
Theorem 3
(
 ). Let \(q \le 2^{n-2}\), and \(E_{K_1}, E_{K_2}, E_{K_3}: \mathcal {K} \times \mathbb {F} _2^n \rightarrow \mathbb {F} _2^n\) be block ciphers with \(K_1, K_2, K_3 \twoheadleftarrow \mathcal {K} \). Then,
). Let \(q \le 2^{n-2}\), and \(E_{K_1}, E_{K_2}, E_{K_3}: \mathcal {K} \times \mathbb {F} _2^n \rightarrow \mathbb {F} _2^n\) be block ciphers with \(K_1, K_2, K_3 \twoheadleftarrow \mathcal {K} \). Then,
First, we can replace the secret-key block ciphers \(E_{K_1}\), \(E_{K_2}\), \(E_{K_3}\) with \(K_1\), \(K_2\), \(K_3 \twoheadleftarrow \mathcal {K} \) by random permutations \(\pi _1, \pi _2, \pi _3 \twoheadleftarrow \mathsf {Perm} (\mathbb {F} _2^n)\). For TNT, the advantage between both settings is upper bounded by
We consider the information-theoretic setting with a computationally unbounded distinguisher \(\mathbf {A}\). W.l.o.g., we assume that \(\mathbf {A}\) is deterministic and non-trivial.
5.1 Oracle Descriptions
The Real Oracle. \(\mathcal {O}_{\text {real}} \) runs \(\textsf {TNT} [\pi _1, \pi _2, \pi _3]\). The transcript random variable \(\varTheta _{\text {real}} \) yields the transcript as the tuple \((\mathcal {T} ^q\), \(\mathcal {M} ^q\), \(\mathcal {C} ^q\), \(\mathcal {X} ^q\), \(\mathcal {Y} ^q\), \(\mathcal {V} ^q)\) where for all queries \(i \in [q]\), the values \(T_i\), \(M_i\), \(C_i\), \(X_i\), \(Y_i\), \(V_i\), \(U_i\), \(\lambda _i\) refer to the variables as given in Fig. 9, which can be compared to those in CLRW2 in Fig. 8. The sets \(\mathcal {U} ^q = \mathcal {C} ^q\) and \(\lambda ^q = \mathcal {T} ^q\) can be derived directly from the transcript.
The Ideal Oracle. \(\mathcal {O}_{\text {ideal}} \) implements \(\widetilde{\varPi } \twoheadleftarrow \mathsf {\widetilde{Perm}} (\mathbb {F} _2^n, \mathbb {F} _2^n)\). Moreover, we treat the first permutation and tweak addition in TNT as equivalent to the first hash function in CLRW2. Thus, the ideal oracle samples \(\pi _1 \twoheadleftarrow \mathsf {Perm} (\mathbb {F} _2^n)\) and gives all values \(X_i\) to \(\mathbf {A}\) after \(\mathbf {A}\) finished its interactions but before it outputs its decision bit. The transcript looks as before, where \(T_i, M_i, C_i\) are the inputs and outputs from \(C_i = \widetilde{\varPi } (T_i, M_i)\) or \(M_i = \widetilde{\varPi } ^{-1}(T_i, C_i)\), \(\lambda _i = T_i\), \(X_i \leftarrow \pi _1(M_i) \oplus T_i\), \(U_i \leftarrow C_i\). The values of the sets \(\mathcal {X} ^q\), \(\mathcal {U} ^q\), and \(\mathcal {T} ^q\) are defined honestly.
Jha and Nandi [JN20] characterized so-called bad hash keys. Given the partial transcript \((\mathcal {T} ^q, \mathcal {M} ^q, \mathcal {C} ^q, \mathcal {X} ^q)\) – plus for CLRW2 also the hash functions \(H_1\) and \(H_2\) – they defined a number of conditions when \((H_1, H_2)\) where considered good or bad, respectively, and defined the sets \(\mathcal {H} _{\textsf {good}}\) and \(\mathcal {H} _{\textsf {bad}}\) for this purpose. While TNT omits hash functions, the predicates were not conditions on the hash keys but instead on equalities of internal variables that can also occur in TNT. Therefore, we consider their cases analogously. A hash key was defined to be bad iff one of the following predicates was true:
-
1.
\(\textsf {badH} _1\): \(\exists ^* i, j \in [q]\) such that \(X_i = X_j \wedge U_i = U_j\).
-
2.
\(\textsf {badH} _2\): \(\exists ^* i, j \in [q]\) such that \(X_i = X_j \wedge T_i = T_j\).
-
3.
\(\textsf {badH} _3\): \(\exists ^* i, j \in [q]\) such that \(U_i = U_j \wedge T_i = T_j\).
-
4.
\(\textsf {badH} _4\): \(\exists ^* i, j, k, \ell \in [q]\) such that \(X_i = X_j \wedge U_j = U_k \wedge X_k = X_{\ell }\).
-
5.
\(\textsf {badH} _5\): \(\exists ^* i, j, k, \ell \in [q]\) such that \(U_i = U_j \wedge X_j = X_k \wedge U_k = U_{\ell }\).
-
6.
\(\textsf {badH} _6\): \(\exists k \ge 2^n/2q\), \(\exists ^* i_1, i_2, \ldots , i_k \in [q]\) such that \(X_{i_1} = \cdots = X_{i_k}\).
-
7.
\(\textsf {badH} _7\): \(\exists k \ge 2^n/2q\), \(\exists ^* i_1, i_2, \ldots , i_k \in [q]\) such that \(U_{i_1} = \cdots = U_{i_k}\).
In the absence of hash keys, we cannot label those as H being bad or good. Thus, we call them bad and good hash equivalent instead.
 If one of the events \(\textsf {badH} _1\) through \(\textsf {badH} _7\) occurs, the ideal oracle samples the values \(\mathcal {Y} ^q\) and \(\mathcal {V} ^q\) as \(Y_i = V_i = 0\) for all \(i \in [q]\).
If one of the events \(\textsf {badH} _1\) through \(\textsf {badH} _7\) occurs, the ideal oracle samples the values \(\mathcal {Y} ^q\) and \(\mathcal {V} ^q\) as \(Y_i = V_i = 0\) for all \(i \in [q]\).
 In the other case, it will be useful to study the transcript graph \(\mathcal {G} (\mathcal {X} ^q, \mathcal {U} ^q)\) of the associations \((\mathcal {X} ^q, \mathcal {U} ^q)\) that arises from the transcript when no \(\textsf {badH} \) event occurs. Figure 10 shows all possible types of components in \(\mathcal {G} (\mathcal {X} ^q, \mathcal {U} ^q)\). There, (star) components of the Types (2) and (3) contain exactly one vertex with a degree of \(\ge 2\). Components of Types (4) and (5) can contain one vertex with a degree of \(\ge 2\) in \(\mathcal {U} \) and one such vertex in \(\mathcal {X} \).
In the other case, it will be useful to study the transcript graph \(\mathcal {G} (\mathcal {X} ^q, \mathcal {U} ^q)\) of the associations \((\mathcal {X} ^q, \mathcal {U} ^q)\) that arises from the transcript when no \(\textsf {badH} \) event occurs. Figure 10 shows all possible types of components in \(\mathcal {G} (\mathcal {X} ^q, \mathcal {U} ^q)\). There, (star) components of the Types (2) and (3) contain exactly one vertex with a degree of \(\ge 2\). Components of Types (4) and (5) can contain one vertex with a degree of \(\ge 2\) in \(\mathcal {U} \) and one such vertex in \(\mathcal {X} \).
Components types of a transcript graph corresponding to a good hash equivalent. Type (1) is the only component with a single edge. Types (2) and (3) are \(\mathcal {X} \)- and \(\mathcal {U} \)-star components, respectively. Types (4) and (5) are the only components that are neither isolated nor stars since they can have vertices of degree \({\ge }2\) in both \(\mathcal {X} \) and \(\mathcal {U} \).
Lemma 4
(Lemma 6.1 in [JN20]). The transcript graph \(\mathcal {G} (\mathcal {X} ^q, \mathcal {U} ^q)\) (\(\mathcal {G} \) for short, hereafter) by a good hash equivalent has the following properties:
-
1.
\(\mathcal {G} \) is simple, acyclic, and possesses no isolated vertices.
-
2.
\(\mathcal {G} \) has no two adjacent edges i and j such that \(T_i \oplus T_j = 0\).
-
3.
\(\mathcal {G} \) has no component of size \(\ge 2^n / 2q\) edges.
-
4.
\(\mathcal {G} \) has no component with more than one vertex of degree \(\ge 2\) in neither \(\mathcal {X} \) or \(\mathcal {U} \) (though, it can have one vertex with degree \(\ge 2\) in \(\mathcal {X} \) and one in \(\mathcal {U} \)).
The proof is given in [JN20].
For the sake of completeness, we describe the sampling process of \(\mathcal {Y} ^q\) and \(\mathcal {V} ^q\) in the case of a good hash equivalent. This is the same process as for CLRW2 in [JN20]. Therefore, this part is only a revisit and attributed to [JN20]:
The indices \(i \in [q]\) are collected in index sets \(\mathcal {I} _1, \ldots , \mathcal {I} _5\), corresponding to the edges in all Type-1, ..., Type-5 components, respectively. The five sets are disjoint and \([q] = \bigcup _{i = 1}^5 \mathcal {I} _i\). Let \(\mathcal {I} = \bigcup _{i = 1}^3 \mathcal {I} _i\) and consider the system of equations

where \(Y_i = Y_j\) (respectively \(V_i = V_j\)) holds iff \(X_i = X_j\) (respectively \(U_i = U_j\)) for all \(i, j \in [q]\). The solution set of \(\mathcal {L} \) is precisely the set

Given these definitions, the ideal-world oracle \(\mathcal {O}_{\text {ideal}}\) samples \((\mathcal {Y} ^q, \mathcal {V} ^q)\) as follows:
-
\((\mathcal {Y} ^{\mathcal {I}}, \mathcal {V} ^{\mathcal {I}}) \twoheadleftarrow \mathcal {S} \). This means, \(\mathcal {O}_{\text {ideal}}\) samples uniformly one valid assignment from the set of all valid assignments.
-
Let \(\mathcal {G} {\setminus } \mathcal {I} \) denote the subgraph of \(\mathcal {G} \) after the removal of edges and vertices corresponding to \(i \in \mathcal {I} \). For each component \(\mathcal {C} \subset \mathcal {G} {\setminus } \mathcal {I} \):
-
If \((X_i, U_i) \in \mathcal {C} \) corresponds to the edge in \(\mathcal {C} \) where both \(X_i\) and \(U_i\) have a degree \(\ge 2\). Then, \(Y_i \twoheadleftarrow \mathbb {F} _2^n\) and \(V_i = Y_i \oplus T_i\).
-
For each edge \((X_{i'}, U_{i'}) \ne (X_i, U_i) \in \mathcal {C} \), either \(X_{i'} = X_i\) or \(U_{i'} = U_i\). Take the case that \(X_{i'} = X_i\). Then, \(Y_{i'} = Y_i\) and \(V_{i'} = Y_{i'} \oplus T_{i'}\). In the other case \(U_{i'} = U_i\). Then, \(V_{i'} = V_i\) and \(Y_{i'} = V_{i'} \oplus T_{i'}\).
-
Then, the transcript in the ideal world is completely defined, maintaining both the consistency of equations of the form \(Y_i \oplus V_i = T_i\) as in the real world and the permutation consistency within each component for good hash equivalents. Still, there can be collisions among the values of \(\mathcal {Y} \) or among the values of \(\mathcal {V} \) from different components.
5.2 Definition of Bad Transcripts
The analysis of bad transcripts and of bad hash equivalents, in particular, is the core aspect wherein the analyses of CLRW2 and TNT differ. However, there can be collisions among the values of \(\mathcal {Y} \) or among the values of \(\mathcal {V} \) from different components that have to be treated in bad transcripts. Their treatment can be done similarly as in [JN20]. They are essential for the proof of TNT and listed in this subsection only for the sake of completeness, but we refer to [JN20] for their proof.
The set of transcripts \(\varOmega \) is the set of all tuples \(\tau = (\mathcal {T} ^q, \mathcal {M} ^q, \mathcal {C} ^q, \mathcal {X} ^q, \mathcal {Y} ^q, \mathcal {V} ^q)\) defined as before. Recall that \(\mathcal {U} ^q = \mathcal {C} ^q\) holds for TNT. Following [JN20], a bad transcript definition needs the following preprocessing steps:
-
1.
Eliminate all tuples \((\mathcal {X} ^q, \mathcal {U} ^q, \mathcal {T} ^q)\) such that both \(\mathcal {Y} ^q\) and \(\mathcal {V} ^q\) are trivially restricted by linear dependencies.
-
2.
Eliminate all tuples \((\mathcal {X} ^q, \mathcal {U} ^q, \mathcal {V} ^q, \mathcal {Y} ^q)\) such that
 or
or 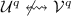 .
.
A transcript \(\tau \) is called a bad hash-equivalent transcript if one of the conditions \(\textsf {badH} _1\) through \(\textsf {badH} _7\) holds. We define a compound event \(\textsf {badH} =^{\text {def}} \bigcup _{i = 1}^7 \textsf {badH} _i\) that ensures that the first requirement is fulfilled.
For the second requirement, all conditions that might lead to  or
or  have to be addressed. The transcript is trivially inconsistent if one of them is fulfilled and we consider that \(\textsf {badH} \) does not hold in the following. If the transcript is still bad, it is called sampling-induced bad iff one of the following conditions from [JN20] holds, for some \(\alpha \in \{1, \ldots , 5\}\) and \(\beta \in \{\alpha , \ldots , 5\}\):
have to be addressed. The transcript is trivially inconsistent if one of them is fulfilled and we consider that \(\textsf {badH} \) does not hold in the following. If the transcript is still bad, it is called sampling-induced bad iff one of the following conditions from [JN20] holds, for some \(\alpha \in \{1, \ldots , 5\}\) and \(\beta \in \{\alpha , \ldots , 5\}\):
-
\(\textsf {ycoll} _{\alpha , \beta }\): \(\exists i \in \mathcal {I} _{\alpha }, j \in \mathcal {I} _{\beta }\) such that \(X_i \ne X_j \wedge Y_i = Y_j\) and
-
\(\textsf {vcoll} _{\alpha , \beta }\): \(\exists i \in \mathcal {I} _{\alpha }, j \in \mathcal {I} _{\beta }\) such that \(U_i \ne U_j \wedge V_i = V_j\),
where \(\mathcal {I} _i\) is defined as before. It holds that

By varying \(\alpha \) and \(\beta \) over all 30 values, one obtains 30 conditions that could yield that  or
or  . Some of these conditions cannot be satisfied due to the sampling mechanism. Those are
. Some of these conditions cannot be satisfied due to the sampling mechanism. Those are
A transcript is called bad if it is a bad hash-equivalent or bad sampling-induced transcript. All other transcripts are called good and all good transcripts are attainable. It holds that
5.3 Analysis of Bad Transcripts
The analysis of bad transcript is the core point where the analysis of CLRW2 and TNT differ. This is mainly because TNT lacks hash functions, but adds the unmodified tweak to the state between the permutation calls. As a result, hash collisions as in CLRW2 cannot occur for distinct tweaks.
Lemma 5
For TNT, it holds in the ideal world that
Proof
We study the probabilities of the individual events \(\textsf {badH} \) in the following. Prior, we note that \(F(T_i, M_i) =^{\text {def}} \pi _1(M_i) \oplus T_i\) is \(\epsilon \)-\(\textsf {AU}\) for \(\epsilon \le 1/(2^n - 1) \le 2^{1-n}\), and at most \(1/(2^n - (q - 1))\) if \(q - 1\) values \(M_i\) had been queried before. Since \(q \le 2^{n-2}\), it holds that \(\epsilon \le 4 / (3 \cdot 2^{n})\).
-
 . This event holds if for some distinct i, j both \(X_i = X_j\) and \(U_i = U_j\). If \(T_i = T_j\), it must hold that \(M_i \ne M_j\), which implies that \(X_i \ne X_j\) and the event cannot hold. If \(T_i \ne T_j\), \(X_i = X_j\) implies \(Y_i = Y_j\) and \(U_i = U_j\) implies \(V_i = V_j\). Thus, it would have to hold that \(T_i = T_j\), which is a contradiction. Hence, the probability is zero.
. This event holds if for some distinct i, j both \(X_i = X_j\) and \(U_i = U_j\). If \(T_i = T_j\), it must hold that \(M_i \ne M_j\), which implies that \(X_i \ne X_j\) and the event cannot hold. If \(T_i \ne T_j\), \(X_i = X_j\) implies \(Y_i = Y_j\) and \(U_i = U_j\) implies \(V_i = V_j\). Thus, it would have to hold that \(T_i = T_j\), which is a contradiction. Hence, the probability is zero. -
 . This event holds if for some distinct i, j both \(X_i = X_j\) and \(T_i = T_j\). Since \(T = T\), it must follow that \(M_i = M_j\). Though, since \(\mathbf {A}\) does not ask duplicate queries, this implies that \(X_i \ne X_j\). So, the probability is zero.
. This event holds if for some distinct i, j both \(X_i = X_j\) and \(T_i = T_j\). Since \(T = T\), it must follow that \(M_i = M_j\). Though, since \(\mathbf {A}\) does not ask duplicate queries, this implies that \(X_i \ne X_j\). So, the probability is zero. -
 . This event holds if for some distinct i, j both \(U_i = U_j\) and \(T_i = T_j\). Again, the latter condition implies that \(M_i \ne M_j\). \(U_i = U_j\) implies that \(V_i = V_j\), which implies that \(Y_i = Y_j\), \(X_i = X_j\), and \(\pi _1(M_i) = \pi _1(M_j)\), which is a contradiction and therefore has zero probability.
. This event holds if for some distinct i, j both \(U_i = U_j\) and \(T_i = T_j\). Again, the latter condition implies that \(M_i \ne M_j\). \(U_i = U_j\) implies that \(V_i = V_j\), which implies that \(Y_i = Y_j\), \(X_i = X_j\), and \(\pi _1(M_i) = \pi _1(M_j)\), which is a contradiction and therefore has zero probability. -
 . This event holds if for some distinct \(i, j, k, \ell \), \(X_i = X_j\), \(U_j = U_k\), and \(X_k = X_{\ell }\). The values of X are results from an \(\epsilon \)-universal hash function. The values U are sampled uniformly at random in the ideal world from a set of at least \(2^{n} - q\) values for the current tweak. Thus, its sampling process can be interpreted to be \(\epsilon \)-\(\textsf {AU}\) with \(\epsilon \le 1/(2^n - q)\). We can apply Lemma 3 to obtain $$\begin{aligned} \Pr \left[ \textsf {badH} _4\right]&\le q^2 \epsilon ^{1.5} \le \frac{4^{1.5} q^2}{(3 \cdot 2^n)^{1.5}} \le \frac{2q^2}{2^{1.5n}}. \end{aligned}$$
. This event holds if for some distinct \(i, j, k, \ell \), \(X_i = X_j\), \(U_j = U_k\), and \(X_k = X_{\ell }\). The values of X are results from an \(\epsilon \)-universal hash function. The values U are sampled uniformly at random in the ideal world from a set of at least \(2^{n} - q\) values for the current tweak. Thus, its sampling process can be interpreted to be \(\epsilon \)-\(\textsf {AU}\) with \(\epsilon \le 1/(2^n - q)\). We can apply Lemma 3 to obtain $$\begin{aligned} \Pr \left[ \textsf {badH} _4\right]&\le q^2 \epsilon ^{1.5} \le \frac{4^{1.5} q^2}{(3 \cdot 2^n)^{1.5}} \le \frac{2q^2}{2^{1.5n}}. \end{aligned}$$ -
 . This event holds if for some distinct \(i, j, k, \ell \), \(U_i = U_j\), \(X_j = X_k\), and \(U_k = U_{\ell }\). From a similar argumentation as for \(\textsf {badH} _4\), it holds that $$\begin{aligned} \Pr \left[ \textsf {badH} _5\right]&\le \frac{2q^2}{2^{1.5n}}. \end{aligned}$$
. This event holds if for some distinct \(i, j, k, \ell \), \(U_i = U_j\), \(X_j = X_k\), and \(U_k = U_{\ell }\). From a similar argumentation as for \(\textsf {badH} _4\), it holds that $$\begin{aligned} \Pr \left[ \textsf {badH} _5\right]&\le \frac{2q^2}{2^{1.5n}}. \end{aligned}$$ -
 . This event holds if there exist distinct \(i_1, \ldots , i_k \in [q]\) for \(k \ge 2^n/2q\) such that \(X_{i_1} = \cdots = X_{i_k}\). Since \((T_{i}, M_i) \ne (T_j, M_j)\) for none of the indices, we can use Corollary 1 with \(a = 2^n/2q\) to upper bound it by $$\begin{aligned} \Pr \left[ \textsf {badH} _6\right]&\le \frac{8q^4 \epsilon }{2^{2n}} \le \frac{16q^4}{2^{3n}}. \end{aligned}$$
. This event holds if there exist distinct \(i_1, \ldots , i_k \in [q]\) for \(k \ge 2^n/2q\) such that \(X_{i_1} = \cdots = X_{i_k}\). Since \((T_{i}, M_i) \ne (T_j, M_j)\) for none of the indices, we can use Corollary 1 with \(a = 2^n/2q\) to upper bound it by $$\begin{aligned} \Pr \left[ \textsf {badH} _6\right]&\le \frac{8q^4 \epsilon }{2^{2n}} \le \frac{16q^4}{2^{3n}}. \end{aligned}$$ -
 . This event holds if there exist distinct \(i_1, \ldots , i_k \in [q]\) for \(k \ge 2^n/2q\) such that \(U_{i_1} = \cdots = U_{i_k}\). From a similar argumentation as for \(\textsf {badH} _6\), we get $$\begin{aligned} \Pr \left[ \textsf {badH} _7\right]&\le \frac{16q^4}{2^{3n}}. \end{aligned}$$
. This event holds if there exist distinct \(i_1, \ldots , i_k \in [q]\) for \(k \ge 2^n/2q\) such that \(U_{i_1} = \cdots = U_{i_k}\). From a similar argumentation as for \(\textsf {badH} _6\), we get $$\begin{aligned} \Pr \left[ \textsf {badH} _7\right]&\le \frac{16q^4}{2^{3n}}. \end{aligned}$$
Lemma 5 follows then from the sum of probabilities of all \(\textsf {badH} \) events. \(\square \)
Lemma 6
For TNT, it holds in the ideal world that
The proof is exactly as in [JN20] and is deferred to the full version of this work.
5.4 Analysis of Good Transcripts
Lemma 7
For an arbitrary good transcript \(\tau \), it holds that
Again, the proof can follow a similar argumentation as the analysis of good transcripts in [JN20] and is therefore deferred to the full version of this work.
6 Summary and Discussion
This work tried to conduct a step towards closing the security gap of TNT. We showed in Sect. 2 that a variant of Mennink’s distinguisher from [Men18] also applies to TNT, which yields a theoretical distinguisher in \(O(\sqrt{n} \cdot 2^{3n/4})\) time, data, and memory complexity. For this purpose, we reduce the complexity of Mennink’s information-theoretic distinguisher from \(O(2^{3n/2})\) to \(O(2^{3n/4})\) computations and show that at least two similar distinguishers exist. Thereupon, we use the distinguisher to mount a partial key-recovery attack on the instance  from an impossible differential. This attack is described in Sect. 3. Since it needs multiple pairs, its complexity is higher than \(O(2^{3n/4})\). We emphasize that our analysis does not break the proposed version of
from an impossible differential. This attack is described in Sect. 3. Since it needs multiple pairs, its complexity is higher than \(O(2^{3n/4})\). We emphasize that our analysis does not break the proposed version of  from [BGGS20].
from [BGGS20].
From a constructive point of view, we followed the rigorous analysis by Jha and Nandi on CLRW2. We show in Sect. 5 that their STPRP security proof of CLRW2 for up to \(O(2^{3n/4})\) queries can be adapted to an TPRP proof of TNT with similar complexity. We could build on the approach by Jha and Nandi on CLRW2 since we restricted the adversary’s queries to the forward direction only. Thus, the first permutation and tweak addition masks the inputs, similar to the first hash function in CLRW2. Since an equivalent is missing at the ciphertext side, one cannot directly derive STPRP security. However, a four-round variant of TNT would possess such hash-function-like masking at the ciphertext-side. This implies that a four-round variant that adds a fourth independent permutation \(\pi _4\) and encrypts M under T as

would directly inherit the \(O(2^{3n/4}\)) STPRP security from CLRW2. Still, it remains a highly interesting work to conduct an STPRP analysis of the three-round construction TNT. In particular, the Mirror-theory approach seems not easily adaptable since the sampling process in the ideal world is unclear.
From our studies, we see strong indications that TNT is STPRP-secure for approximately \(O(2^{3n/4})\) queries if the primitives are secure – although, we were not able to show it at this point of time. However, we found the problem of sampling the variables from both sides consistently in the middle non-trivial. An alternative strategy could be a more precise, but also considerably more sophisticated, study of the original \(\chi ^2\)-based proof of TNT from [BGGS20].
Notes
References
Bao, Z., Guo, C., Guo, J., Song, L.: TNT: how to tweak a block cipher. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12106, pp. 641–673. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_22
Bao, Z., Guo, J., Iwata, T., Minematsu, K.: ZOCB and ZOTR: tweakable blockcipher modes for authenticated encryption with full absorption. IACR Trans. Symmetric Cryptol. 2019(2), 1–54 (2019)
Beierle, C., et al.: The SKINNY family of block ciphers and its low-latency variant MANTIS. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 123–153. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_5
Bogdanov, A., et al.: PRESENT: an ultra-lightweight block cipher. In: Paillier, P., Verbauwhede, I. (eds.) CHES 2007. LNCS, vol. 4727, pp. 450–466. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74735-2_31
Beierle, C., Leander, G., Moradi, A., Rasoolzadeh, S.: CRAFT: lightweight tweakable block cipher with efficient protection against DFA attacks. IACR Trans. Symmetric Cryptol. 2019(1), 5–45 (2019)
Chakraborti, A., Iwata, T., Minematsu, K., Nandi, M.: Blockcipher-based authenticated encryption: how small can we go? In: Fischer, W., Homma, N. (eds.) CHES 2017. LNCS, vol. 10529, pp. 277–298. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66787-4_14
Chakraborti, A., Iwata, T., Minematsu, K., Nandi, M.: Blockcipher-based authenticated encryption: how small can we go? J. Cryptol. 33(3), 703–741 (2019). https://doi.org/10.1007/s00145-019-09325-z
Cid, C., Murphy, S., Robshaw, M.J.B.: Small scale variants of the AES. In: Gilbert, H., Handschuh, H. (eds.) FSE 2005. LNCS, vol. 3557, pp. 145–162. Springer, Heidelberg (2005). https://doi.org/10.1007/11502760_10
Carter, L., Wegman, M.N.: Universal classes of hash functions. J. Comput. Syst. Sci. 18(2), 143–154 (1979)
Grassi, L., Rechberger, C., Rønjom, S.: Subspace trail cryptanalysis and its applications to AES. IACR Trans. Symmetric Cryptol. 2016(2), 192–225 (2016)
Hoang, V.T., Tessaro, S.: Key-alternating ciphers and key-length extension: exact bounds and multi-user security. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 3–32. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_1
Iwata, T., Minematsu, K., Peyrin, T., Seurin, Y.: ZMAC: a fast tweakable block cipher mode for highly secure message authentication. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 34–65. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_2
Jha, A., List, E., Minematsu, K., Mishra, S., Nandi, M.: XHX – a framework for optimally secure tweakable block ciphers from classical block ciphers and universal hashing. In: Lange, T., Dunkelman, O. (eds.) LATINCRYPT 2017. LNCS, vol. 11368, pp. 207–227. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-25283-0_12
Jha, A., Nandi, M.: Tight security of cascaded LRW2. J. Cryptol. 33, 1272–1317 (2020). https://doi.org/10.1007/s00145-020-09347-y
Jean, J., Nikolić, I., Peyrin, T.: KIASU v1.1 (2014). First-round submission to the CAESAR competition
Jean, J., Nikolić, I., Peyrin, T.: Tweaks and keys for block ciphers: the TWEAKEY framework. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 274–288. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_15
Jean, J., Nikolić, I., Peyrin, T.: Deoxys v1.41, 12 October 2016. Third-round submission to the CAESAR competition. http://competitions.cr.yp.to/caesar-submissions.html
Krovetz, T., Rogaway, P.: The software performance of authenticated-encryption modes. In: Joux, A. (ed.) FSE 2011. LNCS, vol. 6733, pp. 306–327. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21702-9_18
Krawczyk, H.: LFSR-based hashing and authentication. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 129–139. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_15
Leander, G.: Small scale variants of the block cipher PRESENT. IACR Cryptology ePrint Archive 2010/143 (2010)
Lee, B.H., Lee, J.: Tweakable block ciphers secure beyond the birthday bound in the ideal cipher model. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018. LNCS, vol. 11272, pp. 305–335. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03326-2_11
List, E., Nandi, M.: ZMAC+ - an efficient variable-output-length variant of ZMAC. IACR Trans. Symmetric Cryptol. 2017(4), 306–325 (2017)
Leurent, G., Nandi, M., Sibleyras, F.: Generic attacks against beyond-birthday-bound MACs. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 306–336. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_11
Liskov, M., Rivest, R.L., Wagner, D.: Tweakable block ciphers. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 31–46. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_3
Landecker, W., Shrimpton, T., Terashima, R.S.: Tweakable blockciphers with beyond birthday-bound security. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 14–30. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_2
Mennink, B.: Optimally secure tweakable blockciphers. In: Leander, G. (ed.) FSE 2015. LNCS, vol. 9054, pp. 428–448. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48116-5_21
Mennink, B.: Towards tight security of cascaded LRW2. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11240, pp. 192–222. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_8
Minematsu, K.: Parallelizable rate-1 authenticated encryption from pseudorandom functions. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 275–292. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_16
Mennink, B., Neves, S.: Encrypted Davies-Meyer and its dual: towards optimal security using mirror theory. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 556–583. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_19
Naito, Y.: Full PRF-secure message authentication code based on tweakable block cipher. In: Au, M.-H., Miyaji, A. (eds.) ProvSec 2015. LNCS, vol. 9451, pp. 167–182. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-26059-4_9
Naito, Y.: On the efficiency of ZMAC-type modes. In: Camenisch, J., Papadimitratos, P. (eds.) CANS 2018. LNCS, vol. 11124, pp. 190–210. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00434-7_10
Patarin, J.: The “coefficients H” technique. In: Avanzi, R.M., Keliher, L., Sica, F. (eds.) SAC 2008. LNCS, vol. 5381, pp. 328–345. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04159-4_21
Patarin, J.: Introduction to mirror theory: analysis of systems of linear equalities and linear non equalities for cryptography. IACR Cryptology ePrint Archive 2010/287 (2010)
Peyrin, T., Seurin, Y.: Counter-in-tweak: authenticated encryption modes for tweakable block ciphers. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 33–63. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_2
Rogaway, P.: Bucket hashing and its application to fast message authentication. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 29–42. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_3
Sibleyras, F.: Generic attack on iterated tweakable FX constructions. In: Jarecki, S. (ed.) CT-RSA 2020. LNCS, vol. 12006, pp. 1–14. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-40186-3_1
Samajder, S., Sarkar, P.: Rigorous upper bounds on data complexities of block cipher cryptanalysis. J. Math. Cryptol. 11(3), 147–175 (2017)
Wang, L., Guo, J., Zhang, G., Zhao, J., Gu, D.: How to build fully secure tweakable blockciphers from classical blockciphers. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 455–483. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_17
Acknowledgments
We are highly thankful to Zhenzhen Bao and Mridul Nandi for the fruitful discussions as well as the reviewers from Asiacrypt 2020 for their inspiring comments, all of which lead to significant improvements in this work. This research has been partially supported by Nanyang Technological University in Singapore under Grant 04INS000397C230, Singapore’s Ministry of Education under Grants RG18/19 and MOE2019-T2-1-060, the National Natural Science Foundation of China (No. 61961146004, 61802399, 61802400, 61732021 and 61772519) and the Youth Innovation Promotion Association CAS.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Guo, C., Guo, J., List, E., Song, L. (2020). Towards Closing the Security Gap of Tweak-aNd-Tweak (TNT). In: Moriai, S., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2020. ASIACRYPT 2020. Lecture Notes in Computer Science(), vol 12491. Springer, Cham. https://doi.org/10.1007/978-3-030-64837-4_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-64837-4_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64836-7
Online ISBN: 978-3-030-64837-4
eBook Packages: Computer ScienceComputer Science (R0)













 each with varying numbers of message pairs with the desired difference
each with varying numbers of message pairs with the desired difference 


 or
or 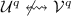 .
. . This event holds if for some distinct i, j both
. This event holds if for some distinct i, j both  . This event holds if for some distinct i, j both
. This event holds if for some distinct i, j both  . This event holds if for some distinct i, j both
. This event holds if for some distinct i, j both  . This event holds if for some distinct
. This event holds if for some distinct  . This event holds if for some distinct
. This event holds if for some distinct  . This event holds if there exist distinct
. This event holds if there exist distinct  . This event holds if there exist distinct
. This event holds if there exist distinct 