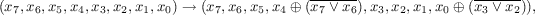The SKINNY Family of Block Ciphers and Its Low-Latency Variant MANTIS

Abstract

We present a new tweakable block cipher family SKINNY, whose goal is to compete with NSA recent design SIMON in terms of hardware/software performances, while proving in addition much stronger security guarantees with regards to differential/linear attacks. In particular, unlike SIMON, we are able to provide strong bounds for all versions, and not only in the single-key model, but also in the related-key or related-tweak model. SKINNY has flexible block/key/tweak sizes and can also benefit from very efficient threshold implementations for side-channel protection. Regarding performances, it outperforms all known ciphers for ASIC round-based implementations, while still reaching an extremely small area for serial implementations and a very good efficiency for software and micro-controllers implementations (SKINNY has the smallest total number of AND/OR/XOR gates used for encryption process).

Secondly, we present MANTIS, a dedicated variant of SKINNY for low-latency implementations, that constitutes a very efficient solution to the problem of designing a tweakable block cipher for memory encryption. MANTIS basically reuses well understood, previously studied, known components. Yet, by putting those components together in a new fashion, we obtain a competitive cipher to PRINCE in latency and area, while being enhanced with a tweak input.

Updated information on SKINNY will be made available via https://sites.google.com/site/skinnycipher/.

1 Introduction

Due to the increasing importance of pervasive computing, lightweight cryptography is currently a very active research domain in the symmetric-key cryptography community. In particular, we have recently seen the apparition of many (some might say too many) lightweight block ciphers, hash functions and stream ciphers. While the term lightweight is not strictly defined, it most often refers to a primitive that allows compact implementations, i.e. minimizing the area required by the implementation. While the focus on area is certainly valid with many applications, most of them require additional performance criteria to be taken into account. In particular, the throughput of the primitive represents an important dimension for many applications. Besides that, power (in particular for passive RFID tags) and energy (for battery-driven device) may be major aspects.

Moreover, the efficiency on different hardware technologies (ASIC, FPGA) needs to be taken into account, and even micro-controllers become a scenario of importance. Finally, as remarked in [3], software implementations should not be completely ignored for these lightweight primitives, as in many applications the tiny devices will communicate with servers handling thousands or millions of them. Thus, even so research started by focusing on chip area only, lightweight cryptography is indeed an inherent multidimensional problem.

Investigating the recent proposals in more detail, a major distinction is eye-catching and one can roughly split the proposals in two classes. The first class of ciphers uses very strong, but less efficient components (like the Sbox used in PRESENT  [5] or LED  [15], or the MDS diffusion matrix in LED or PICCOLO  [31]). The second class of designs uses very efficient, but rather weak components (like the very small KATAN  [9] or SIMON  [2] round function)¹.

From a security viewpoint, the analysis of the members of the first class can be conducted much easily and it is usually possible to derive strong arguments for their security. However, while the second class strategy usually gives very competitive performance figures, it is much harder with state-of-the-art analysis techniques to obtain security guarantees even with regards to basic linear or differential cryptanalysis. In particular, when using very light round functions, bounds on the probabilities of linear or differential characteristics are usually both hard to obtain and not very strong. As a considerable fraction of the lightweight primitives proposed got quickly broken within a few months or years from their publication date, being able to give convincing security arguments turns out to be of major importance.

Of special interest, in this context, is the recent publication of the SIMON and SPECK family of block ciphers by the NSA [2]. Those ciphers brought a huge leap in terms of performances. As of today, these two primitives have an important efficiency advantage against all its competitors, in almost all implementation scenarios and platforms. However, even though SIMON or SPECK are quite elegant and seemingly well-crafted designs, these efficiency improvements came at an essential price. Echoing the above, since the ciphers have a very light round function, their security bounds regarding classical linear or differential cryptanalysis are not so impressive, quite difficult to obtain or even non-existent. For example, in [22] the authors provide differential/linear bounds for SIMON, but, as we will see, one needs a big proportion of the total number of rounds to guarantee its security according to its block size. Even worse, no bound is currently known in the related-key model for any version of SIMON and thus there is a risk that good related-key differential characteristics might exist for this family of ciphers (while some lightweight proposals such as LED  [15], PICCOLO  [31] or some versions of TWINE  [33] do provide such a security guarantee). One should be further cautious as these designs come from a governmental agency which does not provide specific details on how the primitives were built. No cryptanalysis was ever provided by the designers. Instead, the important analysis work was been carried out by the research community in the last few years and one should note that so far SIMON or SPECK remain unbroken.

It is therefore a major challenge for academic research to design a cipher that can compete with SIMON’s performances and additionally provides the essential strong security guarantees that SIMON is clearly lacking. We emphasize that this is both a research challenge and, in view of NSA’s efforts to propose SIMON into an ISO standard, a challenge that has likely a practical impact.

Lightweight Tweakable Block Ciphers and Side-Channel Protected Implementations. We note that tiny devices are more prone to be deployed into insecure environments and thus side-channel protected implementations of lightweight encryption primitives is a very important aspect that should be taken care of. One might even argue that instead of comparing performances of unprotected implementations of these lightweight primitives, one should instead compare protected variants (this is the recent trend followed by ciphers like ZORRO  [14] or PICARO  [28] and has actually already been taken into account long before by the cipher NOEKEON  [13]). One extra protection against side-channel attacks can be the use of leakage resilient designs and notably through an extra tweak input of the cipher. Such tweakable block ciphers are rather rare, the only such candidate being Joltik-BC  [18] or the internal cipher from SCREAM  [34]. Coming up with a tweakable block cipher is indeed not an easy task as one must be extremely careful how to include this extra input that can be fully controlled by the attacker.

Low-Latency Implementations for Memory Encryption. One very interesting field in the area of lightweight cryptography is memory encryption (see e.g. [16] for an extensive survey of memory encryption techniques). Memory encryption has been used in the literature to protect the memory used by a process domain against several types of attackers, including attackers capable of monitoring and even manipulating bus transactions. Examples of commercial uses do not abound, but there are at least two: IBM’s SecureBlue++ [36] and Intel’s SGX whose encryption and integrity mechanisms have been presented by Gueron at RWC 2016². No documentation seems to be publicly available regarding the encryption used in IBM’s solution, while Intel’s encryption method requires additional data to be stored with each cache line. It is optimal in the context of encryption with memory overhead, but if the use case does not allow memory overhead then an entirely different approach is necessary.

With a focus on data confidentiality, a tweakable block cipher in ECB mode would then be the natural, straightforward solution. However, all generic methods to construct a tweakable block cipher from a block cipher suffer from an increased latency. Therefore, there is a clear need for lightweight tweakable block ciphers which do not require whitening value derivation, have a latency similar to the best non-tweakable block ciphers, and that can also be used in modes of operation that do not require memory expansion and offer beyond-birthday-bound security.

While being of great practical impact and need, it is actually very challenging to come up with such a block cipher. It should have three main characteristics. First, it must be executed within a single clock cycle and with a very low latency. Second, a tweak input is required, which in the case of memory encryption will be the memory address. Third, as one necessarily has to implement encryption and decryption, it is desirable to have a very low overhead when implementing decryption on top of encryption. The first and the third characteristics are already studied in the block cipher PRINCE  [7]. However, the second point, i.e. having a tweak input, is not provided by PRINCE. It is not trivial to turn PRINCE into a tweakable block cipher, especially without increasing the number of rounds (and thereby latency) significantly.

Our Contributions. Our contributions are twofold. First, we introduce a new lightweight family of block ciphers: SKINNY. Our goal here is to provide a competitor to SIMON in terms of hardware/software performances, while proving in addition much stronger security guarantees with regard to differential/linear attacks. Second, we present MANTIS, a dedicated variant of SKINNY that constitutes a very efficient solution to the aforementioned problem of designing a tweakable block cipher for memory encryption.

Regarding SKINNY, we have pushed further the recent trend of having a SPN cipher with locally non-optimal internal components: SKINNY is an SPN cipher that uses a compact Sbox, a new very sparse diffusion layer, and a new very light key schedule. Yet, by carefully choosing our components and how they interact, our construction manages to retain very strong security guarantees. For all the SKINNY versions, we are able to prove using mixed integer linear programming (MILP) very strong bounds with respect to differential/linear attacks, not only in the single-key model, but also in the much more involved related-key model. Some versions of SKINNY have a very large key size compared to its block size and this theoretically renders the bounds search space huge. Therefore, the MILP methods we have devised to compute these bounds for a SKINNY-like construction can actually be considered a contribution by itself. As we will see later, compared to SIMON, in the single-key model SKINNY needs a much lower proportion of its total number of rounds to provide a sufficient bound on the best differential/linear characteristic. In the related-key model, the situation is even more at SKINNY’s advantage as no such bound is known for any version of SIMON as of today.

With regard to performance, SKINNY reaches very small area with serial ASIC implementations, yet it is actually the very first block cipher that leads to better performances than SIMON for round-based ASIC implementations, arguably the most important type of implementation since it provides a very good throughput for a reasonably low area cost, in contrary to serial implementations that only minimizes area. We also exhibit ASIC threshold implementations of our SKINNY variants that compare for example very favourably to AES-128 threshold implementations. As explained above, this is an integral part of modern lightweight primitives.

Regarding software, our implementations outperform all lightweight ciphers, except SIMON which performs slightly faster in the situation where the key schedule is performed only once. However, as remarked in [3], it is more likely in practice that the key schedule has to be performed everytime, and since SKINNY has a very lightweight key schedule we expect the efficiency of SKINNY software implementations to be equivalent to that of SIMON. This shows that SKINNY would perfectly fit a scenario where a server communicate with many lightweight devices. These performances are not surprising, in particular for bit-sliced implementations, as we show that SKINNY uses a much smaller total number of AND/NOR/XOR gates compared to all known lightweight block ciphers. This indicates that SKINNY will be competitive for most platforms and scenarios. Micro-controllers are no exception, and we show that SKINNY performs extremely well on these architectures.

We further remark that the decryption process of SKINNY has almost exactly the same description as the encryption counterpart, thus minimizing the decryption overhead.

We finally note that similarly to SIMON, SKINNY very naturally encompasses 64- or 128-bit block versions and a wide range of key sizes. However, in addition, SKINNY provides a tweakable capability, which can be very useful not only for leakage resilient implementations, but also to be directly plugged into higher-level operating modes, such as SCT  [27]. In order to provide this tweak feature, we have generalized the STK construction [17] to enable more compact implementations while maintaining a high provable security level.

The SKINNY specifications are given in Sect. 2. The rationale of our design as well as various theoretical security and efficiency comparisons are provided in Sect. 3. Finally, we conducted a complete security analysis in Sect. 4 and we exhibit our implementation results in Sect. 5 (all the details are provided in the full version of the paper).

Regarding MANTIS, we propose in Sect. 6 a low-latency tweakable block cipher that reuses some design principles of SKINNY ³. It represents a very efficient solution to the aforementioned problem of designing a tweakable block cipher tailored for memory encryption.

The main challenge when designing such a cipher is that its latency is directly related to the number of rounds. Thus, it is crucial to find a design, i.e. a round function and a tweak-scheduling, that ensures security already with a minimal number of rounds. Here, components of the recently proposed block ciphers PRINCE and MIDORI  [1] turn out to be very beneficial.

The crucial step in the design of MANTIS was to find a suitable tweak-scheduling that would ensure a high number of active Sboxes not only in the single-key setting, but also in the setting where the attacker can control the difference in the tweak. Using, again, the MILP approach, we are able to demonstrate that a rather small number of rounds is already sufficient to ensure the resistance of MANTIS to differential (and linear) attacks in the related-tweak setting.

Besides the tweak-scheduling, we emphasize that MANTIS basically reuses well understood, previously studied, known components. It is mainly putting those components together in a new fashion, that allows MANTIS to be very competitive to PRINCE in latency and area, while being enhanced with a tweak. Thus, compared to the performance figures of PRINCE, we get the tweak almost for free, which is the key to solve the pressing problem of memory encryption.

2 Specification of SKINNY

Notations and SKINNY Versions. The lightweight block ciphers of the SKINNY family have 64-bit and 128-bit block versions and we denote n the block size. In both $n=64$ and $n=128$ versions, the internal state is viewed as a $4\times 4$ square array of cells, where each cell is a nibble (in the $n=64$ case) or a byte (in the $n=128$ case). We denote $IS_{i,j}$ the cell of the internal state located at Row i and Column j (counting starting from 0). One can also view this $4\times 4$ square array of cells as a vector of cells by concatenating the rows. Thus, we denote with a single subscript $IS_{i}$ the cell of the internal state located at Position i in this vector (counting starting from 0) and we have that $IS_{i,j}=IS_{4\cdot i+j}$.

SKINNY follows the TWEAKEY framework from [17] and thus takes a tweakey input instead of a key or a pair key/tweak. The user can then choose what part of this tweakey input will be key material and/or tweak material (classical block cipher view is to use the entire tweakey input as key material only). The family of lightweight block ciphers SKINNY have three main tweakey size versions: for a block size n, we propose versions with tweakey size $t=n$, $t=2n$ and $t=3n$ (versions with other tweakey sizes between n and 3n are naturally obtained from these main versions) and we denote $z=t/n$ the tweakey size to block size ratio. The tweakey state is also viewed as a collection of z $4\times 4$ square arrays of cells of s bits each. We denote these arrays TK1 when $z=1$, TK1 and TK2 when $z=2$, and finally TK1, TK2 and TK3 when $z=3$. Moreover, we denote $TKz_{i,j}$ the cell of the tweakey state located at Row i and Column j of the z-th cell array. As for the internal state, we extend this notation to a vector view with a single subscript: $TK1_{i}$, $TK2_{i}$ and $TK3_{i}$. Moreover, we define the adversarial model SK (resp. TK1, TK2 or TK3) where the attacker cannot (resp. can) introduce differences in the tweakey state.

Initialization. The cipher receives a plaintext $m=m_0 \Vert m_1 \Vert \cdots \Vert m_{14} \Vert m_{15}$, where the $m_i$ are s-bit cells, with $s=n/16$ (we have $s=4$ for the 64-bit block SKINNY versions and $s=8$ for the 128-bit block SKINNY versions). The initialization of the cipher’s internal state is performed by simply setting $IS_i=m_i$ for $0 \le i \le 15$:

$$\begin{aligned} IS = \left[ \begin{array}{cccc} m_0 &{} m_1 &{} m_2 &{} m_{3} \\ m_4 &{} m_5 &{} m_6 &{} m_{7} \\ m_8 &{} m_9 &{} m_{10} &{} m_{11} \\ m_{12} &{} m_{13} &{} m_{14} &{} m_{15} \\ \end{array} \right] \end{aligned}$$

This is the initial value of the cipher internal state and note that the state is loaded row-wise rather than in the column-wise fashion we have come to expect from the AES; this is a more hardware-friendly choice, as pointed out in [24].

The cipher receives a tweakey input $tk=tk_0 \Vert tk_1 \Vert \cdots \Vert tk_{30} \Vert tk_{16z-1}$, where the $tk_i$ are s-bit cells. The initialization of the cipher’s tweakey state is performed by simply setting for $0 \le i \le 15$: $TK1_i=tk_i$ when $z=1$, $TK1_i=tk_i$ and $TK2_i=tk_{16+i}$ when $z=2$, and finally $TK1_i=tk_i$, $TK2_i=tk_{16+i}$ and $TK3_i=tk_{32+i}$ when $z=3$. We note that the tweakey states are loaded row-wise.

Table 1. Number of rounds for SKINNY-n-t, with n-bit internal state and t-bit tweakey state.

Table 2. 4-bit Sbox $\mathcal {S}_4$ used in SKINNY when $s=4$.

The Round Function. One encryption round of SKINNY is composed of five operations in the following order: SubCells, AddConstants, AddRoundTweakey, ShiftRows and MixColumns (see illustration in Fig. 1). The number r of rounds to perform during encryption depends on the block and tweakey sizes. The actual values are summarized in Table 1. Note that no whitening key is used in SKINNY. Thus, a part of the first and last round do not add any security. We motivate this choice in Sect. 3.

Fig. 1.

The SKINNY round function applies five different transformations: SubCells (SC), AddConstants (AC), AddRoundTweakey (ART), ShiftRows (SR) and MixColumns (MC).

• SubCells. A s-bit Sbox is applied to every cell of the cipher internal state. For $s=4$, SKINNY cipher uses a Sbox $\mathcal {S}_4$ very close to the PICCOLO Sbox [31]. The action of this Sbox in hexadecimal notation is given by the following Table 2. Note that $\mathcal {S}_4$ can also be described with four NOR and four XOR operations, as depicted in Fig. 2. If $x_0$, $x_1$, $x_2$ and $x_3$ represent the four inputs bits of the Sbox ($x_0$ being the least significant bit), one simply applies the following transformation:

  $$\begin{aligned} (x_3, x_2, x_1, x_0) \rightarrow (x_3, x_2, x_1, x_0 \oplus (\overline{x_3 \vee x_2})), \end{aligned}$$

  followed by a left shift bit rotation. This process is repeated four times, except for the last iteration where the bit rotation is omitted. For the case $s=8$, SKINNY uses an 8-bit Sbox $\mathcal {S}_8$ that is built in a similar manner as for the 4-bit Sbox $\mathcal {S}_4$ described above. The construction is simple and is depicted in Fig. 3. If $x_0$, $\ldots$, $x_7$ represent the eight inputs bits of the Sbox ($x_0$ being the least significant bit), it basically applies the below transformation on the 8-bit state:

  

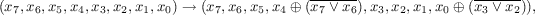
  followed by the bit permutation:

  $$\begin{aligned} (x_7,x_6,x_5,x_4, x_3, x_2, x_1, x_0) \longrightarrow (x_2,x_1,x_7,x_6,x_4,x_0,x_3,x_5), \end{aligned}$$

  repeating this process four times, except for the last iteration where there is just a bit swap between $x_1$ and $x_2$.

• AddConstants. A 6-bit affine LFSR, whose state is denoted (rc$_5$, rc$_4$, rc$_3$, rc$_2$, rc$_1$, rc$_0)$ (with rc$_0$ being the least significant bit), is used to generate round constants. Its update function is defined as:

  $$\begin{aligned} (\mathrm {rc}_5 || \mathrm {rc}_4 || \mathrm {rc}_3 || \mathrm {rc}_2 || \mathrm {rc}_1 || \mathrm {rc}_0) \rightarrow (\mathrm {rc}_4 || \mathrm {rc}_3 || \mathrm {rc}_2 || \mathrm {rc}_1 || \mathrm {rc}_0 || \mathrm {rc}_5 \oplus \mathrm {rc}_4 \oplus 1). \end{aligned}$$

  The six bits are initialized to zero, and updated before use in a given round. The bits from the LFSR are arranged into a $4\times 4$ array (only the first column of the state is affected by the LFSR bits), depending on the size of internal state:

  $$\begin{aligned} \begin{bmatrix} c_{0}&0&0&0\\ c_{1}&0&0&0\\ c_{2}&0&0&0\\ 0&0&0&0\\ \end{bmatrix}, \end{aligned}$$

  with $c_2=\texttt {0x2}$ and

  $$\begin{aligned} (c_{0}, c_{1})&=(\mathrm {rc}_3 \Vert \mathrm {rc}_2 \Vert \mathrm {rc}_1 \Vert \mathrm {rc}_0, \, 0 \Vert 0 \Vert \mathrm {rc}_5 \Vert \mathrm {rc}_4) \text { when } s=4\\ (c_{0}, c_{1})&=(0 \Vert 0 \Vert 0 \Vert 0 \Vert \mathrm {rc}_3 \Vert \mathrm {rc}_2 \Vert \mathrm {rc}_1 \Vert \mathrm {rc}_0, \, 0 \Vert 0 \Vert 0 \Vert 0 \Vert 0 \Vert 0 \Vert \mathrm {rc}_5 \Vert \mathrm {rc}_4) \text { when } s=8. \end{aligned}$$

  The round constants are combined with the state, respecting array positioning, using bitwise exclusive-or.

• AddRoundTweakey. The first and second rows of all tweakey arrays are extracted and bitwise exclusive-ored to the cipher internal state, respecting the array positioning. More formally, for $i=\{0,1\}$ and $j=\{0,1,2,3\}$, we have:

  • $\bullet$ $IS_{i,j} = IS_{i,j} \oplus TK1_{i,j}$ when $z=1$,

  • $\bullet$ $IS_{i,j} = IS_{i,j} \oplus TK1_{i,j} \oplus TK2_{i,j}$ when $z=2$,

  • $\bullet$ $IS_{i,j} = IS_{i,j} \oplus TK1_{i,j} \oplus TK2_{i,j} \oplus TK3_{i,j}$ when $z=3$.

  Then, the tweakey arrays are updated as follows (this tweakey schedule is illustrated in Fig. 4). First, a permutation $P_T$ is applied on the cells positions of all tweakey arrays: for all $0\le i \le 15$, we set $TK1_i\leftarrow TK1_{P_T[i]}$ with

  $$\begin{aligned} P_T=[9,15,8,13,10,14,12,11,0,1,2,3,4,5,6,7], \end{aligned}$$

  and similarly for TK2 when $z=2$, and for TK2 and TK3 when $z=3$. This corresponds to the following reordering of the matrix cells: $(0,\dots ,15) \mathop {\longmapsto }\limits ^{P_T} (9,15,8,13,10,14,12,11,0,1,2,3,4,5,6,7)$, indices being taken row-wise. Finally, every cell of the first and second rows of TK2 and TK3 (for the SKINNY versions where TK2 and TK3 are used) are individually updated with an LFSR. The LFSRs used are given in Table 3 ($x_0$ stands for the LSB of the cell).

• ShiftRows. As in AES, in this layer the rows of the cipher state cell array are rotated, but they are to the right. More precisely, the second, third, and fourth cell rows are rotated by 1, 2 and 3 positions to the right, respectively. In other words, a permutation P is applied on the cells positions of the cipher internal state cell array: for all $0\le i \le 15$, we set $IS_i\leftarrow IS_{P[i]}$ with

  $$\begin{aligned} P=[0,1,2,3,7,4,5,6,10,11,8,9,13,14,15,12]. \end{aligned}$$

• MixColumns. Each column of the cipher internal state array is multiplied by the following binary matrix $\mathbf {M}$:

  $$\begin{aligned} \mathbf {M}= \left( \begin{array}{cccc} 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 \\ 1 &{} 0 &{} 1 &{} 0 \\ \end{array} \right) . \end{aligned}$$

Table 3. The LFSRs used in SKINNY to generate the round constants. The TK parameter gives the number of tweakey words in the cipher, and the s parameter gives the size of cell in bits.

Fig. 2.

Construction of the Sbox $\mathcal {S}_4$.

Fig. 3.

Construction of the Sbox $\mathcal {S}_8$.

Fig. 4.

The tweakey schedule in SKINNY. Each tweakey word TK1, TK2 and TK3 (if any) follows a similar transformation update, except that no LFSR is applied to TK1.

The final value of the internal state array provides the ciphertext with cells being unpacked in the same way as the packing during initialization. Note that decryption is very similar to encryption as all cipher components have very simple inverse (SubCells and MixColumns are based on a generalized Feistel structure, so their respective inverse is straightforward to deduce and can be implemented with the exact same number of operations).

Extending to Other Tweakey Sizes. The three main versions of SKINNY have tweakey sizes $t=n$, $t=2n$ and $t=3n$, but one can easily extend this to any size⁴ of tweakey $n\le t \le 3n$:

• for any tweakey size $n< t < 2n$, one simply uses exactly the $t=2n$ version but the last $2n-t$ bits of the tweakey state are fixed to the zero value. Moreover, the corresponding cells in the tweakey state TK2 will not be updated throughout the rounds with the LFSR.

• for any tweakey size $2n< t < 3n$, one simply uses exactly the $t=3n$ version but the last $3n-t$ bits of the tweakey state are fixed to the zero value. Moreover, the corresponding cells in the tweakey state TK3 will not be updated throughout the rounds with the LFSR.

We note that some of our 64-bit block SKINNY versions allow small key sizes (down to 64-bit). We emphasize that we propose these versions mainly for simplicity in the description of the SKINNY family of ciphers. Yet, as advised by the NIST [26], one should not to use key sizes that are smaller than 112 bits.

Instantiating the Tweakey State with Key and Tweak Material. Following the TWEAKEY framework [17], SKINNY takes as inputs a plaintext or a ciphertext and a tweakey value, which can be used in a flexible way by filling it with key and tweak material. Whatever the situation, the user must ensure that the key size is always at least as big as the block size.

In the classical setting where only key material is input, we use exactly the specifications of SKINNY described previously. However, when some tweak material is to be used in the tweakey state, we dedicate TK1 for this purpose and XOR a bit set to “1” every round to the second bit of the top cell of the third column (i.e. the second bit of $IS_{0,2}$). In other words, when there is some tweak material, we add an extra “1” in the constant matrix from AddConstants). Besides, in situations where the user might use different tweak sizes, we recommend to dedicate some cells of TK1 to encode the size of the tweak material, in order to ensure proper separation. Note that these are only recommendations, thus not strictly part of the specifications of SKINNY.

3 Rationale of SKINNY

Several design choices of SKINNY have been borrowed from existing ciphers, but most of our components are new, optimized for our goal: a cipher well suited for most lightweight applications. When designing SKINNY, one of our main criteria was to only add components which are vital for the security of the primitive, removing any unnecessary operation (hence the name of our proposal). We end up with the sound property that removing any component or using weaker version of a component from SKINNY would lead to a much weaker (or actually insecure) cipher. Therefore, the construction of SKINNY has been done through several iterations, trying to reach the exact spot where good performance meets strong security arguments. We detail in this section how we tried to follow this direction for each layer of the cipher.

We note that one could have chosen a slightly smaller Sbox or a slightly sparser diffusion layer, but our preliminary implementations showed that these options represent worse tradeoff overall. For example, one could imagine a very simple cipher iterating thousands of rounds composed of only a single non-linear boolean operation, an XOR and some bit wiring. However, such a cipher will lead to terrible performance regarding throughput, latency or energy consumption.

When designing a lightweight encryption scheme, several use cases must be taken in account. While area optimized implementations are important for some very constrained applications, throughput or throughput-over-area optimized implementations are also very relevant. Actually, looking at recently introduced efficiency measurements [19], one can see that our designs choices are good for many types of implementations, which is exactly what makes a good general-purpose lightweight encryption scheme.

3.1 Estimating Area and Performances

In order to discuss the rationale of our design, we first quickly describe an estimation in Gate Equivalent (GE) of the ASIC area cost of several simple bit operations (for UMC 180 nm 1.8 V [35]): a NOR/NAND gate costs 1 GE, a OR/AND gate costs 1.33 GE, a XOR/XNOR gate costs 2.67 GE and a NOT gate costs 0.67 GE. Finally, one memory bit can be estimated to 6 GE (scan flip-flop). Of course, these numbers depend on the library used, but it will give us at least some rough and easy evaluation of the design choices we will make.

Besides, even though many tradeoffs exist, we distinguish between a serial implementation, a round-based implementation and a low-latency implementation. In the latter, the entire ciphering process is performed in a single clock cycle, but the area cost is then quite important as all rounds need to be directly implemented. For a round-based implementation, an entire round of the cipher is performed in a single clock cycle, thus ending with the entire ciphering process being done in r cycles and with a moderate area cost (this tradeoff is usually a good candidate for energy efficiency). Finally, in a serial implementation, one reduces the datapath and thus the area to the minimum (usually a few bits, like the Sbox bit size), but the throughput is greatly reduced. The ultimate goal of a good lightweight encryption primitive is to use lightweight components, but also to ensure that these components are compact and efficient for all these tradeoffs. This is what SIMON designers have managed to produce, but sacrificing a few security guarantees. SKINNY offers similar (sometimes even better) performances than SIMON, while providing much stronger security arguments with regard to classical differential or linear cryptanalysis.

3.2 General Design and Components Rationale

A first and important decision was to choose between a Substitution-Permutation Network (SPN), or a Feistel network. We started from a SPN construction as it is generally easier to provide stronger bounds on the number of active Sboxes. However, we note that there is a dual bit-sliced view of SKINNY that resembles some generalized Feistel network. Somehow, one can view the cipher as a primitive in between an SPN and an “AND-rotation-XOR” function like SIMON. We try to get the best of both worlds by benefiting the nice implementation tradeoffs of the latter, while organizing the state in an SPN view so that bounds on the number of active Sboxes can be easily obtained.

The absence of whitening key is justified by the reduction of the control logic: by always keeping the exact same round during the entire encryption process we avoid the control logic induced by having a last non-repeating layer at the end of the cipher. Besides, this simplifies the general description and implementation of the primitive. Obviously, having no whitening key means that a few operations of the cipher have no impact on the security. This is actually the case for both the beginning and the end of the ciphering process in SKINNY since the key addition is done in the middle of the round, with only half of the state being involved with this key addition every round.

A crucial feature of SKINNY is the easy generation of several block size or tweakey size versions, while keeping the general structure and most of the security analysis untouched. Going from the 64-bit block size versions to the 128-bit block size versions is simply done by using a 8-bit Sbox instead of a 4-bit Sbox, therefore keeping all the structural analysis identical. Using bigger tweakey material is done by following the STK construction [17], which allows automated analysis tools to still work even though the input space become very big (in short, the superposition trick makes the TK2 and TK3 analysis almost as time consuming as the normal and easy TK1 case). Besides, unlike previous lightweight block ciphers, this complete analysis of the TK2 and TK3 cases allows us to dedicate a part of this tweakey material to be potentially some tweak input, therefore making SKINNY a flexible tweakable block cipher. Also, we directly obtain related-key security proofs using this general structure.

SubCells. The choice of the Sbox is obviously a crucial decision in an SPN cipher and we have spent a lot of efforts on looking for the best possible candidate. For the 4-bit case, we have designed a tool that searches for the most compact candidate that provides some minimal security guarantees. Namely, with the bit operations cost estimations given previously, for all possible combinations of operations (NAND/NOR/XOR/XNOR) up to a certain limit cost, our tool checks if certain security criterion of the tested Sbox are fulfilled. More precisely, we have forced the maximal differential transition probability of the Sbox to be $2^{-2}$ and the maximal absolute linear bias to be $2^{-2}$. When both criteria are satisfied, we have filtered our search for Sbox with high algebraic degree.

Our results is that the Sbox used in the PICCOLO block cipher [31] is close to be the best one: our 4-bit Sbox candidate $\mathcal {S}_4$ is essentially the PICCOLO Sbox with the last NOT gate at the end being removed (see Fig. 2). We believe this extra NOT gate was added by the PICCOLO designers to avoid fixed points (actually, if fixed points were to be removed at the Sbox level, the PICCOLO candidate would be the best choice), but in SKINNY the fixed points are handled with the use of constants to save some extra GE. Yet, omitting the last bit rotation layer removes already a lot of fixed points (the efficiency cost of this omission being null).

The Sbox $\mathcal {S}_4$ can therefore be implemented with only 4 NOR gates and 4 XOR gates, the rest being only bit wiring (basically free in hardware). According to our previously explained estimations, this should cost 14.68 GE, but as remarked in [31], some libraries provide special gates that further save area. Namely, in our library the 4-input AND-NOR and 4-input OR-NAND gates with two inputs inverted cost 2 GE and they can be used to directly compute a XOR or an XNOR. Thus, $\mathcal {S}_4$ can be implemented with only 12 GE. In comparison, the PRESENT Sbox [5] requires 3 AND, 1 OR and 11 XOR gates, which amounts to 27.32 GE (or 34.69 GE without the special 4-input gates).

All in all, our 4-bit Sbox $\mathcal {S}_4$ has the following security properties: maximal differential transition probability of $2^{-2}$, maximal absolute linear bias of $2^{-2}$, branching number 2, algebraic degree 3 and one fixed point $\mathcal {S}_4(\texttt {0xF})=\texttt {0xF}$.

Regarding the 8-bit Sbox, the search space was too wide for our automated tool. Therefore, we instead considered a subclass of the entire search space: by reusing the general structure of $\mathcal {S}_4$, we have tested all possible Sboxes built by iterating several times a NOR/XOR combination and a bit permutation. Our search found that the maximal differential transition probability and maximal absolute linear bias of the Sboxes are larger than $2^{-2}$ when we have less than 8 iterations of the NOR/XOR combination and bit permutation. With 8 iterations of the NOR/XOR combination and bit permutation, we found Sboxes with desired maximal differential transition probability of $2^{-2}$ and maximal absolute linear bias of $2^{-2}$ with algebraic degree 6. However, the algebraic degree of the inverse Sboxes of all these candidates is 5 rather than 6. In addition, having 8 iterations may result in higher latency when we consider a serial hardware implementation. Therefore, we considered having 2 NOR/XOR combinations in every iteration and reduce the number of iteration from 8 to 4. As a result, we found several Sboxes with the desired maximal differential probability and absolute linear bias, while reaching algebraic degree 6 for both the Sbox and its inverse (thus better than the 8 iterations case). Although such Sbox candidates have 3 fixed points when we omit the last bit permutation layer like the 4-bit case, we can easily reduce the number of fixed points by introducing a different bit permutation from the intermediate bit permutations to the last layer without any additional cost.

With 2 NOR/XOR combinations and a bit permutation iterated 4 times, $\mathcal {S}_8$ can be implemented with only 8 NOR gates and 8 XOR gates (see Fig. 3), the rest being only bit wiring (basically free in hardware). The total area cost should be 24 GE according to our previously explained estimations and using special 4-input AND-NOR and 4-input OR-NAND gates. In comparison, while ensuring a maximal differential transition probability (resp. maximum absolute linear bias) of $2^{-6}$ (resp. $2^{-4}$), the AES Sbox requires 32 AND/OR gates and 83 XOR gates to be implemented, which amounts to 198 GE. Even recent lightweight 8-bit Sbox proposal [10] requires 12 AND/OR gates and 26 XOR gates, which amounts to 64 GE, for a maximal differential transition probability (resp. maximum linear bias) of $2^{-5}$ (resp. $2^{-2}$), but their optimization goal was different from ours.

All in all, we believe our 8-bit Sbox candidate $\mathcal {S}_8$ provides a good tradeoff between security and area cost. It has maximal differential transition probability of $2^{-2}$, maximal absolute linear bias of $2^{-2}$, branching number 2, algebraic degree 6 and a single fixed point $\mathcal {S}_8(\texttt {0xFF})=\texttt {0xFF}$ (for the Sbox we have chosen, swapping two bits in the last bit permutation was probably the simplest method to achieve only a single fixed point).

Note that both our Sboxes $\mathcal {S}_4$ and $\mathcal {S}_8$ have the interesting feature that their inverse is computed almost identically to the forward direction (as they are based on a generalized Feistel structure) and with exactly the same number of operations. Thus, our design reasoning also holds when considering the decryption process.

AddConstants. The constants in SKINNY have several goals: differentiate the rounds (see Sect. 4.2), differentiate the columns and avoid symmetries, complicate subspace cryptanalysis (see Sect. 4.2) and attacks exploiting fixed points from the Sbox. In order to differentiate the rounds, we simply need a counter, and since the number of rounds of all SKINNY versions is smaller than 64, the most hardware friendly solution is to use a very cheap 6-bit affine LFSR (like in LED  [15]) that requires only a single XNOR gate per update. The 6 bits are then dispatched to the two first rows of the first column (this will maximize the constants spread after the ShiftRows and MixColumns), which will already break the columns symmetry.

In order to avoid symmetries, fixed points and more generally subspaces to spread, we need to introduce different constants in several cells of the internal state. The round counter will already naturally have this goal, yet, in order to increase that effect, we have added a “1” bit to the third row, which is almost free in terms of implementation cost. This will ensure that symmetries and subspaces are broken even more quickly, and in particular independently of the round counter.

AddRoundTweakey. The tweakey schedule of SKINNY follows closely the STK construction from [17] (that allows to easily get bounds on the number of active Sboxes in the related-tweakey model). Yet, we have changed a few parts. Firstly, instead of using multiplications by 2 and 3 in a finite field, we have instead replaced these tweakey cells updates by cheap 4-bit or 8-bit LFSRs (depending on the size of the cell) to minimize the hardware cost. All our LFSRs require only a single XOR for the update, and we have checked that the differential cancellation behavior of these interconnected LFSRs is as required by the STK construction: for a given position, a single cancellation can only happen every 15 rounds for TK2, and same with two cancellations for TK3.

Another important generalization of the STK construction is the fact that every round we XOR only half of the internal cipher state with some subtweakey. The goal was clearly to optimize hardware performances of SKINNY, and it actually saves an important amount of XORs in a round-based implementation. The potential danger is that the bounds we obtain would dramatically drop because of this change. Yet, surprisingly, the bounds remained actually good and this was a good security/performance tradeoff to make. Another advantage is that we can now update the tweakey cells only before they are incorporated to the cipher internal state. Thus, half of tweakey cells only will be updated every round and the period of the cancellations naturally doubles: for a certain cell position, a single cancellation can only happen every 30 rounds for TK2 and two cancellations can only happen every 30 rounds for TK3.

The tweakey permutation $P_T$ has been chosen to maximize the bounds on the number of active Sboxes that we could obtain in the related-tweakey model (note that it has no impact in the single-key model). Besides, we have enforced for $P_T$ the special property that all cells located in third and fourth rows are sent to the first and second rows, and vice-versa. Since only the first and second rows of the tweakey states are XORed to the internal state of the cipher, this ensures that both halves of the tweakey states will be equally mixed to the cipher internal state (otherwise, some tweakey bytes might be more involved in the ciphering process than others). Finally, the cells that will not be directly XORed to the cipher internal state can be left at the same relative position. On top of that, we only considered those variants of $P_T$ that consist of a singe cycle.

We note that since the cells of the first tweakey word TK1 are never updated, they can be directly hardwired to save some area if the situation allows.

ShiftRows and MixColumns. Competing with SIMON’s impressive hardware performance required choosing an extremely sparse diffusion layer for SKINNY, which was in direct contradiction with our original goal of obtaining good security bounds for our primitive. Note that since our Sboxes $\mathcal {S}_4$ and $\mathcal {S}_8$ have a branching number of two, we cannot use only a bit permutation layer as in the PRESENT block cipher: differential characteristics with only a single active Sbox per round would exist. After several design iterations, we came to the conclusion that binary matrices were the best choice. More surprisingly, while most block cipher designs are using very strong diffusion layers (like an MDS matrix), and even though a $4 \times 4$ binary matrices with branching number four exist, we preferred a much sparser candidate which we believe offers the best security/performance tradeoff (this can be measured in terms of Figure Of Adversarial Merit [19]).

Due to its strong sparseness, SKINNY binary diffusion matrix $\mathbf {M}$ has only a differential or linear branching number of two. This seems to be worrisome as it would again mean that differential characteristics with only a single active Sbox per round would exist (it would be the same for PRESENT block cipher if its Sbox did not have branching number three, which is the reason of the relatively high cost of the PRESENT Sbox). However, we designed $\mathbf {M}$ such that when a branching two differential transition occurs, the next round will likely lead to a much higher branching number. Looking at $\mathbf {M}$, the only way to meet branching two is to have an input difference in either the second or the fourth input only. This leads to an input difference in the first or third element for the next round, which then diffuses to many output elements. The differential characteristic with a single active Sbox per round is therefore impossible, and actually we will be able to prove at least 96 active Sboxes for 20 rounds. Thus, for the very cheap price of a differential branching two binary diffusion matrix, we are in fact getting a better security than expected when looking at the iteration of several rounds. The effect is the same with linear branching (for which we only need to look at the transpose of the inverse of $\mathbf {M}$, i.e. $(\mathbf {M}^{-1})^{\top }$).

We have considered all possibilites for $\mathbf {M}$ that can be implemented with at most three XOR operations and eventually kept the MixColumns matrices that, in combination with ShiftRows, guaranteed high diffusion and led to strong bounds on the minimal number of active Sboxes in the single-key model.

Note that another important criterion came into play regarding the choice of the diffusion layer of SKINNY: it is important that the key material impacts as fast as possible the cipher internal state. This is in particular a crucial point for SKINNY as only half of the state is mixed with some key material every round, and since there is no whitening keys. Besides, having a fast key diffusion will reduce the impact of meet-in-the-middle attacks. Once the two first rows of the state were arbitrarily chosen to receive the key material, given a certain subtweakey, we could check how many rounds were required (in both encryption and decryption directions) to ensure that the entire cipher state depends on this subtweakey. Our final choice of MixColumns is optimal: only a single round is required in both forward and backward directions to ensure this diffusion.

3.3 Comparing Differential Bounds

Our entire design has been crafted to allow good provable bounds on the minimal number of differential or linear active Sboxes, not only for the single-key model, but also in the related-key model (or more precisely the related-tweakey model in our case). We provide in Table 4 a comparison of our bounds with the best known proven bounds for other lightweight block ciphers at the same security level (all the ciphers in the table use 4-bit Sboxes with a maximal differential probability of $2^{-2}$). We give in Sect. 4 more details on how the bounds of SKINNY were obtained.

Table 4. Proved bounds on the minimal number of differential active Sboxes for SKINNY-64-128 and various lightweight 64-bit block 128-bit key ciphers. Model SK denotes the single-key scenario and model TK2 denotes the related-tweakey scenario where differences can be inserted in both states TK1 and TK2.

First, we emphasize that most of the bounds we obtained for SKINNY are not tight, and we can hope for even higher minimal numbers of active Sboxes. This is not the case of LED or PRESENT for which the bounds are tight.

From the table, we can see that LED obtains better bounds for SK. Yet, the situation is inverted for TK2: due to a strong plateau effect in the TK2 bounds of LED, it stays at 50 active Sboxes until Round 24, while SKINNY already reaches 72 active Sboxes at Round 24. Besides, LED performance will be quite bad compared to SKINNY, due to its strong MDS diffusion layer and strong Sbox.

Regarding PICCOLO, the bounds⁵ are really similar to SKINNY for SK but worse for TK2. Yet, our round function is lighter (no use of a MDS layer), see Sect. 3.4.

No related-key bounds are known for MIDORI, PRESENT or TWINE. Besides, our SK bounds are better than PRESENT. Regarding MIDORI or TWINE in SK, while our bounds are slightly worse, we emphasize again that our round function is much lighter and thus will lead to much better performances.

Comparing differential bounds with SIMON is not as simple as with SPN ciphers. Yet, bounds on the best differential/linear characteristics for SIMON have been provided recently by [22]⁶.

Assuming (very) pessimistically for SKINNY that a maximum differential transition probability of $2^{-2}$ is always possible for each active Sbox in the differential paths with the smallest number of active Sboxes, we can directly obtain easy bounds on the best differential/linear characteristics for SKINNY. We provide in Table 5 a comparison between SIMON and SKINNY versions for the proportion of total number of rounds needed to provide a sufficiently good differential characteristic probability bound according to the cipher block size. One can see that SKINNY needs a much smaller proportion of its total number of rounds compared to SIMON to ensure enough confidence with regards to simple differential/linear attacks. Actually the related-key ratios of SKINNY are even smaller than single-key ratios of SIMON (no related-key bounds are known as of today for SIMON).

Table 5. Comparison between AES-128 and SIMON/SKINNY versions for the proportion of total number of rounds needed to provide a sufficiently good differential characteristic probability bound according to the cipher block size (i.e. $<2^{-64}$ for 64-bit block size and $<2^{-128}$ for 128-bit block size). Results for SIMON are updated results taken from [22].

Finally, in terms of diffusion, all versions of SKINNY achieve full diffusion after only 6 rounds (forwards or backwards), while SIMON versions with 64-bit block size requires 9 rounds, and even 13 rounds for SIMON versions with 128-bit block size [22] (AES-128 reaches full diffusion after 2 of its 10 rounds). Again, the diffusion comparison according to the total number of rounds is at SKINNY’s advantage.

3.4 Comparing Theoretical Performance

After some minimal security guarantee, the second design goal of SKINNY was to minimize the total number of operations. We provide in Table 6 a comparison of the total number of operations per bit for SKINNY and for other lightweight block ciphers, as well as some quality grade regarding its ASIC area in a round-based implementation. We explain in the full version of this article how these numbers have been computed.

Table 6. Total number of operations and theoretical performance of SKINNY and various lightweight block ciphers. N denotes a NOR gate, A denotes a AND gate, X denotes a XOR gate.

One can see from the Table 6 that SIMON and SKINNY compare very favorably to other candidates, both in terms of number of operations and theoretical area grade for round-based implementations. This seems to confirm that when it comes to lightweight block ciphers, SIMON is probably the strongest competitor as of today. Besides, SKINNY has the best theoretical profile among all the candidates presented here, even better than SIMON for area. For speed efficiency, SKINNY outperforms SIMON when the key schedule is taken in account. This scenario is arguably the most important in practice: as remarked in [3], it is likely that lightweight devices will cipher very small messages and thus the back-end servers communicating with millions of devices will probably have to recompute the key schedule for every small message received.

In addition to its smaller key size, we note that KATAN-64-80 [9] theoretical area grade is slightly biased here as one round of this cipher is extremely light and such a round-based implementation would actually look more like a serial implementation and will have a very low throughput (KATAN-64-80 has 254 rounds in total).

While Table 6 is only a rough indication of the efficiency of the various designs, we observe that the ratio between the SIMON and SKINNY best software implementations, or the ratio between the smallest SIMON and SKINNY round-based hardware implementations actually match the results from the table (see full version of the paper).

4 Security Analysis

In this section, we provide a short summary of the in-depth analysis we conducted on the security of the SKINNY family of block ciphers. All details are provided in the full version of this article. We emphasize that we do not claim any security in the chosen-key or known-key model, but we do claim security in the related-key model. Moreover, we chose not to use any constant to differentiate between different block sizes or tweakey sizes versions of SKINNY, as we believe such a separation should be done at the protocol level, for example by deriving different keys (note that, if needed, this can easily be done by encoding these sizes and use them as fixed extra constant material every round).

4.1 Differential/Linear Cryptanalysis

In order to argue for the resistance of SKINNY against differential and linear attacks, we computed lower bounds on the minimal number of active Sboxes, both in the single-key and related-tweakey model. We recall that, in a differential (resp. linear) characteristic, an Sbox is called active if it contains a non-zero input difference (resp. input mask). In contrast to the single-key model, where the round tweakeys are constant and thus do not influence the activity pattern, an attacker is allowed to introduce differences (resp. masks) within the tweakey state in the related-tweakey model. For that, we considered the three cases of choosing input differences in $\mathbf {TK1}$ only, both $\mathbf {TK1}$ and $\mathbf {TK2}$, and in all of the tweakey states $\mathbf {TK1}$, $\mathbf {TK2}$ and $\mathbf {TK3}$, respectively. Table 7 presents lower bounds on the number of differential active Sboxes for 16 up to 30 rounds. For computing these bounds, we generated a Mixed-Integer Linear Programming model following the approach explained in [25, 32].

Table 7. Lowerbounds on the number of active Sboxes in SKINNY for large number of rounds. Note that the bounds on the number of linear active Sboxes in the single-key model are also valid in the related-tweakey model. In case the MILP optimization was too long, we provide upper bounds between parentheses.

For lower bounding the number of linear active Sboxes, we used the same approach. For that, we considered the inverse of the transposed linear transformation $\mathbf {M^{\top }}$. However, for the linear case, we only considered the single-key model. As it is described in [23], there is no cancellation of active Sboxes in linear characteristics. Thus, the bounds for SK give valid bounds also for the case where the attacker is allowed to not only control the message but also the tweakey input.

The above bounds are for single characteristic, thus it will be interesting to take a look at differentials and linear hulls. Being a rather complex task, we leave this as future work.

4.2 Further Cryptanalysis

Meet-in-the-Middle Attacks. Meet-in-the-middle attacks have been applied to block ciphers, e.g. [6, 11]. From its application to the SPN structure [30], the number of attacked rounds can be evaluated by considering the maximum length of three features, partial-matching, initial structure and splice-and-cut. We conclude that meet-in-the-middle attack may work up to at most 22 rounds, so that 32+ rounds of SKINNY-64 provides a reasonable margin.

Remarks on Biclique Cryptanalysis. Biclique cryptanalysis improves the complexity of exhaustive search by computing only a part of encryption algorithm. The improved factor is often evaluated by the ratio of the number of Sboxes involved in the partial computation to all Sboxes in the cipher. The improved factor can be relatively big when the number of rounds in the cipher is small, which is not the case in SKINNY. We do not think improving exhaustive search by a small factor will turn into serious vulnerability in future. Therefore, SKINNY is not designed to resist biclique cryptanalysis with small improvement.

Impossible Differential Attacks. Impossible differential attack [4] finds two internal state differences $\varDelta$ and $\varDelta ^{\prime }$ such that $\varDelta$ is never propagated to $\varDelta ^{\prime }$. The attacker then finds many plaintext/ciphertext pairs and tweakey values leading to $(\varDelta , \varDelta ^{\prime })$. Those tweakey values are wrong values, thus tweakey space can be reduced.

We found that the longest impossible differential characteristics reach 11 rounds and there are 16 such characteristics in total. While several rounds can be appended to turn this into a key-recovery attack, the number of rounds for SKINNY provide a sound security margin.

Integral Attacks. Integral attack [12, 21] prepares a set of plaintexts so that particular cells can contain all the values in the set and the other cells are fixed to a constant value. Then properties of the multiset of internal state values after encrypting several rounds are considered. The integral distinguisher in the best attack we found covers 10 rounds that can be turned into a key-recovery attack on 14 rounds. The division property could be used to slightly extend those results. Again, given the number of rounds for SKINNY, integral attacks do not seem to be a threat for the security of the cipher.

Slide Attacks. In SKINNY, the distinction between the rounds of the cipher is ensured by the AddConstants operation and thus the straightforward slide attacks cannot be applied. We consider possible variants (in the full version of the paper), but we could not turn any of those into a valid attack.

Subspace Cryptanalysis. Invariant subspace cryptanalysis makes use of affine subspaces that are invariant under the round function. Given that SKINNY has a non-trivial key-scheduling, this technique does not seem well suited to launch an attack.

Algebraic Attacks. We detail in the full version of our paper why, not surprisingly, algebraic attacks do not threaten SKINNY.

5 Implementations, Performance and Comparison

We provide a complete study of SKINNY performance on various platforms (software, ASIC, FPGA, micro-controllers, ...) in the full version of the paper. Yet, we describe here our results regarding ASIC round-based implementations since it represents our top performance criterion.

We used Synopsys DesignCompiler version A-2007.12-SP1 to synthesize the designs considering UMCL18G212T3 [35] standard cell library, which is based on the UMC L180 0.18$\mu$m 1P6M logic process with a typical voltage of 1.8 V. For the synthesis, we advised the compiler to keep the hierarchy and use a clock frequency of 100 KHz, which allows a fair comparison with the benchmark of other block ciphers reported in literature.

In a first step, we designed round-based implementations for all SKINNY variants providing a good trade-off between performance and area. All implementations compute a single round of SKINNY within a clock cycle. Besides, our designs take advantage of dedicated scan flip-flops rather than using simple flip-flops and additional multiplexers placed in front in order to hold round states and keys. Note that this approach leads to savings of 1 GE per bit to be stored. In order to allow a better and fairer comparison, we provide both throughput at a maximally achievable frequency and throughput at a frequency of 100 KHz.

Table 8 briefly summarizes the results of the round-based architectures of all SKINNY variants and compares it to other round-based implementations of lightweight ciphers taken from the literature. In particular, SKINNY-64-128 offers the smallest area footprint compared to other lightweight ciphers providing the same security level. Note, that even SIMON-64-128 implemented in a round-based fashion cannot compete with our design in terms of both area and throughput.

Table 8. Round-based implementations of SKINNY-64 and SKINNY-128.

6 The Low-Latency Tweakable Block Cipher MANTIS

In this section, we present a tweakable block cipher design which is optimized for low-latency implementations.

The low-latency block cipher PRINCE already provides a very good starting point for a low-latency design. Its round function basically follows the AES structure, with the exception of using a MixColumns-like mapping with branch number 4 instead of 5. The main difference between PRINCE and AES (and actually all other ciphers) is that the design is symmetric around a linear layer in the middle. This allows to realize what was coined $\alpha$-reflection: the decryption for a key K corresponds (basically) to encryption with a key $K\oplus \alpha$ where $\alpha$ is a fixed constant. Turning PRINCE into a tweakable block cipher is (conceptually) well understood when using e.g. the TWEAKEY framework [17]. First, define a tweakey-schedule and than simply increase the number of rounds until one can ensure that the cipher is secure against related-tweak attacks.

However, the problem is that the latency of a cipher is directly related to the number of rounds. Thus, it is crucial to find a design, i.e. a round function and a tweak-scheduling, that ensures security already with a minimal number of rounds. Here, components of the recently proposed block ciphers MIDORI  [1] turn out to be very beneficial. In MIDORI, again an AES-like design, one of the key observations was that changing ShiftRows into a more general permutation allows to significantly improve upon the number of active Sboxes (in the single key model) while keeping a MixColumns-like layer with branch number 4 only. On top, the designers of MIDORI designed a 4-bit Sbox that was optimized with respect to circuit-depth. This directly leads to an improved version of PRINCE itself: replace the PRINCE round function by the MIDORI-round function while keeping the entire design symmetric around the middle to keep the $\alpha$-reflection property. This simple change would result in a cipher with improved latency and improved security (i.e. number of active Sboxes) compared to PRINCE. It is actually exactly this PRINCE-like MIDORI that we use as a starting point for designing the low-latency block cipher MANTIS. The final step in the design of MANTIS was to find a suitable tweak-scheduling that would ensure a high number of active Sboxes not only in the single-key setting, but also in the setting where the attacker can control the difference in the tweak. Using, again, the MILP approach, we are able to demonstrate that a slight increase in the number of rounds (from 12 to 14) is already sufficient to ensure the resistance of MANTIS to differential (and linear) attacks in the related-tweak setting. Note that MANTIS is certainly not secure in the related-key model, as there always exist a probability one distinguisher caused by the $\alpha$-reflection property.

$\mathtt{MANTIS} _r$ has a 64-bit block length and works with a 128-bit key and 64-bit tweak. The parameter r specifies the number of rounds of one half of the cipher. The overall design is illustrated in Fig. 5.

Fig. 5.

Illustration of $\mathtt{MANTIS} _6$.

We acknowledge the contribution of Roberto Avanzi to the design of MANTIS. He first suggested us to combine PRINCE with the TWEAKEY framework, and also to modify the latter by permuting the tweak independently from the key, in order to save on the Galois multiplications of the tweak cells. He then brainstormed with us on early versions of the design.

6.1 Description of the Cipher

$\mathtt{MANTIS} _r$ is based on the FX-construction [20] and thus applies whitening keys before and after applying its core components. The 128-bit key is first split into $k = k_0 \mid \mid k_1$ with 64-bit subkeys $k_0,k_1$. Then, $(k_0 \mid \mid k_1)$ is extended to the 192 bit key

$$\begin{aligned} ( k_0 \mid \mid k_0^{'}\mid \mid k_1) := (k_0 \mid \mid (k_0 \ggg 1) \oplus (k_0 \gg 63) \mid \mid k_1), \end{aligned}$$

and $k_0,k_0^{'}$ are used as whitening keys in an FX-construction. The subkey $k_1$ is used as the round key for all of the 2r rounds of $\mathtt{MANTIS} _r$. We decided to stick with the FX construction for simplicity., even so other options as described in [8].

Initialization. The cipher receives a plaintext $m=m_0 \Vert m_1 \Vert \cdots \Vert m_{14} \Vert m_{15}$, where the $m_i$ are 4-bit cells. The initialization of the cipher’s internal state is performed by setting $IS_i=m_i$ for $0 \le i \le 15$.

The cipher also receives a tweak input $T=t_0 \Vert t_1 \Vert \cdots \Vert t_{15}$, where the $t_i$ are 4-bit cells. The initialization of the cipher’s tweak state is performed by setting $T_i=t_i$ for $0 \le i \le 15$. Thus,

$$\begin{aligned} IS = \left[ \begin{array}{cccc} m_0 &{} m_1 &{} m_2 &{} m_{3} \\ m_4 &{} m_5 &{} m_6 &{} m_{7} \\ m_8 &{} m_9 &{} m_{10} &{} m_{11} \\ m_{12} &{} m_{13} &{} m_{14} &{} m_{15} \\ \end{array} \right] T = \left[ \begin{array}{cccc} t_0 &{} t_1 &{} t_2 &{} t_{3} \\ t_4 &{} t_5 &{} t_6 &{} t_{7} \\ t_8 &{} t_9 &{} t_{10} &{} t_{11} \\ t_{12} &{} t_{13} &{} t_{14} &{} t_{15} \\ \end{array} \right] \end{aligned}$$

The Round Function. One round $\mathcal {R}_i(\cdot ,tk)$ of $\mathtt{MANTIS} _r$ operates on the cipher internal state depending on the round tweakey tk as

$$\begin{aligned} \mathtt{MixColumns} \circ \mathtt{PermuteCells} \circ \mathtt{AddTweakey}_{tk} \circ \mathtt{AddConstant}_i \circ \mathtt{SubCells}. \end{aligned}$$

In the following, we describe the components of the round function.

• SubCells. The involutory MIDORI Sbox $\mathtt {Sb_0}$ is applied to every cell of the internal state. Using the MIDORI Sbox is beneficial as this Sbox is especially optimized for small area and low circuit depth.

• AddConstant. In the i-th round, the round constant $RC_i$ is XORed to the internal state. The round constants are generated in a similar way as for PRINCE, that is we used the first digits of $\pi$ to generate those constants (actually the very first digits correspond to $\alpha$ defined below). The round constants can be found in the full version of the paper. Note that, in contrast to PRINCE, the constants are added row-wise instead of column-wise.

• AddRoundTweakey. In round $\mathcal {R}_i$, the (full) round tweakey state $h^i(T) \oplus k_1$ is XORed to the cipher internal state. In the i-th inverse round $\mathcal {R}^{-1}_i$, the tweakey state $h^i(T) \oplus \bar{k}_1 := h^i(T) \oplus k_1 \oplus \alpha$ with $\alpha = \mathtt{0x243f6a8885a308d3}$ is XORed to the internal state. Note that this $\alpha$, as the round constants, is chosen as the first digits of $\pi$. Thereby, it is $h(T) = t_{h(0)} \Vert t_{h(1)} \cdot \Vert t_{h(15)}$, where the tweak permutation h is defined as

  $$\begin{aligned} h=[6,5,14,15,0,1,2,3,7,12,13,4,8,9,10,11]. \end{aligned}$$

• PermuteCells. The cells of the internal state are permuted according to the MIDORI permutation

  $$\begin{aligned} P=[0,11,6,13,10,1,12,7,5,14,3,8,15,4,9,2]. \end{aligned}$$

  Note that the MIDORI permutation ensures a higher number of active Sboxes compared to the choice made in PRINCE.

• MixColumns. Each column of the cipher internal state array is multiplied by the binary matrix used in MIDORI.

Encryption. In the following, we define $H_r$ as the application of r rounds $\mathcal {R}_i$ and one additional SubCells layer. Similarly, we define $H_r^{-1}$ as the application on one inverse SubCells layer plus r inverse rounds. Thus,

$$\begin{aligned} H_r(\cdot ,T,k_1)&= \mathtt{SubCells} \circ \mathcal {R}_r(\cdot ,h^r(T) \oplus k_1) \circ \dots \circ \mathcal {R}_1(\cdot ,h(T) \oplus k_1) \\ H_r^{-1}(\cdot ,T,\bar{k}_1)&= \mathcal {R}_1^{-1}(\cdot ,h(T) \oplus \bar{k}_1) \circ \dots \circ \mathcal {R}_r^{-1}(\cdot ,h^r(T) \oplus \bar{k}_1) \circ \mathtt{SubCells}. \end{aligned}$$

With this notation, it is

$$\begin{aligned} \mathbf {Enc}_{(k_0,k'_0,k_1)}(\cdot ,T)&= \mathtt{AddTweakey}_{k'_0 \oplus k_1 \oplus \alpha \oplus T} \circ H_r^{-1}(\cdot ,T,k_1 \oplus \alpha ) \\&\circ \mathtt{MixColumns} \circ H_r(\cdot ,T,k_1) \circ \mathtt{AddTweakey}_{k_0 \oplus k_1 \oplus T} \end{aligned}$$

Decryption. It is $\mathbf {Enc}^{-1}_{(k_0,k'_0,k_1)}(\cdot ,T) = \mathbf {Enc}_{(k'_0,k_0,k_1 \oplus \alpha )}(\cdot ,T)$ because of the $\alpha$-reflection property.

6.2 Design Rationale

The goal was to design a cipher which is competitive to PRINCE in terms of latency with the advantage of being tweakable. In contrast to SKINNY, we distinguish between tweak and key input. In particular, we allow an attacker to control the tweak but not the key. Thus, similar to PRINCE, we do not claim related-key security. In order to reach this goal, again, several components are borrowed from already existing ciphers. In the following, we present the reasons for our design. Note that, as we aim for an efficient unrolled implementation, one is not restricted to a classical round-iterated design.

$\alpha$ -Reflection Property. $\mathtt{MANTIS} _r$ is designed as a reflection cipher such that encryption under a key k equals decryption under a related key. This significantly reduces the implementation overhead for decryption. Therefore, the parameter r denotes only half the number of rounds, as the second half of the cipher is basically the inverse of the first half. It is advantageous that the diffusion matrix $\mathbf {M}$ is involutory since we need the middle part of the cipher to be an involution. Unlike in the description of PRINCE, we use the same round constant for the inverse $\mathcal {R}^{-1}_i$ of the i-th round and apply the addition of $\alpha$ to the round key $k_1$.

The Choice of the Diffusion Layer. To achieve low latency in an unrolled implementation, one is limited in the number rounds to be applied. Therefore, one has to achieve very fast diffusion while guaranteeing a high number of active Sboxes. To reach these requirements, we adopted the linear layer of MIDORI. It provides full diffusion only after three rounds and guarantees a high number of active Sboxes in the single-key setting. We refer to Table 4 for the bounds.

The Choice of the Sbox. For the Sbox in MANTIS we used the same Sbox as in MIDORI. The MIDORI Sbox has a significantly smaller latency than the PRINCE Sbox. The maximal linear bias is $2^{-2}$ and the best differential probability is $2^{-2}$ as well.

The Choice of the Tweakey Permutation h . Our aim was to choose a tweak permutation h such that five rounds (plus one additional SubCells layer) guarantee at least 16 active Sboxes in the related-tweak setting. This would guarantee at least 32 active Sboxes for $\mathtt{MANTIS} _5$ which is enough to bound the differential probability (resp. linear bias) below $2^{-2\cdot 32}$. Since there are 16! possibilities for h, which is too much for an exhaustive search, we restricted ourself on a subclass of 8! tweak permutations. The restriction is that two complete rows (without changing the position of the cells in those rows) are permuted to different rows. In our case, the first and third row are permuted to the second and fourth row, respectively. The bounds were derived using the MILP tool. We tested several thousand choices for the permutation h and found out that 16 active Sboxes were the best possible to reach over $H_5$. Out of these optimal choices, we took the permutation that maximized the bound for $\mathtt{MANTIS} _5$, and as a second step for $\mathtt{MANTIS} _6$. We refer to Table 9 for the actual bounds.

Table 9. Lower bounds on the number of linear (and differential) active Sboxes in the single-key model and of differential active Sboxes in the related-tweak model.

Security Claim. For $\mathtt{MANTIS} _7$, we claim that any adversary who in possession of $2^n$ chosen plain/ciphertext pairs which were obtained under chosen tweaks, but with a fixed unknown key, needs at least $2^{126-n}$ calls to the encryption function in order to recover the secret key. Thus, our security claims are the same as for PRINCE, except that we also claim related-tweak security. Moreover, already for $\mathtt{MANTIS} _5$ we claim security against practical attacks, similar to what has been considered in the PRINCE challenge. More precisely, we claim that no related-tweak attack (better than the generic claim above) is possible against $\mathtt{MANTIS} _5$ with less than $2^{30}$ chosen or $2^{40}$ known plaintext/ciphertext pairs. Note that because of the $\alpha$-reflection, there exists a trivial related-key distinguisher with probability one. We especially encourage further cryptanalysis on the aggressive versions.

6.3 Security Analysis

As one round of MANTIS is almost identical to one round in MIDORI, most of the security analysis can simply be copied from the latter. This holds in particular for meet-in-the-middle attacks, integral attacks and slide attacks. We therefore only focus on the attacks where the changes in round constants and by adding the tweak actually result in different arguments.

Invariant Subspaces. The most successful attack against MIDORI-64 at the moment is an invariant subspace attack with a density of $2^{96}$ weak keys. The main observation here is that the round constants in MIDORI are too sparse and structured to avoid certain symmetries. More precisely, the round constants in MIDORI-64 only affect a single bit in each of the 16 4-bit cells. Together with a property of the Sbox this finally results in the mentioned attack. For MANTIS, the situation is very different as the round constants (in each half) are basically random values. This in particular ensures that the invariant subspace attack on MIDORI does not translate into an attack on MANTIS.

Differential and Linear Related-Tweak Attacks. Using the MILP approach, we are able to prove strong bounds against related-tweak linear and differential attacks. In particular, no related tweak linear or differential distinguisher based on a characteristics is possible for $\mathtt{MANTIS} _5$, that is already for 12 layers of Sboxes. As $\mathtt{MANTIS} _7$ has four more rounds, and additional key-whitening, we believe that is provides a small but sufficient security margin.

The results of unrolled implementations for MANTIS are listed in the full version of the paper.