Keywords

1 Introduction

A stochastic fractional integro-differential equation (SFIDE), where order of derivative is non integer, is a generalization of the fractional Folkker-Plank equation which describes the random walk of a particle [2]. This model has the following form

$$\begin{aligned} \begin{aligned} D^{\alpha }u(t)&= f(t)+\int _{0}^{t}u(s)k_{1}(s,t)ds+\int _{0}^{t}u(s)k_{2}(s,t)dW(s),~t\in [0,T),\\ u(0)&= u_{0}, \end{aligned} \end{aligned}$$
(1)

where \(D^{\alpha },\) \( 0< \alpha < 1,\) denotes the Caputo fractional derivative, \(W(s),s \in [0,T)\) is the standard Wiener process and the integral with respect to it is the It\(\hat{o}\) integral. Presence of the It\(\hat{o}\) integral in Equation (1) causes randomness in the solution and hence it becomes non deterministic. In this paper, we develop a novel approach to quantify this uncertain behavior in the numerical solution.

In recent decade, the need to obtain the numerical solution of SFIDE has increased significantly. However, in literature, only a handful of papers are available that actually discuss about the numerical solution of SFIDE. In [8], Maleknejad et al. provided an operational matrix method based on block pulse functions to solve stochastic Volterra integral equations. In [12], Taheri et al. formulated the spectral collocation method based on shifted Legendre polynomials to solve SFIDE. In [10], Mirzaee and Samadyar constructed an efficient scheme to solve SFIDE based on Bernstein polynomials. In [11], Mirzaee and Samadyar provide a meshless discrete collocation method based on radial basis functions to solve SFIDE.

In this paper, a new scheme is derived based on Legendre wavelet collocation method and block pulse function involving the operational matrix for solving SFIDE (1). In Sect. 2, we give basic definition of fractional calculus and construction of Legendre wavelet based on Multi-resolution analysis. Then in Sect. 3, operational matrix of fractional order integration and integration operational matrix are derived. The proposed scheme for the SFIDE is discussed in Sect. 4, while Sect. 5 provides numerical experiments performed to showcase the effectiveness of the approach. In Sect. 6, we present various applications of SFIDE. Finally, Sect. 7 gives the brief conclusion.

2 Preliminaries

In this section, we discuss the mathematical preliminaries of fractional calculus and construction of wavelet which are required for subsequent development.

Definition 1

[5] The left Riemann-Liouville fractional integral of order \(\alpha \ge 0\) of a function \(f(t),~t\in (a,b)\) is defined as follows

$$\begin{aligned} \begin{aligned} _{a}I_{t}^{\alpha }f(t)&= \frac{1}{\varGamma (\alpha )}\int _{a}^{t}(t-s)^{\alpha -1}f(s)ds, \\ _{a}I_{t}^{0}f(t)&= f(t). \end{aligned} \end{aligned}$$
(2)

Similar to integer order integration, the left Riemann-Liouville fractional integral operator is a linear operator

$$\begin{aligned} _{a}I_{t}^{\alpha }(\lambda f(t)+\mu g(t)) = \lambda _{a}I_{t}^{\alpha }f(t)+\mu _{a}I_{t}^{\alpha }g(t), \end{aligned}$$

where \(\lambda \) and \(\mu \) are constants.

Definition 2

[5] The left Caputo derivative with order \(\alpha > 0\) of the given function \(f(t),~t\in (a,b)\) is defined as

$$\begin{aligned} D_{a,t}^{\alpha }f(t) = \frac{1}{\varGamma (m-\alpha )}\int _{a}^{t}(t-s)^{m-\alpha -1}f^{(m)}(s)ds, \end{aligned}$$
(3)

where m is a positive integer satisfying \(m-1 < \alpha \le m.\)

2.1 Multi-resolution Analysis (MRA)

An MRA is an increasing family of closed subspace \(V^{j} \subset L^{2}(\mathbb {R})\) which satisfies the following axioms [9] :

  1. 1.

    \(V^{j} \subset V^{j+1}\)

  2. 2.

    \(\overline{\cup _{j \in \mathbb {Z}}V^{j}} = L^{2}(\mathbb {R})\)

  3. 3.

    \(\{\phi (x-k) : k \in \mathbb {Z}\}\) is an orthonormal basis of \(V^{0}\)

  4. 4.

    \(f(\cdot ) \in V^{j}\) if and only if \(f(2(\cdot )) \in V^{j+1}\) for all \(j \in \mathbb {Z}\).

For given nested sequence subspace \(V^{j}\), define the space \(W^{j}\) as the orthogonal complement of \(V^{j}\) in \(V^{j+1}\), i.e., \(V^{j} \perp W^{j}\) and

$$\begin{aligned} V^{j+1} = V^{j}\oplus W^{j}, \end{aligned}$$
(4)

applying recursively, we get

$$\begin{aligned} V^{j} = V^{j_{0}}\oplus \bigoplus _{k=j_{0}}^{j-1}W^{k},~~j > j_{0}. \end{aligned}$$
(5)

Now, based on the above analysis, to construct a wavelet define a space \(V_{M}^{J}\) of piecewise polynomial functions as follows :

$$\begin{aligned} \begin{aligned} V_{M}^{J} := \{\phi ~: \text { the restriction of } \phi \text { to the interval } [2^{-J+1}(k-1),2^{-J+1}k) \\ \text {is a polynomial of degree less than M for } k = 1,2,\cdots ,2^{(J-1)},\\ \text { and } \phi \text { vanishes elsewhere} \}. \end{aligned} \end{aligned}$$
(6)

The space \(V_{M}^{J}\) has dimension \(2^{(J-1)}M\) and

$$V_{M}^{1} \subset V_{M}^{2} \subset \cdots V_{M}^{J} \subset \cdots \subset L^{2}([0,1)). $$

Next, consider the \(2^{(J-1)}M\)-dimensional space \(W_{M}^{J}\) which is an orthogonal complement of \(V_{M}^{J}\) in \(V_{M}^{J+1}\), i.e.,

$$V_{M}^{J+1} = V_{M}^{J}\oplus W_{M}^{J+1}.$$

Inductively, one can obtain

$$\begin{aligned} V_{M}^{J} = V_{M}^{1}\oplus \bigoplus _{j=1}^{J-1}W_{M}^{j}. \end{aligned}$$
(7)

Unlike Haar, the element of the space \(W_{M}^{J}\) do not have a general form. To construct the elements of \(W_{M}^{J}\) one can refer [1].

Further, if

$$ V_{M}^{J} = \text {span}\{\phi _{k,m}^{J},~m=0,1,\cdots ,M-1,~k = 1,2,\cdots ,2^{(J-1)}\},$$

then we define the projection operator \(P_{V_{M}^{J}} : L^{2}[0,1] \rightarrow V_{M}^{J}\) as

$$\begin{aligned} P_{V_{M}^{J}}(f(x)) := \sum _{k=1}^{2^{J-1}}\sum _{m=0}^{M-1}c_{k,m}^{J}\phi _{k,m}^{J}(x), \end{aligned}$$
(8)

where \(c_{k,m}^{J} = \int _{\frac{(k-1)}{2^{(J-1)}}}^{\frac{k}{2^{(J-1)}}}f(x)\phi _{k,m}^{J}(x)dx.\) Set

$$W_{M}^{J} = \text {span}\{\psi _{k,m}^{J}(x),~m=0,1,\cdots ,M-1,~k = 1,2,\cdots ,2^{(J-1)}\},$$

where \(\psi _{k,m}^{J}(x) = 2^{\frac{(J-1)}{2}}\psi _{m}(2^{(J-1)}x-k+1)\). The support of \(\psi _{k,m}^{J}\) is \([\frac{k-1}{2^{J-1}},\frac{k}{2^{J-1}})\) and \(\psi _{m}(x)\) satisfies the following property (vanishing moment property)

$$\begin{aligned} \int _{0}^{1}x^{i}\psi _{m}(x)dx = 0,~i = 0,1,\cdots ,M-1. \end{aligned}$$
(9)

Now, using \(V_{M}^{J}\), we introduced the subspace \(V_{M}^{J,2}\) of \(L^{2}([0,)\times [0,1))\) defined by

$$ V_{M}^{J,2} := \{\phi ~|~ \phi = \phi _{1}\phi _{2}~\text {where}~\phi _{1},\phi _{2} \in V_{M}^{J}\}.$$

Moreover,

$$V_{M}^{J,2} = \text {span}\{\phi _{k,m,k',m'}^{J} = \phi _{k,m}^{J}\phi _{k',m'}^{J}~:~k,k' = 1,\cdots ,2^{J-1}~\text {and}~m,m' = 0,\cdots ,M-1 \}.$$

Then, define the projection operator \(P_{V_{M}^{J,2}}:L^{2}([0,1]\times [0,1]) \rightarrow V_{M}^{J,2}\) as

$$\begin{aligned} P_{V_{M}^{J,2}}f(s,t) = \sum _{k=1}^{2^{J-1}}\sum _{m=0}^{M-1}\sum _{k'=1}^{2^{J-1}}\sum _{m'=0}^{M-1}c_{k,m,k',m'}^{J}\phi _{k,m,k',m'}^{J}(s,t), \end{aligned}$$
(10)

where \(c_{k,m,k',m'}^{J} = \int _{\frac{(k-1)}{2^{(J-1)}}}^{\frac{k}{2^{J-1}}}\int _{\frac{(k'-1)}{2^{(J-1)}}}^{\frac{k'}{2^{J-1}}}f(s,t)\phi _{k,m,k',m'}^{J}(s,t)dsdt\).

Next, introduce the space \(W_{M}^{J,2}\) which is defined by

$$W_{M}^{J,2} = \{\psi ~|~ \psi = \psi _{1}\psi _{2}~\text {where}~\psi _{1},\psi _{2} \in W_{M}^{J} \},$$

and

$$W_{M}^{J,2} = \text {span}\{\psi _{k,m,k',m'}^{J} = \psi _{k,m}^{J}\psi _{k',m'}^{J}~:~ k,k'=1,\cdots ,2^{J-1}~\text {and}~m,m'=0,\cdots ,M-1 \},$$

where

$$\begin{aligned} \psi _{k,m,k',m'}^{J}(s,t)&= 2^{J-1}\psi _{m,m'}(2^{J-1}s-k+1,2^{J-1}t-k'+1)\\ {}&:= 2^{J-1}\psi _{m}(2^{J-1}s-k+1)\psi _{m'}(2^{J-1}t-k'+1) \end{aligned}$$

and \(\psi _{m,m'}(s,t)\) satisfies the following property

$$\begin{aligned} \int _{0}^{1}\int _{0}^{1}s^{i}t^{j}\psi _{m,m'}(s,t)dsdt = 0,~i,j=0,\cdots ,M-1. \end{aligned}$$
(11)

The subspace \(W_{M}^{J,2}\) is orthogonal complement of \(V_{M}^{J,2}\) in \(V_{M}^{J+1,2}\). Therefore, one can write

$$V_{M}^{J+1,2} = V_{M}^{J,2}\oplus W_{M}^{J,2},$$

and hence

$$\begin{aligned} V_{M}^{J,2} = V_{M}^{1,2}\oplus \bigoplus _{j=1}^{J-1}W_{M}^{j-1,2}. \end{aligned}$$
(12)

Now, if we choose \(\phi _{k,m}^{J}\) as in [13], i.e., for \(m = 0,1,2,\cdots ,M-1\), and \(\hat{k} = 2k-1\) with \(k=1,2,\cdots ,2^{(J-1)}\)

$$\begin{aligned} \phi _{k,m}^{J}(t) = {\left\{ \begin{array}{ll} \sqrt{m+\frac{1}{2}}2^{J/2}P_{m}(2^{J}t-\hat{k}) &{} \text {for}~~ \frac{\hat{k}-1}{2^{J}} \le t < \frac{\hat{k}+1}{2^{J}}\\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$
(13)

where \(P_{m}(t)\) is a Legendre polynomials of order m are defined in the interval \([-1,1]\) and given by the following recurrence formulas

$$P_{0}(t) = 1,~P_{1}(t) = t,$$
$$P_{m+1}(t) = \Big (\frac{2m+1}{m+1}\Big )tP_{m}(t)-\Big (\frac{m}{m+1}\Big )P_{m-1}(t),~m=1,2,3,\cdots .$$

The wavelet constructed above using Legendre polynomials are called as Legendre wavelet [7].

2.2 Function Approximation

A function f(t) defined over \(L^{2}[0,1)\) can be expanded with Legendre scaling functions \(\phi _{k,m}^{J}(t)\) as

$$\begin{aligned} f(t) = \sum _{k=1}^{2^{J-1}}\sum _{m=0}^{\infty }c_{k,m}^{J}\phi _{k,m}^{J}(t), \end{aligned}$$
(14)

where \(c_{k,m}^{J} = \int _{0}^{1}f(t)\phi _{k,m}^{J}(t)dt\) and \(J\rightarrow \infty \). If the infinite series in (14) is truncated, then (14) can be written as

$$\begin{aligned} f(t) \approx P_{V_{M}^{J}}(f(t)) = \sum _{k=1}^{2^{J-1}}\sum _{m=0}^{M-1}c_{k,m}^{J}\phi _{k,m}^{J}(t) = C^{T}\varPhi (t), \end{aligned}$$
(15)

where C and \(\varPhi (t)\) are \(2^{J-1}M\times 1\) matrices given by

$$\begin{aligned} C =&[c_{1,0}^{J},c_{1,1}^{J},\cdots ,c_{1,M-1}^{J},c_{2,0}^{J},\cdots ,c_{2,M-1}^{J},\cdots ,c_{2^{J-1},0}^{J},\cdots ,c_{2^{J-1},M-1}^{J}]^{T},\\ \varPhi _{2^{J-1}M}(t) =&[\phi _{1,0}^{J}(t),\phi _{1,1}^{J}(t),\cdots ,\phi _{1,M-1}^{J}(t),\cdots ,\phi _{2^{J-1},M-1}^{J}(t)]^{T} \\ =&[\phi _{1}^{J}(t),\dots ,\phi _{2^{J-1}M}^{J}(t)]^{T}. \end{aligned}$$

In similar way, a bivariate function \(f(s,t) \in L^{2}[[0,1)\times [0,1)]\) can be expanded with Legendre wavelets as

$$\begin{aligned} f(s,t) \approx \sum _{i=1}^{2^{J-1}M}\sum _{j=1}^{2^{J-1}M}\phi _{i}^{J}(s)f_{ij}\phi _{j}^{J}(t) = \varPhi ^{T}(s)F\varPhi (t), \end{aligned}$$
(16)

where

$$f_{ij} = \int _{0}^{1}\int _{0}^{1}f(s,t)\phi _{i}^{J}(s)\phi _{j}^{J}(t)dsdt.$$

3 Legendre Wavelet Matrix and Block Pulse Operational Matrix

Let the collocation points be

$$\begin{aligned} t_{i} = \frac{2i-1}{2^{J}M},~ i = 1,2,\dots ,2^{J-1}M. \end{aligned}$$

We denote the Legendre wavelet matrix as \(\phi _{2^{J-1}M\times 2^{J-1}M}\) and define it as the combination of \(\phi _{k,m}^{J}(t_{i})\) at the collocation points \((t_{i})\) as

$$ \phi _{2^{J-1}M\times 2^{J-1}M} = \begin{pmatrix} \phi _{1,0}^{J}(t_{1}) &{} \phi _{1,1}^{J}(t_{2}) &{} \dots &{} \phi _{2^{J-1},M-1}^{J}(t_{2^{J-1}M}) \\ \phi _{1,0}^{J}(t_{1}) &{} \phi _{1,1}^{J}(t_{2}) &{} \dots &{} \phi _{2^{J-1},M-1}^{J}(t_{2^{J-1}M}) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \phi _{1,0}^{J}(t_{1}) &{} \phi _{1,1}^{J}(t_{2}) &{} \dots &{} \phi _{2^{J-1},M-1}^{J}(t_{2^{J-1}M}) \end{pmatrix}. $$

3.1 Legendre Wavelet Operational Matrix of Fractional Order Integration

If f(t) is expanded as in Eq. (14), then the Riemann-Liouville fractional order integration is given by

$$\begin{aligned} _{0}I_{t}^{\alpha }f(t) \approx \frac{1}{\varGamma (\alpha )}\int _{0}^{t}(t-\tau )^{\alpha -1}C^{T}\varPhi (\tau )d\tau = C^{T}(_{0}I_{t}^{\alpha }\varPhi _{2^{J-1}M}(t)). \end{aligned}$$

The \(2^{J-1}M-\)set of block pulse functions (BPFs) are also defined as

$$\begin{aligned} b_{i}(t) = {\left\{ \begin{array}{ll} 1 &{} \frac{(i-1)}{2^{J-1}M} \le t < \frac{i}{2^{J-1}M} \\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$
(17)

where \(i = 1,2,\dots ,2^{J-1}M\). The function \(b_{i}(t)\) has the following disjoint and orthogonal properties

  • \(b_{i}(t)b_{j}(t) = \delta _{ij}b_{i}(t)\),

  • \(\int _{0}^{1}b_{i}(t)b_{j}(t) = \frac{\delta _{ij}}{2^{J-1}M}\),

where \(\delta _{ij}\) is the Kronecker delta. The Legendre wavelet can be expanded into \(2^{J-1}M\) - term block pulse function as

$$\begin{aligned} \varPhi _{2^{J-1}M}(t) = \phi _{2^{J-1}M\times 2^{J-1}M}{} \mathbf{b} _{2^{J-1}M}(t), \end{aligned}$$
(18)

where \(\mathbf{b} _{2^{J-1}M}(t) = [b_{1}(t),\dots ,b_{2^{J-1}M}(t)]^{T}.\) The block pulse operational matrix of fractional-order integration \(G^{\alpha }\) is given in [6] as follows

$$\begin{aligned} _{0}I_{t}^{\alpha }{} \mathbf{b} _{2^{J-1}M}(t) \approx G^{\alpha }{} \mathbf{b} _{2^{J-1}M}(t), \end{aligned}$$
(19)

where

$$ G^{\alpha } = \frac{1}{(2^{J-1}M)^{\alpha }}\frac{1}{\varGamma (\alpha +2)} \begin{pmatrix} 1 &{} \xi _{1} &{} \xi _{2} &{} \xi _{3} &{} \cdots &{} \xi _{2^{J-1}M-1}\\ 0 &{} 1 &{} \xi _{1} &{} \xi _{2} &{} \cdots &{} \xi _{2^{J-1}M-2} \\ 0 &{} 0 &{} 1 &{} \xi _{1} &{} \cdots &{} \xi _{2^{J-1}M-3} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 1 \end{pmatrix}, $$

with \(\xi _{i} = (i+1)^{\alpha +1}-2i^{\alpha +1}+(i-1)^{\alpha +1}\).

Let

$$\begin{aligned} _{0}I_{t}^{\alpha }\varPhi _{2^{J-1}M}(t) = P_{2^{J-1}M\times 2^{J-1}M}^{\alpha }\varPhi _{2^{J-1}M}(t), \end{aligned}$$
(20)

where the matrix \(P_{2^{J-1}M\times 2^{J-1}M}^{\alpha }\) is called the Legendre wavelet operational matrix of fractional order integration. Using Eqs. (18) and (19) in (20), we get

$$\begin{aligned} P_{2^{J-1}M\times 2^{J-1}M}^{\alpha } \approx (\phi _{2^{J-1}M\times 2^{J-1}M})G^{\alpha }(\phi _{2^{J-1}M\times 2^{J-1}M})^{-1}. \end{aligned}$$

3.2 Deterministic Integration Operational Matrix

Let \(m = 2^{J-1}M\) and compute \(\int _{0}^{t}b_{i}(s)ds\) as follows

$$\begin{aligned} \int _{0}^{t}b_{i}(s)ds = {\left\{ \begin{array}{ll} 0 &{} 0 \le t< \frac{i-1}{m}\\ t-\frac{i-1}{m} &{} \frac{i-1}{m} \le t< \frac{i}{m} \\ \frac{1}{m} &{} \frac{i}{m} \le t < 1. \end{array}\right. } \end{aligned}$$
(21)

We approximate \(t-\frac{i-1}{m}\), for \(\frac{i-1}{m} \le t < \frac{i}{m},\) by \(\frac{1}{2m}\) and express \(\int _{0}^{t}b_{i}(s)ds\) in terms of BPFs as follows

$$\begin{aligned} \int _{0}^{t}b_{i}(s)ds \approx \big (0,\dots ,0,\frac{1}{2m},\frac{1}{m},\dots ,\frac{1}{m}\big )\mathbf{b} _{m}(t), \end{aligned}$$
(22)

where \(\frac{1}{2m}\) is the ith component of vector. Therefore

$$\begin{aligned} \int _{0}^{t}{} \mathbf{b} _{m}(s)ds \approx P\mathbf{b} _{m}(t), \end{aligned}$$
(23)

where the operational matrix of integration is given by

$$ P = \frac{1}{2m} \begin{pmatrix} 1 &{} 2 &{} 2 &{} \cdots &{} 2 \\ 0 &{} 1 &{} 2 &{} \cdots &{} 2 \\ 0 &{} 0 &{} 1 &{} \cdots &{} 2 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 \end{pmatrix}_{m\times m} $$

3.3 Stochastic Integration Operational Matrix

The It\(\hat{o}\) integral of each single BPFs \(b_{i}(t)\) can be computed as follows

$$\begin{aligned} \int _{0}^{t}b_{i}(s)dW(s) = {\left\{ \begin{array}{ll} 0 &{} 0 \le t< \frac{i-1}{m}\\ W(t)-W(\frac{i-1}{m}) &{} \frac{i-1}{m} \le t< \frac{i}{m} \\ W(\frac{i}{m})-W(\frac{i-1}{m}) &{} \frac{i}{m} \le t < 1. \end{array}\right. } \end{aligned}$$
(24)

We can approximate \(W(t)-W(\frac{i-1}{m})\), for \(\frac{i-1}{m} \le t < \frac{i}{m}\), by \(W(\frac{i-0.5}{m})-W(\frac{i-1}{m})\) and express \(\int _{0}^{t}b_{i}(s)dW(s)\), in terms of BPFs as follows

$$\begin{aligned} \begin{aligned} \int _{0}^{t}b_{i}(s)dW(s) \approx&\bigg (0,\dots ,0,W(\frac{i-0.5}{m})-W(\frac{i-1}{m}),W(\frac{i}{m})-W(\frac{i-1}{m}),\\ {}&\dots , W(\frac{i}{m})-W(\frac{i-1}{m})\bigg )b_{m}(t), \end{aligned} \end{aligned}$$
(25)

where \(W(\frac{i-0.5}{m})-W(\frac{i-1}{m})\) is the ith component of vector. Therefore, we obtain the following expression (for details, see [8])

$$\begin{aligned} \int _{0}^{t}{} \mathbf{b} _{m}(s)dW(s) \approx P_{s}{} \mathbf{b} _{m}(t), \end{aligned}$$
(26)

where stochastic operational matrix of integration is given by

$$ P_{s} = \begin{pmatrix} W(\frac{1}{2m}) &{} W(\frac{1}{m}) &{} W(\frac{1}{m}) &{} \cdots &{} W(\frac{1}{m}) \\ 0 &{} W(\frac{3}{2m})-W(\frac{1}{m}) &{} W(\frac{2}{m})-W(\frac{1}{m}) &{} \cdots &{} W(\frac{2}{m})-W(\frac{1}{m}) \\ 0 &{} 0 &{} W(\frac{5}{2m})-W(\frac{2}{m}) &{} \cdots &{} W(\frac{3}{m})-W(\frac{2}{m}) \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} W(\frac{2m-1}{2m})-W(\frac{m-1}{m}) \end{pmatrix}_{m\times m} $$

4 Description of Numerical Method

Here we present the wavelet collocation method based on the Legendre wavelets for solving SFIDE (1). We use the relation between the fractional derivative and integral to obtain the solution u(t) derived as follows

  • Let \(D^{\alpha }u(t) \approx C^{T}\varPhi (t)\), this implies that

    $$\begin{aligned} u(t) \approx {C^{T}} {_{0}I^{\alpha }}\varPhi (t)+u_{0}. \end{aligned}$$
    (27)

  • Let \(k_{1}(s,t) \in L^{2}([0,1)\times [0,1))\). It can be expanded with respect to Legendre wavelet as

    $$\begin{aligned} k_{1}(s,t) \approx \varPhi ^{T}(s)K_{1}\varPhi (t) = \varPhi ^{T}(t)K_{1}^{T}\varPhi (s), \end{aligned}$$
    (28)

    where \(K_{1} = (k_{1})_{ij},~i=1,2,\dots ,m,~j=1,2,\dots ,m\) is the \(m\times m\) Legendre wavelets coefficient matrix with

    $$\begin{aligned} (k_{1})_{ij} = \int _{0}^{1}\int _{0}^{1}k_{1}(s,t)\phi _{i}(s)\phi _{j}(t)dsdt. \end{aligned}$$

    Similarly

    $$\begin{aligned} k_{2}(s,t) \approx \varPhi ^{T}(s)K_{2}\varPhi (t) = \varPhi ^{T}(t)K_{2}^{T}\varPhi (s), \end{aligned}$$
    (29)

    where \(K_{2} = (k_{2})_{ij},~i=1,2,\dots ,m,~j=1,2,\dots ,m\) is the \(m\times m\) Legendre wavelets coefficient matrix with

    $$\begin{aligned} (k_{2})_{ij} = \int _{0}^{1}\int _{0}^{1}k_{2}(s,t)\phi _{i}(s)\phi _{j}(t)dsdt. \end{aligned}$$

Substituting the above approximation in (1), we get

$$\begin{aligned} C^{T}\varPhi (t)&= f(t) +\int _{0}^{t}C^{T}(_{0}I^{\alpha }\varPhi (s))\varPhi ^{T}(s)K_{1}\varPhi (t)ds + u_{0}\int _{0}^{t}\varPhi ^{T}(s)K_{1}\varPhi (t)ds\\&+\int _{0}^{t}C^{T}(_{0}I^{\alpha }\varPhi (s))\varPhi ^{T}(s)K_{2}\varPhi (t)dW(s) + u_{0}\int _{0}^{t}\varPhi ^{T}(s)K_{2}\varPhi (t)dW(s) \\&= f(t)+C^{T}P^{\alpha }\big (\int _{0}^{t}\varPhi (s)\varPhi ^{T}(s)ds\big )K_{1}\varPhi (t)+u_{0}\big (\int _{0}^{t}\varPhi ^{T}(s)ds\big )K_{1}\varPhi (t) \\&+C^{T}P^{\alpha }\big (\int _{0}^{t}\varPhi (s)\varPhi ^{T}(s)dW(s)\big )K_{2}\varPhi (t)+u_{0}\big (\int _{0}^{t}\varPhi ^{T}(s)dW(s)\big )K_{2}\varPhi (t) \\&= f(t)+C^{T}P^{\alpha }\phi \big (\int _{0}^{t}{} \mathbf{b} (s)\mathbf{b} ^{T}(s)ds\big )\phi ^{T}K_{1}\varPhi (t)+u_{0}\big (\int _{0}^{t}{} \mathbf{b} ^{T}(s)ds\big )\phi ^{T} K_{1}\varPhi (t) \\&+C^{T}P^{\alpha }\phi \big (\int _{0}^{t}{} \mathbf{b} (s)\mathbf{b} ^{T}(s)dW(s)\big )\phi ^{T}K_{2}\varPhi (t)+u_{0}\big (\int _{0}^{t}{} \mathbf{b} ^{T}(s)dW(s)\big )\phi ^{T} K_{2}\varPhi (t). \end{aligned}$$

Let \(P^{\alpha }\phi = Q_{1},~\phi ^{T}K_{1} = Q_{2},~\phi ^{T}K_{2} = Q_{3}\), \(Q_{2}^{i}\) be the ith row of constant matrix \(Q_{2}\), \(Q_{3}^{i}\) be the ith row of constant matrix \(Q_{3}\), \(R^{i}\) be the ith row of the integration operational matrix P and \(R_{s}^{i}\) be the ith row of the stochastic operational matrix \(P_{s}\). We have

Then

$$\begin{aligned} C^{T}(I-Q_{1}B_{1}-Q_{1}B_{2})\varPhi (t) \approx f(t)+u_{0}(\mathbf{b} ^{T}(t)P^{T}Q_{2}+\mathbf{b} ^{T}(t)P_{s}^{T}Q_{3})\varPhi (t) \end{aligned}$$
(30)

So, by setting

$$ A = \begin{pmatrix} \varPhi ^{T}(t_{1})(I-Q_{1}B_{1}-Q_{1}B_{2})^{T} \\ \vdots \\ \varPhi ^{T}(t_{m})(I-Q_{1}B_{1}-Q_{1}B_{2})^{T} \end{pmatrix}$$

and

$$ F = \begin{pmatrix} f(t_{1})+u_{0}(\mathbf{b} ^{T}(t_{1})P^{T}Q_{2}+\mathbf{b} ^{T}(t_{1})P_{s}^{T}Q_{3})\varPhi (t_{1}) \\ \vdots \\ f(t_{m})+u_{0}(\mathbf{b} ^{T}(t_{m})P^{T}Q_{2}+\mathbf{b} ^{T}(t_{m})P_{s}^{T}Q_{3})\varPhi (t_{m}) \end{pmatrix}, $$

where \(t_{i}\) are the collocation points. We have

$$\begin{aligned} AC = F, \end{aligned}$$
(31)

which is a linear system of equations that gives the Legendre wavelets coefficient.

5 Numerical Experiments

To illustrate the proposed method discussed in Sect. 4, we consider the following examples.

Example 51

Consider the SFIDE (1) with \(f(t) = \frac{t^{2}}{2}+\frac{\varGamma (2)}{\varGamma (2-\alpha )}t^{1-\alpha },~k_{1}(s,t) = 1,~k_{2}(s,t) = 0,\) and \(u_{0} = 0\). For \(\alpha = 0\), \(u(t) = -(2+t)+2e^{t}\) is exact solution of (1).

Example 52

Consider the SFIDE (1) with \(f(t) = -\frac{t^{5}e^{t}}{5}+\frac{6t^{2.25}}{\varGamma (3.25)},~k_{1}(s,t) = e^{t}s,~k_{2}(s,t) = 0,\) and \(u_{0} = 0\). For \(\alpha = 0.75\), \(u(t) = t^{3}\) is exact solution of (1).

Example 53

Consider the SFIDE (1) with \(f(t) = 0,~k_{1}(s,t) = s^{2},~k_{2}(s,t) = s^{3},\) and \(u_{0} = 1\). For \(\alpha = 0\), \(u(t) = e^{\frac{t^{3}}{3}+\int _{0}^{t}s^{3}dW(s)}\) is exact solution of (1).

Let \(u_{num}(t_{i},l)\) denotes the approximate solution of \(l^{th}\) simulation at \(t_{i}\) and \(u_{exact}(t_{i},l)\) denotes the exact solution of \(l^{th}\) simulation at \(t_{i}\). The efficiency of the proposed method, for Examples 51, 52 and 53 are highlighted in Tables 1, 2 and 3, respectively, which showcase the values of maximum absolute error and root mean square (RMS) error that are defined as

$$\begin{aligned} \mathbb {E}\Vert e\Vert _{\infty } = \frac{1}{N}\sum _{l=1}^{N}\max _{1\le i \le m}|u_{exact}(t_{i},l)-u_{num}(t_{i},l)|, \end{aligned}$$
(32)
$$\begin{aligned} \mathbb {E}\Vert e\Vert _{2,m} = \frac{1}{N}\sum _{l=1}^{N}\sqrt{\frac{1}{m}\sum _{i=1}^{m}|u_{exact}(t_{i},l)-u_{num}(t_{i},l)|^{2}} \end{aligned}$$
(33)

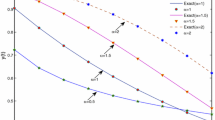
respectively, where N is total number of simulation and \(\mathbb {E}\) is mathematical expectation. For deterministic function \(\mathbb {E}\Vert .\Vert _{\infty } = \Vert .\Vert _{\infty }\) and \(\mathbb {E}\Vert .\Vert _{2,m} = \Vert .\Vert _{2,m}\). Table 1 shows the maximum absolute errors obtained for Example 51 via the proposed method discussed in Sect. 4 for \(\alpha = 0\) and different values of J,  M and m. Table 2 shows the comparison of our method with Gaussian radial basis function (GA RBF) and thin plate splines radial basis function (TBS RBF) in terms of the absolute maximum error and RMS-error obtained for Example 52 with \(\alpha =0.75\) and different values of m. These methods (GA RBF and TBS RBF [11]) need smaller value of shape parameter for higher accuracy which increases the condition number of coefficient matrix and as a result the methods become unstable. However, the method proposed in Sect. 4 has no such behavior. Finally, Table 3 shows the calculation of the mean and standard deviation which are denoted by \(\mathbb {E}\Vert e\Vert _{\infty }\) and \(S_{e}\), respectively, of the maximum absolute error for Example 53 with \(\alpha = 0\) and different number of simulation trajectories (N). For different values of N, the upper and lower limit of \(95\%\) confidence interval (C.I.) are also listed in Table 3. In Fig. 1, we plot the mean approximate solution and mean exact solution of Example 53 along with \(95\%\) confidence interval region for \(\alpha = 0\) and \(m =32\) with different values of N.

Table 1. Maximum absolute error in u(t) corresponding to \(\alpha =0\) with different value of J and M.
Full size table
Table 2. Results of Example 52 for different values of m and \(\alpha = 0.75\)
Full size table
Fig. 1.
figure 1

The trajectory of the approximate solution and exact solution of Example 53 along with 95\(\%\) confidence interval (C.I) for \(M = 2,~J = 5,~m = 32\) and \(\alpha = 0\).

Full size image
Table 3. Mean, Standard deviation and mean confidence interval for maximum absolute error in Example (53) with \(m = 32,~J = 5,~ M = 2\) and \(\alpha =0\).
Full size table

6 Applications

In this section, we present some special cases of the proposed model and their applications in real life examples. SFIDE (1) have many practical applications in scientific field such as physics, finance and biology etc. When \(\alpha =0\), \(f(t)=0\), \(k_1(s,t)=\mu \) and \(k_2(s,t)=\sigma \), the proposed model reduces in the following form

$$\begin{aligned} u(t) = u_{0}+\int _{0}^{t}\mu u(s)ds+\int _{0}^{t}\sigma u(s)dW(s), \end{aligned}$$
(34)

or,

$$\begin{aligned} du(t) = \mu u(t)+\sigma u(t)dW(t). \end{aligned}$$
(35)

The above stochastic differential equation is called geometric Brownian motion model which is used for modeling the stock prices in the finance [3]. Also in physics, (35) is the Langevin equation with multiplicative noise [4]. The Langevin equation is very important tool in physics for describing many physical process. Suppose u(t) is any physical process described by the (35) then we always get probability distribution \(p(u,t|u_{0})\) corresponding to (35) which satisfies the Fokker-Plank equation.

7 Conclusion

In this paper, we develop a wavelet collocation method based on the Legendre wavelets to solve SFIDE (1). For this purpose, we compute the deterministic and stochastic operational matrices based on block pulse function. The SFIDE (1) is then converted to a system of linear equations by employing the collocation method and making use of operational matrices. The solution of SFIDE is obtained using our proposed method. In Sect. 5, we solve several examples to indicate the accuracy and efficiency of the proposed method as discussed in Sect. 4.