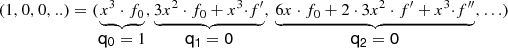Abstract
Non-linear effects in accelerator physics are important both during the design stage and for successful operation of accelerators. Since both of these aspects are closely related, they will be treated together in this overview. Some of the most important aspects are well described by methods established in other areas of physics and mathematics. Given the scope of this handbook, the treatment will be focused on the problems in accelerators used for particle physics experiments. Although the main emphasis will be on accelerator physics issues, some of the aspects of more general interest will be discussed. In particular to demonstrate that in recent years a framework has been built to handle the complex problems in a consistent form, technically superior and conceptually simpler than the traditional techniques. The need to understand the stability of particle beams has substantially contributed to the development of new techniques and is an important source of examples which can be verified experimentally. Unfortunately the documentation of these developments is often poor or even unpublished, in many cases only available as lectures or conference proceedings.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
3.1 Introduction
Non-linear effects in accelerator physics are important both during the design stage and for successful operation of accelerators. Since both of these aspects are closely related, they will be treated together in this overview. Some of the most important aspects are well described by methods established in other areas of physics and mathematics. Given the scope of this handbook, the treatment will be focused on the problems in accelerators used for particle physics experiments. Although the main emphasis will be on accelerator physics issues, some of the aspects of more general interest will be discussed. In particular to demonstrate that in recent years a framework has been built to handle the complex problems in a consistent form, technically superior and conceptually simpler than the traditional techniques. The need to understand the stability of particle beams has substantially contributed to the development of new techniques and is an important source of examples which can be verified experimentally. Unfortunately the documentation of these developments is often poor or even unpublished, in many cases only available as lectures or conference proceedings.
This article is neither rigorous nor a complete treatment of the topic, but rather an introduction to a limited set of contemporary tools and methods we consider useful in accelerator theory.
3.1.1 Motivation
The most reliable tools to study (i.e. description of the machine) are simulations (e.g. tracking codes).
-
Particle Tracking is a numerical solution of the (nonlinear) Initial Value Problem. It is a “integrator” of the equation of motion and a vast amount of tracking codes are available, together with analysis tools (Examples: Lyapunov, Chirikov, chaos detection, frequency analysis, …)
-
It is unfortunate that theoretical and computational tools exist side by side without an undertaking how they can be integrated.
-
It should be undertaken to find an approach to link simulations with theoretical analysis, would allow a better understanding of the physics in realistic machines.
-
A particularly promising approach is based on finite maps [1].
3.1.2 Single Particle Dynamics
The concepts developed here are used to describe single particle transverse dynamics in rings, i.e. circular accelerators or storage rings. This is not a restriction for the application of the presented tools and methods. In the case of linear betatron motion the theory is rather complete and the standard treatment [2] suffices to describe the dynamics. In parallel with this theory the well known concepts such as closed orbit and Twiss parameters are introduced and emerged automatically from the Courant-Snyder formalism [2]. The formalism and applications are found in many textbooks (e.g. [3,4,5]).
In many new accelerators or storage rings (e.g. LHC) the description of the machine with a linear formalism becomes insufficient and the linear theory must be extended to treat non-linear effects. The stability and confinement of the particles is not given a priori and should rather emerge from the analysis. Non-linear effects are a main source of performance limitations in such machines. A reliable treatment is required and the progress in recent years allows to evaluate the consequences. Very useful overview and details can be found in [6,7,8].
3.1.3 Layout of the Treatment
Following a summary of the sources of non-linearities in circular machine, the basic methods to evaluate the consequences of non-linear behaviour are discussed. Since the traditional approach has caused misconception and the simplifications led to wrong conclusions, more recent and contemporary tools are introduced to treat these problems. An attempt is made to provide the physical picture behind these tools rather than a rigorous mathematical description and we shall show how the new concepts are a natural extension of the Courant-Snyder formalism to non-linear dynamics. An extensive treatment of these tools and many examples can be found in [7]. In the last part we summarize the most important physical phenomena caused by the non-linearities in an accelerator.
3.2 Variables
For what follows one should always use canonical variables!
In Cartesian coordinates:
If the energy is constant (i.e. P Z = const.), we use:
This system is rather inconvenient, what we want is the description of the particle in the neighbourhood of the reference orbit/trajectory:
which are considered now the deviations from the reference and which are zero for a particle on the reference trajectory
It is very important that it is the reference not the design trajectory!
(so far it is a straight line along the Z-direction)
3.2.1 Trace Space and Phase Space
A confusion often arises about the terms Phase Space (x, p x, …) or Trace Space (x, x′, …)
It is not laziness nor stupidity to use one or the other:
-
Beam dynamics is strictly correct only with (x, p x, …), (see later chapter) but in general quantities cannot be measured easily
-
Beam dynamics with (x, x′, …) needs special precaution, but quantities based on these coordinates are much easier to measure
-
Some quantities are different (e.g. emittance)
It comes back to a remark made at the beginning, i.e. that we shall use rings for our arguments. In single pass machine, e.g. linac, beam lines, spectrometers, the beam is not circulating over many turns and several hours, therefore there is no interest in stability issues. Instead for most of these applications what counts is the coordinates and angles at a given position (x, x′, y, y′), e.g. at the end of a beam line or a small spot one an electron microscope. When “accelerator physicists” talk about concepts such as tune, resonances, β-functions, equilibrium emittances etc., all these are irrelevant for single pass machine. There is no need to study iterating systems. In these cases the use of the trace space is fully adequate, in fact preferred because the quantities can be measured. In the end, the mathematical tools are very different from the ones discussed in this article.
3.2.2 Curved Coordinate System
For a “curved” trajectory, in general not circular, with a local radius of curvature ρ(s) in the horizontal (X–Z plane), we have to transform to a new coordinate system (x, y, s) (co-moving frame) with:
The new canonical momenta become:
3.3 Sources of Non-linearities
Any object creating non-linear electromagnetic fields on the trajectory of the beam can strongly influence the beam dynamics. They can be generated by the environment or by the beam itself.
3.3.1 Non-linear Machine Elements
Non-linear elements can be introduced into the machine on purpose or can be the result of field imperfections. Both types can have adverse effects on the beam stability and must be taken into account.
3.3.1.1 Unwanted Non-linear Machine Elements
The largest fraction of machine elements are either dipole or quadrupole magnets. In the ideal case, these types of magnets have pure dipolar or quadrupolar fields and behave approximately as linear machine elements. Any systematic or random deviation from this linear field introduces non-linear fields into the machine lattice. These effects can dominate the aperture required and limit the stable region of the beam. The definition of tolerances on these imperfections is an important part of any accelerator design.
Normally magnets are long enough that a 2-dimensional field representation is sufficient. The components of the magnetic field can be derived from the potential and in cylindrical coordinates (r, Θ, s = 0) can be written as:
where R ref is a reference radius and B n and A n are constants. Written in Cartesian coordinates we have:
where z = x + iy = re i Θ. The terms n correspond to 2n-pole magnets and the B n and A n are the normal and skew multipole coefficients. The beam dynamics set limits on the allowed multipole components of the installed magnets.
3.3.1.2 Wanted Non-linear Machine Elements
In most accelerators the momentum dependent focusing of the lattice (chromaticity) needs to be corrected with sextupoles [3, 4]. Sextupoles introduce non-linear fields into the lattice that are larger than the intrinsic non-linearities of the so-called linear elements (dipoles and quadrupoles). In a strictly periodic machine the correction can be done close to the origin and the required sextupole strengths can be kept small. For colliding beam accelerators usually special insertions are foreseen to host the experiments where the dispersion is kept small and the β-function is reduced to a minimum. The required sextupole correction is strong and can lead to a reduction of the dynamic aperture, i.e. the region of stability of the beam. In most accelerators the sextupoles are the dominant source of non-linearity. To minimize this effect is an important issue in any design of an accelerator.
Another source of non-linearities can be octupoles used to generate amplitude dependent detuning to provide Landau damping in case of instabilities.
3.3.2 Beam–Beam Effects and Space Charge
A strong source of non-linearities are the fields generated by the beam itself. They can cause significant perturbations on the same beam (space charge effects) or on the opposing beam (beam-beam effects) in the case of a colliding beam facility.
As an example, for the simplest case of round beams with the line density n and the beam size σ the field components can be written as:
and
In colliding beams with high density and small beams these fields are the dominating source of non-linearities. The full treatment of beam-beam effects is complicated due to mutual interactions between the two beams and a self-consistent treatment is required. in the presence of all other magnets in the ring.
3.4 Map Based Techniques
In the standard approach to single particle dynamics in rings, the equations of motion are introduced together with an ansatz to solve these equations. In the case of linear motion, this ansatz is due to Courant-Snyder [2]. However, this treatment must assume that the motion of a particle in the ring is stable and confined. For a non-linear system this is a priori not known and the attempt to find a complete description of the particle motion must fail.
The starting point for the treatment of the linear dynamics in synchrotrons is based on solving a linear differential equation of the Hill type.
Each element at position s acts as a source of forces, i.e. we must write for the forces K → K(s) which is assumed to be a periodic function, i.e. K(s + C) = K(s)ring
The solution of this Boundary Value Problem must be periodic too!
It is therefore not applicable in the general case (e.g. Linacs, Beamlines, FFAG, Recirculators, …), much better to treat it as an Initial Value Problem.
In a more useful approach we do not attempt to solve such an overall equation but rather consider the fundamental objects of an accelerators, i.e. the machine elements themselves. These elements, e.g. magnets or other beam elements, are the basic building blocks of the machine. All elements have a well defined action on a particle which can be described independent of other elements or concepts such as closed orbit or β-functions. Mathematically, they provide a “map” from one face of a building block to the other, i.e. a description of how the particles move inside and between elements. In this context, a map can be anything from linear matrices to high order integration routines.
A map based technique is also the basis for the treatment of particle dynamics as an Initial value Problem (IVP).
It follow immediately that for a linear, 1st order equation of the type
the solution can always be written as:
where the function K(s) does not have to be periodic. Furthermore, the determinant of the matrix A is always 1. Therefore it is an advantage to use maps (matrices) for a linear systems from the start, without trying to solve a differential equation.
The collection of all machine elements make up the ring pr beam line and it is the combination of the associated maps which is necessary for the description and analysis of the physical phenomena in the accelerator ring or beam line.
For a circular machine the most interesting map is the one which describes the motion once around the machine, the so-called One-Turn-Map. It contains all necessary information on stability, existence of closed orbit, and optical parameters. The reader is assumed to be familiar with this concept in the case of linear beam dynamics (Chap. 2) where all maps are matrices and the Courant-Snyder analysis of the corresponding one-turn-map produces the desired information such as e.g. closed orbit or Twiss parameters.
It should therefore be the goal to generalize this concept to non-linear dynamics. The computation of a reliable one-turn-map and the analysis of its properties will provide all relevant information.
Given that the non-linear maps can be rather complex objects, the analysis of the one-turn-map should be separated from the calculation of the map itself.
3.5 Linear Normal Forms
3.5.1 Sequence of Maps
Starting from a position s 0 and combining all matrices to get the matrix to position s 0 + L (shown for 1D only):
For a ring with circumference C one obtains the One-Turn-Matrix (OTM) at s 0
Without proof, the scalar product:
is a constant of the motion: invariant of the One Turn Map.
With this approach we have a strong argument that the construction of the One Turn Map is based on the properties of each element in the machine. It is entirely independent of the purpose of the machine and their global properties. It is not restricted to rings or in general to circular machine.
Once the One Turn Map is constructed, it can be analysed, but this analysis does not depend on how it was constructed.
As a paradigm: the construction of a map (being for a circular machine or not) and its analysis are conceptual and computational separated undertakings.
3.5.2 Analysis of the One Turn Map
The key for the analysis is that matrices can be transformed into Normal Forms. Starting with the One-Turn-Matrix, and try to find a (invertible) transformation A such that:
-
The matrix R is:
-
A “Normal Form”, (or at least a very simplified form of the matrix)
-
For example (most important case): R becomes a pure rotation
-
-
The matrix R describes the same dynamics as M, but:
-
All coordinates are transformed by A
-
This transformation A “analyses” the complexity of the motion, it contains the structure of the phase space
-
The motion on an ellipse becomes a motion on a circle (i.e. a rotation): R is the simple part of the map and its shape is dumped into the matrix A. R can be obtained by the evaluation of the Eigenvectors and Eigenvalues.
One finds for the two components of the original map:
Please note that the normal form analysis gives the eigenvectors (3.14) without any physical picture related to their interpretation. The formulation using α and β is due to Courant and Snyder. Amongst other advantages it can be used to “normalise” the position x: the normalised position x n is the “non-normalized” divided by \(\sqrt {\beta }\). The variation of the normalised position x n is then smaller than in the non-normalized case. This is also better suited for analytical calculation, e.g. involving perturbation theory.
The Normal Form transformation together with this choice gives the required information:
-
μ x is the “tune” Q x ⋅ 2π (now we can talk about phase advance!)
-
β, α, … are the optical parameters and describe the ellipse
-
The closed orbit (an invariant, identical coordinates after one turn!):
-
M OTM ∘ (x, x′)co ≡ (x, x′)co
3.5.3 Action-Angle Variables
More appropriate for studies of beam dynamics is the use of Action-Angle variables.
Once the particles “travel” on a circle, the motion is better described by the canonical variables action J x and angle Ψx:

with the definitions and the choice is (3.14):
-
the angular position along the ring Ψ becomes the independent variable!
-
The trajectory of a particle is now independent of the position s!
-
The constant radius of the circle \(\sqrt {2 J}\) defines the action J (invariant of motion)
3.5.4 Beam Emittance
A sad and dismal story in accelerator physics is the definition of the emittance. Most foolish in this context is to relate emittance to single particles. This is true in particular when we have a beam line which is not periodic. In that case the Courant-Snyder parameters can be determined from the beam. These parameters are related to the moments of the beam, e.g. the beam size is directly related to the second order moment < x 2 > . Using the expression above for the action and angle, we can write for this expression:
The average of \(\cos ^{2}\) can immediately be evaluated as 0.5 and defining the emittance as:
we write
Using a similar procedure (details and derivation in e.g. [3], and to a much lesser extent in [1]) one can determine the moments
and
Using these expressions, the emittance becomes readily
Therefore, once the emittance is measured, the Courant-Snyder parameters are determined by Eqs. (3.18), (3.19), and (3.20).
Since other definitions often refer to the treatment by Courant and Snyder, here a quote from Courant himself in [9]:
Interlude 1
The invariant J is simply related to the area enclosed by the ellipse:
$$\displaystyle \begin{aligned} {\mathsf{Area~enclosed}}~~~=~~2\pi J. {} \end{aligned} $$(3.22)In accelerator and storage ring terminology there is a quantity called the emittance which is closely related to this invariant. The emittance, however, is a property of a distribution of particles, not a single particle. Consider a Gaussian distribution in amplitudes. Then the (rms) emittance, 𝜖, is given by:
$$\displaystyle \begin{aligned} (x_{rms})^{2}~~=~~\beta_{x}(s)\cdot \epsilon_{x}. {} \end{aligned} $$(3.23)In terms of the action variable, J, this can be rewritten
$$\displaystyle \begin{aligned} \epsilon_{x}~~=~~<J>. {} \end{aligned} $$(3.24)where the bracket indicates an average over the distribution in J.
Other definitions based on handwaving arguments or those approximately valid only in special cases, should be discarded, in particular those relying on presumed distributions, e.g. Gaussian.
3.6 Techniques and Tools to Evaluate and Correct Non-linear Effects
The key to a more modern approach shown in this section is to avoid the prejudices about the stability and other properties of the ring. Instead, we must describe the machine in terms of the objects it consists of with all their properties, including the non-linear elements. The analysis will reveal the properties of the particles such as e.g. stability. In the simplest case, the ring is made of individual machine elements such as magnets which have an existence on their own, i.e. the interaction of a particle with a given element is independent of the motion in the rest of the machine. Also for the study of non-linear effects, the description of elements should be independent of concepts such as tune, chromaticity and closed orbit. To successfully study single particle dynamics, one must be able to describe the action of the machine element on the particle as well as the machine element.
3.6.1 Particle Tracking
The ring being a collection of maps, a particle tracking code, i.e. an integrator of the equation of motion, is the most reliable map for the analysis of the machine. Of course, this requires an appropriate description of the non-linear maps in the code. It is not the purpose of this article to describe the details of tracking codes and the underlying philosophy, such details can be found in the literature (see e.g. [6]). Here we review and demonstrate the basic principles and analysis techniques.
3.6.1.1 Symplecticity
If we define a map through \({\vec {z_{2}}}~=~{{M}}_{12}(\vec {z_{1}})\) as a propagator from a location “1” to a location “2” in the ring, we have to consider that not all possible maps are allowed. The required property of the map is called “symplecticity” and in the simplest case where M 12 is a matrix, the symplecticity condition can be written as:
The physical meaning of this condition is that the map is area preserving in the phase space. The condition can easily be derived from a Hamiltonian treatment, closely related to Liouville’s theorem.
3.6.2 Approximations and Tools
The concept of symplecticity is vital for the treatment of Hamiltonian systems. This is true in particular when the stability of a system is investigated using particle tracking. However, in practice it is difficult to accomplish for a given exact problem. As an example we may have the exact fields and potentials of electromagnetic elements. For a single pass system a (slightly) non-symplectic integrator may be sufficient, but for an iterative system the results are meaningless.
To track particles using the exact model may result in a non-symplectic tracking, i.e. the underlying model is correct, but the resulting physics is wrong.
It is much better to approximate the model to the extend that the tracking is symplectic. One might compromise on the exactness of the final result, but the correct physics is ensured.
As a typical example one might observe possible chaotic motion during the tracking procedure. However, there is always a non-negligible probability that this interpretation of the results may be wrong. To conclude that it is not a consequence of non-symplecticity of the procedure or a numerical artifact it is necessary to identify the physical mechanism leading to this observation.
This may not be possible to achieve using the exact model as input to a (possibly) non-symplectic procedure. Involving approximations to the definition of the problem should reveal the correct physics at the expense of a (hopefully) small error. Staying exact, the physics may be wrong.
As a result, care must be taken to positively identify the underlying process.
This procedure should be based on a approximations as close as possible to the exact problem, but allowing a symplectic evaluation.
An example for this will be shown in Sect. 3.6.3.4.
3.6.3 Taylor and Power Maps
A non-linear element cannot be represented in the form of a linear matrix and more complicated maps have to be introduced [5]. In principle, any well behaved, non-linear function can be developed as a Taylor series. This expansion can be truncated at the desired precision.
Another option is the representation as Lie transformations [8, 10]. Both types are discussed in this section.
3.6.3.1 Taylor Maps
A Taylor map can be written using higher order matrices and in the case of two dimensions we have:
(where z j, j = 1, …, 4, stand for x, x′, y, y′). Let us call the collection: A 2 = (R, T) the second order map A 2. Higher orders can be defined as needed, e.g. for the 3rd order map A 3 = (R, T, U) we add a third order matrix:
Since Taylor expansions are not matrices, to provide a symplectic map, it is the associated Jacobian matrix J which must fulfill the symplecticity condition:
However, in general J ik ≠ const and for a truncated Taylor map it can be difficult to fulfill this condition for all z. As a consequence, the number of independent coefficients in the Taylor expansion is reduced and the complete, symplectic Taylor map requires more coefficients than necessary [7].
The explicit maps for a sextupole is:
Writing the explicit form of the Jacobian matrix:
For k 2 ≠ 0 coefficients depend on initial values, e.g.:
The non-symplecticity can be recovered in the case of elements with L = 0. It becomes small (probably small enough) when the length is small.
As a result, the model is approximated by a small amount, but the symplecticity (and therefore the physics) is ensured. An exact model but compromised integration can fabricate non-existing features and conceal important underlying physics.
The situation is rather different in the case of single pass machines. The long term stability (and therefore symplecticity) is not an issue and the Taylor expansion around the closed orbit is what is really needed. Techniques like the one described in Sect. 3.7.6 provide exactly this in an advanced and flexible formalism.
3.6.3.2 Thick and Thin Lenses
All elements in a ring have a finite length and therefore should be treated as “thick lenses”. However, in general a solution for the motion in a thick element does not exist. It has become a standard technique to avoid using approximate formulae to track through thick lenses and rather perform exact tracking through thin lenses. This approximation is improved by breaking the thick element into several thin elements which is equivalent to a numerical integration. A major advantage of this technique is that “thin lens tracking” is automatically symplectic. In this context it becomes important to understand the implied approximations and how they influence the desired results. We proceed by an analysis of these approximations and show how “symplectic integration” techniques can be applied to this problem.
We demonstrate the approximation using a quadrupole. Although an exact solution of the motion through a quadrupole exists, it is a useful demonstration since it can be shown that all concepts developed here apply also to arbitrary non-linear elements.
Let us assume the transfer map (matrix) for a thick, linearized quadrupole of length L and strength K:
This map is exact and can be expanded as a Taylor series for a “small” length L:
If we keep only terms up to first order in L we get:
This map is precise to order O(L 1), but since we have det M ≠ 1, this truncated expansion is not symplectic.
3.6.3.3 Symplectic Matrices and Symplectic Integration
However, the map (3.34) can be made symplectic by adding a term −K 2 L 2. This term is of order O(L 2), i.e. does not deteriorate the approximation because the inaccuracy is of the same order.
Following the same procedure we can compute a symplectic approximation precise to order O(L 2) from (3.32) using:
It can be shown that this “symplectification” corresponds to the approximation of a quadrupole by a single kick in the centre between two drift spaces of length L∕2:
It may be mentioned that the previous approximation to 1st order corresponds to a kick at the end of a quadrupole, preceded by a drift space of length L. Both cases are illustrated in Fig. 3.1.

Schematic representation of a symplectic kick of first order (left) and second order (right)
One can try to further improve the approximation by adding 3 kicks like in Fig. 3.2 where the distance between kicks and the kick strengths are optimized to obtain the highest order. The thin lens approximation in Fig. 3.2 with the constants:
provides an O(L 4) integrator [11].
This process is a Symplectic Integration [12] and is a formal procedure to construct higher order integrators from lower order ones. From a 2nd order scheme (1 kick) S 2(t) we construct a 4th order scheme (3 kicks = 3 × 1 kick) like: S 4(t) = S 2(x 1 t) ∘ S 2(x 0 t) ∘ S 2(x 1 t) with:
In general: If S 2k(t) is a symmetric integrator of order 2k, then we obtain a symmetric integrator of order 2k + 2 by: S 2k+2(t) = S 2k(x 1 t) ∘ S 2k(x 0 t) ∘ S 2k(x 1 t) with:
Higher order integrators can be obtained in a similar way in an iterative procedure. A very explicit example of the iterative construction of a higher order map from a lower order can be found in [7].
This method can be applied to any other non-linear map and we obtain the same integrators. The proof of this statement and the systematic extension can be done in the form of Lie operators [12].
It should be noted that higher order integrators require maps which drift backwards (3.38) as shown in Fig. 3.2 right. This has two profound consequences. First, a straightforward “physical” interpretation of thin lens models representing drifts and individual small “magnets” (a la MAD) makes no sense and prohibits the use of high order integrators. Secondly, models which require self-consistent time tracking or s tracking (e.g. space charge calculations) must use integrators for which s(t) is monotonic in the magnets.
3.6.3.4 Comparison Symplectic Versus Non-symplectic Integration
A demonstration of a non-symplectic tracking is shown in Fig. 3.3. A particle is tracked through a quadrupole and the poincare section is shown. A quadrupole is chosen because it allows a comparison with the exact solution. The non-symplecticity causes the particle to spiral outwards. As comparison to the exact tracking is shown. In Fig. 3.3 (right) the symplectic integrators of order 1 and 2 as derived above are used instead. The trajectory is now constant and the difference to the exact solution is small. Although the model is approximated but symplectic, the underlying physics (i.e. constant energy in this case) is correct at the expense of a small discrepancy with respect to the exact solution.
3.7 Hamiltonian Treatment of Electro-Magnetic Fields
A frequently asked question is why one should not just use Newton’s laws and the Lorentz force. Some of the main reasons are:
-
Newton requires rectangular coordinates and time, trajectories with e.g. “curvature” or “torsion” need to introduce “reaction forces”. (For example: LHC has locally non-planar (cork-screw) “design” orbits!).
-
For linear dynamics done by ad hoc introduction of new coordinate frame.
-
With Hamiltonian it is free: The formalism is “coordinate invariant”, i.e. the equations have the same form in every coordinate system.
-
The basic equations ensure that the phase space is conserved
3.7.1 Lagrangian of Electro-Magnetic Fields
3.7.1.1 Lagrangian and Hamiltonian
It is common practice to use q for the coordinates when Hamiltonian and Lagrangian formalisms are used. This is deplorable because q is also used for particle charge.
The motion of a particle is usually described in classical mechanics using the Langrange functional:
where q 1(t), …q n(t) are generalized coordinates and \(\dot {q_{1}}(t),\ldots \dot {q_{n}}(t)\) the corresponding generalized velocities. Here q i can stand for any coordinate and any particle, and n can be a very large number.
The integral
defines the action S.
The action S is used with the Hamiltonian principle: a system moves along a path such that the action S becomes stationary, i.e. δS = 0
Is fulfilled when:
It is unfortunate that the term action is used in different contexts and must not be confused with the action-angle variables defined earlier. The action above is a functional rather than a variable.
Without proof or derivation it should be stated that L = T − V = kinetic energy −potential energy.
Given the Lagrangian, the Hamiltonian can be derived as:
The coordinates q i are identical to those in the Lagrangian (3.41), whereas the conjugate momenta p i are derived from L as:
3.7.2 Hamiltonian with Electro-Magnetic Fields
Readers only interested in the final result can skip Eqs. (3.46)–(3.54).
A key for the correct Hamiltonian is the relativistic treatment. An intuitive derivation is presented here, a simpler and elegant derivation should be based on 4-vectors [13]. The action S must be a relativistic invariant and becomes (now using coordinates x and velocities v):
since the proper time τ is Lorentz invariant, and therefore also γ ⋅ L.
The Lagrangian for a free particle is usually a function of the velocity (see classical formula of the kinematic term), but must not depend on its position.
The only Lorentz invariant with the velocity is [13]:
where U is the four-velocity.
For the Lagrangian of a (relativistic) free particle we must write
Using for the electromagnetic Lagrangian a form (without derivation, any textbook):
Combining (3.48) and (3.49) we obtain the complete Lagrangian:
thus the conjugate momentum is derived as:
where \(\vec {p}\) is the ordinary kinetic momentum.
A consequence is that the canonical momentum cannot be written as:
Using the conjugate momentum the Hamiltonian takes the simple form:
The Hamiltonian must be a function of the conjugate variables P and x and after a bit of algebra one can eliminate \(\vec {v}\) using:
With (3.50) and (3.54) we write for the Hamiltonian for a (ultra relativistic, i.e. γ ≫ 1, β ≈ 1) particle in an electro-magnetic field is given by:
where \(\vec {A}(\vec {x}, t)\), \(\Phi (\vec {x}, t)\) are the vector and scalar potentials.
Interlude 2
A short interlude,one may want to skip to Eq.(3.60)
Equation (3.55) is the total energy Eof the particle where the difference is the potential energy eϕ and the new conjugate momentum \(\vec {P}~=~(\vec {p}~-~\frac {e}{c}\vec {A})\) , replacing \(\vec {p}\).
From the classical expression
one can re-write
The expression (mc 2)2 is the invariant mass [ 13 ], i.e.
with the 4-vector for the momentum [ 13 ]:
The changes are a consequence using 4-vectors in the presence of electromagnetic fields (potentials).
An interesting consequence of (3.51) is that the momentum is linked to the fields (\(\vec {A}\)) and the angle x′ cannot easily be derived from the total momentum and the conjugate momentum. That is using (x, x′) as coordinate are strictly speaking not valid in the presence of electromagnetic fields.
In this context using (x, x′) or (x, p x) is not equivalent. A general, strong statement that (x, x′) is used in accelerator physics is at best bizarre.
3.7.3 Hamiltonian Used for Accelerator Physics
In a more convenient (and useful) form, using canonical variables x and p x, p y and the design path length s as independent variable (bending field B 0 in y-plane) and no electric fields (for details of the derivation see [14]):
where \(p~=~\sqrt {E^{2}/c^{2}~-~m^{2}c^{2}}\) total momentum, δ = (p − p 0)∕p 0 is relative momentum deviation and A s(x, y) (normalized) longitudinal (along s) component of the vector potential. Only transverse field and no electric fields are considered.
After square root expansion and sorting the A s contributions:
-
The Hamiltonian describes the motion of a particle through an element
-
Each element has a component in the Hamiltonian
-
Basis to extend the linear to a nonlinear formalism
A short list of Hamiltonians of some machine elements (3D)
In general for multipoles of order n:
We get for some important types (normal components k n only):
Interlude 3
A few remarks are required after this list of Hamiltonian for particular elements.
-
Unlike said in many introductory textbooks and lectures, a multipole of order n is not required to drive a nth order resonance—nothing could be more wrong!!
-
In leading order perturbation theory, only elements with an even order (and larger than 2) in the Hamiltonian can produce an amplitude dependent tune shift and tune spread.
3.7.3.1 Lie Maps and Transformations
In this chapter we would like to introduce Lie algebraic tools and Lie transformations [15,16,17]. We use the symbol z i = (x i, p i) where x and p stand for canonically conjugate position and momentum. We let f(z) and g(z) be any function of x, p and can define the Poisson bracket for a differential operator [18]:
Assuming that the motion of a dynamic system is defined by a Hamiltonian H, we can now write for the equations of motion [18]:
If H does not explicitly depend on time then:
implies that f is an invariant of the motion. To proceed, we can define a Lie operator : f : via the notation:
where : f : is an operator acting on the function g.
We can define powers as:
One can collect a set of useful formulae for calculations:
Some common special (very useful) cases for f:
Once powers of the Lie operators are defined, they can be used to formulated an exponential form:
This expression is call a “Lie transformation”.
Give the Hamiltonian H of an element, the generator f is this Hamiltonian multiplied by the length L of the element.
To evaluate a simple example, for the case H = −p 2∕2 using the exponential form and (3.75):
One can easily verify that for 1D and δ = 0 this is the transformation of a drift space of length L (if p ≈ x′) as introduced previously. The function f(x, p) = −Lp 2∕2 is the generator of this transformation.
Interlude 4
The exact Hamiltonian in two transverse dimensions and with a relative momentum deviation δis (full Hamiltonian with \(\vec {A}(\vec {x}, t)\) = 0):
The exact map for a drift space is now:
In 2D and with δ ≠ 0it is more complicated than Eq.(3.78). In practice the map can (often) be simplified to the well known form.
More general, acting on the phase space coordinates:
is the Lie transformation which describes how to go from one point to another.
While a Lie operator propagates variables over an infinitesimal distance, the Lie transformation propagates over a finite distance.
To illustrate this technique with some simple examples, it can be shown easily, using the formulae above, that the transformation:
corresponds to the map of a thin quadrupole with focusing length f, i.e.
A transformation of the form:
corresponds to the map of a thick quadrupole with length L and strength k:
The linear map using Twiss parameters in Lie representation (we shall call it : f 2 : from now on) is always of the form:
In case of a general non-linear function f(x), i.e. with a (thin lens) kick like:
the corresponding Lie operator can be written as:
An important property of the Lie transformation is that the one turn map is the exponential of the effective Hamiltonian and the circumference C:
The main advantages of Lie transformations are that the exponential form is always symplectic and that a formalism exists for the concatenation of transformations. An overview of this formalism and many examples can be found in [7]. As for the Lie operator, one can collect a set of useful formulae. Another neat package with useful formulae:
With a constant and f, g, h arbitrary functions:
and very important:
3.7.3.2 Concatenation of Lie Transformations
The concatenation is very easy when f and g commute (i.e. [f, g] = [g, f] = 0) and we have:
The generators of the transformations can just be added.
To combine two transformations in the general case (i.e. [f, g] ≠ 0) we can use the Baker–Campbell–Hausdorff formula (BCH) which in our convention can be written as:
In many practical cases, non-linear perturbations are localized and small compared to the rest of the (often linear) ring, i.e. one of f or g is much smaller, e.g. f corresponds to one turn, g to a small, local distortion.
In that case we can sum up the BCH formula to first order in the perturbation g and get:
When g is small compared to f, the first order is a good approximation.
For example, we may have a full ring \(e^{:f_{2}:}\) with a small (local) distortion, e.g. a multipole e :g: with g = kx n then the expression:
allows the evaluation of the invariant h for a single multipole of order n in this case.
In the case that f 2, f 3, f 4, are 2nd, 3rd, 4th order polynomials (Dragt-Finn factorization [19]):
each term is symplectic and the truncation at any order does not violate symplecticity.
One may argue that this method is clumsy when we do the analysis of a linear system. The reader is invited to prove this by concatenating by hand a drift space and a thin quadrupole lens. However, the central point of this method is that the technique works whether we do linear or non-linear beam dynamics and provides a formal procedure. Lie transformations are the natural extension of the linear matrix formalism to a non-linear formalism. There is no need to move from one method to another as required in the traditional treatment.
In the case an element is described by a Hamiltonian H, the Lie map of an element of length L and the Hamiltonian H is:
For example, the Hamiltonian for a thick sextupole is:
To find the transformation we search for:
We can compute:
to get:
Putting the terms together one obtains:
3.7.4 Analysis Techniques: Poincare Surface of Section
Under normal circumstances it is not required to examine the complete time development of a particle trajectory around the machine. Given the experimental fact that the trajectory can be measured only at a finite number of positions around the machine, it is only useful to sample the trajectory periodically at a fixed position. The plot of the rate of change of the phase space variables at the beginning (or end) of each period is the appropriate method and also known as Poincare Surface of Section [20]. An example of such a plot is shown in Fig. 3.4 where the one-dimensional phase space is plotted for a completely linear machine (Fig. 3.4, left) and close to a 5th order resonance in the presence of a single non-linear element (in this case a sextupole) in the machine (Fig. 3.4, right).
It shows very clearly the distortion of the phase space due to the non-linearity, the appearance of resonance islands and chaotic behaviour between the islands. From this plot is immediately clear that the region of stability is strongly reduced in the presence of the non-linear element. The main features we can observe in Fig. 3.4 are that particles can:
-
Move on closed curves
-
Lie on islands, i.e. jump from one island to the next from turn to turn
-
Move on chaotic trajectories
The introduction of these techniques by Poincare mark a paradigm shift from the old classical treatment to a more modern approach. The question of long term stability of a dynamic system is not answered by getting the solution to the differential equation of motion, but by the determination of the properties of the surface where the motion is mapped out. Independent how this surface of section is obtained, i.e. by analytical or numerical methods, its analysis is the key to understand the stability.
3.7.5 Analysis Techniques: Normal Forms
The idea behind this technique is that maps can be transformed into Normal Forms. This tool can be used to:
-
Study invariants of the motion and the effective Hamiltonian
-
Extract non-linear tune shifts (detuning)
-
Perform resonance analysis
In the following we demonstrate the use of normal forms away from resonances. The treatment of the beam dynamics close to resonances is beyond the scope of this review and can be found in the literature (see e.g. [6, 7]).
3.7.5.1 Normal Form Transformation: Linear Case
The strategy is to make a transformation to get a simpler form of the map M, e.g. a pure rotation R( Δμ) as schematically shown in Fig. 3.5 using a transformation like:
with
This transformation corresponds to the Courant-Snyder analysis in the linear case and directly provides the phase advance and optical parameters. The optical parameters emerge automatically from the normal form analysis of the one-turn-map.
Although not required in the linear case, we demonstrate how this normal form transformation is performed using the Lie formalism. Starting from the general expression:
we know that a linear map M in Lie representation is always:
therefore:
and (with U −1 f 2) f 2 expressed in the new variables X, P x it assumes the form:
i.e. with the transformation U −1 the rotation : f 2 : becomes a circle in the transformed coordinates. We transform to action and angle variables J and Φ, related to the variables X and P x through the transformations:
With this transformation we get a simple representation for the linear transfer map f 2:
3.7.5.2 Normal Form Transformation: Non-linear Case
In the more general, non-linear case the transformation is more complicated and one must expect that the rotation angle becomes amplitude dependent (see e.g. [6]). A schematic view of this scheme is shown in Fig. 3.6 where the transformation leads to the desired rotation, however the rotation frequency (phase advance) is now amplitude dependent.
We demonstrate the power by a simple example in one dimension, but the treatment is similar for more complex cases. In particular, it demonstrates that this analysis using the algorithm based on Lie transforms leads easily to the desired result. A very detailed discussion of this method is found in [6].
From the general map we have made a transformation such that the transformed map can be expressed in the form \(e^{:h_{2}:}\) where the function h 2 is now a function only of J x, J y, and δ and it is the effective Hamiltonian.
In the non-linear case and away from resonances we can get the map in a similar form:
where the effective Hamiltonian h eff depends only on J x, J x, and δ.
If the map for h eff corresponds to a one-turn-map, we can write for the tunes:
and the change of path length:
In the non-linear case, particles with different J x, J y, δ have different tunes. Their dependence on J x, J y is the amplitude detuning, the dependence on δ are the chromaticities.
The effective Hamiltonian can always be written (here to 3rd order) in a form:
and then tune depends on action J and momentum deviation δ:
The meaning of the different contributions are:
-
μ x, μ y: linear phase advance or 2π ⋅ i.e. the tunes for rings
-
\(\frac {1}{2}\alpha _{c}, c_{3}, c_{4}\): linear and nonlinear “momentum compaction”
-
c x1, c y1: first order chromaticities
-
c x2, c y2: second order chromaticities
-
c xx, c xy, c yy: detuning with amplitude
The coefficients are the various aberrations of the optics.
As a first example one can look at the effect of a single (thin) sextupole. The map is:
we get for h eff (see e.g. [6, 7]):
Then it follows:
Since it was developed to first order only, there is no non-linear detuning with amplitude.
As a second example one can use a linear rotation followed by an octupole, the Hamiltonian is:
The first part of the Hamiltonian corresponds to the generator of a linear rotation and the second part to the localized octupole.
The map, written in Lie representation becomes:
The purpose is now to find a generator F for a transformation
such that the exponents of the map depend only on J and not on x.
Without going through the algebra (advanced tools exist for this purpose, see e.g. [6]) we quote the result and with
we can write the map:
the term \({{\frac {3}{8} J^{2}}}\) implies a tune shift with amplitude for an octupole.
3.7.6 Truncated Power Series Algebra Based on Automatic Differentiation
It was argued that an appropriate technique to evaluate the behaviour of complex, non-linear systems is by numerically tracking through the individual elements. Schematically this is shown in Fig. 3.7 and the tracking through a complicated system relates the output numerically to the input. When the algorithm depicted in Fig. 3.7 represents the full turn in a ring, we obtained the most reliable one-turn-map through this tracking procedure, assuming we have chosen an appropriate representation of the maps for the individual elements.
3.7.6.1 Automatic Differentiation: Concept
This procedure may not be fully satisfactory in all cases and one might like to get an analytical expression for the one-turn-map or equivalent. Could we imagine something that relates the output algebraically to the input? This might for example be a Taylor series of the type:
Then we have an analytic map (for all z 1).
To understand why this could be useful, we can study the paraxial behaviour. In Fig. 3.8 we show schematically the trajectories of particles close to the ideal orbit. The red line refers to the ideal trajectory while the other lines show the motion of individual particles with small deviations from the ideal path. The idea is that if we understand how small deviations behave, we understand the system much better.
If we now remember the definition of the Taylor series:
we immediately realize that the coefficients determine the behaviour of small deviations Δx from the ideal orbit x. Therefore the Taylor expansion does a paraxial analysis of the system and the main question is how to get these coefficients without extra work?
The problem is getting the derivatives f (n)(a) of f(x) at a:
Numerically this corresponds to the need to subtract almost equal numbers and divide by a small number. For higher orders f″, f‴.., one must expect numerical problems. An elegant solution to this problem is the use of Differential Algebra (DA) [21].
3.7.6.2 Automatic Differentiation: The Algebra
Here we demonstrate the concept, for more details the literature should be consulted [6, 7, 21].
-
1.
Define a pair (q 0, q 1), where q 0, q 1 are real numbers
-
2.
Define operations on such pairs like:
$$\displaystyle \begin{aligned}~~~(q_{0}, q_{1})~{{+}}~(r_{0}, r_{1}) = (q_{0} + r_{0}, q_{1} + r_{1})\end{aligned} $$(3.133)$$\displaystyle \begin{aligned}~~~c~{{\cdot}}~(q_{0}, q_{1}) = (c\cdot q_{0}, c \cdot q_{1})\end{aligned} $$(3.134)$$\displaystyle \begin{aligned}~~~(q_{0}, q_{1})~{{\cdot}}~(r_{0}, r_{1}) = ( q_{0}\cdot r_{0}, q_{0}\cdot r_{1} + q_{1}\cdot r_{0})\end{aligned} $$(3.135) -
3.
We define the ordering like:
$$\displaystyle \begin{aligned}~~~(q_{0},q_{1}) < (r_{0},r_{1})~~~{\mathsf{if}}~~~ q_{0} < r_{0}~~~{\mathsf{or}}~~~(q_{0} = r_{0} ~~~{\mathsf{and}}~~~ q_{1} < r_{1})\end{aligned} $$(3.136)$$\displaystyle \begin{aligned}~~~(q_{0},q_{1}) > (r_{0},r_{1})~~~{\mathsf{if}}~~~ q_{0} > r_{0}~~~{\mathsf{or}}~~~(q_{0} = r_{0} ~~~{\mathsf{and}}~~~ q_{1} > r_{1})\end{aligned} $$(3.137) -
4.
This implies that:
$$\displaystyle \begin{aligned}~~~(0,0) < (0,1) < (r,0) ~~~({\mathsf{for~any}}~r)\end{aligned} $$(3.138)
This means that (0,1) is between 0 and ANY real number, i.e. it is infinitely small, corresponding to the “𝜖” in standard calculus.
Therefore we call this special pair “differential unit” d = (0, 1).
With our rules we can further see that:
In general the inverse of a function f(q 0, q 1) can de derived like:
using the multiplication rules. The inverse is then (r 0, r 1). For example:
gives for the inverse:
3.7.6.3 Automatic Differentiation: The Application
Of course (q, 0) is just the real number q and we define the “real” and the “differential part”:
For a function f(x) we have (without proof, see e.g. [21]):
We use an example instead to demonstrate this with the function:
Using school calculus we have for the derivative:
We now apply Automatic Differentiation instead. For the variable x in (3.145)
we substitute x → (x, 1) = (2, 1) and using our rules:
we arrive at a vector containing the differentials at x = 2. The computation of derivatives becomes an algebraic problem, without need for small numbers. No numerical difficulties are expected and the differential is exact.
3.7.6.4 Automatic Differentiation: Higher Orders
To obtain higher orders, we need higher derivatives, i.e. larger dimension for our vectors:
-
1.
The pair (q 0, 1), becomes a vector of length N and with equivalent rules:
$$\displaystyle \begin{aligned}(q_{0}, 1)~~\Rightarrow~~(q_{0}, 1, 0, 0, \ldots,0)\end{aligned} $$(3.147)$$\displaystyle \begin{aligned}(q_{0}, q_{1}, q_{2}, \ldots q_{N})~{{+}}~(r_{0}, r_{1}, r_{2}, \ldots r_{N}) = (s_{0}, s_{1}, s_{2}, \ldots s_{N})\end{aligned} $$(3.148)$$\displaystyle \begin{aligned}c~{{\cdot}}~(q_{0}, q_{1}, q_{2}, \ldots q_{N})~=~(c\cdot q_{0},c\cdot q_{1},c\cdot q_{2}, \ldots c\cdot q_{N})\end{aligned} $$(3.149)$$\displaystyle \begin{aligned}(q_{0}, q_{1}, q_{2}, \ldots q_{N})~{{\cdot}}~(r_{0}, r_{1}, r_{2}, \ldots r_{N})~=~(s_{0}, s_{1}, s_{2}, \ldots s_{N})\end{aligned} $$(3.150)with:
$$\displaystyle \begin{aligned}s_{i} = \sum_{k=0}^{i} \frac{i!}{k! (i-k)!} q_{k} r_{i-k}\end{aligned} $$(3.151)If we had started with:
$$\displaystyle \begin{aligned}~~~x = (a,1,0,0,0\ldots ) \end{aligned} $$(3.152)we would get:
$$\displaystyle \begin{aligned}~~~f(x) = (~f(a),~ f^{\prime}(a),~ f^{\prime\prime}(a),~ f^{\prime\prime\prime}(a), \ldots~ f^{(n)}(a)~) \end{aligned} $$(3.153)Some special cases are:
$$\displaystyle \begin{aligned} (x, 0, 0, 0, ..)^{n}~=~(x^{n}, 0, 0, 0, ..) {} \end{aligned} $$(3.154)$$\displaystyle \begin{aligned} (0, 1, 0, 0, ..)^{n}~=~(0, 0, 0, ..,{\overbrace{n!}^{n+1}}, 0, 0, ..) {} \end{aligned} $$(3.155)$$\displaystyle \begin{aligned} (x, 1, 0, 0, ..)^{2}~=~(x^{2}, 2x, 2, 0, ..) {} \end{aligned} $$(3.156)$$\displaystyle \begin{aligned} (x, 1, 0, 0, ..)^{3}~=~(x^{3}, 3x^{2}, 6x, 6, ..) {} \end{aligned} $$(3.157)As another exercise one can consider the function f(x) = x −3
\(f(x)~~\rightarrow ~~f(x, 1, 0, 0, ..)~~=~~{\underbrace {(x, 1, 0, 0, ..)^{-3}~~=~~(f_{0}, f^{\prime }f^{\prime \prime }, f^{\prime \prime \prime }, ..)}_{\textstyle \mathsf {next:~multiply~both~sides~with~(x, 1, 0, 0)^{3}}}}\)
(1, 0, 0, ..) = (x, 1, 0, 0, ..)3 ⋅ (f 0, f ′, f ′′, f ′′′, …)
(1, 0, 0, ..) = (x 3, 3x 2, 6x, 6, ..) ⋅ (f 0, f ′, f ′′, f ′′′, …) using (3.157)
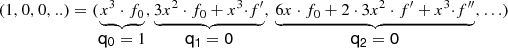
This can easily be solved by forward substitution:
$$\displaystyle \begin{aligned} \begin{array}{lll} 1~=~&x^{3}\cdot f_{0}~~~~~&\rightarrow~~~f_{0}~=~x^{-3} \\ 0~=~&3x^{2}\cdot f_{0}~~+~~x^{3}\cdot f^{\prime}~~~~~&\rightarrow~~~f^{\prime}~=~-3x^{-4}\\ 0~=~&6x\cdot f_{0}~~+~~2\cdot 3x^{2}\cdot f^{\prime}~~+~~{x^{3}}\cdot f^{\prime\prime}~~~~~&\rightarrow~~~f^{\prime\prime}~=~{12}{x^{-5}}\\ .... \end{array} \end{aligned} $$(3.158)Using the same procedure for f(x) = x −1 one obtains:
$$\displaystyle \begin{aligned} (x, 1, 0, 0, ..)^{-1}~=~(\frac{1}{x}. -\frac{1}{x^{2}}, \frac{2}{x^{3}}, \ldots ) {} \end{aligned} $$(3.159)For the function we have used before (3.145) :
$$\displaystyle \begin{aligned} f(x) = x^{2} + \frac{1}{x} \end{aligned} $$(3.160)and using (adding!) the expressions (3.156) and (3.159) one has:
$$\displaystyle \begin{aligned} (f_{0}, f^{\prime}, f^{\prime\prime}, f^{\prime\prime\prime})~~=~~(x^{2}~+~\frac{1}{x},~~~2x~-~\frac{1}{x^{2}},~~ 2~+~\frac{2}{x^{3}},~~ ..) \end{aligned} $$(3.161)
3.7.6.5 Automatic Differentiation: More Variables
It can be extended to more variables x, y and a function f(x, y):
and get (with more complicated multiplication rules):
3.7.6.6 Differential Algebra: Applications to Accelerators
Of course it is not the purpose of these tools to compute analytical expressions for the derivatives, the examples were used to demonstrate the techniques. The application of these techniques (i.e. Truncated Power Series Algebra [6, 21]) is schematically shown in Fig. 3.9. Given an algorithm, which may be a complex simulation program with several thousands of lines of code, we can use the techniques to “teach” the code how to compute the derivatives automatically.
When we push f(x) = (a, 1, 0, 0, 0…) through the algorithm, using our rules, we get all derivatives around a, i.e. we get the Taylor coefficients and can construct the map!
What is needed is to replace the standard operations performed by the computer on real numbers by the algebra defined above. The maps are provided with the desired accuracy and to any order.
Given a Taylor series to high accuracy, the wanted information about stability of the system, global behaviour and optical parameters can be derived more easily. It should be stressed again that the origin is the underlying tracking code, just acting on different data types with different operations.
3.7.6.7 Differential Algebra: Simple Example
A simple example is shown below where the original “tracking code” is shown in the left column (DATEST1) and the corresponding modified code in the right column (DATEST2). The operation is rather trivial to demonstrate the procedure more easily. The code is written in standard FORTRAN 95 which allows operator overloading, but an object oriented language such as C+ + or Python are obviously well suited for this purpose. Standard FORTRAN-95 is however more flexible overloading arbitrary operations. The DA-package used for demonstration only is loaded by the command use my_own_da in the code. To make the program perform the wanted operation we have to make two small modifications:
-
1.
Replace the types real by the type my_taylor (defined in the package).
-
2.
Add the “differential unit” (0, 1), the monomial in this implementation to the variable.


Running these two programs we get the results in the two columns below. In the left column we get the expected result from the real calculation of the expression \(\sin {}(\pi /6))\) = 0.5, while in the right column we get additional numbers sorted according to the array index.


The inspection shows that these numbers are the coefficients of the Taylor expansion of \(\sin {}(x)\) around x = π∕6:
We have indeed obtained the derivatives of our “algorithm” through the tracking code.
Some examples related to the analysis of accelerator physics lattices.
In example 1 a lattice with 8 FODO cells is constructed and the quadrupole is implemented as a thin lens “kick” in the center of the element. Note that the example is implemented in the horizontal and the longitudinal planes. For the second example an octupole kick is added to demonstrate the correct computation of the non-linear effect, i.e. the detuning with amplitude.
The procedure is:
-
1.
Track through the lattice and get Taylor coefficients
-
2.
Produce a map from the coefficients
-
3.
Perform a Normal Form Analysis on the map












Defined assignments:
-
M = z, constructs a map M using the coefficients z
-
NORMAL = M, computes a normal form NORMAL using the map M
-
In FORTRAN95 derived “type” plays the role of “structures” in C, and NORMAL contains:
-
NORMAL%tune is the tune Q
-
NORMAL%dtune_da is the detuning with amplitude \(\frac {dQ}{da}\)
-
NORMAL%R, NORMAL%A, NORMAL%A**-1 are the matrices
-
such that: M = A R A−1
-
from the normal form transformation one obtains α, β, γ …
Below a comparison is shown in Fig. 3.10 using the lattice function (e.g. β) obtained with this procedure and the optical functions from the corresponding MAD-X output.
One finds that β max ≈ 300 m, β min ≈ 170 m and perfect agreement.
3.8 Beam Dynamics with Non-linearities
Following the overview of the evaluation and analysis tools, it is now possible to analyse and classify the behaviour of particles in the presence of non-linearities. The tools presented beforehand allow a better physical insight to the mechanisms leading to the various phenomena, the most important ones being:
-
Amplitude detuning
-
Excitation of non-linear resonances
-
Reduction of dynamic aperture and chaotic behaviour.
This list is necessarily incomplete but will serve to demonstrate the most important aspects.
To demonstrate these aspects, we take a realistic case and show how the effects emerge automatically.
3.8.1 Amplitude Detuning
It was discussed in Sect. 3.7.5 that the one-turn-map can be transformed into a simpler map where the rotation is separated. A consequence of the non-linearities was that the rotation frequency becomes amplitude dependent to perform this transformation. Therefore the amplitude detuning is directly obtained from this normal form transformation.
3.8.1.1 Amplitude Detuning due to Non-linearities in Machine Elements
Non-linear elements cause an amplitude dependent phase advance. The computational procedure to derive this detuning was demonstrated in the discussion on normal for transformations in the case of an octupole Eqs. (3.125) and (3.129). This formalism is valid for any non-linear element.
Numerous other examples can be found in [6] and [5].
3.8.1.2 Amplitude Detuning due to Beam–Beam Effects
For the demonstration we use the example of a beam-beam interaction because it is a very complex non-linear problem and of large practical importance [7, 22].
In this simplest case of one beam-beam interaction we can factorize the machine in a linear transfer map \(e^{:f_{2}:}\) and the beam-beam interaction e :F:, i.e.:
with
where μ is the overall phase, i.e. the tune Q multiplied by 2π, and β is the β-function at the interaction point. We assume the waist of the β-function at the collision point (α = 0). The function F(x) corresponds to the beam-beam potential (3.87):
For a round Gaussian beam we use for f(x) the well known expression:
Here N is the number of particles per bunch, r 0 the classical particle radius, γ the relativistic parameter and σ the transverse beam size.
For the analysis we examine the invariant h which determines the one-turn-map (OTM) written as a Lie transformation e :h:. The invariant h is the effective Hamiltonian for this problem.
As usual we transform to action and angle variables J and Φ, related to the variables x and p x through the transformations:
With this transformation we get a simple representation for the linear transfer map f 2:
The function F(x) we write as Fourier series:
For the evaluation of (3.172) see [7]. We take some useful properties of Lie operators (e.g. [6, 7]):
and the CBH-formula for the concatenation of the maps (3.92):
which gives immediately for h:
Equation (3.175) is the beam-beam perturbed invariant to first order in the perturbation using (3.92).
From (3.175) we observe that for \(\textstyle {\nu ~= \frac {\mu }{2\pi } = \frac {p}{n}}\) resonances appear for all integers p and n when c n(J) ≠ 0.
Away from resonances a normal form transformation gives:
and the oscillating term disappears. The first term is the linear rotation and the second term gives the amplitude dependent tune shift (see (3.114)):
The computation of this tuneshift from the equation above can be found in the literature [7, 23].
3.8.1.3 Phase Space Structure
To demonstrate how this technique can be used to reconstruct the phase space structure in the presence of non-linearities, we continue with the very non-linear problem of the beam-beam interaction treated above. To test our result, we compare the invariant h to the results of a particle tracking program.
The model we use in the program is rather simple:
-
linear transfer between interactions
-
beam-beam kick for round beams
-
compute action \(\textstyle {J~=~\frac {\beta ^{*}}{2 \sigma ^{2}}(\frac {x^{2}}{\beta ^{*}} + p_{x}^{2}\beta ^{*})}\)
-
compute phase \(\Phi ~=~{\mathsf {arctan}}(\frac {p_{x}}{x})\)
-
compare J with h as a function of the phase Φ
The evaluation of the invariant (3.175) is done numerically with Mathematica. The comparison between the tracking results and the invariant h from the analytical calculation is shown in Fig. 3.11 in the (J,Φ) space. One interaction point is used in this comparison and the particles are tracked for 1024 turns. The symbols are the results from the tracking and the solid lines are the invariants computed as above. The two figures are computed for amplitudes of 5 σ and 10 σ. The agreement between the models is excellent. The analytic calculation was done up to the order N = 40. Using a lower number, the analytic model can reproduce the envelope of the tracking results, but not the details. The results can easily be generalized to more interaction points [22]. Close to resonances these tools can reproduce the envelope of the phase space structure [22].
Comparison: numerical and analytical model for one interaction point. Shown for 5σ x (left) and 10σ x (right). Full symbols from numerical model and solid lines from invariant (3.175)
3.8.2 Non-linear Resonances
Non-linear resonances can be excited in the presence of non-linear fields and play a vital role for the long term stability of the particles.
3.8.2.1 Resonance Condition in One Dimension
For the special case of the beam-beam perturbed invariant (3.175) we have seen that the expansion (3.175) diverges when the resonance condition for the phase advance is fulfilled, i.e.:
The formal treatment would imply to use the n-turn map with the n-turn effective Hamiltonian or other techniques. This is beyond the scope of this handbook and can be found in the literature [6, 7]. We should like to discuss the consequences of resonant behaviour and possible applications in this section.
3.8.2.2 Driving Terms
The treatment of the resonance map is still not fully understood and a standard treatment using first order perturbation theory leads to a few wrong conclusions. In particular it is believed that a resonance cannot be excited unless a driving term for the resonance is explicitly present in the Hamiltonian. This implies that the related map must contain the term for a resonance in leading order to reproduce the resonance. This regularly leads to the conclusion that 3rd order resonances are driven by sextupoles, 4th order are driven by octupoles etc. This is only a consequence of the perturbation theory which is often not carried beyond leading order, and e.g. a sextupole can potentially drive resonances of any order. Such a treatment is valid only for special operational conditions such as resonant extraction where strong resonant effects can be well described by a perturbation theory. A detailed discussion of this misconception is given in [6]. A correct evaluation must be carried out to the necessary orders and the tools presented here allow such a treatment in an easier way.
3.8.3 Chromaticity and Chromaticity Correction
For reasons explained earlier, sextupoles are required to correct the chromaticities. In large machines and in particular in colliders with insertions, these sextupoles dominate over the non-linear effects of so-called linear elements.
3.8.4 Dynamic Aperture
Often in the context of the discussion of non-linear resonance phenomena the concept of dynamic aperture in introduced. This is the maximum stable oscillation amplitude in the transverse (x, y)-space due to non-linear fields. It must be distinguished from the physical aperture of the vacuum chamber or other physical restrictions such as collimators.
One of the most important tasks in the analysis of non-linear effects is to provide answers to the questions:
-
Determination of the dynamic aperture
-
Maximising the dynamic aperture
The computation of the dynamic aperture is a very difficult task since no mathematical methods are available to calculate it analytically except for the trivial cases. Following the concepts described earlier, the theory is much more complete from the simulation point of view. Therefore the standard approach to compute the dynamic aperture is done by numerical tracking of particles.
The same techniques can be employed to maximise the dynamic aperture, in the ideal case beyond the limits of the physical aperture. Usually one can define tolerances for the allowed multipole components of the magnets or the optimized parameters for colliding beams when the dominant non-linear effect comes from beam-beam interactions.
3.8.4.1 Long Term Stability and Chaotic Behaviour
In accelerators such as particle colliders, the beams have to remain stable for many hours and we may be asked to answer the question about stability for as many as 109 turns in the machine. This important question cannot be answered by perturbative techniques. In the discussion of Poincare surface-of-section we have tasted the complexity of the phase space topology and the final question is whether particles eventually reach the entire region of the available phase space.
It was proven by Kolmogorov, Arnol’d and Moser (KAM theorem) that for weakly perturbed systems invariant surfaces exist in the neighbourhood of integrable ones. Poincare gave a first hint that stochastic behaviour may be generated in non-linear systems. In fact, higher order resonances change the topology of the phase space and lead to the formation of island chains on an increasingly fine scale. Satisfactory insight to the fine structure of the phase space can only be gained with numerical computation. Although the motion near resonances may be stochastic, the trajectories are constrained by nearby KAM surfaces (at least in one degree of freedom) and the motion remains confined.
3.8.4.2 Practical Implications
In numerical simulations where particles are tracked for millions of turns we would like to determine the region of stability, i.e. dynamic aperture. Since we cannot track ad infinitum, we have to specify criteria whether a particle is stable or not. A straightforward method is to test the particle amplitudes against well defined apertures and declare a particle lost when the aperture is reached. A sufficient number of turns, usually determined by careful testing, is required with this method.
Usually this means to find the particle survival time as a function of the initial amplitude. In general the survival time decreases as the amplitude increases and should reach an asymptotic value at some amplitude. The latter can be identified as the dynamic aperture.
Other methods rely on the assumption that a particle that is unstable in the long term, exhibits features such as a certain amount of chaotic motion.
Typical methods to detect and quantify chaotic motion are:
In all cases care must be taken to avoid numerical problems due to the computation techniques when a simulation over many turns is performed.
References
W. Herr, Mathematical and Numerical Methods for Nonlinear Dynamics Proc. CERN Accelerator School: Advanced Accelerator Physics (2013), published as CERN Yellow Report CERN-2014-009, arXiv:1601.07311.
E. Courant and H. Snyder, Theory of the Alternating Gradient Synchrotron, Ann. Phys. 3 (1958) 1.
A. Wolski, Beam Dynamics in High Energy Particle Accelerators, Imperial College Press (2014).
H. Wiedemann, Particle Accelerator Physics—basic Principles and Linear Beam Dynamics, Springer-Verlag (1993).
A. Chao and M. Tigner, Handbook of Accelerator Physics and Engineering, World Scientific (1998).
E. Forest, Beam Dynamics, Harwood Academic Publishers (1998).
A. Chao, Lecture Notes on Topics in Accelerator Physics, SLAC (2001).
A. Dragt, Lie Methods for Nonlinear Dynamics with Applications to Accelerator Physics, in preparation, Univ. of Maryland (Nov. 2019). https://www.physics.umd.edu/dsat/dsatliemethods.html.
E. Courant and R. Ruth, Stability in Dynamical Systems, Summer School on High Energy Particle Accelerators, Upton, New York, July 6–16, 1983.
A. Dragt and E. Forest, Computation of Nonlinear Behaviour of Hamiltonian Systems using Lie Algebraic Methods, J.Math.Phys. 24, 2734 (1983).
E. Forest and R. Ruth, Physica D43, (1990) 105.
H. Yoshida, Phys. Lett A150 (1990) 262.
W. Herr, Relativity, lecture at CAS-CERN Accelerator School on “Introduction to accelerator Physics”, Budapest, Hungary (2016).
S. Sheehy, Motion of Particles in Electro-magnetic Fields, lecture at CAS-CERN Accelerator School on “Introduction to accelerator Physics”, Budapest, Hungary (2016).
A. Dragt, AIP Proc. 87, Phys. High Energy Accelerators, Fermilab, (1981) 147.
A. Dragt et al., Ann. Rev. Nucl. Part. Sci 38 (1988) 455.
A. Dragt et al, Phys. Rev. A45, (1992) 2572.
H. Goldstein, Classical Mechanics, Addison Wesley, (2001).
A. Dragt and J. Finn, J. Math. Phys., 17, 2215 (1976); A. Dragt et al., Ann. Rev. Nucl. Part. Sci., 38, 455 (1988).
H. Poincare, Les Methods Nouvelles de la Mecanique Celeste, Gauthier-Villars, Paris (1892).
M. Berz, Particle Accelerators 24, (1989) 109.
W. Herr, D. Kaltchev, Effect of phase advance between interaction points in the LHC on the beam-beam interaction, LHC Project Report 1082, unpublished, (2008).
T. Pieloni, A Study of Beam-Beam Effects in Hadron Colliders with a Large Number of Bunches, PhD thesis Nr. 4211, EPFL Lausanne, (2008).
H.S. Dumas, J. Laskar, Phys. Rev. Lett. 70 (1989) 2975.
J. Laskar, D. Robin, Particle Accelerators 54 (1996)183.
G. Benettin et al., Phys. Rev. A14 (1976) 2338.
B.V. Chirikov, At. Energ. 6, (1959) 630.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this chapter
Cite this chapter
Herr, W., Forest, E. (2020). Non-linear Dynamics in Accelerators. In: Myers, S., Schopper, H. (eds) Particle Physics Reference Library . Springer, Cham. https://doi.org/10.1007/978-3-030-34245-6_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-34245-6_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34244-9
Online ISBN: 978-3-030-34245-6
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)