Keywords

1 Introduction and Rationale

Technology is almost everywhere in our lives and there is no process, even educational, that does not deal with it. Moreover, technological resources have been combined with already existing instrumental resources and used in didactic practices supporting the construction of mathematical meanings. In recent years, a considerable corpus of research has focused on the ways in which technologies can influence mathematics learning, in particular how technology could offer new ways to interact with mathematical thinking and generate new kinds of mathematical experiences for students [1,2,3]. However, the digital technologies do not eliminate the need of a synergic relationship between all the educational artefacts, each of them bringing different possibilities and supporting the process of incorporation and conceptualization in a different way [4,5,6,7,8].

Moreover, one of the mathematical topics that need to be supported by artefact is the geometric transformation. In Italy, as in other countries, geometric transformations appear in the curriculum, at different school levels, nevertheless, they do not receive much attention by teachers. Also, in math research geometric transformation has not been a popular topic. More recently, the advent of new technologies and specific micro world for Geometry brought this topic to the forefront, mainly at secondary school level [9].

We think that geometric transformations can become a powerful and effective tool in solving geometrical problems only if they are introduced in a mathematically consistent way, in other terms, if intuitive meanings emerging from actions and observation are suitably formalized into appropriate and well defined mathematical properties.

On the basis of a recent research on the use of two artefacts for the construction of the axial symmetry meaning [10], we report a study that aims to highlight the potentialities of the combined use of both digital and manipulative artefacts for the construction of the meaning of the translation. The study design is based on the Theory of Semiotic Mediation (TMS), developed by Bartolini Bussi and Mariotti [11] in a Vygotskijan perspective, which deals with the complex system of semiotic relations among fundamental elements involved in the use of artefacts to construct mathematical meanings: the artefact, the task, the mathematical knowledge that is the subject of the activity, and the teaching/learning processes that take place in the class.

Our didactic assumption claims that the process of formalization characterizing a geometrical transformation, such as the translation, can be achieved through the mediation of specific artefacts. The TSM provides a reference for the design and the implementation of a teaching sequence, as well as the analysis of the data resulting from the experiment.

The research hypothesis of our study is that, during the resolution of a translation task, the alternating use of a digital and a manipulative artefact generates in students a cognitive interaction between the schema use of one of the two artefacts and the signs exhibited while using the other artefact. This fosters a suitable and coherent construction of the translation meaning and its properties.

In this paper we present the design and implementation of a teaching experiment centered on the combined use of two artefacts. We will focus on the role played by the theoretical frame analyzing the key moments of the teaching sequence where the combination between the two artefacts was assumed to trigger the unfolding of the expected mathematical meanings. The study involved a class of 20 students, aged 13–14, of a Secondary School in the Apulia Region, Italy.

Our research is framed in a broader projection that, exploiting the teaching experimental methodology, it aims at validating the hypothesis regarding the possible synergic effect of the use of the two artefacts [10, 12].

2 Geometric Notion of Translation

The geometric concept referred to is that of translation. It is understood as an isometric transformation of the plane itself. Specifically, it is intended to point out that the translation is a point-to-point correspondence between points of the plane. Therefore it is the domain of the function, which transforms straight lines into congruent/super imposable segments. It also keeps the parallelism and the width of the angles.

Moreover, closer attention will be paid to the properties of the translation through which it is possible to construct the translated point of a given point with respect to a vector, i.e. the parallelism between the joining of the corresponding points and the direction of the vector as well as the preservation of the distance between the point and its translation, and the form of the vector.

3 Theoretical Framework

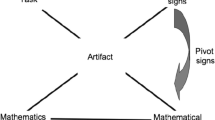
According to Vygotskian view, the Theory of Semiotic Mediation (TSM) concerns the complex system of semiotic relations between the elements taking part in the construction of mathematical meanings through the use of artefacts: the artefact, the task the artefact is used in, the mathematical knowledge which is the objective of the didactic intervention and the teaching/learning processes that take place in the classroom [11].

The concept of artefact used here is consistent with the distinction between artefact and instrument that was introduced by Rabardel [13] and re-elaborated by Bartolini Bussi and Mariotti [11]: an artefact is any device created and realized by human beings for any objective. The notion of artefact and that of schema of utilization [13] is the main focus of the TSM’s construct of semiotic potential, that is the twofold relationship that the artefact has with the personal meanings emerging from its use and the mathematical meanings that might be evoked by such use:

[…] on the one hand, personal meanings are related to the use of the artefact, in particular in relation to the aim of accomplishing the task; on the other hand, mathematical meanings may be related to the artefact and its use. This double semiotic relationship will be named the semiotic potential of an artefact [11, p. 754].

The study of the semiotic potential will describe what could emerge in the classroom, in particular actions and signs produced by the student and its relationship with the mathematical meanings. This is why, it is the main focus of any teaching sequence and it is the fundamental reference for the analysis of any experimental realization of the didactic intervention. In particular, meanings related to the use of the artefact can be referred to the schema of utilization that is shown by the students during a specific task. Consequently, the design of the tasks develops on the base of a fine grain a-priori analysis of the solution processes, and specifically on the identification of the schema of utilization that are expected. According to the TSM, during semiotic activities various signs are produced.

Personal meanings are expressed by the “artefact signs”, that often have a highly subjective nature and are linked to the learner’s specific experience with the artefact and the task to be carried out; these signs may evolve into mathematical meanings expressed by the “mathematics signs”; finally the “pivot signs”, with their hybrid nature, show the evolution between artefact signs and mathematics signs, through the linked meanings. Such an evolution can occur together with specific semiotic activities, in particular, in the peer interaction during the task and in the collective discussions, accompanied by the expert guidance of the teacher. The collective construction of shared mathematical meanings is a complex process, where it is possible to distinguish evolution paths (semiotic chains) described by the appearance and chain of different types of signs: artefact signs, mathematical signs and pivot signs [11].

Finally, the notion of didactic cycle [11, p. 754] constitutes the unit of design: the didactic cycle organizes the coordination between activities with the artefact and semiotic activities finalized to make the expected evolution of signs occur. According to this structure, the description of the sequence will be framed by an iteration of didactic cycles.

4 The Artefacts

As described above, a digital and a manipulative artefact have been employed.

The digital artefact is Geogebra (GG) with some specific tools that correspond to particular elements of the manipulative artefact. To be more specific, the tools chosen are those that allow the construction of some geometric objects (point, straight line, segment, vector, perpendicular and parallel line, and intersection point), the ‘Translation’ artefact and the ‘Trace’ tool. A very important role is also played by the dragging function, boosted by the ‘Trace’ tool that allows observing the invariance of the properties characterizing the figures.

The manipulative artefact consists of a sheet of paper, with a vector line drawn on it marking where to fold it, a transparent sheet of paper used to copy the initial figures and a pin used to pierce both the sheets at the right points in order to construct their translated points (Pa+T+Pi). This artefact allows a translation to be directly created because the sheet naturally models the plane, the transparent sheet of paper allows moving the figure on the plane and sliding the transparent sheet allows the production of translated points using the pin.

The original aspect of this study concentrates on the choice of two different artefacts and of the didactic assumption that by using these two artefacts in an intentionally combined way, it is possible to create a fruitful synergy between them [10].

To be more precise, it is possible to design a teaching sequence so that it can connect the semiotic potential of one artefact with the semiotic potential of the other, in a way that the semiotic potential of an artefact can potentiate the semiotic potential of the other.

5 Research Methodology

According to the TSM and the main assumption concerning the possible synergy between the two artefacts, a teaching sequence following the general scheme of successive ‘didactic cycles’ has been formed; the main hypothesis, however, consists of alternating activities that involve the use of one or the other artefact, and of formulating tasks that could exploit the complement of their semiotic potentials.

All the pupils involved were at an average mathematical level. Data collection of the study is based on student interaction transcriptions and videotapes during experimental task execution, written answers to given questions, and finally the transcripts and videotapes of the collective discussions concluding each experimental cycle. A specific lens of analysis is related to the identification of key elements supporting our synergy hypothesis.

The semiotic potential related to each of the two artefacts and how a synergy between them can influence the construction/conceptualization of translation and its properties, will be shown by the analysis of some episodes.

In this paper we will analyze the data coming from the first two of these cycles and we will demonstrate the unfolding of the semiotic potential related to each of the two artefacts, and how a synergy between them can influence the construction of mathematical meanings.

6 Focus on the First and Second Didactic Cycles

In this section, we present in detail the first and second didactic cycle describing the tasks and the semiotic potentials of the artefacts involved.

6.1 Description of the Tasks of the First Cycle

The first didactic cycle involves two tasks (Task 1 and the Task). Given a figure (convex quadrilateral) drawn (in black) on a sheet, at the moment while handing over the sheet a red vector is drawn on it. The task is:

TASK 1 – first part

Draw in red the translated figure of the black one, with respect to the red vector, with the help of a transparent sheet of paper and a pin:

  • Fold the sheet along the line identified by the red vector so that the folded sheet portion overlap the white sheet;

  • Overlap the transparent sheet of paper over the white sheet, putting it into the fold;

  • Trace the black figure on the transparent sheet of paper and make a notch on it at the point where the vector begins;

  • Slide the transparent sheet into the fold until the notch reaches the tip of the vector arrow;

  • Pierce the transparent sheet and the white sheet by piercing with a pin on the figure on it;

  • Remove the transparent sheet and join the holes by using a red marker.

After completing this task, on the same paper, the teacher draws a blue vector. The task is:

TASK 1 – second part

Draw in blue the translated figure of the black one, with respect to the blue vector, with the help of a transparent sheet of paper and a pin:

  • Fold the sheet along the line identified by the blue vector so that the folded sheet portion overlap the white sheet;

  • Overlap the transparent sheet of paper over the white sheet, putting it into the fold;

  • Trace the black figure on the transparent sheet of paper and make a notch on it at the point where the vector begins

  • Slide the transparent sheet into the fold until the notch reaches the tip of the vector arrow

  • Pierce the transparent sheet and the white sheet by piercing with a pin on the figure on it;

  • Remove the transparent sheet and join the holes by using a blue marker.

In the final task, the pupils are asked:

TASK 2

Observe what you have done and write the answers to the following questions:

  • How many times did you point the pin to draw the red figure?

  • Where did you point the pin?

  • How many times did you point the pin to draw the blue figure?

  • Where did you point the pin?

  • Describe how you drew the translated figure obtained by folding the sheet along the direction identified by the vector and sliding the transparent sheet of paper.

  • Look at the red figure and the blue figure. What looks the same about them? Explain why.

  • What looks different? Explain why.

6.2 Analysis of the Semiotic Potential and the Schemes of Utilization of the Artefacts P+T+P in Relation to the Described Tasks

According to the TSM, we assume that the meanings’ construction and their emergence through signs’ production are based on the development of utilization schemes related with both the artefact and the specific task [11, p. 748].

The artefact Pa+T+Pi, related to Task 1, evokes four important mathematical meanings:

  1. 1.

    The idea of the vector of translation (direction, modulus and orientation), expressed by folding the paper along a line; by sliding the transparent sheet of paper along the straight line for a fixed distance, by sliding the transparent sheet along the straight line in one of the orientation indicated by the arrow;

  2. 2.

    The idea of translation as correspondence of points, expressed by the holes in the paper made by piercing it with a pin;

  3. 3.

    The idea that the translated figure depends on the vector of translation, expressed by comparing what changed and what didn’t change in two translated figures when drawn on different vectors after folding the paper;

  4. 4.

    The idea of translation as a one-to-one correspondence that transforms segments into other congruent and parallel segments: as a matter of fact, this property corresponds to the fact that joining the points obtained with the pin produces a figure that is the translation of the original one.

Taking into account previous results [14] and with the aim of fostering the emergence of specific signs related to the task, some particular expressions, words and phrases, have been chosen purposefully in the formulation:

  • To fold along a line, is used to refer to the direct action when using the vector;

  • Overlap transparent sheet of paper over the white sheet, trace black figure over the transparent sheet and make a notch on the transparent sheet at the point where the vector begins, slide the transparent sheet into the fold until the notch reaches the tip of the vector arrow, with the aim to refer to transfer the original figure on a plane which moves following the direction and orientation vector actions;

  • To point, is used to refer to the direct action when using the pin to point and pierce to find the translated point;

  • To join, is used to refer to the direct action when drawing a segment between two corresponding points;

  • Translated figure, is used to refer to the direct outcome of the six actions (folding along a line, overlap, trace, slide, pointing/piercing on the vertexes of the figure, joining the points/holes);

  • What looks different, is used to refer to the direct action when comparing two translated figures obtained by the same figure with respect to two different vectors.

Let’s now describe the semiotic potential of Pa+T+Pi artefact referring to conceptualizing vector of translation and the point-to-point correspondence. For this we will analyze the possible schema of utilization relating to previous tasks. Given a drawn black figure on the white sheet on which a red vector is drawn consequently, we want to obtain the translated figure of the already given one, with respect to the red vector, by using the fold along the line of the given vector, the transparent sheet on which to trace the black figure and translate it into a new position by sliding it along the fold, with respect to the orientation and modulus of the vector and by using a pin to recognize translated points obtained by piercing the sheets, both the white and the transparent one.

When this task is accomplished, on the same sheet we will draw a further blue vector, giving the same task. So the previously defined parts of Task 1 will be given separately. In Task 2 pupils will be asked to answer some questions.

6.3 Description of the Tasks of the Second Cycle

The second didactic cycle involves two tasks (Task 3 and Task 4) to be carried out using the digital artefact GG and by using the buttons/tools “translation” and “trace” as well as the dragging function.

Task 3

  • Open in a new Geogebra file, graphic view without axis and grid;

  • Draw a quadrangle and call it “t”, then name its vertices A, B, C and D;

  • Draw a vector outside the quadrangle and call it “s”;

  • Using the button/tool ‘translation’, construct the translated figure of figure “t” with respect to the vector “s” and call it “t’”;

  • Call the corresponding vertices respectively A’, B’, C’ and D’.

With new assignments students go on:

  • Activate ‘Trace’ on point A and point A’. Drag point A. What moves? What does not move? Why?

  • Drag point A’. What moves? What does not move? Why?

  • Deactivate “Trace” on point A and A’. Drag side “a” of the figure. What moves? What does not move? Why?

  • Drag “s”. What moves? What does not move? Why?

According to the notion of ‘didactic cycle’ within the TSM, Task 4 aims at fostering the pupils’ personal production of signs related to Task 3. For this reason, the pupils are asked to:

Task 4:

Write down in the summary table below the answers to the questions asked in Task 3:

Drag

What moves?

What does not move?

Why?

Point A

   

Point A’

   

Side a

   

Vectors

   

6.4 Analysis of the Semiotic Potential and the Schemes of Utilization of the Artefacts GG in Relation to the Described Tasks

The artefact GG, related to Task 3 and Task 4, evokes the following mathematical meanings:

  1. 1.

    The idea of translation as a point-to-point correspondence, expressed by clicking on the tool/button “Translation”;

  2. 2.

    The idea that the translated figure depends on the figure of origin, in particular the idea that the translated vertex of the figure depends on the figure vertex of origin expressed by clicking on the tool/button “Trace” for the point of origin and the translated point, and by dragging the point of origin;

  3. 3.

    The idea that the translated point depends on the vector, expressed by clicking on the tool/button “Trace” for the point of origin and the translated point, and by dragging the vector;

  4. 4.

    The idea that the translated point depends on both the point of origin and the vector, expressed by dragging the translated point.

The use of the dragging function in the task 3 allows us to introduce the meanings of co-variation, by means of the dragging action and the observation of the resulting correlated movement of the points. In particular, the request to drag the vector could allow the distinction between independent and dependent variation to emerge. This is related to the different nature of the mutual movements of the points: some points move as a result of the direct action on them that the user achieve with the mouse, and other points indirectly move as the result of the movement of those points from which they have been constructed [15].

Moreover, the request to drag the translated point, allows the user to underline its specific behavior with respect to all the other objects of the configuration. When dragging the translated point, indeed, it can be observed a resulting no movement of the entire configuration. The difference in the movements between the translated point and the point of origin can be compared to the distinction between a dependent variable and an independent variable.

7 Data Analysis

The following episode refers to the class discussion at the end of the first cycle. When Task 1, using a manipulative artefact, was carried out, one student, G., was absent. The following day, during the discussion, the teacher asked others students to tell G. what they did. This teacher’s intervention is a case of “back to the task” which opens up a discussion and aims at pointing in the story the emergence of signs that refer to the activity carried out with the artefact.

The first to speak is A. who says: “First we copied the figure on a transparent sheet of paper and we folded the white sheet on the…”. The teacher focuses attention on an aspect that was drifting away, in an attempt to re-emerge the importance of the vector, asking: “What was the first request, before copying the figure on the transparent sheet?”.

The teacher’s attempt is successful because the importance of the vector is confirmed in the words of C. who answers: “the first request was to fold the sheet on the vector, make a notch at the beginning of the vector” and A. adds: “and then we had to copy the figure on the transparent sheet” and finally M. goes on: “and after make it move along the arrow of the vector”.

The discussion continues and the teacher intervenes by drawing attention to the artefact, bringing out at the same time the point-to-point correspondence (Table 1).

Table 1. Episode 1
Full size table

This episode shows the unfolding of the semiotic potential, as expected, but it also illustrates a first evolution towards the mathematical meanings that are the aims of the teaching intervention. The intervention of the teacher is fundamental in inducing the students to express their personal meanings, and the different reformulations showed how such meanings evolved from the description of the action to the idea of point-to-point correspondence. During the discussion another translation characterizing property emerged, the parallelism among the segments joining correspondent points and the vector of translation.

Indeed F says: “go all along the same direction… that is the arrow goes always on the same direction of the vector”. The sign “go all along the same direction” evokes the idea that the original figure moves following the vector direction. This artefact sign evolves in the mathematical sign “parallel” (Table 2).

Table 2. Episode 2
Full size table

Following episode refers to the collective discussion started after the second cycle, which consists in the Task 3 and Task 4 instructions, in which the students have built the translated figure from an original figure relative to a vector, using the “Translation” tool of the digital environment and dragging for first the original figure’s vertex A, then one side of the original figure and finally one of the translating vector on the display. With the aid of the “trace” tool they have observed what moves and what does not.

The video analysis in the discussion highlights two aspects:

  • In the first one, it is possible to recognize the arising of the digital artefact’s semiotic potential;

  • In the second one, it is also possible to detect an early reminder to the experience already had with the manipulative artefact, in terms such as “like what we did on the sheet”, coupled with gestures referring to something previously occurred.

Moreover, with the aid of the “trace” tool, the dependence of the translated point A’ from the original point A and the translating vector became clear for the students.

Furthermore, the cross-references about the two artefacts’ employment support the mathematical meaning’s structure of the functional dependence between a translation’s points.

Now let us consider the transcription of the discussion’s second phase (Table 3).

Table 3. Episode 3
Full size table

An. is dragging point A’, derived from point A’s translation. Therefore, she can observe nothing moving.

When the teacher asked, “What is moving? And what is not moving?”, M.G. answered confidently, “If I move A, A’ will move too. If I move the vector, A’ moves; and if I move A’… well… it does not move… nothing!”.

This episode shows how when using the digital artefact the meanings of the correspondence between figures and that of the vector of translation emerge once more. In particular, the argumentation by A. in the second part of Table 3, concerning the impossibility of a free movement of translated figure, shows how effective is the cross-reference to the use of the two artefacts, accompanied by an explicit interpretation of the experiences made with them, led to a consolidation of the mathematics meaning of functional dependence.

Finally, the meaning emerges most strongly not through the unfolding of the semiotic potential of the two different artefacts, but through the synergy activated by the comparison between the experiences with them.

8 Concluding Remarks

This paper, in continuity with the research on axial symmetry [11], reported on some preliminary results concerning the validity of the hypothesis about the potentialities of using the combination of artefacts as tool of semiotic mediation.

The analysis of the data coming from a teaching experiment clearly shows how the potentialities of each single artefact can be exploited and combined for constructing and developing some mathematical meanings concerning translation.

A careful analysis of the semiotic potential of each of the two artefacts and the didactical activity goals, guided the design of the tasks.

The results highlight the development of a synergy, created at a cognitive level, in the use of the two artefacts that is capable of enhancing the semiotic mediation functions of each of them. Moreover, we have shown how in passing from the use of manipulative artefacts to virtual artefacts, a synergy is created so that each experience enhances the potential of the other.

The study is still in progress but the results obtained encourage us to go forward and develop a long-term teaching experiment to confirm them. In accordance with the TSM, and in particular with the didactic cycle model, we intend to verify the efficacy of the observed synergy in a longer sequence of didactic cycles.