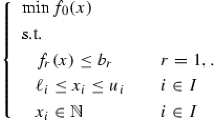Abstract
We consider quadratic programs with pure general integer variables. The objective function is quadratic and convex and the constraints are linear. An exact solution approach is proposed. It is decomposed into two phases. In the first phase, the initial problem is reformulated into an equivalent problem with a separable objective function. This is done by use of a Gauss decomposition of the Hessian matrix of the initial problem and requires the addition of some continuous variables and constraints. In the second phase, the reformulated problem is linearized by an approximation of each squared term by a set of K linear functions that correspond to the tangents of a hyperbola in K points. We give a proof of the intuitive property that when K is large enough, the optimal value of the obtained linear program is very close to optimal value of the two previous problems, the initial problem and the reformulated separable problem. The reminder is dedicated to the implementation of a branch-and-bound algorithm for the solution of linearized problem, and its application to a set of instances. Several points are considered among which choice of the right value for parameter K and the implementation of a sophisticated heuristic solution algorithm. The numerical comparison is done with CPLEX 12.2 since, in this case, the initial problem as well as the problem reformulated by the first step can be solved by CPLEX. We show that with our approach, the total CPU time is divided by a factor ranging from 1.2 to 131.6 for instances with 40–60 variables.




Similar content being viewed by others
Notes
Instances available on the web site http://people.brunel.ac.uk/~mastjjb/jeb/orlib/mknapinfo.html
References
Benson HP, Erenguc SS and Horst R (1990). A note on adapting methods for continuous global optimization to the discrete case. Annals of Operations Research 25 (1): 243–252.
Billionnet A and Soutif E (2004). An exact method based on Lagrangian decomposition for the 0-1 quadratic knapsack problem. European Journal of Operational Research 157 (3): 565–575.
Billionnet A, Elloumi S and Plateau M-C (2009). Improving the performance of standard solvers for quadratic 0-1 programs by a tight convex reformulation: The QCR method. Discrete Applied Mathematics 157 (6): 1185–1197.
Billionnet A, Elloumi S and Lambert A (2013). An efficient compact quadratic convex reformulation for general integer quadratic programs. Computational Optimization and Applications 54 (1): 141–162.
Bretthauer K and Shetty B (1995). A branch and bound algorithm for integer quadratic knapsack problems. INFORMS Journal on Computing 7 (1): 109–116.
Caprara A, Pisinger D and Toth P (1999). Exact solution of the quadratic knapsack problem. INFORMS Journal on Computing 11 (2): 125–137.
Chaillou P, Hansen P and Mahieu Y (1989). Best network flow bounds for the quadratic knapsack problem. Lecture Notes in Mathematics 1403: 225–235.
Chaovalitwongse W, Pardalos PM and Prokopyev OA (2004). A new linearization technique for multi-quadratic 0-1 programming problems. Operations Research Letters 32 (6): 517–522.
Chu PC and Beasley JE (1998). A genetic algorithm for the multidimensional knapsack problem. Journal of Heuristics 4 (1): 63–86.
Djerdjour M (1997). An enumerative algorithm framework for a class of nonlinear integer programming problems. European Journal of Operational Research 101 (1): 104–121.
Djerdjour M, Mathur K and Salkin H (1988). A surrogate relaxation based algorithm for a general quadratic multi-dimensional knapsack problem. Operations Research Letters 7 (5): 253–257.
Dussault JP, Ferland JA and Lemaire B (1986). Convex quadratic programming with one constraint and bounded variables. Mathematical Programming 36 (1): 90–104.
Elloumi S, Faye A and Soutif E (2000). Decomposition and linearization for 0-1 quadratic programming. Annals of Operations Research 99 (1–4): 79–93.
Erenguc SS and Benson HP (1991). An algorithm for indefinite integer quadratic programming. Computational Mathematics and Applications 21 (6–7): 99–106.
Faaland B (1974). An integer programming algorithm for portfolio selection. Management Science 20 (10): 1376–1384.
Gallo G, Hammer PL and Simeone B (1980). Quadratic knapsack problem. Mathematical Programming Study 12: 132–149.
Garey MR and Jonhson DS (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. Freeman: New-York.
Glover F (1975). Improved linear integer programming formulations of nonlinear integer problems. Management Science 22 (4): 455–460.
Gueye S and Michelon P (2009). A linearization framework for unconstrained quadratic (0-1) problems. Discrete Applied Mathematics 157 (6): 1255–1266.
Horst R and Tuy H (1990). Global Optimization: Deterministic Approaches. Springer: Berlin.
Hua Z, Zhang B and Liang L (2006). An approximate dynamic programming approach to convex quadratic knapsack problems. Computers & Operations Research 33 (3): 660–673.
Li D, Sun XL and Wang J (2006). Optimal lot solution to cardinality constrained mean-variance formulation for portfolio selection. Mathematical Finance 16 (1): 83–101.
Lueker GS (1975). Two NP-complete problems in nonnegative integer programming. Computer Science Lavatory, Princeton, NJ report 178 (A6).
Michelon P and Veilleux L (1996). Lagrangean methods for the 0-1 quadratic knapsack problem. European Journal of Operational Research 92 (2): 326–341.
Minjin Z and Wei C (2010). Reducing the number of variables in integer quadratic programming problem. Applied Mathematical Modelling 34 (2): 424–436.
More JJ and Vavasis SA (1991). On the solution of concave knapsack problems. Mathematical Programming 49 (1–3): 397–411.
Ozaltin OY, Prokopyev OA and Schaefer AJ (2012). Two-stage quadratic integer programs with stochastic right-hand sides. Mathematical Programming Series A 133 (1–2): 121–158.
Pisinger W.D. (2007). The quadratic knapsack problem—A survey. Discrete Applied Mathematics 155 (5): 623–648.
Pisinger WD, Rasmussen AB and Sandvik R (2007). Solution of large quadratic knapsack problems through aggressive reduction. INFORMS Journal on Computing 19 (2): 280–290.
Plateau M-C and Rios-Solis Y-A (2010). Optimal solutions for unrelated parallel machines scheduling problems using convex quadratic reformulations. European Journal of Operational Research 201 (3): 729–736.
Quadri D and Soutif E (2010). A roof linearization algorithm to obtain a tight upper bound for integer nonseparable quadratic programming. Electronic Notes in Discrete Mathematics 36: 271–278.
Quadri D, Soutif E and Tolla P (2007). Upper bounds for large scale integer quadratic multidimensional knapsack. International Journal of Operations Research 4 (3): 146–154.
Quadri D, Soutif E and Tolla P (2009). Exact solution method to solve large scale integer quadratic multidimensional knapsack problems. Journal of Combinatorial Optimization 17 (2): 157–67.
Rodrigues CD, Quadri D., Michelon P. and Gueye S. (2012). 0-1 quadratic knapsack problems: An approach based on a t-linearization. SIAM Journal of Optimization 22 (4): 1449–1468.
Sherali H and Adams W (1999). A Reformulation Technique for Solving Discrete and Continuous non Convex Problems. Kluwer Academic Publishers.
Skutella M (2001). Convex quadratic and semidefinite programming relaxations in scheduling. Journal of ACM 48 (2): 206–242.
Van Zandt T (2003). Real-time hierarchical resource allocation with quadratic costs. CEPR Discussion Paper 4022 (2003) Available at SSRN: http://ssrn.com/abstract=454140.
Wilkinson JH (1965). The Algebraic Eigenvalue Problem. Clarendon Press: Oxford.
Zhang B and Hua Z (2012). Simple solution methods for separable mixed linear and quadratic knapsack problem. Applied Mathematical Modelling 36 (7): 3245–3526.
Zhang B and Chen B (2012). Heuristic and exact solution method for convex nonlinear knapsack problem. Asia-Pacific Journal of Operations Research 29 (5): 1250031.
Zheng XJ, Sun XL and Li D (2010). Separable relaxation for nonconvex quadratic integer programming: Integer diagonalization approach. Journal of Optimization Theory and Applications 146 (2): 463–489.
Acknowledgements
Part of this research has been performed thanks to the French Operation Research Group (GdR RO).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Quadri, D., Soutil, E. Reformulation and solution approach for non-separable integer quadratic programs. J Oper Res Soc 66, 1270–1280 (2015). https://doi.org/10.1057/jors.2014.76
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/jors.2014.76