Feedback Based Parametric Actuation with Sensor Nonlinearity and Mass Sensing

Abstract

Purpose

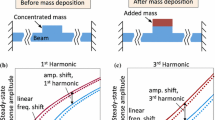
Parametric actuation in a microcantilever beam is analyzed. Here, displacement is given to the clamped end, which is determined through feedback. The sensor output has been considered with nonlinear characteristics. One of the motives of the article is to analyze the parametric excitation in a closed-loop system, where the feedback is having a feature of cubic nonlinearity. Also, the influence of noise on the response has been studied, where the power spectral density gets squeezed to certain frequencies. Another motive is to utilize the feedback based parametric excitation for a sensing application. Here, a novel scheme of mass sensing is presented for improved sensitivity, where the sensor nonlinearity and closed-loop excitation provides the scope for 3–7 times higher sensitivity.

Method

Dynamics of the cantilever beam model is studied using the multiple scales technique. For numerical analysis, discrete element method has been used. Parametric excitation based noise reduction has been demonstrated through numerical simulations, where the effect of thermal forces is considered through lumped forces.

Results

Comparing the outcome of perturbation analysis with the results of numerical simulations shows an excellent agreement. Analyzing the power spectrum of the sensor output, a novel method of mass detection has been proposed. It can provide superior performance in comparison to conventional resonant mass sensing.

A Appendix

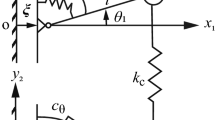
For the numerical study of the considered cantilever beam model, DEM is chosen for which a schematic diagram is presented in Fig. 3a. The relation between rotation angle ($\theta$) and transverse displacement(y) of the block is shown in the Fig. 3b. The first block of discretized system is considered to have zero rotation angle to realize the clamped boundary condition. For two rigid masses in the sequence, free body diagrams are shown in Fig. 3c. The equation of motion for the ith block can be written using Newtonian laws.

$$\begin{aligned}&J_{i} \frac{d^2 \theta _{i}}{d t^2} =J_{i} \ddot{\theta _{i}}=M_{i+1}-M_{i} + \frac{l_{i}}{2}\left( s_{i+1}+s_{i}\right) , \;\; and \end{aligned}$$

(31a)

$$\begin{aligned}&m_{i} \frac{d^2 y_{i}}{d t^2}=m_{i} \ddot{y_{i}}=s_{i+1}-s_{i} - f_{i}^d, \text { where}\, i=2,3...N-1 . \end{aligned}$$

(31b)

Similarly, for the Nth block,

$$\begin{aligned} J_{N} \ddot{\theta }_{N}&=-M_{N} + \frac{l_{N}}{2} s_{N}, \text { and } \end{aligned}$$

(32a)

$$\begin{aligned} m_{N} \ddot{y}_{N}&=-s_{N}-f_{N}^d \end{aligned}$$

(32b)

For the discrete element model, different parameters can be calculated.

$$\begin{aligned} l_{i}=\frac{l}{N-1}, \;\; m_{i}=\rho A \; l_{i}=l_i, \;\; J_{i}=\frac{m_{i}}{12} \left( l_{i}^2+h^2\right) , \;\; i=2,3...N-1, \end{aligned}$$

In the similar way for the Nth block,

$$\begin{aligned} l_{N}=\frac{l}{2(N-1)}, \;\; m_{N}= l_{N}, \;\; J_{N}=\frac{m_{N}}{12} \left( l_{N}^2+h^2\right) . \end{aligned}$$

Here, $l_i$, $m_i$, and $J_i$ are the length, mass, and mass moment of inertia of ith the elements, respectively. From the governing equation in the nondimensionalized form (7), $\rho A = 1$ and $EI=C_0$. Value of $C_0$ is taken as, $C_0= 1.8751^{-4}$. That simplifies the nondimensionalized model with the natural frequency, $\omega _1=1$. For a detailed study on discrete element method, one can refer to [41]. For the discretized model, the damping force is assumed lumped, acting on each block. For ith block, it can be written as

$$\begin{aligned} f_{i}^d = c_{i}^d \frac{\mathrm {d}y_i}{\mathrm {d}t}, \end{aligned}$$

where the damping coefficient is given as,

$$\begin{aligned} c_{i}^d = \mu l_i, where i=2,3,..N \end{aligned}.$$

Equivalent stiffness of torsional springs can be given as

$$\begin{aligned} k_{i}=\frac{C_0}{l_{i}}. \end{aligned}$$

In the considered cantilever beam model, clamped end is given transverse displacement. To realize that, rotation of the first block is restricted ($\theta _1=0$) and $y_1$ will be equivalent to the given displacement. One can get the expression for $y-\theta$ relation as

$$\begin{aligned} y_{i}-y_{i-1}=\frac{l_{i-1}}{2} \theta _{i-1}+\frac{l_{i}}{2} \theta _{i}, \; \; i=2,3,..N. \end{aligned}$$

Using the above expression, following relation between ${\mathop {Y}\limits _{\thicksim }}$ and $\Theta$ can be obtained.

$$\begin{aligned} -\varvec{A}^T {\mathop {Y}\limits _{\thicksim }} -y_{1} {\mathop {a}\limits _{\thicksim }}_1=\frac{1}{2} \varvec{B}^T \varvec{L} {\mathop {\Theta }\limits _{\thicksim }} \end{aligned}$$

(33)

That can be also written as

$$\begin{aligned} {\mathop {\Theta }\limits _{\thicksim }}=-2\varvec{L}^{-1} \left( \varvec{B}^{T}\right) ^{-1} \varvec{A}^T {\mathop {Y}\limits _{\thicksim }} - 2\varvec{L}^{-1} \left( \varvec{B}^{T}\right) ^{-1} {\mathop {a}\limits _{\thicksim }} y_{1}. \end{aligned}$$

(34)

${\mathop {a}\limits _{\thicksim }}_{1}$, vectors of transverse displacement ${\mathop {Y}\limits _{\thicksim }}$ and rotation of blocks ${\mathop {\Theta }\limits _{\thicksim }}$, vectors for transverse forces ${\mathop {S}\limits _{\thicksim }}$ and moments acting on blocks ${\mathop {M}\limits _{\thicksim }}$ are given as

$$\begin{aligned} {\mathop {a}\limits _{\thicksim }}_1 =\begin{Bmatrix} 1\\ 0\\ \vdots \\ \\ 0 \end{Bmatrix}, \; \; {\mathop {Y}\limits _{\thicksim }} =\begin{Bmatrix} y_2\\ y_3\\ \vdots \\ \\ y_N \end{Bmatrix}, \; \; {\mathop {\Theta }\limits _{\thicksim }}=\begin{Bmatrix} \theta _2\\ \theta _3\\ \vdots \\ \\ \theta _N \end{Bmatrix}, \; \; {\mathop {S}\limits _{\thicksim }} =\begin{Bmatrix} S_2\\ S_3\\ \vdots \\ \\ S_N \end{Bmatrix}, \; \; {\mathop {M}\limits _{\thicksim }} =\begin{Bmatrix} M_2\\ M_3\\ \vdots \\ \\ M_N \end{Bmatrix}. \end{aligned}$$

Here, matrices are marked using bold letters, and vectors are represented by letters with tilde symbols. Matrices representing mass $\varvec{m}$, damping coefficient $\varvec{C_d}$, length $\varvec{L}$, mass moment of inertia $\varvec{J}$ of the blocks are diagonal. Stiffness matrix $\varvec{K}$, whose elements give the torsional stiffness of the spring is also diagonal.

$$\begin{aligned} \varvec{m}= & {} \begin{bmatrix} m_{2} &{} &{} \\ &{} \ddots &{} \\ &{} &{} m_{N} \end{bmatrix}, \; \; \varvec{C_d} = \begin{bmatrix} c_{2}^d &{} &{} \\ &{} \ddots &{} \\ &{} &{} c_{N}^d \end{bmatrix}, \; \; \varvec{L} = \begin{bmatrix} l_{2} &{} &{} \\ &{} \ddots &{} \\ &{} &{} l_{N} \end{bmatrix}, \; \;\\ \varvec{J}= & {} \begin{bmatrix} J_{2} &{} &{} \\ &{} \ddots &{} \\ &{} &{} J_{N} \end{bmatrix}, \; \; \varvec{K} = \begin{bmatrix} k_{2} &{} &{} \\ &{} \ddots &{} \\ &{} &{} k_{N} \end{bmatrix} \end{aligned}$$

Assembling the equation of motion for all the blocks, using (31) and (32), one can get the following sets of equations.

$$\begin{aligned}&\varvec{J} \ddot{{\mathop {\Theta }\limits _{\thicksim }}}\ =\varvec{A} {\mathop {M}\limits _{\thicksim }}+\frac{1}{2} \varvec{L} \varvec{B} {\mathop {S}\limits _{\thicksim }} \end{aligned}$$

(35a)

$$\begin{aligned}&\varvec{m} \ddot{{\mathop {Y}\limits _{\thicksim }}} + \varvec{C_d} \dot{{\mathop {Y}\limits _{\thicksim }}} =\varvec{A} {\mathop {S}\limits _{\thicksim }} \end{aligned}$$

(35b)

Matrices, $\varvec{A}$ and $\varvec{B}$ have the form like,

$$\begin{aligned} \varvec{A} = \begin{bmatrix} -1 &{} 1 &{} 0 &{} \cdots &{} &{} 0\\ 0 &{} -1 &{} 1 &{} 0 &{} \cdots &{} 0\\ \vdots &{} &{} &{} &{} &{} \vdots \\ &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} -1&{} 1\\ 0 &{} \cdots &{} &{} &{} 0&{} -1 \end{bmatrix}, \; \; \varvec{B}= \begin{bmatrix} 1 &{} 1 &{} 0 &{} \cdots &{} &{} 0\\ 0 &{} 1 &{} 1 &{} 0 &{} \cdots &{} 0\\ \vdots &{} &{} &{} &{} &{} \vdots \\ &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} 1&{} 1\\ 0 &{} \cdots &{} &{} &{} 0&{} 1 \end{bmatrix} \end{aligned}$$

Moments acting on the rigid blocks and their rotations are related as,

$$\begin{aligned} M_{i} =k_{i} \left( \theta _{i}-\theta _{i-1}\right) , \end{aligned}$$

writing it in the vector form

$$\begin{aligned} {\mathop {M}\limits _{\thicksim }} =-\varvec{K} \varvec{A}^T {\mathop {\Theta }\limits _{\thicksim }} \end{aligned}$$

Substituting the above expression for ${\mathop {M}\limits _{\thicksim }}$, equation of moment balance (35)b, can be written as,

$$\begin{aligned} -\varvec{A} \varvec{K} \varvec{A}^T {\mathop {\Theta }\limits _{\thicksim }} + \frac{1}{2} \varvec{L} \varvec{B} {\mathop {S}\limits _{\thicksim }} = \varvec{J} \ddot{{\mathop {\Theta }\limits _{\thicksim }}} \end{aligned}$$

(36)

Using the expression for ${\mathop {\Theta }\limits _{\thicksim }}$ and Eqs (36)b, (36)a can be written in following format so that, ${\mathop {Y}\limits _{\thicksim }}$ will only be the dependent variable.

$$\begin{aligned} \varvec{\beta _{1}} \ddot{{\mathop {Y}\limits _{\thicksim }}} + {\mathop {\beta }\limits _{\thicksim }}_{2} \ddot{y_{1}} + \varvec{\beta _{3}} {\mathop {Y}\limits _{\thicksim }} + {\mathop {\beta }\limits _{\thicksim }}_{4} y_{1}= \varvec{A}^{-1} \varvec{m} \ddot{{\mathop {Y}\limits _{\thicksim }}} + \varvec{A}^{-1} \varvec{C_d} \dot{{\mathop {Y}\limits _{\thicksim }}} \end{aligned}$$

(37)

Coefficients of the system of eq, (37) are,

$$\begin{aligned} \varvec{\beta _{1}}&= -4 \varvec{B}^{-1} \varvec{L}^{-1} \varvec{J} \varvec{L}^{-1} \left( \varvec{B}^{T}\right) ^{-1} \varvec{A}^T \\ {\mathop {\beta }\limits _{\thicksim }}_{2}&= -4 \varvec{B}^{-1} \varvec{L}^{-1} \varvec{J} \varvec{L}^{-1} \left( \varvec{B}^{T}\right) ^{-1} {\mathop {a}\limits _{\thicksim }}\\ \varvec{\beta _{3}}&= -4 \varvec{B}^{-1} \varvec{L}^{-1} \varvec{A K A}^T \varvec{L}^{-1} \left( \varvec{B}^{T}\right) ^{-1} \varvec{A}^T \\ {\mathop {\beta }\limits _{\thicksim }}_{4}&= -4 \varvec{B}^{-1} \varvec{L}^{-1} \varvec{A K A}^T \varvec{L}^{-1} \left( \varvec{B}^{T}\right) ^{-1} {\mathop {a}\limits _{\thicksim }} \\ \end{aligned}$$

(37) can be further simplified as,

$$\begin{aligned} \ddot{{\mathop {Y}\limits _{\thicksim }}} + \varvec{\alpha } {\mathop {\beta }\limits _{\thicksim }}_{2} \ddot{y_{1}} + \varvec{\alpha \beta _{3}} {\mathop {Y}\limits _{\thicksim }} + \varvec{\alpha } {\mathop {\beta }\limits _{\thicksim }}_{4} y_{1} = \varvec{\alpha } \varvec{A}^{-1} \varvec{C_d} \dot{{\mathop {Y}\limits _{\thicksim }}} \end{aligned}$$

(38)

Where, $\varvec{\alpha }=(\varvec{\beta _{1}}-\varvec{A}^{-1} \varvec{m})^{-1}$.

To study the effect of thermal noise, random forces (having the white noise characteristics) are considered acting on each block of the discretized system, and the resulting system of equation of motion is shown below.

$$\begin{aligned} \ddot{{\mathop {Y}\limits _{\thicksim }}} + \varvec{\alpha } {\mathop {\beta }\limits _{\thicksim }}_{2} \ddot{y_{1}} + \varvec{\alpha \beta _{3}} {\mathop {Y}\limits _{\thicksim }} + \varvec{\alpha } {\mathop {\beta }\limits _{\thicksim }}_{4} y_{1} = \varvec{\alpha } \varvec{A}^{-1} \varvec{C_d} \dot{{\mathop {Y}\limits _{\thicksim }}} - \varvec{\alpha } \varvec{A}^{-1} {\mathop {F}\limits _{\thicksim }}_{th}. \end{aligned}$$

(39)

Sensor noise is considered as a white noise added to the sensor output. The resulting sensor output will be further used for the calculation of the base displacement.

The given base displacement $y_1$ is calculated as,

$$\begin{aligned} y_1=2 G \cos (2\Omega t) \left( y_N +\alpha y_N^3 + n_d \right) \end{aligned}$$

Here, ${\mathop {F}\limits _{\thicksim }}_{th}$ is the random force vector, and $n_{d}$ is the detection noise present in the sensor output.